1. Introduction
Our study investigates the macroeconomic dynamics of household indebtedness within a neoclassical growth model that integrates quasi-hyperbolic discounting, financial intermediation, and resource constraints. Indebtedness is one of the defining economic challenges of our time, significantly impacting consumption decisions, investments, and financial stability, particularly in the context of environmental sustainability. The 2008 global financial crisis highlighted the macroeconomic risks of excessive household debt, as emphasized by (
Bernanke, Gertler, & Gilchrist, 1999) in connection with the financial accelerator mechanism. Additionally, the depletion of natural resources, as predicted decades ago by (
Meadows, Meadows, Randers, & Behrens III, 1972), underscores the urgency of finding a balance between economic growth and sustainability. For modern economies, a deeper understanding of these dynamics is essential for designing stable and sustainable growth trajectories.
Our model assumes a single representative household that makes time-inconsistent decisions due to present-biased behavior modeled by quasi-hyperbolic discounting, as described by
Laibson (
1997). The explicit modeling of the financial sector enables the analysis of interest-bearing loan intermediation and the dynamics of borrowing, which amplify behavioral biases. Production occurs under resource constraints, accounting for the finite nature of natural resources, making the joint analysis of indebtedness and sustainability more realistic. This approach offers a new perspective compared to traditional neoclassical models, which often neglect behavioral and environmental considerations. The elements integrated in our model—time-inconsistent decision-making, financial intermediation, and resource constraints—enable a deeper understanding of the complex challenges facing modern economies.
The study focuses on three main research questions:
How do quasi-hyperbolic discounting and interest rates affect the dynamics of indebtedness and equilibrium variables, such as capital intensity and debt stock?
What is the impact of the tax rate, savings rate, and financial intermediation on economic growth and stability in a resource-constrained environment?
Which parameters ensure a stable equilibrium point, and how can the results of numerical simulations be interpreted from the perspective of economic stability?
These questions are particularly relevant for modern economies, where rising household debt, financial market volatility, and environmental sustainability pose simultaneous challenges. We employ dynamic optimization techniques and the Routh–Hurwitz criterion for stability analysis, complemented by numerical simulations to provide practical insights into the effects of parameters.
The structure of the study is as follows: the literature review outlines the theoretical foundations of the research, followed by the presentation of model assumptions and equations of motion. This is followed by the determination of equilibrium solutions, stability analysis with numerical simulations and a phase diagram, and finally, the conclusion and summary. The study’s contribution lies in integrating behavioral, financial, and sustainability considerations into a unified neoclassical framework, supported by numerical simulations. The results offer new perspectives on the interaction between interest rates and debt cycles, particularly in the context of sustainable economic growth. For example, the model highlights how quasi-hyperbolic discounting can lead to excessive borrowing, amplified by the financial sector, while resource constraints tighten growth opportunities.
2. Literature Review
Our study examines the dynamics of household indebtedness within a neoclassical growth model that integrates insights from behavioral economics, financial intermediation, and sustainable growth. The macroeconomic significance of household indebtedness is particularly pronounced today, as global economic crises and environmental sustainability challenges have highlighted the complex interactions between consumption decisions, credit markets, and resource constraints. Our model analyzes time-inconsistent decision-making, financial frictions, and the depletion of natural resources within a unified framework, contributing to a deeper understanding of economic stability and sustainability. Below, we review the relevant literature that forms the basis of our study.
Neoclassical growth theory provides a fundamental framework for examining the long-term dynamics of economic growth. The works of
Ramsey (
1928),
Koopmans (
1965), and
Cass (
1965) centered on the intertemporal optimization of a representative household, assuming rational decision-making in which households uniformly discount future utility. However, these models do not account for behavioral biases or the role of the financial sector and neglect resource constraints. The model by
Solow (
1956) emphasizes exogenous technological progress as the driver of economic growth but does not address the effects of credit markets or the depletion of natural resources. Due to these limitations, neoclassical models are not well-suited for the joint analysis of complex issues in modern economies, such as indebtedness and sustainability.
Behavioral economics has made significant strides in understanding non-rational decision-making, which is crucial for modeling household indebtedness.
Laibson (
1997) introduced the concept of quasi-hyperbolic discounting, which models time-inconsistent preferences and explains households’ propensity for excessive consumption and indebtedness. According to quasi-hyperbolic discounting, households overvalue near-term utility compared to distant future utility, leading to short-term consumption decisions and long-term debt accumulation.
Koltay & Vincze (
2009) comprehensively analyze consumer decisions from the perspective of behavioral economics, highlighting that non-standard preferences, such as social preferences or cognitive errors, do not lead to Pareto-efficient equilibria. Their findings suggest that the emotional impact of advertising can significantly exacerbate consumption biases, particularly in credit markets.
Phelps & Pollak (
1968) examined the macroeconomic effects of present-biased decision-making, emphasizing that time-inconsistent preferences can lead to lower savings rates and increased economic instability.
The literature on financial intermediation is essential for our model, as credit markets and financial frictions fundamentally influence the dynamics of indebtedness.
Bernanke, Gertler, & Gilchrist (
1999) introduced the concept of the financial accelerator mechanism, which posits that financial frictions amplify economic cycles, particularly during crises. Their work highlights that credit constraints and the state of corporate balance sheets significantly affect macroeconomic performance.
Kiyotaki & Moore (
1997) modeled the interaction between credit constraints and asset prices, demonstrating how collateral constraints can lead to debt cycles and economic instability.
Gertler & Karadi (
2011) analyzed the role of banks in monetary policy, emphasizing that the activities of financial intermediaries are crucial for understanding the relationship between interest rates and economic activity. These works support our model’s assumption that explicit modeling of the financial sector is essential for analyzing the macroeconomic effects of indebtedness.
The literature on sustainable growth focuses on the economic consequences of natural resource depletion, which inspired the design of our model’s production function. The pioneering work of
Meadows, Meadows, Randers, & Behrens III (
1972),
The Limits to Growth, drew attention to the tension between resource constraints and economic growth, predicting that unlimited growth is unsustainable given finite resources.
Nordhaus (
1992) further developed these ideas, analyzing the trade-offs between economic growth and environmental sustainability. His work emphasizes that the depletion of natural resources and environmental externalities pose significant long-term economic costs for growth models. These studies support our model’s assumption that explicitly accounting for resource constraints is essential for modeling sustainable economic growth.
In our view, relatively few studies attempt to jointly model indebtedness, behavioral biases, financial intermediation, and resource constraints. Neoclassical growth models often neglect behavioral and financial considerations, while behavioral economics research rarely addresses macroeconomic dynamics or sustainability issues. For example, the works of
Laibson (
1997) and
Koltay & Vincze (
2009) focus on micro-level decision-making but do not examine the macroeconomic effects of resource constraints. Similarly,
Bernanke, Gertler, & Gilchrist (
1999) and
Kiyotaki & Moore (
1997) focus on financial frictions but do not integrate behavioral biases or environmental constraints. Our study fills this research gap with an analytical and numerical analysis that examines quasi-hyperbolic discounting, financial intermediation, and resource constraints within a unified neoclassical framework, providing new insights into the interplay of economic stability and sustainability.
3. Materials and Methods
Our model describes a closed economy, ignoring the foreign trade dimension, with a single household, a corporate sector, a financial sector, and a government sector. The household makes decisions using quasi-hyperbolic discounting, the financial sector intermediates loans, and production is resource-constrained.
The household’s utility function depends on consumption (
) and resources (
). The utility function is given by
where
measures present bias, and
measures concern for resources. The household allocates its income (
) to consumption and savings, borrowing loans (
) at an interest rate (
).
The production function is resource-constrained. The production function is given by
and the resource dynamics are described by
Banks intermediate savings (
) in the form of loan disbursements (
,
), with their balance sheet given by
where the debt dynamics are
Investments are determined by the following equation:
The study makes the following assumptions:
The production function is homogeneous, so
The government collects taxes (
), which are spent on public goods
The economy’s equilibrium conditions are
Effective labor (
) grows:
,
, so
. The intensive production function is
where
. The factor prices and debt are
4. Results
4.1. Equations of Motion and the Existence and Uniqueness of Equilibrium
In this subsection, we derive the model’s equations of motion, taking into account the financial sector, and prove the existence of equilibrium. The model considers a single household and resource constraints.
The household’s optimization problem is
The corresponding Hamiltonian function is
The necessary conditions are
The consumption growth rate is
where
is a relatively small friction parameter.
The dynamics of capital intensity are
The resource dynamics are
The equations of motion are continuous, so the Cauchy–Peano theorem ensures the existence of a solution. The Lipschitz property guarantees uniqueness for .
4.2. Stability of Equilibrium Solutions
In this subsection, we analyze the stability of the model’s equilibrium points () using the Routh–Hurwitz criterion, examining the three-dimensional system shaped by the financial sector and resource constraints. Our goal is to determine which parameters—such as the interest rate (i), savings rate (), or resource utilization rate ()—ensure the dynamic system describing the economy returns to equilibrium. We complement the analysis with numerical simulations and a phase diagram to illustrate stability behavior.
We linearize the equations of motion around the equilibrium point. The system in vector form is
where
The Jacobian matrix of the linearized system is
The elements of the Jacobian matrix at the equilibrium point are
The consumption derivatives are derived from the equilibrium consumption equation (), and the friction ensures nonzero elements.
We examine stability using the characteristic polynomial
The coefficients are calculated as
The stability conditions (Routh–Hurwitz criteria) are: , , , . The second and third inequalities hold. If , then the first and last conditions are also satisfied. Thus, and guarantee the stability conditions.
Using numerical simulations (
,
,
,
,
,
,
,
,
,
,
,
,
,
), we obtain:
The Routh–Hurwitz criteria are satisfied, as , , , . However, we note that at high interest rates (), may become negative, potentially leading to instability.
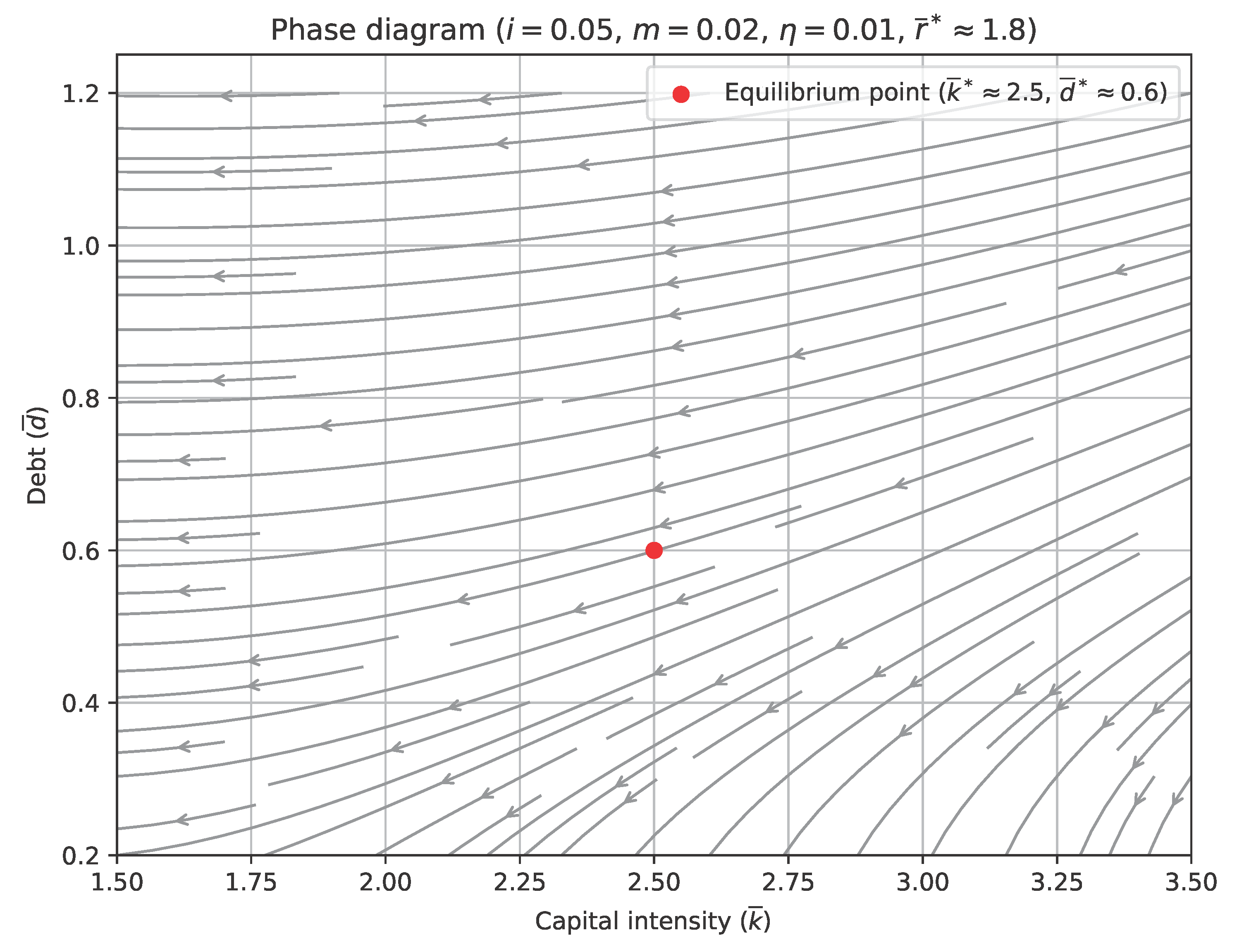
4.2.1. Phase Diagram Analysis
We illustrate the system’s dynamics with a phase diagram showing the trajectories of capital intensity (
) and debt (
), with the resource stock fixed (
). The diagram was created for a low consumption friction parameter (
) and is shown in
Figure 1 below.
The diagram’s trajectories indicate convergence toward the equilibrium point, supporting stability for low . For high or , the system may exhibit saddle-point instability, indicated by the violation of the Routh–Hurwitz criteria, but this is not separately illustrated here.
The stability analysis can be interpreted at three levels:
Mathematical conclusions: The friction ensures stability if and . High or may cause a saddle point.
Economic implications: High consumption friction or technological progress rate increases the debt burden, potentially causing instability. High and low stabilize the system.
Policy recommendations: Regulating consumption dynamics and interest rates promotes stability.
The phase diagram visually confirms that the system can be stabilized with appropriate parameters.
5. Discussion
Our study examined the dynamics of household indebtedness within a neoclassical growth model, incorporating quasi-hyperbolic discounting, an explicit financial sector, and resource constraints. The model demonstrated that time-inconsistent decisions, modeled by quasi-hyperbolic discounting, significantly increase households’ propensity to borrow, particularly under high interest rates. Resource constraints, however, limit economic growth, underscoring the need for sustainable resource management. Numerical simulations (, , ) indicated a stable equilibrium point, supported by the Routh–Hurwitz criteria and phase diagram analysis. A low consumption friction parameter () and a positive difference between the interest rate and the technological progress rate () are critical for ensuring stability. However, high interest rates or significant consumption frictions can lead to instability, such as saddle-point dynamics, as indicated by our numerical analyses.
Increasing the tax rate reduces capital intensity, which may moderate economic growth in the long term but can contribute to regulating debt dynamics. A high savings rate () and a low resource utilization rate () stabilize the system, enabling the maintenance of economic equilibrium. The financial sector plays a key role in amplifying behavioral biases, as the availability of interest-bearing loans encourages present-biased consumption. Therefore, targeted monetary policy interventions, such as regulating interest rates or introducing borrowing constraints, are necessary to promote stability. Sustainable resource management is essential for ensuring long-term economic growth, particularly given the threat of natural resource depletion.
The interaction between the financial sector and behavioral biases raises further policy considerations. Time-inconsistent decisions generated by quasi-hyperbolic discounting are particularly sensitive to changes in interest rates, posing challenges for central banks in designing monetary policy. For example, excessively low interest rates may stimulate consumption and economic growth in the short term but lead to debt accumulation in the long term, while excessively high interest rates can destabilize the system, as indicated by numerical simulations. Therefore, fine-tuning monetary policy, such as targeted interest rate reductions or tightening credit market regulations, is crucial for maintaining economic stability.
The issue of sustainability is significant not only economically but also socially. The resource constraints applied in our model highlight global economic trends, such as the depletion of fossil fuels or environmental degradation. To promote sustainable resource management, economic policy should incentivize the use of renewable resources and technological innovations that reduce the resource utilization rate (). This aligns with international sustainability goals, such as the United Nations Sustainable Development Goals, and contributes to long-term economic stability.
6. Conclusions
Further development of the model offers numerous research opportunities. Introducing heterogeneous households instead of a single representative household would allow the examination of the effects of diverse consumption and savings preferences. Modeling variable or stochastic interest rates could make the financial sector dynamics more realistic, particularly during crises. Additional research could focus on more detailed modeling of environmental externalities, such as carbon emissions or natural resource depletion, which would more closely link economic growth with sustainability goals. These developments could further enhance the model’s practical relevance and offer new policy recommendations for modern economies.
Author Contributions
Conceptualization, B.Sz. and Zs.N.; methodology, B.Sz.; software, B.Sz.; validation, B.Sz. and Zs.N.; formal analysis, B.Sz.; investigation, B.Sz.; resources, Zs.N.; writing—original draft preparation, B.Sz.; writing—review and editing, Zs.N.; visualization, B.Sz.; supervision, Zs.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created in this study. Data sharing is not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bernanke, B. S., M. Gertler, and S. Gilchrist. 1999. Edited by B. Taylor J. and M. Woodford. The financial accelerator in a quantitative business cycle framework. In Handbook of macroeconomics. Elsevier: pp. 1341–1393. [Google Scholar]
- Cass, D. 1965. Optimum growth in an aggregative model of capital accumulation. Review of Economic Studies 32, 3: 233–240. [Google Scholar] [CrossRef]
- Gertler, M., and P. Karadi. 2011. A model of unconventional monetary policy. Journal of Monetary Economics 58, 1: 17–34. [Google Scholar] [CrossRef]
- Kiyotaki, N., and J. Moore. 1997. Credit cycles. Journal of Political Economy 105, 2: 211–248. [Google Scholar] [CrossRef]
- Koltay, G., and J. Vincze. 2009. Consumer decisions from the perspective of behavioral economics. Közgazdasági Szemle 56, 6: 495–525. [Google Scholar]
- Koopmans, T. C. 1965. On the concept of optimal economic growth. In The econometric approach to development planning. North-Holland: pp. 225–287. [Google Scholar]
- Laibson, D. 1997. Golden eggs and hyperbolic discounting. Quarterly Journal of Economics 112, 2: 443–478. [Google Scholar] [CrossRef]
- Meadows, D. H., D. L. Meadows, J. Randers, and W. W. Behrens, III. 1972. The limits to growth. Universe Books. [Google Scholar]
- Nordhaus, W. D. 1992. Lethal model 2: The limits to growth revisited. Brookings Papers on Economic Activity 1992, 2: 1–43. [Google Scholar] [CrossRef]
- Phelps, E. S., and R. A. Pollak. 1968. On second-best national saving and game-equilibrium growth. Review of Economic Studies 35, 2: 185–199. [Google Scholar] [CrossRef]
- Ramsey, F. P. 1928. A mathematical theory of saving. Economic Journal 38, 152: 543–559. [Google Scholar] [CrossRef]
- Solow, R. M. 1956. A contribution to the theory of economic growth. Quarterly Journal of Economics 70, 1: 65–94. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).