A Novel Mathematical Formalism for Modeling Physical Phenomena

1. Introduction

This paper is about physics, an essential part of which is the activity of knowledge exchange among physicists, at different locations, different eras, different orientations etc. The Lagrangian formalism, also referred to as the (extremum-) action principle, is one of several equivalent tools designed to achieve the common ground necessary for such social activity. Physicist A (mathematically) representing a studied system by $\phi$, is guaranteed that $\phi$ could (in principle) appear in physicist B’s notes if they use a common action to generate the set of their permissible $\phi$’s. To facilitate communication between any two physicists there must also exist a consistent set of dictionaries, translating ${\phi }_{\mathrm{A}}\leftrightarrow {\phi }_{\mathrm{B}}$, which is elegantly provided by the symmetry group of the action. The central role of the Poincaré group in this regard stems from the fact that it provides a necessary and sufficient set of such dictionaries for the vast majority of physicists ever registered. In this paper we ask: Why not extend our Poincaré community of physicists to include also physicists of arbitrary scale?

A cynical reviewer might at this point recommend that this manuscript be resubmitted to a scaled journal, for which there are two good replies. First, to this very day the social activity of physicists is limited to the firm ground of planet earth and at small relative velocities. Yet the mere act of imagining the existence of physicists anywhere else and at large velocities relative to us is what brought as so far, rescuing physics multiple times from long periods of stagnation. Rejecting even the possibility that physicists could have a size other than that of a physics professor, would be a blatant repetition of the original sin of anthropocentrism. So why not imagine a giant observer for whom our galaxy, or even the entire universe is a mere spec of dust? Or miniature ones, experiencing the creation and subsequent annihilation of a short-lived subatomic particle over multiple generations?—which leads to the second reply: We currently don’t know how to identify a scaled physicist. The cynic might object that we do: Just take all the dynamical fields, $\phi$, and scale them according to

$$\phi \left(x\right)\mapsto S_{\lambda }\phi ={\lambda }^{\alpha }\phi \left(\lambda x\right)$$

(1)

for some $\phi$-specific scaling exponent $\alpha$ (its inverse ‘length dimension’); that’s the only way to preserve the multiplicative group property

$$S_{{\lambda }_2}{S}_{{\lambda }_1}\phi =S_{{\lambda }_2{\lambda }_1}\phi$$

(2)

he would argue. This implies that scaled physicists comprise scaled hydrogen atoms, which are seen nowhere. Moreover, scaling (1) without alteration of the constants of nature requires physics to be scale covariant, which it isn’t according to our best understanding.

A detailed model addressing the cynic’s concerns has previously been proposed by the author. It accepts the premise (1) hence also the conventional action principle which was never meant to be invariant under (1). There is only a handful of non trivial scale invariant actions, none of which come close to being realistic. Attempting realism therefore required a very unorthodox application of the action principle manifesting in various technical subtleties, which is never a good sign. However, this is not the main motivation for the current paper. Rather, the form (1) of a scale transformation is too simplistic for two reasons: First, it is only one part of what occurs when, e.g., zooming out of a picture, the other part being a coarsening/smoothing operator. Such coarsening is familiar from the Renormalization Group formalism where $\phi$ is assumed to be a scale-dependent effective representation of some fundamental underlying reality. However, since we can’t allow such assignment of ontological privilege to any particular scale, $\phi (x,\lambda )$ are equally fundamental irrespective of their $\lambda$. Second, even standalone, (1) presupposes too much about $\phi$. The Hubble expansion, for example, can formally be viewed as a scale transformation satisfying (2), with the cosmological time playing the role of (the log of-) $\lambda$, but not conforming with (1), in which different structures scale differently depending on their ‘$\phi$’. As (1) results from integrating infinitesimal ‘naive’ scale transformations

$$\lambda {\partial }_{\lambda }\phi =x·{\partial }_x\phi +\alpha \phi ,$$

a more flexible rescaling would ensue from substituting $x·{\partial }_x\phi \mapsto Z·{\partial }_x\phi$ (generalizing to a Lie derivative along Z for tensors) where Z is a $\phi$-dependent scaling field determined on consistency grounds, reducing to x in the appropriate limit. The $\alpha$-term could likewise locally depend on Z. Combined with some $\lambda$-independent, local coarsening operator $\widehat{C}$, (1) is replaced with

$$\lambda {\partial }_{\lambda }\phi =\widehat{S}\phi ,\mathrm{with}\widehat{S}\phi :=Z·{\partial }_x\phi +\alpha \phi +\widehat{C}\phi$$

(3)

That prescription (3) for scale transformations respects the group property (2) is easily seen by changing the scale variable to $s=ln\lambda$, $s\in \left(-\infty ,\infty \right)$, in which case (3) becomes

$${\partial }_s\phi =\widehat{S}\phi$$

(4)

and (2) becomes the group property of a flow. Above and throughout the paper $\phi$ stands for $\phi (e^s,x)$ whenever the logarithmic scale s is involved, which should be clear from the context. Crucially, while the effect of $\widehat{C}$, as that of its RG counterpart, is to smooth $\phi$ (equivalently, attenuate its high frequencies) it must not result in a projection, or else scale-flow would be possible only in the forward, viz. $+s$ direction, with some $\phi (x,s_0)$ as initial condition, implicitly privileging the scale $s_0$.1 Nonetheless, since $\widehat{C}$is a coarsener, flowing backwards in scale typically leads to a singularity, often at finite-s, as the high frequencies grow without bound. It further turns out that compatibility with Lorentz transformations creates a similar problem also in the $+s$ direction. In the proposed formalism, the tiny subset of solutions of (3) which are well-behaved at any scale, $s=\pm \infty$ included, and any x, denoted by $\mathcal{S}$, plays the role of the set of all extrema of an action.

The set $\mathcal{S}$ is determined solely by the form of $\widehat{S}$ in (3). In other words, given a definition of what a scale transformation is, the mere requirement of consistency between the descriptions of physical phenomena at any scale is what defines the laws of physics. Thus each member of $\mathcal{S}$, referred to as a scale orbit, consists of infinitely many fixed-scale sections, each corresponding to distinct yet compatible representations of spacetime phenomena at different scales. It should therefore not come as a surprise that analyzing an individual section not in the context of its full orbit could lead to ‘bizarre physics’. Critically, unlike in the RG formalism, the scale, s, is not a resolution parameter an experimenter can always control by changing the equipment with which he observes a system, but rather his native scale, encapsulating the totality of instruments and materials he uses when arriving at measurement results. The native scale is an identifier facilitating the dictionary between distinct-scale physicists. A dwarf and a giant can determine whether they are studying the same system, i.e., whether their sections are taken from a common orbit, by propagating in scale their sections at their native scale, to the native scale of the other. Note that by $s-$translation invariance of (4) one’s native scale is only defined up to a communal constant, i.e. only relative scales matter. Thus a spacetime phenomenon (section) which we, humans, regard as being in the realm of condensed matter physics, a dwarf might label “astrophysical", and so would be his attitude towards us, when slicing the orbit on which we reside at ${\lambda }_{\mathrm{dwarf}}$. However, when slicing his orbit at ${\lambda }_{\mathrm{dwarf}}$ he must arrive at a self-representation which is isomorphic to ours, i.e., ${\phi }_{\mathrm{dwarf}}(x,s_{\mathrm{dwarf}})\sim {\phi }_{\mathrm{human}}(x,s_{\mathrm{human}})$, or else we would not belong to the same community of physicists (Such distinction between the representations of one’s self and of others exists also in action based theories, perhaps the most radical example being a physicist boosted to near light-speed becoming nearly two dimensional). The s-translation invariance of (4) then implies ${\phi }_{\mathrm{dwarf}}(x,s)\sim {\phi }_{\mathrm{human}}(x,s-\Delta s)$ with $\Delta s=s_{\mathrm{dwarf}}-s_{\mathrm{human}}$.

Irrespective of its philosophical merits, the proposed formalism could be used as a phenomenological tool for modeling physical phenomena, with multi-scale phenomena, e.g., turbulent flow, being the most natural candidates. However in this paper the main focus is on a model pretending to be ‘fundamental’. As such, it inevitably interfaces with diverse fields, ranging from astronomy and cosmology to quantum foundations and the nature of matter. Obviously, no single paper and no single brain can fully cover the relevant existing body of knowledge. Moreover, the high degree of novelty involved in the proposed formalism meant that, compromises in mathematical rigor in some of the proofs/arguments had to be made. Nonetheless, consistent equations for observables are eventually presented, and solved in simple cases. Hopefully, by the end of the paper, the reader will be more open to the possibility that the major open problems in physics are all different facets of a common problem: An outdated modeling language, still clutching to the belief that we, humans, are special.

2. Exactly Solvable Linear Toy Model

In order for the notion of native scale to be fully meaningful, $\phi$ must be rich enough to be able to describe: the system being observed; the observer—his equipment included; electromagnetic phenomena involved in most observations etc. This ambitious task is differed to sect.3. A gentle introduction to the jargon and techniques used in that section is provided by the flow (4) of a time-independent scalar field in Euclidean D-dimensional space. In choosing the generator of coarsening, $\widehat{C}$, the following properties should be included:

• Averaging. If $\phi \left(x_{\mathrm{m}}\right)$ is a local maximum (minimum) then $\widehat{C}\phi \left(x_{\mathrm{m}}\right)\le 0$ ($\ge 0$ resp.)
• Locality. $\widehat{C}$ is second order and does not contain higher order derivatives or higher powers of the second derivative.
• Equivariance. $\widehat{C}$ must commute with translations, rotations and reflections in ${\mathbb{R}}^D$.

The simplest $\widehat{C}$ satisfying the above is the (D-dimensional) Laplacian, corresponding to the (weighted) arithmetic average of $\phi$ in the neighborhood of a point. There are, of course, other choices corresponding to different averages2 such as: $\nabla ·\left(\nabla f\left(\phi \right)\right)$ for a monotonically increasing f, or ${\nabla }^2\phi +{|\nabla g\left(\phi \right)|}^2$ for any g and combinations thereof (∇ and · are both D-dimensional). The locality clause is a corollary of averaging. Indeed, in 1-dimension for simplicity, a ${\partial }_x^4$ term added to the Laplacian would increase a local maximum of $\phi =-x^2+a{x}^4$ at $x=0$ for a large enough, and similarly with an added $b{\left({\partial }^2\phi \right)}^2$ term for $b>1/2$. However, when $\phi$ takes values in spaces lacking a clear-cut definition of local extremum, locality becomes an independent clause, defining the local, infinitesimal neighborhood of a point. Clause 3 is obviously needed due to the arbitrariness in positioning an orienting one’s coordinate system. Equivalently, it is what defines the community of physicists in Euclidean space.

Sticking with the Laplacian, and using the simplest scaling field, $Z^i=x^i$, (4) becomes

$${\partial }_s\phi ={\ell }_0^2{\nabla }^2\phi +x·\nabla \phi +\alpha \phi$$

(5)

with ${\ell }_0$ some parameter. It is tempting to attribute a ‘physical dimension of length’ to ${\ell }_0$, balancing the double derivative it multiplies. However, being a description of physics on all scales, the prorposed formalism is inexorably an attempted ‘theory of everything’ and as such aught to be able to represent any measurement process. And since the result of any measurement is ultimately a dimensionless number, e.g., the number pointed to by a pointer, or the minimal number of standard-length rods exactly fitting a line segment, the notion of physical dimensions should ultimately be abolished. Moreover, since (5) describes a flow in scale, endowing ${\ell }_0$ with a dimension of length may lead to the wrong expectation that it too would flow in scale. Nonetheless, the developmental stage of the proposed theory is currently insufficient to internally represent any measurement. To make contact with empirical data associated with sections at our native scale, arbitrarily assigned the value $s=0$ or $\lambda =1$, dimensions will occasionally appear in this paper. Unless stated otherwise, ${\ell }_0=1$ is assumed, i.e., the coordinate x at $s=0$ is measured in multiples of ${\ell }_0$. Note that even this innocuous statement relies on the existence of an affine structure of space whose physical validation requires an affine structure of space! Thus without doing away with this circularity via a general covariant extension of (5) (section 3), our proposal cannot even pretend to be a fundamental physical theory.

2.1. The Particle Basis of $\phi$

Of special interest are fixed-point solutions of the flow (5), i.e. scale-invariant $\phi$, of which fixed-points which are further global or local attractors stand out. To find the latter we note that, if $\phi$ is integrable at $s=0$—the case of a non-integrable $\phi$ is dealt with later—its zeroth moment, $m_0$, satisfies ${\partial }_s{m}_0=(\alpha -D)m_0$ and $m_0$ explodes for $\left|s\right|\to \infty$, implying $\phi \notin \mathcal{S}$, unless $\alpha =D$ and $m_0\left(s\right)\equiv 1$ without loss of generality by the linearity of (5), or else $m_0\left(0\right)=0$. Assuming the former for now, it is helpful to represent $\phi$ by its cumulants. Taking the Fourier transform of (5) and dividing by the Fourier transform $\tilde{\phi }:=\mathcal{F}\phi$, which is also the generating function of its moments assumed all to exist, leads to the following equation for the generating function of the cumulants, $\mathcal{Ƶ}(k,s):=ln\tilde{\phi }$

$${\partial }_s\mathcal{Ƶ}=-k^2-k·\nabla \mathcal{Ƶ},(v·w\equiv v_i{w}_i,v^2\equiv v·v)$$

(6)

Equation (6) is an infinite set of uncoupled o.d.e.’s for the coefficients of multinomials $k_1^{n_1}\dots k_D^{n_D}$, whose solutions, $\propto exp\left(-s{\sum }_i{n}_i\right)$, all vanish for $s\to \infty$ except that of $k_1^2,\dots ,k_D^2$, approaching $-\frac{1}{2}$. Solving back, $\phi ={\mathcal{F}}^{-1}exp\mathcal{Ƶ}$, we get the Gaussian

$${\phi }_{\mathrm{G}}={\left(2\pi \right)}^{D/2}{e}^{-\frac{1}{2}{\sum }_i{x}_i^2}$$

which is therefore a global attractor of the flow (5) for (moment-determinate) functions with well defined moments to any order at $s=0$. However, not all moment determinate $\phi (x,s=0)$ are sections of orbits in $\mathcal{S}$. A large subset that is, consists of linear combinations, discrete or continuous, of shifted fixed-point Gaussians. This is so because any such sum has well defined moments to any order and the effect of the flow on individual Gaussians is a trivial shift

$${\phi }_{\mathrm{G}}(x-x_0){|}_{s=0}\mapsto {\phi }_{\mathrm{G}}\left(x-e^{-s}{x}_0\right)$$

(7)

We strongly suspect that the converse is also true, namely, that any $\phi \in \mathcal{S}$ can be decomposed into a linear combination of shifting Gaussians. A formal proof will not be attempted here but the intuition must be clear: The Laplacian increases (decreases) and ‘sharpens’ $\phi$ at its local maximum (resp. minimum) when flowing in the $-s$ direction of (5), and if the scaling part does not sufficiently compensate for this, $\phi$ wildly diverges at a local extremum. Any section of $\phi \in \mathcal{S}$ must therefore be ‘round’ enough on the scale set by ${\ell }_0$($=1$) and if so it should be decomposable into Gaussians of width ${\ell }_0$. A clear illustration of the fate of a function not sufficiently round is provided by a Gaussian of width less than 1 at $s=0$, i.e., $\mathcal{Ƶ}\left(0\right)=-(\frac{1}{2}-ϵ)k^2$. A finite-s singularity is reached at $s=\frac{1}{2}ln\left(2ϵ\right)$ where $\mathcal{Ƶ}$ vanishes, corresponding to $\phi$ which is a ‘delta-function Gaussian’.

Closure under continuous sums is what distinguishes the shifted Gaussians basis of $\mathcal{S}$, referred to as the ‘particle basis’, from the scaled Fourier basis,

$${\lambda }^{\alpha }{e}^{i\lambda k·x-\frac{1}{2}{\lambda }^2{k}^2};k\in {\mathbb{R}}^D,\lambda \equiv e^s$$

(8)

Although individually in $\mathcal{S}$, infinite sums thereof may still lie outside $\mathcal{S}$, as the above narrow-Gaussian example demonstrates. Nonetheless, the pseudo basis (8) is not entirely useless. It clearly shows the rapid decay of waves when their wave-vector is contracted beyond the cuttoff frequency (${\ell }_0^{-1}$) and will serve us in the sequel.

Returning to the case of non-integrable, or integrable but zero $m_0$, the corresponding fixed-points of (5) are $f_l\left(r\right)Y_l^m(\Omega )$ in $D=3$ for a suitable $f_l$, $l\ge 1$, vanishing at $r=0$, which happen to have a $r^{-3}$ asymptotic tail hence are non-integrable. It can be shown that the basin of attraction of each consists only of itself, rendering it uninteresting from our perspective.

Full justification for the name “particle" attached to Gaussians of width ${\ell }_0$ and $0^{\mathrm{th}}$-moment equal to 1 (or any other normalization) will have to await section 3 but some can already be given at this stage. If physicists of different native scales are to have isomorphic self-representations—their laboratory etc. included—and if physicists exist at arbitrarily large or small scales (but not necessarily at any scale) then they must all consist of the same particles and their ‘oppositely charged’ antiparticles—Gaussians of width ${\ell }_0$ and $0^{\mathrm{th}}$-moment $-1$. Otherwise particle-antiparticle pairs would not get fully annihilated when flowing via (7) in the $+s$ direction. As a result, the ‘vacuum’ would get increasingly contaminated with particles of arbitrary charge. Conversely, the vacuum could only acquire content when zooming into an empty patch of it, if particle-antiparticle pairs are created out of it. Note that the decomposablility of $\phi$ into a discrete sum of particles is required by the fact that $\phi$ would otherwise trivialize to a uniform $\phi \equiv 0$ for $s\to -\infty$. Thus our model requires for its consistency both particles and the quantization of their charge. Moreover, in the point-particle limit, ${\ell }_0\to 0$, it would take $s\to \infty$ for any pair to annihilate even approximately, contradicting the existence of scaled physicists. Point-particles, which are the source of all evil in mathematical physics, are excluded from the outset.

2.2. Adding Time Dependence

How should the flow (5) be generalized for a time-dependent $\phi$? Guided by the equivariance clause with the Poincaré group replacing the isometry group of Euclidean space, the unique generalization reads

$${\partial }_s\phi ={\nabla }^2\phi -{\partial }_{tt}\phi +x·\nabla \phi +t{\partial }_t\phi +\alpha \phi$$

(9)

Multiplying the ${\partial }_{tt}\phi$ term is a ${({\ell }_0/c)}^2$ coefficient, assumed to equal 1 unless stated otherwise. In covariant notations (9) reads

$${\partial }_s\phi ={\square }^2\phi +x^{\mu }{\partial }_{\mu }\phi +\alpha \phi$$

(10)

with ${\square }^2\equiv {\eta }^{\mu \nu }{\partial }_{\mu }{\partial }_{\nu }$ and ${\eta }^{\mu \nu }={\eta }_{\mu \nu }:=\mathrm{diag}(-1,1,1,1)$. Readers experiencing unease from the appearance of Lorentz symmetry out of the blue are referred to [3]; It has been known since the early years of Relativity Theory that Lorentz transformations were only serendipitously discovered within the framework of electrodynamics. This symmetry group (the Galilean group being a limiting case thereof) is an inevitability when the meaning of synchronized clocks is logically analyzed—which is essentially what is being done in this paper with regard to scale transformations. Thus our proposed time-dependent generalization of ${\mathit{\nabla }}^2\phi (\mathit{x},t)$ inexorably involves values of $\phi$ at times other than t, but not because space and time form a ‘spacetime’ continuum—the Minkowskian/geometric view (if that were the case then ${\partial }_{tt}$ would be expected to have the opposite sign). Instead, space and time are fundamentally distinct and are mixed together on consistency grounds; without such mixing no community of physicists would exist.

Generalizing static particles are—naturally—moving particles and in particular uniformly so, obtained by boosting a static particle solution. In $D=1$ for simplicity, the boost explicitly reads ${\phi }_{\mathrm{G}}(x,s)\mapsto {\phi }_{\mathrm{G}}\left(\gamma (x-vt),s\right)$ with $\gamma =\sqrt{1/(1-v^2)}$, making the Lorentz contraction of the particle in the direction of motion manifest. Uniformly moving particles are therefore all members of $\mathcal{S}$, but are all members of $\mathcal{S}$ such? More accurately: Do they form a basis for $\mathcal{S}$? To answer this question, (9) is first integrated over three-space. Assuming the integral exists results in the following equation for the zeroth moment

$${\partial }_s{m}_0=-{\partial }_{tt}{m}_0+t{\partial }_t{m}_0+(\alpha -D)m_0$$

(11)

Plugging a scaled Fourier ansatz $m_0(\omega ;t,s)=f_{\omega }\left(s\right)exp\left(i{e}^s\omega t\right)$ and continuing with the $\alpha =D$ case, we get: ${\displaystyle \frac{\mathrm{d}}{\mathrm{d}s}}{f}_{\omega }={\omega }^2{f}_{\omega }$ implying $f_{\omega }\equiv 0$$\forall \omega \ne 0$ or else it explodes for $s\to \infty$. For $\omega =0$, $f_{\omega }$ is some constant which can be assumed to equal 1 by the linearity of (9). We conclude that $m_0$ which is constant in both time and scale is a necessary condition for the corresponding $\phi$ to lie in $\mathcal{S}$. Next, consider the generalization of equation (6) for the time-dependent cumulants of $\phi$,

$$\lambda {\partial }_{\lambda }\mathcal{Ƶ}=-k^2-{\partial }_{tt}\mathcal{Ƶ}+{\left({\partial }_t\mathcal{Ƶ}\right)}^2+t{\partial }_t\mathcal{Ƶ}-k·\nabla \mathcal{Ƶ}$$

(12)

similarly obtained by Fourier transforming (9) and dividing by $\tilde{\phi }(k,t,\lambda )$. Using (12) we first argue that the instability of the flow (9) in the $-s$ direction, which mandates particles, in and of itself does not further mandate their uniform motion. To show this we plug the following ansatz into (12), continuing with $D=1$ for clarity

$$\mathcal{Ƶ}(k,\lambda ,t)=\sum _{n=1}^{\infty }{c}_n(\lambda t,\lambda )k^n=\sum _{n=1}^{\infty }\left(\sum _{m=n-1}^{\infty }{c}_n^m\left(\lambda t\right){\lambda }^{2m-n}\right)k^n$$

(13)

where $c_n^m$ is a double-indexed function of the scaled time alone. Equating the coefficient of each power of k to zero in increasing powers of $\lambda$ (note that the series is missing the $n=0$ term by our result $c_0\equiv ln{m}_0=0$). Starting with $c_1^{-1}$, dictating the asymptotic scaling form of the center-of-mass, i.e. ${\lambda }^{-1}{c}_1^{-1}\left(\lambda t\right)$, we see that it decouples from all other terms in the limit $\lambda \to 0$ and can be an arbitrary function. Successive terms, $c_1^k$, can then be iteratively computed as the ${\left({\partial }_{t}Z\right)}^2$ term does not contain the first power of k, and the ${\partial }_{tt}$ term pulls out an extra factor of ${\lambda }^2$, e.g., $c_1^1=-\frac{1}{2}{\ddot{c}}_1^{-1},c_1^3=-{\displaystyle \frac{1}{4}}{\ddot{c}}_1^1,\dots$ (all evaluated at the scaled time $\lambda t$). For $c_1^{-1}$ with bounded time derivatives to all orders, the power series of $c_1$ clearly converges for $\lambda <1$. Moving to $n=2$, the leading order of (minus the-) variance reads $c_2^0=-\frac{1}{2}(1-v^2)$ with $v={\dot{c}}_1^{-1}$ again manifesting the Lorentz contraction. Higher order corrections, $c_2^k$, can then be calculated in terms of ${\ddot{c}}_2^{k-2}$ and products ${\dot{c}}_1^p{\dot{c}}_1^q$, $p+q=k-2$ coming from the nonlinear term, e.g., $c_2^2={\displaystyle \frac{1}{4}}\left(-{\ddot{c}}_2^0+2{\dot{c}}_1^{-1}{\dot{c}}_1^1\right)\dots$. The leading order term of the third cumulant, the so called “skewness", reads $\lambda c_3^1=\lambda {\displaystyle \frac{2}{3}}{v}^2\dot{v}$. It is likewise a relativistic effect in which the ‘front’ and ‘back’ of an accelerating (extended) particle experience different Lorentz contractions. Continuing this way, $c_n^m$ can be computed in terms of $c_1^{-1}$ and its first $n-1$ derivatives. The results in a convergent power series for each at $\lambda <1$. As $c_n=O\left({\lambda }^{n-2}\right)$, at small enough scale the shape of a particle is approximated arbitrarily well by that of a uniformly moving particle (appropriately Lorentz contracted in the direction of motion). The leading order correction appear in the form of a particle’s skewness in the direction of acceleration (predicated on relativistic velocities). We conclude that a sufficient condition for $\phi$ to well-behave at small scales is that it approaches a scaling particle solutions, generalizing the static-particle result and, as in that case, we conjecture that any $\phi \in \mathcal{S}$ approaches a sum of moving-particle solutions at small scales. Although much more difficult to prove, there is no apparent reason why this conclusion should not carry to nonlinear scale-flows in the case of a single particle, and this conjecture shall play a central role in Section 3. However, unlike in the linear case, single particle solutions cannot be superposed, hence the “‘basis" in “particle basis" becomes a misnomer. Instead, it is conjectured that any $\phi \in \mathcal{S}$ must approach at small scales a discrete sum of non-overlapping moving-particle solutions.

Returning to our original question, of whether $c_1^{-1}$ necessarily describes a uniformly moving particle, we turn to the fate of such a well localized moving particle solution at small $\lambda$, entirely encoded in the single function $c_1^{-1}$, when it flows to large $\lambda$, outside the convergence radius of the each cumulant’s power series. We prove that the answer is positive, viz., unless $c_1^{-1}$ describes a globally freely moving particles, ${\lambda }^{-1}{c}_1^{-1}\left(\lambda t\right)={\zeta }_{\mathrm{free}}:={\lambda }^{-1}{x}_0+vt$ for some $x_0$ and v, its corresponding $\phi$ is not in $\mathcal{S}$. This is due to a new flow instability in the $+\lambda$ direction, introduced by the minus sign of the ${\partial }_{tt}$ term in (9). To prove this, consider the equation for the center of the particle $\zeta \equiv c_1$ (switching notations in order to not overload the upper index)

$$\lambda {\partial }_{\lambda }{\zeta }^i=-{\partial }_{tt}{\zeta }^i+t{\partial }_t{\zeta }^i-{\zeta }^i,i=1,\dots ,D$$

(14)

obtained by equating the coefficients of $k^i$ in (12) to zero (i not a power!). Now plug into (14) the most general solution

$${\zeta }^i(t,\lambda )={\zeta }_{\mathrm{free}}^i(\lambda ,t)+{\lambda }^{-1}\sum _{\omega }{A}_{\omega }^i{e}^{i\lambda \omega t+\frac{1}{2}{\omega }^2{\lambda }^2}$$

(15)

with the sum representing also an integral, and the $A_{\omega }$’s are the Fourier coefficients of ${\zeta }^i(1,t)$. Clearly, unless $A_{\omega }^i\equiv 0$, and insofar as $\phi$ still describes a localized particle, this particle (wildly) moves around unbounded for $\lambda \to \infty$ which in and of itself implies $\phi \notin \mathcal{S}$. However, moving to higher order cumulants, which are all morphological attributes of a particle-like $\phi$ hence independent of ${\zeta }^i$, a similar divergence occurs, implying either the divergence $\phi$ or its complete delocalization.

Another way of seeing why only uniformly moving particles appear in $\mathcal{S}$ is by decomposing a non-uniformly moving particle solution at $s=0$ into its space-time Fourier components, and letting them each flow to $s=\infty$. Their evolution in scale is just (8) with $k·x$ meaning $k_{\mu }{x}^{\mu }$ (and $k^2\equiv k_{\mu }{k}^{\mu }$). Waves with $k^2>0$ are strongly attenuated at large $\lambda$, while those with $k^2<0$ blow-up. Now, it is easily verified that any non-uniform, or uniform but superluminal motion at $s=0$, must have some time-like ($k^2<0$) Fourier components in its decomposition, expelling the orbit on which it resides from $\mathcal{S}$. This method is applicable also to possible superpositions of non-uniformly moving particles having $\zeta ={\zeta }_{\mathrm{free}}$ for their joint $\phi$. Rather than resorting to murky causal paradoxes, or to our current inability to accelerate masses beyond the speed of light, the proposed formalism rejects Tachyons on simple mathematical grounds. The dominance of waves with light-like k’s can also be appreciated even before moving to more complicated models.

3. A Realistic Model

The alert reader must have anticipated the main result of the previous section, namely, that $\mathcal{S}$ consists of freely moving particles. By linearity, particles can move through one another uninterrupted and if so, they are non interacting particles which should better have straight paths. Enabling their mutual interaction therefore requires some form of nonlinearity, either in the coarsener, $\widehat{C}$, or in the scaling part. Further recalling our commitment to general covariance as a precondition for any fundamental physical theory, nonlinearity is inevitably and, in a sense, uniquely forced upon us. A nonlinear model also supports a plurality of particles, having different sizes which are different from the common ${\ell }_0$ in a linear theory. This frees ${\ell }_0$, ultimately estimated at $\sim {10}^{20}$ km, to play a role at astrophysical scales.

Our realistic model involves a spin-1, $\alpha =1$ field: The A-field. A straightforward (and unique up to terms involving the curvature) way to render a differential operator generally covariant is through the minimal-coupling prescription, of ‘dotting the commas’ which can be applied to the ‘Maxwell coarsener’ ${\eta }_{\mu \nu }{\square }^2-{\partial }_{\mu }{\partial }_{\nu }$. The scaling piece of an $\alpha =1$ covariant vector is just its Lie derivative with respect to the scaling field, $Z^{\mu }$, defined below. Combined, the scale flow of $A_{\mu }$ reads

$${\partial }_s{A}_{\mu }={\ell }_0^2\left({\nabla }^{\nu }{\nabla }_{\nu }{A}_{\mu }-{\nabla }^{\nu }{\nabla }_{\mu }{A}_{\nu }\right)+{\mathcal{L}}_Z{A}_{\mu }$$

(16)

with

$${\mathcal{L}}_Z{A}_{\mu }\equiv Z^{\nu }{\nabla }_{\nu }{A}_{\mu }+{\nabla }_{\mu }{Z}^{\nu }{A}_{\nu }$$

(17)

the Lie derivative of $A_{\mu }$ with respect to $Z^{\mu }$. In flat spacetime and $Z^{\mu }\left(x\right)=x^{\mu }$, (17) reduces to ‘naive’ $\alpha =1$ scaling, ${\mathcal{L}}_Z{A}_{\mu }\to x^{\nu }{\partial }_{\nu }{A}_{\mu }+A_{\mu }$. Equation (16) prescribes the generally covariant scale-flow of a vector in one particular coordinate system common to all scales. Thus $\mathcal{S}$ is partitioned into equivalence classes, the members of each are related by some coordinate transformation.

Analyzing an $\alpha =1$ model in $D=3$ space is much more difficult as no moment of the associated particle exists. This is clearly seen already in a linear, naive scaling, flat-space model. A non-spinning, viz., $\mathit{A}\equiv 0$, fixed-point reads

$$A_0\left(r\right):={\displaystyle \frac{1}{r}}\mathrm{erf}\left({\displaystyle \frac{r}{\sqrt{2}{\ell }_0}}\right)$$

(18)

having a non-integrable $r^{-1}$ tail. To facilitate the analysis of such extended particles, we define a auxiliary $\alpha =3$ model for the ‘center’ of $A_{\mu }$

$$J_{\mu }:=-{\nabla }^{\nu }{\nabla }_{\nu }{A}_{\mu }+{\nabla }^{\nu }{\nabla }_{\mu }{A}_{\nu }\equiv -{\nabla }^{\nu }{F}_{\nu \mu }\equiv -{\displaystyle \frac{1}{\sqrt{-g}}}{\partial }^{\nu }\left(\sqrt{-g}{F}_{\nu \mu }\right)$$

(19)

Operating with ${\nabla }^{\mu }$ on (19), using the antisymmetry of $F_{\mu \nu }:={\nabla }_{\mu }{A}_{\nu }-{\nabla }_{\nu }{A}_{\mu }$, the commutators of covariant derivatives

$$\left[{\nabla }_{\mu },{\nabla }_{\nu }\right]V^{\alpha }=R_{\phantom{1}\rho \mu \nu }^{\alpha }{V}^{\rho },\left[{\nabla }_{\mu },{\nabla }_{\nu }\right]T^{\alpha \beta }=R_{\phantom{1}\rho \mu \nu }^{\alpha }{T}^{\rho \beta }+R_{\phantom{1}\rho \mu \nu }^{\beta }{T}^{\alpha \rho },\mathrm{etc}.$$

(20)

and the symmetries of the Riemann tensor, gives ${\nabla }^{\mu }{J}_{\mu }\equiv 0$, i.e., $J_{\mu }$ is covariantly conserved at any scale, s. Operating with ${\widehat{W}}_{\rho }^{\phantom{1}\mu }:=-{\nabla }_{\alpha }{\nabla }^{\alpha }{g}_{\rho }^{\phantom{1}\mu }+{\nabla }_{\rho }{\nabla }^{\mu }$ on (16), the second term of this operator annihilates the coarsener by the above remarks. The scaling piece combines the covariant generalization of the flat spacetime conversion $\alpha =1\mapsto 3$ with a novel nonlinear term (see sect.3.2 below). On the l.h.s. we have ${\widehat{W}}_{\rho }^{\phantom{1}\mu }{\partial }_s{A}_{\mu }$. We would like to swap the order of W and ${\partial }_s$, which would give ${\partial }_s{J}_{\nu }$ by (19). However, ${\widehat{W}}_{\rho }^{\phantom{1}\mu }$ could implicitly depend on the scale s through $g_{\mu \nu }$. Nonetheless the order is swapped and we shall review the approximation involved in doing so once $g_{\mu \nu }$ is determined. The combined result finally reads

$${\partial }_s{J}_{\nu }={\ell }_0^2{\nabla }_{\alpha }{\nabla }^{\alpha }{J}_{\nu }+{\widehat{W}}_{\nu }^{\phantom{1}\mu }{\mathcal{L}}_Z{A}_{\mu }$$

(21)

more suited for analysis. For example, in the case of flat spacetime and naive scaling, $Z^{\mu }=x^{\mu }$, the particle solution of the J-field associated with (18) is the familiar Gaussian $J_0=e^{-r^2/2{\ell }_0^2}$ from the previous sections. It is emphasized that $J_{\mu }$ and its associated scale flow are merely analytic tools, not to be put on equal footing with $A_{\mu }$ and its flow. As the nonlinear term arising from scaling does not involve $J_{\mu }$ but rather $A_{\mu }$, for a given $A_{\mu }$ and $g_{\mu \nu }$ equation (21) describes the linear but inhomogeneous (in both spacetime and scale) flow of $J_{\mu }$.

Relation (19) is formally equivalent to Maxwell’s equations with $J_{\mu }$ sourcing $A_{\mu }$’s wave equation. However, $J_{\mu }$ is not an independent object as in classical electrodynamics but a marker of the locus of privileged points at which the Maxwell coarsener does not annihilate $A_{\mu }$ (distinct $A_{\mu }$’s differing by some ${\partial }_{\mu }\Lambda$ therefore have identical $J_{\mu }$’s). For $J_{\mu }$ and $A_{\mu }$ to mimic those of classical electrodynamics, $J_{\mu }$ must also be localized along curved worldlines traced by solutions of the Lorentz force equation in $A_{\mu }$ (which as already shown in the scalar case, necessitates a nonlinear scale flow). And just like in the scalar-particle case, where higher order cumulants ($n>2$) are ‘awakened’ by its center’s nonuniform motion, deforming its stationary shape, so does the $A_{\mu }$ “adjunct" (in the jargon of action-at-a-distance electrodynamics) to each such $J_{\mu }$ gets deformed. Due to the extended nature of an A-particle, and unlike in $\alpha =3$ models3, these deformations at $(t,\mathit{x})$ are not encoded in the local motion of its center at time t, but rather on its motion at retarded and advanced times, $t\pm \left|\mathit{x}\right|$ (assuming flat spacetime for simplicity). However, associating such temporal incongruity with ‘radiation’ can be misleading, as it normally implies the freedom to add any homogeneous solution of Maxwell’s equations to $A_{\mu }$ which is clearly nonsensical from our perspective. Consequently, the retarded solution cannot be imposed on $A_{\mu }$ and in general, $A_{\mu }$ contains a mixture of both advanced and retarded parts, which varies across spacetime. The so-called radiation arrow of time manifested in every macroscopic phenomenon must therefore receive an alternative explanation (see sect.3.4.2).

Now, why should $J_{\mu }$ be confined to the neighborhood of a worldline? As already seen in the linear, time-dependent case, a scale-flow such as (16) suffers from instability in both s-directions: In the $-s$ direction it is due to the spatial part of the coarsener, whereas in $+s$ direction it is its temporal part. If we examine the scale flow of $A_{\mu }$ inside a ‘lab’ of dimension much smaller than ${\ell }_0$, centered at the origin without loss of generality, then the coarsener completely dominates the flow. It follows that $A_{\mu }\in \mathcal{S}$ requires that it be almost annihilated by ${\widehat{W}}_{\rho }^{\phantom{1}\mu }$, or else it would rapidly diverge. This can be true if either: the scale of variation of $A_{\mu }$ is on par with ${\ell }_0$ or greater—as in the case of our static, Gaussian fixed-point; or else ${\widehat{W}}_{\rho }^{\phantom{1}\mu }{A}_{\rho }\approx 0$, except around privileged points where the scaling-field grows to the order of ${\ell }_0$, balancing the non-vanishing coarsener piece. This is where $J_{\mu }$ is focused, as shown in sect.3.1.2 below. “Almost" is emphasized above because exact annihilation would leave a flow governed entirely by scaling. It is precisely the fact that, at distances from $J_{\mu }$ that are much smaller than ${\ell }_0$, the action of the coarsener is on the order of that of the scaling piece, which gives rise to nontrivial physics. This will be a recurrent theme in the rest of the paper.

3.1. Determining the Metric and the Scaling Field

The flow (16) of $A_{\mu }$ requires specifying both $g_{\mu \nu }(x,\lambda )$ and $Z^{\mu }(x,\lambda )$ in a generally covariant way. Starting with the former, we seek the scale flow of $g_{\mu \nu }$. It is well known that, in Riemannian geometry, the Ricci tensor is the unique, symmetric generally covariant tensor which can be constructed from the metric tensor and its first two derivatives and does not contain higher power than the first of its second derivative. By our definition of a coarsener, this leaves $\widehat{C}=R_{\mu \nu }+b{g}_{\mu \nu }R$ with $R_{\mu \nu }:=R_{\phantom{1}\mu \alpha \nu }^{\alpha }$ and $R:=R_{\phantom{1}\mu }^{\mu }$, as the only permissible coarsener for some constant b. Now, the flow (16) of $A_{\mu }$ is ‘guided’ by $g_{\mu \nu }$ via the minimal coupling prescription. On consistency grounds the flow of $g_{\mu \nu }$ must also be guided by $A_{\mu }$, or else the gravitational field would not focus around matter. The simplest way to achieve this mutuality is through the use of the (symmetric) canonical energy-momentum tensor

$${\Theta }_{\mu \nu }=F_{\mu \rho }{F}_{\nu }^{\phantom{1}\rho }-\frac{1}{4}{g}_{\mu \nu }{F}^{\rho \sigma }{F}_{\rho \sigma }$$

(22)

peaking around $J_{\mu }$, which leads to the following scale flow of $g_{\mu \nu }$:

$${\partial }_s{g}_{\mu \nu }={\ell }_g^2\left(-R_{\mu \nu }-b{g}_{\mu \nu }R+4\pi G{\Theta }_{\mu \nu }\right)+{\mathcal{L}}_Z{g}_{\mu \nu }$$

(23)

with ${\ell }_g$, G and b some constants, and

$${\mathcal{L}}_Z{g}_{\mu \nu }\equiv Z^{\rho }{\nabla }_{\rho }{g}_{\mu \nu }+g_{\rho \nu }{\nabla }_{\mu }{Z}^{\rho }+g_{\rho \mu }{\nabla }_{\nu }{Z}^{\rho }={\nabla }_{\mu }{Z}_{\nu }+{\nabla }_{\nu }{Z}_{\mu }$$

(24)

The global sign of the coarsener piece reflects the following sign conventions for the Riemann tensor

$${R^{\mu }}_{\alpha \beta \gamma }=\left({\Gamma }_{\alpha \gamma ,\beta }^{\mu }-{\Gamma }_{\alpha \beta ,\gamma }^{\mu }+{\Gamma }_{\sigma \beta }^{\mu }{\Gamma }_{\gamma \alpha }^{\sigma }-{\Gamma }_{\sigma \gamma }^{\mu }{\Gamma }_{\beta \alpha }^{\sigma }\right)$$

Taking the covariant divergence of (23), and using ${\nabla }^{\mu }\left(R_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }R\right)\equiv 0$ (as a result of the Bianchi identity) implies that

$${\nabla }^{\mu }\left(4\pi G{\ell }_g^2{\Theta }_{\mu \nu }+{\mathcal{L}}_Z{g}_{\mu \nu }-{\partial }_s{g}_{\mu \nu }+\left(b+\frac{1}{2}\right){\ell }_g^2{g}_{\mu \nu }R\right)=0$$

(25)

is a necessary condition for (23) to have a solution. Defining

$$4\pi G{\ell }_g^2{P}_{\mu \nu }:={\mathcal{L}}_Z{g}_{\mu \nu }$$

(26)

equation (25) can be rewritten as

$${\nabla }^{\mu }\left({\Theta }_{\mu \nu }+P_{\mu \nu }\right)={\displaystyle \frac{1}{4\pi G{\ell }_g^2}}{\nabla }^{\mu }{\partial }_s{g}_{\mu \nu }-{\displaystyle \frac{b+\frac{1}{2}}{4\pi G}}{\partial }_{\nu }R$$

(27)

Postulating that energy-momentum conservation is recovered in the limit $g_{\mu \nu }\to {\eta }_{\mu \nu }$ mandates $b=-\frac{1}{2}$, nullifying the last term on the r.h.s. of (27), which is assumed henceforth. The possibility that gravity is essentially involved in the structure of elementary matter [4], and consequently $g_{\mu \nu }\to {\eta }_{\mu \nu }$ is nonphysical, has not been explored.

3.1.1. Determining $Z^{\mu }$ in the Flat Spacetime Approximation

Assuming $g_{\mu \nu }={\eta }_{\mu \nu }$ leads to significant simplification when determining $Z^{\mu }$, and is therefore considered first. In this approximation covariant derivatives appear as ordinary derivatives, (27) reduces to energy-momentum conservation

$${\partial }^{\mu }{T}_{\mu \nu }\equiv {\partial }^{\mu }\left({\Theta }_{\mu \nu }+P_{\mu \nu }\right)=0$$

(28)

and ${\mathcal{L}}_Z{g}_{\mu \nu }={\partial }_{\mu }{Z}_{\nu }+{\partial }_{\nu }{Z}_{\mu }$. By virtue of definition (19) of $J^{\mu }$ (Maxwell’s equations) and ${\partial }_{\mu }{\tilde{F}}^{\mu \nu }\equiv 0$ (${\tilde{F}}_{\mu \nu }:={ϵ}_{\mu \nu \rho \sigma }{F}^{\rho \sigma }$) alone, Poynting theorem is satisfied identically

$${\partial }^{\mu }{\Theta }_{\mu \nu }=-F_{\nu \mu }{J}^{\mu }$$

(29)

hence (28) implies

$${\partial }^{\mu }{P}_{\mu \nu }=F_{\nu \mu }{J}^{\mu }$$

(30)

Maxwell’s equations (19), along with (29) and (30), referred to henceforth as the basic tenets of classical electrodynamics, are nowadays taken as the definition of classical electrodynamics, encapsulating its experimental success while avoiding the traditional use of the Lorentz force equation of a point charge, with its infamous, unresolved classical self-force problem.

Equations (26) and (30) result in four second order equations for the four components of the scaling vector $Z^{\mu }$,

$${\square }^2{Z}_{\nu }+{\partial }_{\nu }{\partial }^{\mu }{Z}_{\mu }=4\pi G{\ell }_g^2{F}_{\nu \mu }{J}^{\mu }$$

(31)

which, together with the boundary condition $Z^{\mu }\to x^{\mu }$ away from matter, define $Z^{\mu }$ up to a solution of the homogeneous equation (31). Continuity in s severely, if not completely, removes this remaining freedom.

Summarizing, as a corollary of defining the scale flow of the metric, a definition of the scaling field at each scale $\lambda$ was obtained, constrained by continuity in $\lambda$. A generalization to curved spacetime follows by adding the r.h.s. of (27) (with $b=-\frac{1}{2}$) to the r.h.s. of (31),

$${\nabla }^{\mu }{\nabla }_{\mu }{Z}_{\nu }+{\nabla }^{\mu }{\nabla }_{\nu }{Z}_{\mu }=4\pi G{\ell }_g^2{F}_{\nu \mu }{J}^{\mu }+{\nabla }^{\mu }{\partial }_s{g}_{\mu \nu }$$

(32)

and using a covariant form for the boundary condition

$$P_{\mu \nu }\to {\displaystyle \frac{1}{2\pi G{\ell }_g^2}}{g}_{\mu \nu }\mathrm{far}\mathrm{away}\mathrm{from}\mathrm{matter}$$

(33)

3.1.2. Time Independent Fixed-Point $A_{\mu }$

Now that $A_{\mu }$ depends on $Z^{\mu }$ via (16), and $Z^{\mu }$ on $A_{\mu }$ via (31), the nonlinear nature of the flow (16) can be appreciated, as well as the indirect mixing of $A_0$ and $\mathit{A}$ through $Z^{\mu }$, even in the time-independent case. Analyzing and solving the fixed-point solutions of the nonlinear system (16)(31) in the general, time-independent case, deserves a separate paper. Here we analyze the spherically symmetric, non-spinning ($\mathit{A}\equiv 0$) case in order to demonstrate how the nonlinearity introduces a second length scale, governing particle physics, which unlike ${\ell }_0$ is an attribute of the solution rather than a parameter of the model.

For $A_0\equiv \phi \left(r\right)$, $\mathit{A}\equiv 0$, the r.h.s. of (30) is an outwards-pointing radial force $x_{i}f\left(r\right)$ with

$$f\left(r\right):=\left(2{\displaystyle \frac{{\phi }^{\prime 2}}{r^2}}+{\displaystyle \frac{{\phi }^{\prime }{\phi }^{″}}{r}}\right)$$

Plugging

$$Z_i=x_i+z_i\equiv x_i+x_{i}z\left(r\right),Z_0=x_0+h\left(r\right)$$

(34)

into (31) with boundary conditions $z(\infty )=0$, $z^{\prime }\left(0\right)=0$ (for the Laplacian to be well-defined at the origin) and $h^{\prime }\left(0\right)=h(\infty )=0$ translates into $h=0$ and a second order ODE for $z\left(r\right)$

$$2z^{″}+{\displaystyle \frac{8z^{\prime }}{r}}=4\pi G{\ell }_g^{2}f,z(\infty )=0,z^{\prime }\left(0\right)=0$$

(35)

Setting ${\partial }_s{A}_0=0$ in (16) gives

$${\ell }_0^2\left({\phi }^{″}+{\displaystyle \frac{2{\phi }^{\prime }}{r}}\right)+r(1+z){\phi }^{\prime }+\phi =0,{\phi }^{\prime }\left(0\right)=\phi (\infty )=0$$

(36)

The system (35)(36) is symmetric under $A_{\mu }\mapsto -A_{\mu }$, $z^{\mu }\mapsto z^{\mu }$, guaranteeing that fixed-points come in particle-antiparticle pairs, which is true also in the general case. Since $z(\infty )=0\Rightarrow \phi (\infty )=0$, the system is underdetermined, i.e., its solutions involve four integration constants satisfying only three independent conditions. Solutions of (35) are

$$z\left(r\right)=2\pi G{\ell }_g^2{\int }_0^r{ṛ}^{\prime }{\displaystyle \frac{{\int }_0^{r^{\prime }}{ṛ}^{″}{r^{″}}^{4}f\left(r^{″}\right)}{r^{\prime 4}}}-2\pi G{\ell }_g^2{\int }_0^{\infty }{ṛ}^{\prime }{\displaystyle \frac{{\int }_0^{r^{\prime }}{ṛ}^{″}{r^{″}}^{4}f\left(r^{″}\right)}{r^{\prime 4}}}$$

(37)

A particle solution is defined by $f\left(r\right)\approx 0$ for $r\gtrsim r_{\mathrm{p}}$, where $r_{\mathrm{p}}$ is the radius of the support of $J_0$ (‘matter’), on the order of the proton radius. Inside matter $f\left(r\right)>0$, implying $z\left(0\right)<0$. Since $J_0=-{\mathbf{\nabla }}^2\phi$, at $r\ll {\ell }_0$ it must (almost) vanish by (36), unless $\left|z\right|\gg 1$ there. Indeed, by (37) z is on the order of the huge dimensionless number $q^{2}G{\ell }_g^2/r_{\mathrm{p}}^4\sim {10}^{36}$ inside $J_0$, assuming that the particle’s mass is entirely of electrostatic origin (which it is; see next) and using an estimate ${\ell }_g\sim {10}^{23}$km based on cosmological observations (sect.3.4.2). Using $f\left(0\right)=\frac{1}{3{\ell }_0^4}{\phi }^2\left(0\right)$ the system (35)(36) can be integrated from $r=0$ using $\phi \left(0\right)$ as a free parameter, adjusting $z\left(0\right)$ to meet $z(\infty )=0$. It can then be shown that $r_{\mathrm{p}}$ is monotonically decreasing with increasing $\phi \left(0\right)$, i.e., the support of $\left|z\right|$ shrinks with increasing $\left|f\right(0\left)\right|$. Remarkably, parameters involved in gravity, viz., ${\ell }_0,{\ell }_g,G$ all appear in such fixed-point equations for microscopic matter, even in the flat spacetime approximation.

The Poincaré stress-energy tensor (26) reads

$$P_{ij}={\displaystyle \frac{1}{2\pi G{\ell }_g^2}}\left({\eta }_{ij}(1+z)+{\displaystyle \frac{x_i{x}_j}{r}}{z}^{\prime }\right),P_{00}=-{\displaystyle \frac{1}{2\pi G{\ell }_g^2}},P_{0i}=0$$

(38)

consisting of an $A_{\mu }$-independent (negative) ‘vacuum energy-momentum’ piece, ${\displaystyle \frac{1}{2\pi G{\ell }_g^2}}{\eta }_{\mu \nu }$, entirely due to the boundary condition (33), and an $A_{\mu }$-specific, G-and ${\ell }_g$-independent piece, $p_{\mu \nu }$, which is colocalized with $J_0$. The trace of $p_{ij}$ is negative inside matter; Poincaré would have interpreted this as the negative pressure holding the particle against its internal Coulomb expansion, and the non-trivial scaling field, $x^{i}z$, as (minus) the displacement vector due to the Coulomb stress. Outside matter $z\sim -r^{-3}$, rendering $p_{ij}$ traceless. The $p_{00}$ component vanishes thus the particle’s energy is attributable entirely to its electrostatic self-energy ${\Theta }_{00}$.

In conclusion of this section, a few final remarks. First, the above particle solution, although involving a nonlinearity, must not be conflated with soliton solutions of nonlinear PDEs, having a long history in modeling of particles. The existence of particles in the proposed formalism does not hinge on the flow being nonlinear (as seen in sect.2), but rather on a unique scaling operation countering the coarsener. Second, at large r, the scaling piece completely dominates the fixed-point equation, exactly annihilating only the monopole, $\sim r^{-1}$, of $J_{\mu }$. No higher order multipoles are therefore part of a fixed-point solution at $r>{\ell }_0$ (it would take, e.g., $\alpha =2$ for the dipole). However, since electro- and magneto-statics are only testable at scales much smaller than ${\ell }_0$, higher order multipoles, required by a spinning particle, need only extend to distances$\ll {\ell }_0$, where the coarsener completely dominates when $\left|\mathit{z}\right|\ll 1$, exactly annihilating any term in the multipole expansion. Second, charge quantization could be explained by cosmological considerations, of the type discussed at the end of sec.2.1. As in the linear case, and as seen in the spherically symmetric solution, fixed-points depend on a continuous parameter, controlling both their charge and size this time, which is ‘spontaneously’ fixed at its observed value by a global consistency condition. Alternatively, charge quantization may arise just from the fixed-point condition for a spinning particle. Finally, some/most/all real-world particles are more likely represented by time-dependent solutions, which are fixed-points only in the statistical sense, when averaged over sufficiently long yet microscopic time intervals. Since $p_{00}\propto {\partial }_0{z}_0$, the time-averaged energy $\int {\mathrm{d}}^{3}x{p}_{00}$ would vanish nonetheless. The time dependence of such solutions would need to be chaotic, with a scale invariant power spectrum up to some cutoff frequency. Analyzing the properties of such dynamical fixed-points is suited for a statistical theory, complementing the proposed realistic model on such issues, which allegedly is quantum mechanics and its generalization; see sect.3.3

3.1.3. A Particle’s Gravitational Field

Moving one step beyond the the flat spacetime approximation, the distortion to ${\eta }_{\mu \nu }$ caused by a fixed-point particle is calculated, assuming first that it is a static particle. To this end the flat metric is replaced with a static metric

$$g_{00}=-(1-\Phi ),g_{ij}={\eta }_{ij}(1+\Phi ),g_{i0}=g_{0i}=0,|\Phi |\ll 1$$

(39)

and we seek a fixed-point solution of the metric flow (23), with $T_{\mu \nu }:={\Theta }_{\mu \nu }+P_{\mu \nu }$ now calculated using (39) instead of ${\eta }_{\mu \nu }$. Substituting (39) into (23) and setting ${\partial }_s{g}_{\mu \nu }=0$ gives

$${\mathbf{\nabla }}^2\Phi +{\displaystyle \frac{2}{{\ell }_g^2}}=4\pi G\left({\Theta }_{00}+p_{00}^{\mathrm{met}}\right)$$

(40)

with $p_{00}^{\mathrm{met}}$ being the metric part of $p_{00}$, resulting from ${\partial }_0{z}_0\mapsto {\nabla }_0{z}_0$ in (26) (the matter part vanishes; see previous section), and the the vacuum piece (33) of $P_{\mu \nu }$, now reading $P_{\mu \nu }^{\mathrm{vac}}=-(1-\Phi )/\left(2\pi G{\ell }_g^2\right)\approx -1/\left(2\pi G{\ell }_g^2\right)$ moved to the l.h.s.

In arriving at (40) we assumed $Z^i\approx x^i$ to leading order in $\Phi$, which can be verified given ${\nabla }^2\Phi =0$. The scaling piece coming from the Lie derivative, explicitly appearing in the fixed-point equation (36) for $A_{\mu }$, appears to be missing from (40). This is because it has been absorbed into $p_{00}^{\mathrm{met}}$:

$$p_{00}^{\mathrm{met}}\approx {\displaystyle \frac{1}{4\pi G{\ell }_g^2}}\left(x^i+z^i\right){\partial }_i\Phi$$

(41)

Moving $p_{00}^{\mathrm{met}}$ to the l.h.s. of (40), using $z^i\ll x^i$ outside matter from the previous section, we obtain the fixed-point equation for an inhomogeneous flow of a scalar $\Phi$

$$-{\ell }_g^2\left({\mathbf{\nabla }}^2\Phi -4\pi G{\Theta }_{00}\right)-2+x^i{\partial }_i\Phi =0$$

(42)

with the $z^i{\partial }_i\Phi$ term inside matter omitted by our assumption that gravity plays a negligible role in the structure of matter. At distances from the source smaller than ${\ell }_g$, ultimately estimated at ${\ell }_g\sim {10}^{23}$km, solutions of (42) are approximately the usual solutions of Newtonian gravity, ${\Phi }_m=-m/\left|\mathit{x}\right|$, with $m=\int {\mathrm{d}}^{3}x{\Theta }_{00}$. A covariant generalization of (40) would be

$$R_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }R-{\displaystyle \frac{2}{{\ell }_g^2}}{g}_{\mu \nu }=4\pi G\left({\Theta }_{\mu \nu }+p_{\mu \nu }\right)$$

(43)

which is just Einstein’s fields equation with a cosmological constant and $G\mapsto -\frac{1}{2}G$. The physical meaning of $g_{\mu \nu }$ solving (43) is only revealed through its effect on $A_{\mu }$, and in the following sections the reason for this peculiar coefficient of G becomes apparent.

In most realistic scenarios, ${\Theta }_{\mu \nu }$ is time-dependent, focused on the worldline, $\zeta (t,\lambda )$, of a particle, and the adjunct metric perturbation solving

$$\lambda {\partial }_{\lambda }\Phi =-{\ell }_g^2\left({\nabla }^2\Phi -{\partial }_{tt}\Phi -4\pi G{\Theta }_{00}\right)+x^i{\partial }_i\Phi +t{\partial }_t\Phi$$

(44)

becomes more complicated. For a uniformly moving $\zeta$ we can simply boost the previous static perturbation as in sect.2.2. For non-relativistic non-uniform motion, we first note the freedom to choose the scaling center at will: If $\Phi (\mathit{x},t,\lambda )$ solves (44) with ${\Theta }_{00}$ focused on $\zeta (t,\lambda )$, then so does $\Phi (\mathit{x}-{\lambda }^{-1}{\mathit{x}}^{\prime },t-{\lambda }^{-1}{t}^{\prime },\lambda )$ with $\zeta \mapsto \zeta (t-{\lambda }^{-1}{t}^{\prime },\lambda )+{\lambda }^{-1}{\mathit{x}}^{\prime }$ for any ${\mathit{x}}^{\prime },t^{\prime }$. Using this freedom we can focus on any point on the worldline traced by $\zeta$, assuming $t=0$. It is then readily verified that at sufficiently small accelerations, $\ddot{\zeta }$ (e.g., for a path $\zeta :={\lambda }^{-1}{\zeta }_{\mathrm{scl}}\left(\lambda t\right)$ in its scaling regime), ${\Phi }_m(\mathit{x}-\zeta )$ becomes a pointwise, arbitrarily good solution for (44) in a neighborhood,

$$\left|\mathit{x}-\zeta \right|\le c^2{\left|\ddot{\zeta }\right|}^{-1}\ll {\ell }_g$$

(45)

Since outside this neighborhood ${\Phi }_m\approx 0$, the standard, Newtonian approximation

$$\Phi (\mathit{x},t,\lambda )\approx \sum _k{\Phi }_{m_k}\left(\mathit{x}-{\zeta }_k(t,\lambda )\right)$$

(46)

where k is a particle label, becomes an arbitrarily good, point-wise, global solution of (44). The scale dependence of $\Phi$ is therefore inherited from that of $\left\{{\zeta }_k\right\}$. Note that the time-independence of $\Phi$ in (39) must be relaxed to include this quasi-static change, resulting from the time dependence of $\left\{{\zeta }_k\right\}$.

As $\Phi$ (46) flows to larger $\lambda$, the approximation (45) it involves gradually breaks due to the shrinkage of that neighborhood of $\zeta$ at large accelerations. A better approximation is obtained as follows. Choosing the scaling center such that all relevant particles contributing to ${\Theta }_{00}$ are in a ‘lab’ of radius much smaller than ${\ell }_g$, the terms in (44) multiplied by ${\ell }_g^2$ completely dominate the flow, and ${\mathbf{\nabla }}^2\Phi -{\partial }_{tt}\Phi -4\pi G{\Theta }_{00}\approx 0$ must be satisfied at any $\lambda$ for $\Phi$ not to rapidly blow up due to the instability of the flow (44). In other words, $\Phi$ must be approximately a solution of a massless wave equation sourced by that part of $4\pi G{\Theta }_{00}$ which is associated with particles inside the lab. A weak-field metric ansatz more general than (39), $g_{\mu \nu }={\eta }_{\mu \nu }-\frac{1}{2}{h}_{\mu \nu }$, $\left|h_{\mu \nu }\right|\ll 1$, would have resulted in the standard, linearized Einstein field equations.

3.2. The Motion of Matter Lumps in a Weak Gravitational Field

Equation (46) prescribes the scale flow of the metric (in the Newtonian approximation), given the a set, $\left\{{\zeta }_k(t,\lambda )\right\}$, of worldlines associated with matter lumps. To determine this set, an equation for each ${\zeta }_k(t,\lambda )$, given $\Phi (t,\mathit{x},\lambda )$, is obtained in this section. This is done by analyzing the scale flow of the first moment of $J_0$ associated with a general matter lump, using (21). An obstacle to doing so comes from the fact that, $\zeta (t,\lambda )$ now incorporates both gravitation and electromagnetic interactions in a convoluted way, as the existence of gravitating matter depends on it being composed of charged matter. In order to isolate the effect of gravity on $\zeta (t,\lambda )$, we first analyze the motion of a body in the absence of gravity, i.e., $g_{\mu \nu }\equiv {\eta }_{\mu \nu }$, $Z^{\mu }=x^{\mu }+z^{\mu }$ with $x^{\mu }$ the Minkowskian coordinates. To this end we first need to better understand the scale flow (21) of $J_{\mu }$. Using (24) and (19) plus some algebra the scaling piece in (21) reads

$${\widehat{W}}_{\nu }^{\phantom{1}\mu }{\mathcal{L}}_Z{A}_{\mu }=x^{\mu }{\partial }_{\mu }{J}_{\nu }+3J_{\nu }+M_{\nu }$$

(47)

with

$$M_{\nu }:={\partial }_{\mu }{M}_{\phantom{1}\nu }^{\mu }:={\partial }_{\mu }\left({\partial }_{\rho }{z}^{\mu }{F}_{\nu }^{\phantom{1}\rho }+{\partial }^{\mu }{z}_{\rho }{F}_{\nu }^{\phantom{1}\rho }+{\partial }_{\nu }{z}^{\rho }{F}_{\rho }^{\phantom{1}\mu }-{\partial }_{\rho }{z}^{\rho }{F}_{\nu }^{\phantom{1}\mu }+z^{\mu }{J}_{\nu }\right)$$

(48)

The first two terms in (47) are the familiar $\alpha =1\mapsto \alpha =3$ conversion, to which a ‘matter vector’, $M_{\nu }$, is added, consisting of inhomogeneous terms, and the homogeneous, ${\partial }_{\mu }\left(z^{\mu }{J}_{\nu }\right)$ term, modifying naive scaling in a way which conserves-in-scale charge for a time-independent $J_0$

$$Z^{\mu }=x^{\mu }\mapsto x^{\mu }+z^{\mu },\alpha =3\mapsto 3+{\partial }_{\mu }{z}^{\mu }$$

(49)

In the absence of gravity, the swapping of ${\widehat{W}}_{\nu }^{\phantom{1}\mu }$ and ${\partial }_s$ leading to the l.h.s. of (21) is fully justified. Combined, we then get

$${\partial }_s{J}_{\nu }={\ell }_0^2{\square }^2{J}_{\nu }+x^{\mu }{\partial }_{\mu }{J}_{\nu }+3J_{\nu }+M_{\nu }$$

(50)

Since ${\partial }^{\nu }{J}_{\nu }\equiv 0$, taking the divergence of (50) implies ${\partial }^{\nu }{M}_{\nu }\equiv 0\Rightarrow \int {\mathrm{d}}^{3}x{M}_0:=M\left(s\right)$, viz., a conserved-in-time ‘matter charge’. Defining $q\left(s\right):=\int {\mathrm{d}}^{3}x{J}_0$ the (conserved in time-) electric charge, and integrating (50) over three-space implies ${\displaystyle \frac{\mathrm{d}}{\mathrm{d}s}}q=M\left(s\right)$ i.e., electric charge is conserved in scale if and only if the matter charge vanishes. That the latter is identically true follows from

$$M=\int {\mathrm{d}}^{3}x{\partial }_j{M}_{\phantom{1}0}^j+\int {\mathrm{d}}^{3}x{\partial }_0{M}_{\phantom{1}0}^0=0+0$$

(51)

where the vanishing of the second integral follows, after integration by parts, from the explicit form (48) of ${\partial }_0{M}_{\phantom{1}0}^0.$

Next, multiplying (50) by $x^i/q$ and integrating over a ball, B, containing a body of charge q, results in

$$\lambda {\partial }_{\lambda }{\zeta }^i=-{\ell }_0^2{\partial }_{tt}{\zeta }^i+t{\partial }_t{\zeta }^i-{\zeta }^i+q^{-1}{\int }_B{\mathrm{d}}^{3}x{x}^i{M}_0(\mathit{x},t,s)$$

(52)

where ${\zeta }^i(t,s)=q^{-1}{\int }_B{\mathrm{d}}^{3}x{x}^i{J}_0(\mathit{x},t,s)$ is an object’s ‘center-of-charge’. Above and in the rest of this section, the charge of a body, assumed nonzero for simplicity, is only used as a convenient tracer of matter.

The integral in (52) is the first moment of a distribution, $M_0$, whose zeroth moment vanishes. It vanishes identically for a spherically symmetric $M_0$, and even for a skewed $M_0$, the result is a constant, $w\ll {\ell }_0$, at most on the order of the support of $M_0$. For a particle’s path not passing close to the scaling enter (without loss off generality), $w\ll \left|\zeta \right|$. This integral term is therefore ignored for the rest of the paper, and the reader can easily verify that its inclusion would have had a negligible influence on the results.

With said integral ignored, (52) becomes (14). And as proved in that case, solutions for ${\zeta }^i$ must all be straight, non tachyonic worldlines. The effect of gravity on those is derived by including a weak field in the the flow of the first-moment projection of (21). Since gravity is assumed to play a negligible role in the structure of matter, the way this field enters the flat spacetime analysis is via the scaling field, $Z^{\mu }=x^{\mu }+z^{\mu }\mapsto {\tilde{z}}^{\mu }+z^{\mu }$, with ${\tilde{z}}^{\mu }$ incorporating the metric, and by ‘dotting the commas’ in partial derivatives. Before analyzing the first moment we note that, the previous zeroth-moment analysis can be repeated with $\partial \mapsto \nabla$, at most introducing curvature-terms corrections due to the non-commutativity of covariant derivatives (20), which can be neglected in the Newtonian approximation. As for the the swapping of ${\widehat{W}}_{\phantom{1}\mu }^{\nu }$ and ${\partial }_s$ made in arriving at (50), using $F_{\mu \nu }\equiv {\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }$ (viz., ordinary derivatives can replace covariant ones) in the definition (19) of $J^{\mu }$, it is easily established that the swapping introduces an error equal to $\frac{1}{2}{F}_{\nu \mu }{\partial }_s{\partial }^{\nu }ln(-g)\approx F_{\nu \mu }{\partial }_s{\partial }^{\nu }\Phi$ with the determinant $g=|g_{\mu \nu }|\approx -1-2\Phi$. This error is negligible when competing with ${\partial }_s{\partial }^{\nu }{F}_{\nu \mu }$, containing extra spatial derivatives of $A_{\mu }$ at its center. Thus $J_0$ is not only covariantly conserved in time, which can be written ${\partial }^{\mu }\left(\sqrt{-g}{J}_{\mu }\right)=0$, by virtue of the last identity in (19), but also in scale,

$$\int {\mathrm{d}}^{3}x\sqrt{-g}{J}_0(\mathit{x},t,\lambda )\equiv q$$

(53)

Continuing in the Newtonian approximation of the metric (39) for simplicity, and further assuming non-relativistic motion, i.e., $\left|\right|J^i\left|\right|\ll \left|\right|J^0\left|\right|$ (say, in the $L^1$ sense), a straightforward calculation of the Christoffel symbols to first order in $\Phi$ incorporating ${\nabla }^2\Phi =0$ gives

$${\square }_{\mathrm{GR}}^2{J}_0\equiv {\nabla }^{\alpha }{\nabla }_{\alpha }{J}_0\approx -(1+\Phi ){\partial }_{tt}{J}_0+(1-\Phi ){\partial }_j\left({\partial }_j{J}_0+{\partial }_j\Phi J_0\right)$$

(54)

Ignoring $O(\Phi )$ corrections to the isotropic coarsener, the net effect of of the potential in the Newtonian approximation is to render the coarsener unisotropic through its gradient. Multiplying (50) with the modified d’Alembertian (54) by $\sqrt{-g}{x}^i/q\approx (1+\Phi )x^i/q$ and integrating over B, the $(1+\Phi )$ cancels (to first order in $\Phi$) the $(1-\Phi )$ factor multiplying the spatial piece in (54), which is then integrated by parts, assuming ${\partial }_i\Phi$ is approximately constant over the extent of the body. Since ${\tilde{z}}^{\mu }=x^{\mu }+O(\Phi )$ and ${\nabla }_{\mu }{J}_0\approx {\partial }_{\mu }\left(J_0(1+O(\Phi ))\right)$ the modification to the scaling piece (47) only introduces an $O(\Phi )$ correction to the $-{\zeta }^i$ term in (52) which is neglected in the Newtonian approximation. Further neglecting the $O(\Phi )$ contribution to the double time-derivative piece, the first moment projection of (21) finally reads

$$\lambda {\partial }_{\lambda }{\zeta }^i={\ell }_0^2\left(-{\partial }_{tt}{\zeta }^i-{\partial }^i\Phi (\zeta ,t,\lambda )\right)-{\zeta }^i+t{\partial }_t{\zeta }^i$$

(55)

This equation is just (14) with an extra ‘force-term’ on its r.h.s. which could salvage a non uniformly moving solution, ${\zeta }^i$, from the catastrophic fate at $\lambda \to \infty$ suffered by its linear counterpart.

At sufficiently large scales, $\lambda$, when all relevant masses contributing to $\Phi$ occupy a small ball of radius $\ll {\ell }_0$ centered at the origin of scaling without loss of generality, the scaling part on the r.h.s of (55) becomes negligible compared with the force term, rather benefiting from such crowdedness ($t\ll {\ell }_0$ can similarly be assumed without loss of generality). It follows that each $\left|\zeta \right|$ would grow—extremely rapidly as we show next—with increasing $\lambda$ even when the weak-field approximation is still valid, implying that the underlying $A_{\mu }$ is not in $\mathcal{S}$. The only way to keep the scale evolution of $\zeta$ under control is for the acceleration term to similarly grow, almost canceling the force term but not quite, which is critically important; it is the fact that the sum of these two terms, both originating from the coarsener, remains on the order of the scaling term, which is responsible for a nontrivial, non pure scaling $\zeta$. This means that each worldline converges at large scales to that satisfying Newton’s equation

$${\partial }_{tt}{\zeta }^i=-{\partial }^i\Phi (\zeta ,t,\lambda )$$

(56)

At small scales the opposite is true. The scaling part dominates and any scaling path, i.e., ${\zeta }^i(t,\lambda )={\lambda }^{-1}{\zeta }_{\mathrm{scl}}^i\left(\lambda t\right)$ is well behaved. Combined: at large scales ${\zeta }^i$ is determined, then simply scaled at small scales, gradually converging locally to a freely moving particle. Finally, (56) must be true also for a loosely bound system, e.g. a wide binary moving in a strong external field, implying that Newton’s law applies also to their relative vector, not merely to their c.o.m.

Deriving a manifestly covariant generalization of (55) is certainly a worthwhile exercise. However, in a weak field the result could only be

$$\lambda {\partial }_{\lambda }{\zeta }^{\mu }={\left(\lambda {\ell }_0\right)}^2\left(-{\partial }_{\tau \tau }{\zeta }^{\mu }-{\overline{\Gamma }}_{\nu \rho }^{\mu }{\partial }_{\tau }{\zeta }^{\nu }{\partial }_{\tau }{\zeta }^{\rho }\right)-z^{\mu }$$

(57)

with $\tau$ some scalar parameterization of the worldline traced by ${\zeta }^{\mu }$. Above, ${\overline{\Gamma }}_{\nu \rho }^{\mu }$ is the Christoffel symbols associated with $g_{\mu \nu }(x,\lambda ;-2G)$, i.e., the analytic continuation of the metric, seen as a function of Newton’s constant, to $-2G$. Recalling from sect.3.1.3 that the fixed-point $g_{\mu \nu }$ is a solution of the standard EFE analytically continued to $G\mapsto -\frac{1}{2}G$, $\overline{\Gamma }$ in that case is therefore just the Christoffel symbol associated with standard solutions of EFE’s. The previous, Newtonian approximation is a private case of this, where $\Phi$ contains a factor of G. Note however that the path of a particle in our model is a covariantly defined object irrespective of the analytic properties of $g_{\mu \nu }$. Resorting to analyticity simply provides a constructive tool for finding such paths whenever $g_{\mu \nu }$ is analytic in G. In such cases, the covariant counterpart of (56) becomes the standard geodesic equation of GR which gives great confidence that this is also the case for non-analytic $g_{\mu \nu }$.

The reasons for trusting (57) are the following. It it is manifestly covarinat, as is our model; At nonrelativistic velocities and weak field, (57) implies ${\zeta }^t\equiv t\approx {\lambda }^{-1}\tau$ which, when substituted into the i-components of (57), recovers (55); It only involves local properties of ${\zeta }^{\mu }\left(\tau \right)$ and $g_{\mu \nu }\left(x\right)$, i.e., their first two derivatives, which must also be a property of a covariant derivation, as is elucidated by the non-relativistic case. Thus (57) is the only candidate up to covariant, higher derivatives terms involving ${\zeta }^{\mu }$ and $g_{\mu \nu }$, or nonlinear terms in their first or second derivatives, all becoming negligible in weak fields/ at small accelerations.

In conclusion of this section we wish to relate (57) to the fact that $T_{\mu \nu }$ is not covariantly conserved by virtue of (27). It was well known already to Einstein that the geodesic equation follows from local energy-momentum conservation under reasonable assumptions. Similarly, the Lorentz force equation follows quite generally from the basic tenets of classical electrodynamics (30),(29),(19). 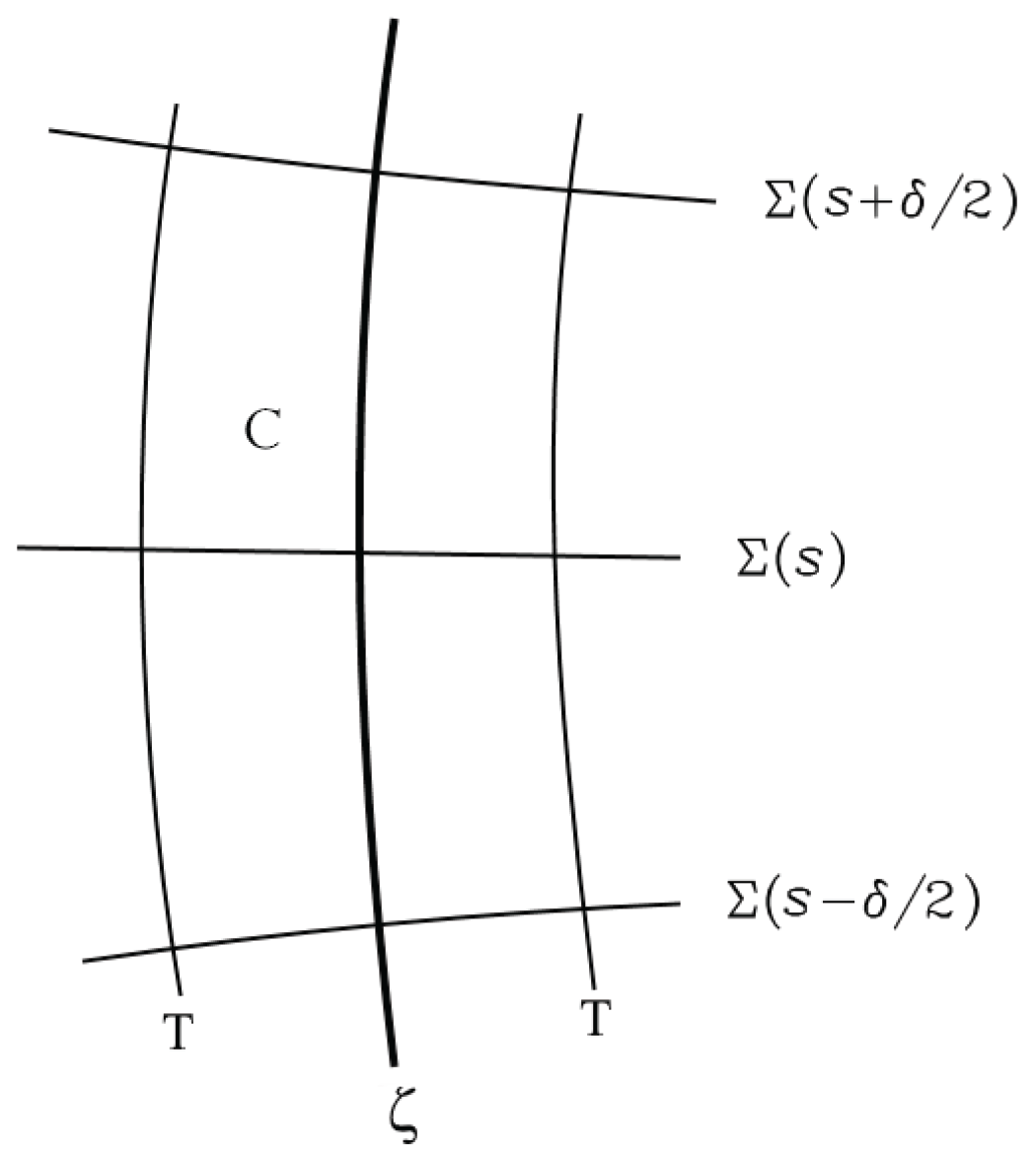Referring to fig.1, both results are derived by integrating ${\nabla }_{\mu }{T}^{\mu \nu }=0$ over a world-cylinder, C, with the ${\partial }_{\tau \tau }{\zeta }^{\nu }$ term obtained by converting part of the volume integral into a surface integral over the $\Sigma$’s via (a relativistic generalization of-) Stoke’s theorem, leaving the remaining part for the ‘force term’, which gives ${\overline{\Gamma }}_{\nu \rho }^{\mu }{\partial }_{\tau }{\zeta }^{\nu }{\partial }_{\tau }{\zeta }^{\rho }$ in the case of gravity. The integral over T represents small radiative corrections to the geodesic/Lorentz-force equation which can be ignored in what follows. A crucial point in that derivation is that the result is insensitive to the form of C so long as the $\Sigma$’s contain the support of the particle’s energy-momentum distribution. This insensitivity would not carry to the r.h.s. of (27) should it be transferred sides, whether or not $g_{\mu \nu }$ is to include the self-field of the particle. Thus attempting to generalize the geodesic equation based on (27) in the hope that it would reproduce fixed-$\lambda$ solutions of (57) is bound to fail. Nonetheless, since the conservation-violating r.h.s. of (27) is a tiny $O\left({\ell }_g^{-2}\right)$, it can consistently be ignored for any reasonable choice of C whenever the individual terms in the geodesic equation are much larger, i.e., at large scales; it is only at small scales that each term becomes comparable to the r.h.s. even for reasonable choices of C. And since in the limit ${\ell }_0\to \infty$ paths become simple geodesics at any scale according to (57), the two length parameters, ${\ell }_0$, ${\ell }_g$ are not independent, constrained by consistency of solutions such as the above, and likely additional ones involving the structure of matter, as hinted to by the fixed-point example in sect.3.1.2.

3.2.1. Application: The Rotation Curve of Disc Galaxies

As a simple application of (55), let us calculate the rotation curve, $v\left(r\right)$, of a scale-invariant mass, M, located at the origin, as it appears to an astronomer of native scale $\lambda =1$. Above, r is the distance to the origin of a test mass orbiting M in circles at velocity v. Since $\Phi$ in (55) is time-independent, the time-dependence of ${\zeta }^i$ can only be through the combination $\Omega \left(\lambda \right)t$ for some function $\Omega$. Looking for a circular motion solution in the $x^1-x^2$ plane,

$${\zeta }^1(\lambda ,t)=r\left(\lambda \right)sin\left(\Omega \left(\lambda \right)t\right),{\zeta }^2(\lambda ,t)=r\left(\lambda \right)cos\left(\Omega \left(\lambda \right)t\right)$$

and equating coefficients of $sin\left(\Omega t\right)$ and $cos\left(\Omega t\right)$ for each component, the system (55) reduces to two, first order ODE’s for $\Omega \left(\lambda \right)$ and $r\left(\lambda \right)$. The equation for $\Omega$ readily integrates to $\Omega =\omega \lambda$ for some integration constant $\omega$, and for r it reads

$$\lambda {\displaystyle \frac{\mathrm{d}r}{\mathrm{d}\lambda }}={\ell }_0^2\left({\lambda }^2{\omega }^{2}r-{\displaystyle \frac{GM}{r^2}}\right)-r$$

(58)

Solutions of (58) with $r\left(1\right)\equiv r_1$ as initial condition, all diverge in magnitude for $\lambda \to \infty$ except for a single value of $\omega$ for which $r\left(\lambda \right)\to 0$ in that limit; for any other ${\omega }^{\prime }\gtrless \omega$, $r\left(\lambda \right)$ rapidly diverges to $\pm \infty$ respectively; the map $r_1\mapsto \omega$ is invertible. We note in advance that, for a mistuned $\omega$ this divergence starts well before the the weak field approximation breaks down due to the $r^{-2}$ term, and neglected relativistic and self-force terms become important, and being so rapid, $\sim e^{{\lambda }^2}$, those would not tame a rogue solution. It follows that there is no need to complicate our hitherto simple analysis in order to conclude that ${\omega }^{\prime }=\omega$ is a necessary conditions for r to correspond to an $A_{\mu }\in \mathcal{S}$.

Solutions of (58) which are well-behaved for $\lambda \to \infty$ admit a relatively simple analytic form. Reinstating c and defining $\overline{\lambda }:=\omega {\ell }_0\lambda /c$ the result is

$$r\left(\overline{\lambda }\right):={\left({\displaystyle \frac{GM{\ell }_0^2}{6c^2}}\right)}^{1/3}{\displaystyle \frac{1}{\overline{\lambda }}}{\left[6\overline{\lambda }-\sqrt{6\pi }{e}^{{\displaystyle \frac{3}{2}}{\overline{\lambda }}^2}\left(\mathrm{erf}\left(\sqrt{3/2}\overline{\lambda }\right)-1\right)\right]}^{1/3},$$

(59)

having the following power law asymptotic forms

$$r\left(\overline{\lambda }\right)\sim {\left({\displaystyle \frac{GM{\ell }_0^2}{c^2}}\right)}^{1/3}\times \left\{\begin{array}{cc}{\overline{\lambda }}^{-2/3}\hfill & \mathrm{for}\overline{\lambda }\gg 1,‘\mathrm{coarsening}\mathrm{regime}’\hfill \\ {\left({\displaystyle \frac{\pi }{6}}\right)}^{1/6}{\overline{\lambda }}^{-1}\hfill & \mathrm{for}\overline{\lambda }\ll 1,‘\mathrm{scaling}\mathrm{regime}’\hfill \end{array}\right.$$

(60)

with the corresponding asymptotic circular velocity, $v=\left(\omega \lambda \right)r$

$$v\left(\overline{\lambda }\right)\sim {\left({\displaystyle \frac{GMc}{{\ell }_0}}\right)}^{1/3}\times \left\{\begin{array}{cc}{\overline{\lambda }}^{1/3}\hfill & \mathrm{for}\overline{\lambda }\gg 1,\hfill \\ {\left({\displaystyle \frac{\pi }{6}}\right)}^{1/6}\hfill & \mathrm{for}\overline{\lambda }\ll 1\hfill \end{array}\right.$$

(61)

With these asymptotic forms the reader can verify that, in the large $\overline{\lambda }$ regime, (56), which in this case takes the form:

$${\displaystyle \frac{v^2}{r}}={\displaystyle \frac{GM}{r^2}}$$

(62)

is indeed satisfied for any $\overline{\lambda }$. This almost certainly generalizes to the following: The paths, ${\zeta }_k(t,\lambda )$, solving (55)(46) for a bound system of scale-independent masses (indexed by k), approach at large $\lambda$ the form

$${\zeta }_k(t,\lambda )\underset{\lambda \gg 1}{\sim }{\lambda }^{-2/3}{\zeta }_k^{\mathrm{N}}\left(\lambda t\right)$$

(63)

where ${\zeta }_k^{\mathrm{N}}$ are the Newtonian paths of such a system; (63) is an exact symmetry of Newtonian gravity. Finally, for a scale-dependent mass in (58), an $r(\lambda ;\omega )$ is obtained by the large-scale regularity condition which is not of the form $r\left(\overline{\lambda }\right)$. This results in a rotation curve $v\left(r_1\right)\equiv \omega \left(r_1\right)r_1$ which is not flat at large $r_1$, and an $r\left(\lambda \right)$ which, depending on the form of $M\left(\lambda \right)$, may not even converge to zero at large $\lambda$.

Moving, next, to a more realistic representation of disc galaxies. For a general gravitational potential, $\Phi$, sourced via (46) by a planar, axially symmetric mass density $T_{00}^{\mathrm{mat}}\left(\rho \right)$—$\rho$ being the radial distance from the galactic axis in the galactic plane—and for a test mass circularly orbiting the symmetry axis in the galactic plane, the counterpart of (58) reads

$$\lambda {\displaystyle \frac{\mathrm{d}r}{\mathrm{d}\lambda }}={\ell }_0^2\left({\omega }^2{\lambda }^{2}r-{\partial }_{\rho }\Phi (r,\lambda )\right)-r$$

(64)

The time-independent mass density, $T_{00}^{\mathrm{mat}}$, is approximated by a (sufficiently dense) collection of concentric line-rings, each composed of a (sufficiently dense) collection of particles evenly spaced along the circumference. Next, recall that in the above warm-up exercise, the solution of (64) for each such particle is well behaved only for one, carefully tuned value of $\omega$. This sensitivity results form instability of the the o.d.e. (64) in the $+\lambda$ direction, inherited from that of $A_{\mu }$, and is not a peculiarity of the Coulomb potential. To find the rotation curve one needs to simultaneously propagate with (64) each ring—or rather a single representative particle from each ring—$r_{r_1}\left(\lambda \right)$, using an initial guess for $\omega \left(r_1\right)$ (where $r_1$ is now a ring index, labeling the ring whose radius at $\lambda =1$ equals $r_1$, viz., $r_{r_1}\left(1\right)=r_1$). Unlike in the previous case, the (mean-field) Newtonian potential of the disc at scale $\lambda$, $\Phi (\rho ,\lambda )$, solution of (40), must be re-computed at each $\lambda$. The rotation curve is obtained as that (unique) guess, $\omega \left(r_1\right)$, for which no ring diverges in the limit $\lambda \to \infty$. In so finding the rotation curve the scale dependence of individual particles comprising the disc needs to be specified. If those are fixed-point particles then their mass is scale-independent by definition. Moreover, as mentioned above, a scale-dependent mass leads to manifest contradictions with observations. In light of this, a scale independent mass is assumed modulo some caveats discussed in sect.3.4. Note the implication of the scale-invariant-mass approximation, applicable to any gravitating system: Although ${\zeta }^i(t,s=0)$ is the desired spacetime path, by construction and the s-translation invarinace of (55), ${\zeta }^i(t,s)$ for any s would also be a permissible path at $s=0$. In other words, (55) with the regularity condition at $s\to \infty$, generates a continuous family of spacetime paths which could be observed at any fixed native scale, $s=0$ in particular.

The algorithm described above for finding the rotation curve, although conceptually straightforward, could be numerically challenging and will be attempted elsewhere. However, much can be inferred from it without actually running the code. Mass tracers lying at the outskirts of a disc galaxy, experience almost the same, $-MG/r$ potential, where M is the galactic mass, independently of $\lambda$. This is clearly so at $\lambda =1$, as higher order multipoles of the disc are negligible far away from the galactic center, but also at larger $\lambda$, as all masses comprising the disc converge towards the center, albeit at different paces. The analytic solution (60) can therefore be used to a good approximation for such traces, implying the following power-law relation between the asymptotic velocity, $v_{\mathrm{f}}$, of a galaxy’s rotation curve and its mass, M,

$$M={\left({\displaystyle \frac{6}{\pi }}\right)}^{1/2}{\displaystyle \frac{{\ell }_0}{Gc}}{v}_{\mathrm{f}}^3$$

(65)

Such an empirical power law, relating M and $v_{\mathrm{f}}$, is known as the Baryonic Tully-Fisher Relation (BTFR), and is the subject of much controversy. There is no concensus regarding the conssistency of observations with a zero intrinsic scatter, nor is there an agreemnet about the value of the slope—3 in our case—when plotting $logM$ vs. $log{v}_{\mathrm{f}}$. Some groups [5] see a slope $\sim 3$ while other [6] insisting it is closer to 4 (both ‘high quality data’ representatives, using primary distance indicaors). While some of the discrepancy in slope estimates can be attributed to selection bias and different methods of estimating the galactic mass, the most important factor is the inclusion of relatively low-mass galaxies in the latter. When restricting the mass to lie above $\sim {10}^{10}{M}_{\odot }$, almost all studies support a slope close to 3. The recent study [7] which includes some new, super heavy galaxies, found a slope $\sim 3.26$ and a $logM/M_{\odot }$-axis intercept of $\sim 3.3$ for the massive part of the graph. Since the optimization method used in finding those two parameters is somewhat arbitrary, imposing a slope of 3 and fitting for the best intercept is not a crime against statistics. By inspection this gives an intercept of $\sim 4.2$, consistent with [5], which by (65) corresponds to ${\ell }_0\sim 4.6\times {10}^{20}$ km.

With an estimate of ${\ell }_0$ at hand, yet another prediction of our model can be put to test, pertaining to the radius at which the rotation curve transitions to its flat part. The form (60) of $r\left(\lambda \right)$ implies that the transition from the scaling to the coarsening regime occurs at $\overline{\lambda }\approx \sqrt{2/3}$. At that scale the radius assumes a value $r_{\mathrm{tr}}\approx {\left(MG{\ell }_0^2/c^2\right)}^{1/3}=v_{\mathrm{f}}{\ell }_0/c$. Using standard units where velocities are given in km/s and distances in kpc, gives $r_{\mathrm{tr}}\approx {\displaystyle \frac{1}{20}}{v}_{\mathrm{f}}$. Now, in galaxies with a well-localized center—a combination of a massive bulge and (exponential) disc—most of the mass is found within a radius $r_{\mathrm{M}}<r_{\mathrm{tr}}$, lying to the right of the Newtonian curve’s maximum. Approximating the potential at $r\ge r_{\mathrm{M}}$ by $-GM/r$, the transition of the rotation curve from scaling to coarsening, with its signature rise from a flat part seen in fig.2, is expected to show at $r_{\mathrm{tr}}$, followed by a convergence to the galaxy-specific Newtonian curve. This is corroborated in all cases—e.g. galaxies NGC2841, NGC3198, NGC2903, NGC6503, UGC02953, UGC05721, UGC08490... in fig.12 of [8]

The above sanity checks indicate that the rotation curve predicted by our model cannot fall too far from that observed, at least for massive galaxies; it is guarantied to coincide with the Newtonian curve near the galactic center, depart from it approximately where observed, eventually flattening at the right value.

However, the above checks do not apply to diffuse, typically gas dominated galaxies, several orders of magnitude lighter. More urgently, a slope$=3$ is difficult to reconcile with [6] which finds a slope$\approx 4$ when such diffuse galaxies are included in the sample. Below we therefore point to two features of the proposed model possibly explaining said discrepancy. First, our model predicts that $v_{\mathrm{f}}$ attributed in [6] to such galaxies would turn out to be a gross overestimation should their rotation curves be significantly extended beyond the handful of data points of the flat portion. To see why, consider an alternative solution strategy for finding a rotation curve (which may also turn out to be computationally superior):

• 1. Start with a guess for the mass distribution of a galaxy at some large enough scale, ${\lambda }_{>}$, such that its rotation curve is fully Newtonian (If our conjecture regarding (63) is true then the flow to even larger $\lambda$ is guaranteed not to diverge for any such initial guess).
• 2. Let this Newtonian curve flow via (64)(46) to $\lambda =1$—no divergence problem in this, stable direction of the flow—comparing the resultant mass distribution at $\lambda =1$ with the observed distribution
• 3. Repeat step 1 with an improved guess based on the results of 2, until an agreement is reached.

By construction the solution curve is Newtonian at ${\lambda }_{>}$, having a $v\sim \sqrt{GM/r}$ tail past the maximum, whose rightmost part ultimately evolves into the flat segment at $\lambda =1$. We can draw two main distinctions between the flows to $\lambda =1$ of massive and diffuse galaxies’ rotation curves. First, since the hypothetical Newtonian curve at $\lambda =1$—that which is based on baryonic matter only—is rising/leveling at the point of the outmost velocity tracer in the diffuse galaxies of [6], we can be certain that this tracer was at the the rising part/maximum of the ${\lambda }_{>}$ curve, rather than on its $v\sim \sqrt{GMr}$ tail as in massive galaxies. This means that, in massive galaxies, the counterpart of the short, flat segment of a diffuse galaxy’s r.c., is rather the short flat segment near its maximum, seen in most such galaxies near the maximum of the hypothetical Newtonian curve. Second, had tracers further away from the center been measured in diffuse galaxies, the true flat part would have been significantly lower relative to this maximum than in massive galaxies. With some work this can be shown via the inhomogeneous flow of $v\equiv \lambda \omega r$ derived from (64)

$$\overline{\lambda }{\partial }_{\overline{\lambda }}v={\overline{\lambda }}^{2}v-{\partial }_{\rho }\Phi (r,\overline{\lambda })\overline{\lambda }$$

(66)

where r is a solution of (64) (re- expressed as a function of $\overline{\lambda }$). The gist of the argument is that, solutions of (66) deep in the coarsening regime, upon flowing to smaller $\overline{\lambda }$, decay approximately as ${\overline{\lambda }}^{1/3}$, whereas in the scaling regime they remain constant (see (61)). In massive galaxies the entire flow from ${\overline{\lambda }}_{>}$ to $\overline{\lambda }=1$ of a tracer originally at the maximum of the r.c. is in the coarsening regime, while in diffuse galaxies it is mostly in a hybrid, coarsening scaling intermediate mode. The velocity of that tracer relative to the true $v_{\mathrm{f}}$ therefore decays more slowly in diffuse galaxies. Note that to make the comparison meaningful a common ${\lambda }_{>}$ must be chosen for both galaxies such that $v\left({\overline{\lambda }}_{>}\right)/v_{\mathrm{f}}$ is equal in both.

The second possible explanation for the slopes discrepancy, which could further contribute to an intrinsic scatter around a straight BTFR, involves a hitherto ignored transparent component of the energy-momentum tensor. As emphasized throughout the paper, the A-field away from a non-uniformly moving particle (almost solving Maxwell’s equations in vacuum) necessarily involves both advanced and retarded radiation. Thus even matter at absolute zero constantly ‘radiates’, with advanced fields compensating for (retarded) radiation loss, thereby facilitating zero-point motion of matter. The A-field at spacetime point $(t,\mathit{x})$ away from neutral matter is therefore rapidly fluctuating, contributed by all matter at the intersection of its worldline with the light-cone of $(t,\mathit{x})$. We shall refer to it as the Zero Point Field (ZPF), a name borrowed from Stochastic Electrodynamics although it does not represent the very same object. Being a radiation field, the ZPF envelopes an isolated body with an electromagnetic energy ‘halo’, decaying as the inverse distance squared—which by itself is not integrable!—merging with other halos at large distance. Such ‘isothermal halos’ served as a basis for a ‘transparent matter’ model in a previous work by the author [2] but in the current context its intensity likely needs to be much smaller to fit observations. Space therefore hosts a non-uniform ZPF peaking where matter is concentrated, in a way which is sensitive to both the type of matter and its density. This sensitivity may result both in an intrinsic scatter of the BTFR, and in a systematic departure from ZPF-free slope=3 at lower mass. Indeed, in heavy galaxies, typically having a dominant massive center, the contribution of the halo to the enclosed mass at $r_{\mathrm{tr}}$ is tiny. Beyond $r_{\mathrm{tr}}$ orbiting masses transition to their scaling regime, minimally influenced by additional increase in the enclosed mass at r. The situation is radically different in light, diffuse galaxies, where the ratio of ${\rho }_{\mathrm{ZPF}}/{\rho }_{\mathrm{baryon}}$ is much higher throughout the galaxy, and much more of the non-integrable tail of the halo contributes to the enclosed mass at the point where velocity tracers transition to their scaling regime. This under estimation of the effective galactic mass, increasing with decreasing baryonic mass, would create an illusion of a BTFR slope greater than 3.

3.2.2. Other Probes of ‘Dark Matter’

Disc galaxies are a fortunate case in which the worldline of a body transitions from scaling to coarsening at a common scale along its entire worldline (albeit different scales for different bodies). They are also the only systems in which the velocity vector can be inferred solely from its projection on the line-of-sight. In pressure supported systems, e.g., globular clusters, elliptical galaxies or galaxy clusters, neither is true. Some segments of a worldline could be deep in their scaling regime while others in the coarsening, rendering the analysis of their collective scale flow more difficult. One solution strategy leverages the fact that, all the worldlines of a bound system are deep in their coarsening regime at sufficiently large scale, where their fixed-$\lambda$ dynamics is well approximated using Newtonian gravity. Starting with such a Newtonian system at sufficiently large ${\lambda }_{>}$, the integration of (55) to small $\lambda$ is in its stable direction, hence not at risk of exploding for any initial choice of Newtonian paths. If the Newtonian system at ${\lambda }_{>}$ is chosen to be virialized, a ‘catalog’ of solutions of pressure supported systems extending to arbitrarily small $\lambda$ can be generated, and compared with line-of-sight velocity projections of actual systems. As remarked above, the transition from coarsening to scaling generally doesn’t take place at a common scale along the worldline of any single member of the system. However, if we assume that there exists a rough transition scale, ${\lambda }_{\mathrm{tr}}$, for the system as a whole in the statistical sense, which is most reasonable in the case of galaxy clusters, then immediate progress can be made. Since in the scaling regime velocities are unaltered, the observed distribution of the line-of-sight velocity projections should remain approximately constant for $\lambda <{\lambda }_{\mathrm{tr}}$, that of a virialized system, viz., Gaussian of dispersion ${\sigma }_v$. On the other hand, at $\lambda >{\lambda }_{\mathrm{tr}}$ a virialized system of total mass M satisfies

$${\sigma }_v\approx \sqrt{GM/r}$$

(67)

where ${\sigma }_v$ is the velocity dispersion, and r is the radius of the system, which is just (62) with ${\sigma }_v\mapsto v$. On dimensional grounds it then follows that ${\sigma }_v$ would be the counterpart of $v_f$ from (65), implying ${\sigma }_v\propto M^{1/3}$ which is in rough agreement with observations. The proportionality constant can’t be exactly pinned using such huristic arguments, but its observed value is on the same order of magnitude as that implied by (65).

Applying our model to gravitational lensing in the study of dark matter requires better understanding of the nature of radiation. This is murky territory even in conventional physics and in next section initial insight is discussed. To be sure, Maxwell’s equations in vacuum are satisfied away from $J_{\mu }$, although only ‘almost so’, as discussed in sect.3. However, treating them as an initial value problem, following a wave-front from emitter to absorber is meaningless for two reasons. First, tiny, $O\left({\ell }_0^{-1}\right)$ local deviations from Maxwell’s equations could become significant when accumulated over distances on the order of ${\ell }_0$. Second, in the proposed model extended particles ‘bump into one another’ and their centers jolt as a result—some are said to emit radiation and other absorb it, and an initial-value-problem formulation is, in general, ill-suited for describing such process. Nonetheless, incoming light—call it a photon or a light-ray—does posses an empirical direction when detected. In flat spacetime this could only be the spatial component of the null vector connecting emission and absorption events, as it is the only non arbitrary direction. A simple generalization to curved spacetime, involving multiple, freely falling observers, selects a path, ${\zeta }^{\mu }$, everywhere satisfying the light-cone condition ${\dot{\zeta }}^2\left(\tau \right)\equiv 0$. Every null geodesic satisfies the light-cone condition, but not the converse. In ordinary GR, the only non arbitrary path connecting emission and absorption events which respects the light-cone condition and locally depends on the metric and its first to derivatives is indeed a null geodesic. In our model, a solution of (57) which is well behaved on all scales, further satisfying the light-cone condition for $\lambda \to \infty$, is an appealing candidate: It becomes a null geodesic at large scales, while the scaling operator alone preserves the light-cone condition.

Furthermore, in GR the deflection angle of a light ray due to gravitational lensing, by a compact gravitating system of mass M, is $\varphi =4GM/\left(c^{2}R\right)$, where R is the impact parameter. When ${\zeta }^{\mu }$ is in its scaling regime, our model’s $\varphi$ remains constant. If the system is likewise in its scaling regime, (67) implies that its virial mass, $M_{\mathrm{vir}}={\sigma }_v^{2}r/G$, scales according to $M_{\mathrm{vir}}\mapsto {\lambda }^{-1}{M}_{\mathrm{vir}}$, as does the impact parameter of ${\zeta }^{\mu }$, $R\mapsto {\lambda }^{-1}R$. The conventional mass estimate based on the virial theorem, of this $\lambda$-dependent family of gravitating systems, would then agree with that which is based on (conventional) gravitational lensing, $M_{\mathrm{lens}}=c^{2}R\varphi /4G$, up to a constant, common to all members—recall that this entire family appears in the ‘catalog’ of $\lambda =1$ systems. Extending this family to large $\lambda$, the two estimates will coincide by construction. Thus if the system and ${\zeta }^i$ transition approximately at a common $\lambda$, this proportionality constant can only be close to 1. This is apparently the case in most observations pertaining to galaxy clusters. Nonetheless, the two methods according to our model need not, in general, produce identical results. The degree to which they disagree depends on the exact scale-flow of ${\zeta }^{\mu }$, which is one of those calculations avoided thus far, involving a path non-uniformly (in scale) transitioning from coarsening to scaling.

A final caveat regarding the application of (57) to imaging, is that it is not clear whether the light-cone condition is automatically satisfied by all paths thus defined or that it should be imposed as an additional constraint. Nor is it even obvious that this condition must be satisfied exactly. In trying to figure this out one should remember that, in general, solutions of (57) that are well behaved on all scales are not solutions of any o.d.e. in $\tau$ for a fixed $\lambda$.

3.3. Quantum Mechanics as a Statistical Description of the Realistic Model

The basic tenets of classical electrodynamics (19), (29) and (30), which must be satisfied at any scale on consistency grounds (up to neglected curvature terms), strongly constrain also statistical properties of ensembles of members in $\mathcal{S}$, and in particular constant-$\lambda$ sections thereof. In a previous paper by the author [1] it was shown that these constraints could give rise to the familiar wave equations of QM, in which the wave function has no ontological significance, merely encoding certain statistical attributes of the ensemble via the various currents which can be constructed from it. It is through this statistical description that ℏ presumably enters physics, and so does ‘spin’ (see below).

This somewhat non-committal language used to describe the relation between QM wave-equations and the basic tenets is for a reason. Most attempts to provide a realist (hidden variables) explanation of QM follow the path of statistical mechanics, starting with a single-system theory, then postulating a ‘reasonable’ ensemble of single-systems—a reasonable measure on the space of single-system solutions—which reproduces QM statistics. Ignoring the fact that no such endeavor has ever come close to fulfillment, it is rarely the case that the measure is ‘natural’ in any objective way, effectively defining the statistical theory/measure (uniformity over the impact parameter in an ensemble representing a scattering experiment being an example of an objectively natural attribute of an ensemble). Even the ergodicity postulate, as its name suggests, is a postulate—external input. When sections of members in $\mathcal{S}$ are the single-systems, the very task of defining a measure on such a space, let alone a natural one, becomes hopeless. The alternative approach adopted in [1] is to derive constraints on any statistical theory of single-systems respecting the basic tenets, showing that QM non-trivially satisfies them. QM then, like any measure on the space of single-system solutions, is postulated rather than derived, and as such enjoys a fundamental status, on equal footing with the single-system theory. Nonetheless, the fact that the QM analysis of a system does not require knowledge of the system’s orbit makes it suspicious from our perspective. And since a quantitative QM description of any system but the simplest ones involves no less sorcery than math, that fundamental status is still pending confirmation (refutation?).

Of course, the basic tenets of classical electrodynamics are respected by all (sections of-) members of $\mathcal{S}$, not only those associated Dirac’s and Schrödinger’s equations. The focus in [1] on ‘low energy phenomena’ is only due to the fact that certain simplifying assumptions involving the self-force can be justified in this case. In fact, the current realization of the basic tenets, involving fields only instead of interacting particles, is much closer in nature to the QFT statistical approach than to Schrödinger’s.

3.3.1. The Origin of Quantum Non-Locality

“Multiscale locality", built into the proposed formalism, readily dispels one of QM’s greatest mysteries—its apparent non-local nature. In a nutshell: Any two particles, however far apart at our native scale, are literally in contact at sufficiently large scale.

Two classic example where this simple observation invalidates conventional objections to local-realist interpretations of QM are the following. The first is a particle’s ability to ‘remotely sense’ the status of the slit through which it does not pass, or the status of the arm of an interferometer not traversed by it (which could be a meter away). To explain both, one only needs to realize that for a giant physicist, a fixed-point particle is scattered from a target not any larger than the particle itself, to which he would attribute some prosaic form-factor; At large enough $\lambda$ the particle literally passes though both arms of the interferometer (and through none!). This global knowledge is necessarily manifested in the paths chosen by it at small $\lambda$. Of course, at even larger $\lambda$ the particle might also pass through two remote towns etc., so one must assume that the cumulative statistical signature of those infinitely larger scales is negligible. A crucial point to note, though, is that the basic tenets, which imply local energy-momentum conservation at laboratory scales, are satisfied at each $\lambda$ separately. For this large-$\lambda$ effect to manifest at $\lambda =1$, local energy-momentum conservation alone must not be enough to determine the particle’s path, which is always the case in experiment manifesting this type of non-locality. Inside the crystal serving as mirror/beam-splitter in, e.g., a neutron interferometer, the neutron’s classical path (=paths of bulk-motion derived from energy-momentum conservation) is chaotic. Recalling that, what is referred to as a neutron—its electric neutrality notwithstanding—only marks the center of an extended particle, and that the very decomposition of the A-field into particles is an approximation, even the most feeble influence of the A-field awakened by the neutron’s scattering, traveling through the other arm of the interferometer, could get amplified to a macroscopic effect. This also provides an alternative, fixed-scale explanation for said ‘remote sensing’. In the double-slit experiment such amplification is facilitated by the huge distance of the screen from the slits compared with their mutual distance.

The second kind of non-locality is demonstrated in Bell’s inequality violations. As with the first kind, the conflict with one’s classical intuition can be explained both at a fixed scale, or as a scale-flow effect. Starting with the former, and ever so slightly dumbing down his argument, Bell assumes that physical systems are small machines, with a definite state at any given time, propagating (deterministically or stochastically) according to definite rules. This generalizes classical mechanics, where the state is identified with a point in phase-space and the evolution rule with the Hamiltonian flow. However, even the worldlines of particles in our model, represented by sections of members in $\mathcal{S}$, are not solutions of any (local) differential equation in time. Considering also the finite width of those worldlines, whose space-like slices Bell would regard as possibly encoding their ‘internal state’, it is clear that his modeling of a system is incompatible with our model; particles are not machines, let alone particle physicists. Spacetime ‘trees’ involved in Bell’s experiments—a trunk representing the two interacting particles, branching into two, single particle worldlines—must therefore be viewed as a single whole, with Bell’s inequality being inapplicable to the statistics derived from ‘forests’ of such trees.4 This spacetime-tree view gives rise to a scale-flow argument explaining Bell’s inequality violations: The two branches of the tree shrink in length when moving to larger scale, eventually merging with the trunk and with one another. Thus the two detectors at the endpoints of the branches cannot be assumed to operate independently, as postulated by Bell.

3.3.2. Fractional Spin

Fractional spin is regarded as one of the hallmarks of quantum physics, having no classical analog, but according to [1], much like ℏ, it is yet another parameter—discrete rather than continuous—entering the statistical description of an ensemble. At the end-of-the-day, the output of this statistical description is a mundane statement in ${\mathbb{R}}^3$, e.g., the scattering cross-section in a Stern-Gerlach experiment, which can be rotated with $O\left(3\right)$. Neither Bell’s- nor the Kochen-Specker theorems are therefore relevant in our case as the spin is not an attribute of a particle. For this reason the spin-0 particle from sect.3.1.2 is a legitimate candidate for a fractional-spin particles, such as the proton, for its ‘spin measurement/polarization’ along some axis is by definition a dynamical happening, in which its extended world-current bends and twists, expands and contracts in a way compatible with- but not dictated by the basic tenets. As stressed above, there is no natural measure on the space of such objects, and the appearance of two strips on Stern$\&$Gerlach’s plate rather than one, or three etc. need not have raised their eyebrows. Nonetheless, the proposed model does support spinning solutions, viz. $\mathit{J}\not\equiv 0$ in the rest frame of the particle, and there is a case to be made that those are more likely candidates for particles normally attributed with a spin, integer or fractional.

3.3.3. Photons and Neutrinos (or Illusion Thereof?)

Einstein invented the ‘photon’ in order to explain the apparent violation of energy conservation occurring when an electron is jolted at a constant energy from an illuminated plate even when the plate is placed far enough from the source, such that the time-integrated Poynting flux across it becomes smaller than that of the jolted electron. It is entirely possible that Einstein’s explanation can be realized in the proposed formalism, although the rest-frame analysis of a fixed-point particle from sect.3.1.2 must obviously be modified for massless (neutral) particles which might further require extending $A_{\mu }$ and $Z^{\mu }$ to include distributions. Maxwell’s equations would then act as the photonic counterpart of a massive-particle’s QM wave equation, describing the statistical aspects of ensembles of photons. Indeed, since in a ‘lab’ of dimension $\ll {\ell }_0$ individual photons (almost) satisfy the basic tenets of classical electrodynamics (and (31)) for a chargeless current (i.e., $\int {\mathrm{d}}^3{J}_0=0$), the construction from [1] would result in Maxwell’s equations, with the associated ${\Theta }_{\mu \nu }$ being the ensemble energy-momentum tensor. However, since the A-field (almost) satisfies Maxwell’s equations regardless of it being a building block of photons, it is highly unlikely that photons exhaust all radiation-related phenomena. For example, is there any reason to think that a radio antenna transmits its signal via radio photons, rather than radio (A-) waves? This suggests an alternative explanation for photon-related phenomena, which does not require actual, massless particles. Its gist is that, underlying the seeming puzzle motivating Einstein’s invention of the photon, is the assumption that an electron’s radiation field is entirely retarded which, as emphasized throughout the paper, cannot be the case for the A-field. Advanced radiation converging on the electron could supply the energy necessary to jolt it, further facilitating violation of Bell’s inequality in entangled ‘photons’ experiments. This proposal, first appearing in [1] and further developed in [2], was, at the time, the only conceivable realist explanation of photon related phenomena. In the proposed model, apparently capable of representing ‘light corpuscles’, it may very well be the wrong explanation. Photons would then be just ephemeral massless particles created in certain structural transitions of matter, then disappearing when detected. Note that these two processes are entirely mundane, merely representing a relatively rapid changes in $A_{\mu }$ and $Z^{\mu }$ at the endpoints of a photon’s (extended) worldline. Such unavoidable transient regions might result in an ever-so-slight smoothing of said distributions, which are otherwise excluded from $\mathcal{S}$.

“God is subtle but not malicious" was Einstein’s response to claims that further repetitions of the Michelson-Morley experiment did show a tiny directional dependence of the speed of light. This attitude is adopted vis-a-vis the neutrino’s mass problem. All direct measurements based on time-of-flight are consistent with the neutrino being massless; the case for a massive neutrino relies entirely on indirect measurements and a speculative extension of the Standard Model. Neutrinos would then be quite similar to photons, only probably spinning ($\mathit{J}\ne 0$), whose creation and annihilation involve structural transitions at the subatomic scale. However, as with photons, and even more so due to their elusiveness, neutrinos might not be the full story, or even the real one. The classical model of photons cited above assumes that only $A_{\mu }$ contributes to the radiative $T_{\mu \nu }$ which is therefore identified with ${\Theta }_{\mu \nu }$. In the proposed model $T_{\mu \nu }$ consists also of

$$P_{\mu \nu }={\displaystyle \frac{1}{4\pi G{\ell }_g^2}}\left({\partial }_{\mu }{Z}_{\nu }+{\partial }_{\nu }{Z}_{\mu }\right)$$

with $Z_{\nu }$ satisfying (31) in the flat spacetime approximation, rewritten here

$${\square }^2{Z}_{\nu }+{\partial }_{\nu }{\partial }^{\mu }{Z}_{\mu }=4\pi G{\ell }_g^2{F}_{\nu \mu }{J}^{\mu }$$

This is a massless wave equation, not too dissimilar to Maxwell’s, therefore expected to participate in radiative, energy-momentum transfer. However, two features set it apart. First, the two terms on the l.h.s. of (31) enter with the ‘wrong’ relative sign, spoiling gauge covariance. As a result an extra longitudinal mode exists, i.e., $Z^{\mu }={ϵ}^{\mu }f\left(k_{\nu }{x}^{\nu }\right)$ with ${ϵ}^{\mu }\propto k^{\mu }$ (which in the Maxwell case is a pure gauge), on top of the two transverse modes, ${ϵ}^{\mu }{k}_{\mu }=0$. Second, unlike ${\Theta }_{\mu \nu }$, $P_{\mu \nu }$ is only linear in $Z^{\mu }$, an impossibility for a Noether current. Combined, these two features imply that only the longitudinal mode can radiate energy-momentum and only during transient, ‘structural changes’ to the radiating system. Indeed, consider the integral of the energy flux of $P_{\mu \nu }$ over $T=S^2\times \mathbb{R}$ in fig.1.

$$\int \mathrm{d}t{\int }_{S^2}{P}_{0i}\mathrm{d}{\sigma }^i\equiv \int \mathrm{d}t{\int }_{S^2}\mathit{P}·\mathrm{d}\sigma$$

(68)

where $S^2$ is a large sphere centered at the location of the system and $\mathrm{d}\sigma$ is an outward pointing vector orthogonal to $S^2$ of length $\mathrm{d}\sigma$. Clearly, only the longitudinal mode, whose energy flux at each point on $S^2$ is $\propto k_0\mathit{k}\Vert \mathrm{d}\sigma$, contributes to the integral (68). Moreover, we saw in sect.3.1.1 that outside of fixed-points, $z^{\mu }$ must be negligible. So long as the system qualifies as a fixed-point, as during bulk acceleration, no net flux is being generated by it, and it is therefore only while transitioning between distinct fixed-points that $\mathit{P}$ is involved in energy changes (and even then only its ${\partial }_r{Z}_0$ piece—r being the radial coordinate when $S^2$ and the system are co-centered at the origin—as the ${\partial }_t{Z}_r$ piece integrates to zero over time). The Z-field is therefore a natural candidate for a ‘classical neutrino field’, whose relation to neutrino phenomena parallels that of the A-field to photon phenomena. As with photons, it is a particle’s advanced Z-field converging on it which supplies the energy-momentum necessary to jolt it, conventionally interpreted as the result of being struck by a neutrino. Similarly, hitherto ignored retarded Z-field is allegedly generated in structural changes of a system, e.g., when nuclei undergo $\beta$-decay. As pointed out in sect.3.3.2 above, the (fractional) spin-$\frac{1}{2}$ attributed to the neutrino, as is the spin-1 of the photon, only labels the statistical description of phenomena involving such jolting of charged particles.

3.4. Cosmology

Cosmological models are stories physicists entertain themselves with; they can’t truly know what happened billions of years ago, billions of light-years away, based on the meager data collected by telescopes. Moreover, in the context of the proposed model, the very ambition implied by the term “cosmology" is at odds with the humility demanded of a physicist, whose entire observable universe could be another physicist’s microwave oven. On the other hand, astronomical observations associated with cosmology, also serve as a laboratory for testing ‘terrestrial’ physical theories, e.g., atomic-, nuclear-, quantum-physics, and this would be particularly true in our case, where the large and the small are so intimately interdependent. When the most compelling cosmological story we can devise requires contrived adjustments to terrestrial-physics theories, confidence in those, including GR, should be shaken.

Reluctantly, then, a cosmological model is outlined below. Its purpose at this stage is not to challenge $\Lambda$CDM in the usual arena of precision measurements, but to demonstrate that it plausibly avoids the aforementioned flaw, while also addressing the infamous dipole problem [9], which undermines the very foundations of any Friedmann cosmological model.

3.4.1. A Newtonian Cosmological Model

As a warm-up exercise, we wish to solve the system (55)(46) for a spherical, uniform, expanding cloud of massive particles originating from the scaling center (without loss of generality), described by

$${\zeta }_n^i(t,\lambda )=r_n^{i}a(t,\lambda )$$

(69)

where n is a particle index, $r_n^i$ a constant vector, and $\left\{{\mathit{r}}_n\right\}$ are uniformly distributed when averaged over a large enough volume. It is easily verified that the same homogeneous expanding cloud would appear to an observer fixed to any particle, not just the one at the origin. The mass density of the cloud depends on a via $\rho \propto a^{-3}$, retaining its uniformity at any time and scale. The gravitational force acting on particle n is given by $f_n^i=-{\displaystyle \frac{4\pi G}{3}}\rho (t,\lambda )r_n^{i}a$ (the uniform vacuum energy is ignored as its contribution to the force can only vanish by symmetry) and (55) gives a single, particle-independent equation for a

$$\lambda {\partial }_{\lambda }a={\ell }_0^2\left(-\ddot{a}-{\displaystyle \frac{4\pi G}{3}}\rho a\right)-a+t\dot{a}$$

(70)

with $\dot{a}\equiv {\partial }_{t}a$ etc.

Two types of solutions for (70) that are well behaved on all scales should be distinguished: Bounded and unbounded. In the former $a(t,\lambda )$ becomes arbitrarily small $\forall t$ at sufficiently large $\lambda$, and is identically zero at $t=0$ and a $\lambda$-dependent ‘big-crunch’ time, $t_{\mathrm{f}}$. By our previous remarks, at large scale the coarsening terms—those multiplied by ${\ell }_0^2$ on the r.h.s. of (70)—dominate the flow and must almost cancel each other or else a would rapidly blow up with increasing $\lambda$. The resulting necessary condition for a regular $a(t,\lambda )$ on all scales is a $\lambda$-dependent o.d.e. in time, which is simply the time derivative of the (first) Friedmann equation for non-relativistic matter

$${\dot{a}}^2+k\left(\lambda \right)={\displaystyle \frac{8\pi G}{3}}\rho a^2,\rho \propto a^{-3}$$

(71)

Note that k disappears as a result of this derivative, meaning that it resurfaces as a second integration constant of any magnitude—not just $k\in \left\{-1,0,1\right\}$. During the flow of $a(t,\lambda )$ to large $\lambda$, k increases without bound, and as a consequence ${max}_{t}a(t,\lambda )$ shrinks to zero for $\lambda \to \infty$. In other words, as $\lambda$ grows the initial explosion becomes increasingly less energetic—as evaluated at some fixed, small $t>0$ to avoid a trivial infinity. Given a solution of (71) at large enough $\lambda$ one can then integrate (70) in its stable, small $\lambda$ direction, where the scaling piece becomes important, but due to the $a(t=0,\lambda )=a(t_{\mathrm{f}},\lambda )\equiv 0$ constraint, some parts of a solution remain deep in their coarsening regime. The same is true for unbounded solutions, but in this case there is no $a(t,{\lambda }_{\mathrm{large}})$ to start from. This renders the task of finding solutions more difficult, which is addressed below, in the appropriate, relativistic context.

The Newtonian-cloud model, while mostly pedagogical, nonetheless captures a way—perhaps the only way—cosmology is to be viewed within the proposed framework: It does not pertain to the Universe but rather to a universe—an expanding cloud as perceived by a dwarf amidst it. A relative giant, slicing the cloud’s orbit at a much larger $\lambda$, might classify the corresponding section as the expanding phase of a Cepheid, or that of a red-giant, supernova, etc. An even mightier giant may see a decaying radioactive atom. Of course, matter must disappear in such flow to larger and larger scales—a phenomenon already encountered in the linear case which is further discussed below. A simplifying aspect of the proposed formalism already exploited in the case of galaxies is that dynamical aspects of small-$\lambda$ sections can be analyzed independently of those large-$\lambda$ sections. However, one must not lose sight of the orbit view. For example, a possible singularity at $t=0$ should not be interpreted as “the beginning of time" or what have you, but merely the breakdown of the dwarf’s phenomenological description of his section.

Suppose for concreteness that a giant’s section is an expanding star. The dwarf’s entire observable universe would in this case correspond to a small sphere, non-concentrically cut from the star. The hot thermal radiation inside that sphere at ${\lambda }_{\mathrm{giant}}$, after flowing with (16) to ${\lambda }_{\mathrm{dwarf}}$, would be much cooler, much less intense, and much more uniform, except for a small dipole term pointing towards the star’s center, approximaely proportional to the star’s temperature gradient at the sphere, multiplied by the sphere’s diameter. Similarly for the matter distribution at ${\lambda }_{\mathrm{dwarf}}$, only in this case the distribution of accumulated matter created during the flow is expected to decrease in uniformity if new matter is created close to existing matter. Thus the distribution of matter at ${\lambda }_{\mathrm{dwarf}}$ is proportional to the density at ${\lambda }_{\mathrm{giant}}$ only when smoothed over a large enough ball, whose radius coresponds to a distance at ${\lambda }_{\mathrm{giant}}$ much larger than the scale of density fluctuations. This would elegantly explain the so-called dipole problem [9]—the near perfect alignment of the CMB dipole with the dipole deduced from matter distribution, but with over $5\sigma$ discrepancy in magnitude; Indeed, the density and temperature inside a star typically have co-linear, inward-pointing gradients, but which differ in magnitude. Note that a uniform cloud ansatz is inconsistent with the existence of such a dipole discrepancy and should therefore be taken as a convenient approximation only, rendering the entire program of precision cosmology futile. The horizon problem of pre inflation cosmology is also trivially explained away by such orbit view of the CMB. Similarly, the tiny but well-resolved deviations from an isotropic CMB (after correcting for the dipole term) might be due to acoustic waves inside the star.

Returning to the scale-flow of $\phi \equiv \left(A_{\mu },g_{\mu \nu }\right)$ interpolating between ‘a universe’ and a star, and recalling that $\phi (x,s)$ stands for a spacetime phenomenon as represented by a physicist of native scale s, a natural question to ask is: What would this physicist’s lab notes be? A primary anchor facilitating this sort of note-sharing among physicists of different scales is a fixed-point particle, setting both length and mass standard gauges. We can only speculate at this stage what those are, but the fact that the mass of macroscopic matter must be approximately scale invariant—or else rotation curves would not flatten asymptotically—makes atomic nuclei, where most of the mass is concentrated, primary candidates. Note that in the proposed formalism the elementarity of a particle is an ill-defined concept, and the entire program of reductionism must be abandoned. For if zooming into a particle were to ‘reveal its structure’, even a fixed-point would comprise infinitely many copies of itself as part of its attraction basin.

If nuclei approximately retain their size under scale-flow to large $\lambda$, while macroscopic molecular matter shrinks, a natural question to ask is: What aspects of spacetime physics (at a fixed-scale section) have changed? Instinctively, one would attribute the change to a RG flow in parameter space of spacetime theories, e.g., the Yukawa couplings of the Standard Model of particle physics, primarily that of the electron. However, this explanation runs counter to the view advocated in this paper, that (spacetime) sections should always be viewed in the context of their (scale) orbit; If the proposed model is valid, then the whole of spacetime physics is, at best, a useful approximation with a limited scope. Moreover, an RG flow in parameter space cannot fully capture the complexity involved in such a flow, where, e.g., matter could annihilate in scale (subject to charge conservation); ‘electrons’ inside matter, which in our model simply designate the A-field in between nuclei—the same A-field peaking at the location of nuclei—‘merging’ with those nuclei (electron capture?); atomic lattices, whose size is governed by the electronic Bohr radius $\sim m_{\mathrm{e}}^{-1}$, might initially scale, but ultimately change structure. At sufficiently large $\lambda$ an entire star or even a galaxy would condense into a fixed-point—perhaps a mundane proton, or some more exotic black-hole-like fixed-point which cannot involve a singularity by definition. Finally, we note that, by definition, the self-representation of that scaled physicist slicing $\phi (x,s)$ at his native scale s, is isomorphic to ours, viz., he reports being made of the same organic molecules as we are made of, which are generically different from those he observes, e.g., in the intergalactic medium. So either actual physicists (as opposed to hypothetical ones, serving as instruments to explain the mathematical flow of $\phi$) do not exist in a continuum of native scales, only at those (infinitely many) scales at which hydrogen atoms come in one and the same size; or else they do, in which case we, human astronomers, should start looking around us for odd-looking spectra, which could easily be mistaken for Doppler/gravitational shifts.

3.4.2. Relativistic Cosmology

In order to generalize the Newtonian-cloud universe to relativistic velocities, while retaining the properties of no privileged location and statistical homogeneity, it is convenient to transfer the expansion from the paths of the particles to a maximally symmetric metric—a procedure facilitated by the general covariance of the proposed formalism. Formally, this corresponds to an ‘infinite Newtonian cloud’ which is a good approximation whenever the size of the cloud and the distance of the observer from its edge are both much greater than ${\ell }_0$ and ${\ell }_g$. Consider first a spatially flat ($k=0$ in the FLRW metric), maximally symmetric space, with metric

$$g_{tt}=-b^2\left(\lambda \right),g_{ij}={\eta }_{ij}{a}^2(t,\lambda ),g_{it}=0$$

(72)

for which the only non-vanishing Christoffel symbols are

$${\Gamma }_{ij}^t={\displaystyle \frac{a{\partial }_{t}a}{b^2}}{\delta }_{ij},{\Gamma }_{tj}^i\equiv {\Gamma }_{jt}^i{\displaystyle \frac{{\partial }_{t}a}{a}}{\delta }_{\phantom{1}j}^i$$

(73)

The gravitational part, ${\tilde{z}}^{\mu }$, of the scaling field, appropriate for the description of a universe which is electrically neutral on large enough scales, i.e., $〈J_{\mu }〉\approx 0$, is given by solutions of (32) which, for the metric (72), reads

$${\nabla }^{\mu }{\nabla }_{\mu }{\tilde{z}}_{\nu }+{\nabla }^{\mu }{\nabla }_{\nu }{\tilde{z}}_{\mu }=\left\{\begin{array}{cc}-6\left(\lambda {\partial }_{\lambda }a/a\right)\left({\partial }_{t}a/a\right)\hfill & \mathrm{for}\nu =0\hfill \\ 0\hfill & \mathrm{for}\nu =1,2,3\hfill \end{array}\right.$$

(74)

However, the generally covariant boundary condition (33) “far away from matter" is not applicable here. Instead, ${\nabla }_i{\tilde{z}}_j+{\nabla }_j{\tilde{z}}_i$ is required to be compatible with the (maximal) symmetry of space—its Lie derivative along any Killing field of space must vanish.

Equation (74) is tricky; we need ${\tilde{z}}^{\mu }$ to calculate the scale flow (23) of the metric, yet ${\partial }_{\lambda }a$ appears in the that equation for ${\tilde{z}}^{\mu }$! The most general cosmological model will therefore not be attempted here, but progress can still be made. The general form of ${\tilde{z}}^{\mu }$ consistent with the metric (72) is

$${\tilde{z}}^t=\varphi (t,\lambda ),{\tilde{z}}^i=x^i\psi (t,\lambda )\Rightarrow {\tilde{z}}_t=-b^2\varphi ,{\tilde{z}}_i=a^2{x}_i\psi$$

(75)

for which the $\nu =0$ and $\nu =i$ components of (74) respectively become

$$2\ddot{\varphi }+6{\displaystyle \frac{\dot{a}}{a}}\dot{\varphi }+3\dot{\psi }-6{\displaystyle \frac{\dot{a}}{a}}\left(\psi +{\displaystyle \frac{\dot{a}}{a}}\varphi \right)=-6{\displaystyle \frac{\lambda {\partial }_{\lambda }a}{a}}{\displaystyle \frac{\dot{a}}{a}}$$

(76)

$$\ddot{\psi }+5{\displaystyle \frac{\dot{a}}{a}}\dot{\psi }=0$$

(77)

For an expanding universe, i.e., $H\equiv \dot{a}/a>0$, equation (77) describes the dumped, otherwise free motion of $\psi \left(t\right)$, stabilizing at $\psi =1$ (without loss of generality) for $t\to \infty$ and H bounded from below. For a general $\psi$, (76) becomes analytically intractable. Assuming therefore $\psi \equiv 1$, it is readily verifies that for a of the form

$$a(t,\lambda )=a_{\sigma }\left(\lambda t\right)\Rightarrow \lambda {\partial }_{\lambda }a=t{\partial }_{t}a$$

(78)

$\varphi =t$ is a solution, hence

$${\tilde{z}}^t=t,{\tilde{z}}^i=x^i\Rightarrow {\tilde{z}}_t=-b^{2}t,{\tilde{z}}_i=a^2{x}_i$$

(79)

No generalization exists for a $k\ne 0$ FLRW metric. A formal proof will be provided elsewhere, but for $k=1$ the reader can easily be convinced by (unsuccessfully) trying to visualize such a field on a sphere. The flatness problem of pre-inflation cosmology is thus solved.

Calculating the metric-flow (23) for the above, maximally symmetric metric and associated scaling field is somewhat more subtle than the transition from EFE to cosmology. The energy-momentum tensor on its r.h.s. of EFE is a phenomenological device, equally valid whether applied to the hot plasma inside a star or to the ‘cosmic fluid’. In contrast, ${\Theta }_{\mu \nu }$ and the scaling field from which $P_{\mu \nu }$ is derived, both enter (23) as fundamental quantities, on equal footing with $g_{\mu \nu }$. To make progress, this fundamental status must be relaxed, and $T_{\mu \nu }:={\Theta }_{\mu \nu }+P_{\mu \nu }$ is to be seen as the phenomenological $T_{\mu \nu }$ in standard cosmology—a step that can be made fairly rigorous. Specifically, for $Z^{\mu }=z^{\mu }+{\tilde{z}}^{\mu }$, with $z^{\mu }$ the scaling field inside matter, we shall use a maximally symmetric ansatz

$$T_{00}(t,\lambda )=b^2\left(\rho (t,\lambda )-{\displaystyle \frac{1}{2\pi G{\ell }_g^2}}\right),T_{ij}(t,\lambda )=a^2\left(p(t,\lambda )+{\displaystyle \frac{1}{2\pi G{\ell }_g^2}}\left(1+{\displaystyle \frac{\dot{a}}{a}}t\right)\right){\delta }_{ij}$$

(80)

with $\rho$ and p incorporating ${\Theta }_{\mu \nu }$ and $p_{\mu \nu }$, while the remaining terms are entirely due to ${\tilde{z}}^{\mu }$. Plugging (80) and (72) into the metric flow (23), results in space-space and time-time components given, respectively, by

$$2a\lambda {\partial }_{\lambda }a={\ell }_g^2\left(-{\displaystyle \frac{2a\ddot{a}}{b^2}}-{\displaystyle \frac{{\dot{a}}^2}{b^2}}+4a^2\pi Gp\right)+2a^2+2a\dot{a}t$$

(81)

$$2b\lambda {\partial }_{\lambda }b={\ell }_g^2\left(3{\displaystyle \frac{{\dot{a}}^2}{a^2}}+4\pi G{b}^2\rho \right)-2b^2$$

(82)

Another equation which can be extracted from those two, or directly from energy-momentum (non-)conservation (27) is

$${\partial }_{t}p{a}^3-{\partial }_t\left(a^3(\rho +p)\right)=-{\displaystyle \frac{3}{2\pi G{\ell }_g^2}}a\dot{a}\left(\lambda {\partial }_{\lambda }a-\dot{a}t\right)$$

(83)

Only two of the above equations are independent due to the Bianchi identity. 5

The gravitational scaling field (79) is predicated on the special form, $a_{\sigma }$ (78), of a. Further recalling that paths solving (57) can be deduced by analytically continuing solutions $g_{\mu \nu }\left(G\right)$, $G\mapsto -2G$, and solving (57) in the resultant metric, we might as well solve the above equations directly for $G\mapsto -2G$. Combined, (82) becomes

$${\lambda }^2{\displaystyle \frac{{a_{\sigma }^{\prime }}^2}{a_{\sigma }^2}}-{\displaystyle \frac{8\pi G{b}^2}{3}}\rho -{\displaystyle \frac{2}{3{\ell }_g^2}}\left(b^2+b\lambda {\partial }_{\lambda }b\right)=0$$

(85)

where $a_{\sigma }^{\prime }$ is the (ordinary) derivative of $a_{\sigma }$ with respect to its argument. At $\lambda =1$ and for $b(\lambda =1)=1$, (85) is the first Friedman equation with a positive cosmological constant. Moreover, for $a\mapsto a_{\sigma }$ in (83), the r.h.s. vanishes and energy conservation is recovered.

As in standard cosmology, solutions of the Friedman equation require additional physical input regarding the nature of the energy-momentum tensor, e.g., an equation of state relating p and $\rho$. In the proposed model, both $\rho$ and p represent some large-volume average of ${\Theta }_{\mu \nu }+P_{\mu \nu }$ removed of $P_{\mu \nu }$’s trivial cosmological constant component. The contribution from inside matter (where $J_0\not\equiv 0$), denoted ${\rho }_{\mathrm{m}}$, can be assumed to be that of non-relativistic (“cold") matter, i.e., $p_{\mathrm{m}}\approx 0$. Outside matter the A-field is nearly a vacuum solution of Maxwell’s equations with an associated traceless ${\Theta }_{\mu \nu }$ contributing ${\rho }_{\mathrm{r}}$ and $p_{\mathrm{r}}=\frac{1}{3}{\rho }_{\mathrm{r}}$ to the total $\rho$ and p. The scaling field, $Z^{\mu }$, outside matter, which is responsible for the cosmological constant, might have an additional, radiative contribution to $P_{\mu \nu }$ which is neglected due to $P_{\mu \nu }$ being oscillatory and linear in $Z^{\mu }$—the cosmological constant being the sole survivor of a volume average. If we proceed as usual, identifying ${\rho }_{\mathrm{r}}$ with the energy of retarded radiation emitted by matter, observations would then imply ${\rho }_{\mathrm{r}}\ll {\rho }_{\mathrm{m}}$ in the current epoch. However, ${\rho }_{\mathrm{r}}$ incorporates also the ZPF which could outweigh ${\rho }_{\mathrm{m}}$. The contribution of the ZPF, being an ‘extension’ of matter outside the support of its $J_{\mu }$, although having a distinct $p\left(\rho \right)$ dependence, is not an independent component. Properly modeling the combined matter-ZPF fluid, e.g. as interacting fluids, or using some exotic equation-of-state, will be attempted elsewhere. Nonetheless, unlike contrived cold dark matter, a transparent component of the energy-momentum tensor is an inevitability in the proposed model, as is a positive cosmological constant.

With a solution at $\lambda =1$ for $a_{\sigma }\left(t\right)\equiv a\left(t\right)$, $\rho (t,\lambda =1)$ and $p(t,\lambda =1)$, a unique extension of $\rho$ and p to $\lambda \ne 1$ follows from (85) and (83), namely

$$\rho (t,\lambda )={\displaystyle \frac{3}{8\pi G}}\left({\lambda }^2{\displaystyle \frac{{a_{\sigma }^{\prime }}^2\left(\lambda t\right)}{a_{\sigma }^2\left(\lambda t\right)}}-{\displaystyle \frac{2}{3{\ell }_g^2}}\left(b^2+b\lambda {\partial }_{\lambda }b\right)\right)$$

(86)

with $p(t,\lambda )$ obtained by solving (83) at a fixed $\lambda$ with $a_{\sigma }$ and the above $\rho$. We mention this extension, despite only the $\lambda =1$ quantities being of empirical interest to us, because a solution for $a_{\sigma }$ is valid only if it results in $\rho$ and p which are non negative for any $\lambda$. This mandates $b\left(\lambda \right)=\lambda$, hence a cosmological constant term $-4{\lambda }^2/3{\ell }_g^2$, and

$$\rho (t,\lambda )={\lambda }^{-2}{\rho }_{\sigma }\left(\lambda t\right),p(t,\lambda )={\lambda }^{-2}{p}_{\sigma }\left(\lambda t\right)$$

(87)

where ${\rho }_{\sigma }(·)=\rho (·,\lambda =1)$ and $p_{\sigma }(·)=p(·,\lambda =1)$. The ${\lambda }^{-2}$ multiplying $\rho$ above, merely compensates for the $g_{tt}=-{\lambda }^2$ in (72). Namely, the energy density measured by a physicist of native scale $\lambda$ is $g_{tt}\rho ={\rho }_{\sigma }$. For the pressure, the proper scale factor of a scaled physicist is $a_{\mathrm{pr}}={\lambda }^{-1}{a}_{\sigma }$—see point (c) in footnote 5. Thus $a^{2}p=a_{\sigma }^2{\lambda }^{-2}{p}_{\sigma }=a_{\mathrm{pr}}^2{p}_{\sigma }$.

Having determined the form of the cosmological constant at $\lambda =1$, an estimate of ${\ell }_g$ can be obtained. Since the Friedman equation (85) is satisfied (also) at $\lambda =1$, reasonably assuming that $\rho {|}_{t=t_0,\lambda =1}$ is on the order of the current baryonic density based on direct ‘count’, ${\rho }_b\approx 3\times {10}^{-19}$kg/${\mathrm{km}}^3$, most likely a lower bound, we get

$${\ell }_g\gtrsim 2c{\left({\displaystyle \frac{2}{3H_0^2-8\pi G{\rho }_b}}\right)}^{1/2}=3\times {10}^{23}\mathrm{km},H_0:={\displaystyle \frac{\dot{a}}{a}}{|}_{a=a_0=1}=70\mathrm{km}/\sec /\mathrm{Mpc}$$

(88)

(Note that $a_0=1$ is assumed, which is a standard practice in cosmology, equivalent to ‘absorbing’ $a_0$ into the definition of the standard length gauge).

Deducing astronomical observations from a solution, $a_{\sigma }\left(t\right)$ ($\lambda =1$) entails extra steps, which must be modified in the proposed model. To calculate the redshift, two time-ordered points along the worldline of a distant, comoving standard clock are to be matched with similar two points on earth. The matching is done by finding two solutions of (57) which are well behaved on all scales, satisfying the light-cone condition, connecting the corresponding points at $\lambda =1$. Using (72), the equation for ${\zeta }^1$ (assuming ${\zeta }^2={\zeta }^3=0$ without loss of generality) of such a light signal becomes

$$\lambda {\partial }_{\lambda }{\zeta }^1={\left(\lambda {\ell }_0\right)}^2\left(-{\partial }_{\tau \tau }{\zeta }^1-2{\displaystyle \frac{{\partial }_{\tau }\overline{a}}{\overline{a}}}{\partial }_{\tau }{\zeta }^1\right)-{\zeta }^1$$

(89)

$$\lambda {\partial }_{\lambda }{\zeta }^t={\left(\lambda {\ell }_0\right)}^2\left(-{\partial }_{\tau \tau }{\zeta }^t-{\displaystyle \frac{\overline{a}{\partial }_{\tau }\overline{a}}{{\partial }_{\tau }{\zeta }^t}}{\left({\partial }_{\tau }{\zeta }^1\right)}^2\right)-{\zeta }^t$$

(90)

with $\overline{a}(\tau ,\lambda ):=a\left({\zeta }^t(\tau ,\lambda ),\lambda \right)$. The reader can then easily verify that, for $a=a_{\sigma }$, solutions of the system (89)(90) are ${\zeta }^1={\lambda }^{-1}{\overline{\zeta }}^1\left(\tau \right)$, ${\zeta }^t={\lambda }^{-1}{\overline{\zeta }}^t\left(\tau \right)$ where $\overline{\zeta }$ are just the standard geodesics in the FLRW metric (72). Adding the light-cone condition, these satisfy: ${\partial }_{\tau }{\overline{\zeta }}^1={\overline{a}}^{-2}$, ${\partial }_{\tau }{\overline{\zeta }}^t={\overline{a}}^{-1}$, parameterizing a trajectory $\mathrm{d}{x}^1=a^{-1}\mathrm{d}t$.

Finally, the seemingly remarkable fact, that ‘at cosmological scales’ all physicists observe a common universe, could in fact have been anticipated; compared with infinity, everyone is equally small.