Propagation of Uncertainties in Doppler Effect Current-Meters and Current Profilers

1. Introduction

Subsurface currents are one of the essential climate variables defined by the Global Climate Observing System or GCOS (https://gcos.wmo.int/en/essential-climate-variables). In situ measurements can be made by Eulerian methods where instruments are on fixed moorings, or Lagrangian methods where instruments are surface or subsurface buoys ‘anchored’ in a water mass, the trajectory of which can be followed by satellites. This study concentrates on the Eulerian method where measurements are made with Doppler effect acoustic instruments that can be standalone or vessel-mounted. The assessment of uncertainties in current measurements made by these instruments, is a task that has been unsatisfactorily or at best incompletely solved to date, because of the inherent complexity of the measurement principle and also because of multiple factors contributing to the velocity uncertainty. This paper proposes a method to fill this gap.

Standalone instruments can be single-points or profilers that is to say, they can measure the velocity of water masses in a single layer or in several layers from the seabed or from the surface. They can be mounted on mooring cages deployed on the seabed or on mooring lines. On mooring lines or on the seabed they can be inclined compared to the vertical position. This inclination must be corrected to retrieve the vertical and the horizontal components of the current, and for this purpose they are equipped with tilt sensors. The direction and the amplitude of currents is retrieved at first, in the instrument body by at least three slanted beams that make a vectoral measurement of the velocity and then in the Earth framework by a matrix calculation that uses measured tilt angles and angular directions. For standalone instruments, the angular direction in relation to the magnetic North, is retrieved with a magnetic compass, and the direction in relation with the true North is retrieved by applying a correction of magnetic declination. For vessel mounted instruments, the direction and inclination are given by the inertial navigation system of the boat.

The velocity measured by standalone current-meters and current profilers can be calibrated, and an estimate of their measurement uncertainties can be made in hydrodynamic channels [1] or by carrying out inter-comparisons at sea as it was carried out in 2012 [2] or in rivers [3], but these inter-comparisons are expensive, difficult to organize, and they allow only one part of the velocity range of instruments to be tested. In addition, these two methods do not allow an estimation of errors of each sensor of the instrument separately and the calibration uncertainty can be hardly determined. In 2007 a first publication described a method to calibrate the compass of current-meters [4], and in 2014, a second publication described a method to calibrate the compass and the tilt sensors of these instruments [5] (see Figure 1). In 2020, a third publication described a method to detect the Doppler effect measurement errors made by the transducers of current-meters and profilers, and it quantified the uncertainty of this calibration [6]. It should be noted that in 2015, another method was published by von Appen to correct compass errors linked to nearby metal masses, and applied to ADCP-equipped (Acoustic Doppler Current Profiler) buoys deployed in Greenland [7]. In 2023, another publication demonstrated the impact of different elements of moorings, on the accuracy of compass measurements, and it opened the way to best practices [8].

However, if the uncertainties of direction and velocity measurements can be assessed by these techniques, a method is missing to propagate the uncertainties they quantify, on the current measurements made in situ. The “Guide to the expression of uncertainty in measurement” or GUM [9] edited by the BIPM, proposes a method based on the law of variance composition to assess a combined measurement uncertainty from a physical relation called measurement model. This model must describe the impact of the variations of input quantities on a single output quantity. The supplement 2 to the GUM [10] edited in 2011 or JCGM102: 2011, proposes a standardized method that can be applied to measurement models having any number of input and output quantities. The multi-beams Doppler current-meters and profilers respond to this kind of measurement model. Each acoustic transducer is sensitive to the same input variables and the velocities components U, V, W calculated in the earth framework are sensitive to the same measured velocities and direction quantities. The difficulty lies in the assessment of the standard uncertainties of the input variables.

This publication proposes to apply the JCGM102: 2011 method to evaluate the impact on current measurements of uncertainties on the input quantities that participate to standalone Doppler current-meters and profiler’s measurement, in the case of four-beam current profilers. Numerical applications and simulations based on two commonly used instruments, are given to validate the theoretical developments.

2. Operating Principles of Doppler Current-Meters and Profilers

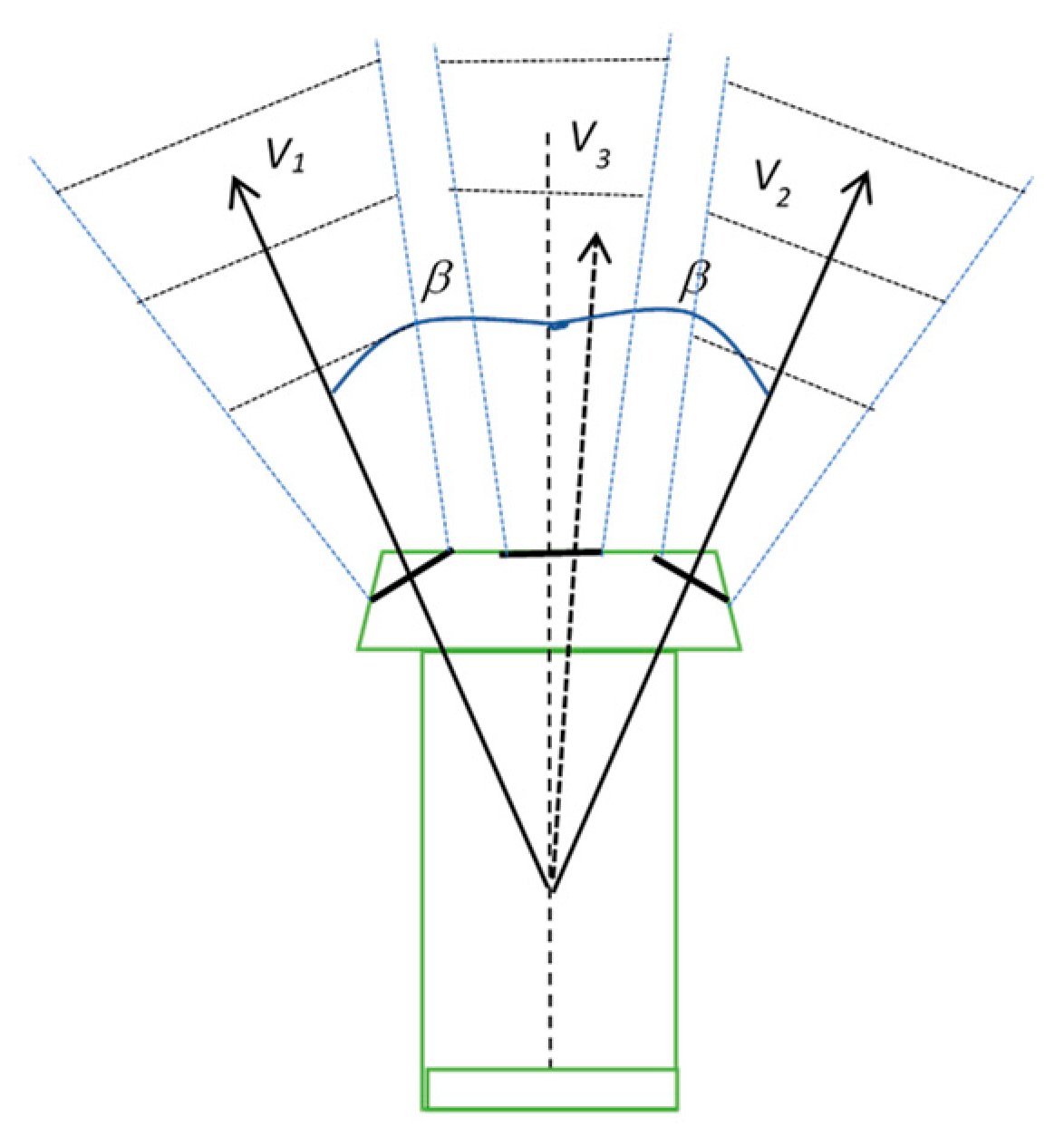
Current-meters and profilers compute velocities (V₁, V₂, V₃) obtained by Doppler shifts measurements in their beam axes (radial velocities). The transducers are tilted 20 °, 25 ° or 45 ° (angle β). β is the Janus angle or slant angle which is accurately determined by the manufacturer (Figure 2). Most of recent instruments are equipped with a fourth transducer used as rescue when the signal detection is too much degraded for one of the other beams.

Speeds (V₁, V₂, V₃) or (V₁, V₂, V₃, V₄) are obtained after the detection of echoes resulting from the reflection of acoustic pulses on the successive layers of particles. To improve measurement trueness, pulses are repeated at a frequency f_r. Some instruments can be used in narrowband or broadband mode. A narrowband instrument transmits a single tone burst and uses an autocovariance function to measure the phase or the frequency shift of the return pulses. It is worth noting that broadband techniques so that averaging improve the detection limits of pings in the noise and the profiling range of measurements or the conditions of detection in waters with low levels of particles.

The document [11] gives formulas to calculate the low limits of the velocity measurement uncertainties of narrow and broadband systems, along the beam path. For a single ping and a narrowband system, the standard deviation σ_NB of the horizontal velocity component can be obtained by the Formula (1):

$${\sigma }_{NB}={\displaystyle \frac{1.6x{10}^5}{f_{0}D}}$$

(1)

where f₀ is the transmit frequency in Hz and D the depth cell length in m. For a broadband system, the standard deviation σ_BB of the horizontal velocity component can be obtained by the relationship (2):

$${\sigma }_{BB}={\displaystyle \frac{{\left(R^{-2}-1\right)}^{1/2}c}{{4\pi \sqrt{2}f}_0{T}_L}}$$

(2)

where R is the correlation at the time T_L. R = 0.5 for a 2-pulses system. T_L is the time separating the transmission of two pulses in a 2-pulses system and c the speed of sound. In this case, the autocorrelation function results are a major peak centred on zero and two side peaks centred on ± T_L.

In order to obtain the velocities (V_x, V_y, V_z) in the referential of the instrument, manufacturers provide transfer matrix that can take different forms according to the orientation given to transducers. Figure 3 compares the enumeration of transducers and the orientation of rotation axis for the instruments Nortek Signature profiler and Teledyne RD Instruments Workhorse ADCP.

The matrix (3) can be used in the case of Nortek Signature profilers which head orientation is given in Figure 3:

$$\left[\begin{array}{c}\begin{array}{c}{V}_x\\ V_y\\ V_z\end{array}\\ V_e\end{array}\right]=\left[\begin{array}{c}\begin{array}{ccc}{\displaystyle \frac{1}{2\mathit{sin}\left(\beta \right)}}& 0& {\displaystyle \frac{-1}{2\mathit{sin}\left(\beta \right)}}\\ 0& {\displaystyle \frac{1}{2\mathit{sin}\left(\beta \right)}}& 0\\ {\displaystyle \frac{1}{4\mathit{cos}\left(\beta \right)}}& {\displaystyle \frac{1}{4\mathit{cos}\left(\beta \right)}}& {\displaystyle \frac{1}{4\mathit{cos}\left(\beta \right)}} \end{array}\begin{array}{c}0\\ {\displaystyle \frac{-1}{2\mathit{sin}\left(\beta \right)}}\\ {\displaystyle \frac{1}{4\mathit{cos}\left(\beta \right)}}\end{array}\\ \begin{array}{cc} 0 & 0 \end{array} \begin{array}{cc}0 & 0\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{V}_1\\ V_2\\ V_3\end{array}\\ V_4\end{array}\right]$$

(3)

In the case when the beam angle can vary independently for each beam, the angle β can be declined in different values β₁, β₂ or β₃. For Teledyne RDI ADCP’s, this matrix takes another form. According to RDI Instruments (1998), for a convex transducer head we have:

$$\left[\begin{array}{c}\begin{array}{c}{V}_x\\ V_y\\ V_z\end{array}\\ V_e\end{array}\right]=\left[\begin{array}{c}\begin{array}{ccc}{\displaystyle \frac{1}{2\mathit{sin}\left(\beta \right)}} & {\displaystyle \frac{-1}{2\mathit{sin}\left(\beta \right)}} & 0 \\ 0& 0& {\displaystyle \frac{-1}{2\mathit{sin}\left(\beta \right)}} \\ {\displaystyle \frac{1}{4\mathit{cos}\left(\beta \right)}} & {\displaystyle \frac{1}{4\mathit{cos}\left(\beta \right)}} & {\displaystyle \frac{1}{4\mathit{cos}\left(\beta \right)}} \end{array}\begin{array}{c}0\\ {\displaystyle \frac{1}{2\mathit{sin}\left(\beta \right)}}\\ {\displaystyle \frac{1}{4\mathit{cos}\left(\beta \right)}}\end{array}\\ \begin{array}{cc} {\displaystyle \frac{1}{2\sqrt{2}\mathit{sin}\left(\beta \right)}} & {\displaystyle \frac{1}{2\sqrt{2}\mathit{sin}\left(\beta \right)}} \end{array} \begin{array}{cc}{\displaystyle \frac{-1}{2\sqrt{2}\mathit{sin}\left(\beta \right)}} & {\displaystyle \frac{-1}{2\sqrt{2}\mathit{sin}\left(\beta \right)}}\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{V}_1\\ V_2\\ V_3\end{array}\\ V_4\end{array}\right]$$

(4)

The first three rows are the generalized inverse of the beam directional matrix representing the components of each beam in the instrument coordinate system. The last row representing the error velocity, is orthogonal to the other three rows and has been normalized so that its magnitude (root-mean-square) matches the mean of the magnitudes of the first two rows. This normalization has been chosen so that in horizontally homogeneous flows, the variance of the error velocity will indicate the portion of the variance of each of the nominally-horizontal components (X and Y) attributable to instrument noise (short-term error). If one beam is marked bad due to low correlation or fish detection, then a three-beam solution is calculated by the ADCP. If, for example, the beam 4 is bad, the term ${\displaystyle \frac{1}{2\sqrt{2}\mathit{sin}\left(\beta \right)}}$ is replaced by a 0 value which is equivalent to a 3-beam solution.

Current-meters are equipped with ‘flux-gate’, ‘Hall effect’ or magneto-resistive compasses to retrieve the amplitude of current components (U, V, W) in reference to the magnetic North (angle α), and considering the magnetic declination at the place of measurements, in relation to the true North. Moreover, their inclination is corrected thanks to a tilt sensor measuring roll angles θ and pitch angles Ψ. For vessel-mounted instruments, these data come from the attitude sensors of the boat. According to [12], between 1 and 12 equations can be found to describe a rotation in the three dimensions.

Concerning the reference frame given in Figure 3 for the Nortek instruments, a Nortek routine called “signatureAD2CP_beam2xyz_enu.m” (https://support.nortekgroup.com/hc/en-us/articles/360029820971-How-is-a-coordinate-transformation-done?) can be used to calculate a rotation matrix for instruments in the Signature range. That gives:

$$\left[\begin{array}{c}U\\ V\\ W\end{array}\right]=\left[\begin{array}{ccc}{C}_{\psi }{C}_{\alpha }& (-S_{\psi }{S}_{\theta }{C}_{\alpha }+C_{\theta }{S}_{\alpha })& (-S_{\psi }{C}_{\theta }{C}_{\alpha }-S_{\theta }{S}_{\alpha })\\ -C_{\psi }{S}_{\alpha }& (S_{\psi }{S}_{\theta }{S}_{\alpha }+C_{\theta }{C}_{\alpha })& (S_{\psi }{C}_{\theta }{S}_{\alpha }-S_{\theta }{C}_{\alpha })\\ S_{\psi }& C_{\psi }{S}_{\theta }& C_{\psi }{C}_{\theta }\end{array}\right]\left[\begin{array}{c}{V}_x\\ V_y\\ V_z\end{array}\right]$$

(5)

Teledyne RD Instruments describes an inverse rotation matrix to retrieve the values of components (U, V, W), in its document of 1998, upgraded in 2010 [13]. For profilers installed on boats, they use the names starboard S, forward F, and mast M, instead of pitch, roll, and heading for the axes. If the beam 3 is aligned with the keel on the forward side of the ADCP, for the downward-looking orientation, these axes are identical to the instrument axes: S = X, F = Y, M = Z. For the upward-looking orientation, S = -X, F = Y, M = -Z. In earth coordinates, the roll, pitch, and heading angles correspond to Y axis, X axis andZaxis(downward looking). This description corresponds to the right schematic of Figure 3. To retrieve the components (U, V, W), they use the following rotation matrix [6]:

$$\left[\begin{array}{c}U\\ V\\ W\end{array}\right]=\left[\begin{array}{ccc}{(C}_{\alpha }{C}_{\theta }+S_{\alpha } S_{\alpha } S_{\psi })& \left(C_{\psi }{S}_{\alpha }\right)& (S_{\alpha }{C}_{\alpha }-S_{\psi }{S}_{\alpha }{C}_{\alpha })\\ (-C_{\theta }{S}_{\alpha }+S_{\theta }{C}_{\alpha }{S}_{\psi })& \left(C_{\psi }{C}_{\alpha }\right)& (-S_{\alpha }{S}_{\alpha }-S_{\psi }{C}_{\alpha }{C}_{\alpha })\\ -{C_{\psi }S}_{\alpha }& S_{\psi }& C_{\psi }{C}_{\theta }\end{array}\right]\left[\begin{array}{c}{V}_x\\ V_y\\ V_z\end{array}\right]$$

(6)

Velocities V₁, V₂, V₃ and V₄ of matrix (3) and (4) are obtained after the detection of echoes resulting from the reflection of pulses on successive layers of particles that are carried along by the currents. This displacement creates a frequency shift δf_i (i ∈{1, 2, 3, 4}) called Doppler shift. Echoes are measured continuously, allowing the size of measurement cells in the water column to be determined (Figure 2), considering the value of the speed of sound in seawater c and the duration t_p of pulses. The lowest uncertainty that can be obtained for the measurements of (V₁, V₂, V₃, V₄) is limited by the standard deviation of the Doppler noise σ_δ, which is inversely proportional to t_p. This noise is generated by the random displacement of particles, the multiple echoes and the detection limits of the instrument electronics. Different techniques exist to extract the signal from the noise and to improve the detection limit (see [14], or [15], or [11], or [16]). If f₀ is the emitted frequency, the measured radial velocity is obtained by the Doppler effect relationship:

$$V_i=\pm {\displaystyle \frac{\delta f_{i}c}{2f_0}} i\in \left\{\mathrm{1,2},\mathrm{3,4}\right\}$$

(7)

In this relation, c is programmed in the instrument by the user or calculated by a relation using temperature, pressure measurements and sometimes a value of practical salinity.

3. Method to Evaluate the Currents Measurements Uncertainties

3.1. Uncertainties on the Instrument Body Velocities

It is necessary to consider at first, the matrix (3) and (4) that allow to transform the measured velocities (V₁, V₂, V₃, V₄) in the instrument body velocities (V_x, V_y, V_z, V_e). β is affected by a manufacturing uncertainty. Manufacturers never communicated about this uncertainty but they characterize to the best each type of instrument’s head to obtain a unique transformation matrix. The remaining uncertainty is given to be included in the accuracy given in the specification sheet established by the manufacturer. This uncertainty will be called u_β. The sensitivity of this uncertainty can be evaluated thanks to the matrix products (3) or (4). For example, considering a Nortek Signature 500 kHz where β = 25 °, if V₁ = -1 m/s, V₂ = 1 m/s, V₃ = - 5 m/s and V₄ = 5 m/s, V_x value changes of 0.018 m/s, V_y of 0.004 m/s, V_z of 0.001 m/s and per 0.1 ° in error. The measurement range of this instrument is ± 5 m/s along the beams. Therefore, its maximal sensitivity to the slant angle is 0.18 m/s/° (see Table 1).

The same simulation can be made on a Teledyne RD Instrument Workhorse Sentinel 600 kHz. On this instrument, β = 20 °. In order to obtain instrument body velocities less than 5 m/s to compare calculated values with the Signature values, it is necessary to take V₁ = 4.4 m/s, V₂ = 1 m/s, V₃ = 3.3 m/s and V₄ = 1 m/s. In this case, V_x value changes of 0.024 m/s, V_y of 0.023 m/s, V_z of 0.001 m/s and per 0.1 ° in error. Therefore, its sensitivity at 5 m/s to the slant angle is 0.24 m/s/°. A reduced slant angle increases the sensitivity to the manufacturing tolerance on this angle.

Velocities (V₁, V₂, V₃, V₄) measured from the Doppler effect, have three sources of uncertainties:

- the first comes from the accuracy in which this effect is measured by the instrument. It is dependent on the linearity of its electronic or on the stability of its oscillator. This part can be evaluated during the calibration of transducers as described in [6]. It participates to the uncertainty u_δf.

- The second comes from the conditions of reflection in the medium and of the detection techniques employed. This part also participates to the uncertainty u_δf, and it is hard to assess. If pings average are made, some instruments can also generate a standard deviation per measurement cell to quantify the uncertainty of Doppler shifts real-time measurement. In this case, the resulting standard deviation can be quadratically add to the transducer’s calibration uncertainty.

- The third source depends on the difference between the speed of sound programmed in the instrument, and the true speed of sound in the medium. It can be evaluated thanks to Formula (7). Considering that f₀ is perfectly determined, and that c has an uncertainty u_c on its determination, as δf_i and c are two independent quantities, we can write that the uncertainty u_vi on V_i is:

$$u_{Vi}^2=V_i^2\left[{\left({\displaystyle \frac{u_{\delta f}}{\delta f}}\right)}^2+{\left({\displaystyle \frac{u_c}{c}}\right)}^2\right]$$

(8)

Considering again a Signature 500 kHz, if 1500 m/s is programmed in the instrument and the true velocity is unknow but estimated to be inferior to 1520 m/s, according to BIPM (2008), $u_c=20/\sqrt{3}$ or 11.5 m/s. If V_i = 1 m/s, for f₀ = 500 kHz, δf_i = 758 Hz. The uncertainty on the calibration of transducers is generally close to 0.002 m/s, what makes u_δf = 1.6 Hz. In this case, the first member of the Equation (8) is 4 10^-6 and the second member is 5.8 10^-5. The uncertainty on the speed of sound dominates largely the uncertainty on the measured velocity. For V_i = 1 m/s, the uncertainty on V_i is 0.008 m/s or 0.76 % of the measured speed. This uncertainty decreases as V_i increases.

From a measurement point of view, velocities (V₁, V₂, V₃, V₄) are determined independently, in the same layer of water. However, there is a spatial correlation between the beams due to their angle of inclination. Their covariance is proportional to the cosine of the slant angle. If the slant β was 90 °, cov(V_i, V_j) = 0 pour i # j ∈ {1, 2, 3, 4}. Therefore, it is possible to estimate the covariance of V_i’s by the relation: cov(V_i, V_j) = u_Vi u_Vj cos(β), to form the variance matrix V_vi, which diagonal is composed of the squared of the standard uncertainties u_Vi of the velocities V_i, i ∈ {1, 2, 3, 4}. V_vi has the form:

$${\mathit{V}}_{vi}=\left[\begin{array}{c}\begin{array}{c}\begin{array}{ccc}{u}_{v1}^2& c_{12}& c_{13} c_{14} 0\\ c_{21}& u_{v2}^2& c_{23} c_{24} 0\\ c_{31}& c_{32}& u_{v3}^2 { c}_{34} 0\end{array}\\ \begin{array}{ccc}{c}_{41} c_{42}& c_{43}& u_{v4}^2 0\end{array}\end{array}\\ \begin{array}{ccc}0 & 0& 0 0 u_{\beta }^2\end{array}\end{array}\right]$$

(9)

where c_ij = cov(V_i, V_j) i # j ∈ {1, 2, 3, 4}. β is a variable independent of V_i, i ∈ {1, 2, 3, 4}. The uncertainty on the speeds (V_x, V_y, V_z) of matrix (3) or (4) can be obtained, according to [10], from the matrix product (10):

$${\mathit{V}}_{v_{xyz}}=\mathit{M}{\mathit{V}}_{\mathit{v}\mathit{i}}{\mathit{M}}^T$$

(10)

V_x, V_y, V_z and V_e are functions of V₁, V₂, V₃, V₄ and β. In the case of a 4-beam ADCP, M will take the form:

$$\mathit{M}=\left[\begin{array}{c}\begin{array}{ccc}{\displaystyle \frac{\partial V_x}{\partial V_1}} & {\displaystyle \frac{\partial V_x}{\partial V_2}} & {\displaystyle \frac{\partial V_x}{\partial V_3}} \\ {\displaystyle \frac{\partial V_y}{\partial V_1}} & {\displaystyle \frac{\partial V_y}{\partial V_2}} & {\displaystyle \frac{\partial V_y}{\partial V_3}} \\ {\displaystyle \frac{\partial V_z}{\partial V_1}} & {\displaystyle \frac{\partial V_z}{\partial V_2}} & {\displaystyle \frac{\partial V_z}{\partial V_3}} \end{array}\begin{array}{c}{\displaystyle \frac{\partial V_x}{\partial V_4}} {\displaystyle \frac{\partial V_x}{\partial \beta }}\\ {\displaystyle \frac{\partial V_y}{\partial V_4}} {\displaystyle \frac{\partial V_y}{\partial \beta }}\\ {\displaystyle \frac{\partial V_z}{\partial V_4}} {\displaystyle \frac{\partial V_z}{\partial \beta }}\end{array}\\ \begin{array}{cc}{\displaystyle \frac{\partial V_e}{\partial V_1}} & {\displaystyle \frac{\partial V_e}{\partial V_2}} \end{array} \begin{array}{cc}{\displaystyle \frac{\partial V_e}{\partial V_3}}& {\displaystyle \frac{\partial V_e}{\partial V_4}}\end{array} {\displaystyle \frac{\partial V_e}{\partial \beta }}\end{array}\right]$$

(11)

M^T is the transposed matrix of M. The derivatives of V_x, V_y, V_z and V_e with respect to V₁, V₂, V₃, V₄ correspond to the elements of matrix (3) or (4) according to the chosen ADCP. The derivatives of V_x, V_y, V_z and V_e with respect to β can be obtained with the Equations (12) and (13):

$$\left[\begin{array}{c}{\displaystyle \frac{\partial V_x}{\partial \beta }}={\displaystyle \frac{1}{2}}\left(V_3-V_1\right){\displaystyle \frac{cos\left(\beta \right)}{{\left(sin\left(\beta \right)\right)}^2}}\\ {\displaystyle \frac{\partial V_y}{\partial \beta }}={\displaystyle \frac{1}{2}}\left(V_2-V_4\right){\displaystyle \frac{cos\left(\beta \right)}{{\left(sin\left(\beta \right)\right)}^2}}\\ {\displaystyle \frac{\partial V_z}{\partial \beta }}={\displaystyle \frac{1}{4}}\left({V_1+V}_2+V_3+V_4\right){\displaystyle \frac{sin\left(\beta \right)}{{\left(cos\left(\beta \right)\right)}^2}}\end{array}\right.$$

(12)

Equation (12) can be used for the matrix (3) and the following Equation (13) can be used for the matrix (4):

$$\left[\begin{array}{c}\begin{array}{c}{\displaystyle \frac{\partial V_x}{\partial \beta }}={\displaystyle \frac{1}{2}}\left(V_2-V_1\right){\displaystyle \frac{cos\left(\beta \right)}{{\left(sin\left(\beta \right)\right)}^2}}\\ {\displaystyle \frac{\partial V_y}{\partial \beta }}={\displaystyle \frac{1}{2}}\left(V_3-V_4\right){\displaystyle \frac{cos\left(\beta \right)}{{\left(sin\left(\beta \right)\right)}^2}}\\ {\displaystyle \frac{\partial V_z}{\partial \beta }}={\displaystyle \frac{1}{4}}\left({V_1+V}_2+V_3+V_4\right){\displaystyle \frac{sin\left(\beta \right)}{{\left(cos\left(\beta \right)\right)}^2}}\end{array}\\ {\displaystyle \frac{\partial V_e}{\partial \beta }}={\displaystyle \frac{1}{2\sqrt{2}}}\left({{-V}_1-V}_2+V_3+V_4\right){\displaystyle \frac{cos\left(\beta \right)}{{\left(sin\left(\beta \right)\right)}^2}}\end{array}\right.$$

(13)

It is well known that ADCP do not provide reliable water velocity measurements near the sea surface or near the bottom, because acoustic sidelobe reflections from the boundary contaminate the Doppler velocity measurements [17]. For the surface, the bias will depend on the sea state or surface wind conditions. Higher velocities are measured in the upper layer. In 2022, Lentz et al. formulated a relationship suggesting that the contaminated region is deeper than traditionally suggested, with a dependence on the bin size Δz [18]. The depth z_sl was calculated with the relationship z_sl = h_a[1 - cos(β)], where h_a is the distance from the ADCP acoustic head to the sea surface. According to [18], the true depth z of this region must be assessed with the relation: z < z_sl + 3Δz/2. However, this publication does not provide a method or a relationship for assessing the magnitude of the error or of the uncertainty on the measured velocity as a function of depth, and there is no way in post-processing to separate the bias effect of side-lobes. Consequently, the measurements made in a depth inferior to z are excluded of the field of our publication.

3.2. Uncertainties on Velocities Calculated in the Earth Framework

The determination of U, V and W just requires 3 beams. Let us consider that the measurements of V_x, V_y, V_z are of a good quality and that V_e is not required. In the same way, U, V and W of matrix (5) and (6), are determinist functions of 6 independent variables V_x, V_y, V_z, α, θ and $\psi$ that have measurement uncertainties u_vx, u_vy, u_vz, u_α, u_θ, $u_{\psi }$. That gives the diagonal variance matrix V_6v:

$${\mathit{V}}_{6v}=\left[\begin{array}{c}\begin{array}{ccc}{u}_{vx}^2& 0& 0\\ 0& u_{vy}^2& 0\\ 0& 0& u_{vz}^2\end{array}\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\\ \begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\begin{array}{ccc}{u}_{\alpha }^2& 0& 0\\ 0& u_{\theta }^2& 0\\ 0& 0& u_{\psi }^2\end{array}\end{array}\right]$$

(14)

The uncertainties on the speeds (U, V, W) of matrix (5) or (6) can be obtained with the product:

$${\mathit{V}}_{U,V,W}={\mathit{M}}_{\mathit{f}}{\mathit{V}}_{6\mathit{v}}{\mathit{M}}_{\mathit{f}}^{\mathit{T}}$$

(15)

with:

$${\mathit{M}}_f=\left[\begin{array}{ccc}{\displaystyle \frac{\partial U}{\partial V_x}}& {\displaystyle \frac{\partial U}{\partial V_y}}& {\displaystyle \frac{\partial U}{\partial V_z}} \\ {\displaystyle \frac{\partial V}{\partial V_x}}& {\displaystyle \frac{\partial V}{\partial V_y}}& {\displaystyle \frac{\partial V}{\partial V_z}} \\ {\displaystyle \frac{\partial W}{\partial V_x}}& {\displaystyle \frac{\partial W}{\partial V_y}}& {\displaystyle \frac{\partial W}{\partial V_z}} \end{array}\begin{array}{ccc}{\displaystyle \frac{\partial U}{\partial \alpha }}& {\displaystyle \frac{\partial U}{\partial \theta }}& {\displaystyle \frac{\partial U}{\partial \psi }}\\ {\displaystyle \frac{\partial V}{\partial \alpha }}& {\displaystyle \frac{\partial V}{\partial \theta }}& {\displaystyle \frac{\partial V}{\partial \psi }}\\ {\displaystyle \frac{\partial W}{\partial \alpha }}& {\displaystyle \frac{\partial W}{\partial \theta }}& {\displaystyle \frac{\partial W}{\partial \psi }}\end{array}\right]$$

(16)

M_f^T is the transposed matrix of M_f. The equations of derivatives of the matrix (15) applied to the matrix (5) and (6), are given in the supplementary materials.

4. Numerical Applications and Results

There are so many different current-meters and current profilers and so many ways of configuring and using them, that it is impossible to obtain a unique numerical result representing the measurement uncertainty that can be expected from these instruments. In order to see how the relationships of the section 3 can be applied and in order to give an order of magnitude of the final uncertainties that can be found, numerical applications have been made based on a Nortek Signature 500 kHz and on a 600 kHz RD Instrument Workhorse Sentinel. These instruments have frequencies in the average of the frequency range of the commercially available instruments and they are widely used in oceanography.

The Nortek Signature 500 kHz has a slant angle β = 25 °. The uncertainty u_β on the determination of this slant angle is unknown, but the standard ISO 2768 [19] determines classes of tolerances on angles in mechanical parts manufacturing. The higher class allows to define angles to 0° 5′ or 0.083 ° (0.0014 rad). This value will be taken as an example to define the uncertainty u_β, but without any real knowledge of what can be obtained by manufacturers.

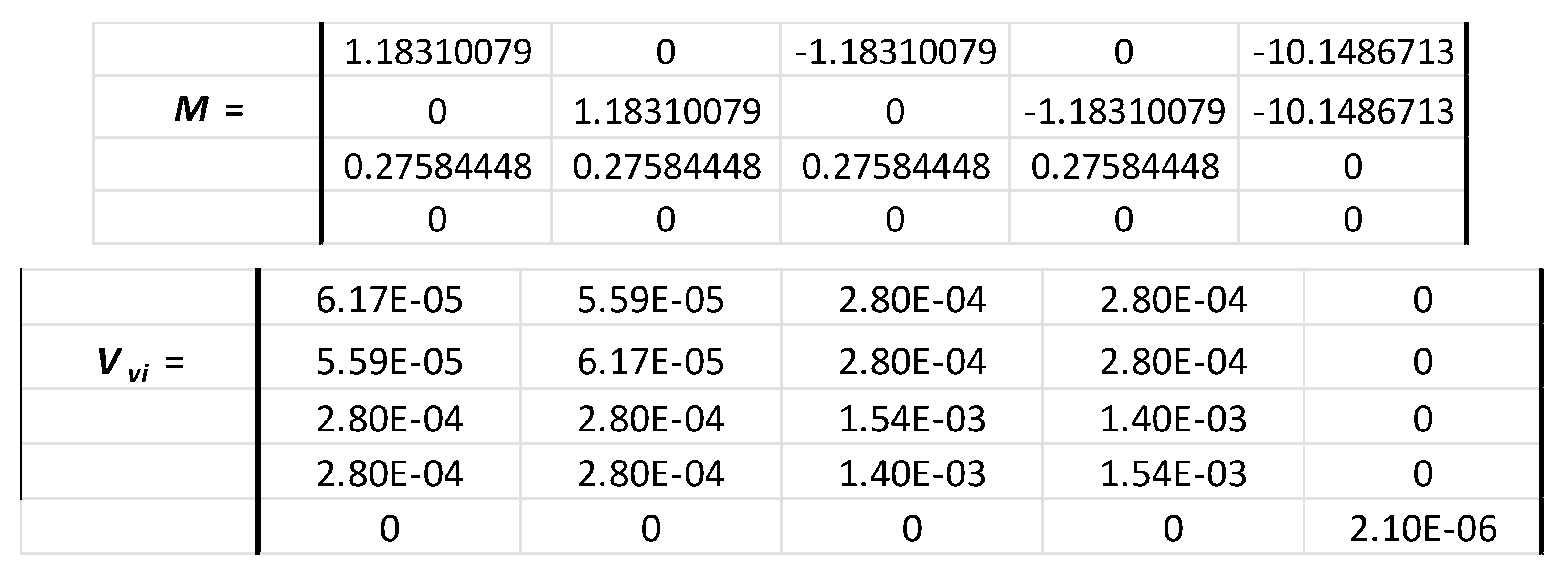
With V₁ = -1 m/s, V₂ = 1 m/s, V₃ = - 5 m/s and V₄ = 5 m/s, we have u_V1 = u_V2 = 0.008 m/s, and u_V3 = u_V4 = 0.039 m/s by considering a maximal uncertainty of 20 m/s on the speed of sound c. That gives the matrix:

and u_Vx = u_Vy = 0.041 m/s, and u_Vz = 0.025 m/s, with V_x = 4.732 m/s, V_y = 1.183 m/s and V_z = - 1.379 m/s. If we consider now that β is perfectly determined and has no uncertainty, the values of u_Vx and u_Vy become a little bit smaller: u_Vx = u_Vy = 0.038 m/s, and we have always u_Vz = 0.025 m/s. Therefore, this calculation shows that the uncertainties on the measured speeds are slightly sensitive to the slant angle of beams and that the smallest uncertainty allowed on the manufacturing has a small impact on the horizontal measured velocities. That highlights the necessity for manufacturers to compensate it with adjusted values of β in matrix (3) and (4), and to communicate about it.

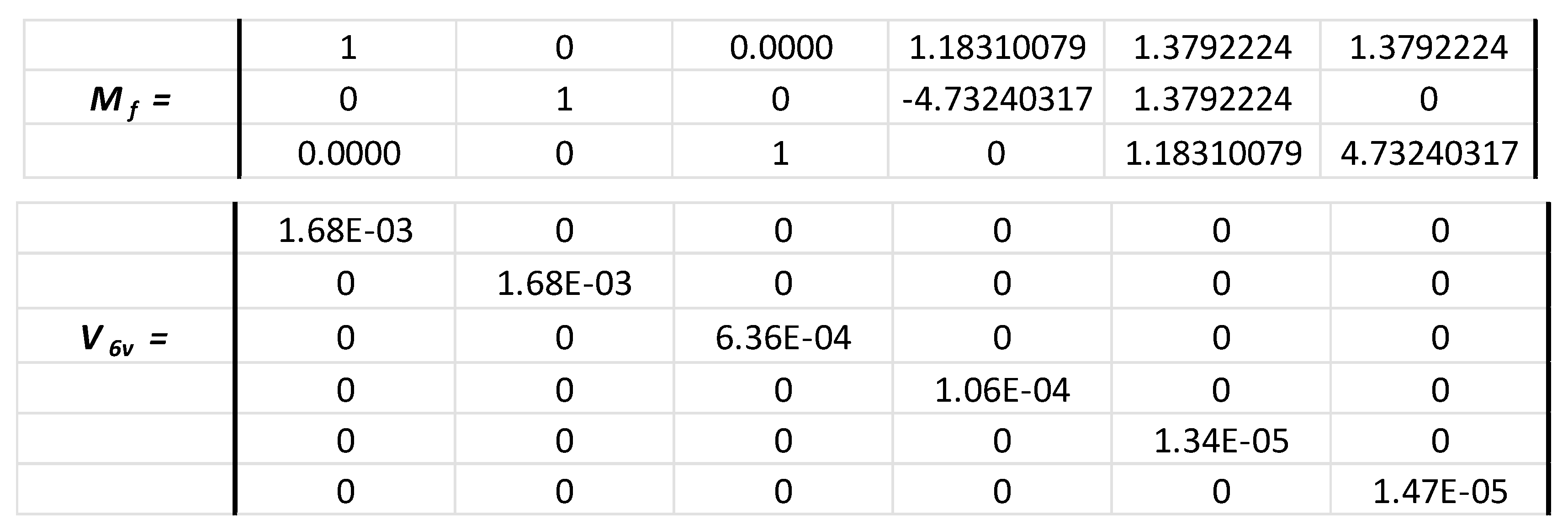
If the heading, roll and pitch angles are taken to be 0 °, U = V_x, V = V_y and W = V_z. Using the calibration platform described in [8] or [5], the typical standard uncertainties that can be obtained on heading, roll and pitch angles are: u_α = 0.59 °, u_θ = 0.21 ° and $u_{\psi }$ = 0.22 °. That gives the matrix:

The relationship (15) gives u_U = 0.043 m/s, u_V = 0.064 m/s and u_W = 0.021 m/s. In the case when u_β = 0 °, u_U = 0.041 m/s, u_V = 0.062 m/s and u_W = 0.021 m/s.

If now the profiler is turned by α = 70 ° and tilted by θ = $\psi$ = 5 °, the values of U, V and W are different (U = 2.87 m/s, V = - 4.09 m/s and W = - 0.85 m/s) so that their measurement uncertainties: u_U = 0.059 m/s, u_V = 0.051 m/s and u_W = 0.032 m/s. If u_β = 0 °, u_U = 0.057 m/s, u_V = 0.048 m/s and u_W = 0.032 m/s.

Bias are often found on compass and tilt sensors after several years of using. Let us suppose that these biases are not corrected and considered as uncertainties, and that u_α = 6 °, u_θ = 1 ° and $u_{\psi }$= 1 ° which are error values currently found. In this case, the calculation gives: u_U = 0.43 m/s, u_V = 0.30 m/s and u_W = 0.09 m/s. If u_β = 0 °, the uncertainties remain the same: u_U = 0.43 m/s, u_V = 0.30 m/s and u_W = 0.09 m/s. The uncertainties on U and V are very large and dominated by the compass uncertainty. They represent 15 % and 7 % of the measured value. To check their trueness, we just need to look at how U, V and W vary when α, θ and $\psi$ go respectively from 70 ° to 76 ° and from 5 ° to 5.8 °. The differences obtained by using the matrix (5) is δU = 0.42 °, δV = 0.28 ° and δW = 0.08 ° which is very close of values found for u_U, u_V and u_W.

This simulation shows the importance of correcting the compass and tilt sensors errors to make these uncertainties equivalent to the calibration uncertainties. All these results are resumed in Table 2.

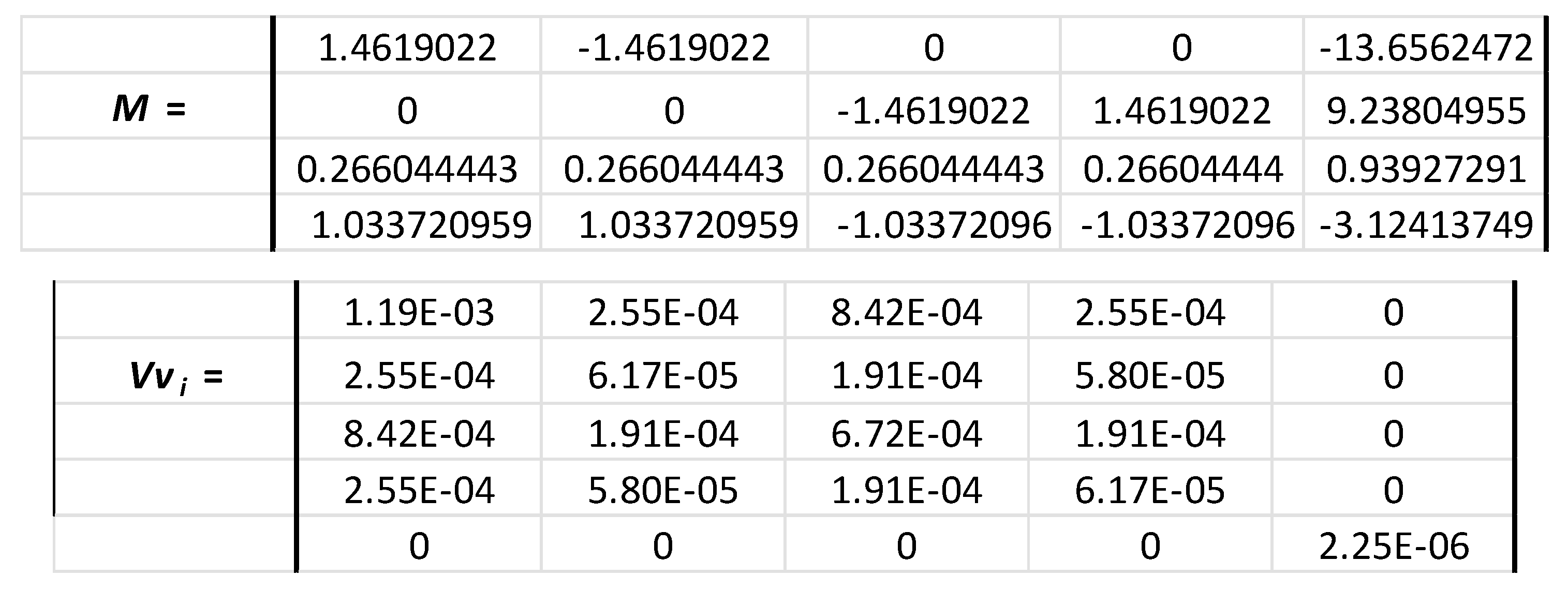
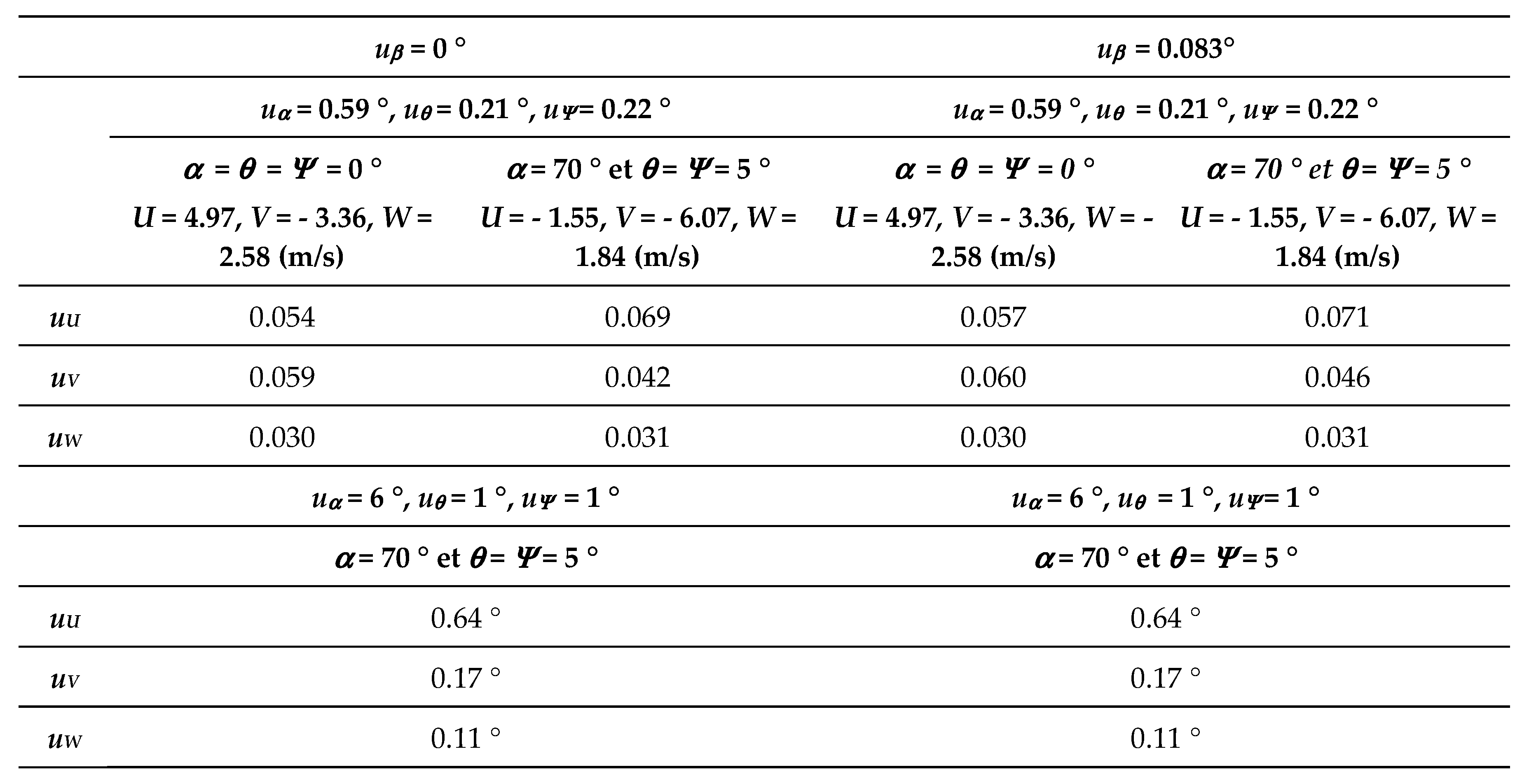
The same numerical applications can be made on RD Instrument Workhorse Sentinel. The specifications of the 600 kHz are the closest of the 500 kHz Signature. For this instrument, β = 20 °. With V₁ = 4.4 m/s, V₂ = 1 m/s, V₃ = 3.3 m/s and V₄ = 1 m/s, we have u_V1 = 0.036 m/s, u_V3 = 0.026 m/s, and u_V2 = u_V4 = 0.008 m/s by considering again a maximal uncertainty of 20 m/s on the speed of sound c. That gives the matrix:

and u_Vx = 0.045 m/s, u_Vy = 0.030 m/s, u_Vz = 0.020 m/s and u_Ve = 0.015 m/s, with V_x = 4.97 m/s, V_y = - 3.36 m/s, V_z = 2.58 m/s and V_e = 1.14 m/s. If we consider now that β is perfectly determine and has no uncertainty, like for the Signature, the values of u_Vx, u_Vy are smaller and u_Vz is unchanged: u_Vx = 0.040 m/s, u_Vy = 0.027 m/s, u_Vz = 0.020 m/s and u_Ve = 0.014 m/s.

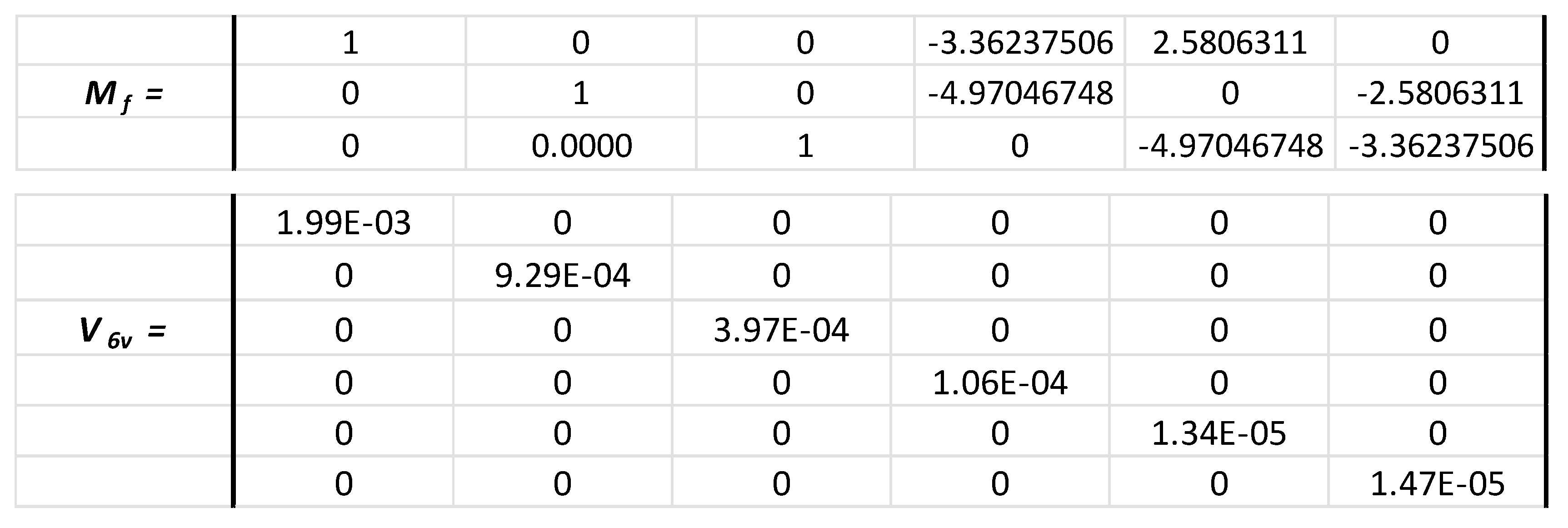
If the heading, roll and pitch angles are taken to be 0 °, U = V_x, U = V_y and W = V_z. Using the previous heading, roll and pitch uncertainty values (u_α = 0.59 °, u_θ = 0.21 ° and $u_{\psi }$ = 0.22 °), that gives the matrix:

We have again u_U = 0.057 m/s u_V = 0.060 m/s but u_W = 0.030 m/s. In the case when u_β = 0 °, u_U = 0.054 m/s, u_V = 0.059 m/s and u_W = 0.030 m/s. These values are of the same order of magnitude as those obtained with the Signature.

If now the profiler is turned by α = 70 ° and tilted by θ = $\psi$ = 5 °, the values of U, V and W are different (U = - 1.55 m/s, V = - 6.07 m/s and W = + 1.84 m/s) and the uncertainties on U, V and W are distributed differently: u_U = 0.071 m/s, u_V = 0.046 m/s and u_W = 0.031 m/s. If u_β = 0 °, u_U = 0.069 m/s, u_V = 0.042 m/s and u_W = 0.031 m/s.

Let us suppose again that u_α = 6 °, u_θ = 1 ° and u_Ψ = 1 ° which are error values currently found. In this case, the calculation gives: u_U = 0.637 m/s, u_V = 0.172 m/s and u_W = 0.112 m/s. If u_β = 0 °, u_U = 0.637 m/s, u_V = 0.170 m/s and u_W = 0.112 m/s. The uncertainties on U and V are again very large and dominated by the compass uncertainty. They represent respectively 41 %, 3 % and 6 % of the measured value. To check their trueness, we just need to look at how U, V and W vary when α, θ and $\psi$ go respectively from 70 ° to 76 ° and from 5 ° to 5.8 °. The differences obtained by using the matrix (6) is δU = 0.64 °, δV = 0.16 ° and δW = 0.13 ° which is very close of values found for u_U, u_V and u_W. All these results are resumed in Table 3. This simulation demonstrates again the importance of correcting the compass and tilt sensors errors to make these uncertainties equivalent to the calibration uncertainties.

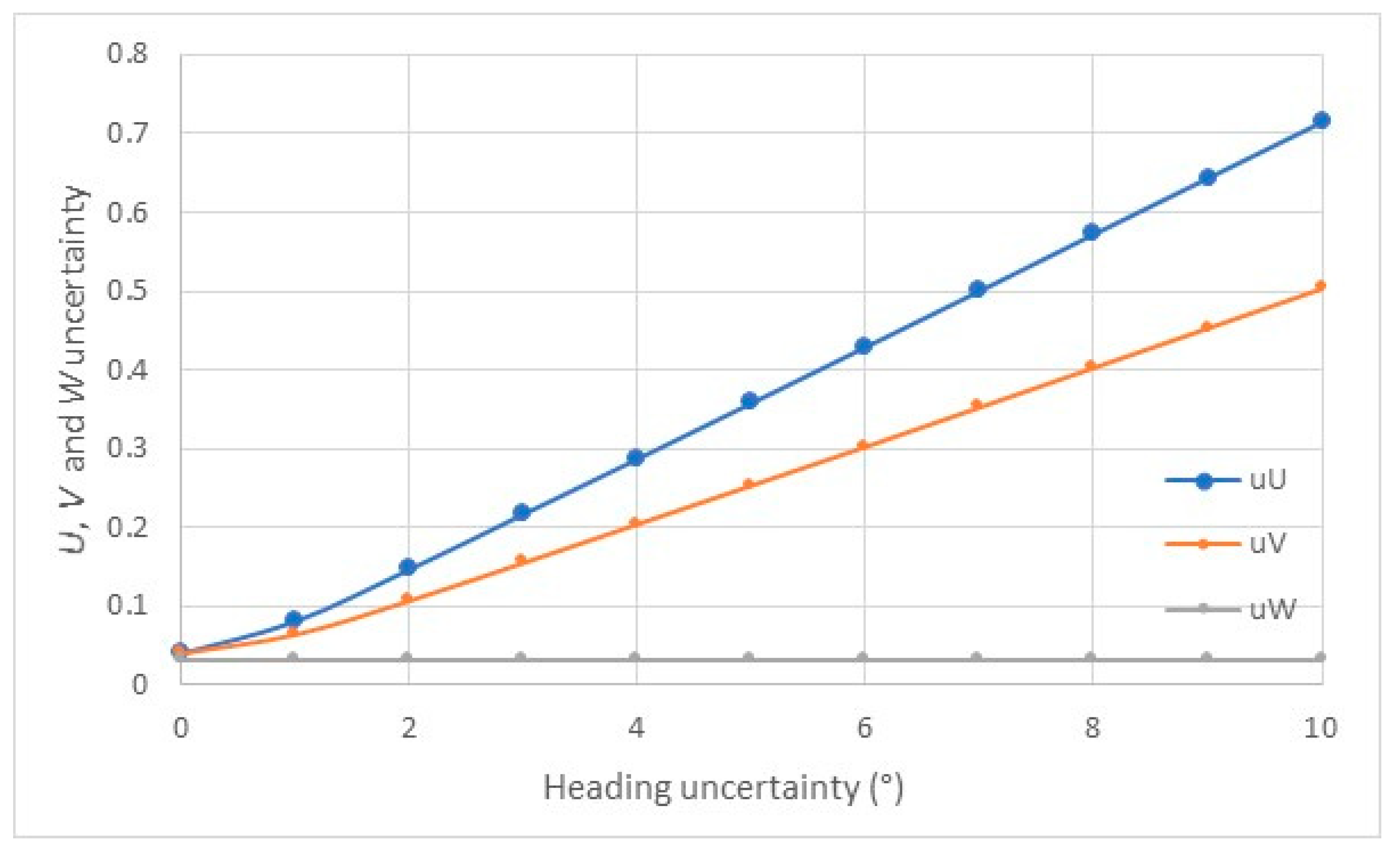
In order to illustrate the possibilities of simulation offered by this method, four graphs have been plotted (Figure 4, Figure 5 and Figure 6). The first one (Figure 4) shows the evolution of U, V and W uncertainties when the uncertainty on the heading increases from 0 to 10 °, for the values used in Table 1: α = 70 ° and θ = Ψ = 5 °, U = 2.87 m/s, V = - 4.09 m/s, W = - 0.85 m/s, u_θ = 0.21 °, u_Ψ = 0.22 °. As expected, u_W remains constant and u_U and u_V increase linearly.

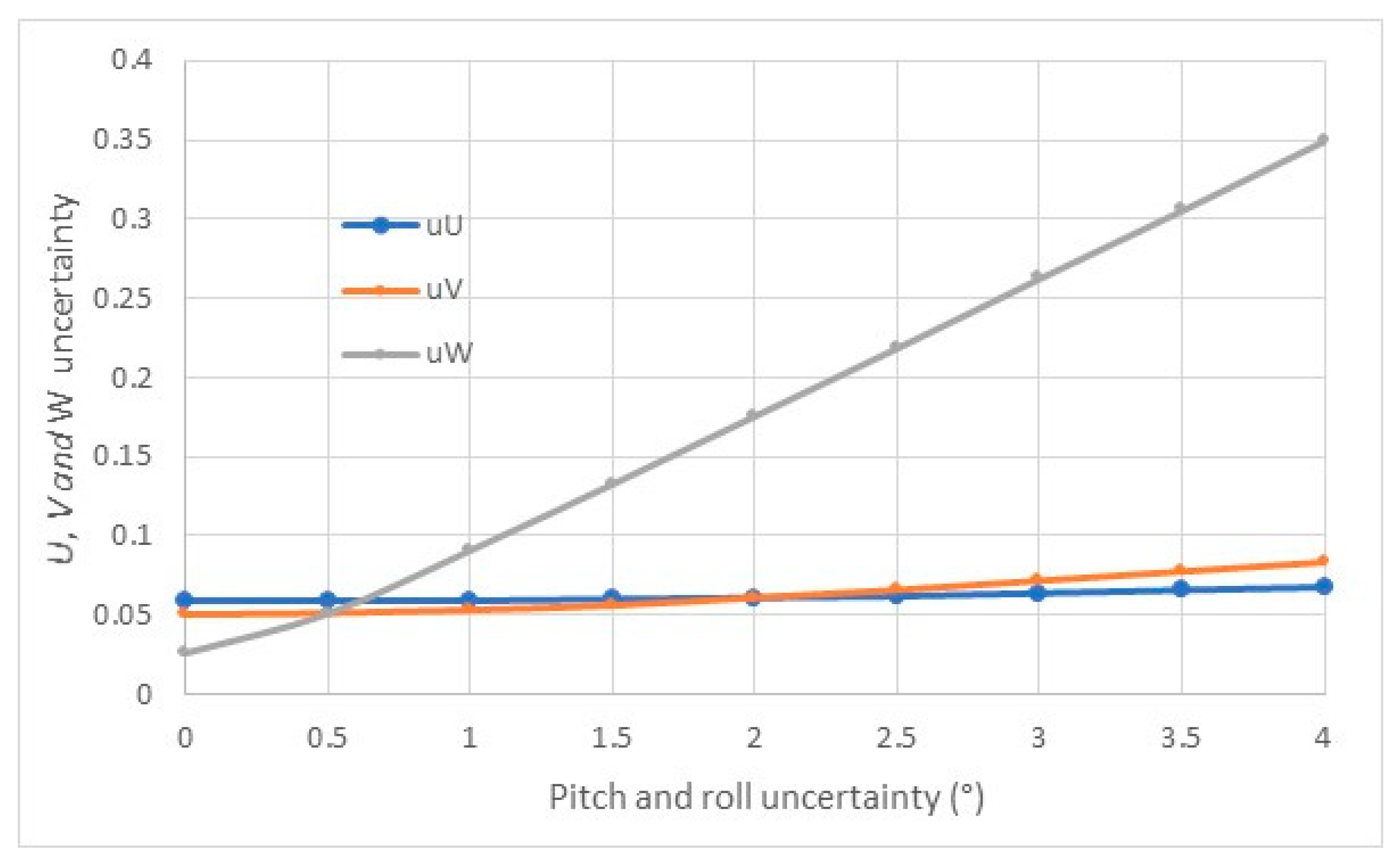
The second one, (Figure 5) shows the evolution of U, V and W uncertainties when the uncertainties on the roll and pitch measurements increase of the same value from 0 to 4 °, again for the values used in Table 1: α = 70 ° and θ = Ψ = 5 °, U = 2.87 m/s, V = - 4.09 m/s, W = - 0.85 m/s, u_α= 0.59 °. As expected, the uncertainties on U and V evolve moderately and the uncertainty on W increases linearly.

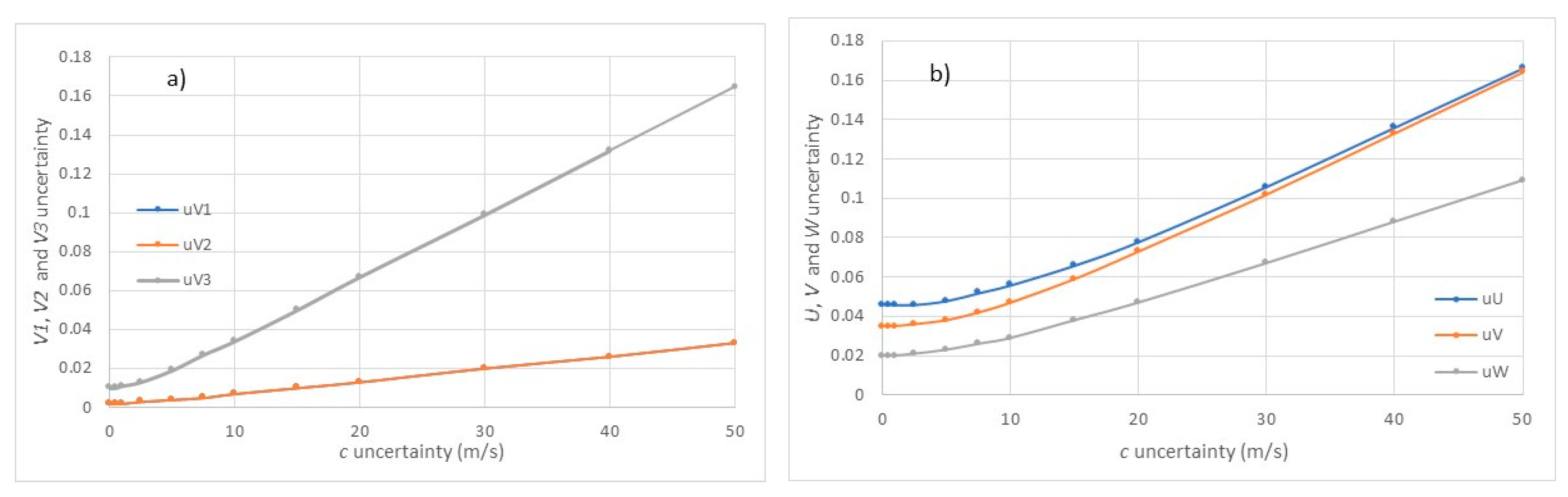
To quantify the effect of a large uncertainty on the speed of sound, we have plotted the evolution of the uncertainties in V₁, V₂ and V₃ (Figure 6a) and the evolution of the uncertainties in U, V and W, as a function of the uncertainty in c (Figure 6b). When the relative uncertainty u_Vi/V_i increases from 0.2 to 3.3 % as u_c increases from 0 to 50 m/s, the relative uncertainty u_U/U increases from 1.2 % to 5.7 %, which corresponds to a 4.5 % increase, and u_W/W increases from 2.3 % to 12.8 %, which corresponds to a 10.5 % increase.

5. Conclusions

Doppler effect current meters and profilers are technologically complex measuring instruments. They enable massive quantities of data to be collected on marine currents, but the complexity of their operation has always been an obstacle to a rigorous assessment of the uncertainties of their measurements. The method described in this publication takes into account all the elements involved in calculating the amplitude and direction of currents and the restitution made by the software of the instrument that rest on using of a transfer and a rotation matrix. This functioning responds to the method described in the Supplement 2 to the “Guide to the expression of uncertainty in measurement” edited by the BIPM [10].

Applying this method with available values of uncertainties, allows us to highlight a few important points:

- for velocities (V₁, V₂, V₃, V₄) resulting directly from the Doppler shift measurements, the uncertainty coming from a bad knowledge of the speed of sound c at the place of measurements is much greater than that on the measurement of the Doppler shift. The determination of this value is often neglected so that it can impact the measured velocity from 0.2 to 3.3 % for an uncertainty on c that vary from 0 to 50 m/s, and this impact on U, V and W components is still more important.

- The beams slant angle of ADCPs is an important element that participates to the final uncertainty on the amplitude of currents components. This is ignored in instruments specifications sheets.

- However, the compass and tilt sensors effects are the more influent sources of uncertainties. The compass errors can be the result of elements like battery packs that create magnetic anomalies or other devices as showed in [8]. As they often are ignored or not precisely quantified, they become sources of uncertainties.

The method proposed in this publication can be used to simulate the uncertainties that can be expected in different configurations and different practical applications.