Submitted:
12 June 2025
Posted:
16 June 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Methods
2.1. Modeling Software
2.2. Model Parameters
2.3. Numerical Simulations
3. Modular Model
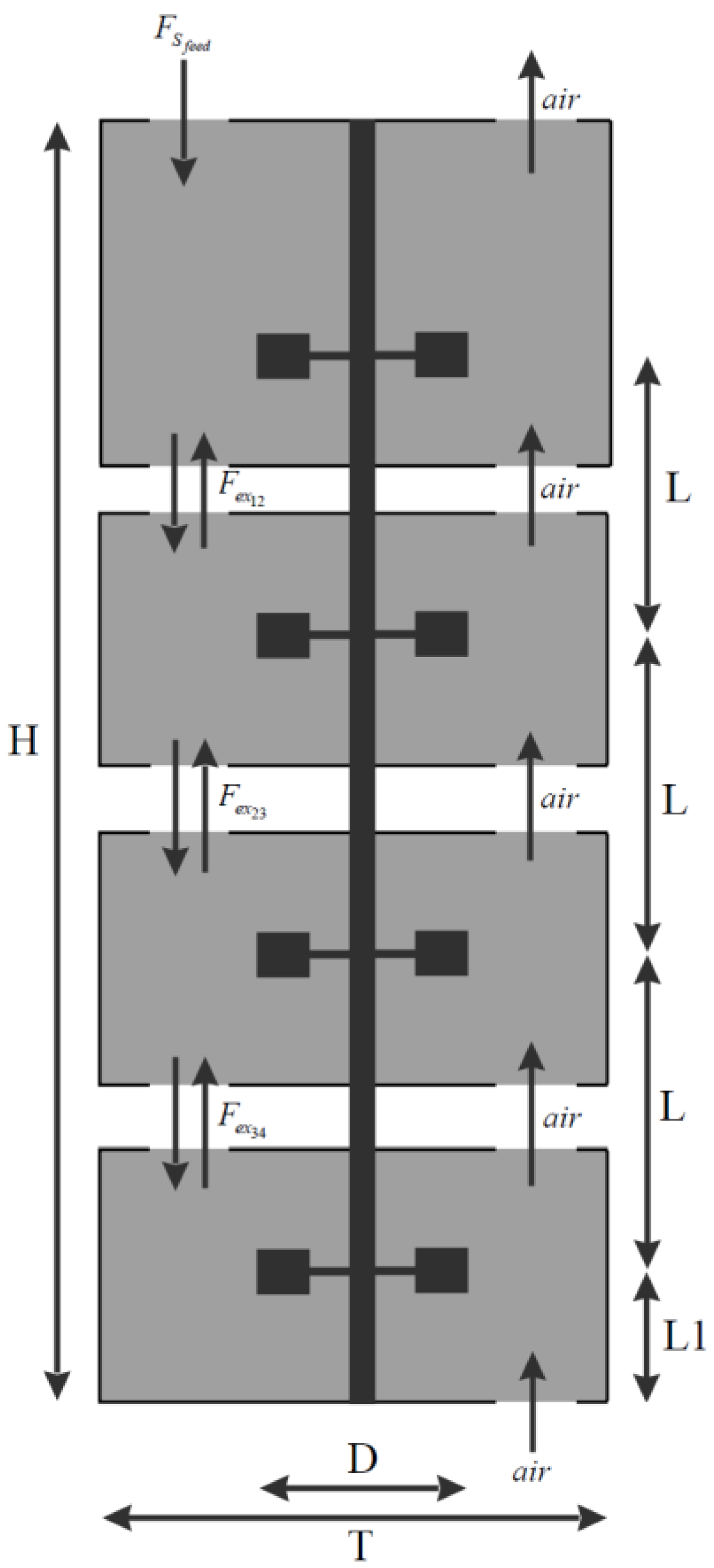
3.1. Bioreactor Compartmentalization
3.2. Modular Model Structure
3.3. Main Equations of the Modular Model
4. Results
4.1. Preliminary Information
4.2. Simulation Results for the Boundary Mixing Regimes
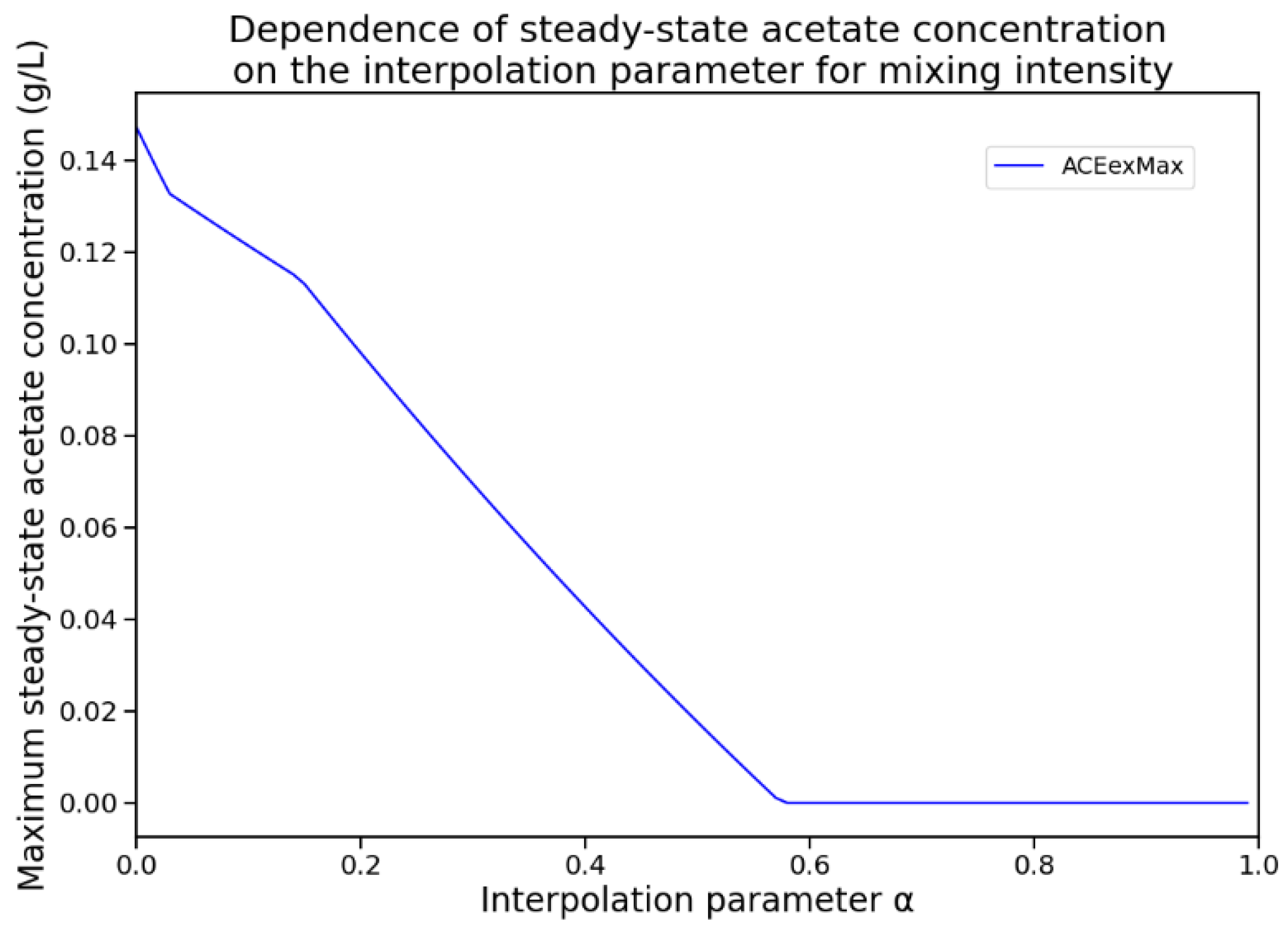
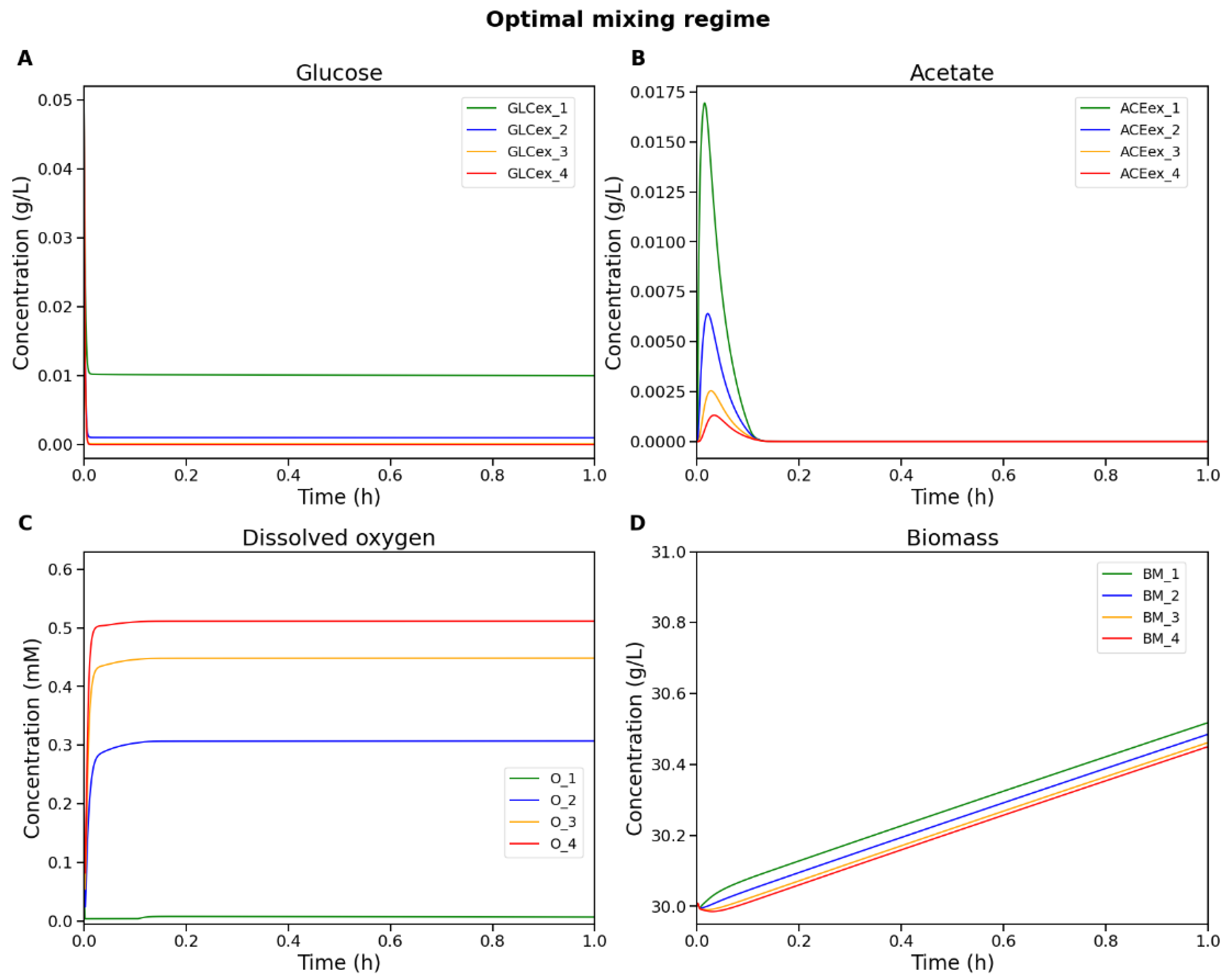
4.3. Optimal Mixing Regime Identification
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Calvin, K.; Dasgupta, D.; Krinner, G.; Mukherji, A.; Thorne, P.W.; Trisos, C.; Romero, J.; Aldunce, P.; Barrett, K.; Blanco, G.; et al. Climate change 2023: Synthesis report. Contribution of Working Groups I, II and III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Lee, H., Romero, J., Eds.; Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2023. [Google Scholar] [CrossRef]
- Cordell, W.T.; Avolio, G.; Takors, R.; Pfleger, B.F. Milligrams to kilograms: Making microbes work at scale. Trends in Biotechnology 2023, 41, 1442–1457. [Google Scholar] [CrossRef]
- Noorman, H.J.; Heijnen, J.J. Biochemical engineering’s grand adventure. Chemical Engineering Science 2017, 170, 677–693. [Google Scholar] [CrossRef]
- Straathof, A.J.J.; Wahl, S.A.; Benjamin, K.R.; Takors, R.; Wierckx, N.; Noorman, H.J. Grand research challenges for sustainable industrial biotechnology. Trends in Biotechnology 2019, 37, 1042–1050. [Google Scholar] [CrossRef] [PubMed]
- Keasling, J.D. Manufacturing molecules through metabolic engineering. Science 2010, 330, 1355–1358. [Google Scholar] [CrossRef] [PubMed]
- Stephanopoulos, G. Synthetic biology and metabolic engineering. ACS Synthetic Biology 2012, 1, 514–525. [Google Scholar] [CrossRef]
- Casini, A.; Chang, F.-Y.; Eluere, R.; King, A.M.; Young, E.M.; Dudley, Q.M.; Karim, A.; Pratt, K.; Bristol, C.; Forget, A.; et al. A pressure test to make 10 molecules in 90 days: External evaluation of methods to engineer biology. Journal of the American Chemical Society 2018, 140, 4302–4316. [Google Scholar] [CrossRef]
- Lee, S.Y.; Kim, H.U.; Chae, T.U.; Cho, J.S.; Kim, J.W.; Shin, J.H.; Kim, D.I.; Ko, Y.-S.; Jang, W.D.; Jang, Y.-S. A comprehensive metabolic map for production of bio-based chemicals. Nature Catalysis 2019, 2, 18–33. [Google Scholar] [CrossRef]
- Voigt, C.A. Synthetic biology 2020–2030: Six commercially-available products that are changing our world. Nature Communications 2020, 11, 6369. [Google Scholar] [CrossRef] [PubMed]
- Jullesson, D.; David, F.; Pfleger, B.; Nielsen, J. Impact of synthetic biology and metabolic engineering on industrial production of fine chemicals. Biotechnology Advances 2015, 33, 1395–1402. [Google Scholar] [CrossRef]
- Hemmerich, J.; Noack, S.; Wiechert, W.; Oldiges, M. Microbioreactor systems for accelerated bioprocess development. Biotechnology Journal 2018, 13, 1700141. [Google Scholar] [CrossRef]
- Crater, J.S.; Lievense, J.C. Scale-up of industrial microbial processes. FEMS Microbiology Letters 2018, 365, fny138. [Google Scholar] [CrossRef]
- Noorman, H. An industrial perspective on bioreactor scale-down: What we can learn from combined large-scale bioprocess and model fluid studies. Biotechnology Journal 2011, 6, 934–943. [Google Scholar] [CrossRef]
- Nadal-Rey, G. Modelling of gradients in industrial aerobic fed-batch fermentation processes. Ph.D. Thesis, Technical University of Denmark, Denmark, 2020. https://backend.orbit.dtu.dk/ws/portalfiles/portal/244849808/201001_PhDThesis_GiselaNadalRey.pdf.
- Biggs, B.W.; Alper, H.S.; Pfleger, B.F.; Tyo, K.E.J.; Santos, C.N.S.; Ajikumar, P.K.; Stephanopoulos, G. Enabling commercial success of industrial biotechnology. Science 2021, 374, 1563–1565. [Google Scholar] [CrossRef]
- Kampers, L.F.C.; Asin-Garcia, E.; Schaap, P.J.; Wagemakers, A.; Martins dos Santos, V.A.P. From innovation to application: Bridging the valley of death in industrial biotechnology. Trends in Biotechnology 2021, 39, 1240–1242. [Google Scholar] [CrossRef]
- de Lorenzo, V.; Couto, J. The important versus the exciting: Reining contradictions in contemporary biotechnology. Microbial Biotechnology 2018, 12, 32–34. [Google Scholar] [CrossRef]
- Nadal-Rey, G.; McClure, D.D.; Kavanagh, J.M.; Cornelissen, S.; Fletcher, D.F.; Gernaey, K.V. Understanding gradients in industrial bioreactors. Biotechnology Advances 2021, 46, 107660. [Google Scholar] [CrossRef]
- Vrábel, P.; van der Lans, R.G.J.M.; Luyben, K.Ch.A.M.; Boon, L.; Nienow, A.W. Mixing in large-scale vessels stirred with multiple radial or radial and axial up-pumping impellers: Modelling and measurements. Chemical Engineering Science 2000, 55, 5881–5896. [Google Scholar] [CrossRef]
- Xu, B.; Jahic, M.; Enfors, S.-O. Modeling of overflow metabolism in batch and fed-batch cultures of Escherichia coli. Biotechnology Progress 1999, 15, 81–90. [Google Scholar] [CrossRef]
- Wolfe, A.J. The acetate switch. Microbiology and Molecular Biology Reviews 2005, 69, 12–50. [Google Scholar] [CrossRef]
- Neubauer, P.; Åhman, M.; Törnkvist, M.; Larsson, G.; Enfors, S.-O. Response of guanosine tetraphosphate to glucose fluctuations in fed-batch cultivations of Escherichia coli. Journal of Biotechnology 1995, 43, 195–204. [Google Scholar] [CrossRef]
- Almquist, J.; Cvijovic, M.; Hatzimanikatis, V.; Nielsen, J.; Jirstrand, M. Kinetic models in industrial biotechnology – Improving cell factory performance. Metabolic Engineering 2014, 24, 38–60. [Google Scholar] [CrossRef]
- Vrábel, P.; van der Lans, R.G.J.M.; Cui, Y.Q.; Luyben, K.Ch.A.M. Compartment model approach. Chemical Engineering Research and Design 1999, 77, 291–302. [Google Scholar] [CrossRef]
- Oosterhuis, N.M.G.; Kossen, N.W.F. Dissolved oxygen concentration profiles in a production-scale bioreactor. Biotechnology and Bioengineering 1984, 26, 546–550. [Google Scholar] [CrossRef]
- Reuss, M.; Bajpai, R. Stirred tank models. In Biotechnology; Wiley: 1991; pp. 299–348. [CrossRef]
- Spann, R.; Glibstrup, J.; Pellicer-Alborch, K.; Junne, S.; Neubauer, P.; Roca, C.; Kold, D.; Lantz, A.E.; Sin, G.; Gernaey, K.V.; Krühne, U. CFD predicted pH gradients in lactic acid bacteria cultivations. Biotechnology and Bioengineering 2018, 116, 769–780. [Google Scholar] [CrossRef]
- Kuschel, M.; Takors, R. Simulated oxygen and glucose gradients as a prerequisite for predicting industrial scale performance a priori. Biotechnology and Bioengineering 2020, 117, 2760–2770. [Google Scholar] [CrossRef]
- Spann, R.; Gernaey, K.V.; Sin, G. A compartment model for risk-based monitoring of lactic acid bacteria cultivations. Biochemical Engineering Journal 2019, 151, 107293. [Google Scholar] [CrossRef]
- Bafna-Rührer, J. Strategies and tools to select E. coli fermenterphiles for industrial application. Ph.D. Thesis, Technical University of Denmark, Denmark, 2024. https://orbit.dtu.dk/files/375573898/Submission_version_PhD_thesis_JBR.pdf.
- Jahan, N.; Maeda, K.; Matsuoka, Y.; Sugimoto, Y.; Kurata, H. Development of an accurate kinetic model for the central carbon metabolism of Escherichia coli. Microbial Cell Factories 2016, 15, 112. [Google Scholar] [CrossRef]
- Kolpakov, F.; Akberdin, I.; Kashapov, T.; Kiselev, I.; Kolmykov, S.; Kondrakhin, Y.; Kutumova, E.; Mandrik, N.; Pintus, S.; Ryabova, A.; et al. BioUML: An integrated environment for systems biology and collaborative analysis of biomedical data. Nucleic Acids Research 2019, 47, W225–W233. [Google Scholar] [CrossRef]
- Kolpakov, F.; Akberdin, I.; Kiselev, I.; Kolmykov, S.; Kondrakhin, Y.; Kulyashov, M.; Kutumova, E.; Pintus, S.; Ryabova, A.; Sharipov, R.; et al. BioUML—towards a universal research platform. Nucleic Acids Research 2022, 50, W124–W131. [Google Scholar] [CrossRef]
- Hucka, M.; Bergmann, F.T.; Chaouiya, C.; Dräger, A.; Hoops, S.; Keating, S.M.; König, M.; Novère, N.L.; Myers, C.J.; Olivier, B.G.; et al. The Systems Biology Markup Language (SBML): Language specification for Level 3 Version 2 Core Release 2. Journal of Integrative Bioinformatics 2019, 16, jib-2019-0021. [Google Scholar] [CrossRef] [PubMed]
- Novère, N.L.; Hucka, M.; Mi, H.; Moodie, S.; Schreiber, F.; Sorokin, A.; Demir, E.; Wegner, K.; Aladjem, M.I.; Wimalaratne, S.M.; et al. The Systems Biology Graphical Notation. Nature Biotechnology 2009, 27, 735–741. [Google Scholar] [CrossRef]
- Kutumova, E.O.; Akberdin, I.R.; Egorova, V.S.; Kolesova, E.P.; Parodi, A.; Pokrovsky, V.S.; Zamyatnin, A.A. Jr; Kolpakov, F.A. Physiologically based pharmacokinetic model for predicting the biodistribution of albumin nanoparticles after induction and recovery from acute lung injury. Heliyon 2024, 10, e30962. [Google Scholar] [CrossRef]
- Miroshnichenko, M.I.; Kolpakov, F.A.; Akberdin, I.R. A modular mathematical model of the immune response for investigating the pathogenesis of infectious diseases. Viruses 2025, 17, 589. [Google Scholar] [CrossRef]
- Hindmarsh, A.C.; Brown, P.N.; Grant, K.E.; Lee, S.L.; Serban, R.; Shumaker, D.E.; Woodward, C.S. SUNDIALS. ACM Transactions on Mathematical Software 2005, 31, 363–396. [Google Scholar] [CrossRef]
- Nadal-Rey, G.; McClure, D.D.; Kavanagh, J.M.; Cassells, B.; Cornelissen, S.; Fletcher, D.F.; Gernaey, K.V. Development of dynamic compartment models for industrial aerobic fed-batch fermentation processes. Chemical Engineering Journal 2021, 420, 130402. [Google Scholar] [CrossRef]
- Oosterhuis, N.M.G. Scale-up of bioreactors: A scale-down approach. Ph.D. Thesis, TU Delft, Netherlands, 1984. http://resolver.tudelft.nl/uuid:03a887b7-8c20-4052-8d6b-7fe76918d7ec.
- Noorman, H.J.; van Winden, W.; Heijnen, J.J.; van der Lans, R.G.J.M. Intensified fermentation processes and equipment. In Intensification of Biobased Processes; The Royal Society of Chemistry: 2018; pp. 1–41. [CrossRef]
- Lapin, A.; Müller, D.; Reuss, M. Dynamic behavior of microbial populations in stirred bioreactors simulated with Euler−Lagrange methods: Traveling along the lifelines of single cells. Industrial & Engineering Chemistry Research 2004, 43, 4647–4656. [Google Scholar] [CrossRef]
- Hewitt, C.J.; Boon, L.A.; McFarlane, C.M.; Nienow, A.W. The use of flow cytometry to study the impact of fluid mechanical stress on Escherichia coli W3110 during continuous cultivation in an agitated bioreactor. Biotechnology and Bioengineering 1998, 59, 612–620. [Google Scholar] [CrossRef]
- Guardia Alba, M.J.; García Calvo, E. Characterization of bioreaction processes: Aerobic Escherichia coli cultures. Journal of Biotechnology 2000, 84, 107–118. [Google Scholar] [CrossRef]
- Lapin, A.; Schmid, J.; Reuss, M. Modeling the dynamics of E. coli populations in the three-dimensional turbulent field of a stirred-tank bioreactor—A structured–segregated approach. Chemical Engineering Science 2006, 61, 4783–4797. [Google Scholar] [CrossRef]
- Glazyrina, J.; Materne, E.-M.; Dreher, T.; Storm, D.; Junne, S.; Adams, T.; Greller, G.; Neubauer, P. High cell density cultivation and recombinant protein production with Escherichia coli in a rocking-motion-type bioreactor. Microbial Cell Factories 2010, 9, 42. [Google Scholar] [CrossRef]
- Zambrano, J.; Carlsson, B.; Diehl, S. Optimal steady-state design of zone volumes of bioreactors with Monod growth kinetics. Biochemical Engineering Journal 2015, 100, 59–66. [Google Scholar] [CrossRef]
- Garcia-Ochoa, F.; Gomez, E. Bioreactor scale-up and oxygen transfer rate in microbial processes: An overview. Biotechnology Advances 2009, 27, 153–176. [Google Scholar] [CrossRef]
- Tarlak, F. The use of predictive microbiology for the prediction of the shelf life of food products. Foods 2023, 12, 4461. [Google Scholar] [CrossRef]
- de Mello, A.F.M.; de Souza Vandenberghe, L.P.; Herrmann, L.W.; Letti, L.A.J.; Burgos, W.J.M.; Scapini, T.; Manzoki, M.C.; de Oliveira, P.Z.; Soccol, C.R. Strategies and engineering aspects on the scale-up of bioreactors for different bioprocesses. Systems Microbiology and Biomanufacturing 2023, 4, 365–385. [Google Scholar] [CrossRef]
- de Lamotte, A.; Delafosse, A.; Calvo, S.; Delvigne, F.; Toye, D. Investigating the effects of hydrodynamics and mixing on mass transfer through the free-surface in stirred tank bioreactors. Chemical Engineering Science 2017, 172, 125–142. [Google Scholar] [CrossRef]
- Garcia-Ochoa, F.; Gomez, E.; Santos, V.E. Fluid dynamic conditions and oxygen availability effects on microbial cultures in STBR: An overview. Biochemical Engineering Journal 2020, 164, 107803. [Google Scholar] [CrossRef]

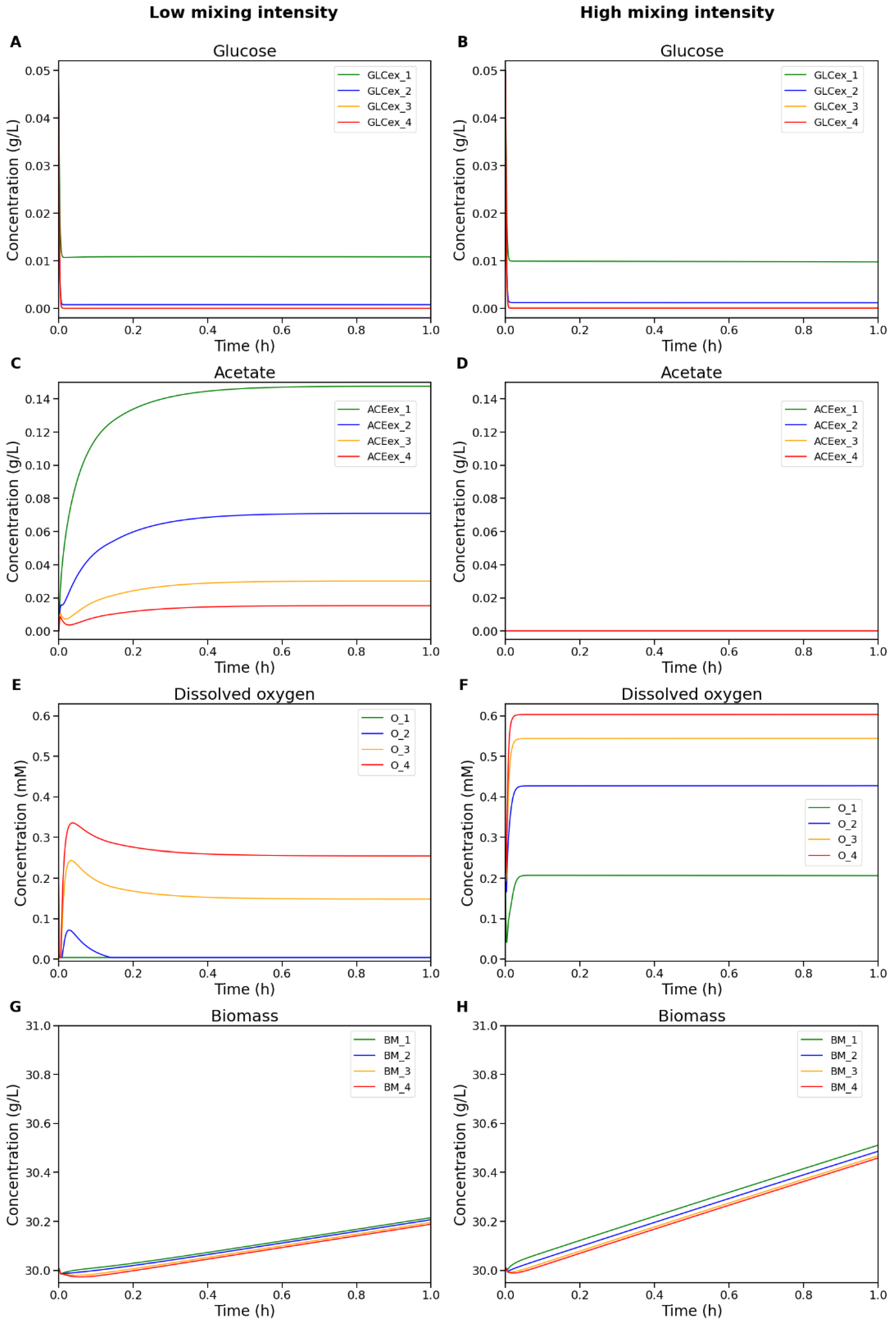
| Compartment | Total substrate uptake (gS/gX/h) |
Anaerobic substrate uptake (gS/gX/h) |
Metabolic regime |
|---|---|---|---|
| 1 (top) | 0.2245 | 0.1984 | Oxygen limitation |
| 2 | 0.0196 | 0.0 | Substrate starvation |
| 3 | 0.0015 | 0.0 | Substrate starvation |
| 4 (bottom) | 1.2522 × 10–4 | 0.0 | Substrate starvation |
| Compartment | Total substrate uptake (gS/gX/h) |
Anaerobic substrate uptake (gS/gX/h) |
Metabolic regime |
|---|---|---|---|
| 1 (top) | 0.2123 | 0.0 | Substrate limitation |
| 2 | 0.0304 | 0.0 | Substrate starvation |
| 3 | 0.0038 | 0.0 | Substrate starvation |
| 4 (bottom) | 5.4551 × 10–4 | 0.0 | Substrate starvation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





