Revisiting The Universe Expansion and Dark Energy Problem

1. Introduction

The general understanding today is that the Universe is expanding and accelerating based on experimental evidence and modeling considerations [1,2]. However there have been reservations questioning the acceleration evidence [e.g., [3,4]) mainly due to data and interpretation uncertainties. One of the key parameters affecting universe expansion is the Hubble Parameter (H), (e.g., [5]), quantifying the rate at which the universe is expanding at any given time (t):

$$H(t)={\displaystyle \frac{\dot{R}\left(t\right)}{R\left(t\right)}}$$

(1)

where R(t) is the length scale factor, describing how distances in the universe expand with time.

On the other hand, the general relativity formulated by Einstein [6], is the prevailing theoretical framework to describe the Universe evolution and dynamics. More specifically, the Friedman equations are the set of equations in cosmology that govern the expansion of space in homogeneous and isotropic models of the universe. They are derived from Einstein’s field equations of general relativity under the assumption of the Friedmann–Lemaître–Robertson–Walker (FLRW) metric (e.g., [5]). These equations describe the universe expansion, acceleration and energy conservation. A widely used approach to study universe dynamics, is based on the introduction of dark energy [7] described through the cosmology constant(Λ) [6]. In practice, Λ has been introduced into the original Friedmann Equations leading to modification (e.g., [5]).

It is noticed that the nature of dark energy has not been fully understood today and the constant value of Λ although it has been extensively used, it lacks yet adequate global acceptance. In fact, there are findings giving a preference towards a more dynamic behavior of the dark energy (e.g., [8]).

It should be noticed in addition, that quantum theory based on Heisenberg Uncertainty principle, predicts a rather significant energy density for empty space, but astronomical observations show that the energy density associated with the above cosmological constant, is quite small in serious discrepancy with the above quantum field theory ptredictions [9]. It is noticed that this very high discrepancy consists one of the major unresolved problems in cosmology today.

Another major challenge to the standard model is the “Hubble tension”—a significant discrepancy between measurements of the Hubble constant obtained from the early Universe (via cosmic microwave background data) and those derived from the local Universe (using Type Ia supernovae and Cepheid variables) [10]. Despite increasing precision on both fronts, the disagreement persists and has prompted speculation about possible new physics beyond the standard ΛCDM framework.

From the discussion above, it is rather clear that concerning the universe expansion and dark energy problem, there are important open questions that is worth revisiting. The present study pays such a revisit, trying to start from the basics. The ambition of the effort is to be conceptually in agreement with (a) the principle of the Least Action [11], (b) Newton’s Third Law of Motion [12] and (c) the logical principle: ‘simplicity first’. The whole approach starts with the Hubble parameter considerations and associated hypotheses.

2. The Present Approach and the Results

In this work, the Universe spatial curvature is considered flat (k=0). It has been a common approximation since several observations show that universe is very close to flat (e.g., [5]).

2.1. The Hubble Parameter and the Total Energy Density

As mentioned above, the Hubble parameter (H(t)) is given by Equation (1). A range of estimations for the H(t) for present time (H₀) based on observation data and their analysis [13,14] is:

H₀ ≈ (2,17÷2.37) × 10^-18 sec^-1

The above value seems to correlate rather well with the age of Universe (t₀ ≈ 4.4 x 10¹⁷ sec) (e.g., [5]):

$$H_0\approx {\displaystyle \frac{1}{t_0}}\approx 2.29\times {10}^{-18}{sec}^{-1}$$

(2)

a value well within the range given above.

It is logical to examine to what degree such an observation might not be a coincidence. Therefore, we are introducing the following two key hypotheses:

1st Key Hypothesis: The Hubble parameter is proposed to be given for the whole universe time by the following equation:

$$H\left(t\right)={\displaystyle \frac{\dot{R}\left(t\right)}{R\left(t\right)}}={\displaystyle \frac{1}{t}}$$

(3)

where t is the elapsed time after the Big Bang.

In consistency with above hypothesis, we introduce the additional key hypothesis.

2st Key Hypothesis: The concept of dark energy remains as the repulsive gravity constituent directly related to the attractive gravity constituents (e.g., matter, radiation). Such a hypothesis introduces a dynamic form of dark energy expressed through the dark energy density $\left({\rho }_{de}\right).$Thus, the total energy density (ρ) consists of the sum of the attractive gravity constituents $\left({\rho }_{ag}\right)$ (mainly matter (${\rho }_m)$ and radiation $\left({\rho }_{rad}\right))$and the repulsive gravity constituent (i.e., dark energy $\left({\rho }_{de}\right)):$

$$\rho ={{\rho }_{ag}+{\rho }_{de}\approx \rho }_m+{\rho }_{rad}+{\rho }_{de}$$

(4)

Equation (4) underlines the assumption that in the present concept, the universe exists due to the balancing coexistence of gravity attractive and gravity repulsing forces pointing out towards the 3rd Newton Law of Motion [12] concept.

The key questions here are: (a) to what degree such a concept meets the reality and (b) can it generate new knowledge useful to lead to new considerations on Universe nature and evolution?

We concentrate first at the total density evolution.

Let us consider the original first Friedmann equation for the total energy density (ρ):

$$({\displaystyle \frac{\dot{R}}{R}}{)}^2={\displaystyle \frac{8\pi G}{3c^2}}\rho$$

(5)

Equation (5) can be used to estimate the present time value ( ${\rho }_0$) using the $H_0$ value of Equation (2).

$${\rho }_0\approx 8.46\times {10}^{-10}Joules/m^3$$

(6)

a value rather close to the critical density given in literature (e.g., [5]): $7.8\times {10}^{-10}Joules/sec$The solution of Equation (5), taken into consideration Equation (3), gives the following simple relationship for the total density as a function of time:

$${\displaystyle \frac{\rho \left(t\right)}{{\rho }_b}}=({\displaystyle \frac{t}{t_b}}{)}^{-2}$$

(7)

where $t_b$ is the time when Equation (7) starts to apply and ${\rho }_b$ is the corresponding density.

$t_b$ is most likely to relate to the Planck time scale ( $t_{Pl}$) which is widely regarded as the transition point from a quantum gravitational epoch, to a classical, expanding universe and when the general relativity starts to apply. In that case, it is plausible to assume $t_b\approx t_{Pl}$. It is reminded that $t_{Pl}$ is given by the relationship [15].

$$t_{Pl}~\sqrt{{\displaystyle \frac{h·G}{2\pi c^5}}}=5.39\times {10}^{-44}sec$$

(8)

We can apply Equation (7) with ρ and t of the present time and estimate ${\rho }_b$ setting $t_b=t_{Pl}$ as estimated from Equation (8), The result has as follows:

$${\rho }_b~5.5\times {10}^{112}Joules/m^3$$

(9)

We can compare now this value with the Planck energy density scale. Recall that the Plank Energy density scale is given by the relationship:

$${\rho }_{Pl}~{\displaystyle \frac{2\pi c^7}{h{G}^2}}=4.63\times {10}^{113}Joules/m^3$$

(10)

It is clear that ${\rho }_b$ and ${\rho }_{Pl}$ are comparable!

This result is quite interesting if one takes also into consideration, that Planck energy density is directly related to the vacuum energy density $\left({\rho }_{QFT}\right)$ arising from quantum fluctuations of fields in space, when confined within the Planck regime. It is derived by summing the zero-point energies of quantum fields up to the Planck scale [16].

$${\rho }_b~{\rho }_{pl}~{\rho }_{QFT}~{10}^{113}Joules/m^3$$

(11)

Thus, the above findings have led to the following proposal for the universe energy density estimation:

$$\rho \left(t\right)~{\rho }_{Pl}·({\displaystyle \frac{t}{t_{Pl}}}{)}^{-2}{~\rho }_{QFT}·({\displaystyle \frac{t}{t_{Pl}}}{)}^{-2}$$

(12)

It should be underlined that Equation (12) expresses a very important finding i.e., it seems to resolve the cosmological constant problem controversy as mentioned above. Before proceeding and trying to have a better understanding, let us examine the problem in the inverse way. Recall from above, that ${\rho }_{QFT}~{10}^{113}Joules/m^3$and ${\rho }_0~{10}^{-9}Joules/m^3.$ Thus we can estimate the ratio: ${\displaystyle \frac{{\rho }_{QFT}}{{\rho }_0}}~{10}^{122}Joules/m^3$. On the other hand, by taken the estimations: $t_0\approx 4.4x{10}^{17}$sec and $t_{Pl}\approx 5.39\times {10}^{-44}sec,$ we obtain: ${\displaystyle \frac{t_0}{t_{PL}}}~{10}^{61}$. If we try to fit those two ratios into a power function with exponent n , the solution is clear: n= -2, reproducing Equation (7). It should be also undelined that by setting n= -2 we end up, through the Friedmann Equation (5), to the 1st hypothesis Equation (3).

The conclusion that can be derived here is that, if the abovementioned two hypotheses are proved to be valid, the cosmological constant problem does not exist anymore. It can be interpreted also that, if the above quantum field theory is adopted , this important finding can be considered as a first step towards the validity of the present theory.

2.2. The Universe Expansion and Total Energy

If we can derive the second derivative of R(t) expressing the Universe acceleration. We find the interesting result:

$$\ddot{R}\left(t\right)=0\left(13\right)$$

(13)

Equation (13) marks a significant departure from the present understanding on university acceleration. As discussed before, the latter seems to be widely supported but without full universal acceptance. It is worth noting, that Nielsen et al. [3] have revisited the existing evidence for the universe accelerated expansion by analyzing the dataset of Type Ia SuperNovae (SN Ia) [17]. A key conclusion was that the data were quite consistent with a constant rate of universe expansion.

The solution of Equation (13) gives the universe expansion:

$$R=c·t$$

(14)

Let us recall the original 2nd Friedmann Equation dealing with Universe acceleration:

$$\ddot{R}=-{\displaystyle \frac{4\pi G}{3c^2}}R(\rho +3P)$$

(15)

This leads to following relation for the pressure:

$$p=-{\displaystyle \frac{1}{3}}·\rho$$

(16)

To what degree Equation (16) makes sense, it is discussed later.

First, in order to get the whole picture, we consider the Friedmann energy conservation equation

$$\dot{\mathsf{\rho }}=-3{\displaystyle \frac{\dot{\mathrm{R}}}{\mathrm{R}}}(\mathsf{\rho }+\mathrm{P})$$

(17)

Recall that the universe total energy (E) can be approximated:

$$\mathrm{E}\approx \mathsf{\rho }·{\displaystyle \frac{4\pi }{3}}{\mathrm{R}}^3$$

(18)

We differentiate:

$${\displaystyle \frac{\partial \mathrm{E}}{\partial \mathrm{t}}}\approx {\displaystyle \frac{4\pi }{3}}(\dot{\mathsf{\rho }}·{\mathrm{R}}^3+3{\mathrm{R}}^2\mathsf{\rho })$$

(19)

Substituting $\dot{\mathsf{\rho }}$ given by Equation (17), we end up with the following relation regarding universe energy rate (ER):

$$ER={\displaystyle \frac{\partial \mathrm{E}}{\partial \mathrm{t}}}\approx -4\pi ·\dot{\mathrm{R}}·{\mathrm{R}}^2·\mathrm{P}$$

(20)

Equation (20) indicates that the universe energy evolution is controlled by the pressure P and consequently by the factors shaping up this pressure. Negative pressure is directly related to the energy inflow, contributing to the universe expansion.

Substituting now the pressure given by Equation (16) in the Equation (20), we obtain for the energy rate (ER):

$$ER={\displaystyle \frac{4\pi }{3}}·\dot{\mathrm{R}}·{\mathrm{R}}^2·\rho$$

(21)

Taking into consideration Equations (5), (14) and (21) we can express and estimate ER as follows:

$$\mathrm{E}\mathrm{R}\approx {{\displaystyle \frac{\mathrm{c}}{2\mathrm{G}}}}^5=1.81·{10}^{52}\mathrm{J}\mathrm{o}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{s}/\mathrm{s}\mathrm{e}\mathrm{c}$$

(22)

This result is also interesting: ER is a constant. If this is true, energy is pumped into the universe with a constant rate. In other words, the universe evolution is characterized by an additional global constant (ER): the expectation value of the universe inflow Energy Rate (ER).

It should be noted, in addition, that the relation (22) is expected to be valid up to the Planck epoch.

Recall that the Planck time scale (${\mathrm{t}}_{\mathrm{P}\mathrm{l}}$ ) is given by Equation (8) whereas the Planck energy scale (${\mathrm{E}}_{\mathrm{P}\mathrm{l}}$ ) is given by the relationship [17]:

$$E_{Pl}~\sqrt{{\displaystyle \frac{h·c^5}{2\pi G}}~}{10}^{9}Joules$$

(23)

The relations (8) and (23) can lead to the following scaling for ER:

$$ER={\displaystyle \frac{c^5}{2G}}~{\displaystyle \frac{E_{Pl}}{t_{Pl}}}$$

(24)

The above relationship, if it is true, is quite significant at least for the following reasons:

a)

The Universe seems to have its roots within its Planck regime exporting vacuum energy at a rate ER.

b)

The expectation value of ER is continuous and constant i.e., another new universal constant dictating the Universe dynamics.

It would be interesting to investigate further, whether this vacuum energy is exported to universe in the form of energy ‘$E_{Pl}$ bursts’ with a frequency ${\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$t_{Pl}$}\right.}$.

We are closing this topic by estimating the universe total energy evolution starting from Equation (24):

$$(E-E_{Pl})~ER·(t-t_{Pl})$$

(25)

In obtaining Equation (25) we have made the plausible assumption that the initial energy is scaled by the Planck energy $E_{Pl}$.

2.3. Universe Composition and Pressure

We have to go back to Equation (16) addressing the pressure vs density relationship. It is reminded that the current state-of-the art suggests that at the present time, the universe is composed mainly by matter and dark energy. Keeping in mind that (a) the present study is concentrating more on setting rather refine the present concept and (b) seeking for first order approximations drawn from the state of the art, we can claim that at the present time the matter energy density (${\rho }_{0,m}$ ) is given by the relationship ${\rho }_{0,m}\approx {\displaystyle \frac{1}{3}}{\rho }_0$ , which implies for the dark energy density $\left({\rho }_{0,de}\right)$:

$${\rho }_{0,de}\approx {\displaystyle \frac{2}{3}}·{\rho }_0$$

(26)

It is widely accepted that the matter related pressure is negligible and therefore, the universe total pressure mainly consists of the dark energy related pressure. Thus, for the present time:

$$P_0\approx {\mathrm{p}}_{0,\mathrm{d}\mathrm{e}}=-w_{0,de}·{\mathsf{\rho }}_{0,\mathrm{d}\mathrm{e}}\approx {\displaystyle \frac{2}{3}}·{\rho }_0$$

(27)

Concerning the value of $w_{de}$, the observation data analysis based on the cosmological constant approximates $w_{de}\approx w_{0,de}\approx -1$ .

In the frame of the present concept and taking into consideration Equations (4) and (27) we propose:

$$w_{0,de}\approx -{\displaystyle \frac{1}{2}}$$

(28)

It should be noted that there have been data past analyses considering $w_{de}$ as a variable suggesting higher values up to $w_{0,de}\approx 0.8$ [18]. In addition, they have been theoretical approaches considering a dynamic behavior of dark energy, like the quintessence (e.g., [19]), in which $w_{de}$ is a variable with values always greater than -1.

Furthermore, concerning Equation (28), a remark that could be made here, is the similarity to a fluid with a motion obeying Bernoulli theorem [20]. It is noticed that such a theorem is applicable to steady, inviscid and isentropic flows. However, Equation (28) has been derived from the present universe properties, a universe grown enough, allowing probably to characterize transient and non-isentropic effects as marginal. This remark could make sense for one trying to get further insight into the nature of dark energy.

Departing from the present time and moving backwards to the early universe, we are entering the regime where the main attractive gravity constituent is mainly radiation. Taking into consideration that in this case, $w_{ag}\approx {\displaystyle \frac{1}{3}}$ we can estimate from Equation (16), the dark energy density for early universe:

$${\rho }_{de}\approx {\displaystyle \frac{4}{5}}·\rho$$

(29)

If this is the case, we can observe that as we move from early universe to the universe of today, a mild decrease of the dark energy content from 0.8 to 0.7 is taking place. This finding needs further investigation, especially how the inflow energy is transformed to the various universe components over time.

It should be also underlined the key role of the dark energy, in ensuring a sustainable expansion of the universe, acting as a reactive force to gravity force, in conceptual agreement with the 3rd Newton Law of motion. The corresponding forcing symmetry is expressed through the conservation of ‘universe total pressure (PT)’ defined as follows:

$$PT=P-{\displaystyle \frac{1}{3}}·\rho =0$$

(30)

2.4. The Hubble Tension Problem

It is also worth examining to what degree the present theory affects the Hubble tension problem mentioned in Section 1. Looking for a representative set of observation data to work with, we ended up with the data presented in [21]. It is a collection of data covering a good range of redshift z=0.07- 3.30. It is noted that the application of Equation (3), leads to the following simple relationship for the Hubble parameter H(z):

$${\displaystyle \frac{H\left(z\right)}{H_0}}=1+z$$

(31)

It is reminded that value of $H_0$ is given in Equation (2).

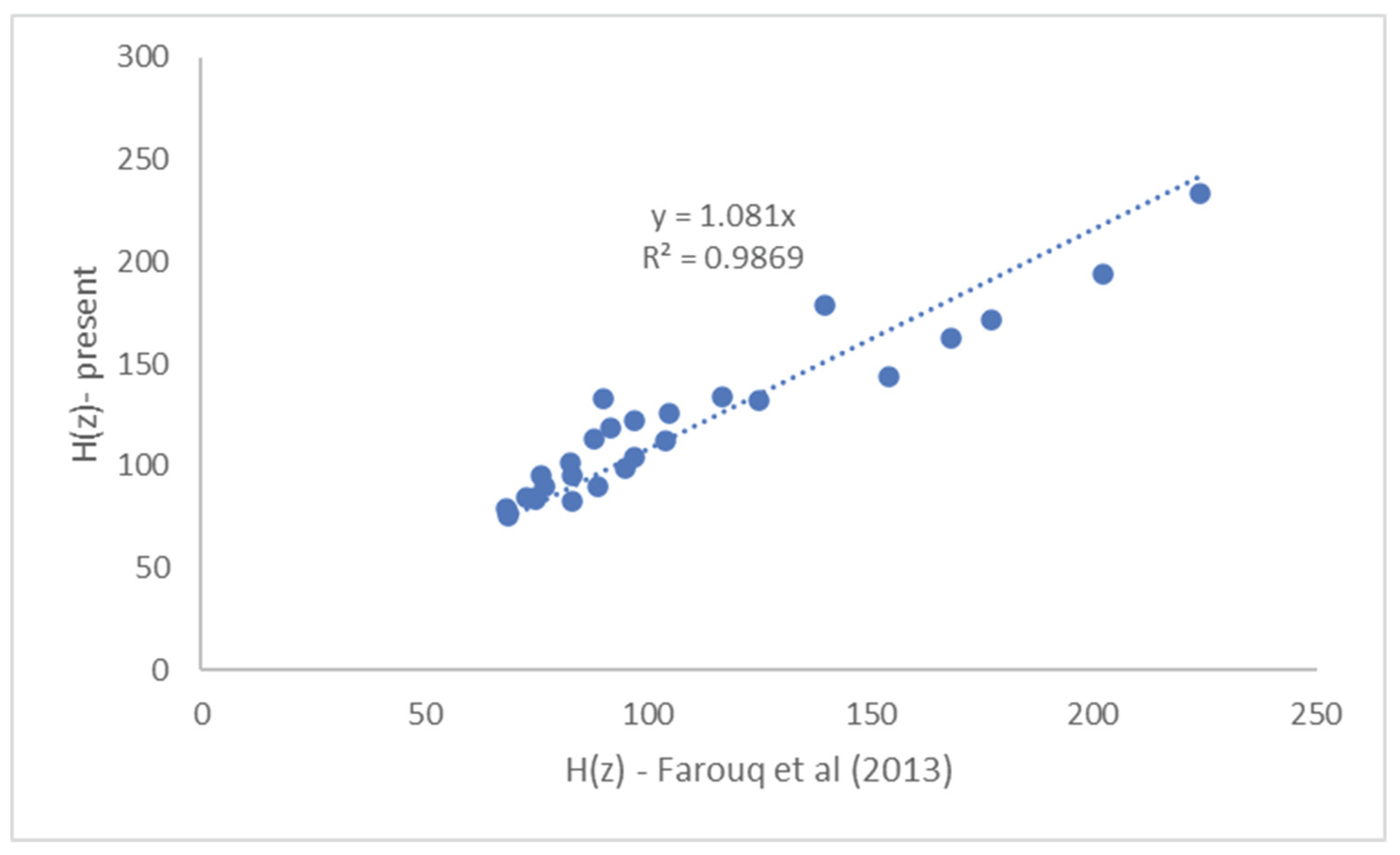
Figure 1 compares the presently produced H(z) values against the corresponding mean values reported in [21]. The results are quite comparable if one takes into consideration that the present model shows an average overprediction over 8% which is well within the reported uncertainties. It is noticed that the H(z) data [21] give an uncertainty which in terms of standard deviation over mean ratio, exceeds the 18%.

In conclusion the obtained results seem to confront with success the Hubble tension problem since it does not appear as a problem under the present theory. The recommendation is the present approach to be seriously considered for further observation data analysis

3. Concluding Remarks

Revisiting the problem of the universe expansion and dark energy and starting from first principles and introducing two key hypotheses (subsection 2.1), it has opened the way for various interesting and surprising findings that could guide into new considerations and theories concerning the birth of universe, its evolution and its sustainability.

The new concept obeys the general relativity theory and applies the Friedmann Equations but without the cosmological constant.

The proposed concept has led to universe energy density predictions (Section 2.1) up to the Planck epoch, quite comparable with the corresponding vacuum energy density predictions leading to an end of the cosmological constant problem controversy still pending today.

The present results (Section 2.2) support the theory that the Universe is born and maintained by quantum vacuum energy filling space. Such energy seems to be stable and dictated by a universal constant: the expectation value of the universe incoming Energy Rate (ER). It would be interesting also to investigate further, whether this vacuum energy is exported to universe in the form of energy ‘$E_{Pl}$ bursts’ with a frequency ${\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$t_{Pl}$}\right.}$.

Nevertheless, the universe seems macroscopically expanding but without acceleration. In other words, the universe remains sustainable with ’a minimum effort’ (i.e., zero acceleration) in conceptual agreement with the fundamental principle of least action.

The Universe composition evolution (Section 2.3) needs further in-depth investigation. Concerning the dark energy, the present preliminary analysis points out to a Bernoulli type behavior and estimates moderately higher contribution in the early universe era. What is also interesting is that the dark energy seems to be the constituent to set a sustainable balance between gravity attractive and repulsive forces in conceptual agreement with the 3rd Newton law of motion. The corresponding forcing symmetry is expressed through the conservation of the universe total pressure as defined by Equation (30).

The present concept seems to confront successfully the Hubble tension problem (Section 2.4) by proposing a single H0= 70.64 km/s/Mpc and H(z) given by the simple Equation (31)

It should be underlined that this study is a first attempt that needs further considerations aided by old and new observations and further theory ideas and refinements.