Structural Information Cosmology: A Novel Framework for Dark Matter and Quantum Gravity

1. Introduction

1.1. Fundamental Challenges in Modern Physics

Modern physics has successfully described the microscopic world and the cosmos through two revolutionary 20th-century theories: the Standard Model and General Relativity [1,2]. The Standard Model provides the foundation for particle physics by unifying the electromagnetic, weak, and strong forces within the framework of gauge symmetry [3]. General Relativity, which interprets gravity as the curvature of spacetime, has become the cornerstone of cosmology and astrophysics [1]. Both theories have demonstrated remarkable predictive power and accuracy within their respective domains. However, despite these successes, as we enter the 21st century, modern physics faces unresolved fundamental problems. The identities of dark matter [4] and dark energy [5,6,7], which are estimated to constitute about 95% of the total energy-matter content of the universe, remain elusive. The Grand Unified Theory (GUT) of the four fundamental forces has achieved only partial success, and a complete unification, especially one including gravity, remains an unfinished task. The black hole information paradox [8,9,10] reveals a fundamental conflict between General Relativity and quantum mechanics, while the absence of a complete quantum gravity [11,12] theory limits our understanding of physical phenomena at the Planck scale.

1.2. The Emergence of the Information Paradigm and the Need for a New Approach

In recent decades, there has been a surge of interest in the role of “information” in physics [13,14]. The holographic principle [3,15,16] suggests that all information contained within a three-dimensional volume can be encoded on its two-dimensional boundary. The AdS/CFT correspondence [17,18] demonstrates an informational link between gravitational theories and quantum field theories. Furthermore, advancements in quantum information theory [19], with concepts such as entanglement and information scrambling [20], are providing new insights into the nature of black holes and spacetime [21,22,23,24,25].

These developments suggest that information may play a role as fundamental as, or even more fundamental than, matter and energy in the description of physical phenomena. However, existing approaches have predominantly focused on the quantity of information (as exemplified by the Bekenstein-Hawking formula, where black hole entropy is proportional to its area [26,27]). The impact of information’s structural complexity and hierarchical organization on physical phenomena has, by contrast, been insufficiently explored in a systematic manner.

1.3. Proposal of Structural Information Cosmology (SIC)

Against this backdrop, this paper proposes a new theoretical framework termed “Structural Information Cosmology (SIC)”. The core idea of SIC is to perceive the fundamental constituents of the universe not only in terms of the distribution of matter and energy but also through the structural complexity and hierarchical organization of information. SIC introduces a structural information field, $\mathcal{C}(\overrightarrow{x},t)$, to describe the structural complexity of information at each point in spacetime. In this paper, as an initial approximation, this field is treated as a dynamical scalar field. However, its intrinsic nature is not merely to represent the quantity of information but to capture how information is hierarchically organized and forms patterns. All physical phenomena, including gravity, are interpreted as consequences of the spatial distribution and temporal evolution of this structural information field. Future research will explore the possibility that this field may possess a more complex dynamical structure through its connection with quantum wavefunctions, which is anticipated to serve as a bridge between quantum information theory [19] and macroscopic physical phenomena.

1.4. Purpose and Scope of the Paper

The primary objectives of this paper are as follows:

First, to clearly present the basic assumptions and mathematical framework of SIC, including the derivation of a modified Lagrangian and field equations that incorporate the structural information field.

Second, to calculate one of the specific predictions of SIC, namely the spatial modulation of the effective gravitational coupling constant $G_{\mathrm{eff}}\left(\overrightarrow{x}\right)$, and to explore how this might offer an explanation for dark matter phenomena.

Third, to present, at a conceptual level, new perspectives that SIC can offer on the unification of the four fundamental forces, the interpretation of black holes, and various cosmological problems.

Fourth, to propose specific directions for future theoretical development and experimental or observational verification. This paper focuses on presenting the foundational theoretical framework of SIC, aiming to explore the potential of a new paradigm that includes a concrete mathematical structure and testable physical predictions. Although detailed calculations and precise comparisons with observational data are left for future work, this paper will present the core mathematical structure and key predictions of SIC to demonstrate its potential for empirical verification, thereby intending to stimulate active discussion within the physics community and foster systematic follow-up research.

2. Core Assumptions and Framework of SIC

2.1. Introduction of the Structural Information Field and Basic Assumptions

The core of SIC lies in introducing a new physical entity, the structural information field $\mathcal{C}(\overrightarrow{x},t)$. This field possesses a fundamentally different character from conventional matter or energy fields.

Basic Assumption 1: All regions of the universe are filled with the structural information field $\mathcal{C}(\overrightarrow{x},t)$, which represents the structural complexity of information at a given spacetime point. Here, structural complexity refers not merely to the quantity of information (e.g., Shannon entropy [28] or thermodynamic entropy), but to how information is hierarchically organized and forms patterns[23]. (This could potentially be related to measures like Kolmogorov complexity or other metrics in algorithmic information theory [29], but in this paper, it is primarily introduced as a phenomenological field.)

Basic Assumption 2: The $\mathcal{C}$ field is a dynamical entity that evolves over time and possesses self-interactions. Furthermore, this field directly couples to spacetime geometry, thereby influencing all physical interactions, including gravitational phenomena. (This bears similarities to how scalar fields couple to gravity in scalar-tensor theories [30,31], but SIC differentiates itself in the physical interpretation of $\mathcal{C}$ and its dynamical terms.)

Basic Assumption 3: In this paper, as an initial approximation, $\mathcal{C}$ is treated as a scalar field. This is for mathematical simplicity, and future research may explore more complex tensor structures or quantum mechanical properties (such as the complex phase discussed in Section 3.2.4). (Various scalar field models, such as inflaton or quintessence fields [32], have been studied in cosmology.)

2.2. Construction of the SIC Lagrangian

To describe a physical system that includes the structural information field, we propose the following SIC Lagrangian:

$${\mathcal{L}}_{\mathrm{SIC}}=\left({\displaystyle \frac{c^4}{16\pi G_N}}+\beta {\mathcal{C}}^2\right)R+\lambda {\left(g^{\mu \nu }{\nabla }_{\mu }\mathcal{C}{\nabla }_{\nu }\mathcal{C}\right)}^2-V\left(\mathcal{C}\right)+{\mathcal{L}}_M$$

The physical meaning of each term is as follows:

Standard Gravitational Term: ${\displaystyle \frac{c^4}{16\pi G_N}}R$ is the Einstein-Hilbert action, representing the spacetime curvature term in standard General Relativity [1,2,33].

Information-Gravity Coupling Term: $\beta {\mathcal{C}}^{2}R$ represents a non-minimal coupling between the structural information field and spacetime curvature. This form of coupling is significantly explored in scalar-tensor theories [30,31] and modified gravity theories [12,34]. Here, the coupling constant $\beta$ can have the following physical implications (its value should be determined by future observations or theoretical consistency):

−

$\beta >0$: As the structural information becomes more complex (i.e., as the value of $\mathcal{C}$ increases), the response to spacetime curvature changes, potentially leading to an effect of weakened effective gravity.

−

$\beta <0$: As the structural information becomes more complex, it could lead to an effect of strengthened effective gravity.

−

$\beta =0$: The direct non-minimal coupling between the information field and gravitational curvature vanishes, approaching standard minimally coupled gravity.

−

$\mathcal{C}$ Field Kinetic Term: $\lambda {\left(g^{\mu \nu }{\nabla }_{\mu }\mathcal{C}{\nabla }_{\nu }\mathcal{C}\right)}^2$ is the term describing the kinetic energy of the structural information field.

−

Coupling Constant $\lambda$: This constant determines the dynamical characteristics of the information structure. The sign and magnitude of $\lambda$ significantly influence the stability of the information structure dynamics (e.g., the appearance of ghost states) and the propagation characteristics of its perturbations, which requires detailed analysis in future work.

−

$\lambda =0$: The higher-order kinetic term (of the ${(\nabla \mathcal{C})}^4$ form) for the $\mathcal{C}$ field vanishes. If a standard kinetic term (of the form $-{\displaystyle \frac{1}{2}}{(\nabla \mathcal{C})}^2$) is not included in this Lagrangian, this could mean that the $\mathcal{C}$ field might lack dynamical degrees of freedom. Self-interaction due to $V\left(\mathcal{C}\right)$ would still exist.

−

This term is of a k-essence form [32], suggesting that the rate of change of the information structure itself can produce new physical effects. Notably, this implies the potential to provide dynamical characteristics similar to dark energy [9,35] or an inflaton field.

−

Self-Interaction Potential: $V\left(\mathcal{C}\right)$ is the self-interaction potential of the structural information field, indicating the extent to which certain values of the information structure are energetically favored. The form of this potential determines properties such as the mass of the $\mathcal{C}$ field (if any), its vacuum states, and its cosmological evolution (e.g., symmetry breaking, phase transitions). This is a crucial element in cosmological scalar field models [5,32].

−

Matter Lagrangian: ${\mathcal{L}}_M$ is the Lagrangian for standard matter fields (fermions, gauge fields, etc.). (A general description of this can be found in standard quantum field theory textbooks. This paper focuses on the interaction with the $\mathcal{C}$ field rather than the specific form of ${\mathcal{L}}_M$.)

2.3. Theoretical Justification for Parameter Introduction

The parameters $\beta$ and $\lambda$ (and those within $V\left(\mathcal{C}\right)$), introduced with the new field and interactions, are core parts of the theory. Their introduction is based on the following general principles and theoretical considerations in constructing physical theories.

• Generality and Systematic Construction of the Theory: When systematically considering physically possible interactions, it is a natural approach to include the simplest yet significant forms of coupling that the structural information field $\mathcal{C}$ can have with established fields (e.g., the Ricci scalar R representing spacetime curvature, and terms representing the self-dynamics of $\mathcal{C}$ like ${\nabla }_{\mu }\mathcal{C}$). This aligns with the spirit of Effective Field Theory, which considers all allowed terms under certain symmetries and dimensions, and similar systematic approaches are pursued in constructing general scalar-tensor theories such as Horndeski theory [31] or DHOST theories [36]. The proposed $\beta {\mathcal{C}}^{2}R$ term and the $\lambda {(\nabla \mathcal{C})}^4$ term in this paper are examples considered in this context.
• Dimensional Analysis and Adherence to Fundamental Symmetries: Each term in the Lagrangian must have the correct physical dimensions (the action is dimensionless, while the Lagrangian density typically has dimensions of ${\left[energy\right]}^4$ or ${\left[length\right]}^{-4}$). Furthermore, to ensure the universality of physical laws, the simplest forms that satisfy fundamental symmetries such as Lorentz invariance (locally) and general covariance are prioritized. General covariance is one of the core principles of General Relativity [1,2].
• Consistency with Existing Theories (Correspondence Principle): A new theory should be able to reproduce previously successful and well-verified theories in certain limits. The SIC Lagrangian precisely reduces to standard General Relativity [1,2,33] coupled minimally to matter systems in the limit where the coupling constants $\beta \to 0$, $\lambda \to 0$, and the potential $V\left(\mathcal{C}\right)$ becomes a constant (or zero). This is an important feature ensuring that SIC theory aligns with well-established physics at low energies or under specific conditions. Consequently, the values of $\beta$ and $\lambda$ can be strongly constrained by the results of existing high-precision gravitational experiments [37].
• Predictive Power and Falsifiability: For a theory to be scientific, it must make testable predictions. Specific (non-zero) values of the parameters $\beta$ and $\lambda$ lead to predictions of new physical phenomena not present in standard theories (e.g., the modulation of $G_{\mathrm{eff}}$ discussed in Section 3.1). This provides the possibility to verify the theory or at least constrain its parameter space through astronomical observations (e.g., gravitational wave observations [38], black hole shadow observations [39]) or precision experiments [37].

Based on these theoretical grounds, the main terms and parameters of the SIC Lagrangian have been introduced, forming the mathematical structure of the theory and the basis for deriving concrete physical predictions.

2.4. Derivation of Field Equations

The field equations describing the dynamics of the physical system from the SIC Lagrangian ${\mathcal{L}}_{\mathrm{SIC}}$ presented in Section 2.2 are derived by applying the principle of least action, i.e., the variational principle $\delta S=\int \delta \left(\sqrt{-g}{\mathcal{L}}_{\mathrm{SIC}}\right)d^{4}x=0$. This is a standard procedure for deriving field equations in modern theoretical physics [2,33]. By varying the action with respect to the spacetime metric $g_{\mu \nu }$, we obtain the gravitational field equations, i.e., the Modified Einstein Field Equations:

$$\left({\displaystyle \frac{c^4}{16\pi G_N}}+\beta {\mathcal{C}}^2\right)G_{\mu \nu }+\beta \left({\nabla }_{\mu }{\nabla }_{\nu }{\mathcal{C}}^2-g_{\mu \nu }\square {\mathcal{C}}^2\right)={\displaystyle \frac{8\pi G_N}{c^4}}\left(T_{\mu \nu }^{\left(M\right)}+T_{\mu \nu }^{\left(\mathcal{C}\right)}\right)$$

The terms here signify:

• $G_{\mu \nu }\equiv R_{\mu \nu }-{\displaystyle \frac{1}{2}}R{g}_{\mu \nu }$ is the Einstein tensor, representing the curvature of spacetime.
• ${\nabla }_{\mu }$ denotes the covariant derivative, and $\square \equiv g^{\alpha \beta }{\nabla }_{\alpha }{\nabla }_{\beta }$ signifies the d’Alembertian operator. Thus, the term $\beta ({\nabla }_{\mu }{\nabla }_{\nu }{\mathcal{C}}^2-g_{\mu \nu }\square {\mathcal{C}}^2)$ is a geometric term related to the second derivatives of the $\mathcal{C}$ field.
• $T_{\mu \nu }^{\left(M\right)}$ is the energy-momentum tensor of standard matter, derived from the standard matter Lagrangian ${\mathcal{L}}_M$.
• $T_{\mu \nu }^{\left(\mathcal{C}\right)}$ is the energy-momentum tensor of the structural information field, derived from the $\mathcal{C}$ field’s dynamical part, i.e., ${\mathcal{L}}_{\mathcal{C}}=\lambda {\left(g^{\alpha \beta }{\nabla }_{\alpha }\mathcal{C}{\nabla }_{\beta }\mathcal{C}\right)}^2-V\left(\mathcal{C}\right)$, in the standard manner ($T_{\alpha \beta }=-2{\displaystyle \frac{\delta {\mathcal{L}}_{\mathcal{C}}}{\delta g^{\alpha \beta }}}+g_{\alpha \beta }{\mathcal{L}}_{\mathcal{C}}$) [2]. This term represents the energy and momentum distribution of the $\mathcal{C}$ field itself.

This modified Einstein field equation shows that the effective gravitational coupling becomes dependent on $\mathcal{C}$, as seen in the first term on the left-hand side (see Section 3.1.2 for $G_{\mathrm{eff}}$), and additionally, that the dynamics of the $\mathcal{C}$ field and its direct coupling to spacetime contribute to gravitational phenomena.

Furthermore, from the Euler-Lagrange equation for the structural information field $\mathcal{C}$, its equation of motion is given by:

$${\nabla }_{\mu }\left[{\displaystyle \frac{\partial {\mathcal{L}}_{\mathrm{SIC}}}{\partial \left({\nabla }_{\mu }\mathcal{C}\right)}}\right]-{\displaystyle \frac{\partial {\mathcal{L}}_{\mathrm{SIC}}}{\partial \mathcal{C}}}=0$$

Substituting the specific form of ${\mathcal{L}}_{\mathrm{SIC}}$ and simplifying, we get:

$${\nabla }_{\mu }\left[4\lambda \left(g^{\alpha \beta }{\nabla }_{\alpha }\mathcal{C}{\nabla }_{\beta }\mathcal{C}\right){\nabla }^{\mu }\mathcal{C}\right]+V^{\prime }\left(\mathcal{C}\right)-2\beta R\mathcal{C}=0$$

where $V^{\prime }\left(\mathcal{C}\right)\equiv dV/d\mathcal{C}$. This equation shows that the spacetime evolution of the structural information field $\mathcal{C}$ is determined by its self-dynamics (higher-order kinetic term, potential $V^{\prime }\left(\mathcal{C}\right)$) and its non-minimal coupling to spacetime curvature R ($-2\beta R\mathcal{C}$). These two field equations (the modified EFE and the equation of motion for $\mathcal{C}$) are coupled and form the complete dynamical system of the SIC theory.

2.5. Theoretical Consistency and Exploration Directions

The proposed SIC framework presents the following theoretical considerations and directions for future exploration:

• Causality and Stability: The kinetic term $\lambda {\left(g^{\mu \nu }{\nabla }_{\mu }\mathcal{C}{\nabla }_{\nu }\mathcal{C}\right)}^2$ in the presented Lagrangian is a form of k-essence [32]. In such models, the propagation speed of $\mathcal{C}$ field perturbations can depend on the background value of $\mathcal{C}$ and its rate of change. Under certain conditions, there is a mathematical possibility that the propagation speed of perturbations in these k-essence models could differ from the speed of light, potentially exceeding it [32,35]. This is an important research topic in general scalar-tensor theories [31,36] and modified gravity theories [11,12]. This aspect is currently regarded as an open possibility. The physical meaning of such solutions, their stability (e.g., the appearance of ghost issues or Laplacian instabilities), and their consistency with macroscopic causality are crucial research topics requiring careful analysis in the future. In this paper, we primarily focus on the solutions of the classical field equations and their phenomenological implications, aiming to explore physically plausible solutions.
• Energy Conditions: For the $\mathcal{C}$ field to play a cosmologically significant role, its energy-momentum tensor $T_{\mu \nu }^{\left(\mathcal{C}\right)}$ may need to satisfy certain energy conditions (e.g., Weak Energy Condition (WEC), Null Energy Condition (NEC), Dominant Energy Condition (DEC), etc. [2,33]). These conditions are generally considered to characterize physically reasonable matter or fields and are related, for example, to the validity of singularity theorems or the possibility of exotic spacetime structures like wormholes. Whether $T_{\mu \nu }^{\left(\mathcal{C}\right)}$ satisfies these conditions largely depends on the form of the potential $V\left(\mathcal{C}\right)$ and the value of the kinetic coefficient $\lambda$. For instance, explaining dark energy often requires a negative pressure ($p<-\rho /3$), which might violate certain energy conditions [35]. To ensure the physical viability of the SIC theory, it is crucial to find parameter regions that satisfy these energy conditions or to clearly understand the physical implications if certain conditions are violated.
• Reduction to Standard Theories: As mentioned in Section 2.3, in the limit where the coupling constants $\beta =0$, $\lambda =0$, and the potential $V\left(\mathcal{C}\right)$ is a constant (or zero), the SIC theory exactly reduces to standard General Relativity [1,2,33] minimally coupled to matter systems. This is an important feature ensuring that the theory satisfies the correspondence principle, aligning with well-established physics at low energies or under specific conditions. Therefore, the predictions of SIC theory can be strongly constrained by comparison with the results of existing precision gravitational experiments [37].

In the next section, based on this theoretical framework, we will explore specific physical predictions, such as how the $\mathcal{C}$ field might alter the effective gravitational coupling constant, and discuss potential applications of the SIC theory.

3. Key Predictions and Applications

3.1. Spatial Modulation of the Effective Gravitational Coupling Constant

3.1.1. Theoretical Background

One of the most direct and verifiable predictions of Structural Information Cosmology (SIC) is that the effective gravitational coupling constant, $G_{\mathrm{eff}}$, can be spatiotemporally modulated according to the local value of the structural information field $\mathcal{C}(\overrightarrow{x},t)$. This is a natural consequence of the SIC Lagrangian presented in Chapter 2 and the modified Einstein field equations derived therefrom. In standard General Relativity, Newton’s constant $G_N$, which represents the strength of gravitational interaction, is considered a fundamental constant, invariant throughout the universe [1,2]. However, in SIC, as discussed in Section 2.2, the existence of a non-minimal coupling term ($\beta {\mathcal{C}}^{2}R$) between the structural information field $\mathcal{C}$ and spacetime curvature R opens up new possibilities for the way gravity acts locally—that is, for its “strength” to vary—depending on the distribution of the $\mathcal{C}$ field. This approach can find similarities and differences in the context of scalar-tensor theories such as Brans-Dicke theory [30], which explored the idea that the gravitational constant could vary cosmologically, or more general modified gravity theories [11,12].

3.1.2. Derivation of the Effective Gravitational Coupling Constant

The modified Einstein field equations presented in Section 2.4 are as follows:

$$\left({\displaystyle \frac{c^4}{16\pi G_N}}+\beta {\mathcal{C}}^2\right)G_{\mu \nu }+\beta ({\nabla }_{\mu }{\nabla }_{\nu }-g_{\mu \nu }\square ){\mathcal{C}}^2={\displaystyle \frac{8\pi G_N}{c^4}}\left(T_{\mu \nu }^{\left(M\right)}+T_{\mu \nu }^{\left(\mathcal{C}\right)}\right)$$

Here, the first term on the left-hand side, i.e., $({\displaystyle \frac{c^4}{16\pi G_N}}+\beta {\mathcal{C}}^2)G_{\mu \nu }$, is the part that directly couples with the Einstein tensor $G_{\mu \nu }$, corresponding to the ${\displaystyle \frac{c^4}{16\pi G_N}}{G}_{\mu \nu }$ term in standard General Relativity [2,33]. If we wish to approximately describe some of the effects of this modified gravity theory in the form of a standard Einstein equation with an effective gravitational constant $G_{\mathrm{eff}}$—that is, if we consider the main gravitational term on the left-hand side as ${\displaystyle \frac{c^4}{16\pi G_{\mathrm{eff}}}}{G}_{\mu \nu }$ (interpreting the remaining terms of the equation, such as $\beta ({\nabla }_{\mu }{\nabla }_{\nu }-g_{\mu \nu }\square ){\mathcal{C}}^2$ and $T_{\mu \nu }^{\left(\mathcal{C}\right)}$, as part of an effective energy-momentum tensor or considering them separately)—we can set up the following equality by comparing the coefficients of $G_{\mu \nu }$:

$${\displaystyle \frac{c^4}{16\pi G_{\mathrm{eff}}}}={\displaystyle \frac{c^4}{16\pi G_N}}+\beta {\mathcal{C}}^2$$

From this relation, the effective gravitational coupling constant $G_{\mathrm{eff}}$ is expressed as a function of the $\mathcal{C}$ field as follows:

$$G_{\mathrm{eff}}(\overrightarrow{x},t)={\displaystyle \frac{G_N}{1+\frac{16\pi G_N}{c^4}\beta \mathcal{C}{(\overrightarrow{x},t)}^2}}$$

This equation is one of the core predictions of SIC theory, clearly demonstrating that the effective strength of gravitational interaction can deviate from the standard value $G_N$ depending on the local value of the structural information field $\mathcal{C}$. Depending on the sign and magnitude of the coupling constant $\beta$, and the distribution of the $\mathcal{C}$ field, $G_{\mathrm{eff}}$ can be larger or smaller than $G_N$, leading to spatiotemporally varying gravitational effects. In this section, we will primarily focus on the spatial aspects of this gravitational modulation effect, considering a static distribution $\mathcal{C}\left(\overrightarrow{x}\right)$ and exploring its implications.

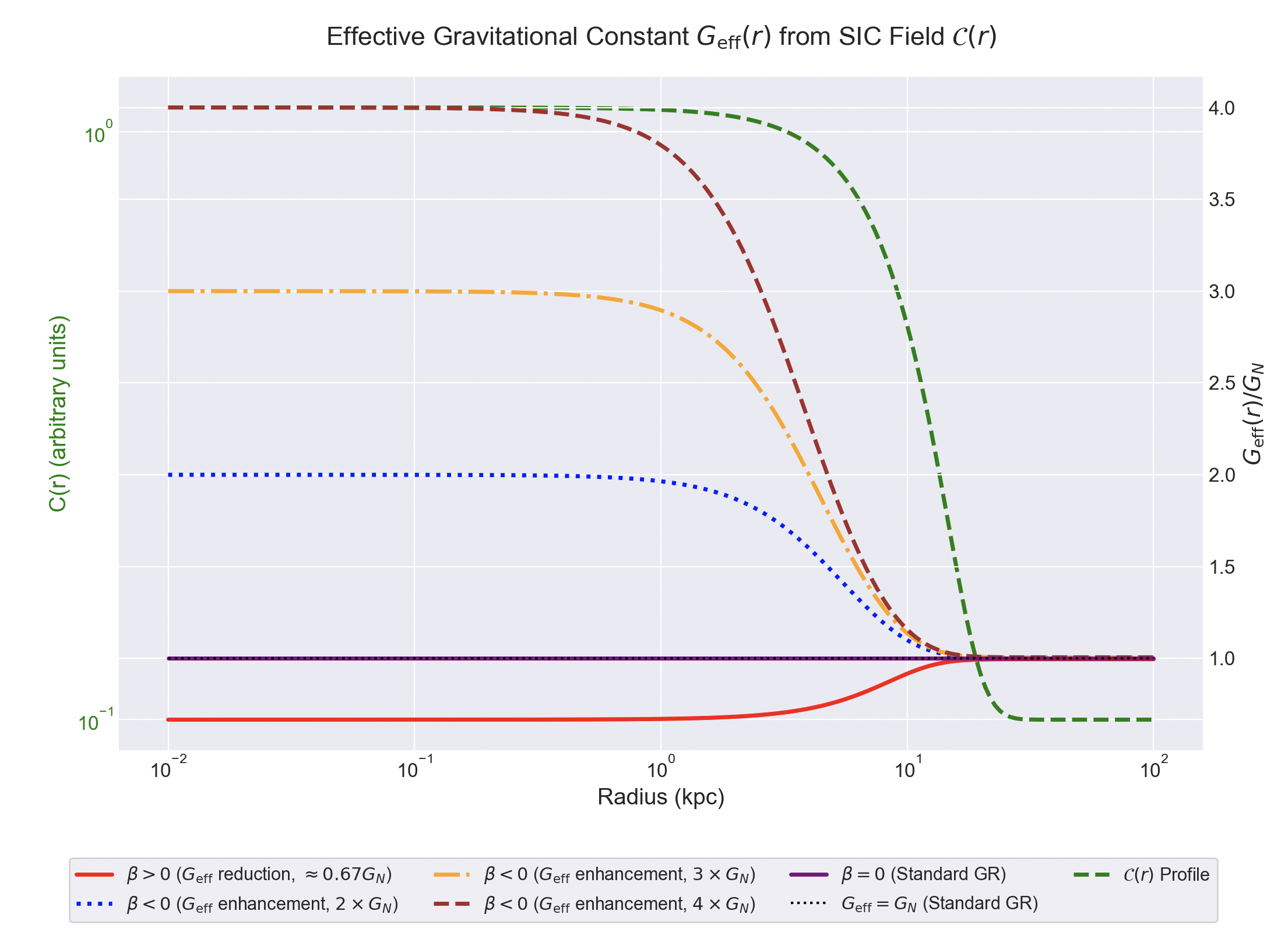
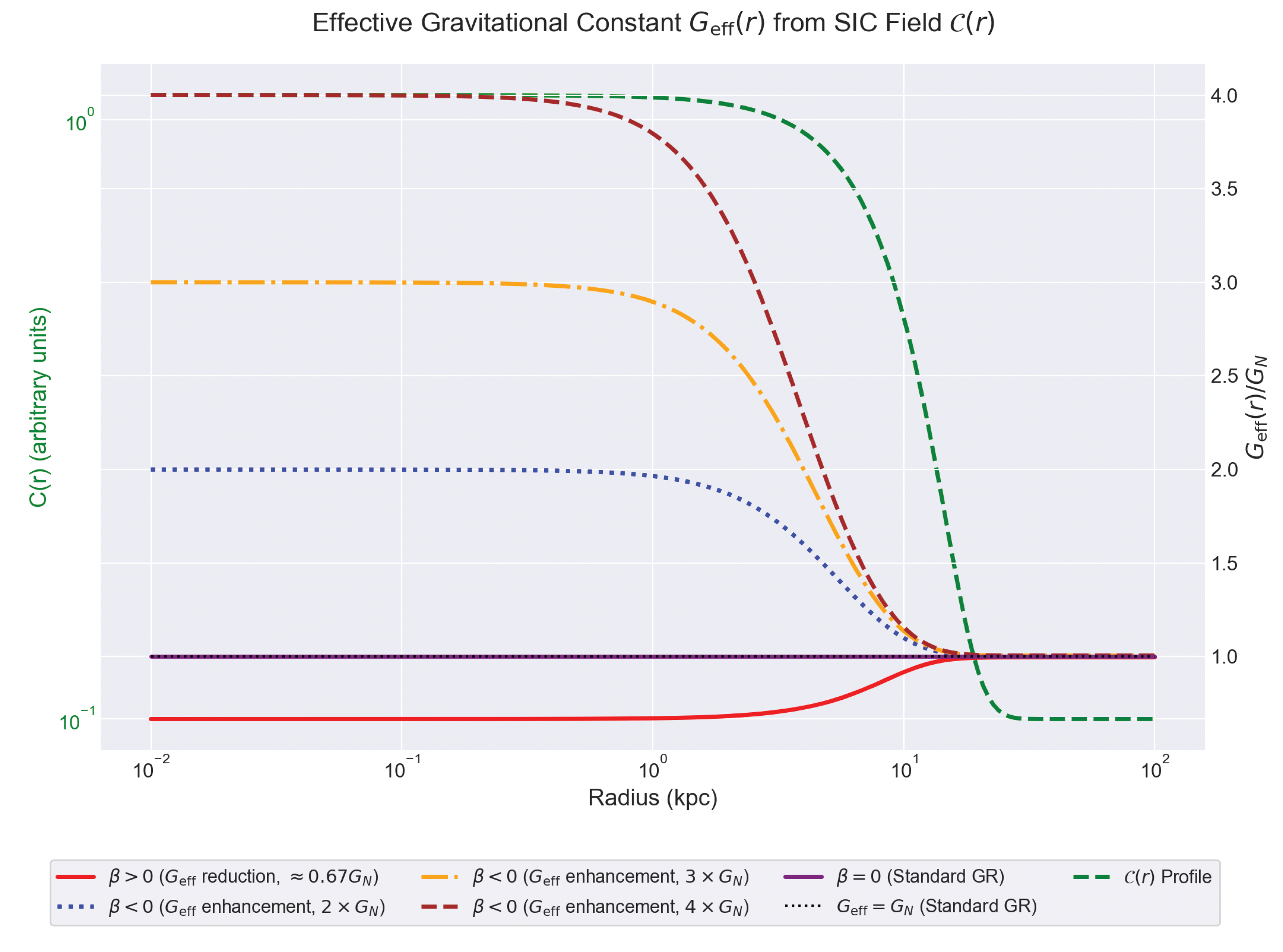
3.1.3. Calculation Model Setup

As a first step to exploring the effects of SIC theory on galactic-scale dynamics, this paper employs an approximation assuming a static, spherically symmetric situation. This approach allows us to prioritize the analysis of spatial distribution effects (r) under the assumption that the evolution of the C field with cosmological time (t) is sufficiently slow at the present epoch ($t=t_{\mathrm{today}}$). A complete analysis of the C field’s full spacetime dynamics remains an important subject for future work. To specifically analyze the spatial variation of the effective gravitational coupling constant, it is necessary to model the distribution of the structural information field $\mathcal{C}\left(r\right)$ around specific celestial objects (e.g., galaxies). Considering the general trend on galactic scales where the distribution of matter (such as stars, gas, and dark matter halos) is concentrated in the central region and its density decreases outwards, this paper assumes that the structural information field $\mathcal{C}\left(r\right)$ may also exhibit a similar spatial distribution.

Theoretically, the $\mathcal{C}$ field has its own physical dimension, derived from the Lagrangian in Section 2.2 to be ${\left[M\right]}^{1/2}{\left[L\right]}^{1/2}{\left[T\right]}^{-1}$ for theoretical consistency. However, for the convenience of calculation in this phenomenological model, we use values made dimensionless by a specific physical scale, such as the Planck scale ($M_{Pl}$) or a new intrinsic scale of the theory ($M_{SIC}$). Therefore, the numerical values for $\mathcal{C}$ presented below should be interpreted as illustrative, dimensionless values representing the relative magnitude with respect to this fundamental scale.

For this purpose, the following simplified Gaussian-form profile is used as an example. (This is a specific functional form for illustrative purposes; the actual distribution of $\mathcal{C}\left(r\right)$ in a physical environment should, in principle, be determined from the solution obtained by simultaneously solving the $\mathcal{C}$ field’s equation of motion and the modified Einstein field equations presented in Section 2.4.):

$$\mathcal{C}\left(r\right)={\mathcal{C}}_{\mathrm{bg}}+{\mathcal{C}}_{0}exp\left(-{\displaystyle \frac{r^2}{r_s^2}}\right)$$

Here, it is assumed that each parameter has the following example values:

• ${\mathcal{C}}_{\mathrm{bg}}$: Background value of the structural information field in the cosmic background (e.g., 0.1 arbitrary units). This is the asymptotic value as $r\to \infty$ and can represent the background level of the $\mathcal{C}$ field uniformly distributed throughout the universe.
• ${\mathcal{C}}_0$: Additional value of the information field at the celestial center ($r=0$) (e.g., 1.0 arbitrary units). This represents the degree to which information is locally concentrated at the center.
• $r_s$: Characteristic scale radius of the information field distribution (e.g., 10 kpc). This radius indicates the approximate size of the region where the $\mathcal{C}\left(r\right)$ value is significantly higher than the background value. It can have a physical scale similar to that of the stellar distribution in galaxies or the core radius of dark matter halos.

This model is an example intended to represent a realistic distribution where the information structure is highly concentrated locally, such as in the galactic center, and asymptotically decreases to the cosmic average background value with increasing distance from the center. Figure 1 below shows the radial dependence of this $\mathcal{C}\left(r\right)$ profile and the ratio of the effective gravitational coupling constant $G_{\mathrm{eff}}\left(r\right)/G_N$ calculated from it, for various values of the coupling constant $\beta$. (See Python code in Appendix for detailed calculations)

3.1.4. Quantitative Analysis and Physical Interpretation

Graph Configuration and Numerical Results:Figure 1 illustrates the radial dependence of the effective gravitational coupling constant ratio $G_{\mathrm{eff}}\left(r\right)/G_N$, calculated using Equation (3.1.2.3) for various values of the coupling constant $\beta$, based on the structural information field $\mathcal{C}\left(r\right)$ profile assumed in Section 3.1.3 (e.g., ${\mathcal{C}}_{\mathrm{bg}}=0.1,{\mathcal{C}}_0=1.0,r_s=10\mathrm{kpc}$). Central Region Effects (at $r\to 0$, i.e., the point where $\mathcal{C}\left(0\right)={\mathcal{C}}_{\mathrm{bg}}+{\mathcal{C}}_0$):

• $\beta <0$ (Gravitational Strengthening Scenario): As can be clearly seen in the figure, for selected negative values of $\beta$, $G_{\mathrm{eff}}\left(0\right)/G_N$ can be larger than $G_N$ (e.g., 2, 3, or even 4 times in the examples). This implies that in regions such as the galactic center, where the structural information field $\mathcal{C}$ is very dense, gravity can act much more strongly than predicted by standard theory. Such gravitational strengthening effects could hold significant implications in attempts to explain the dynamical characteristics of galaxies without invoking dark matter [4].
• $\beta >0$ (Gravitational Weakening Scenario): Conversely, for certain positive values of $\beta$, $G_{\mathrm{eff}}\left(0\right)/G_N$ can be less than 1 (e.g., approximately 0.67 times in the examples). This indicates an effect where gravity is weakened in regions where the $\mathcal{C}$ field is dense. Such scenarios could be employed in exploring specific cosmological models or gravitational effects in high-energy environments.
• $\beta =0$ (Standard GR): In this case, $G_{\mathrm{eff}}\left(r\right)/G_N=1$, showing results identical to standard gravity at all radii. This demonstrates that SIC theory naturally reduces to General Relativity in the $\beta \to 0$ limit [1,2].

Spatial Transition Characteristics: In all cases, the gravitational strengthening or weakening effect varies spatially following the profile of $\mathcal{C}\left(r\right)$. That is, the effect is most pronounced in the region where the $\mathcal{C}\left(r\right)$ value is large, primarily $r\lesssim r_s$ (e.g., within tens of kpc in the examples). Conversely, as $r\gg r_s$ towards the galactic outskirts, $\mathcal{C}\left(r\right)\approx {\mathcal{C}}_{\mathrm{bg}}$, and the value of $G_{\mathrm{eff}}\left(r\right)/G_N$ converges towards a value close to 1 (specifically, to $G_N/(1+{\displaystyle \frac{16\pi G_N}{c^4}}\beta {\mathcal{C}}_{\mathrm{bg}}^2)$). This suggests that the gravitational modulation effect by SIC may be primarily confined to local regions where the information structure is dense. This characteristic offers the possibility of good agreement with standard gravitational experimental results [37] in regions like the Solar System, where changes in the $\mathcal{C}$ field are expected to be minimal and its value itself small, which is an important condition for the theory to pass existing precision gravitational tests.

3.1.5. Quantitative Evaluation of the Capability to Replace Dark Matter Effects

Conceptual Comparison with the Standard Dark Matter Model: According to the current standard cosmological model, the $\Lambda$CDM model, dark matter accounts for about 27% of the total matter-energy density of the universe, while ordinary (baryonic) matter, which we can directly observe, accounts for about 5% [5]. This implies that to explain the gravitational effects observed in astronomical structures such as galaxies and galaxy clusters – for example, the rotation speeds of stars within galaxies [4] or gravitational lensing effects – an invisible dark matter component, approximately 5 to 6 times the mass of baryonic matter ($\approx 27\%/5\%$), is needed in addition to the visible baryonic matter. This “missing mass problem” is one of the greatest mysteries in modern astrophysics.

One can estimate the extent to which the strengthening effect of the effective gravitational coupling constant $G_{\mathrm{eff}}$, which occurs when the coupling constant $\beta <0$ in SIC theory, could replace or account for this need for dark matter. If the effect of dark matter makes the actual total gravity appear to be N times that of baryonic matter alone (i.e., $G_{\mathrm{total}}\approx N·G_N$), then the crucial point is how close the $G_{\mathrm{eff}}/G_N$ value from SIC theory can get to this factor N. For example, let us assume that in a particular galaxy, the total effective gravity, including dark matter effects, appears to be 6 times stronger than what baryonic matter alone would produce (i.e., $N=6$). In this case, the extent to which the SIC model can account for this “additional gravitational effect” via its predicted $G_{\mathrm{eff}}/G_N$ value can be assessed as follows: - $G_{\mathrm{eff}}/G_N=2$ (2-fold enhancement): Can account for $(2-1)/(6-1)=1/5=20\%$ of the additionally required gravity. - $G_{\mathrm{eff}}/G_N=4$ (4-fold enhancement): Can account for $(4-1)/(6-1)=3/5=60\%$ of the additionally required gravity.

Implications for Galaxy Rotation Curves: The rotation speed $v_{\mathrm{rot}}$ of stars or gas orbiting within a galactic disk, under a simplified Newtonian approximation, approximately follows the relationship $v_{\mathrm{rot}}^2\left(r\right)\propto G{M}_{\mathrm{enc}}\left(r\right)/r$ (where $M_{\mathrm{enc}}\left(r\right)$ is the total mass enclosed within radius r) [2,33]. If $M_{\mathrm{enc}}\left(r\right)$ is limited to the observed baryonic matter $M_{\mathrm{visible}}\left(r\right)$, then in SIC theory, the gravitational constant G would be replaced by the effective gravitational constant $G_{\mathrm{eff}}\left(r\right)$, leading to $v_{\mathrm{rot},\mathrm{SIC}}^2\left(r\right)\propto G_{\mathrm{eff}}\left(r\right)M_{\mathrm{visible}}\left(r\right)/r$. Therefore, if $G_{\mathrm{eff}}\left(r\right)$ has a profile that increases appropriately from the galactic center outwards (which, in principle, can be modulated by the spatial distribution of $\mathcal{C}\left(r\right)$ and the choice of $\beta$), it opens up the possibility of explaining part or all of the observed flat or even rising galaxy rotation curve phenomena without assuming a dark matter halo. In the example model presented in Figure 1 (where $\mathcal{C}\left(r\right)$ decreases from the center), $G_{\mathrm{eff}}$ is most significantly enhanced in the central region, which would primarily affect the dynamics of the galactic core. To accurately fit the entire rotation curve of a galaxy, more sophisticated modeling of the $\mathcal{C}\left(r\right)$ distribution, reflecting the actual structure of the galaxy (bulge, disk, halo regions, etc.), is necessary, along with a process to ensure that the model is consistent with the $\mathcal{C}$ field’s dynamical equations.

3.1.6. Theoretical Consistency and Physical Constraints

A new theory must ensure consistency with existing, well-established physical laws and principles, while also possessing its own internal theoretical consistency and stability. In the case of SIC theory, the following key constraints should be considered, and their validity must be established through future research.

Compatibility with the Weak Equivalence Principle: If the effective gravitational coupling constant $G_{\mathrm{eff}}$ in SIC becomes a function of spacetime coordinates, this naturally raises questions about potential violations of the Weak Equivalence Principle (WEP), much like in scalar-tensor theories [30,31]. The WEP could be preserved if all forms of matter and energy couple universally to the $\mathcal{C}$ field (i.e., the coupling mechanism does not depend on the type of matter) and if all matter experiences gravity through the same effective metric $g_{\mu \nu }^{\mathrm{eff}}$ (which could be defined in a way that includes $G_{\mathrm{eff}}$). However, the spatial variation of $G_{\mathrm{eff}}$ itself could lead to different tidal effects or deviations in the free-fall trajectories of objects compared to standard gravity. Therefore, comparisons with high-precision gravitational experimental results within the Solar System [37] and others could place strong constraints on the value of $\beta$ or the spatial variation rate of the $\mathcal{C}$ field.

Satisfaction of Energy Conditions: In General Relativity, various energy conditions (e.g., Weak Energy Condition (WEC), Null Energy Condition (NEC), Strong Energy Condition (SEC), Dominant Energy Condition (DEC), etc. [2,33]) are used to characterize physically meaningful matter distributions or spacetime structures. Whether the energy-momentum tensor of the structural information field, $T_{\mu \nu }^{\left(\mathcal{C}\right)}$, satisfies these energy conditions largely depends on the form of the potential $V\left(\mathcal{C}\right)$ and the coefficient $\lambda$ of the kinetic term in the SIC Lagrangian. For example, if a particular form of $V\left(\mathcal{C}\right)$ or the $\lambda {(\nabla \mathcal{C})}^4$ term induces negative pressure to explain cosmic acceleration, it might violate certain energy conditions (e.g., the SEC) [35]. To ensure the physical viability of the SIC theory and the reliability of its cosmological predictions, it is crucial to find parameter regions that satisfy these energy conditions or to clearly understand the physical implications if certain conditions are violated.

Causality and Stability: As mentioned in Section 2.5, the kinetic term $\lambda {\left(g^{\mu \nu }{\nabla }_{\mu }\mathcal{C}{\nabla }_{\nu }\mathcal{C}\right)}^2$ in the SIC Lagrangian is a form of k-essence [32]. This implies that the propagation speed of $\mathcal{C}$ field perturbations can depend on the background state of $\mathcal{C}$ and its rate of change. Under certain conditions, there is a mathematical possibility that the propagation speed of these perturbations could differ from the speed of light. Such superluminal propagation possibilities in classical field theories can lead to issues with causality (e.g., formation of closed timelike curves) or theoretical stability (e.g., the appearance of ghost states or Laplacian instabilities [31,36]). Therefore, an in-depth analysis of the conditions required to avoid these potential problems and to obtain physically valid solutions (e.g., the sign and value of $\lambda$, the form of $V\left(\mathcal{C}\right)$, etc.) is essential. In this paper, we primarily assume that these theoretical challenges can be resolved or appropriately controlled within a viable parameter space in future research. Our current focus is on the solutions of the classical field equations and their phenomenological implications, aiming to explore physically plausible scenarios. A profound consideration of any potential connection with non-local phenomena, as suggested by the nature of information structure, is left as a task for future investigation, to be conducted in tandem with analyses of stability and causality.

3.1.7. Observational Verification Strategy

The SIC theory, particularly the modulation effect of $G_{\mathrm{eff}}$, can be tested or constrained through various astronomical and cosmological observations. Such verification strategies will test the predictive power of the theory and provide limits on its free parameters (such as $\beta$, $\lambda$, and the form of $V\left(\mathcal{C}\right)$). Direct Verification Methods:

• Precision Gravitational Lensing Analysis: Strong gravitational lensing images (Einstein rings, multiple images, etc.) and weak gravitational lensing distortions of background galaxy shapes at galactic or cluster scales directly probe the curvature of spacetime. The spatial distribution of $G_{\mathrm{eff}}\left(r\right)$ predicted by SIC theory could induce lensing effects different from those predicted by standard General Relativity (with constant $G_N$). These could be precisely measured by next-generation observational facilities (e.g., the Euclid satellite, the LSST camera on the Vera C. Rubin Observatory) [12,35].
• Celestial Orbit Dynamics: A long-term analysis of precise orbital data of S-stars orbiting the supermassive black hole at the center of our galaxy (Sgr A*) [39], or rotation curve data from stars or gas in external galaxies [4], can be used to verify minute deviations in the gravitational field due to changes in $G_{\mathrm{eff}}\left(r\right)$.
• Gravitational Wave Observations: The waveforms of gravitational waves emitted during the merger of binary black holes or neutron stars, especially during the inspiral, merger, and ringdown phases, are highly sensitive to the value of $G_{\mathrm{eff}}$ and spacetime curvature [38]. A spatially varying $G_{\mathrm{eff}}$ or the dynamical effects of the $\mathcal{C}$ field itself could cause subtle modulations in the gravitational wave signal (e.g., additional polarization modes, changes in propagation speed, or alterations in the ringdown frequencies and damping times) different from standard General Relativity. These could be searched for with LIGO-Virgo-KAGRA and future detectors like LISA.

Indirect Verification Indicators:

• Large-Scale Structure Formation Simulations: By incorporating the modified gravitational effects predicted by SIC (such as $G_{\mathrm{eff}}\left(r\right)$ and, if necessary, pressure effects from the $\mathcal{C}$ field itself) into N-body simulations, one can predict how the formation and evolution of cosmic large-scale structures (galaxy cluster distributions, cosmic web, voids, etc.) would compare with observed statistical properties (e.g., matter power spectrum, galaxy cluster mass function).
• Cosmic Microwave Background (CMB) Spectrum: Quantum fluctuations of the $\mathcal{C}$ field in the early universe or temporal variations of $G_{\mathrm{eff}}$ could leave imprints on the temperature and polarization anisotropy angular power spectra of the CMB. A precise calculation of these effects and comparison with observational data from missions like the Planck satellite [5] could provide constraints on early universe conditions and SIC parameters.
• Galaxy Scaling Relations and Evolution: Examining whether the evolution of scaling relations in galaxies observed at different redshifts (i.e., different cosmic epochs)—such as the mass-luminosity relation or mass-velocity dispersion relations (e.g., Tully-Fisher, Faber-Jackson relations)—is consistent with the predictions of SIC (which might include a cosmological evolution of $G_{\mathrm{eff}}$).

3.1.8. Outlook

The model of spatial $G_{\mathrm{eff}}$ modulation presented in this section, along with its quantitative analysis, demonstrates that SIC theory can make phenomenologically significant predictions. In particular, the effective gravitational strengthening that occurs when $\beta <0$ holds the potential to explain a part or a significant portion of observed phenomena currently attributed to dark matter (e.g., galaxy rotation curves [4], mass discrepancies in galaxy clusters) without invoking the existence of dark matter. The 3-4 fold gravitational enhancement for specific parameter values, as exemplified in Figure 1, suggests that a substantial fraction (around 40-60% in the example calculation) of the additionally required gravity could be accounted for by the effects of the $\mathcal{C}$ field.

This represents an attempt to explain observed cosmic phenomena within a single theoretical framework without assuming separate dark components, offering an approach distinct in its fundamental motivation and mathematical structure from other modified gravity theories (e.g., MOND [40], $f\left(R\right)$ gravity [34]). Given that the $\mathcal{C}$ field is rooted in the fundamental concept of “information structure,” it is hoped that further development of the theory could provide a unified and novel understanding of the dark matter and dark energy problems [5,6,7].

Of course, to realize this potential, more precise and systematic comparative analyses with a wide range of astronomical and cosmological observational data are essential. Furthermore, cosmological-scale verification through N-body simulations and the establishment of constraints on the theory’s fundamental parameters (such as $\beta ,\lambda$, and the form of $V\left(\mathcal{C}\right)$) must follow. If the validity of SIC theory is borne out and its predictive power demonstrated through such follow-up studies, it could provide a significant breakthrough in addressing the unresolved problems of modern cosmology.

3.2. Expansive Applications and Unification Potential of SIC Theory

The basic framework of SIC, beyond the direct prediction of the modulation of the effective gravitational coupling constant discussed in Section 3.1, holds the potential to offer new approaches to various fundamental problems facing modern physics. In this section, we explore four major expansion directions proposed by SIC at a conceptual level and present the foundational mathematical ideas and connections with existing theories for each. These expansions demonstrate the rich potential of SIC theory, but each is an initial-stage proposal requiring in-depth theoretical development, mathematical formulation, and verification through observation and experiment in the future.

3.2.1. Unifying Framework for the Four Fundamental Forces

Theoretical Motivation: The Standard Model of modern particle physics very successfully describes the electromagnetic, weak, and strong forces within a unified mathematical framework of gauge symmetry (a general description of the Standard Model can be indirectly referenced, for example, in the discussion of particle dark matter in [4], or found in general particle physics textbooks). However, gravity remains separate from this gauge-theoretic description and is treated as a geometric phenomenon of spacetime in General Relativity [1,2]. One of the long-standing goals of physics is to understand these four fundamental forces integratively within a single theoretical framework, and there have been many efforts towards Grand Unified Theories (GUTs) or a Theory of Everything (TOE) [11,35]. SIC proposes new possibilities for describing these forces integratively by considering the structural information field $\mathcal{C}$ as a common medium that could be the source of all interactions or form their underlying background.

Mathematical Framework (Conceptual Proposal): In SIC, the unification of the four fundamental forces can be conceptually approached through an extended Lagrangian of the following form:

$${\mathcal{L}}_{\mathrm{unified}}={\mathcal{L}}_{\mathrm{gravity}+\mathrm{C}}[\mathcal{C},g_{\mu \nu }]+{\mathcal{L}}_{\mathrm{gauge}}[\mathcal{C},A_{\mu },F_{\mu \nu }]+{\mathcal{L}}_{\mathrm{matter}}[\mathcal{C},\psi ,D_{\mu }]$$

Here, each sector can be associated with the $\mathcal{C}$ field as follows: - Gravity and $\mathcal{C}$ Sector: ${\mathcal{L}}_{\mathrm{gravity}+\mathrm{C}}$ includes the gravitational and $\mathcal{C}$ field parts of the SIC Lagrangian presented in Section 2.2. - Gauge Sector: ${\mathcal{L}}_{\mathrm{gauge}}$ includes each gauge field $A_{\mu }^A$ and its field strength $F_{\mu \nu }^A$. Through coupling with the $\mathcal{C}$ field, the effective coupling constants or gauge dynamics can be modified. For example, the kinetic term for each gauge field could be modified to a form such as:

$${\mathcal{L}}_{\mathrm{gauge}}\approx \sum _A-{\displaystyle \frac{1}{4}}{f}_A\left(\mathcal{C}\right)F_{\mu \nu }^A{F}^{A\mu \nu }$$

where $f_A\left(\mathcal{C}\right)$ is a function dependent on $\mathcal{C}$, which can modulate the effective gauge coupling constant (e.g., $g_{\mathrm{eff},A}^2\sim 1/f_A\left(\mathcal{C}\right)$ or another relation). This idea can be explored in a context similar to some theories where effective coupling constants may vary cosmologically [12,35]. - Matter Sector: ${\mathcal{L}}_{\mathrm{matter}}$ includes fermion fields $\psi$. Through coupling with the $\mathcal{C}$ field, particle masses $m\left(\mathcal{C}\right)$ or their interactions can be modified. For instance, the coupling constant within the covariant derivative $D_{\mu }$ might depend on $\mathcal{C}$, or the mass term could take a form like:

$${\mathcal{L}}_{\mathrm{matter}}\approx \sum _{\psi }\overline{\psi }(i{\gamma }^{\mu }{D}_{\mu }[A_{\mu },g_A\left(\mathcal{C}\right)]-m_{\psi }\left(\mathcal{C}\right))\psi$$

Core Mechanism Ideas: 1. Unification of Coupling Constants: One can explore scenarios where, under specific conditions in the early universe (e.g., at a particular value of $\mathcal{C}$, ${\mathcal{C}}_{\mathrm{unification}}$), all effective coupling constants $g_A\left(\mathcal{C}\right)$ (and constants related to the effective gravitational coupling $G_{\mathrm{eff}}\left(\mathcal{C}\right)$) converge to a single value or satisfy a specific symmetry relation. This idea is inspired by Grand Unified Theories. 2. Mass Generation: It can be hypothesized that particle masses are dynamically determined by the vacuum expectation value $\langle \mathcal{C}\rangle$ of the $\mathcal{C}$ field, or by direct interaction with the $\mathcal{C}$ field (e.g., Yukawa couplings $y_i\left(\mathcal{C}\right)$), similar to the Higgs mechanism in the Standard Model: $m_i=\mathrm{function}(y_i\left(\mathcal{C}\right),\langle \mathcal{C}\rangle ,\mathcal{C})$. 3. Symmetry Breaking: The possibility that the dynamical evolution of the $\mathcal{C}$ field or a cosmological phase transition driven by its potential $V\left(\mathcal{C}\right)$ could induce or significantly contribute to the symmetry breaking of the Standard Model (e.g., $SU{\left(2\right)}_L\times U{\left(1\right)}_Y\to U{\left(1\right)}_{\mathrm{EM}}$) can be investigated.

These ideas suggest that SIC may offer new conceptual pathways towards the unification of forces. Concrete model development, mathematical formulation for each mechanism, and subsequent phenomenological predictions for comparison with existing theories and observations will be crucial research tasks for the future.

3.2.2. Information Structural Interpretation of Black Hole Physics

Exploration of the Information Singularity Hypothesis: In General Relativity, it is predicted that a physical singularity, where spacetime curvature becomes infinite, exists at the center of a black hole [1,2]. In SIC, beyond considering a black hole merely as such a singularity formed by the extreme collapse of matter, we explore the possibility of reinterpreting it as a specific state where the structural information field $\mathcal{C}$ is compressed to its limit. From this perspective, the event horizon can be understood as a boundary where the structural complexity of information (${\mathcal{C}}_H$) reaches a certain threshold, informationally separating it from the external universe. This approach seeks possibilities to alleviate existing singularity problems or understand them in different ways through new concepts such as an information singularity or an extreme state of information structure.

Possibility of a Modified Black Hole Entropy: The Bekenstein-Hawking formula ($S_{\mathrm{BH}}=k_B{c}^{3}A/(4G_N\hslash )$) [26,27], stating that a black hole possesses an entropy proportional to its area, is a cornerstone of black hole thermodynamics. In the SIC framework, since the effective gravitational constant $G_{\mathrm{eff}}$ depends on the $\mathcal{C}$ field, the black hole entropy formula can also be naturally modified. Furthermore, considering the possibility that the structural information field $\mathcal{C}$ itself directly contributes to entropy, the following extended form can be proposed:

$$S_{\mathrm{BH},\mathrm{SIC}}={\displaystyle \frac{k_B{c}^{3}A}{4G_{\mathrm{eff}}\left({\mathcal{C}}_H\right)\hslash }}+S_{\mathrm{info}}({\mathcal{C}}_H,A)$$

where: - ${\mathcal{C}}_H$: The (average) value of the structural information field on the event horizon. - $G_{\mathrm{eff}}\left({\mathcal{C}}_H\right)$: The effective gravitational coupling constant on the horizon, as defined in Section 3.1.2. - $S_{\mathrm{info}}({\mathcal{C}}_H,A)$: An SIC-specific contribution to entropy from the information structure. This term could be related to the complexity of the information structure stored on the horizon or its entropic content, and could take a form such as $\alpha k_B{\mathcal{C}}_H^{\gamma }·f(A/L_{Pl}^2)$, for example. Here, $\alpha$ and $\gamma$ are new parameters of the SIC theory, $f(A/L_{Pl}^2)$ is a dimensionless function dependent on area, and $L_{Pl}$ is the Planck length. - The first term represents a kind of geometric entropy part, proportional to the area via the modified gravitational constant. The second term, $S_{\mathrm{info}}$, could represent an additional entropy contribution related to the complexity of the information structure itself stored in the black hole or its information content.

Conceptual Approach to the Information Paradox: The information paradox [8,9,10], concerning whether initial information is completely lost when a black hole evaporates via Hawking radiation [26], is one of the significant unresolved problems in modern physics. In SIC, new clues to resolving this problem might be found from the perspective that information can be stored and released in deep connection with the $\mathcal{C}$ field. For example, the following ideas can be explored: 1. ${\mathcal{C}}_H$ as an Information Storage Medium: Information falling into a black hole could be encoded in the state of the ${\mathcal{C}}_H$ field near the event horizon. 2. Information Release during Evaporation: Information might not only be carried away by thermal Hawking radiation but could also be indirectly preserved or released through changes in the state of the ${\mathcal{C}}_H$ field or variations in $G_{\mathrm{eff}}\left({\mathcal{C}}_H\right)$ as the black hole evaporates. 3. Hierarchical Information Release: If the information structure possesses a hierarchy, macroscopic information (e.g., mass, charge, angular momentum of the black hole) might be quickly lost or transmitted, while microscopic information (e.g., quantum states of individual particles) could be preserved or released over a long period through subtle correlations involving the $\mathcal{C}$ field or non-local connections (see quantum information linkage ideas in Section 3.2.4 and 4.2.4). Recent attempts to resolve the information paradox, such as those involving quantum extremal surfaces, the “island” formula, and analogies with quantum error correction codes (QECC) [21,22,23,25], provide important insights into how information might be preserved. It is worth exploring whether SIC’s $\mathcal{C}$ field could serve as a physical realization or an effective description of such mechanisms. These SIC interpretations regarding black holes are very preliminary conceptual proposals. To elucidate concrete mechanisms and provide a complete solution to the information paradox, future sophisticated theoretical research, grounded in a deep understanding of quantum gravity and black hole thermodynamics, is essential.

3.2.3. Cosmological Dynamics and Dark Energy

The $\mathcal{C}$ Field as Dynamical Dark Energy: The simplest model explaining the current accelerated expansion of the universe [6,7] is the introduction of a cosmological constant $\Lambda$, but this faces theoretical difficulties such as the fine-tuning problem and the coincidence problem. SIC proposes the possibility that this dark energy is not a static entity like the cosmological constant but can be explained by the dynamical evolution of the structural information field $\mathcal{C}$ itself. The potential $V\left(\mathcal{C}\right)$ and the kinetic term $\lambda {(\nabla \mathcal{C})}^4$ of the $\mathcal{C}$ field can provide an effective energy density and negative pressure on cosmological scales, naturally driving the accelerated expansion of the universe. That is, the $\mathcal{C}$ field itself can play a role similar to a quintessence field [32,35], possessing an effective dark energy density ${\rho }_{\mathrm{DE},\mathrm{eff}}(\mathcal{C},\dot{\mathcal{C}})$ and pressure $p_{\mathrm{DE},\mathrm{eff}}(\mathcal{C},\dot{\mathcal{C}})$ that vary with spacetime.

Connection with Inflation and the ${\rho }_{\mathcal{C}}$ Formula: The rapid expansion of the early universe (inflation) can also be explained by a specific dynamical state of the $\mathcal{C}$ field, for example, by the $\mathcal{C}$ field slowly rolling in a particular flat region of its potential $V\left(\mathcal{C}\right)$, or by a k-essence type kinetic energy dominating the cosmic expansion [32]. In this case, the standard Friedmann equation [2,33] is modified to include the energy density of the $\mathcal{C}$ field as follows:

$$H^2={\displaystyle \frac{8\pi G_N}{3c^2}}\left[{\rho }_{\mathrm{matter}}+{\rho }_{\mathrm{radiation}}+{\rho }_{\mathcal{C}}\right]$$

Here, the energy density of the structural information field $\mathcal{C}$ (assuming a homogeneous and isotropic universe where $\mathcal{C}=\mathcal{C}\left(t\right)$, and $c=1$, from the SIC Lagrangian in Section 2.2) is:

$${\rho }_{\mathcal{C}}=3\lambda {\dot{\mathcal{C}}}^4+V\left(\mathcal{C}\right)$$

This equation is the energy density derived from the ${\mathcal{L}}_{\mathcal{C}}=\lambda X^2-V\left(\mathcal{C}\right)$ term (where $X=g^{\mu \nu }{\nabla }_{\mu }\mathcal{C}{\nabla }_{\nu }\mathcal{C}$, which is $X=-{\dot{\mathcal{C}}}^2$ in a homogeneous universe, utilizing $\rho =2X{\displaystyle \frac{\partial {\mathcal{L}}_{\mathcal{C}}}{\partial X}}-{\mathcal{L}}_{\mathcal{C}}=3\lambda X^2+V\left(\mathcal{C}\right)$). If a standard kinetic term $-{\displaystyle \frac{1}{2}}X$ were additionally included in the SIC Lagrangian, its corresponding energy density contribution ${\displaystyle \frac{1}{2}}{\dot{\mathcal{C}}}^2$ would be added to the above equation. Since the Lagrangian presented in Section 2.2 currently includes only the higher-order kinetic term, the modified formula above is used.

Possibility of Cosmological Phase Transitions: During the evolution of the universe, characteristic changes in the information structure, for example, the $\mathcal{C}$ field undergoing a phase transition by moving between different vacuum states of its potential $V\left(\mathcal{C}\right)$, can occur. One can explore the idea that such transitions could be the physical origin of major cosmological epoch distinctions (e.g., the transition from radiation dominance to matter dominance, or from matter dominance to dark energy dominance) or have played a significant role in these transitions. This can also be closely related to structure formation on cosmological scales.

The specific evolution and predictions of these cosmological scenarios depend heavily on the precise form of $V\left(\mathcal{C}\right)$ and the fundamental parameter values of SIC theory. Therefore, future research must proceed towards constraining these parameters and verifying the model’s validity through precise comparisons with various cosmological observational data (e.g., CMB anisotropies [5], supernova distance-redshift relations [6,7], large-scale structure distributions, etc.).

3.2.4. Fundamental Link with Quantum Information

Exploring the Quantum Origins of Information Structure: Although the structural information field $\mathcal{C}$ of SIC is currently described in this paper as a classical real scalar field, exploring the possibility that its ultimate origin can be interpreted as a macroscopic manifestation of quantum information is a very important research direction. This approach aligns with Wheeler’s famous “It from Bit” or “It from Qubit” proposal [14] and reflects the trend in modern physics that information may be a more fundamental aspect of physical reality [13]. This can be considered through the following conceptual connections:

Possibility of a Complex Phase Representation for the $\mathcal{C}$ Field: The wavefunction $\Psi$ in quantum mechanics inherently takes complex values, containing phase information crucial for interference phenomena and physical phenomena like U(1) gauge symmetry (electromagnetism), in addition to probability amplitude information [19]. If the $\mathcal{C}$ field is to more profoundly reflect these microscopic quantum informational characteristics, one could consider extending $\mathcal{C}$ beyond a simple real scalar field to a complex scalar field $\mathcal{C}=\varphi (\overrightarrow{x},t)e^{i\theta (\overrightarrow{x},t)}$ (or $\mathcal{C}={\mathcal{C}}_R+i{\mathcal{C}}_I$).

−

In this case, the amplitude $\varphi =\left|\mathcal{C}\right|$ of the field could represent the density or strength of the information structure, while the phase $\theta$ could represent internal states of information, cyclical flows, or dynamical degrees of freedom associated with certain symmetries.

−

Each term in the SIC Lagrangian ${\mathcal{L}}_{\mathrm{SIC}}$ could be naturally modified accordingly. For example, the kinetic term $\lambda {\left(g^{\mu \nu }{\nabla }_{\mu }\mathcal{C}{\nabla }_{\nu }\mathcal{C}\right)}^2$ could be generalized to forms like $\lambda |g^{\mu \nu }{\nabla }_{\mu }\mathcal{C}{\nabla }_{\nu }{\mathcal{C}|}^2$ or $\lambda {\left(g^{\mu \nu }{\left({\nabla }_{\mu }\mathcal{C}\right)}^{*}\left({\nabla }_{\nu }\mathcal{C}\right)\right)}^2$, and could include separate dynamical terms for $\varphi$ and $\theta$ (e.g., ${(\nabla \varphi )}^2$, ${\varphi }^2{(\nabla \theta )}^2$). The potential $V\left(\mathcal{C}\right)$ could take the form $V\left(\right|\mathcal{C}\left|\right)$ or $V(\mathcal{C},{\mathcal{C}}^{*})$. The information-gravity coupling term $\beta {\mathcal{C}}^{2}R$ could naturally be extended to ${\beta \left|\mathcal{C}\right|}^{2}R$ (or $\beta {\mathcal{C}}^{*}\mathcal{C}R$).

−

In particular, the dynamics of the phase $\theta$ (e.g., a term like ${\varphi }^2\left({\nabla }_{\mu }\theta \right)\left({\nabla }^{\mu }\theta \right)$) might induce structures analogous to new U(1) gauge symmetries or provide new insights into the unification of the four fundamental forces (Section 3.2.1) through interaction with existing gauge fields. For example, one could explore the possibility of ${\nabla }_{\mu }\theta$ acting like an effective gauge potential. This extends ideas from condensed matter physics, where phase degrees of freedom of superfluids or superconductors describe macroscopic quantum phenomena, to cosmological scales.

−

$\mathcal{C}$ and the Information Content of Quantum States: If $\mathcal{C}$ includes complex phase information as above, one could more sophisticatedly hypothesize that various informational characteristics of a collective quantum system state $|{\Psi }_{\mathrm{total}}\rangle$ (e.g., expectation values of certain “information structure operators” $\widehat{I}$, measures of multipartite entanglement, or phase correlations) are macroscopically averaged or cohere through some mechanism to form the observable classical field $\mathcal{C}\left(\overrightarrow{x}\right)$:

$$\mathcal{C}\left(\overrightarrow{x}\right)\sim \mathrm{CoarseGraining}/\mathrm{Averaging}\left[\sum _k{\mathcal{F}}_k\langle {\Psi }_{\mathrm{total}}|{\widehat{I}}_k\left(\overrightarrow{x}\right)|{\Psi }_{\mathrm{total}}\rangle \right]$$

Here, ${\widehat{I}}_k\left(\overrightarrow{x}\right)$ could now represent a quantum operator that extracts specific structural aspects of information, potentially taking complex values, and ${\mathcal{F}}_k$ is an appropriate filter or weighting function.

−

Relationship between $\mathcal{C}$ and Entanglement Entropy: Certain aspects of $\mathcal{C}$ representing the complexity of the structural information field (e.g., $\left|\mathcal{C}\right|$ or its spatial variation rate) could be related to some measure reflecting the total amount of multi-scale quantum entanglement present within a specific spacetime region. For instance, it is hypothesized that it could be expressed as a hierarchical sum or a more complex function of entanglement entropies $S_{\mathrm{ent}}^{\left(n\right)}$ of subregions defined at different scales (inspired by the Ryu-Takayanagi formula [21,31]):

$$\left|\mathcal{C}\right|\approx \Phi \left(\left\{w_n{S}_{\mathrm{ent}}^{\left(n\right)}\right\}\right)$$

where $w_n$ are weighting factors representing the contribution of each hierarchy or scale, and $\Phi$ is a function combining them. This could also connect with recent research trends suggesting that spacetime geometry emerges from entanglement [21,23,25].

−

Analogy with Quantum Error Correction Codes (QECC): The way information appears to exist stably and evolve coherently in the universe, maintaining macroscopic structures despite local fluctuations, may bear a deep analogy to how fragile quantum information is protected from external noise and stably stored through quantum error correction codes [19,22]. The information structure $\mathcal{C}$ of SIC (now potentially including complex phase information) could be a macroscopic manifestation of such a cosmic-scale information stability and error correction mechanism, and could be related to an encoding map $\mathcal{R}\left[\mathcal{C}\right]$ between physical states and fundamental logical information states:

$$|{\mathrm{State}}_{\mathrm{physical}}\rangle \approx \mathcal{R}\left[\mathcal{C}\right]|{\mathrm{Information}}_{\mathrm{logical}}\rangle$$

This perspective is inspired by recent research findings where quantum error correction codes play an important role in the AdS/CFT correspondence [21,22,23,25].

−

Integrative Extension of the Holographic Principle: SIC offers the idea that the holographic principle [3,15,16] can be extended beyond a mere correspondence of information quantity between the bulk of spacetime and its boundary, to a more abstract “information structure space.” That is, physical phenomena in a higher-dimensional bulk might not only correspond to a quantum field theory on a lower-dimensional boundary (as in the AdS/CFT correspondence [17,18]) but also to a specific state of information structure described by the (complex phase-including) $\mathcal{C}$ field:

$$\mathrm{Bulk}\mathrm{Physics}\iff \mathrm{Boundary}\mathrm{QFT}\iff \mathrm{State}\mathrm{in}\mathrm{Information}\mathrm{Structure}\mathrm{Space}(\mathrm{described}\mathrm{by}\mathrm{complex}\mathcal{C})$$

These ideas could serve as important bridges connecting SIC theory to more fundamental physical theories such as quantum gravity or string theory. They are very preliminary conceptual proposals, and rigorous mathematical formulation and profound theoretical investigation will be essential in the future to substantiate each idea and clarify its physical meaning. In particular, extending the $\mathcal{C}$ field to a complex field could bring significant changes to the mathematical structure and predictions of the theory, so its motivation and consequences must be carefully examined and developed.

3.2.5. Integrative Outlook and Future Development Directions

The four major expansion directions presented in this section (3.2) – namely, exploring a unifying framework for the four fundamental forces via the structural information field $\mathcal{C}$ (Section 3.2.1), an information structural reinterpretation of black hole physics (Section 3.2.2, e.g., concerning the information paradox [8,9,10] and entropy [26,27]), describing cosmological dynamics (inflation, dark energy [6,7,32,35]) based on the $\mathcal{C}$ field, and the fundamental link with quantum information theory (Section 3.2.4, e.g., entanglement, holography [3,17,19,21,22,23,25]) – demonstrate the rich potential for SIC theory to evolve beyond a simple modified gravity model [11,12] into an integrative framework for various fundamental problems in physics.

Progress in each of these areas is not independent but rather interconnected. For example, understanding the quantum informational origins of the $\mathcal{C}$ field could be essential for addressing the black hole information problem or quantum fluctuations in early universe inflation, while a mechanism for force unification might naturally emerge from specific symmetries or dynamical properties of the $\mathcal{C}$ field.

Therefore, a key long-term task will be to establish a microscopic foundation for SIC, particularly by elucidating its connection with quantum information theory [19] and the holographic principle [3,15,16], and thereby to clarify the fundamental nature of the $\mathcal{C}$ field (i.e., what “structural complexity of information” precisely means). These expansive applications all, in principle, offer testable predictions (to be discussed in Section 4.3) or new perspectives on existing problems. Consequently, it is anticipated that through future in-depth theoretical development, coupled with efforts in astronomical observation and experimental verification, the validity of the SIC framework can be systematically evaluated.

4. Discussion and Future Work

4.1. Main Content and Current Significance of SIC Theory

The Structural Information Cosmology (SIC), as presented in this paper, attempts an integrative approach to fundamental problems in modern physics by introducing the new physical concept of structural complexity of information. The main content of SIC and its current significance can be summarized as follows.

Proposal of a Theoretical Framework: SIC posits a structural information field $\mathcal{C}$ as a fundamental element of the universe and presents a Lagrangian and field equations to describe its dynamics and interactions (see Chapter 2). This is an attempt to incorporate an information-theoretic perspective (the idea that information is fundamental to physical systems [13,14]) into the existing geometric view of gravity (General Relativity [1,2]), providing a theoretical framework that could potentially connect insights from the holographic principle [3,15,16] and quantum information theory [19] with macroscopic cosmology [5,33].

Demonstration of Concrete Predictive Capability: Through the example calculation model presented in Section 3.1 of this paper, it was shown that SIC can make concrete physical predictions, specifically the spatial modulation of the effective gravitational coupling constant $G_{\mathrm{eff}}$. Under certain parameter assumptions, a 2 to 4-fold enhancement of effective gravity can occur in regions where the $\mathcal{C}$ field is dense, demonstrating the potential to explain a portion (approximately 40-60% in the example model of this paper) of phenomena currently attributed to dark matter [4]. This suggests that SIC has the potential to develop into a scientific theory capable of concrete and quantitative predictions, moving beyond a purely abstract conceptual proposal.

Exploration of Paths to Verifiability: The modulation effect of $G_{\mathrm{eff}}$ predicted by SIC, and its potential impacts on the observational features of black holes (e.g., observations by the Event Horizon Telescope [39]) or on gravitational lensing phenomena (utilized as a verification method for various modified gravity theories [12,35]), open up avenues through which the theory could, in principle, be verified via various astronomical observations and experiments (see Section 3.1.7). This is an essential element for assessing and developing the scientific validity of the theory.

4.2. Priority Research Tasks for Theoretical Development

To develop SIC theory into a more sophisticated and reliable physical theory, the following systematic follow-up research is essential.

4.2.1. Realistic Modeling of the Structural Information Field

• Dynamical Determination of the $\mathcal{C}(\overrightarrow{x},t)$ Profile: The Gaussian-form $\mathcal{C}\left(r\right)$ profile used as an example in this paper is based on a static assumption and serves as a simplified model. In the future, it is necessary to simultaneously solve the equation of motion for the $\mathcal{C}$ field and the modified Einstein equations, as presented in Section 2.4, in various astrophysical and cosmological environments (e.g., during galaxy formation and evolution [4], in galaxy clusters, and within the cosmic large-scale structure [5]). This will allow for the exploration of the dynamical distribution and temporal evolution of the $\mathcal{C}$ field that forms spontaneously in such environments. This includes modeling the $\mathcal{C}$ distribution according to the multi-component structures of galaxies (bulge, disk, halo) and researching the evolution of the $\mathcal{C}$ field in the cosmological background (e.g., its value in the early universe and at present).
• Concretization of the Potential $V\left(\mathcal{C}\right)$: The form of the self-interaction potential $V\left(\mathcal{C}\right)$ is a key element determining the dynamical characteristics of SIC theory and its cosmological consequences, such as the mass of the $\mathcal{C}$ field, its vacuum states, and the possibility of phase transitions. Based on various theoretical motivations (e.g., specific symmetry assumptions, stability conditions, consistency with models of inflation or dark energy [32,35]), polynomial forms like $V\left(\mathcal{C}\right)={\displaystyle \frac{m_{\mathcal{C}}^2}{2}}{\mathcal{C}}^2+{\displaystyle \frac{{\lambda }_3}{3!}}{\mathcal{C}}^3+{\displaystyle \frac{{\lambda }_4}{4!}}{\mathcal{C}}^4+\dots$ or other functional forms (e.g., exponential, logarithmic, trigonometric) should be considered. The physical meaning of each parameter and observational constraints must be systematically analyzed. In particular, the possibility of a cyclic universe model, as discussed in Section 4.5.1, may be closely related to specific forms of $V\left(\mathcal{C}\right)$.

4.2.2. Comparative Analysis with Precise Observational Data

• Detailed Analysis of Galaxy Rotation Curves and Mass Distributions: A systematic fitting of the SIC model (using dynamically determined or reasonably modeled $\mathcal{C}$ distributions and the resulting $G_{\mathrm{eff}}$) should be performed on the hundreds or thousands of precisely measured rotation curve data [4] and total mass distributions (inferred from stellar and gas distributions, and gravitational lensing effects) available for various types and sizes of galaxies (e.g., spiral, elliptical, dwarf galaxies). Through this, the explanatory power of SIC should be quantitatively assessed via statistical comparison (e.g., ${\chi }^2$ analysis, Bayesian Information Criterion (BIC) for model selection) with the standard $\Lambda$CDM model (including dark matter) [5] and other leading modified gravity theories such as MOND [40], to obtain constraints on the model parameters.
• In-depth Analysis of Gravitational Lensing Phenomena: Strong gravitational lensing (e.g., multiple images, Einstein rings) and weak gravitational lensing (cosmic shear) are very powerful tools for directly probing the distribution of gravitational fields on different scales. The effects of the $G_{\mathrm{eff}}\left(r\right)$ variation predicted by SIC on these lensing phenomena must be precisely calculated and compared with actual observational data (e.g., existing data from HST, DES, KiDS, and vast high-quality data expected from next-generation observational projects such as Euclid, LSST (Vera C. Rubin Observatory), and the Roman Space Telescope [12,35]) to constrain model parameters and verify the theory’s validity.

4.2.3. SIC Interpretation in Black Hole Physics

• Numerical Relativity Simulations: In the extreme gravitational field environment around black holes, obtaining analytical solutions is often difficult. Therefore, the modified Einstein equations and the $\mathcal{C}$ field equation of motion must be solved numerically using numerical relativity codes. Through this, the following observable effects can be predicted and quantified:
  • Changes in black hole shadow size and shape: The standard GR prediction for a Schwarzschild black hole shadow radius is approximately $R_{\mathrm{shadow}}\approx \sqrt{27}GM/c^2\approx 5.196GM/c^2$. In SIC, not only is G replaced by $G_{\mathrm{eff}}\left({\mathcal{C}}_H\right)$, but the $\mathcal{C}$ field itself can also affect spacetime, so changes in the shadow, which could be expressed in the form $R_{\mathrm{shadow},\mathrm{SIC}}=f({\mathcal{C}}_H,\beta ,\mathrm{black}\mathrm{hole}\mathrm{parameters})·R_{\mathrm{GR}}$, must be calculated.
  • Changes in the dynamics, temperature distribution, and electromagnetic radiation spectrum of black hole accretion disks.
  • Alterations in gravitational wave waveforms (inspiral, merger, ringdown phases) from binary black hole/neutron star mergers [38].
• Utilizing Event Horizon Telescope (EHT) Data: Predictions from the SIC model should be compared with EHT data [39] on the observed shadow size and shape of M87* and Sgr A* at the center of our galaxy to explore the possibility of obtaining concrete constraints on the value of the $\mathcal{C}$ field or the coupling constant $\beta$ near black holes.
• Possibility of an Informational Description of Black Hole Interiors: Furthermore, SIC could lead to attempts to describe the extreme environment inside black holes—particularly the classical singularity problem, which is difficult to describe with spacetime geometry alone—using purely informational degrees of freedom, such as specific configurations of the $\mathcal{C}$ field or quantum information states. This is an exploratory area that could provide important clues for resolving the black hole singularity problem and the information paradox [8,9,10].

4.2.4. Deepening the Fundamental Link with Quantum Information Theory

• Exploring the Microscopic Foundation of the $\mathcal{C}$ Field: As suggested by the ideas in Section 3.2.4, research is needed to substantiate the hypothesis that the $\mathcal{C}$ field, introduced classically, is a macroscopic manifestation of quantum information (e.g., entanglement entropy [21,23,25,31], or information content inherent in quantum states). For instance, this could involve attempts to extend the AdS/CFT correspondence [17,18] to the SIC framework (elucidating a relationship like ${\mathcal{C}}_{\mathrm{bulk}}\leftrightarrow {\mathcal{O}}_{\mathcal{C},\mathrm{boundary}}$) or research on information preservation mechanisms through analogies with quantum error correction codes (QECC) [21,22,23,25]. The formula

  $${\mathcal{C}}_{\mathrm{bulk}}(r,\theta ,\varphi )\stackrel{?}{=}{\int }_{\mathrm{Boundary}}{d}^{D}xK(r,\theta ,\varphi ;x){\mathcal{O}}_{\mathcal{C}}\left(x\right)$$
  (where K is a bulk-boundary propagator, and ${\mathcal{O}}_{\mathcal{C}}$ is a specific operator in the boundary theory) represents such a connection. These connections are very challenging but could provide a profound physical basis for SIC theory and enrich its meaning.

4.3. Experimental Verification Strategy and Observational Signatures

The SIC theory, particularly the modulation effect of the structural information field $\mathcal{C}$ and the resulting effective gravitational constant $G_{\mathrm{eff}}$, can, in principle, be verified or constrained through various laboratory-scale precision measurements and astronomical observations. The following are verification strategies and potential observational signatures that can be considered in the short and mid-to-long term.

4.3.1. Short-Term Verification Goals (Within 5 Years)

• Analysis of Terrestrial Precision Gravity Experiment Data: Data from ongoing or planned high-precision gravity experiments, such as tests of the equivalence principle or measurements of the gravitational field using atom interferometry, or tests of the gravitational law at short distances using torsion balance experiments [37], can be re-analyzed from the perspective of SIC theory, or new experiments can be proposed. If the $\mathcal{C}$ field exhibits minute local variations or interacts weakly with matter, this might manifest as tiny deviations from Newton’s inverse square law or minute variations in fundamental constant values. One should examine whether upper limits can be set for the coupling constant $\beta$ or $\mathcal{C}$ field-related parameters through these.
• Reviewing the Feasibility of Using Satellite Gravity Mission Data: Data from existing satellite missions that precisely measure Earth’s gravitational field, such as GRACE-FO (Gravity Recovery and Climate Experiment Follow-On), or from next-generation precision gravity missions that may be planned in the future, can be utilized. If there is a significant distribution or variation of the $\mathcal{C}$ field within the Earth or the Solar System, one should investigate the possibility of detecting minute gravitational field variation signals (differences from standard GR predictions) on terrestrial or Solar System scales, or of placing constraints on the theory’s parameters [37].

4.3.2. Mid-to-Long-Term Verification Goals (10–20 Years)

Utilizing Next-Generation Gravitational Wave Observatories: In addition to the current LIGO-Virgo-KAGRA network [38], future space-based gravitational wave observatories like LISA (Laser Interferometer Space Antenna) and ground-based third-generation observatories such as the Einstein Telescope and Cosmic Explorer will provide new opportunities to test gravitational theories in extreme environments with extremely high precision. SIC theory may predict gravitational wave phenomena different from standard GR:

−

Extreme Mass Ratio Inspiral (EMRI) Systems: Gravitational waves emitted from a small black hole or neutron star spiraling into a supermassive black hole carry highly precise information about spacetime geometry. Spatial variations in the $\mathcal{C}$ field or $G_{\mathrm{eff}}$ could have subtle but cumulative effects on the orbital evolution and gravitational waveforms of such systems, which could be searched for with LISA and others.

−

Cosmological Gravitational Wave Background: The spectrum of a stochastic gravitational wave background, potentially generated during inflation or phase transitions in the early universe, could be sensitive to the early universe dynamics of the $\mathcal{C}$ field and the temporal evolution of $G_{\mathrm{eff}}$.

−

Modified Propagation Characteristics: If the $\mathcal{C}$ field affects the propagation speed or polarization states of gravitational waves, this could lead to verifiable effects in distance measurements to gravitational wave sources (standard sirens) or in multi-messenger astronomy.

−

Exploring Phenomena Approaching Planck Scale and Theoretical Consistency: Developing experimental or observational methodologies to directly verify the quantum nature of the $\mathcal{C}$ field or its fundamental connection with quantum gravity theories [21,22] will be a very challenging and long-term goal. This must be pursued in tandem with theoretical research into the quantization of SIC, its renormalizability, and its UV completion at the Planck scale. For example, it might be indirectly explored through phenomenological predictions in extreme environments such as the early universe or near black holes.

4.4. Comparison with Other Theories and Current Limitations of SIC

4.4.1. Comparison with Existing Modified Gravity Theories (Conceptual)

Structural Information Cosmology (SIC) shares similarities and differences in its motivations and approaches with several modified gravity theories proposed to explain phenomena such as dark matter or dark energy. The following table provides a conceptual comparison of major modified gravity theories with SIC.

Theory/Approach	Primary Motivation/Goal	Modification Method (Example)	Comparative Perspective with SIC (Potential & Differentiation)
MOND[40]	Galaxy rotation curves (explanation without dark matter)	Modification of Newtonian dynamics or inertia at low accelerations ($a\ll a_0$)	SIC has the potential to explain similar phenomena (e.g., gravity enhancement at galactic scales) by varying $G_{\mathrm{eff}}$ through the $\mathcal{C}$ distribution. However, while MOND primarily focuses on phenomenological modification, SIC proposes a more fundamental motivation (information structure) and aims to encompass cosmology as a whole.
$f\left(R\right)$ Gravity[34]	Dark energy, early universe inflation, gravity modification	Replacing the Ricci scalar R in the Einstein-Hilbert Lagrangian with a general function $f\left(R\right)$	SIC also modifies the gravitational Lagrangian via the information-gravity coupling term $\beta {\mathcal{C}}^{2}R$ (i.e., effectively an $F\left(\mathcal{C}\right)R$ form). However, unlike $f\left(R\right)$ theories, the independent dynamics of the $\mathcal{C}$ field itself (kinetic term, potential) provide additional degrees of freedom and richer phenomenology. Under certain conditions, $f\left(R\right)$ theories might be encompassed as a special case of SIC.

Theory/Approach	Primary Motivation/Goal	Modification Method (Example)	Comparative Perspective with SIC (Potential & Differentiation)
Scalar-Tensor Theory[30,31]	Brans-Dicke principle, varying gravitational constant, dark energy, inflation, etc.	One or more scalar fields coupling to gravity in (non-)minimal forms	SIC introduces a scalar field $\mathcal{C}$ intended to impart a specific physical meaning of “structural complexity of information.” In addition to the non-minimal coupling typical of standard scalar-tensor theories, SIC considers more general and complex dynamics from the outset by including a unique higher-order kinetic term ($\lambda {(\nabla \mathcal{C})}^4$) [32,36].
Extra Dimension Theory	Hierarchy problem, force unification, dark matter candidates, etc.	Assumption of higher-dimensional spacetime beyond 4D (e.g., gravity alone can propagate into extra dimensions)	SIC, for now, attempts to explain phenomena through information structure within standard 4D spacetime. However, as discussed in Section 3.2.4, the possibility that the $\mathcal{C}$ field might be an effective theoretical representation of a more fundamental higher-dimensional “information structure space” can be explored as a separate issue in the future. (General reviews on extra dimension theories can be found, for example, in [35] etc.)

]@ >p() * 0.2857 >p() * 0.2500 >p() * 0.1786 >p() * 0.2857@ [b]Theory/Approach	[b]Primary Motivation/Goal	[b]Modification Method (Example)	[b]Comparative Perspective with SIC (Potential & Differentiation)
SIC (This Proposal)	Information structure-centric cosmology, attempt at unified explanation	Proposing ${\mathcal{L}}_{\mathrm{SIC}}$ (non-minimal coupling of $\mathcal{C}$ field and R, unique dynamics of $\mathcal{C}$)	Attempts a unified approach to the modulation of effective gravity, potential unification of forces, resolution of cosmological problems (dark matter, dark energy, etc.) through a new physical entity $\mathcal{C}$. The calculation example in Section 3.1 showed the potential to explain a significant portion of dark matter effects.

(Note: The table above is a highly simplified comparison of each theory and approach, and each has various specific models and variations. The “gravity enhancement effect” of SIC is based on the specific example calculation in Section 3.1 of this paper and is not a general quantitative prediction of the theory.)

4.4.2. Current Limitations of SIC Theory

As SIC theory presented in this paper is still in its nascent, conceptual stage, it possesses the following clear limitations, and future research is essential to overcome them.

• Extensiveness and Indeterminacy of Parameter Space: The free parameters of the theory, including the coupling constants ($\beta ,\lambda$) and the specific functional form of the self-interaction potential $V\left(\mathcal{C}\right)$ in the current SIC Lagrangian, are not yet sufficiently constrained by observations or fundamental theoretical principles. This limits the concrete predictive power of the theory. Systematic exploration of the parameter space and the establishment of constraints through various astronomical observational data (e.g., CMB [5], supernovae [6,7], large-scale structure distribution, etc.) are essential for future work.
• Lack of Quantum Foundation and Consistency Issues: SIC is currently described primarily at the level of classical field theory. Crucial theoretical challenges, such as a complete method for quantizing the $\mathcal{C}$ field, the renormalizability of the theory, and its consistent integration with quantum gravity [21,22] at the Planck scale, remain unresolved. Without understanding these quantum aspects, it is difficult to ascertain the fundamental validity of the theory.
• Concrete Physical Reality and Measurement of the $\mathcal{C}$ Field: The concept of the $\mathcal{C}$ field as “structural complexity of information” still has an abstract aspect regarding its definition and physical content. A clearer understanding and methodology are needed concerning how it quantitatively connects to existing physical quantities (e.g., entropy [27,28], entanglement measures [19], etc.) and how it can be independently measured or observed. Finding experimental or observational evidence that can directly confirm the existence of the $\mathcal{C}$ field will be a key part of verifying the theory.

4.5. Long-Term Development Directions and Physical Implications

4.5.1. Potential for Expansion into an “Information Physics” Paradigm

SIC, in itself, is an attempt to overcome the limitations of cosmology and gravitational theory. Simultaneously, it can contribute to the formation of a broader “Information Physics” paradigm, which fundamentally re-examines and highlights the role of “information” in physics. This may include new ways of exploring fundamental questions such as:

• What is the relationship between information and spacetime, and which is more fundamental? Or how do they emerge from each other? (e.g., Wheeler’s “It from Bit” [14], the holographic principle [3,15,16], and recent ideas about spacetime emerging from entanglement [21,23,25]). The ordering of causality may be perceived as time, and this perception itself could be a phenomenon that emerges at the moment information becomes structured.
• Can physical laws themselves be understood as manifestations of rules for processing, storing, and transmitting information? (e.g., Landauer’s “Information is Physical” principle [13] and its extensions)
• Can the evolution of the universe be understood as a process of storing, processing, and transmitting information? In this regard, if dark energy in SIC originates from the dynamics of the $\mathcal{C}$ field (see Section 3.2.3), then a specific potential $V\left(\mathcal{C}\right)$ for the $\mathcal{C}$ field opens the possibility for a cyclic universe model [explored in some modified gravity or scalar field cosmology models, see, e.g., discussions in [35]] where the universe re-contracts after the current phase of accelerated expansion. In this case, one could explore the intriguing hypothesis that the extremely compressed information structure (the final state of the $\mathcal{C}$ field) at the end of each cosmic cycle might, like genetic information, determine or influence some of the initial conditions or physical laws of the next universe. This would further deepen the information-centric perspective on the origin and ultimate fate of the universe.
• The Gap Between the Probabilistic Description of Quantum Mechanics and Macroscopic Causality: Quantum field theory describes the microscopic world probabilistically, which sometimes leads to interpretational difficulties regarding clear causal continuity in physical processes. If the universe fundamentally operates only in a probabilistic and indeterminate manner, how can the coherent and orderly macroscopic world as we observe it exist? One of the fundamental motivations of SIC theory is an attempt to answer such questions. One could explore the hypothesis that the structural information field $\mathcal{C}$ plays a role in mediating or ensuring causal continuity and coherence when quantum-level probabilistic possibilities manifest as concrete, determinate physical phenomena in the macroscopic world. That is, the $\mathcal{C}$ field, through the structuring of information, might play a role in “selecting” or “reinforcing” specific causal paths amidst probabilistic degrees of freedom, thereby providing an information-based explanation for the emergence of physical laws and the orderly evolution of the universe. This is a very challenging and profound topic, but it could be one of the ultimate implications of the information-centric paradigm pursued by SIC. (Such issues are also related to the measurement problem and interpretations of quantum mechanics [19]).

4.5.2. Potential Technological Applications and Exploration of Exotic Phenomena (Very Long-Term Perspective)

If SIC theory is successfully developed and the existence and controllability of the $\mathcal{C}$ field are confirmed, it could lead to innovative technological applications that are currently in the realm of science fiction. (It is explicitly stated that these are highly abstract and long-term speculations, based more on conceptual ideas than current scientific evidence).

• New forms of quantum computing or information processing systems (related to quantum information theory [19]).
• If the theory permits and technological means are secured, techniques for local spacetime structure manipulation through $\mathcal{C}$ field control.
• Novel communication or energy transmission methods based on information structure.
• Furthermore, deeper research into $\mathcal{C}$ field dynamics might explore the possibility of solutions allowing for stable yet non-standard information propagation characteristics (see causality discussions in Section 2.5 and 3.1.6). If such solutions exist and are physically meaningful, they would pose fundamental questions to our understanding of causality in spacetime and, at a very abstract level, could open possibilities for explaining phenomena that appear to transcend spatiotemporal constraints through efficient connectivity (`shortcuts’) within an `information structure space’ (e.g., effects appearing like effective superluminal information transfer). However, this currently lies purely in the realm of theoretical speculation and must be preceded by rigorous mathematical formulation and verification of physical consistency (especially consistency with macroscopic causality).

4.6. Concluding Outlook

Structural Information Cosmology (SIC) is a theoretical framework possessing the potential to offer new and integrative solutions to some of the most fundamental challenges facing 21stcentury physics—such as the problems of dark matter [4,5] and dark energy [5,6,7], the unification of fundamental forces (including the absence of a quantum gravity theory that unifies gravity and quantum mechanics [11,12,21,22]), and the black hole information paradox [8,9,10]. The initial ideas and calculation examples presented in this paper, particularly the possibility of explaining a significant portion of dark matter effects through the modulation of the effective gravitational coupling constant Geff (under the specific model assumptions of Section 3.1), suggest that this theory has the potential to develop beyond a mere conceptual fancy into a substantive physical theory

However, for SIC to establish itself as one of the major theories in physics, it must successfully address key challenges, as discussed in detail in Sections 4.2 and 4.3. These include systematic theoretical development (model refinement, determination of free parameters, establishment of a quantum foundation, etc.), rigorous verification through precise observations and experiments (e.g., gravitational lensing [12,35], celestial mechanics, gravitational wave observations [38], CMB analysis [5], terrestrial precision gravity experiments [37], etc.), and the clarification of its relationship with other existing theories (see Section 4.4). These tasks are difficult to achieve through individual research alone and can be more effectively pursued through broad discussions and critical reviews within the physics community, as well as through international collaboration.

If the “information-centric” paradigm proposed by SIC theory is successfully developed and verified, it could fundamentally change our understanding of the universe and the laws of nature, perhaps even being recorded as one of the important turning points in physics since Einstein’s General Relativity [1]. It is hoped that this paper will serve as a small but meaningful first step towards such a future.