Submitted:
02 June 2025
Posted:
03 June 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Background
2.1. Existing REC Solutions
| Ref. | Energy Forecasting |
Energy Optimisation |
Fairness | Privacy | ML Pipeline |
Continual Evaluation |
|---|---|---|---|---|---|---|
| [6] | √ | √ | X | X | X | X |
| [7] | √ | X | X | √ | X | X |
| [8] | √ | √ | √ | √ | X | X |
| [9] | √ | √ | X | X | X | X |
| [10] | √ | X | X | √ | X | X |
| [11] | X | √ | X | X | X | √ |
| [12] | X | √ | P2P | X | X | X |
| [13] | X | √ | √ | X | X | X |
| [14] | Concept | Concept | X | X | Concept | Concept |
| Count | 5 | 6 | 3 | 3 | 0 | 1 |
2.2. Predictive Models in REC Settings
| Ref. | Target | TR | U/M | Lookback Window |
Forecast Window |
Performance |
|---|---|---|---|---|---|---|
| [6] | PV production (kW) | 15m | U | 60h | 24h | MAE: 1.60 |
| Consumption | MAE: 2.15 | |||||
| [7] | Congestion | 15m | M | - | - | RMSE: 0.88 |
| [9] | Consumption | 30m | M | 24h | 24h | RMSE: 4.13 |
| [15] | Demand | 15m | U | 2w | 48h | MAPE: 10.00% |
| [16] | Electricity Price | 1h | U | 7d | 24h | MAE: 18.86 |
| [17] | PV production (kWh) | 1h | M | 10h | 1h | RMSE: 1.08 |
| [18] | Consumption | 1M | U | 5Y | 1Y | MAPE 2.67% |
| [19] | Electricity Price | 1h | M | 30d | 2d | rMAE: 8.18% |
3. Methodology
3.1. Application Context
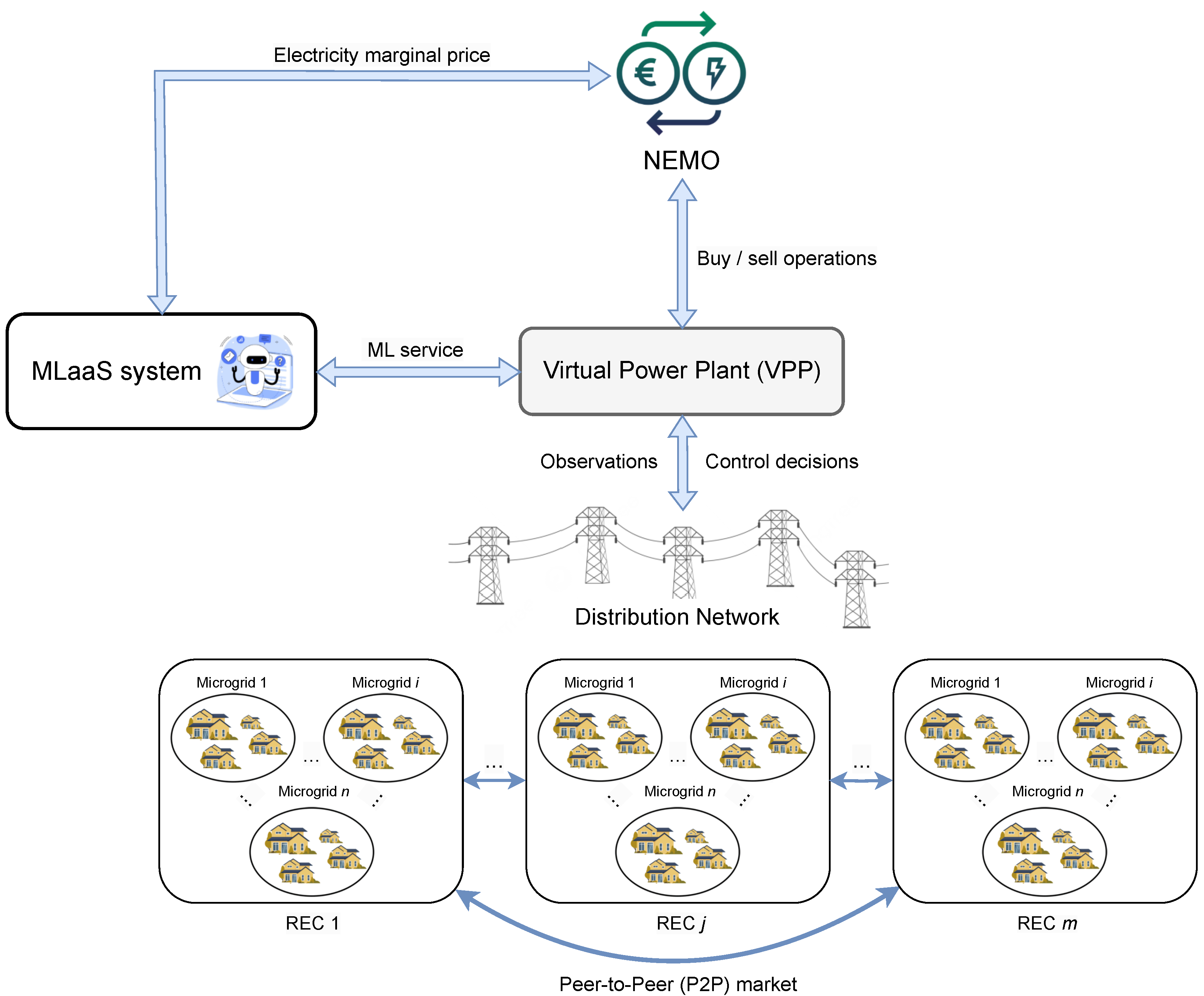
3.2. Proposed MLaaS Solution
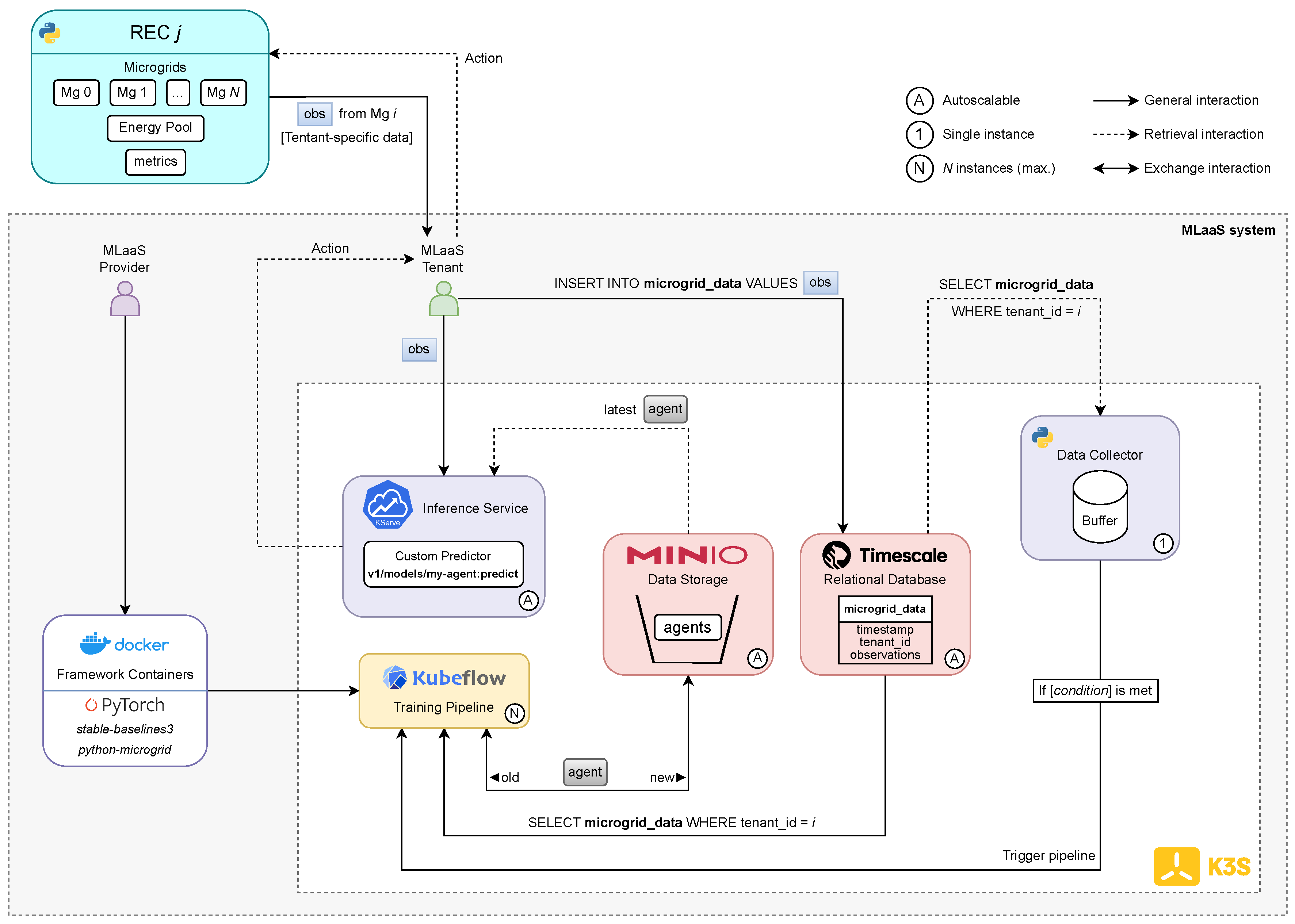
3.3. Trainable Environment
| No. | Operation(s) | Entities | Load Supply | Surplus Handling |
|---|---|---|---|---|
| 0 | Charge battery | Battery | X | √ |
| 1 | Discharge battery | Battery | √ | X |
| 2 | Import from grid | Grid | √ | X |
| 3 | Export to grid | Grid | X | √ |
| 4 | Use genset | Genset | √ | X |
| 5 | Charge battery (fully) with energy from PV panels and/or the grid, then export PV surplus | Battery + Grid |
X | √ |
| 6 | Discharge battery, then use genset | Battery + Genset | √ | X |
3.4. Available Energy Profiles
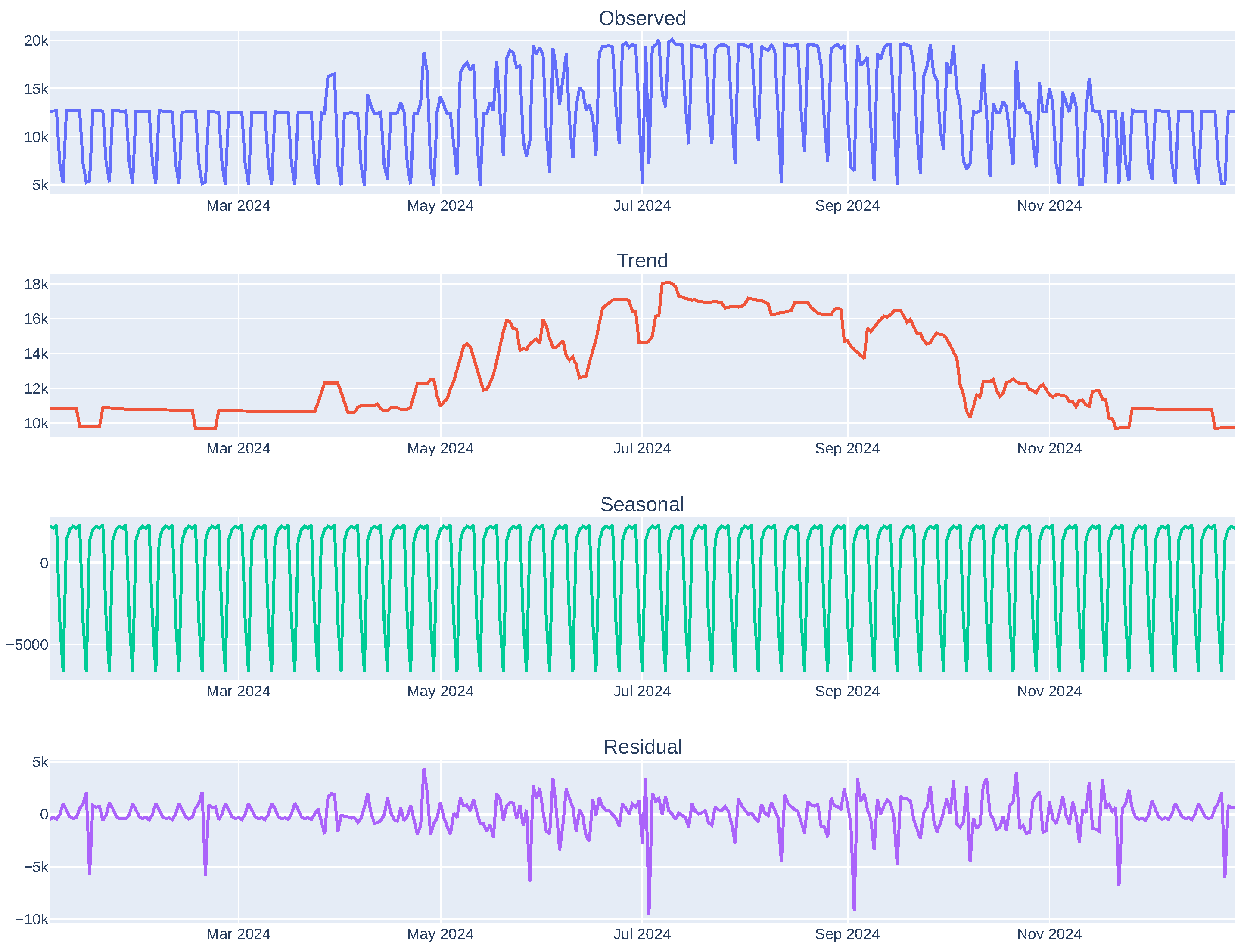
4. Development
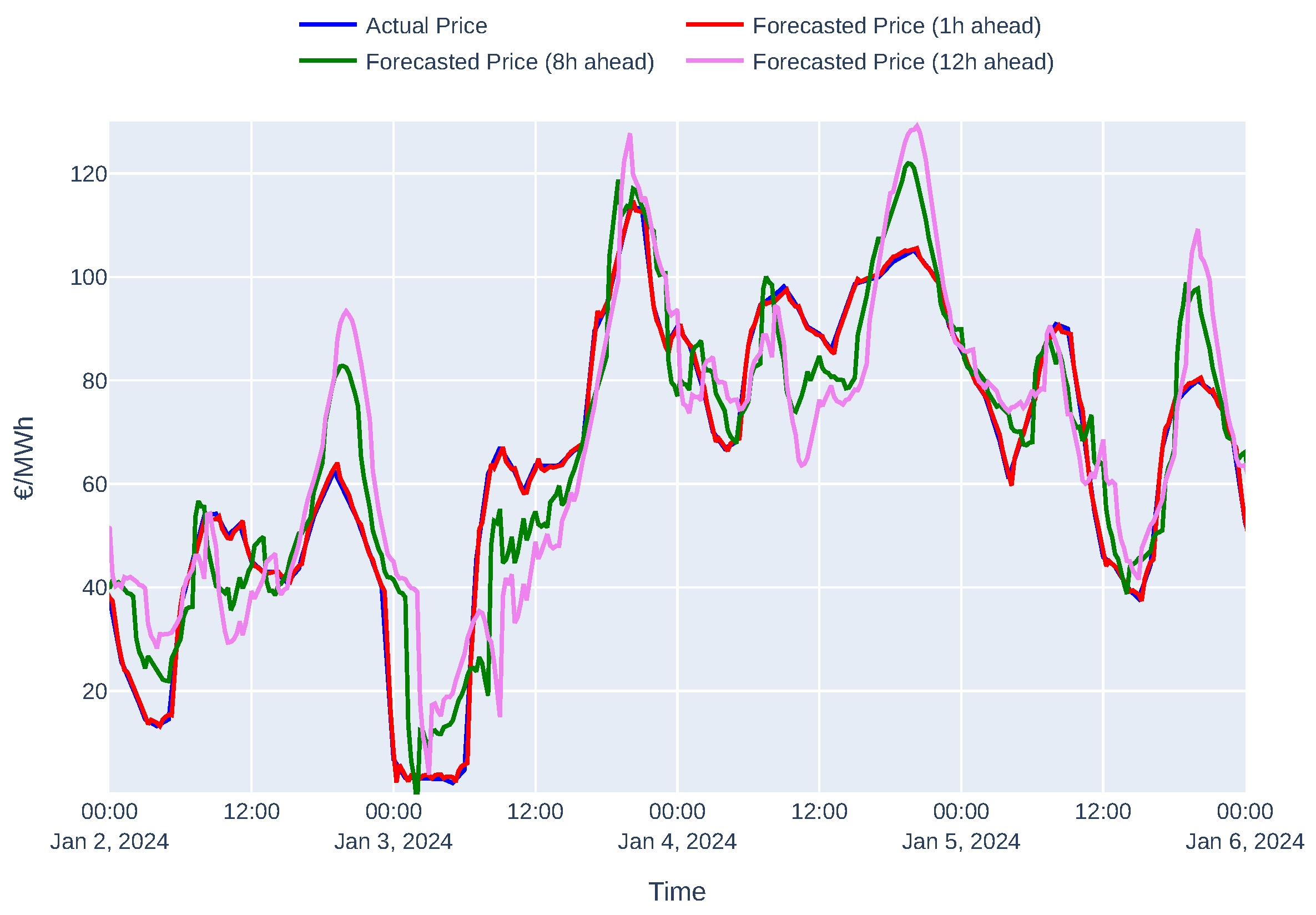
4.1. Energy Price Forecasting
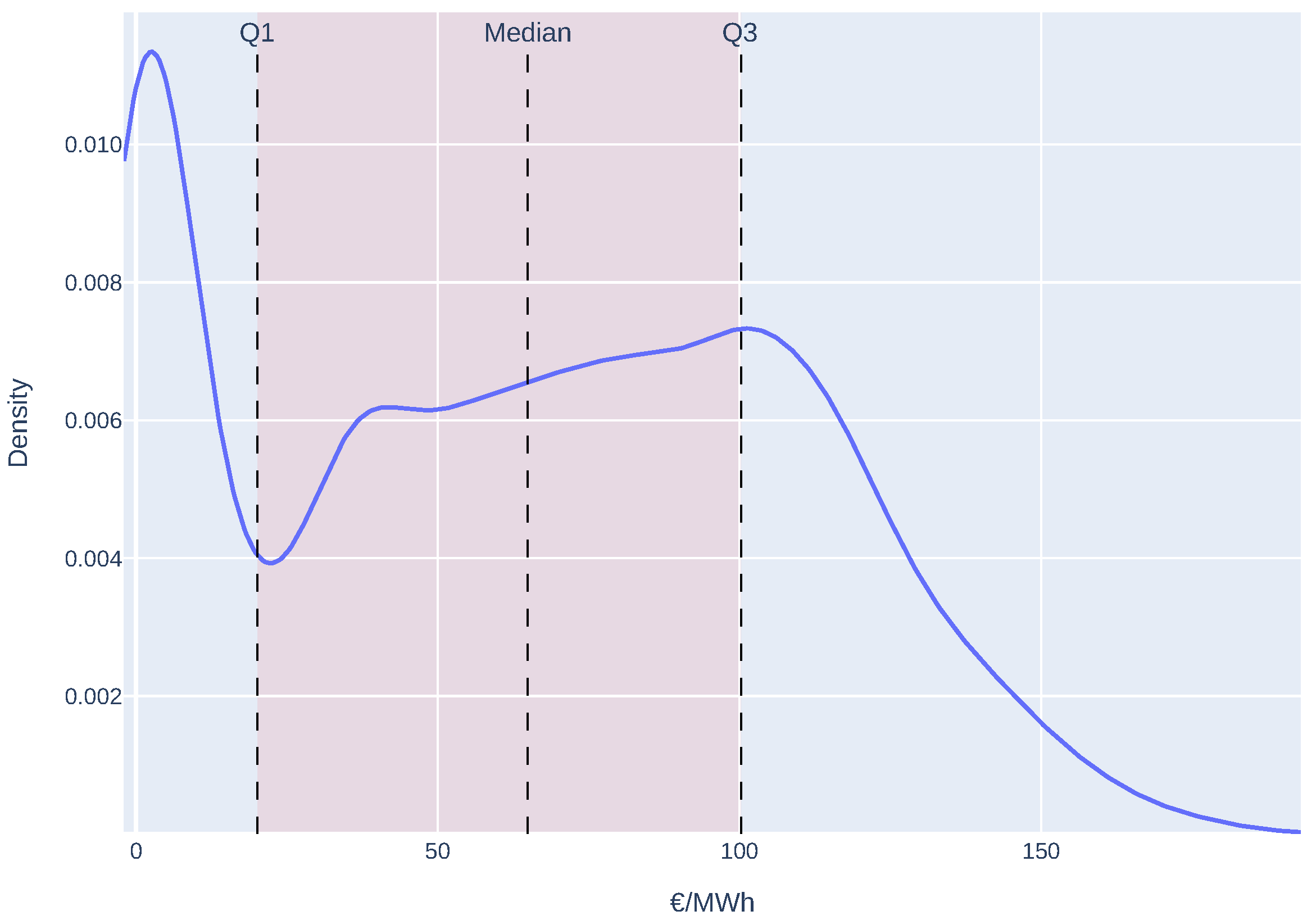
4.2. Intelligent Agents
4.2.1. Heuristics-Based Agent (Baseline)
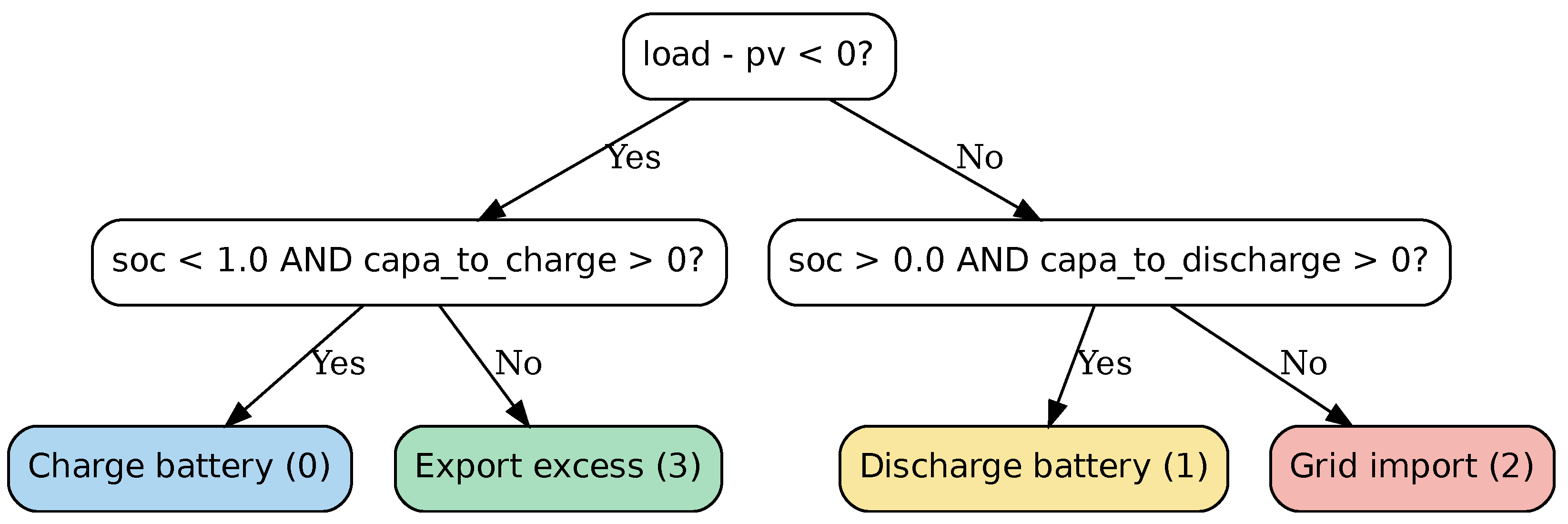
4.2.2. Algorithm 1: Deep Q-Learning (DQN)
- :
- Optimal action-value function;
- r:
- Immediate reward after taking action a in state s;
- :
- Discount factor that controls the importance of future rewards;
- :
- Next state;
- :
- Next action.
| Hyperparameter | Value |
|---|---|
| Replay buffer size | 50,000 |
| Number of transitions before start learning | 1,000 |
| Exploration initial | 1.0 |
| Exploration final | 0.02 |
| Exploration fraction | 0.25 |
| Steps between target network updates | 10,000 |
| Reward discount factor () | 0.99 |
4.2.3. Algorithm 2: Proximal Policy Optimisation (PPO)
- :
- Discount factor that controls the importance of future rewards.
- :
- GAE parameter that controls the bias-variance tradeoff.
- :
- Temporal difference error between expected and actual returns.
- :
- Reward at time step t.
- :
- Estimated value function at state s.
- :
- Policy ratio at time step t.
- :
- Advantage estimate at time step t.
- :
- Clipping parameter that constrains the ratio.
| Hyperparameter | Value |
|---|---|
| Number of epochs per policy update | 10 |
| Number of steps until policy update | 2048 |
| Mini-batch size | 32 |
| Reward discount factor () | 0.99 |
| GAE bias-variance parameter () | 0.95 |
| Clipping parameter () | 0.2 |
4.2.4. Algorithm 3: Advantage Actor-Critic (A2C)
| Hyperparameter | Value |
|---|---|
| Number of steps until policy update | 5 |
| Mini-Batch size | 1 |
| Reward discount factor () | 0.99 |
| GAE bias-variance parameter () | 1.0 |
4.2.5. Algorithm Comparison
| Aspect | DQN | PPO | A2C |
|---|---|---|---|
| Policy Type | Implicit via Q-values | Directly parametrised | Directly parametrised |
| Action Space | Discrete | Discrete/Continuous | Discrete/Continuous |
| Exploration | -greedy | Stochastic policy | Stochastic policy |
| Stability | Moderate (replay buffer) |
High | Low |
| Computational Cost |
Moderate (replay buffer) |
High (multiple epochs) |
Low (1 update / rollout) |
4.3. Inter-REC Energy Trading
- / :
- Price of the buyer’s / seller’s bid.
- / :
- Amount of energy in the buyer’s / seller’s bid.
- c:
- A constant that determines the weight of each price in the final transaction price. For mid-price bidding, which is our case, c is set to 0.5, meaning that the transaction price is the average of the buyer’s and seller’s prices.
4.4. Intra-REC Energy Exchange
- i, j:
- Tenant indexes;
- N:
- Number of tenants in the community;
- :
- Amount of energy exported (positive) or imported (negative) by tenant x;
- :
- Current market’s energy marginal price;
- :
- Amount of energy available in the energy pool.
5. Evaluation
5.1. Experiment Setup
5.2. Quality of Energy Price Forecasts
- :
- actual value / predicted value of the energy price at index i.
- n:
- number of samples in the test / validation set.
| Lookback Window |
Forecasting Window |
MAE | Val. MAE | RMSE | Val. RMSE |
|---|---|---|---|---|---|
| 12 | 8 | 3.78 ± 0.16 | 5.18 ± 1.00 | 6.29 ± 0.38 | 8.73 ± 2.05 |
| 12 | 4.99 ± 0.23 | 7.42 ± 1.63 | 7.97 ± 0.56 | 11.75 ± 2.74 | |
| 24 | 7.23 ± 0.33 | 11.93 ± 3.02 | 10.74 ± 0.69 | 17.32 ± 4.14 | |
| 24 | 8 | 3.92 ± 0.30 | 4.98 ± 0.93 | 6.45 ± 0.42 | 8.51 ± 2.17 |
| 12 | 5.11 ± 0.29 | 6.81 ± 1.40 | 8.11 ± 0.57 | 11.11 ± 2.86 | |
| 24 | 7.36 ± 0.36 | 11.09 ± 2.53 | 10.92 ± 0.68 | 16.29 ± 3.91 | |
| 48 | 8 | 3.91 ± 0.41 | 4.88 ± 0.93 | 6.38 ± 0.46 | 8.26 ± 2.20 |
| 12 | 5.19 ± 0.32 | 6.80 ± 1.08 | 8.15 ± 0.57 | 11.03 ± 2.47 | |
| 24 | 7.33 ± 0.43 | 11.32 ± 2.75 | 10.86 ± 0.73 | 16.44 ± 4.03 |
| i | Agent | Activation Function |
Network Arch. |
Learning Rate |
Baseline (M$) |
Cost (M$) |
Diff. (M$) |
% |
|---|---|---|---|---|---|---|---|---|
| 0 | A2C | ReLU | [128, 128] | 0.001 | 0.19 | 0.05 | 0.14 | 72.68 |
| 1 | DQN | ReLU | [64, 64] | 0.0001 | 23.70 | 3.65 | 20.00 | 84.61 |
| 2 | DQN | ReLU | [64, 64] | 0.0001 | 36.00 | 1.75 | 34.30 | 95.14 |
| 3 | DQN | Tanh | [64, 64] | 0.001 | 35.90 | 1.58 | 34.40 | 95.60 |
| 4 | DQN | ReLU | [64, 64] | 0.0001 | 32.40 | 4.38 | 28.10 | 86.51 |
| 5 | PPO | Tanh | [128, 128] | 0.001 | 114.00 | 4.07 | 109.00 | 96.41 |
| 6 | PPO | Tanh | [128, 128] | 0.001 | 46.30 | 1.76 | 44.50 | 96.20 |
| 7 | DQN | ReLU | [64, 64] | 0.0001 | 15.40 | 1.21 | 14.20 | 92.14 |
| 8 | PPO | Tanh | [128, 128] | 0.001 | 9.74 | 3.64 | 6.09 | 62.58 |
| 9 | DQN | ReLU | [64, 64] | 0.0001 | 3.57 | 1.94 | 1.63 | 45.67 |
| Agent | Activation Function |
Network Arch. |
Learning Rate |
% |
|---|---|---|---|---|
| PPO | Tanh | [64, 64] | 0.001 | < +0.01 |
| PPO | Tanh | [64, 64] | 0.0001 | < +0.01 |
| A2C | Tanh | [64, 64] | 0.001 | < +0.01 |
| DQN | Tanh | [128, 128] | 0.0001 | < +0.01 |
| A2C | Tanh | [128, 128] | 0.0001 | +0.13 |
| DQN | Tanh | [64, 64] | 0.0005 | +0.77 |
| DQN | ReLU | [64, 64] | 0.0001 | +0.94 |
| DQN | ReLU | [128, 128] | 0.0001 | +0.40 |
| DQN | Tanh | [64, 64] | 0.001 | +0.36 |
| DQN | Tanh | [128, 128] | 0.001 | 6.22* |
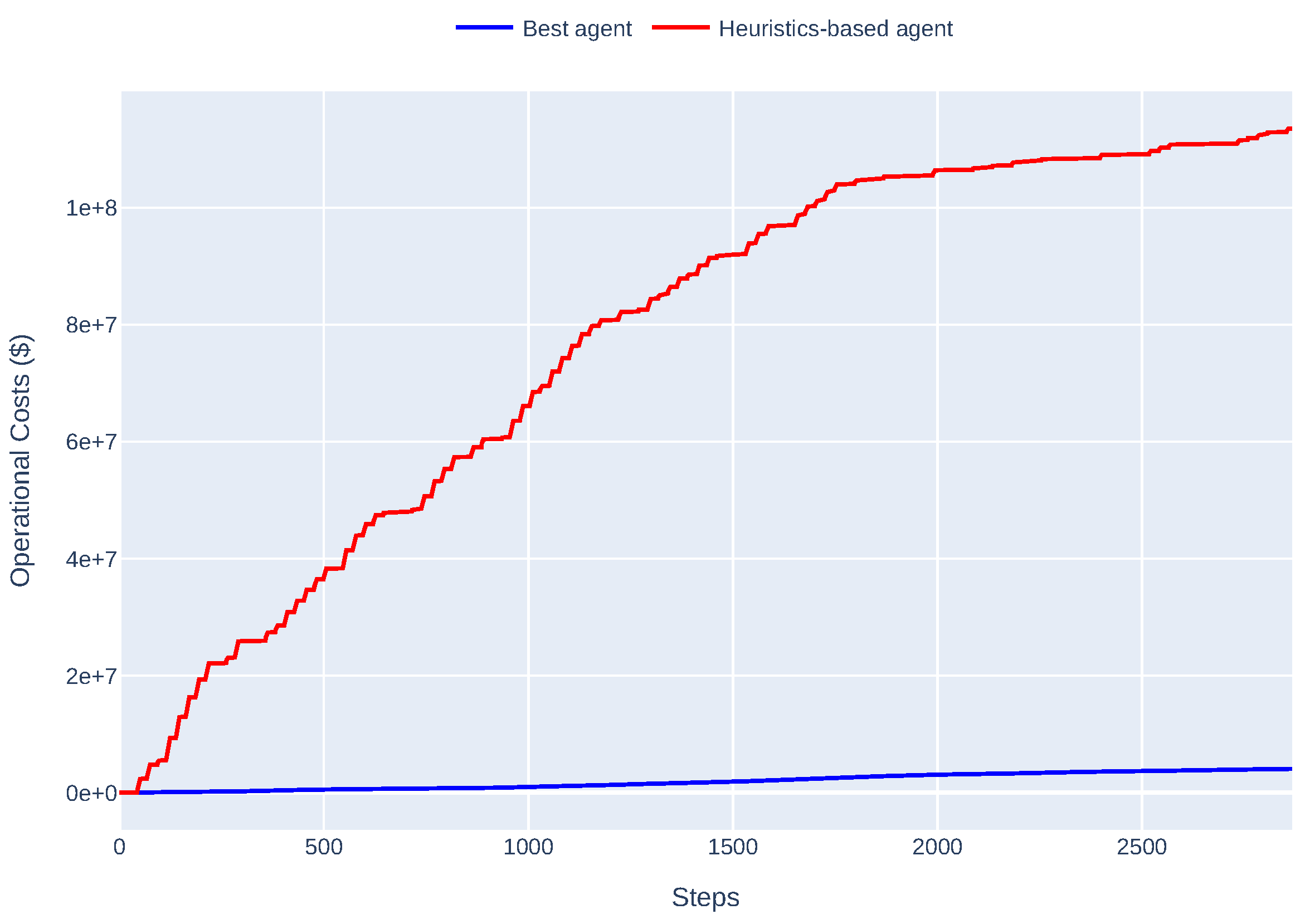
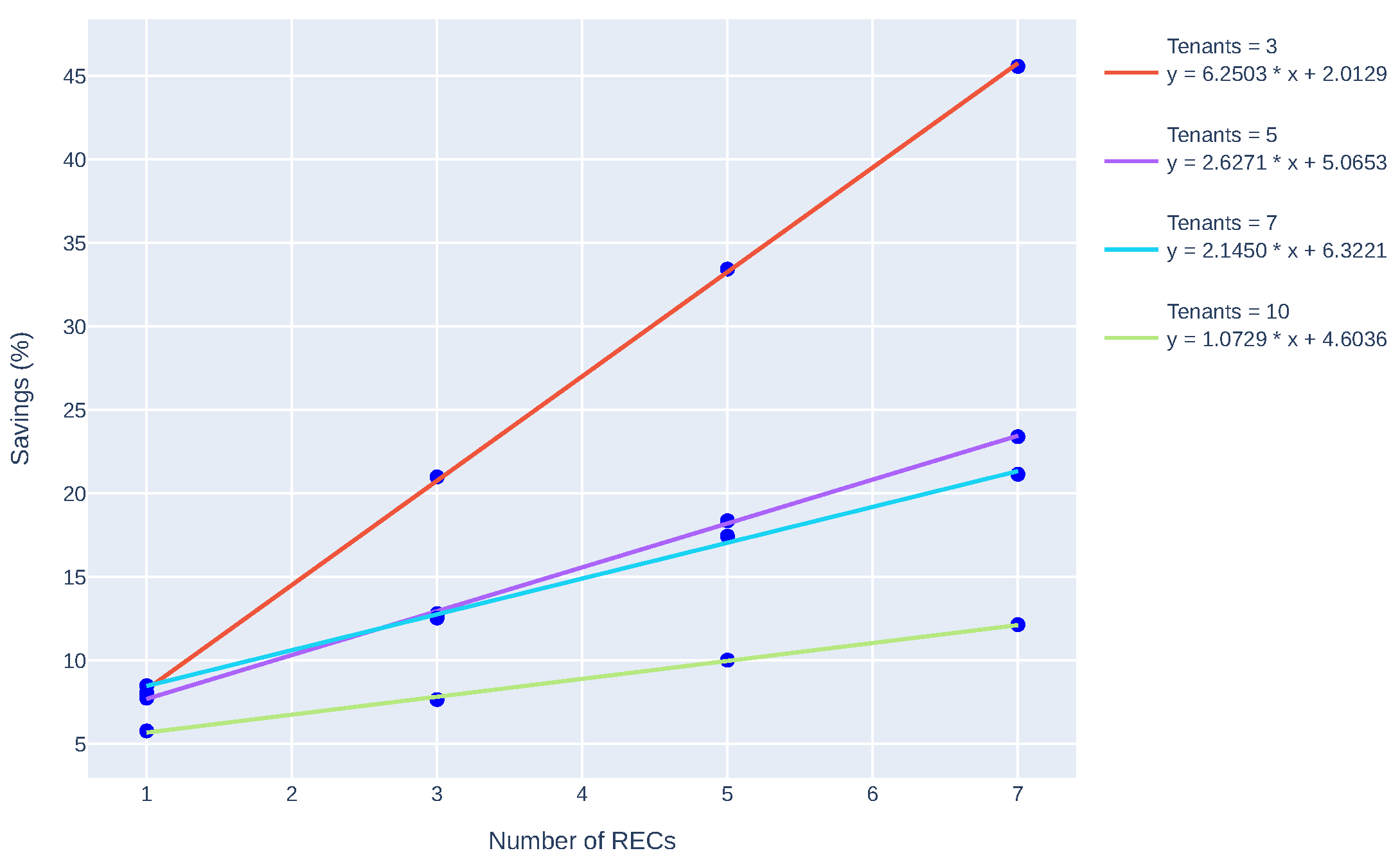
5.3. Simulation Benchmark
| R | T | Heuristics-based Agent | Best Agent | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| NN | NY | YY | Sav. | % | NN | NY | YY | Sav. | % | ||
| 1 | 3 | 8.39 | 8.19* | 0.21 | 2.47 | 7.37 | 6.78* | 0.59 | 8.06 | ||
| 1 | 5 | 17.60 | 17.00* | 0.54 | 3.05 | 15.50 | 14.30* | 1.20 | 7.74 | ||
| 1 | 7 | 27.20 | 26.30* | 0.98 | 3.61 | 23.30 | 21.30* | 1.98 | 8.48 | ||
| 1 | 10 | 37.30 | 36.60* | 0.72 | 1.92 | 32.80 | 30.90* | 1.89 | 5.77 | ||
| 3 | 3 | 8.35 | 8.18 | 7.90 | 0.45 | 5.41 | 7.36 | 7.22 | 5.82 | 1.55 | 20.99 |
| 3 | 5 | 17.50 | 16.80 | 16.30 | 1.21 | 6.95 | 15.60 | 15.00 | 13.60 | 1.99 | 12.80 |
| 3 | 7 | 27.20 | 26.30 | 25.50 | 1.69 | 6.20 | 23.40 | 22.60 | 20.50 | 2.94 | 12.54 |
| 3 | 10 | 37.30 | 36.50 | 35.80 | 1.50 | 4.02 | 32.80 | 32.10 | 30.30 | 2.51 | 7.65 |
| 5 | 3 | 8.37 | 8.20 | 7.62 | 0.74 | 8.88 | 7.40 | 7.25 | 4.93 | 2.47 | 33.43 |
| 5 | 5 | 17.50 | 16.90 | 15.60 | 1.88 | 10.75 | 15.60 | 15.00 | 12.70 | 2.86 | 18.36 |
| 5 | 7 | 27.20 | 26.30 | 24.70 | 2.53 | 9.28 | 23.40 | 22.60 | 19.40 | 4.09 | 17.44 |
| 5 | 10 | 37.30 | 36.50 | 35.30 | 2.06 | 5.53 | 32.80 | 32.10 | 29.60 | 3.29 | 10.02 |
| 7 | 3 | 8.88 | 8.19 | 7.39 | 0.99 | 11.76 | 7.42 | 7.27 | 4.04 | 3.38 | 45.58 |
| 7 | 5 | 17.50 | 16.80 | 15.10 | 2.44 | 13.94 | 15.60 | 15.00 | 12.00 | 3.65 | 23.40 |
| 7 | 7 | 27.30 | 26.30 | 24.10 | 3.21 | 11.76 | 23.50 | 22.60 | 18.50 | 4.97 | 21.15 |
| 7 | 10 | 37.30 | 36.60 | 34.80 | 2.56 | 6.87 | 32.90 | 32.20 | 28.90 | 3.99 | 12.14 |
5.4. Infrastructure Validation
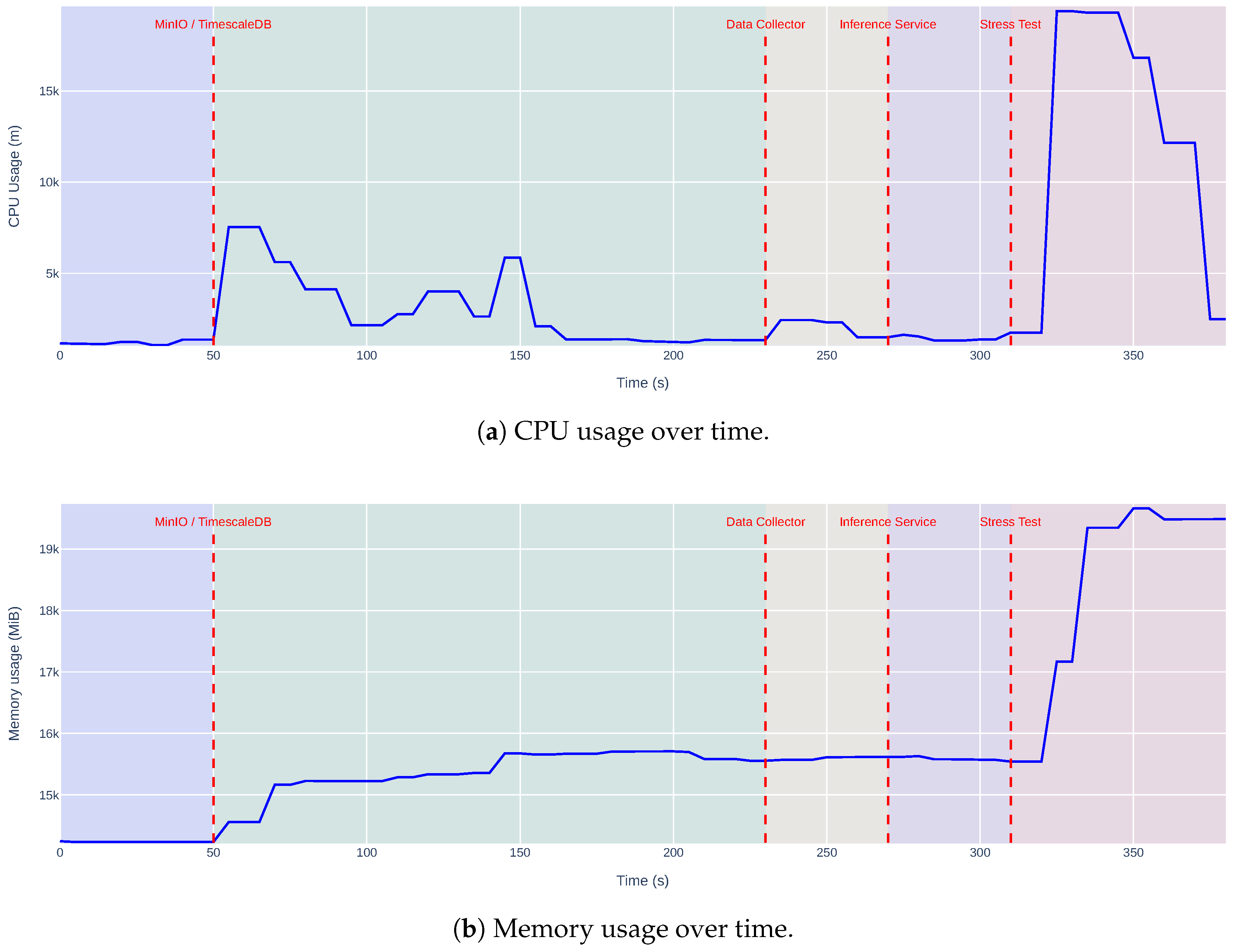
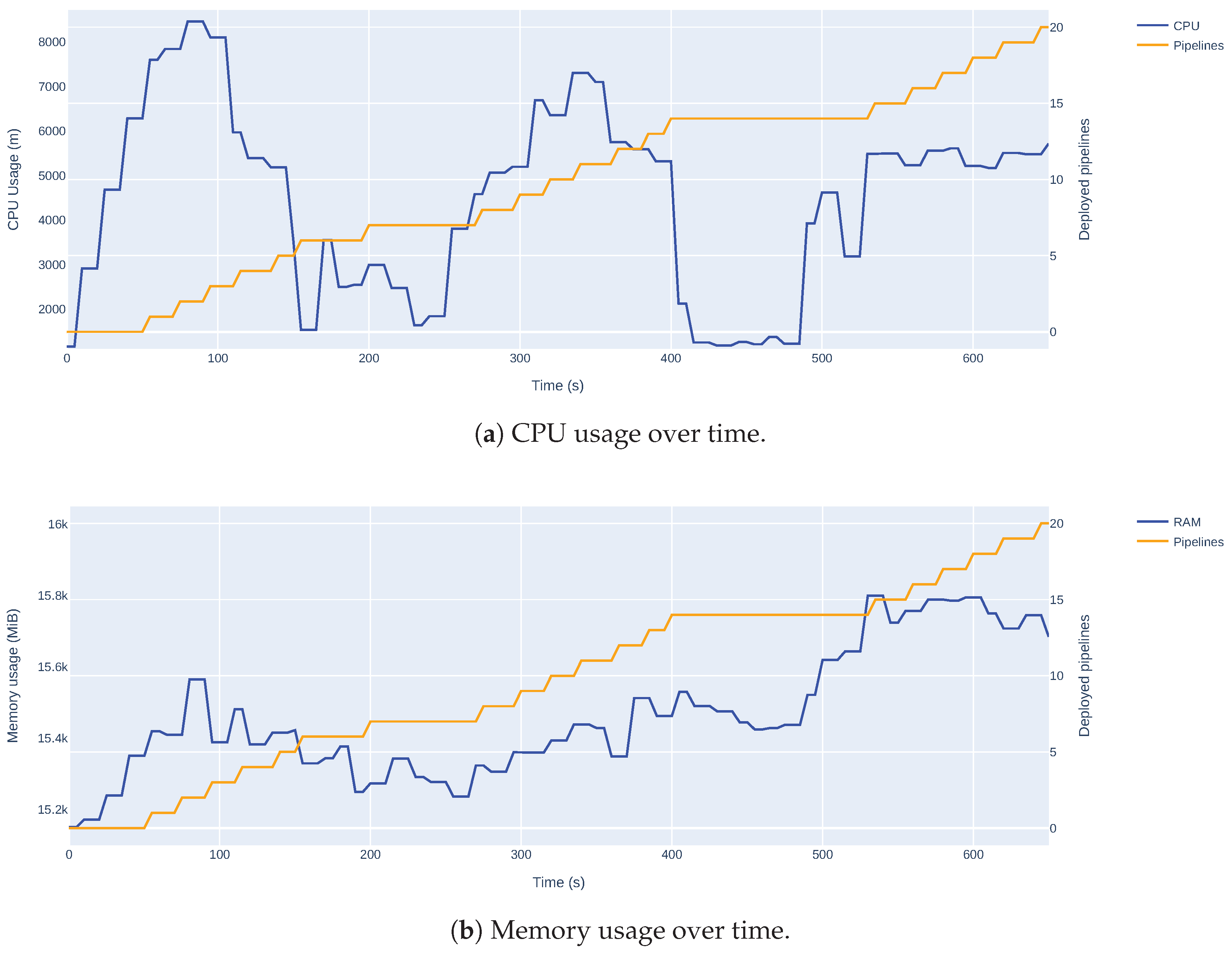
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ML | Machine Learning |
| DL | Deep Learning |
| RL | Reinforcement Learning |
| MLaaS | Machine Learning as a Service |
| MLOps | Machine Learning Operations |
| REC | Renewable Energy Community |
| VPP | Virtual Power Plant |
| NEMO | Nominated Electricity Market Operator |
| OMIE | Operador do Mercado Ibérico de Energia |
| EMS | Energy Management System |
| PV | Photovoltaic |
| BESS | Battery Energy Storage System |
| P2P | Peer-to-Peer |
| ANN | Artificial Neural Network |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| RMSE | Root Mean Squared Error |
| MAPE | Mean Absolute Percentage Error |
| EDA | Exploratory Data Analysis |
| HPA | Horizontal Pod Autoscaler |
| KFP | Kubeflow Pipelines |
| kWh | Kilowatt-hour |
| MWh | Megawatt-hour |
References
- Gielen, D.; Boshell, F.; Saygin, D.; Bazilian, M.D.; Wagner, N.; Gorini, R. The role of renewable energy in the global energy transformation. Energy Strategy Reviews 2019, 24, 38–50. [Google Scholar] [CrossRef]
- Soeiro, S.; Ferreira Dias, M. Renewable energy community and the European energy market: main motivations. Heliyon 2020, 6, e04511. [Google Scholar] [CrossRef] [PubMed]
- Nations, U. Transforming our world: The 2030 agenda for sustainable development. New York: United Nations, Department of Economic and Social Affairs 2015, 1, 41. [Google Scholar]
- Notton, G.; Nivet, M.L.; Voyant, C.; Paoli, C.; Darras, C.; Motte, F.; Fouilloy, A. Intermittent and stochastic character of renewable energy sources: Consequences, cost of intermittence and benefit of forecasting. Renewable and Sustainable Energy Reviews 2018, 87, 96–105. [Google Scholar] [CrossRef]
- Zhang, L.; Ling, J.; Lin, M. Artificial intelligence in renewable energy: A comprehensive bibliometric analysis. Energy Reports 2022, 8, 14072–14088. [Google Scholar] [CrossRef]
- Conte, F.; D’Antoni, F.; Natrella, G.; Merone, M. A new hybrid AI optimal management method for renewable energy communities. Energy and AI 2022, 10, 100197. [Google Scholar] [CrossRef]
- Mai, T.T.; Nguyen, P.H.; Haque, N.A.N.M.M.; Pemen, G.A.J.M. Exploring regression models to enable monitoring capability of local energy communities for self-management in low-voltage distribution networks. IET Smart Grid 2022, 5, 25–41. [Google Scholar] [CrossRef]
- Du, Y.; Mendes, N.; Rasouli, S.; Mohammadi, J.; Moura, P. Federated Learning Assisted Distributed Energy Optimization, 2023, [arXiv:eess.SY/2311.13785].
- Matos, M.; Almeida, J.; Gonçalves, P.; Baldo, F.; Braz, F.J.; Bartolomeu, P.C. A Machine Learning-Based Electricity Consumption Forecast and Management System for Renewable Energy Communities. Energies 2024, 17. [Google Scholar] [CrossRef]
- Giannuzzo, L.; Minuto, F.D.; Schiera, D.S.; Lanzini, A. Reconstructing hourly residential electrical load profiles for Renewable Energy Communities using non-intrusive machine learning techniques. Energy and AI 2024, 15, 100329. [Google Scholar] [CrossRef]
- Kang, H.; Jung, S.; Jeoung, J.; Hong, J.; Hong, T. A bi-level reinforcement learning model for optimal scheduling and planning of battery energy storage considering uncertainty in the energy-sharing community. Sustainable Cities and Society 2023, 94, 104538. [Google Scholar] [CrossRef]
- Denysiuk, R.; Lilliu, F.; Reforgiato Recupero, D.; Vinyals, M. Peer-to-peer Energy Trading for Smart Energy Communities. 02 2020. [CrossRef]
- Limmer, S. Empirical Study of Stability and Fairness of Schemes for Benefit Distribution in Local Energy Communities. Energies 2023, 16. [Google Scholar] [CrossRef]
- Karakolis, E.; Pelekis, S.; Mouzakitis, S.; Markaki, O.; Papapostolou, K.; Korbakis, G.; Psarras, J. Artificial intelligence for next generation energy services across Europe–the I-Nergy project. In Proceedings of the International Conferences e-Society 2022 and Mobile Learning 2022. ERIC; 2022. [Google Scholar]
- Coignard, J.; Janvier, M.; Debusschere, V.; Moreau, G.; Chollet, S.; Caire, R. Evaluating forecasting methods in the context of local energy communities. International Journal of Electrical Power & Energy Systems 2021, 131, 106956. [Google Scholar] [CrossRef]
- Aliyon, K.; Ritvanen, J. Deep learning-based electricity price forecasting: Findings on price predictability and European electricity markets. Energy 2024, 308, 132877. [Google Scholar] [CrossRef]
- Dimitropoulos, N.; Sofias, N.; Kapsalis, P.; Mylona, Z.; Marinakis, V.; Primo, N.; Doukas, H. Forecasting of short-term PV production in energy communities through Machine Learning and Deep Learning algorithms. In Proceedings of the 2021 12th International Conference on Information, Intelligence, Systems & Applications (IISA), 2021, pp. 1–6. [CrossRef]
- Krstev, S.; Forcan, J.; Krneta, D. An overview of forecasting methods for monthly electricity consumption. Tehnički vjesnik 2023, 30, 993–1001. [Google Scholar]
- Belenguer, E.; Segarra-Tamarit, J.; Pérez, E.; Vidal-Albalate, R. Short-term electricity price forecasting through demand and renewable generation prediction. Mathematics and Computers in Simulation 2025, 229, 350–361. [Google Scholar] [CrossRef]
- Sousa, H.; Gonçalves, R.; Antunes, M.; Gomes, D. Privacy-Preserving Energy Optimisation in Home Automation Systems. In Proceedings of the Joint International Conference on AI, Big Data and Blockchain. Springer; 2024; pp. 3–14. [Google Scholar]
- Gonçalves, R.; Magalhães, D.; Teixeira, R.; Antunes, M.; Gomes, D.; Aguiar, R.L. Accelerating Energy Forecasting with Data Dimensionality Reduction in a Residential Environment. Energies 2025, 18, 1637. [Google Scholar] [CrossRef]
- Raffin, A.; Hill, A.; Gleave, A.; Kanervisto, A.; Ernestus, M.; Dormann, N. Stable-Baselines3: Reliable Reinforcement Learning Implementations. Journal of Machine Learning Research 2021, 22, 1–8. [Google Scholar]
- Fuente, N.D.L.; Guerra, D.A.V. A Comparative Study of Deep Reinforcement Learning Models: DQN vs PPO vs A2C, 2024, [arXiv:cs.LG/2407.14151].
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with Deep Reinforcement Learning, 2013, [arXiv:cs.LG/1312.5602].
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal Policy Optimization Algorithms, 2017, [arXiv:cs.LG/1707.06347].
- Schulman, J.; Moritz, P.; Levine, S.; Jordan, M.; Abbeel, P. High-Dimensional Continuous Control Using Generalized Advantage Estimation, 2018, [arXiv:cs.LG/1506.02438].
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.P.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous Methods for Deep Reinforcement Learning, 2016, [arXiv:cs.LG/1602.01783].
- Huang, S.; Kanervisto, A.; Raffin, A.; Wang, W.; Ontañón, S.; Dossa, R.F.J. A2C is a special case of PPO, 2022, [arXiv:cs.LG/2205.09123].
- Kiedanski, D.; Kofman, D.; Horta, J. PyMarket - A simple library for simulating markets in Python. Journal of Open Source Software 2020, 5, 1591. [Google Scholar] [CrossRef]
- OMIE. European Market. Last Accessed: 4 January 2025.
- Henri, G.; Levent, T.; Halev, A.; Alami, R.; Cordier, P. pymgrid: An Open-Source Python Microgrid Simulator for Applied Artificial Intelligence Research, 2020, [arXiv:cs.AI/2011.08004].
- Mystakidis, A.; Koukaras, P.; Tsalikidis, N.; Ioannidis, D.; Tjortjis, C. Energy Forecasting: A Comprehensive Review of Techniques and Technologies. Energies 2024, 17. [Google Scholar] [CrossRef]
| 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




