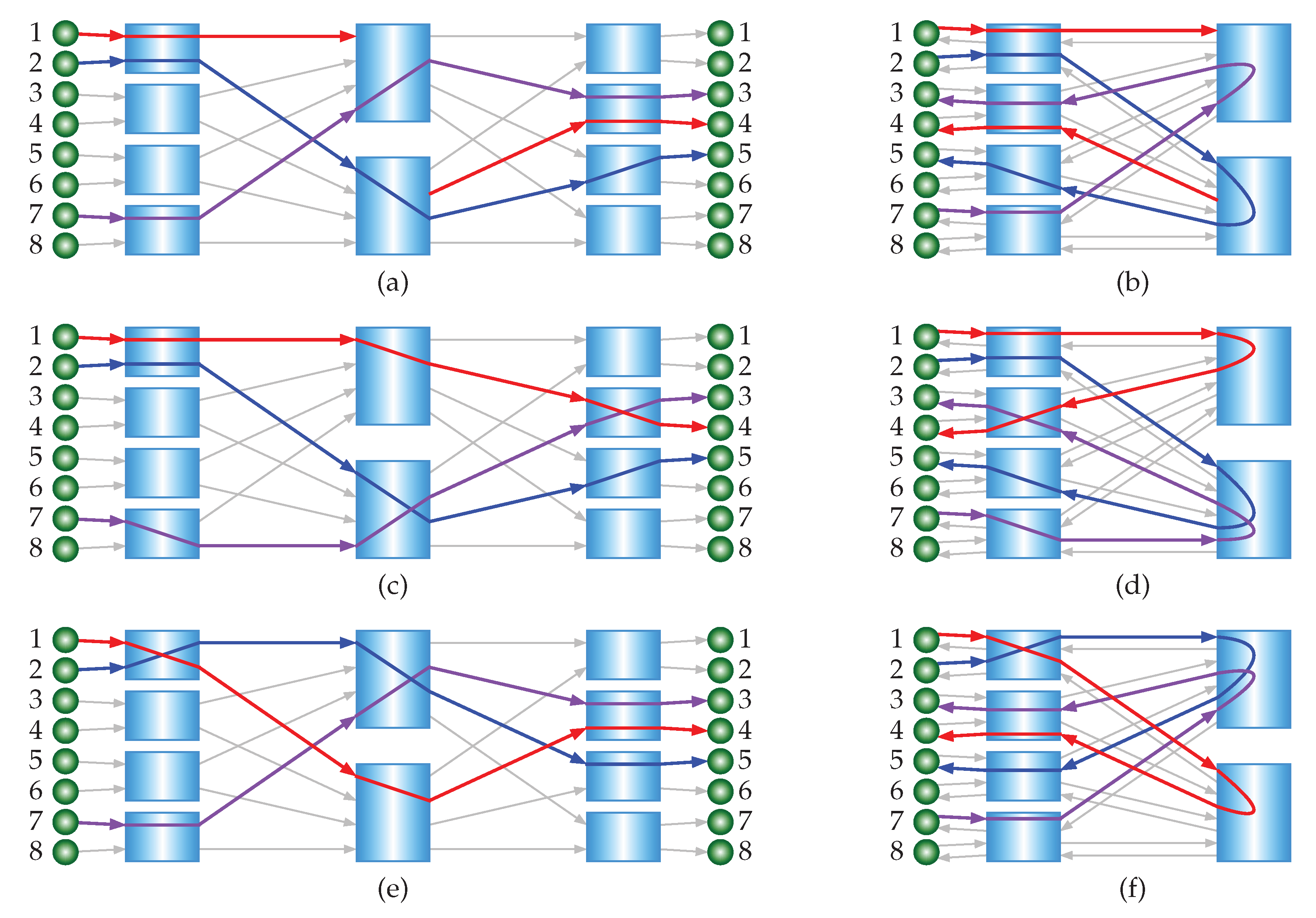
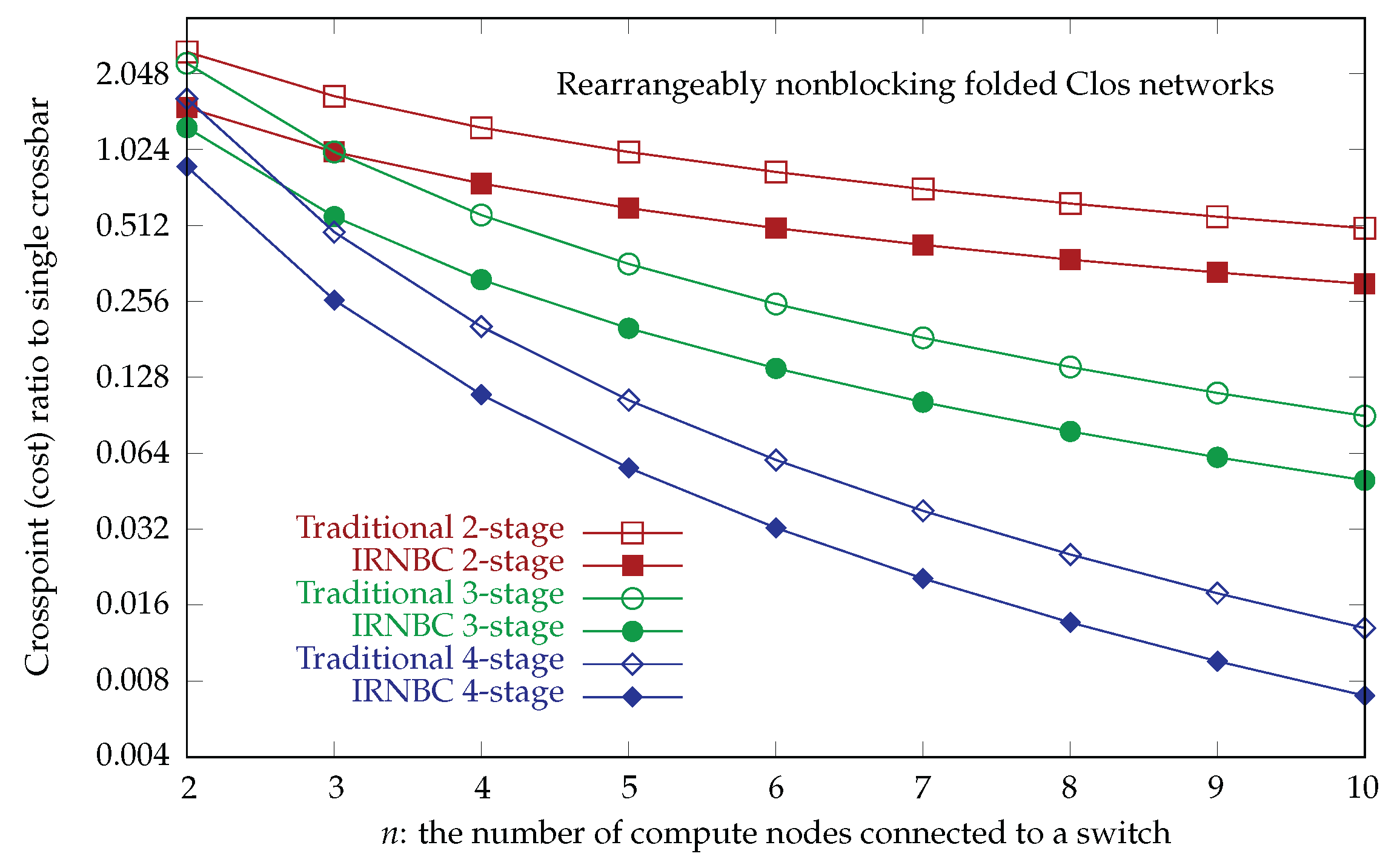
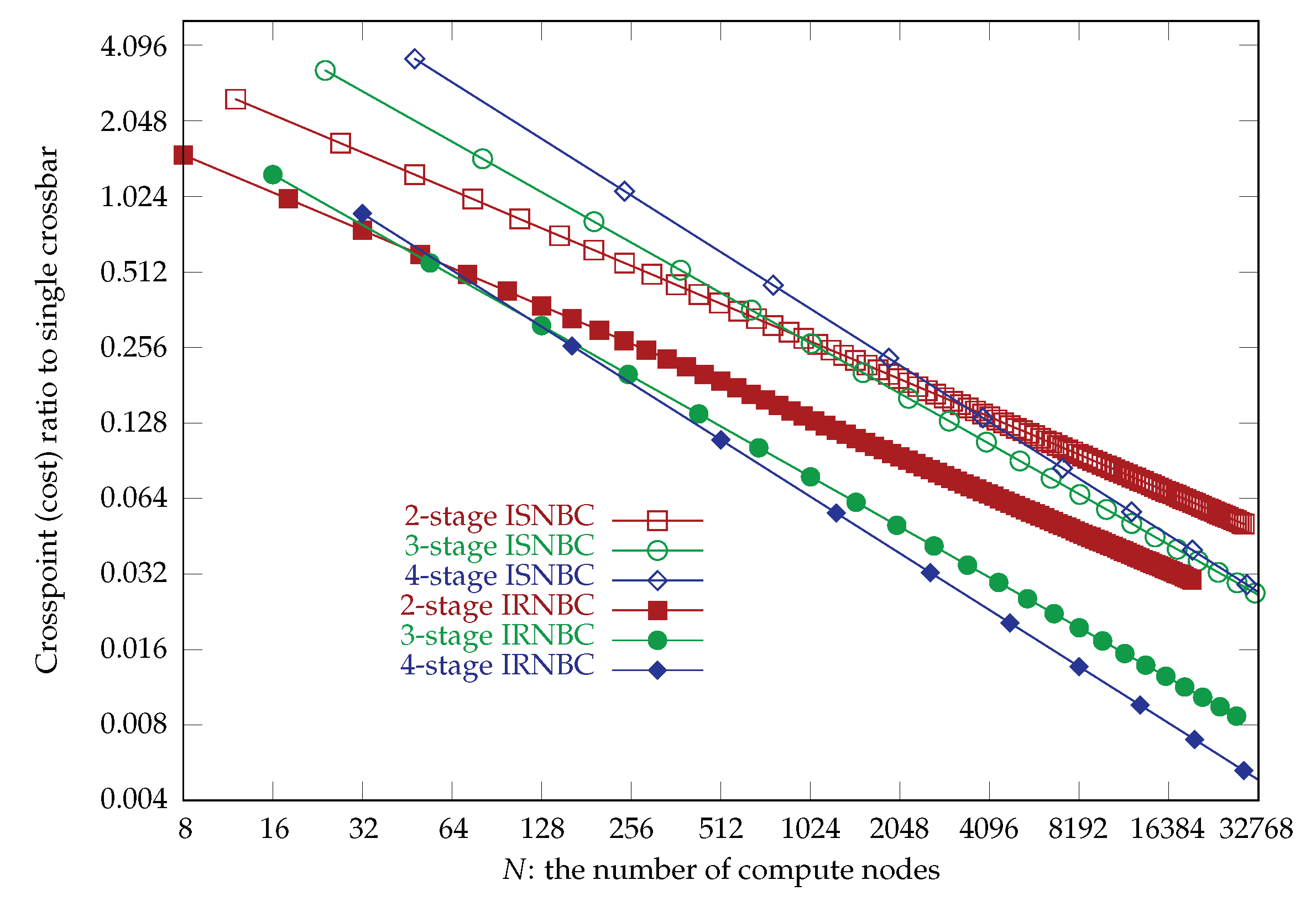
In this subsection, we investigate the crosspoint ratios for Unidirectional Strictly Nonblocking Clos (USNBC) networks and Identical Strictly Nonblocking Folded Clos (ISNBC) networks relative to a single crossbar. These ratios are compared to the corresponding traditional Clos networks.
4.1.1. Cost Evaluations of USNBC Networks
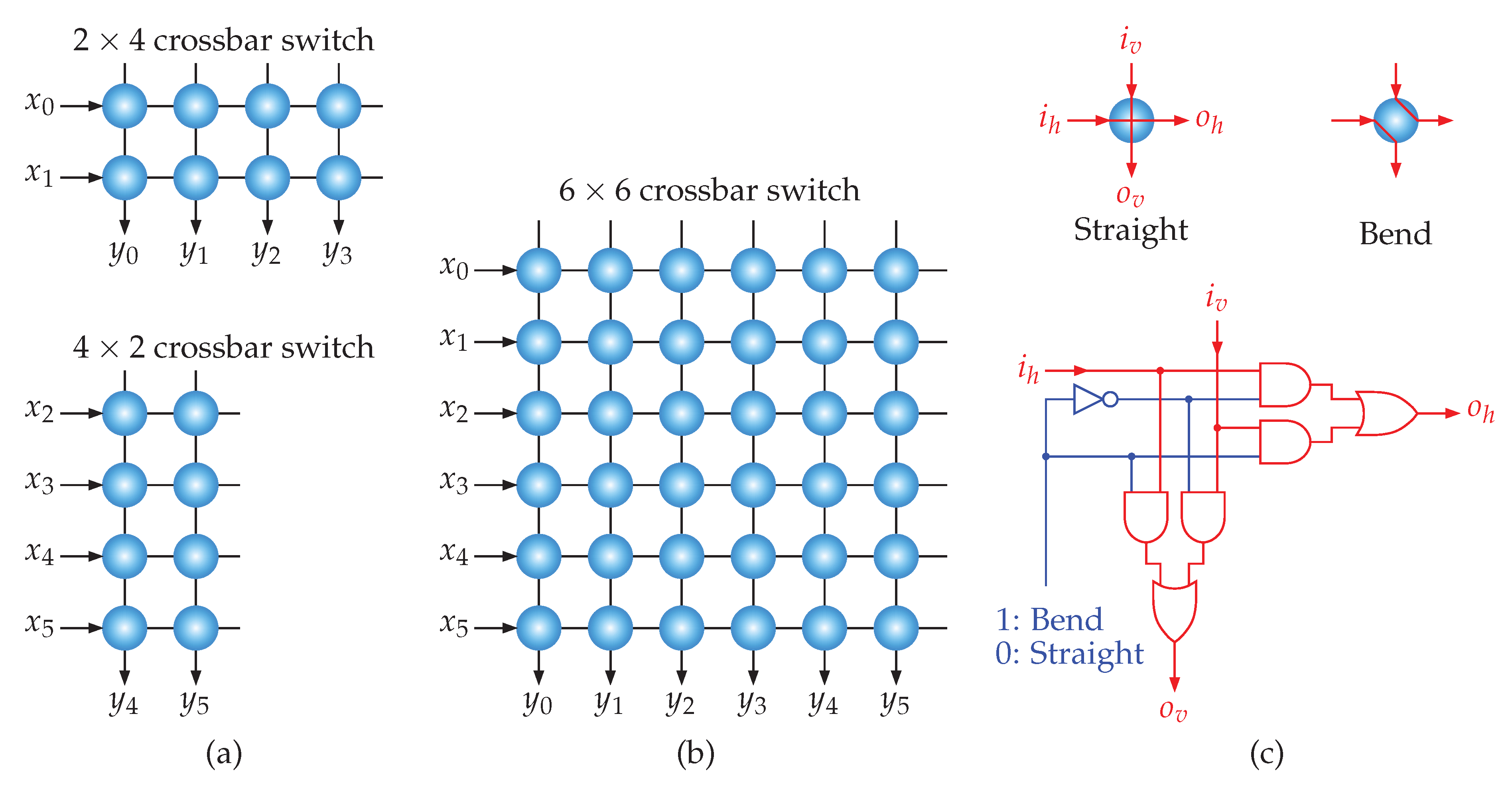
An
crossbar (
n inputs and
m outputs) has
crosspoints. In our strictly nonblocking Clos networks, we have
. Referring to
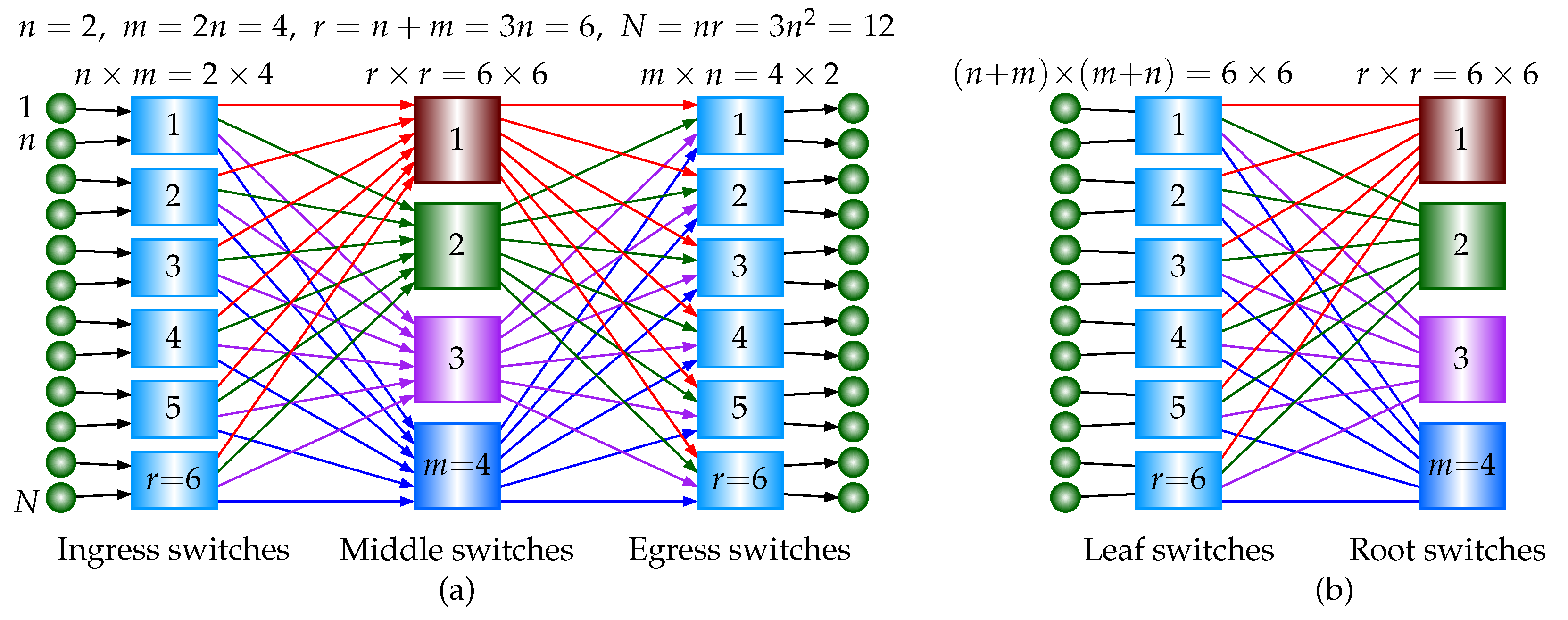
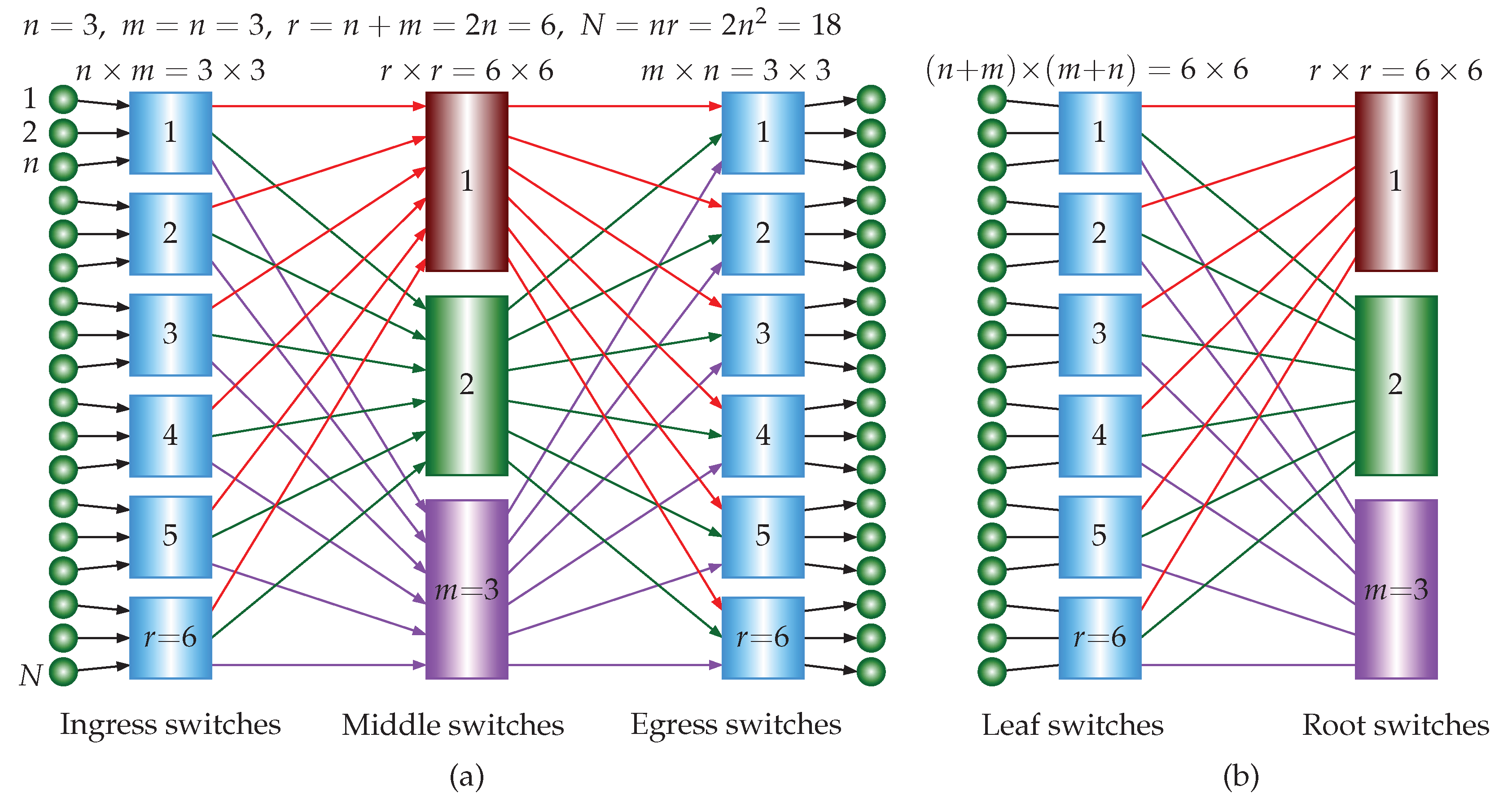
Figure 1(a), in a 3-stage USNBC network, there are
switches in the ingress stage and each switch is an
crossbar. There are
m switches in the middle stage and each switch is an
crossbar. There are
switches in the egress stage and each switch is an
crossbar. The number of total crosspoints is
. There are
inputs and
outputs. If we use a single
crossbar, it requires
crosspoints. The crosspoint ratio of the 3-stage USNBC network to the single crossbar is
that is less than 1 if
. For example, when
, the 3-stage USNBC network requires
crosspoints, less than
crosspoints in the single crossbar’s implementation. In contrast, a traditional strictly nonblocking Clos network requires
, as mentioned in
Section 2.
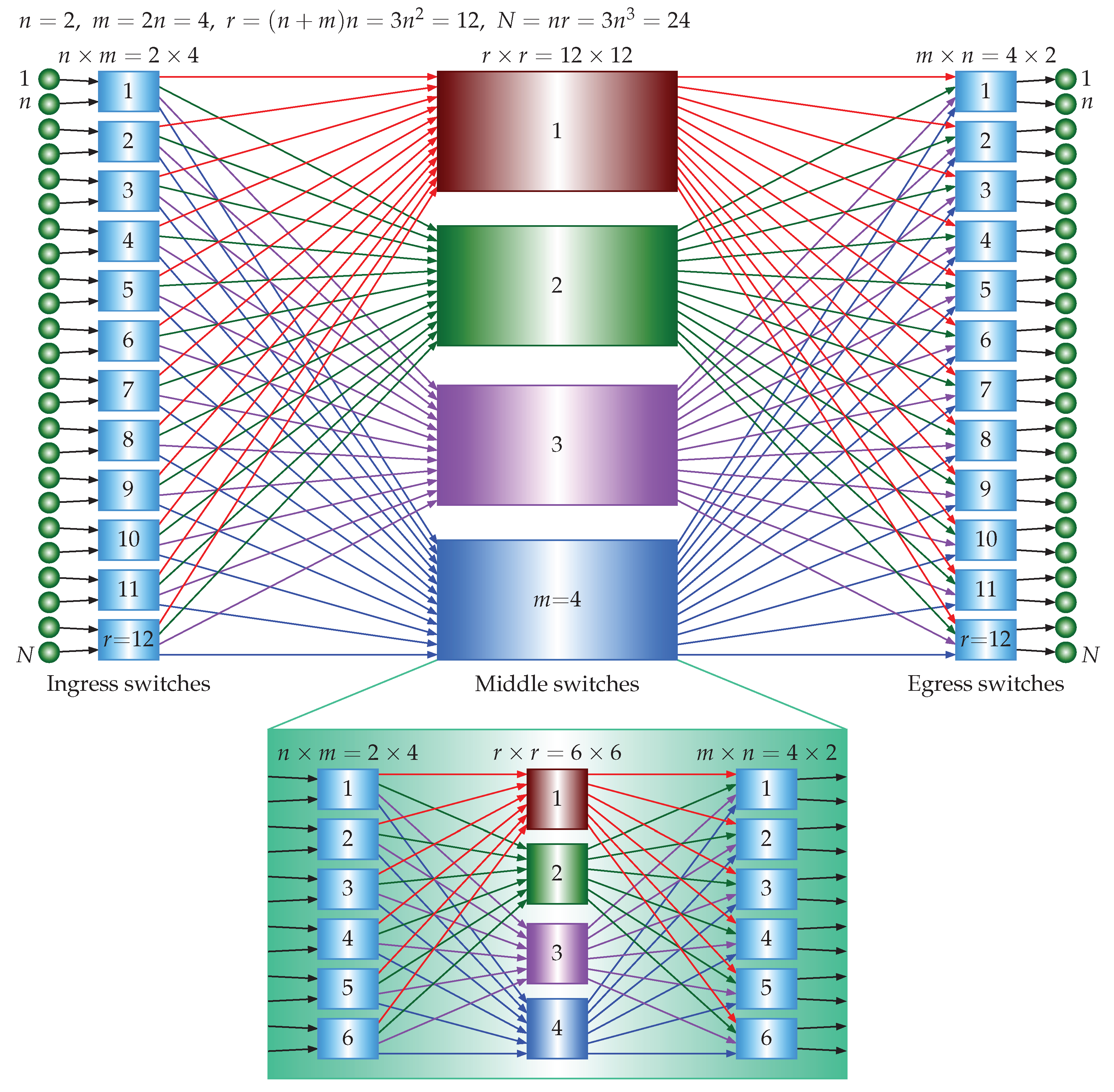
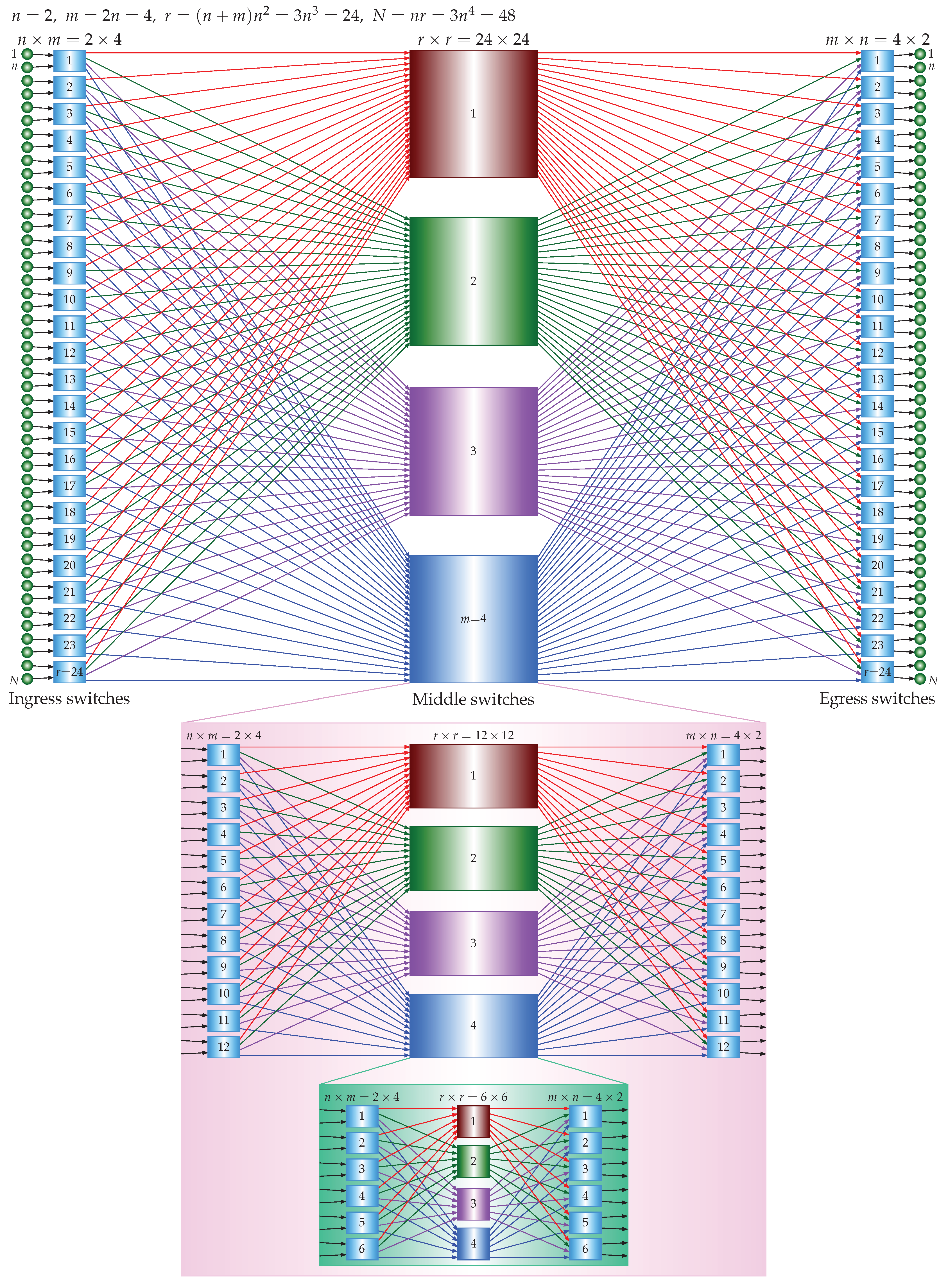
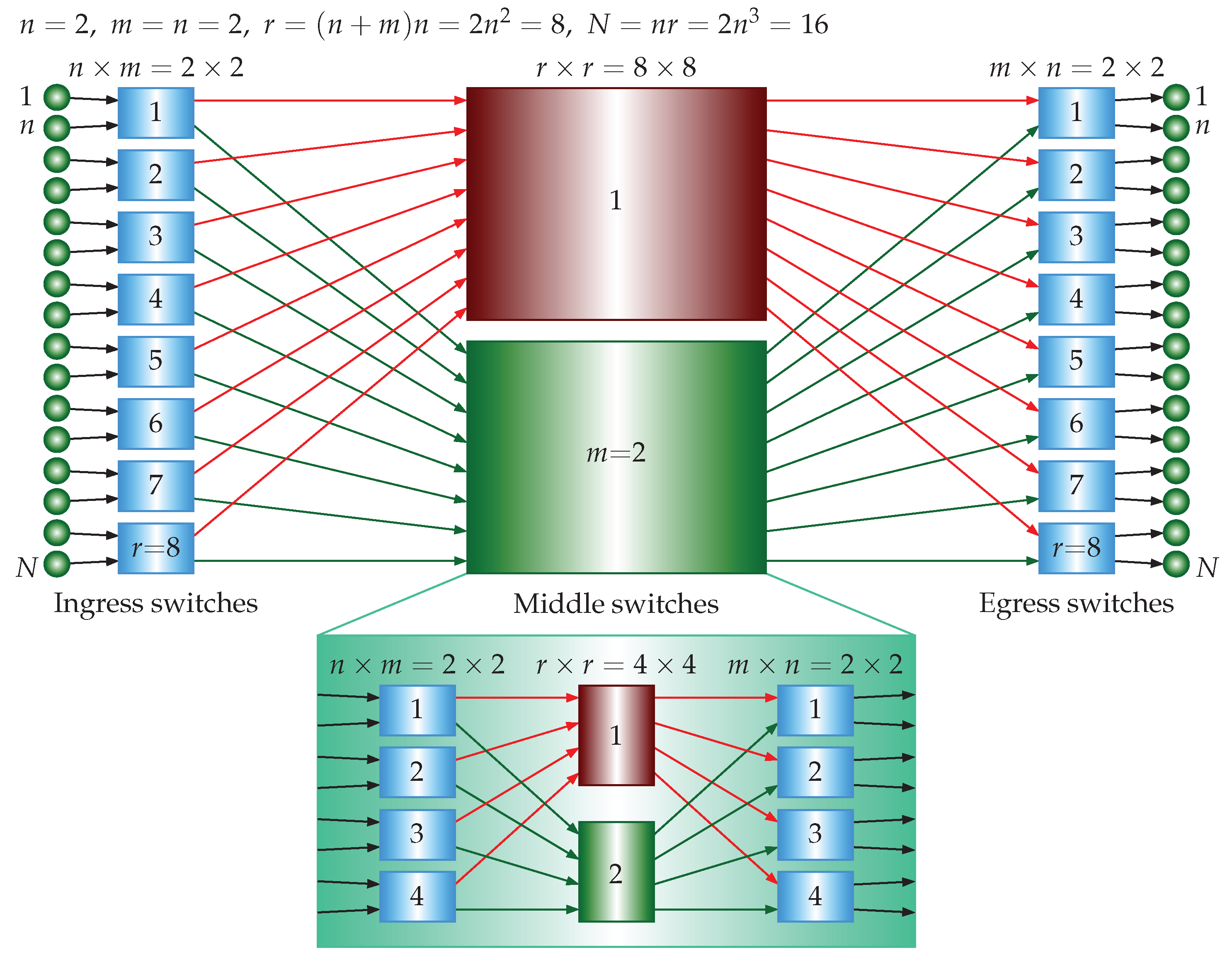
Referring to
Figure 4, in the 5-stage case, there are
crosspoints in the ingress stage, there are
crosspoints in the middle stage, and there are
crosspoints in the egress stage, where
is the number of crosspoints in a 3-stage USNBC network, as derived above. The total number of the crosspoints is
. There are
inputs and
outputs. A single
crossbar requires
crosspoints. The crosspoint ratio of the 5-stage USNBC network to the single crossbar is
which is less than 1 if
.
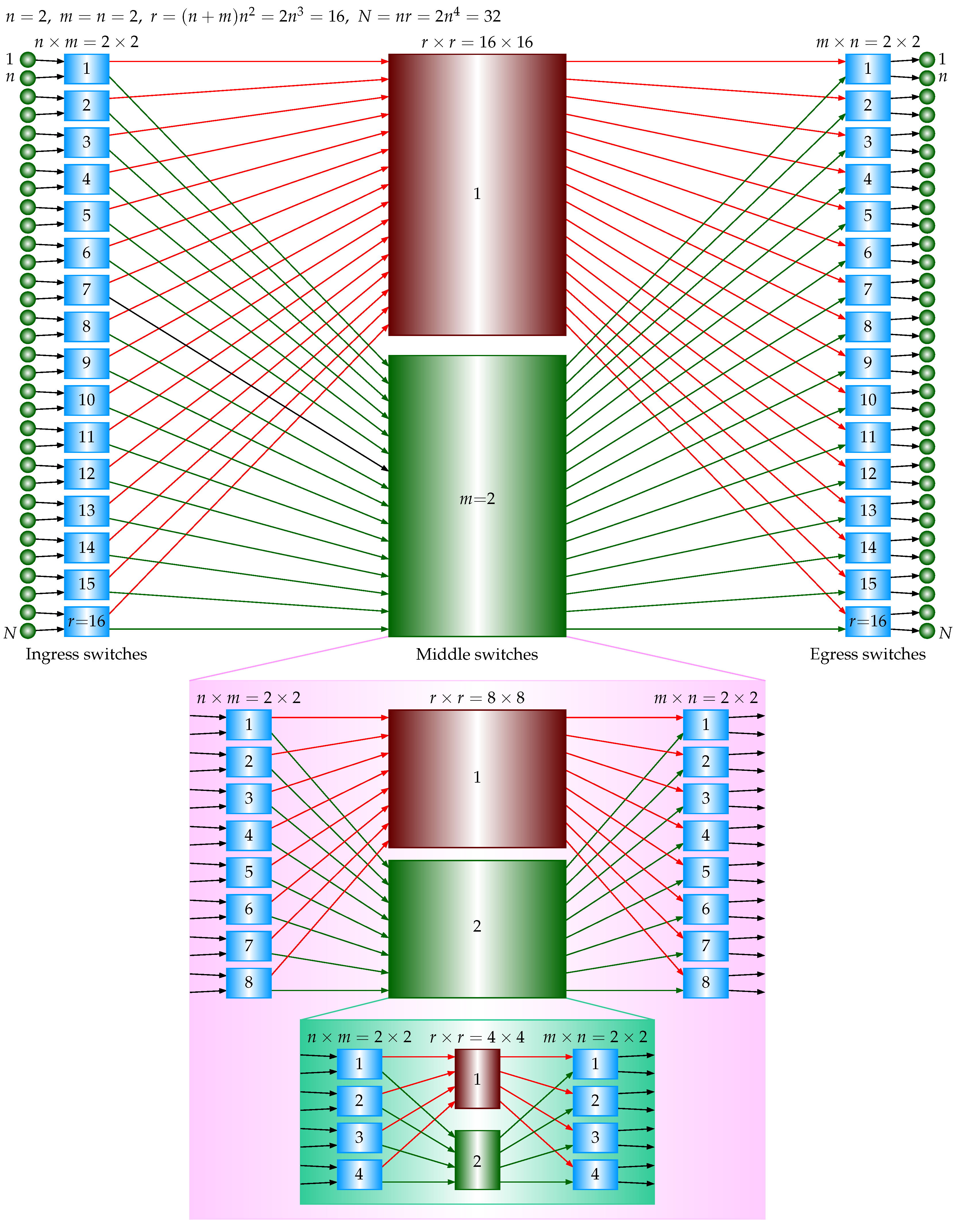
Referring to
Figure 6, in the 7-stage case, there are
crosspoints in the ingress stage, there are
crosspoints in the middle stage, and there are
crosspoints in the egress stage, where
is the number of crosspoints in a 5-stage USNBC network, as derived above. The total number of the crosspoints is
. There are
inputs and
outputs. A single
crossbar requires
crosspoints. The crosspoint ratio of the 7-stage USNBC network to the single crossbar is
which is less than 1 if
.
Now we examine the number of crosspoints for the traditional unidirectional strictly nonblocking Clos network [
1]. The 3-stage traditional unidirectional strictly nonblocking Clos network has
n switches in the ingress stage,
switches in the middle stage, and
n switches in the egress stage. An ingress stage switch is an
crossbar, a middle stage switch is an
crossbar, and an egress stage switch is an
crossbar. Then, the total number of crosspoints is
. The total number of compute nodes is
. If we use a single
crossbar, it requires
crosspoints. The crosspoint ratio of the 3-stage traditional unidirectional strictly nonblocking Clos network to the single crossbar is
. To guarantee that the ratio is less than 1,
is needed.
Consider the case of 5-stage. There are crosspoints in the ingress stage, there are crosspoints in the middle stage, and there are crosspoints in the egress stage, where is the number of crosspoints in a 3-stage traditional unidirectional strictly nonblocking Clos network, as derived above. The total number of crosspoints is . The total number of compute nodes is . A single crossbar requires crosspoints. The crosspoint ratio of the 5-stage traditional unidirectional strictly nonblocking Clos network to the single crossbar is . To guarantee that the ratio is less than 1, is needed.
Consider the case of 7-stage. There are crosspoints in the ingress stage, there are crosspoints in the middle stage, and there are crosspoints in the egress stage, where is the number of crosspoints in a 5-stage traditional unidirectional strictly nonblocking Clos network, as derived above. The total number of crosspoints is . The total number of compute nodes is . A single crossbar requires crosspoints. The crosspoint ratio of the 7-stage traditional unidirectional strictly nonblocking Clos network to the single crossbar is . To guarantee that the ratio is less than 1, is needed.
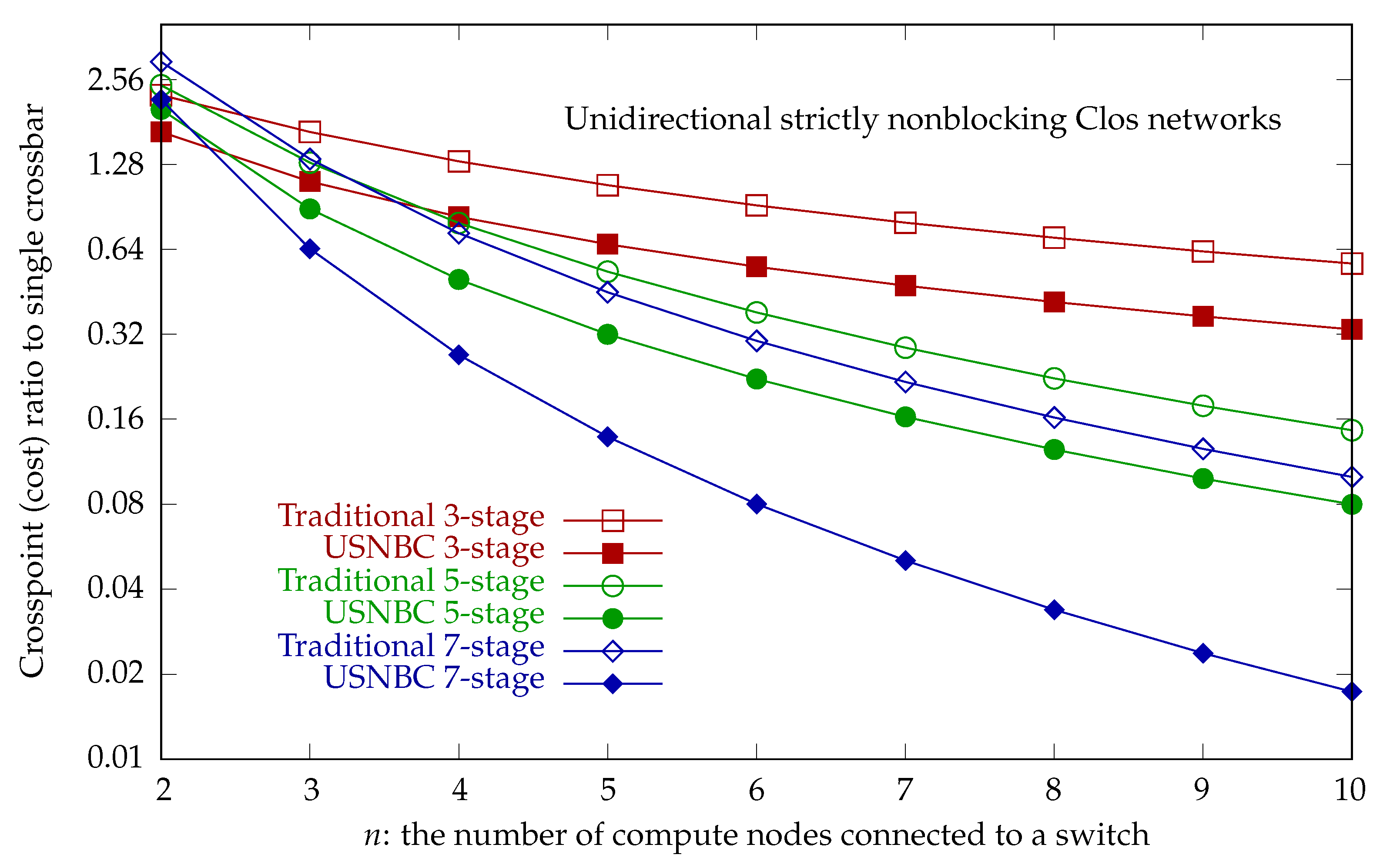
We summarize the crosspoint ratio to the single crossbar for the traditional unidirectional strictly nonblocking Clos networks and USNBC networks in
Table 5.
Figure 15 plots the crosspoint ratio to the single crossbar for the unidirectional strictly nonblocking Clos networks, showing that USNBC networks have a lower crosspoint cost than traditional strictly nonblocking Clos networks.
4.1.2. Cost Evaluations of ISNBC Networks
Now we examine the number of crosspoints for the ISNBC network that uses the equally sized square crossbar of
for
. Referring to
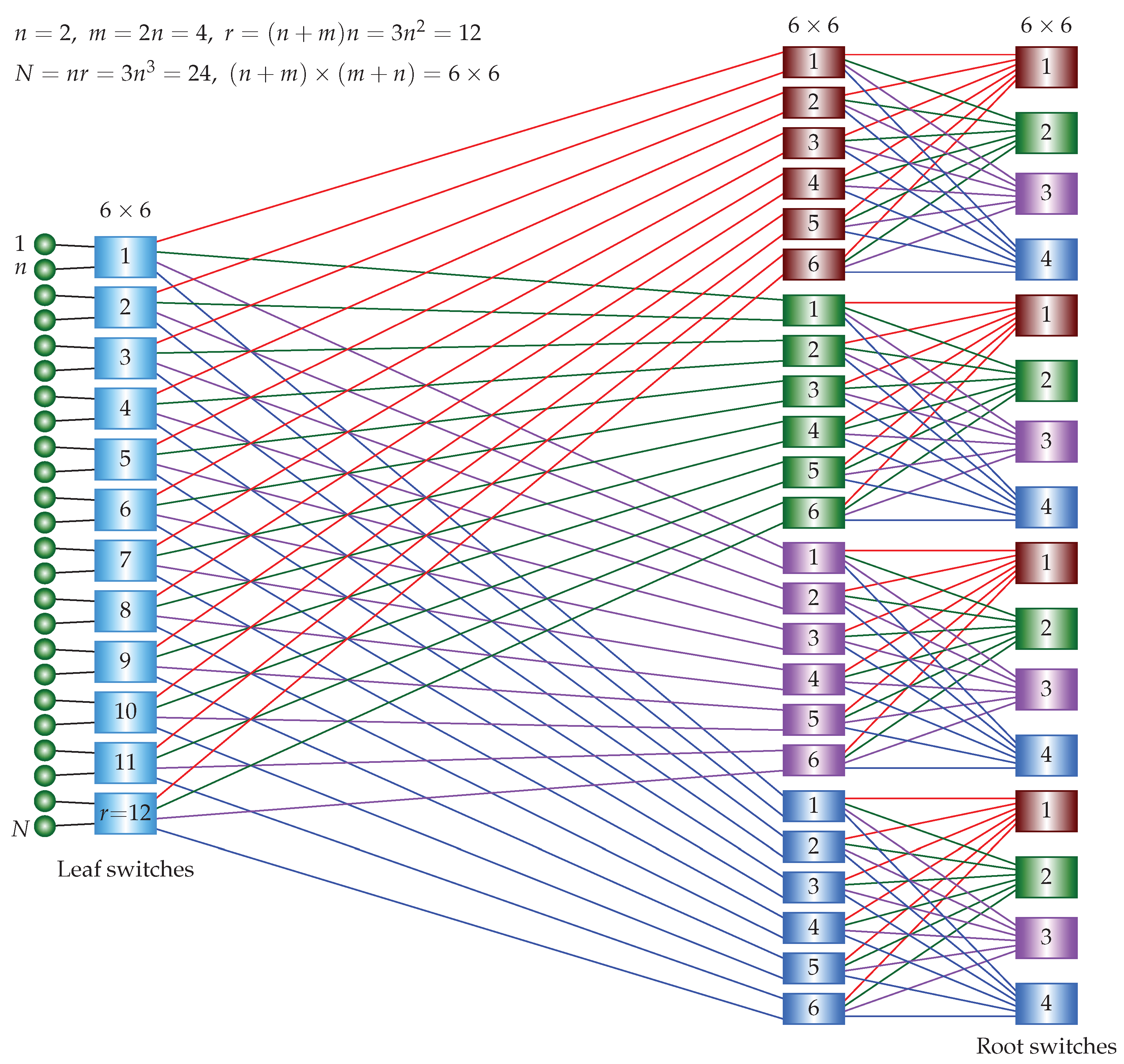
Figure 1(b), the ISNBC network based on the 3-stage USNBC network has two stages. There are
leaf switches and
m root switches. The total number of switches is
and each switch is a square
crossbar. Then, the total number of crosspoints is
. The total number of compute nodes is
. A single
crossbar requires
crosspoints. The crosspoint ratio of the 2-stage ISNBC network to the single crossbar is
. To guarantee that the ratio is less than 1,
is needed.
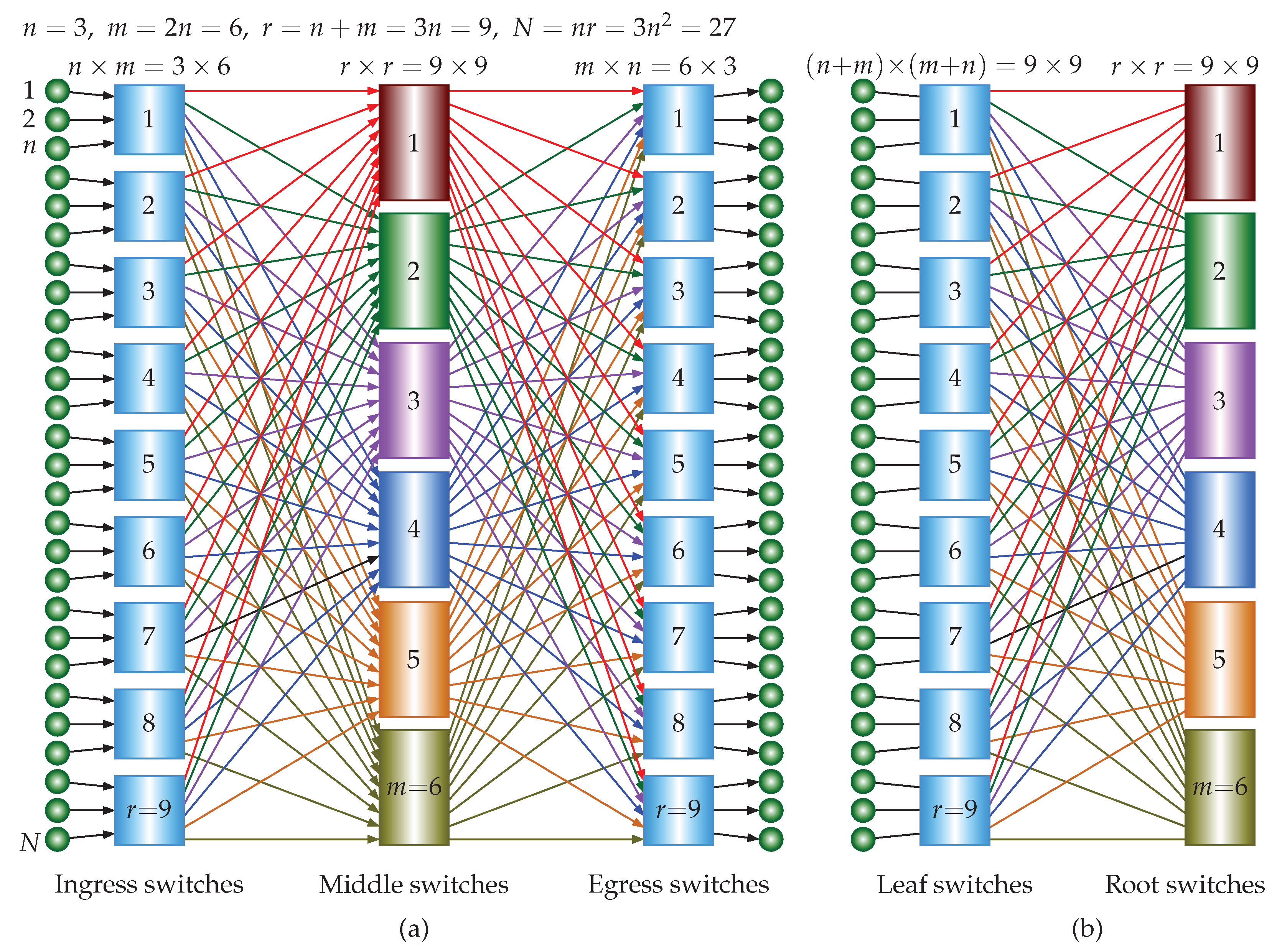
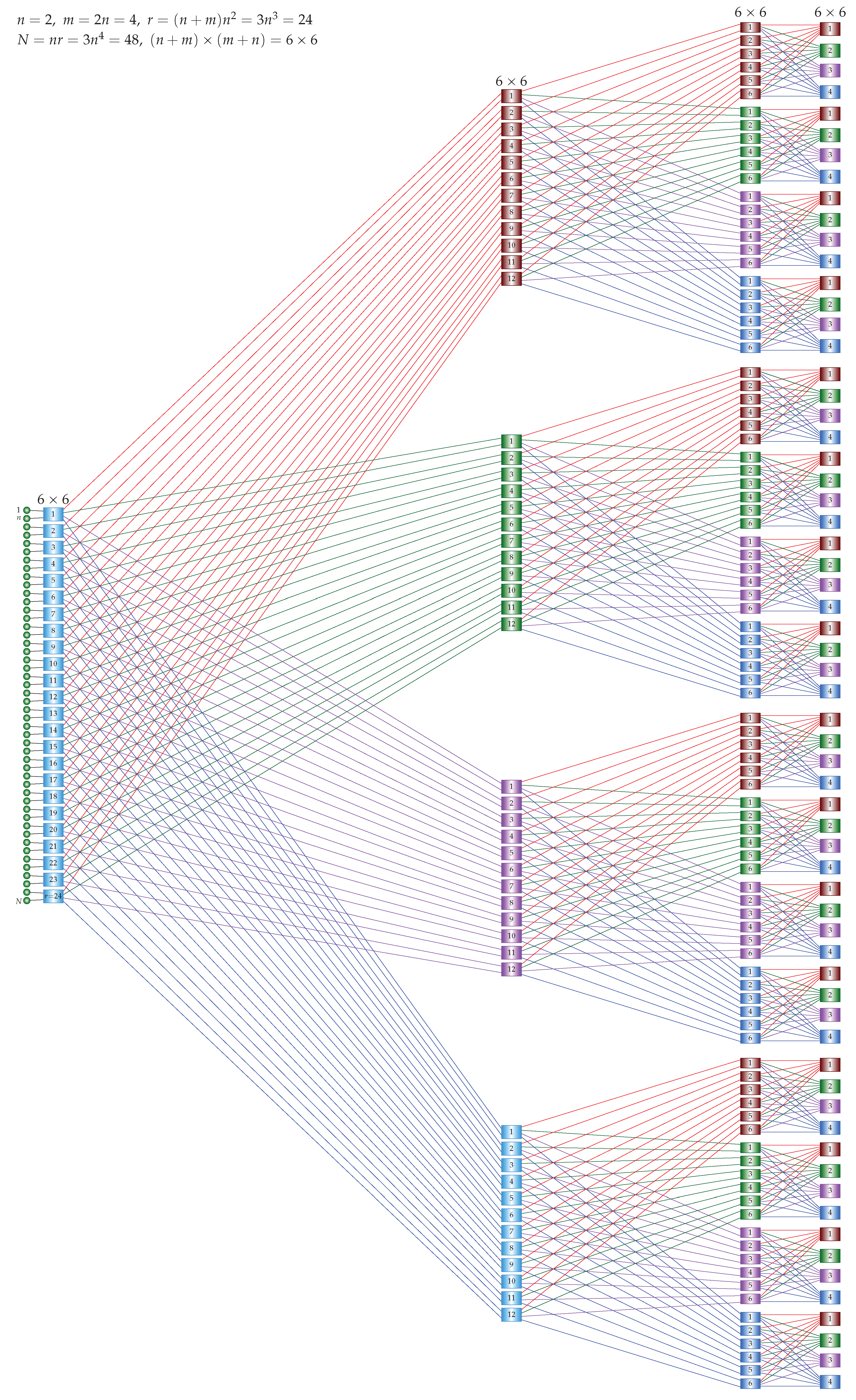
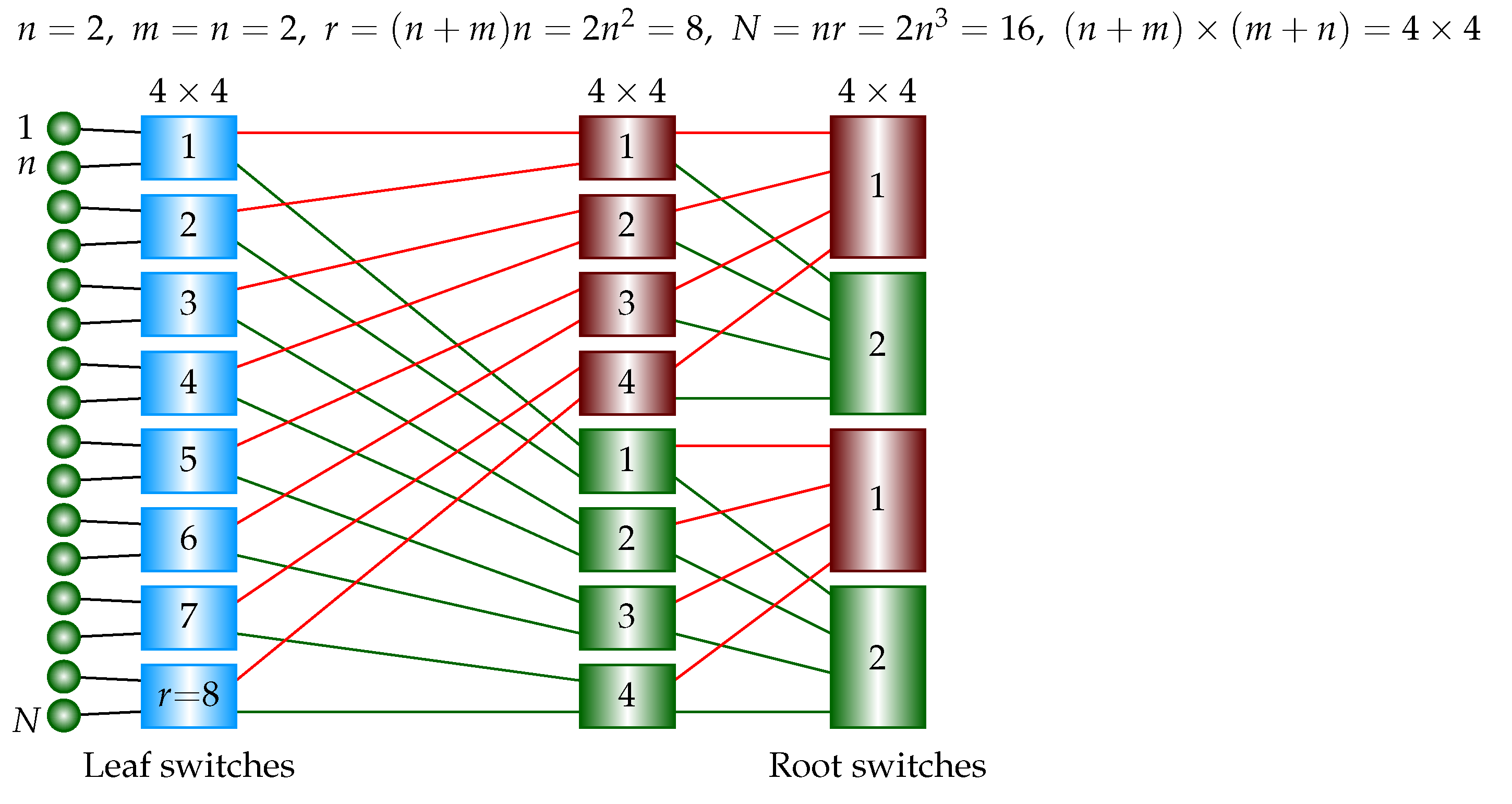
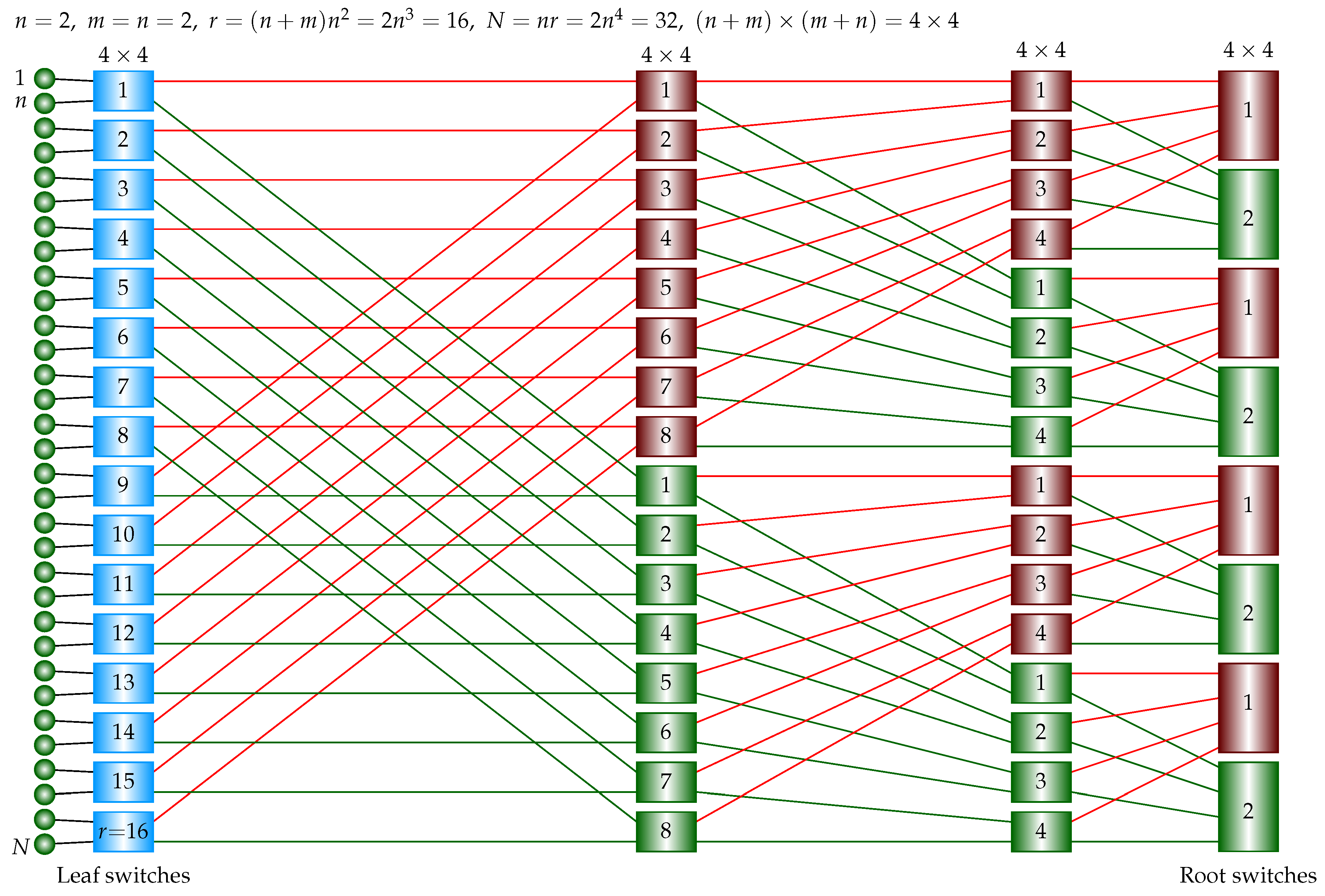
Consider the 3-stage ISNBC network. Referring to
Figure 5, there are
switches in the leaf stage, and there are
m building blocks and each building block is a 2-stage ISNBC network whose number of switches is
, as derived above. The total number of switches is
and each switch is a square
crossbar. Then, the total number of crosspoints is
. The total number of compute nodes is
. A single
crossbar requires
crosspoints. The crosspoint ratio of the 3-stage ISNBC network to the single crossbar is
. To guarantee that the ratio is less than 1,
is needed.
Consider the 4-stage ISNBC network. Referring to
Figure 7, there are
switches in the leaf stage, and there are
m building blocks and each building block is a 3-stage ISNBC network whose number of switches is
, as derived above. The total number of switches is
and each switch is a square
crossbar. Then, the total number of crosspoints is
. The total number of compute nodes is
. A single
crossbar requires
crosspoints. The crosspoint ratio of the 4-stage ISNBC network to the single crossbar is
. To guarantee that the ratio is less than 1,
is needed.
Table 6 lists the crosspoints of ISNBC networks. The “Crossbar” column shows the number of crosspoints in the single crossbar. The “ISNBC” column shows the number of crosspoints in the ISNBC network. The crosspoint number in blue color is better (smaller) than the number of the single crossbar.
Now we examine the number of crosspoints for the traditional strictly nonblocking folded Clos network that uses crossbars of different sizes. The 2-stage traditional strictly nonblocking folded Clos network has n switches in the leaf stage and switches in the root stage. A leaf switch is an crossbar. A root switch is an crossbar. Then, the total number of crosspoints is . The total number of compute nodes is . A single crossbar requires crosspoints. The crosspoint ratio of the 2-stage traditional strictly nonblocking folded Clos network to the single crossbar is . To guarantee that the ratio is less than 1, is needed.
Consider the case of 3-stage. There are switches in the leaf stage and each switch is an crossbar. There are building blocks and each building block has crosspoints, as derived above. Then the total number of crosspoints is . The total number of compute nodes is . A single crossbar requires crosspoints. The crosspoint ratio of the 3-stage traditional strictly nonblocking folded Clos network to the single crossbar is . To guarantee that the ratio is less than 1, is needed.
Consider the case of 4-stage. There are switches in the leaf stage and each switch is an crossbar. There are building blocks and each building block has crosspoints, as derived above. Then the total number of crosspoints is . The total number of compute nodes is . A single crossbar requires crosspoints. The crosspoint ratio of the 4-stage traditional strictly nonblocking folded Clos network to the single crossbar is . To guarantee that the ratio is less than 1, is needed.
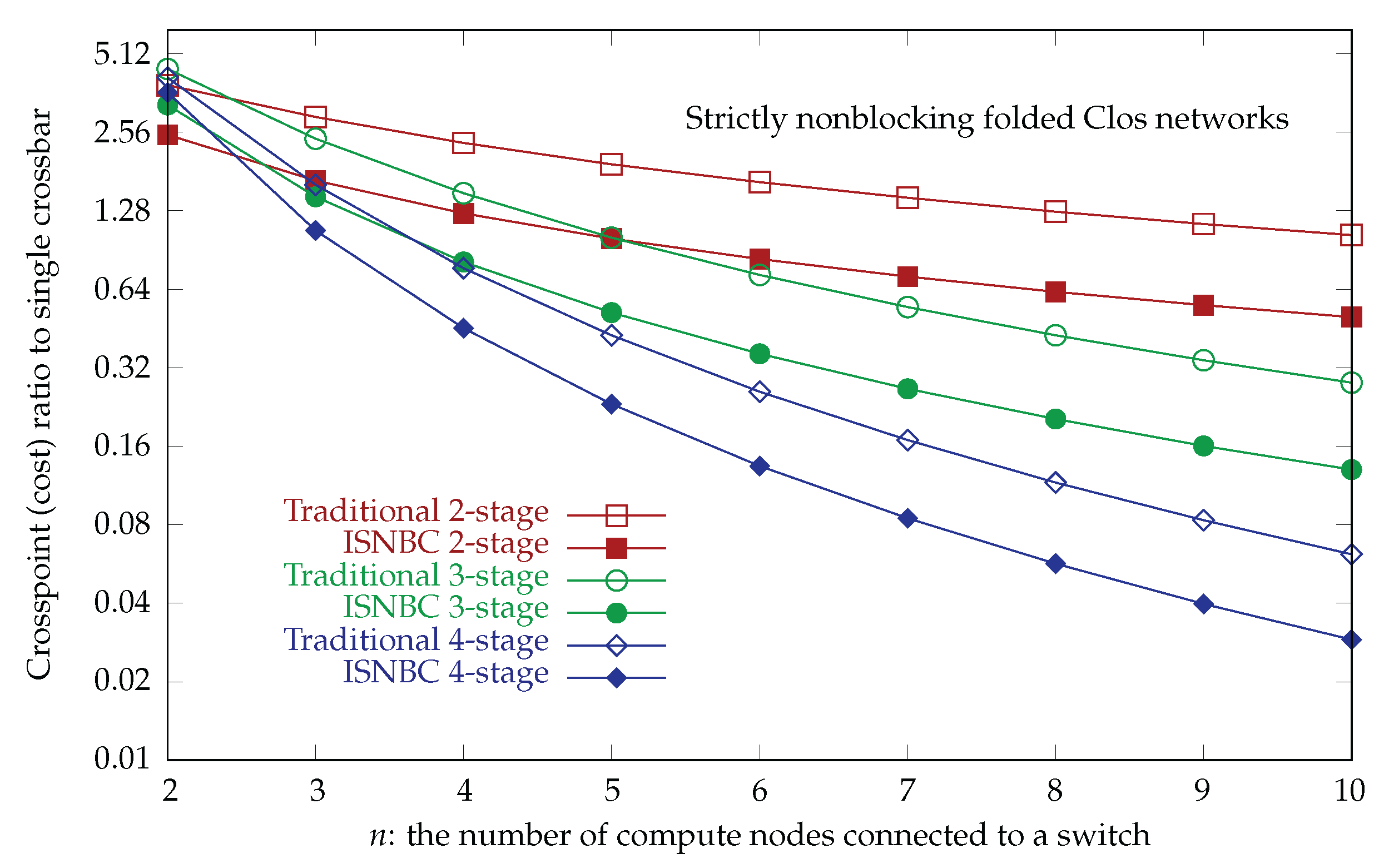
We summarize the crosspoint ratio to the single crossbar for the traditional strictly nonblocking folded Clos networks and ISNBC networks in
Table 7. The general formula for calculating the ISNBC crosspoint ratio to the single crossbar is
, where
s is the number of stages, and the number of compute nodes is
.
Figure 16 plots the crosspoint ratio to the single crossbar for the strictly nonblocking folded Clos networks, showing that the ISNBC networks have a lower crosspoint cost than the traditional strictly nonblocking folded Clos networks. Also note that the ISNBC networks use the equally sized square crossbar for all switches in the network.