Non-Isolated Ultra-High Step-Up DC-DC Converter Topology Using Coupled-Inductor Based Inverting Buck-Boost and Voltage Multipliers

1. Introduction

Nowadays, renewable energy sources such as fuel cells (FCs) and photovoltaic (PV) modules have become important energy sources which can replace fossil fuels. However, due to their low output voltage characteristics, normally ranging from 24V to 48V, it is necessary to boost the voltage up to 380V, which is suitable for the DC link of a single-phase or 700V for a three-phase grid-tie inverter [1].

The simplest way to achieve high step-up voltage gain is by using an isolated converter by adjusting the turns ratio of the transformer. However, due to their disadvantages of high losses, large volume, and high cost, since a greater number of turns for the transformer is required, they are not a suitable choice for applications that do not require isolation between input and output [17].

Conventional non-isolated boost converters could be a candidate. However, in order to achieve high step-up voltage gain, they have to work with an extreme duty cycle, which leads to decreased efficiency and increased system cost since high voltage rating components have to be used due to high voltage stress [2].

Recently, many high step-up voltage gain topologies have been introduced [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. They can be divided into two groups: single-inductor based converters [4,5,6,7,8,9,10,11,12,13,14] and coupled-inductor based converters [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. Single-inductor based converters include interleaved boost or buck-boost converters [4,5,6], switched-inductor and voltage lift techniques [7,8,11,12], voltage multiplier (VM) and their combination topologies [13,14,15]. These types of converters can achieve higher step-up voltage gain than conventional ones with high efficiency. However, for an ultra-high step-up voltage ratio, more converter stages must be cascaded, resulting in the use of more components, which decreases efficiency and increases volume and cost.

Coupled-inductor based topologies can easily meet the high step-up voltage gain requirement by adjusting the turns ratio of the coupled inductor. However, there are still some issues that need to be solved to achieve high efficiency, high power density, and low cost, high turns ratio and leakage inductance of the coupled inductor, switching losses, and voltage stress on components.

The first issue is the high turns ratio of the coupled inductor, which leads to increased inductor volume and winding resistance, thereby reducing the power density and efficiency of the system. Moreover, the leakage inductance causes a very high voltage spike applied to the switches, resulting in high power losses and the need for high voltage rating components, thereby increasing the cost. The leakage inductance problem can be solved by using a passive snubber [16,17,18,19,20,21,22,23,24,25,26,27,28,33], or an active snubber [29,30,31,32], or passive clamping [36,37] so low voltage rating switches can be used with low internal resistance $R_{ds\left(on\right)}$ , hence increasing the overall efficiency. However, this requires more components, increases control complexity for the active snubber, and consequently increases the losses, volume, and cost of the converter.

Another issue that mainly affects the efficiency of the converter is switching losses. Even though the voltage spike applied to the switches caused by leakage inductance is eliminated, the efficiency of the converters in [16,18,31] is still low because of hard switching, resulting in high switching losses in the switches. Moreover, these losses are proportional to the increase in switching frequency. So, in order to maintain efficiency, the converter must work at a low switching frequency, which leads to larger required values for the capacitor and inductor, thus decreasing the power density. The topologies introduced in [21,23,24,26,27,29,30,32,33,35,36] can achieve soft switching to improve efficiency. In these converters, the snubbers or clamped circuits not only eliminate the voltage spike applied to semiconductor devices by absorbing the energy of the leakage inductance but also use this energy to provide Zero-Voltage Switching (ZVS) or Zero-Current Switching (ZCS) for the switches and diodes.

The third issue that increases the volume and cost of the converter is the voltage stress on components. Because of the asymmetrical configuration, the voltage stress on components in converters proposed in [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,37,38] are not evenly distributed. The components on the output side have higher voltage stress. So, all of them need to have higher voltage ratings, leading to increased volume and cost of the system. For example, the converter in [18] has voltage stress on output capacitor equal to output voltage and voltage stress on output diode is nearly equal to the output voltage. Similarly, the converter in [21] has the voltage stress on output diode nearly equal to output voltage.

In order to overcome all of these issues, the proposed converter has been introduced with the following features:

• Ultra-high step-up voltage gain with a low turns-ratio of the coupled inductor.
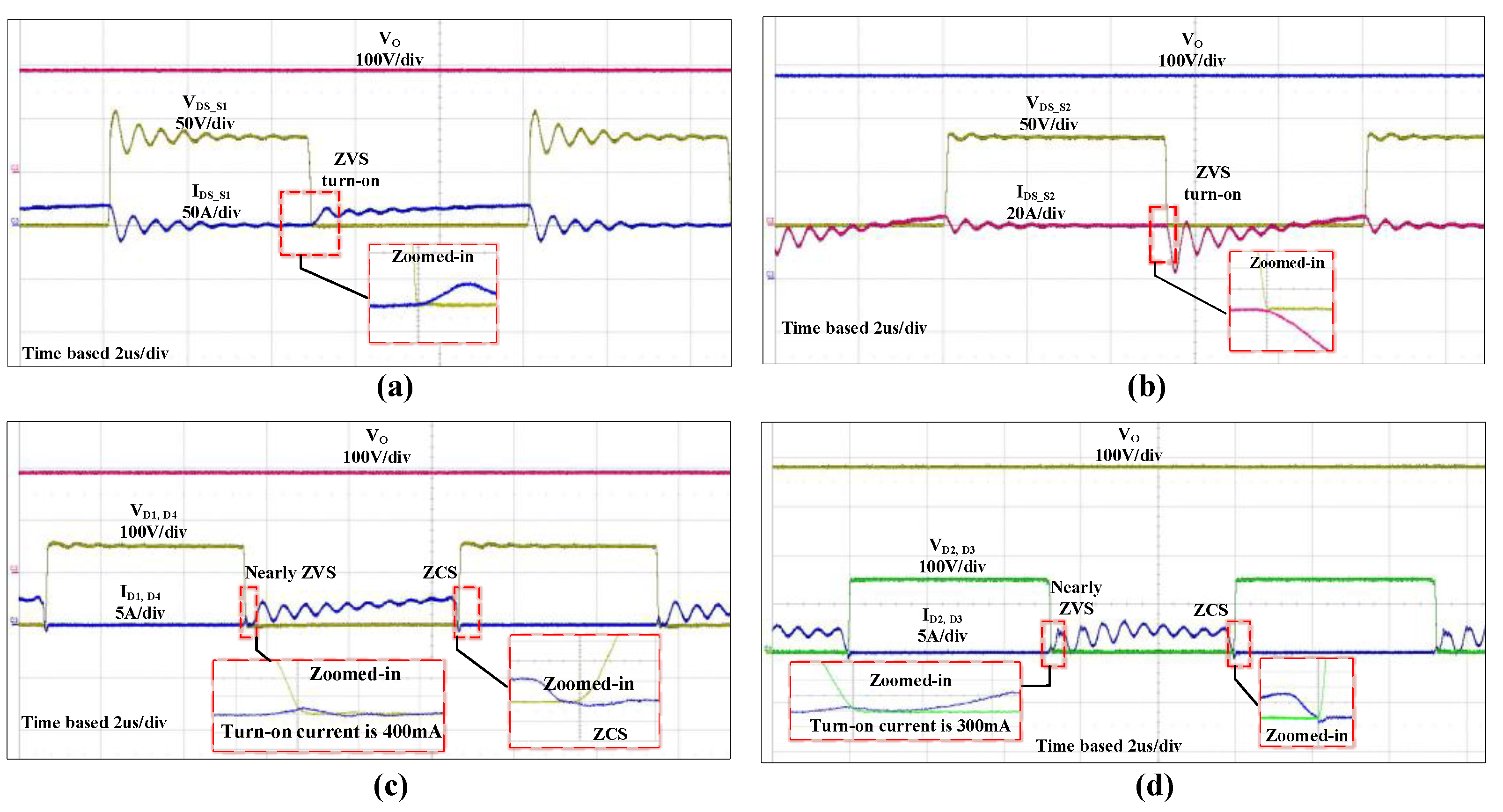
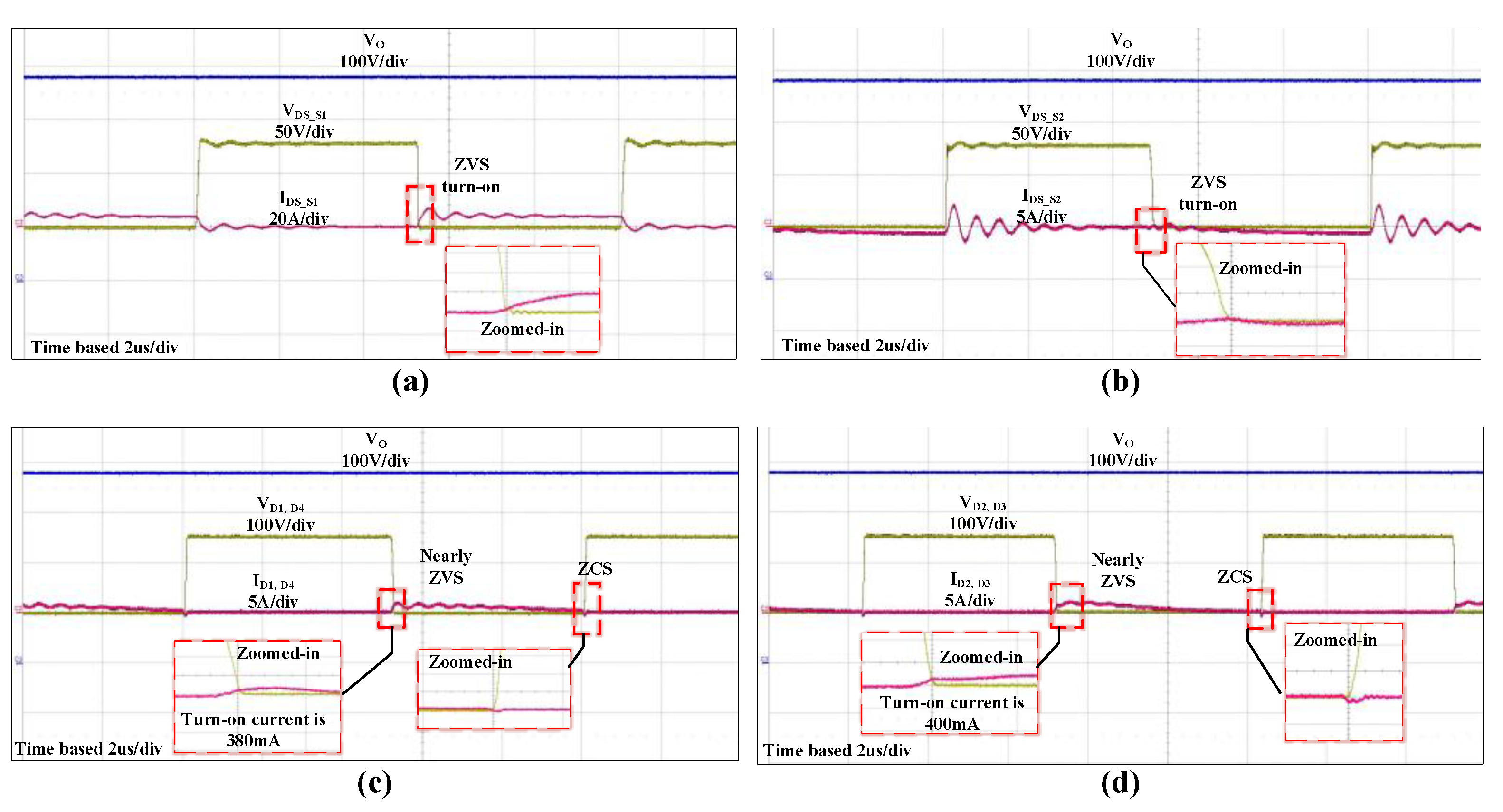
• ZVS turn-on for switches and ZCS turn-off for all diodes
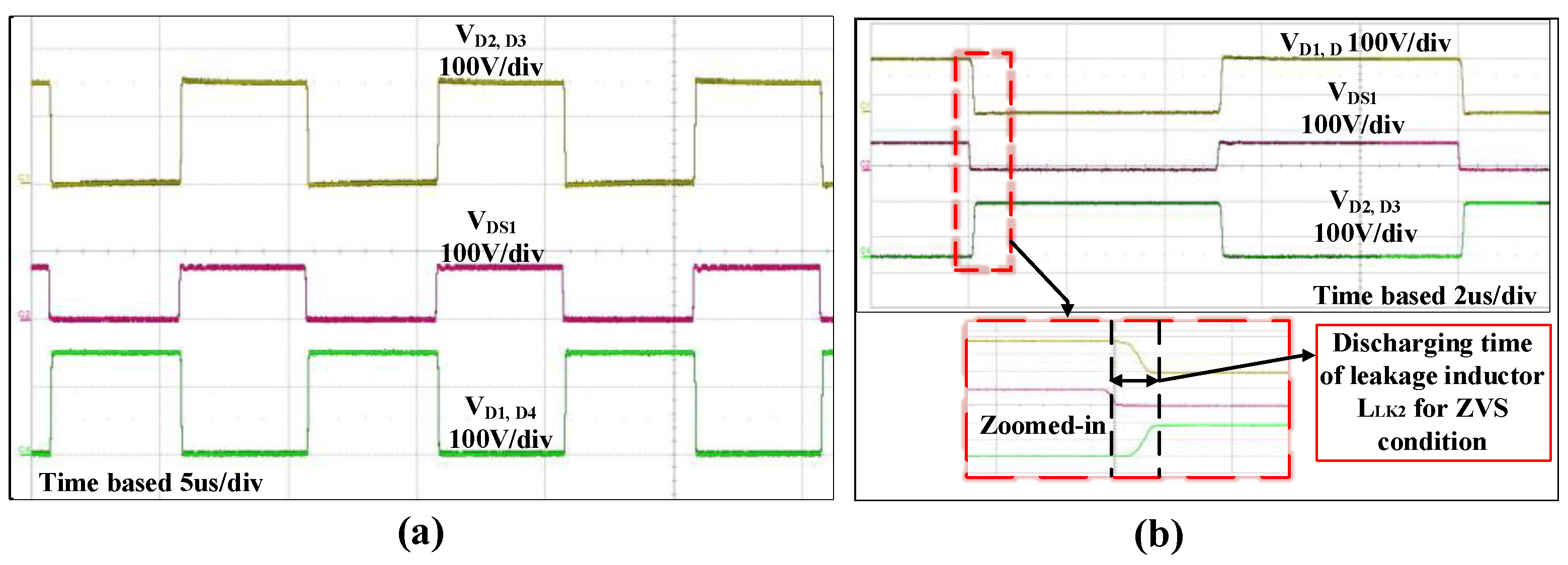
• No voltage spike problem caused by leakage inductance without using an extra snubber circuit.
• Low voltage stress on all components due to the symmetrical configuration.
• Flexibly achieving higher step-up voltage gain with low duty cycle by either adjusting the turns ratio of coupled inductor or cascading a greater number of VM stages.

This paper is divided into six sections. The working principle of the proposed converter is presented in Section 2. The design procedure of the proposed converter is presented in Section 3. In Section 4, the experimental results demonstrating the superiority of the proposed converter are discussed. The comparison between the proposed converter and other topologies is shown in Section 5. Finally, the conclusion is in Section 6.

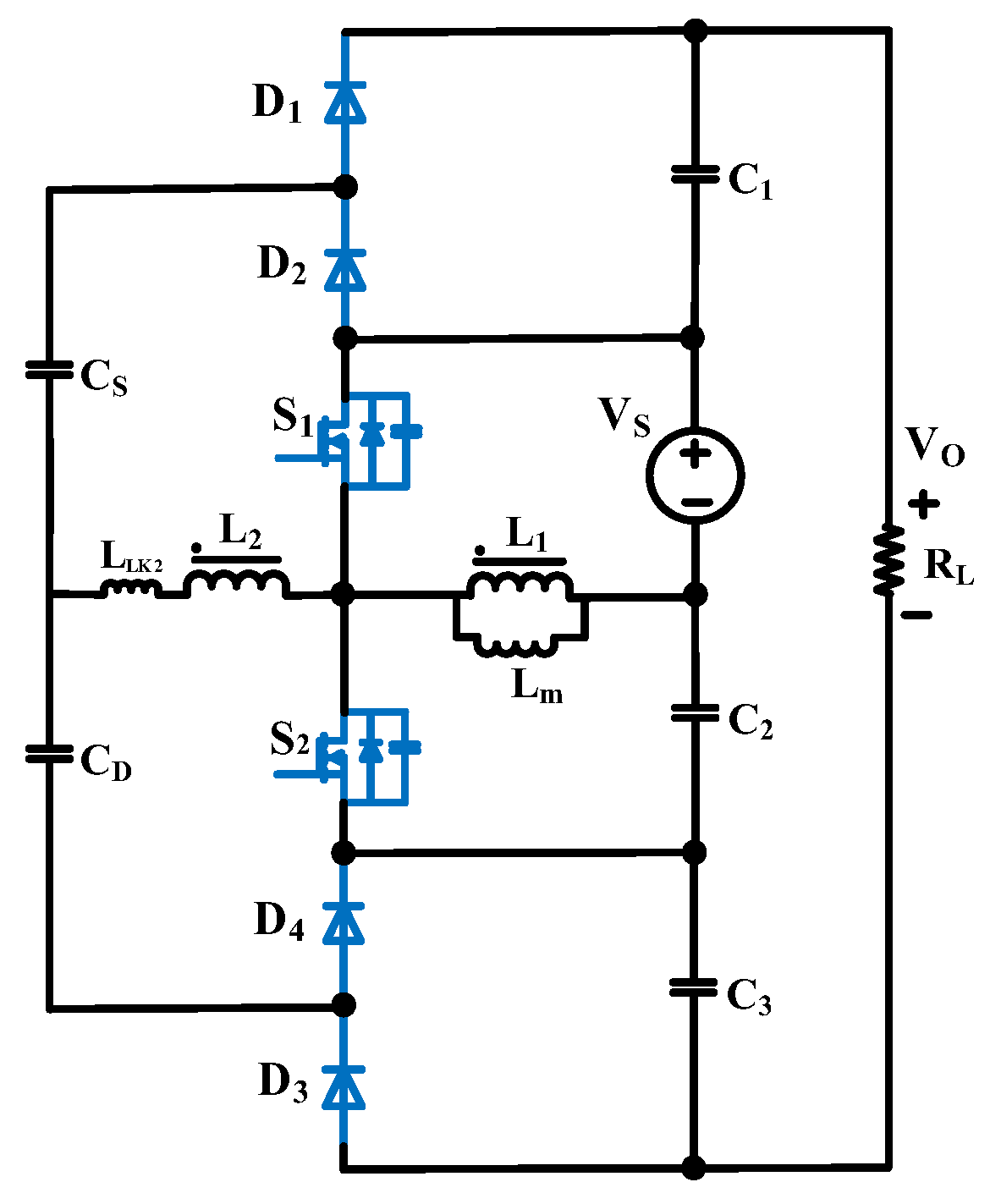
2. Proposed Converter Structure

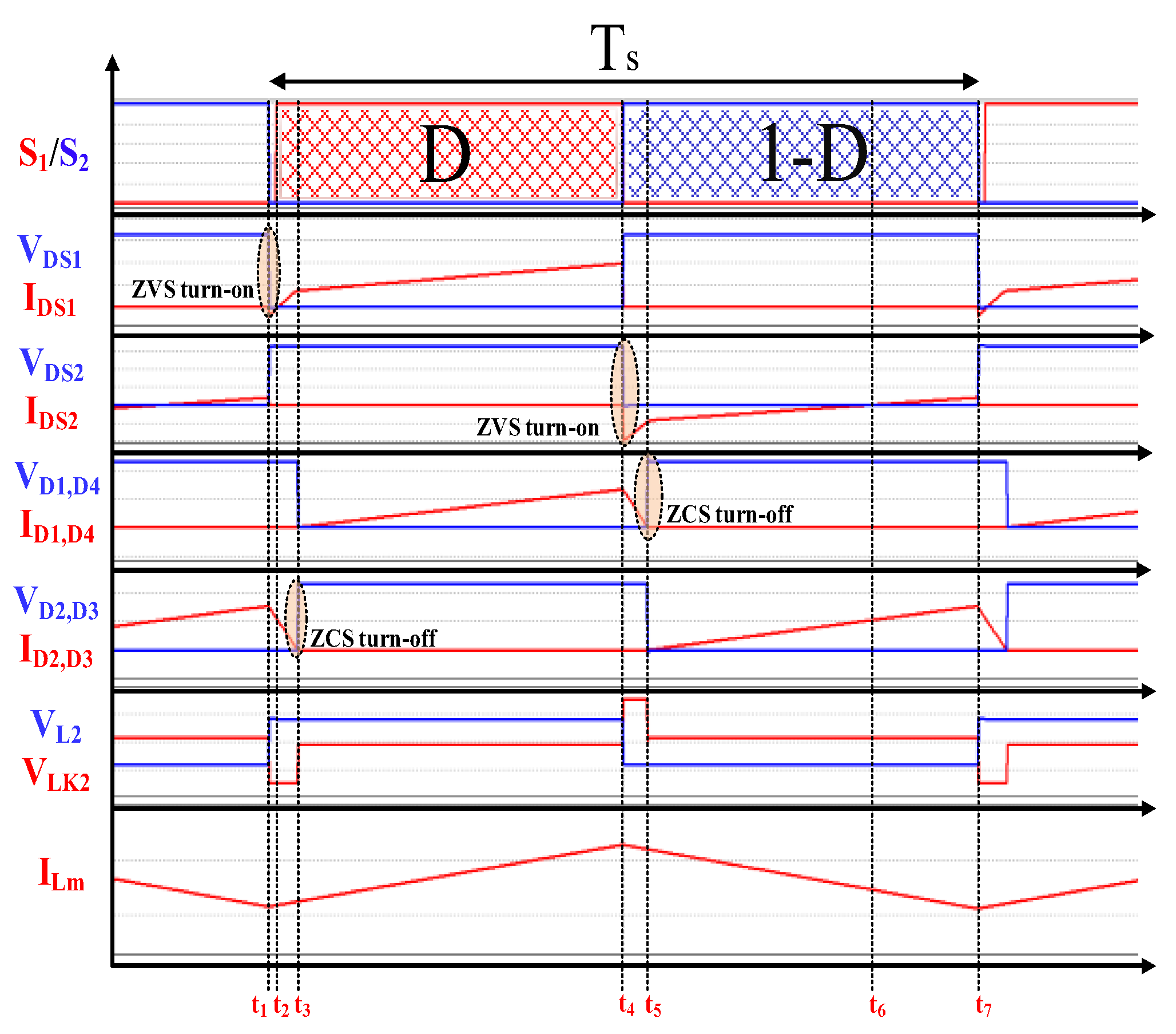
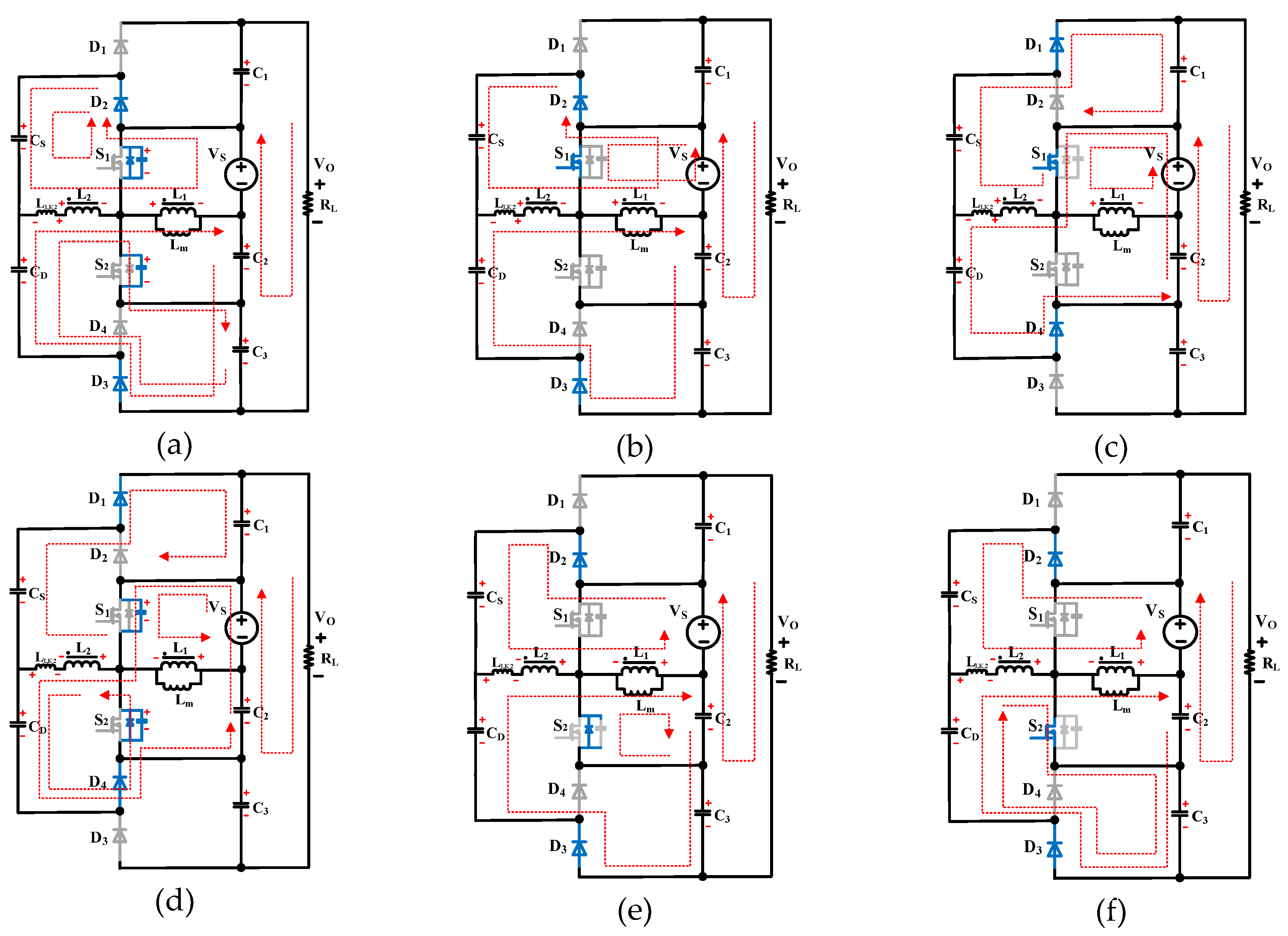
2.1. Operating Principle

As shown in Figure 1, the proposed topology consists of two voltage multipliers (VM): positive VM (which includes diodes $D_1$, $D_2$ and capacitors $C_1$, $C_s$) and negative VM (which includes diodes $D_3$, $D_4$ and capacitors $C_3$, $C_D$) connected to the synchronous Inverting Buck-Boost (IBB) converter. Moreover, the main inductor of IBB is replaced by a coupled inductor, and the secondary side of the coupled inductor is placed at the common path between two blocking capacitors $C_s$ and $C_D$ of the positive VM and negative VM, respectively, not only for creating the ZVS turn-on for switches and ZCS turn-off for diodes but also to increase the overall voltage gain of the proposed converter. In the proposed topology, the leakage inductance referred to the secondary side is used for the ZVS condition, and its energy is absorbed by blocking capacitors $C_s$ and $C_D$. Hence, no snubber is needed in the proposed topology. Furthermore, symmetrical configuration ensures that the voltage stress and current stress are evenly shared among all output components. Consequently, low-cost and small-volume components with low voltage ratings can be used.

In this section, the working principle of the proposed converter is described in Continuous Conduction Mode (CCM). From the key waveform shown in Figure 2, one switching cycle is divided into six modes based on the working status of the main switches. The equivalent circuit for each mode is shown in Figure 3. In the proposed two-stage converter, the main switches and the synchronous rectifier switches are synchronized in operation. To describe the operating principle of the proposed converter, the following assumptions are made:

• The circuit is operating in steady state mode, and the magnetizing inductor current is continuous.
• All the components are ideal, and the parasitic components are neglected.
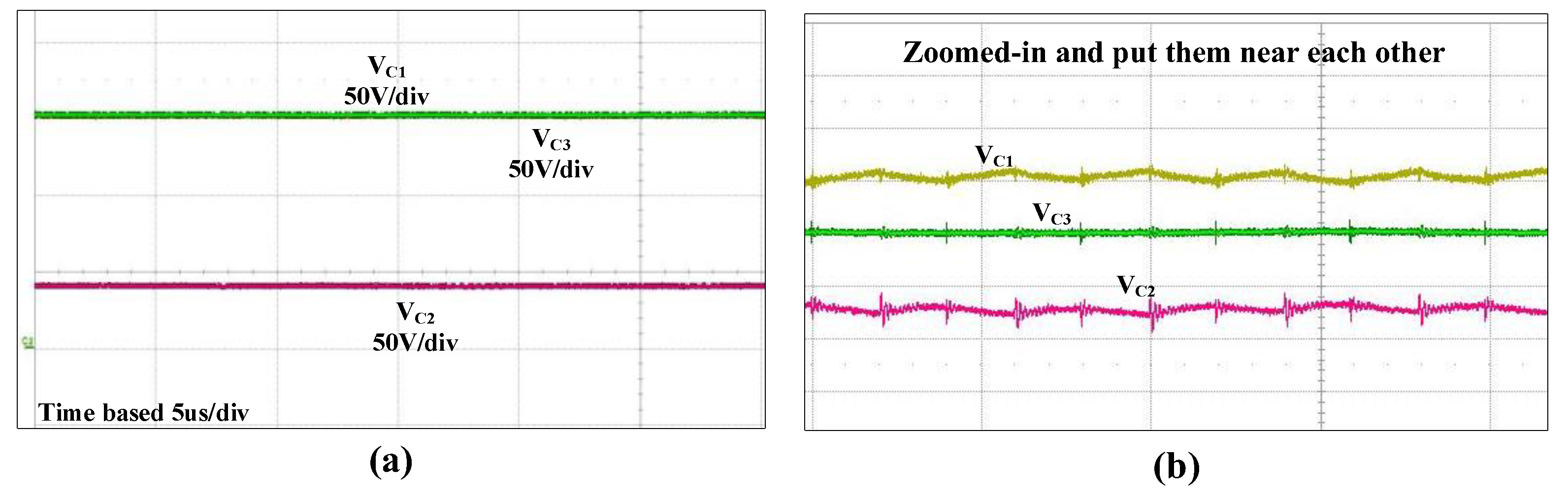
• All the capacitors are large enough to maintain their voltages constant during a switch-off period.
• All the output capacitors have the same value (C₁ = C₂ = C₃), and all the blocking capacitors have the same value (C_S = C_D).
• The switching period is T_s; the switch S₁ is closed for time DT_s and open for time (1-D) T_s and vice versa.
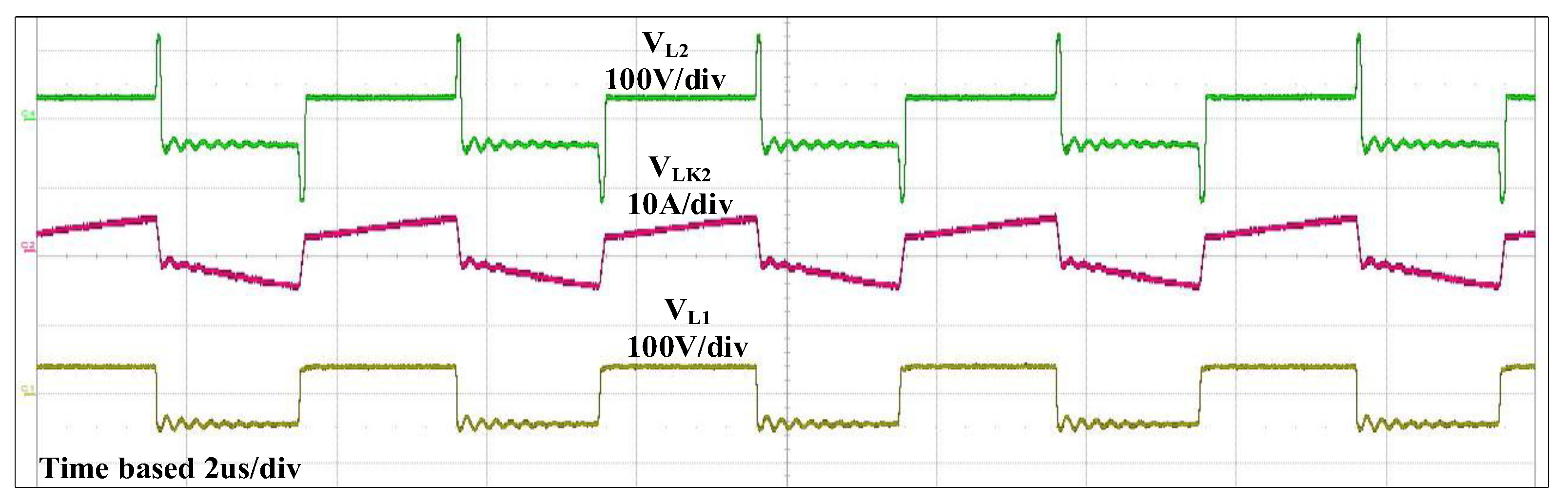
• The turns ratio of the coupled inductor and the relationship between the voltage of each winding are defined in (1)

$$N={\displaystyle \frac{N_2}{N_1}} , V_{L_2}={\displaystyle \frac{N_2}{N_1}}{V}_{L_1}$$

(1)

where: N is turns-ratio, $N_1$ and $N_2$ are the number turns of primary and secondary winding, respectively. $V_{L_1}$ and $V_{L_2}$ are voltage of the primary and secondary winding of the coupled inductor.

Mode 1 ($t_1$-$t_2$)

Before $t_1$, $S_1$ is off, $D_1$ and $D_4$ are reverse biased and $S_2$, $D_2$ and $D_3$ were conducting. At $t$ = $t_1$, $S_2$ turns off, the parasitic capacitor $C_{oss1}$ of $S_1$ is discharged. The coupled inductor starts to charge. Due to the charging of the parasitic capacitor $C_{oss2}$ of $S_2$ and the discharging of leakage inductor $L_{LK2}$, the voltage across $S_2$ is raised up and the body diode of $S_1$ is forward biased to create the ZVS turn-on for $S_1$_.

Mode 2 ($t_2$-$t_3$)

At $t$ = $t_2$, $S_2$ is off, the parasitic capacitor of $S_2$ is fully charged and that of $S_1$ is fully discharged. $S_1$ turns on with ZVS condition as created from Mode 1. Since the $S_1$ is fully on, its body diode is reverse biased, hence the current will flow through $S_1$ instead of its body diode. At the end of this mode, the $L_{LK2}$ is fully discharged, the current through the diodes $D_2$ and $D_3$ decrease to zero and ZCS turn-off for these diodes is achieved.

Mode 3 ($t_3$-$t_4$)

At $t$ = $t_3$, $S_1$ is on, and $S_2$ is off, and the coupled inductor is being charged. Due to the secondary winding voltage of the coupled inductor, $D_1$ and $D_4$ are forward biased, $D_2$ and $D_3$ are reverse biased, causing capacitors $C_D$ and $C_1$ are discharged, $C_s$ is charged. During this mode, the leakage inductor $L_{LK2}$ stores the energy.

By using Kirchhoff’s Voltage Law (KVL), the equation expression in this mode can be expressed as follows.

$$V_{L_1}=V_S,V_{L_2}=N{V}_{L_1}=N{V}_S$$

(2a)

$$V_{C_S}+V_{L_2}=V_{C_1}+V_{L_{LK2}}$$

(2b)

$$V_{L_1}+V_{L_2}+V_{C_2}=V_{C_D}+V_{L_{LK2}}$$

(2c)

$$V_O=V_{C_1}+V_{C_2}+V_{C_3}+V_S$$

(2d)

By using Kirchhoff’s Current Law (KCL), the current $I_{LLK2}$ of leakage inductor $L_{LK2}$ can be calculated as in (3).

$$I_{L_{LK2}}={\displaystyle \frac{C_1\Delta V_{C1}}{(t_4-t_3)}}+{\displaystyle \frac{V_{L_1}(t_4-t_3)}{N{L}_1}}+{\displaystyle \frac{C_2\Delta V_{C2}}{(t_4-t_3)}}$$

(3)

Since the output current ripple is very small and can be neglected, the voltage of capacitor $C_3$ can be considered constant. Then the total ripple of the output voltage is only contributed by the voltage ripple of capacitors $C_1$ and $C_2$. Moreover, from the earlier assumption, capacitors $C_1$, $C_2$, and $C_3$ have the same value. Then the leakage inductor current can be rewritten as follows.

$$I_{L_{LK2}(t_4-t_3)}={\displaystyle \frac{2C_1\Delta V_O}{(t_4-t_3)}}+{\displaystyle \frac{V_{L_1}(t_4-t_3)}{N{L}_1}}$$

(4)

And the voltage of the leakage inductor in this mode can be calculated as follows.

$$V_{L_{LK2}\left(t_4-t_3\right)}={\displaystyle \frac{L_{LK2}d{i}_{L_{LK2}}}{dt}}={\displaystyle \frac{L_{LK2}\left(2C_O\Delta V_{O}N{L}_1+V_{L_1}(t_3-t_2{)}^2\right)}{(t_3-t_2{)}^{2}N{L}_1}}$$

(5)

Mode 4 ($t_4$-$t_5$)

At $t$ = $t_4$, $S_1$ turns off, $S_2$ turns on. The diodes $D_2$ and $D_3$ are reverse biased, $D_1$ and $D_4$ are forward biased. The body diode of $S_2$ is forward biased and conducted, the parasitic capacitor $C_{oss2}$ of $S_2$ is discharged and the parasitic capacitor $C_{oss1}$ of $S_1$ is charged. The coupled inductor and leakage inductor $L_{LK2}$ start to discharge. Due to the discharging of leakage inductor $L_{LK2}$, the currents through diodes $D_1$ and $D_4$ are decreased and create ZCS turn off for these diodes. At the end of this mode, the leakage inductor $L_{LK2}$ is fully discharged.

Mode 5 ($t_5$-$t_6$)

In this mode, the energy stored in the core of coupled inductor is discharged to the output capacitor $C_2$, and the blocking capacitor $C_D$ of negative VM is discharged to the output capacitor $C_3$. The secondary side leakage inductor $L_{LK2}$ is charged after being fully discharged in Mode 3. The blocking capacitor $C_s$ of positive VM is charged for the next discharging cycle. The voltage applied to capacitor $C_s$ is not only the input voltage but also the voltage of primary and secondary winding of coupled inductor minus the voltage drop on leakage inductor $L_{LK2}$ while it is charging. Similarly, the voltage applied to the output capacitor $C_3$ is not only the voltage of blocking capacitor $C_D$ but also the voltage of secondary winding of coupled inductor resulting in the increasing of the overall voltage gain of proposed converter without increasing the voltage stress on components.

By using KVL, the equations of this mode can be expressed as in (6).

$$V_L=V_{C_2},V_{L_2}=N{V}_{L_1}=N{V}_{C_2}$$

(6a)

$$V_{L_1}+V_{L_2}+V_S=V_{C_S}+V_{L_{LK2}}$$

(6b)

$$V_{C_D}+V_{L_2}=V_{C_3}+V_{L_{LK2}}$$

(6c)

$$V_O=V_{C_1}+V_{C_2}+V_{C_3}+V_S$$

(6d)

Mode 6 ($t_6$-$t_7$).

At $t$ = $t_6$, the voltage of the capacitor $C_2$ is raised up higher to the primary winding voltage of the coupled inductor, the body diode of $S_2$ reverse biased. Hence the current flows through $S_2$ instead of its body diode. At the end of this mode $t$ = $t_7$, one switching period is done, everything is ready for the next cycle.

The leakage inductor $L_{LK2}$ is charged in whole time of Mode 5 and Mode 6. Similar in Mode 3, the current $I_{LLK2}$ flow through the leakage inductor $L_{LK2}$ can be calculated as in (7) by using KCL.

$$I_{L_{LK2}\_(t_7-t_5)}={\displaystyle \frac{2C_1\Delta V_o}{(t_7-t_5)}}+{\displaystyle \frac{V_{L_1}(t_7-t_5)}{N{L}_1}}$$

(7)

Hence, the voltage of the leakage inductor $L_{LK2}$ in this mode can be calculated as follows.

$$V_{L_{LK2}(t_7-t_5)}={\displaystyle \frac{L_{LK2}d{i}_{L_{LK2}}}{dt}}={\displaystyle \frac{L_{LK2}\left(2C_O\Delta V_{O}N{L}_1+V_{L_1}(t_7-t_5{)}^2\right)}{(t_7-t_5{)}^{2}N{L}_1}}$$

(8)

2.2. Steady State Analysis of the Proposed Converter

2.2.1. Voltage Gain and Voltage Stress on Components

Since Mode 1, Mode 2 and Mode 4 occur in a very short period of time, we can neglect these three modes in steady-state analysis. Hence, the period ($t_2$ – $t_4$) will be ${DT}_S$ and period ($t_7$ – $t_5$) will be $(1-D)T_S$. Applying the voltage-second balance, the following equations can be obtained as in (9),

$${\bar{V}}_{L_1}=D{V}_S-(1-D)V_{C_2}=0$$

(9a)

$${\bar{V}}_{L_1}=D{V}_S-\left(1-D\right)\left(V_{C_S}+V_{L_{LK2}\left(t_7-t_5\right)}-N{V}_{C_2}-V_S\right)=0$$

(9b)

$${\bar{V}}_{L_1}=D(V_{C_D}+V_{L_{LK2(t_4-t_3)}}-N{V}_S-V_{C_2})-(1-D)V_{C_2}=0$$

(9c)

$$V_O=V_{C_1}+V_{C_2}+V_{C_3}+V_S$$

(9d)

Hence, the voltage of capacitors can be calculated by using (10).

$$V_{C_2}={\displaystyle \frac{D{V}_S}{1-D}}$$

(10a)

$$V_{C_D}=\left(N+{\displaystyle \frac{1}{1-D}}\right)V_S-{\displaystyle \frac{L_{LK2}\left(2C_1\Delta V_{o}N{L}_1+V_{L_1}(D{T}_s{)}^2\right)}{N{L}_1(D{T}_s{)}^2}}$$

(10b)

$$V_{C_S}=\left({\displaystyle \frac{1+ND}{1-D}}\right)V_S-{\displaystyle \frac{L_{LK2}\left(2C_1\Delta V_{o}N{L}_1+V_{L_1}\left(\right(1-D)T_s{)}^2\right)}{N{L}_1\left(\right(1-D)T_s{)}^2}}$$

(10c)

$$V_{C_1}=V_{C_3}=\left({\displaystyle \frac{1+N}{1-D}}\right)V_S-{\displaystyle \frac{L_{LK2}\left(2C_1\Delta V_{o}N{L}_1+V_{L_1}\left(\right(1-D)T_s{)}^2\right)}{N{L}_1\left(\right(1-D)T_s{)}^2}}-{\displaystyle \frac{L_{LK2}\left(2C_1\Delta V_{o}N{L}_1+V_{L_1}(D{T}_s{)}^2\right)}{N{L}_1(D{T}_s{)}^2}}$$

(10d)

And the output voltage equation can be derived as in (11).

$$V_o=\left({\displaystyle \frac{3+2N}{1-D}}\right)V_S-{\displaystyle \frac{2L_{LK2}\left(2C_1\Delta V_{o}N{L}_1+V_{L_1}\left(\right(1-D)T_s{)}^2\right)}{N{L}_1\left(\right(1-D)T_s{)}^2}}-{\displaystyle \frac{2L_{LK2}\left(2C_1\Delta V_{o}N{L}_1+V_{L_1}(D{T}_s{)}^2\right)}{N{L}_1(D{T}_s{)}^2}}$$

(11)

The voltage stress on semiconductors can be calculated as follows.

$$V_{S_1}=V_{S_2}={\displaystyle \frac{V_S}{1-D}}$$

(12a)

$$V_{D_1}=V_{D_2}=V_{D_3}=V_{D_4}=V_{C_1}=V_{C_3}$$

(12b)

From (11) it is noted that the voltage gain is not only contributed by the VM stages but also by the turns-ratio of the coupled inductor. This means that we can flexibly achieve the ultra-high voltage gain by either cascading more VM stages, increasing the turn-ratio of the coupled inductor or both. Moreover, Equation (12) shows that the voltage stress is shared evenly among the components. Hence the output components will work with low voltage stress. This is an advantage of using the symmetrical configuration mentioned before.

2.2.2. ZVS Condition

In Mode 1, to achieve ZVS turn-on for $S_1$, the voltage of leakage inductor $L_{LK2}$, while it is discharging, must be larger than the sum of the voltage of blocking capacitor $C_s$ and secondary winding voltage as shown in (13)

$$V_{L_{LK2}}-V_{C_S}-V_{L_2}\ge 0$$

(13a)

$$V_{L_2}=N{V}_{L_1}=N{V}_S$$

(13b)

The voltage of the leakage inductor can be found from the change of the current through it. As mentioned in Mode 1, the leakage inductor is fully discharged at the end of this mode. So, the change of the current in Mode 1 can be calculated as in (14).

$$\Delta I_{LK2}=I_{LK2\left(t_1\right)}-0$$

(14)

The leakage inductance current at $t$ = $t_1$ actually is the leakage inductance current at $t$ = $t_7$ of the previous switching period and can be derived as in (15).

$$I_{LK2\_\left(t_1\right)}=I_{LK2\_(t_7-t_5)}$$

(15)

Then the ZVS condition equation can be expressed as in (16).

$${\displaystyle \frac{L_{LK2}\Delta I_{L_{LK2}\_(t_7-t_5)}}{T_r}}\ge V_{C_S}+N{V}_S$$

(16)

From (8) and (13), the value of secondary side leakage inductor can be calculated as follows.

$$L_{LK2}\ge {\displaystyle \frac{\left(V_{C_S}+N{V}_S\right)T_r}{\Delta I_{L_{LK2}\_(t_7-t_5)}}}={\displaystyle \frac{(t_7-t_5)N{L}_1\left(V_{C_S}+N{V}_S\right)T_r}{2C_1\Delta V_{o}N{L}_1+V_{L_1}(t_7-t_5{)}^2}}$$

(17)

As mentioned at the beginning of part B, the period ($t_7$ – $t_5$) is denoted by $(1-D)T_S$, then (17) becomes (18).

$$L_{LK2}\ge {\displaystyle \frac{(1-D)T_{s}N{L}_1\left(V_{C_S}+N{V}_S\right)T_r}{2C_1\Delta V_{o}N{L}_1+V_{L_1}\left(\right(1-D)T_s{)}^2}}$$

(18)

where: $T_r$ is the discharging time of secondary side leakage inductor.

3. Design of the Proposed Converter

3.1. Design of the Output Capacitors

The output capacitors can be calculated from the maximum allowable output ripple voltage $\Delta V_O$ as in (19).

$$C_{Oeq}\ge {\displaystyle \frac{I_{O}D}{f_S\times \Delta V_O}}$$

(19)

where: $f_S$ is switching frequency, $I_o$ is the output current, and $C_{Oeq}$ is the equivalent output capacitor, that can be calculated as in (20).

$$C_{Oeq}={\displaystyle \frac{C_1{C}_2{C}_3}{C_1{C}_2+C_2{C}_3+C_3{C}_1}}$$

(20)

To keep the symmetrical configuration, all the output capacitors must have the same value and can be calculated as in (21).

$$C_1=C_2=C_3=3C_{Oeq}\ge {\displaystyle \frac{3I_{O}D}{f_{SW}\times \Delta V_O}}$$

(21)

The leakage inductors $L_{LK2}$, duty cycle D, and the dead time $T_d$_.

Firstly, the minimum duty cycle $D_{min}$ can be calculated from the required voltage gain in the case when the leakage inductor $L_{LK2}$ equals to zero.

$$D_{min}=1-\left(3+2N\right){\displaystyle \frac{V_S}{V_O}}$$

(22)

The voltage of blocking capacitor $C_s$ in the case of minimum duty cycle $D_{min}$ can be calculated as follows.

$${V_{C_S\_D_{min}}=\left({\displaystyle \frac{1+N{D}_{min}}{1-D_{min}}} \right)V}_s$$

(23)

By using (18) and (23), the minimum required value of leakage inductor $L_{LK2}$ can be calculated with an assumption that the discharging time $T_r$ is equal to the deadtime $T_d$ of switches.

After choosing the value for leakage inductor $L_{LK2}$, the right value for duty cycle can be found from the output voltage equation shown in (11).

It should be noted that, if the value of the leakage inductor is too large, the voltage gain will be reduced much. Moreover, the $S_1$ has to be turned on before the leakage inductor $L_{LK2}$ gets fully discharged, then the dead time $T_d$ of switches must be smaller than the discharging time $T_r$ of the leakage inductor $L_{LK2}$ to maintain ZVS condition.

In mode 1, since the body diode of $S_1$ and $D_2$ are forward biased, the leakage inductor $L_{LK2}$ will resonate with capacitor $C_s$. To maintain ZVS condition, the resonant frequency must be much smaller than switching frequency. Moreover, as an assumption before, the capacitors $C_s$ and $C_D$ have the same value to keep the symmetrical configuration, those values can be calculated by using (24).

$$C_S=C_D>>{\displaystyle \frac{1}{(2\pi f_S{)}^2{L}_{LK2}}}$$

(24)

3.2. Design of the Main Inductor

The magnetizing inductance of coupled inductors is designed to operate the proposed converter in CCM mode. Then its value can be calculated as in (25).

$$L_m\ge {\displaystyle \frac{V_{S}D}{\Delta I_{L_m}{f}_{SW}}}$$

(25)

where: $\Delta I_{L_m}$ is the current ripple of the magnetizing inductor $L_m$_.

Then, the primary winding inductance $L_1$ and secondary inductance $L_2$ can be expressed by using (26).

$$L_1=L_m+L_{LK1}$$

(26a)

$$L_2=N^2{L}_1$$

(26b)

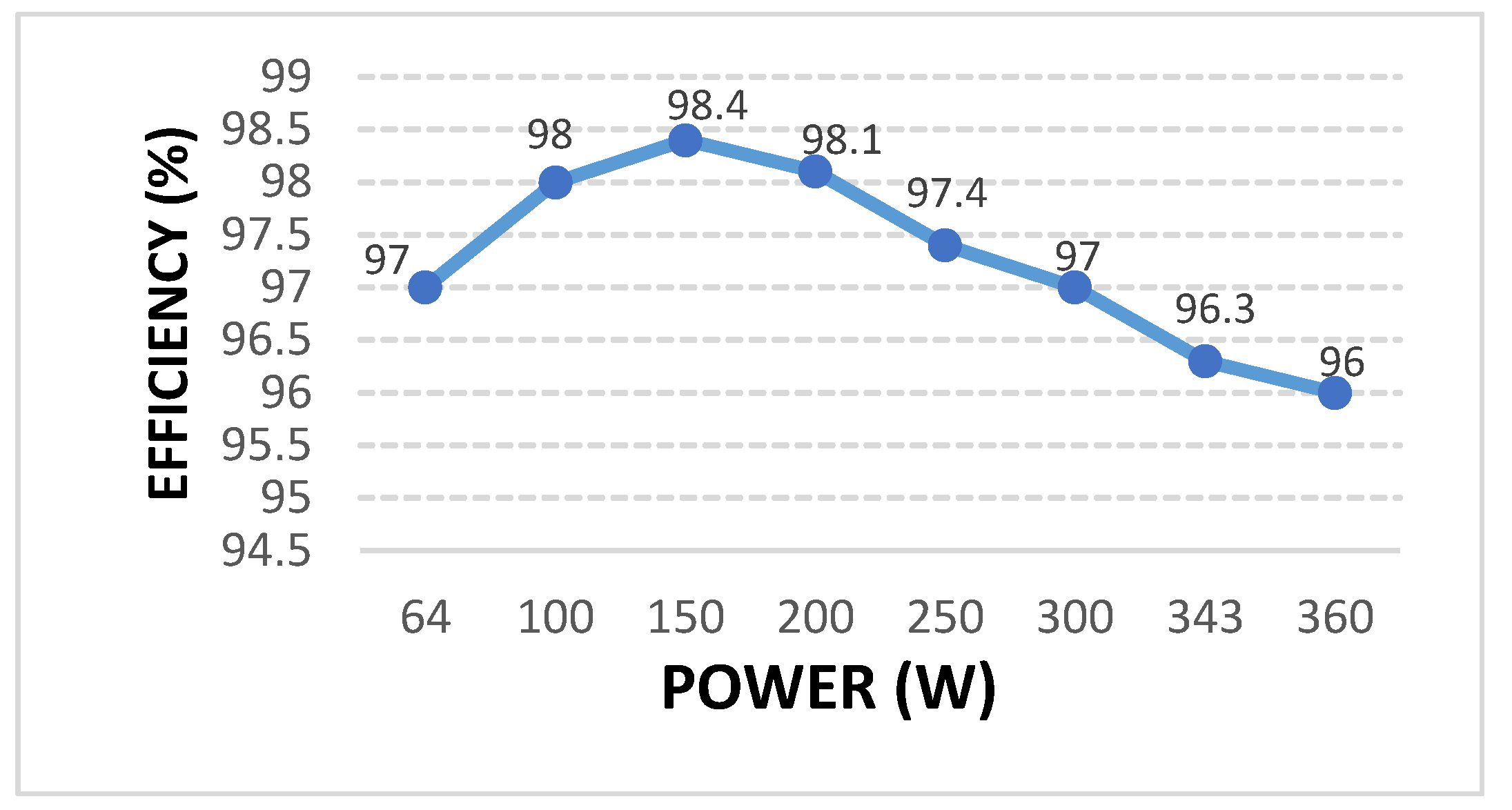
4. Experiment Results

In order to verify the validity of the proposed converter, a 380V, 360W prototype converter is built for a photovoltaic module (Hyundai RI Series 360W, 72 Cell Solar Module). The specifications of the proposed converter are shown on Table 1, and the information about the switches and passive components are shown in Table 2.

In the experiments, the gate signals ($V_{GS1}$, $V_{GS2}$) are generated by a DSP TMS320F28335. The prototype converter is shown in Figure 4. All the through-hole components are placed on the top side, the gate drivers are placed on the bottom side. All the capacitors are film capacitors.

The duty cycle of the main MOSFET ($S_1$) is 0.52 to boost the input voltage 40V to the output voltage of 380V. The deadtime between the two switches is 100ns.

The experimental results in full load condition are shown in Figure 5. In Figure 5(a), it is clear to see that $S_1$ is turned on with ZVS condition. The waveform in Figure 5(b) shows the body diode of $S_2$ is forward biased at the first part of on-time of $S_2$ (as in Mode 4 of working principal part) and it is reverse biased then the current is changed the direction at the last part of on-time of $S_2$ (as in Mode 5 of working principal part). Figure 5(c) and (d) show the voltage and current waveforms of the diodes. It is obvious that all the diodes are turned off with ZCS. Figure 6 shows the voltage and current waveforms of switches and diodes in light load (20%) condition. The switch $S_1$ still achieves ZVS turn-on, and the diodes still achieve ZCS turn-off as in full load condition. It is strong evidence to show the proposed converter can achieve ZVS turn on for switches and ZCS turn-off for diodes in the whole range of load. It should be noted that the oscillation of current when switches are off is observed because of a small snubber capacitor used to eliminate the hot-loop issue in half-bridge configuration.

Figure 7 shows the waveforms of output capacitors. Due to the symmetrical configuration, the voltage of output capacitors $C_1$ and $C_3$ of two voltage multiplier stages are the same. And the voltage of the IBB output capacitor $C_2$ is lower as compared to those of voltage multipliers as a result of the small duty cycle. Moreover, from Figure 7(b), it shows that the capacitors $C_1$ and $C_2$ are interleaved with each other, then their voltage ripples will be canceled out each other and then contribute to the low voltage ripple for output voltage. Hence the smaller value output capacitor can be used to achieve the required output voltage ripple.

Figure 8(a) shows the voltage waveforms of the diodes and MOSFET $S_1$. These waveforms are exactly matched with the simulation. In Figure 8(b) zoomed in voltage waveforms of diodes and MOSFET $S_1$, it is observed that the MOSFET $S_1$ is turned on before the diodes $D_1$ and $D_4$ turn on, and $D_2$ and $D_3$ turn off, at the period of 160ns, which is 60ns longer than the dead time of switches. This is the required time to achieve ZVS turn-on for $S_1$ and ZCS turn-off for diodes as explained before in Part II.

Figure 9 shows the waveforms of coupled inductors at full load. It can be noted that the leakage inductor $L_{LK2}$ is discharging causing high voltage spikes in secondary winding of the coupled inductor in a small period of time before the voltage of the coupled inductor changes its polarity. It is another requirement for ZVS turn-on for $S_1$ and ZCS turn-off for the diodes.

A Power analyzer (Xitron 2802) is used for measuring the converter efficiency. Figure 10 shows the measured efficiency plot of the proposed converter when V_S = 40 V, V_O = 380V and $f_{sw}$=100 kHz. As shown in Figure 10, efficiency achieves 97% at light load (20% load) and 96% at heavy load (100% load). The maximum efficiency of 98.4% is obtained at 150W.

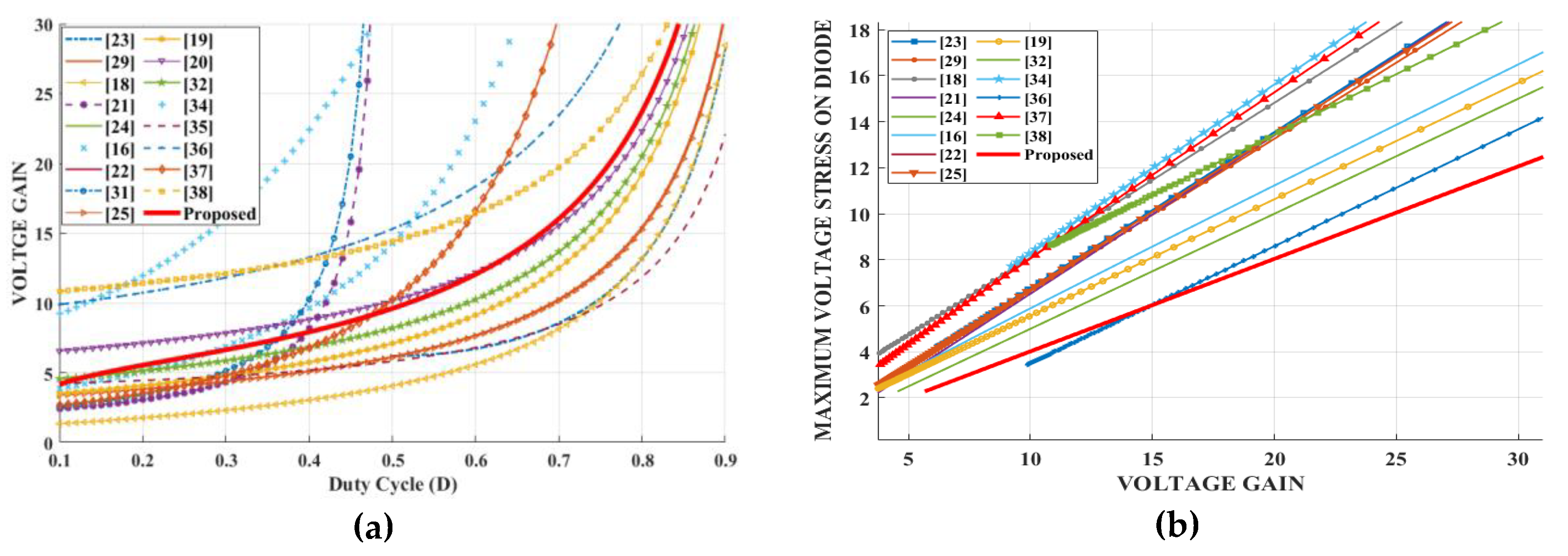
5. Comparison Study

The comparison between the proposed converter and other converters is shown in Table 3. From Table 3, it is clear that the proposed converter has the highest efficiency with a low voltage stress on components and a low number of components. The voltage gain comparison is shown in Figure 11 for the turns-ratio of 1.05. The converters in [16,21,31,34,36,37,38] have higher voltage gain than the proposed topology. However, the voltage stress on output diodes and capacitors is much higher, and the efficiency is much lower than that of the proposed converter. Therefore, it can be concluded that the proposed converter has superior advantages compared to other new topologies. Moreover, the converters in [21,31,34] have a small range of duty cycle, from 0.1 to 0.5. Thus, with applications requiring several hundred watts and very high step-up voltage conversion, the current stress on components will increase significantly, leading to a reduction in the efficiency of the converter. From Figure 12, the comparison of the graphs of stress on diodes with different converters is shown with the proposed converter.

6. Conclusions

In this paper an ultra-high step-up converter using coupled inductor with low voltage stress on components and high efficiency while achieving a high step-up voltage gain characteristic is proposed. The proposed topology is advantageous in terms of the following features:

• No spike voltage applied to semiconductor devices and hence no need for extra snubber.
• Very high efficiency with ZVS turn-on for MOSFET and ZVZCS for diodes.
• Reduced voltage stress on the components due to the symmetric configuration.
• Easy to get higher voltage gain by either choosing turns ratio of coupled inductor, duty cycle or cascading more VM stages.

The proposed converter can be a very good choice for ultra-high voltage step-up applications such as the distributed power generation systems with renewable energy sources, which requires a high voltage gain without using a transformer.