Geometry and Constants in Finite Ring Continuum

1. Introduction

In [1] we proposed the relativistic algebra over a finite field ${\mathbb{F}}_p$ equipped with its gauge-covariant symmetry triple—translation, dilation and powering—as an arithmetic object able to represent every affine change-of-coordinates map $k\mapsto ak+b(modq)$ (see also [2,3]). By arranging these three operators orthogonally to a cardinality axis, we showed that ${\mathbb{F}}_p$ forms a 2-spheroid (the discrete analog of $S^2$)—sitting diagonally in a 4-dimensional coordinate cube of symmetries—that already encodes the combinatorial signature of the topological sphere [4]. Furthermore, in [1] we have demonstrated that the resultant mathematical construct is capable of supporting the full extent of arithmetical apparatus provided by the conventional number classes $\mathbb{Z},\mathbb{Q},\mathbb{R}$ and $\mathbb{C}$.

The present work advances our program from purely discrete to pseudo-smooth geometry. Leveraging a non-principal ultrafilter [5], we pass from the finite field ${\mathbb{F}}_p$ to the ultrapower ${\mathbb{R}}_p$, a characteristic-p continuum whose diagonal copy of ${\mathbb{F}}_p$ forms an infinitesimal lattice, where we let p to be an odd prime $p\equiv 1(mod4)$, and ${\mathbb{R}}_p:={\prod }_n{\mathbb{F}}_p/U$ for its ultrapower. Within ${\mathbb{R}}_p^4$ we lift the discrete spheroid to the internal surface

$${\mathcal{S}}_p=\{(\sigma (u,v),c):u,v,c\in {[0,1]}_p\},$$

where $\sigma$ is the rational stereographic chart [6] and ${[0,1]}_p$ the pseudo-unit interval. Transfer principles [7] guarantee that ${\mathcal{S}}_p$ is an internal $C^{\infty }$ two-manifold1, while its hyperfinite trace reproduces the original ${\displaystyle \frac{{(p-1)}^2}{2}}+1$-point lattice exactly. Three consequences follow.

(i)

Every affine gauge of ${\mathbb{F}}_p$ extends to an internal diffeomorphism of ${\mathcal{S}}_p$, so the pseudo-smooth surface inherits the full relativistic covariance of the finite algebra.

(ii)

Loeb-measure shadows [8] show that the combinatorial curvature of the lattice converges, up to infinitesimals, to the Gauss curvature of ${\mathcal{S}}_p$ [9]. This tangible bridge between discrete and smooth geometry in characteristic p also paves the way for harmonic analysis [10,11], heat flow [12], and gauge theory [13] on finite relativistic geometries.

(iii)

The framed field ${\mathbb{F}}_p$ contains three fundamental structural constants—$i_p,{\pi }_p,e_p$—canonically singled out by its cyclic order. These constants serve as finite-field analogs of the classical $i,\pi ,e$ that underpin calculus on $\mathbb{R}$ and $\mathbb{C}$.

By exhibiting a genuine differential structure generated solely from the finite ring data, we provide concrete evidence that the proposed relativistic algebra can support the full extent of modern geometric ideas. This pseudo-smooth realization is therefore an essential incremental step toward our long-term goal: a unified algebraic foundation capable of expressing and interrelating the languages of mathematics, encompassing both the number theory, and the complete reconstruction of the classical analytic toolkit within a single, finite and gauge-covariant framework.

2. Finite Fields and Arithmetic Symmetries

Let ${\mathbb{Z}}_q:=\mathbb{Z}/q\mathbb{Z}=\{0,1,2,\dots ,q-1\}$ be a finite ring of integers modulo a natural number q. The elements of ${\mathbb{Z}}_q$ form a complete and closed set of relational representations of ${\mathbb{Z}}_q$ under modular addition and multiplication. However, the specific numeric labels assigned to these elements—particularly the designation of 0 and 1 as the additive and multiplicative identities—are intrinsically relative and carry no absolute meaning within the ring itself [1].

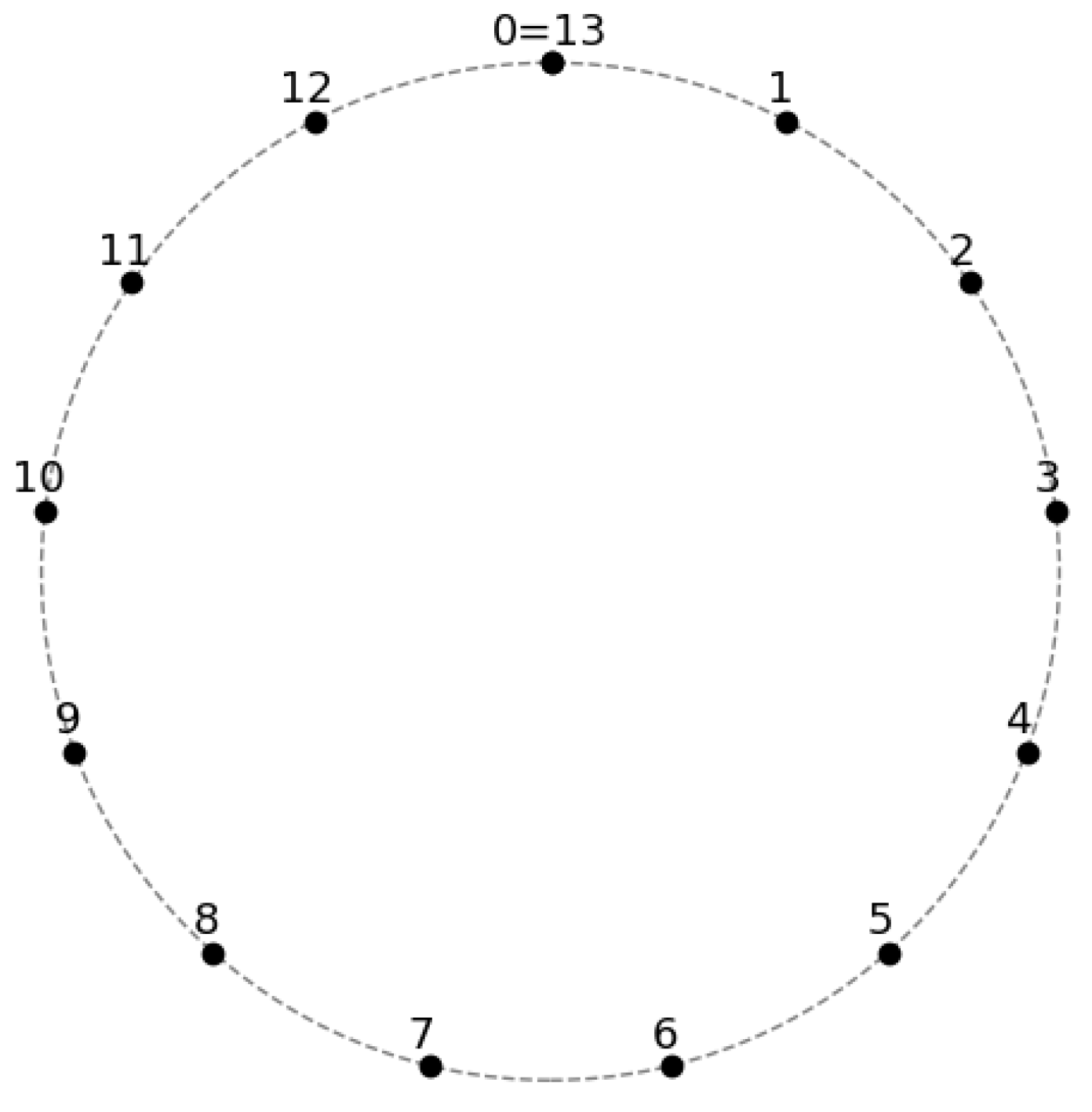
A typical diagram of a finite ring ${\mathbb{Z}}_q$, where $q=13$, is shown in Figure 1. We would like to specifically note that such a diagram is typically visualized as a circle on a 2D plane that illustrates its periodicity and rotational symmetry under the arithmetic operation of addition, thus assigning an intuitive geometric interpretation to the arithmetic structure of the additive group $({\mathbb{Z}}_q,+)$. However, the association between arithmetic operations and symbolic geometry can be extended further. In the finite ring ${\mathbb{Z}}_q$, the basic arithmetic operations of counting, addition, multiplication, and exponentiation can be all understood as manifestations of the underlying symmetries of structural transformations of the field [14].

Counting corresponds to the selection of the cardinality q of the underlying set. While typically taken for granted, the act of counting is an ontologically and informationally significant degree of freedom that both presupposes the existence of the ring ${\mathbb{Z}}_q$, and determines the entirety of its structural properties. Furthermore, the counting operation establishes a translation symmetry successor map $n⟼n+1(modq)$ that underpins the operation of addition as its iterative application.

Addition corresponds to the iterative application of counting. The additive group $({\mathbb{Z}}_q,+)$ forms a finite cyclic group of order q, generated by the element 1. Each addition operation $a\mapsto a+k$ (mod q) can be viewed as a rotation by k steps around a circular configuration of the elements of ${\mathbb{Z}}_q$. This symmetry reflects the homogeneity and periodicity of the additive structure [14].

Multiplication corresponds to the iterative application of addition, and furthermore reflects a scaling symmetry within the ring. The operation $a\mapsto a·k$ (mod q) corresponds to a dilation or contraction of the additive structure, where the effect of multiplication is constrained by the modulus. The multiplicative structure of ${\mathbb{Z}}_q$ is more subtle: if q is prime, ${\mathbb{Z}}_q^{\times }={\mathbb{Z}}_q\setminus \left\{0\right\}$ forms a finite multiplicative group, and multiplication becomes a permutation of the nonzero elements. If q is composite, the presence of zero divisors disrupts this structure, but the operation still defines a transformation governed by modular symmetry [15].

Exponentiation, or the operation $a\mapsto a^n$ (mod q), represents iterative applications of multiplication. When restricted to the multiplicative group ${\mathbb{Z}}_q^{\times }$, this operation defines power maps and automorphisms that reveal the group-theoretic structure and internal symmetries of the ring. In particular, when q is prime, exponentiation captures cyclic subgroup structures and encodes deep number-theoretic properties such as primitive roots and residue classes [16].

Thus, the basic arithmetic operations in ${\mathbb{Z}}_q$ are not arbitrary—they are algebraic expressions of the ring’s internal symmetries. They define how elements of the system transform under structured, invertible actions, and they reveal the harmonious regularity inherent in finite arithmetic.

Proposition 1

(3-Manifold Geometry of ${\mathbb{Z}}_q$). For a fixed value of cardinality q, the finite ring ${\mathbb{Z}}_q$, together with its triplet of arithmetic symmetries, may be interpreted as a discrete symbolic three-dimensional manifold embedded in an abstract four-dimensional symmetry space.

The detailed proof and the precise description of the resultant mathematical structure for non-prime values of q involve additional complexities, such as zero divisors and loss of multiplicative inverses, which are beyond the immediate scope of this publication and will be addressed in detail in our future work. Here, we would like to restrict ourselves to the important case of odd prime q, where the structure simplifies significantly, allowing for a clearer analysis and demonstration of the resultant symbolic geometry.

More specifically, when q is a prime, the ring ${\mathbb{Z}}_q$ becomes a field, and the exponentiation symmetry becomes algebraically reducible to multiplication due to the cyclic nature of ${\mathbb{Z}}_q^{\times }$. As a result, the independent exponential symmetry collapses, and the effective symmetry structure reduces from three to two dimensions. In this sense, the symbolic 3-manifold degenerates to a 2-spheroid within the same 4D space, reflecting a reduction in the degrees of algebraic freedom. In order to emphasize that q is an odd prime, we will henceforth denote it as p and the corresponding finite framed field as ${\mathbb{F}}_p$.

2.1. The Discrete 2-Spheroid Inside Symmetry Space

Throughout this subsection p denotes an odd prime and ${\mathbb{F}}_p$ its finite field. Write ${\mathbb{F}}_p^{\times }={\mathbb{F}}_p\setminus \left\{0\right\}$ for the multiplicative group, and fix a primitive root $g\in {\mathbb{F}}_p^{\times }$.

Definition 1

(Arithmetic symmetries). For $k,n\in {\mathbb{F}}_p$ define endomorphisms of ${\mathbb{F}}_p$

$$T_k\left(a\right)=a+k,S_k\left(a\right)=ka,P_n\left(a\right)=a^n,a\in {\mathbb{F}}_p.$$

The translation maps $T_k$ form the additive group $({\mathbb{F}}_p,+)$; the scaling maps $S_k$ form ${\mathbb{F}}_p^{\times }$; and $P_n$ is called exponentiation.

Lemma 2.1

(Exponentiation collapses to scaling). For every $n\in {\mathbb{F}}_p$ there exists a unique $m\in \{0,\dots ,p-2\}$ such that $P_n=S_{g^m}$ on ${\mathbb{F}}_p$.

Proof. 

Because ${\mathbb{F}}_p^{\times }$ is cyclic of order $p-1$ there is m with $g^m\equiv g^n(modp)$; hence $a^n=g^{m{log}_{g}a}=g^{m}a$ for all $a\in {\mathbb{F}}_p^{\times }$, and trivially for $a=0$. □

The symmetry triple $(T_k,S_k,P_n)$ therefore contains only two algebraically independent directions, namely translation and scaling.

Definition 2

(Carrier cube and diagonal embedding). Set

$${\mathcal{S}}_p:={\left({\mathbb{F}}_p\right)}^4=\{(c,a,m,e)\mid c,a,m,e\in {\mathbb{F}}_p\},$$

the carrier cube whose coordinates record

count(c), add(a), multiply(m), exponentiate(e).

Embed the field diagonally by $\iota :{\mathbb{F}}_p\hookrightarrow {\mathcal{S}}_p,a\mapsto (a,a,a,a).$

Definition 3

(Orbit complex). Let

$${\mathcal{N}}_p:=\left\{T_{k_1}{S}_{k_2}\left(\iota \left(a\right)\right)|a,k_1,k_2\in {\mathbb{F}}_p\right\}\subset {\mathcal{S}}_p.$$

Equip ${\mathcal{S}}_p$ with the cubical adjacency relation: two vertices are adjacent when they differ in exactly one coordinate by 1 modulo p. The sub-complex ${\mathcal{N}}_p$ inherits this incidence structure.

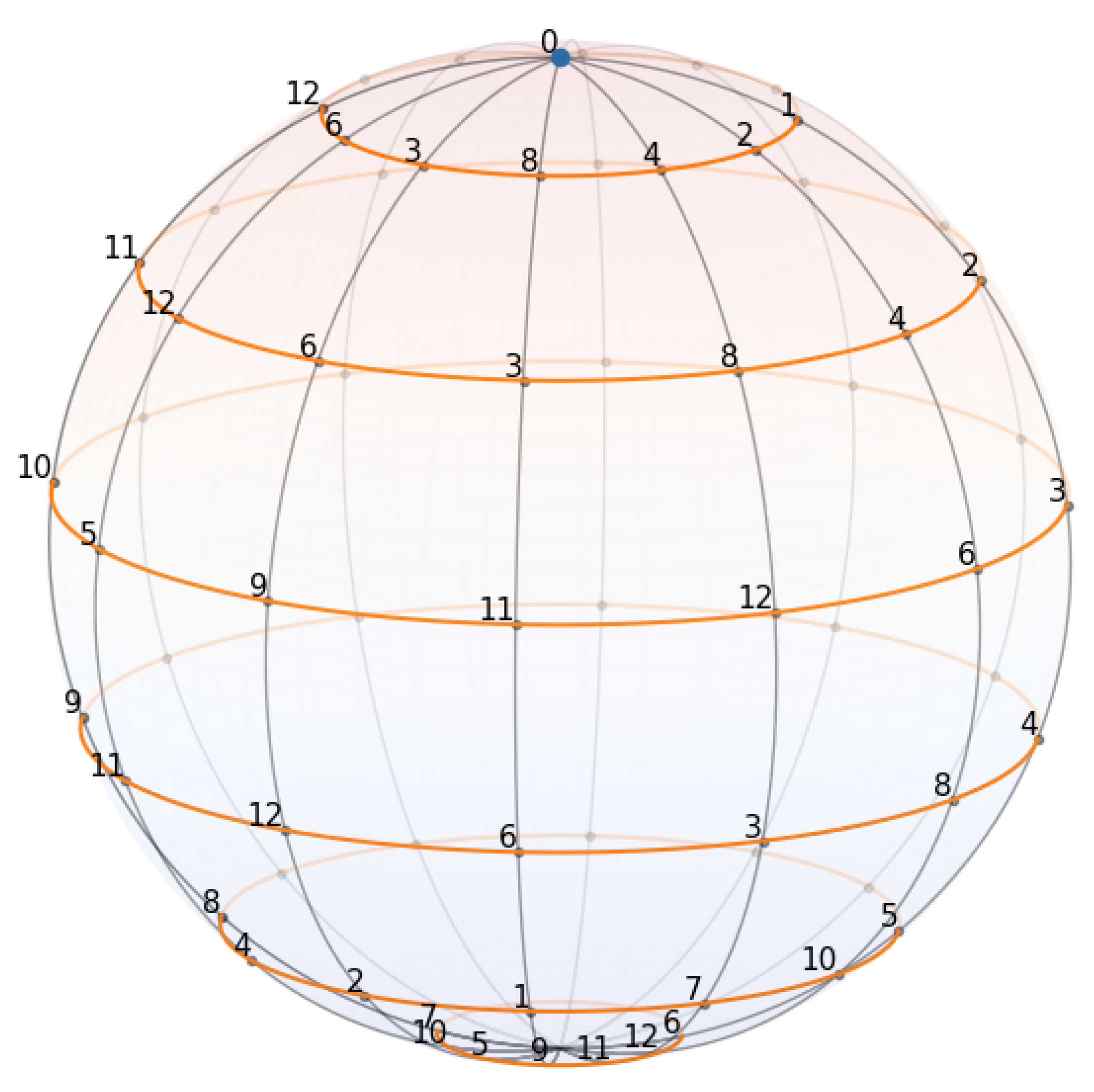
Proposition 2

(Finite 2-spheroid). The orbit complex ${\mathcal{N}}_p$ is a regular CW-complex [17] whose links of vertices are combinatorial circles; consequently ${\mathcal{N}}_p$ is combinatorially isomorphic to the boundary of a 3-simplex, i.e. to the 2-sphere $S^2$. Thus, ${\mathbb{F}}_p$, together with translation and scaling, realizes a finite discrete 2-spheroid embedded in the 4-dimensional lattice ${\mathcal{S}}_p$ as depicted in Figure 2.

Proof. 

• Two-parameter generation. By the lemma any composition of $T_k,S_k,P_n$ reduces to $T_{k^{\prime }}{S}_{k^{\prime \prime }}$; hence ${\mathcal{N}}_p$ is exactly the orbit of $\iota \left(0\right)$ under the commuting group ${\mathbb{F}}_p\times {\mathbb{F}}_p^{\times }$.
• Dimension. Each orbit point is obtained by at most two independent moves (T and S), so every cell in the induced cubical structure has dimension $\le 2$. Non-degeneracy of the actions ensures that two-dimensional faces do appear, making the complex pure of dimension 2.
• Local sphericality. At a vertex v adjacent vertices differ from v in exactly one of the two active coordinates. The four resulting neighbours form a 4-cycle, i.e. the link of v is a combinatorial 1-sphere.
• Global structure. A finite, pure 2-dimensional CW-complex with cyclic vertex links is necessarily a triangulation of a topological 2-sphere (Alexander duality or direct enumeration). Hence ${\mathcal{N}}_p\cong S^2$.

□

Remark 2.2.

No additional topology is required—the compactness of ${\mathcal{N}}_p$ follows from finiteness. The term “spheroid” refers to the regular 2-sphere CW-structure obtained above, serving as the symbolic analogue of a smooth sphere.

2.2. Pseudo-Smooth Lift to $S^2$

Let p be a fixed odd prime. All constructions below are carried out inside one and the same finite field ${\mathbb{F}}_p$.

Definition 4

(Pseudo-reals [1]). Fix a non-principal ultrafilter $\mathcal{U}$ on $\mathbb{N}$ and set

$${\mathbb{R}}_p:=\prod _{n\in \mathbb{N}}{\mathbb{F}}_p/\mathcal{U},\iota :{\mathbb{F}}_p\hookrightarrow {\mathbb{R}}_p,a⟼{\left[(a,a,a,\dots )\right]}_{\mathcal{U}}.$$

$R_p$ is an internal field of characteristic p that is $\kappa$-saturated for every standard $\kappa <card\left(\mathbb{R}\right)$. The diagonal copy $\iota \left({\mathbb{F}}_p\right)$ is a hyperfinite lattice which is $\epsilon$-dense in every compact interval of ${\mathbb{R}}_p$ for any infinitesimal $\epsilon$.

We write ${[0,1]}_p:=\{x\in {\mathbb{R}}_p:0\le x\le 1\}$ for the pseudo-unit interval, a totally ordered, internally compact subset of ${\mathbb{R}}_p$.

Definition 5

(Internal stereographic map). Define

$$\sigma :{\mathbb{R}}_p^2\setminus \{u^2+v^2=-1\}⟶{\mathbb{R}}_p^3,\sigma (u,v):=\left({\displaystyle \frac{2u}{D}},{\displaystyle \frac{2v}{D}},{\displaystyle \frac{u^2+v^2-1}{D}}\right),D:=u^2+v^2+1.$$

Transfer of the classical estimate shows that $\sigma$ is internally 1-Lipschitz on ${[0,1]}_p^2$.

Definition 6

(Pseudo-smooth surface and lattice). Set

$${\mathcal{S}}_p:=\left\{(\sigma (u,v),c)|u,v,c\in {[0,1]}_p\right\}\subset {\left({\mathbb{R}}_p\right)}^4,L_p:={\mathcal{S}}_p\cap {\left(\iota \left({\mathbb{F}}_p\right)\right)}^4.$$

The set $L_p$ is finite with $p^3$ points and inherits from the cubical lattice $\iota {\left({\mathbb{F}}_p\right)}^4$ a regular CW-complex isomorphic to the discrete 2-spheroid of Proposition 2 (each vertex link is a 4-cycle).

Theorem 2 3

(Pseudo-smooth realisation for fixed p). Let p be any odd prime and ${\mathbb{R}}_p$ the pseudo-real field from Definition 4. Then:

• ${\mathcal{S}}_p$ is an internal $C^{\infty }$ two-dimensional submanifold of ${\left({\mathbb{R}}_p\right)}^4$.
• $L_p$ is a finite 2-sphere CW-complex combinatorially identical to the discrete 2-spheroid of ${\mathbb{F}}_p$.
• For every infinitesimal $\epsilon \in R_p$ the lattice $L_p$ is an ε-net in ${\mathcal{S}}_p$; equivalently, $\overline{L_p}={\mathcal{S}}_p$ in the internal topology.
• The internal Gaussian curvature of ${\mathcal{S}}_p$, computed by infinitesimal triangles, is identically 1. (Proof: transfer of the classical formula for σ.)

Proof.(a) Smoothness follows from transfer of the real inverse-function theorem applied to $\sigma$ and the coordinate projection $c\mapsto c$. (b)Each vertex of $L_p$ has valency 4; the link is a square; the resulting complex is a flag triangulation of $S^2$. (c)Given $x=(\sigma (u,v),c)\in {\mathcal{S}}_p$ choose $k_1,k_2,k_3\in {\mathbb{F}}_p$ with $|u-\iota \left(k_1\right)|,|v-\iota \left(k_2\right)|,|c-\iota \left(k_3\right)|<\delta$ for an arbitrary infinitesimal $\delta$. Lipschitz continuity of $\sigma$ yields a point of $L_p$ within distance $C\delta$. (d)Because $\sigma$ is the standard rational stereographic chart, the induced first fundamental form satisfies $E=G=\frac{4}{D^2},F=0$; direct transfer of the classical Gauss formula gives $K\equiv 1$. □

The pseudo-smooth 2-spheroid ${\mathcal{S}}_p$ provides the geometric arena on which finite analogs of differential forms, spinors, and gauge fields can be developed. In forthcoming sections we connect the algebraic observer formalism of the companion paper [1] with the differential geometry of ${\mathcal{S}}_p$, paving the way toward a finite-field approach to relativistic dynamics.

Remark 2.4

(Optional characteristic-zero shadow). If one embeds ${\mathbb{R}}_p$ into a characteristic-0 non-standard field (e.g. via Witt vectors), the standard-part map sends ${\mathcal{S}}_p$ to an honest smooth round 2-sphere in ${\mathbb{R}}^4$, while collapsing $L_p$ to a ${\displaystyle \frac{1}{p}}$-mesh refinement thereof. No such embedding is needed for the internal differential calculus used in this paper, but it can be convenient when comparing with classical geometry.

The theorem shows that every finite framed field ${\mathbb{F}}_p$ already carries within itself—via its pseudo-real completion—a fully fledged smooth-like 2-sphere on which the lattice of field elements forms an arbitrarily fine pixelation.

2.3. Intrinsic Curvature of the Pseudo-Smooth 2-Spheroid ${\mathcal{S}}_p$

Recall the internal stereographic chart

$$\sigma (u,v)=\left(X(u,v),Y(u,v),Z(u,v)\right)=\left(\frac{2u}{D},\frac{2v}{D},\frac{u^2+v^2-1}{D}\right),D:=u^2+v^2+1,$$

defined for $(u,v)\in {[0,1]}_p^2\subset {\mathbb{R}}_p^2$. The pseudo-smooth surface of Section 2.2 is ${\mathcal{S}}_p=\left\{(\sigma (u,v),c)\mid u,v,c\in {[0,1]}_p\right\}\subset {\left({\mathbb{R}}_p\right)}^4.$

Set ${\sigma }_u:={\partial }_u\sigma ,{\sigma }_v:={\partial }_v\sigma$ and abbreviate $E:=\langle {\sigma }_u,{\sigma }_u\rangle ,F:=\langle {\sigma }_u,{\sigma }_v\rangle ,G:=\langle {\sigma }_v,{\sigma }_v\rangle$ for the metric coefficients with respect to the $\langle ·,·\rangle$ coming from the standard dot-product on ${\left({\mathbb{R}}_p\right)}^3$. A direct internal computation—identical to the real one—gives

$$E={\displaystyle \frac{4}{D^2}},F=0,G={\displaystyle \frac{4}{D^2}}.$$

Because $\parallel \sigma \parallel =1$ we may take the inward unit normal $\mathbf{n}:=\sigma$. Let $L:=\langle {\sigma }_{uu},\mathbf{n}\rangle ,M:=\langle {\sigma }_{uv},\mathbf{n}\rangle ,N:=\langle {\sigma }_{vv},\mathbf{n}\rangle$ denote the second-fundamental-form coefficients. Using $\langle {\sigma }_u,\sigma \rangle =\langle {\sigma }_v,\sigma \rangle =0$ one finds

$$L={\displaystyle \frac{2}{D^2}},M=0,N={\displaystyle \frac{2}{D^2}}.$$

With $K={\displaystyle \frac{LN-M^2}{EG-F^2}},H={\displaystyle \frac{EN+GL-2FM}{2(EG-F^2)}}$ (see, e.g., [9]) one obtains

$$K(u,v)=1,H(u,v)=1,\mathrm{for}\mathrm{all}(u,v)\in {[0,1]}_p^2.$$

In conclusion, every point of the pseudo-smooth surface ${\mathcal{S}}_p$ has constant positive Gaussian curvature $K\equiv 1$ and mean curvature $H\equiv 1$. This explicit calculation confirms Theorem 2.3(d).

Remark. Because the fourth “count” coordinate in $F(u,v,c):=\left(\sigma \right(u,v),c)$ is flat, all curvature is carried by the three stereographic coordinates. Hence ${\mathcal{S}}_p$ is internally isometric to the unit round sphere in ${\left({\mathbb{R}}_p\right)}^3$.

3. Canonical Constants in ${\mathbb{F}}_p$

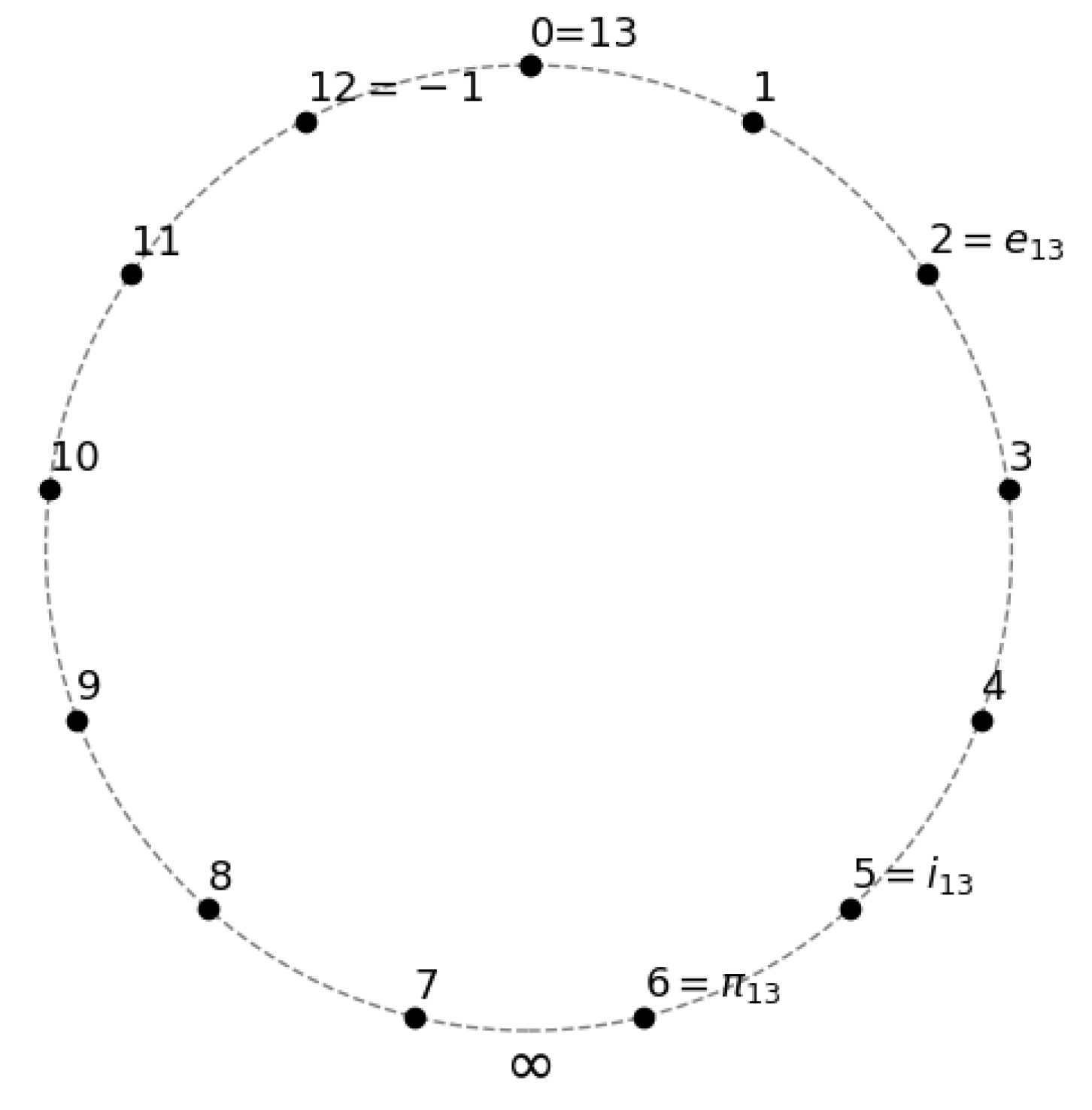
3.1. Finite-Field Multiplicative Half-Turn Generator $i_p$

Recall from [1] that, for every prime $p\equiv 1(mod4)$, $-1$ is a quadratic residue in ${\mathbb{F}}_p$. Define the imaginary unit

$$i_p:=min\left\{x\in {\mathbb{F}}_p|x^2=-1,1\le x<\frac{p-1}{2}\right\}.$$

The interval restriction makes $i_p$ the unique square-root in the forward half-cycle of the frame order.

On the additive circle ${\mathcal{C}}_p:=\{(x,y)\in {\mathbb{F}}_p^2:x^2+y^2=1\}$ the map $Q:(x,y)\mapsto (-y,x)$ corresponds to multiplication by $i_p$; it is the quarter-turn rotation, the discrete analog of $e^{i\pi /2}$.

3.2. Natural Exponential Base $e_p$

In the real calculus the number e is characterized by the minimal-deviation property ${\displaystyle \frac{d}{dx}}{e}^x{|}_{x=0}=1,$ i.e. the exponential map coincides with the identity to first order at the origin. We translate this idea into the finite setting by choosing, among the primitive roots of ${\mathbb{F}}_p^{\times }$, the one that sits closest to 0 in the chosen cyclic order $0\prec 1\prec 2\prec \dots \prec p-1\prec 0.$

Cyclic distance. For $x\in {\mathbb{F}}_p$ define the additive-circle distance to the origin

$$d_0\left(x\right):=min\left\{x,p-x\right\}\in \left\{0,1,\dots ,\frac{p-1}{2}\right\}.$$

Forward-time convention. To avoid the duplicity $(g,-g)$ of primitive roots we restrict attention to the forward half-circle

$${\mathcal{P}}_{+}:=\left\{g\in {\mathbb{F}}_p^{\times }\mathrm{primitive}:0<g<\frac{p-1}{2}\right\}.$$

Every unordered pair $\{g,-g\}$ of primitive roots contributes exactly one element to ${\mathcal{P}}_{+}$, so the selection below is unambiguous for all odd primesp.

Definition 7

(Natural base $e_p$). Set

$$e_p:=\underset{x\in {\mathcal{P}}_{+}}{arg\; min}{d}_0\left(x\right)=min{\mathcal{P}}_{+}.$$

(1)

Lemma 3.1

(Uniqueness and minimal increment). $e_p$ is theuniqueprimitive root in the interval $(0,\frac{p-1}{2})$, hence the unique primitive root that minimizes both $d_0\left(x\right)$ and $|x-1|$.

Proof. 

The interval $(0,\frac{p-1}{2})$ contains no pair of additive inverses, so $min{\mathcal{P}}_{+}$ is a single element. For any primitive root $g\ne e_p$ we have $d_0\left(g\right)\ge d_0\left(e_p\right)+1$, whence $|g-1|\ge d_0\left(g\right)-1\ge d_0\left(e_p\right)=|e_p-1|$. □

Discrete exponential and logarithm. Using $e_p$ as base define

$${exp}_p:\mathbb{Z}⟶{\mathbb{F}}_p^{\times },{exp}_p\left(k\right):=e_p^k,{log}_{e_p}:{\mathbb{F}}_p^{\times }⟶\mathbb{Z}/(p-1)\mathbb{Z},{log}_{e_p}\left(x\right)=k\iff x=e_p^k.$$

Because $|e_p-1|$ is minimal among primitive roots, ${exp}_p$ realises the smallest forward difference at the origin, $\Delta {exp}_p\left(0\right)=e_p-1,$ mirroring $e^{\prime }\left(0\right)=1$.

Gauge covariance. Let $x\mapsto ax+b$ be an affine gauge transformation with $a\in {\mathbb{F}}_p^{\times }$. Multiplication by a is an automorphism of the cyclic group ${\mathbb{F}}_p^{\times }$, so it permutes primitive roots and preserves the order of their residues in $(0,\frac{p-1}{2})$. Translation by b fixes ${\mathbb{F}}_p^{\times }$. Consequently the image of $e_p$ under the gauge is the minimiser of (1) in the new frame; hence $e_p$ is a frame-invariant constant of the theory.

Remark 3.2.

For primes $p\equiv 1(mod4)$ the forward-time convention coincides with choosing the representative of a $\{\pm g\}$ pair that is closest to 0; for $p\equiv 3(mod4)$ it simply avoids the fact that $-1$ itself is a primitive root.

Thus the number $e_p$ inherits inside ${\mathbb{F}}_p$ the defining property of the real constant e: it generates the discrete exponential map that deviates least from the identity at the origin, and its logarithm turns multiplicative structure into additive increments with maximal linear fidelity.

3.3. Finite-Field Additive Half-Turn ${\pi }_p$

The real number $\pi$ is simultaneously a half-period for the rotation group of the unit circle and the factor that converts the sphere’s constant curvature into the length of a half-meridian. Both rôles have exact analogs in every finite field ${\mathbb{F}}_p$.

Primitive root and half-turn. Fix an odd prime p and let

$$g_{min}:=min\left\{x\in \{2,\dots ,p-1\}\mid x\mathrm{generates}{\mathbb{F}}_p^{\times }\right\}$$

be the least positive primitive root in the framed order $0\prec 1\prec \dots \prec p-1\prec 0$. Euler’s criterion gives the well-known identity $g_{min}^{(p-1)/2}=-1.$

Definition 8

(Half-period integer). Set

$${\pi }_p:={\displaystyle \frac{p-1}{2}}\in \mathbb{Z}.$$

${\pi }_p$ is the unique positive integer for which $g_{min}^{{\pi }_p}=-1$.

Because $(p-1)/2$ depends only on p, the quantity ${\pi }_p$ is gauge-covariant: any affine relabelling $x\mapsto ax+b$ of the frame transports $g_{min}$ to the new least primitive root but leaves the integer ${\pi }_p$ unchanged.

Rotation-group interpretation. Define the additive circle ${\mathcal{C}}_p:=\{(x,y)\in {\mathbb{F}}_p^2:x^2+y^2=1\}.$ Multiplication by $g_{min}$ acts on ${\mathcal{C}}_p$ by

$$\rho :(x,y)⟼(g_{min}x,g_{min}y),$$

and the map $\langle \rho \rangle \stackrel{\cong }{⟶}{\mathbb{F}}_p^{\times },{\rho }^k\mapsto g_{min}^k$ identifies the rotation group of ${\mathcal{C}}_p$ with the cyclic group of units. Under this identification

$${\rho }^{{\pi }_p}(x,y)=(-x,-y)$$

is the half-turn (antipodal) map, so ${\pi }_p$ counts exactly half the lattice points around the discrete circle, mirroring the classical equation $e^{i\pi }=-1$.

Geometric role on the pseudo-smooth spheroid. Embed ${\mathbb{F}}_p$ diagonally into the pseudo-real line $R_p$ and let

$${\mathcal{S}}_p:=\left\{(\sigma (u,v),c):u,v,c\in {[0,1]}_p\right\}\subset {\left(R_p\right)}^4$$

be the pseudo-smooth 2-spheroid of Theorem 2.3. Its prime meridian ${\mathcal{M}}_p:=\{(0,y,z,0)\in {\mathcal{S}}_p\}$ inherits the same rotation group as ${\mathcal{C}}_p$. Stepping ${\pi }_p$ times along the lattice $L_p={\mathcal{S}}_p\cap {\left(\iota \left({\mathbb{F}}_p\right)\right)}^4$ therefore

• advances halfway around ${\mathcal{M}}_p$;
• sends each lattice point to its meridian antipode; and
• realizes a geodesic length proportional to ${\pi }_p$.

Since ${\mathcal{S}}_p$ has constant internal curvature $K\equiv 1$ (Section 2.3), the Gauss-Bonnet integrand along any meridian satisfies ${\int }_{\mathrm{half}-\mathrm{meridian}}Kds={\pi }_p.$ Thus, ${\pi }_p$ converts the local curvature normalized to 1 into the global half-circumference factor, exactly as real $\pi$ does on the classical unit sphere.

In summary, the constant ${\pi }_p={\displaystyle \frac{p-1}{2}}$ plays inside ${\mathbb{F}}_p$ the dual rôle of the real constant $\pi$: 1. It is the half-period of the discrete rotation group on the framed circle ${\mathcal{C}}_p$; and 2. It supplies the universal conversion factor between constant curvature and half-meridian length on the pseudo-smooth spheroid ${\mathcal{S}}_p$.

Together with the imaginary unit $i_p=-1$ from Section 3.1 and $e_p$ from Section 3.2, the value ${\pi }_p$ completes the triple of canonical constants ${\pi }_p,e_p,i_p$ underpinning finite-field calculus over ${\mathbb{R}}_p$ and ${\mathbb{C}}_p$. The triplet of canonical constants for the finite field ${\mathbb{F}}_{13}$ is summarized in Table 1 and further depicted in Figure 3, where the three constants $i_{13}=5,{\pi }_{13}=6,e_{13}=2$ are represented as specific elements of the finite field ${\mathbb{F}}_{13}$.

4. Harmonic Analysis in Finite Relativistic Algebra

Building on the broader aims outlined in [1]—notably the links to Approximate Lie Groups and a finite-field analog of the Langlands programme—we now turn our attention to the harmonic analysis. We show how the constants $i_p,{\pi }_p,e_p\in {\mathbb{F}}_p$ constructed in Section 3 provide a bridge between the continuous and finite harmonic analysis. The key idea is to embed the finite field ${\mathbb{F}}_p$ into its pseudo-real completion ${\mathbb{R}}_p$ and to interpret the primitive root $e_p$ as an infinitesimal rotation. This allows us to define a kernel that simultaneously serves as a Fourier kernel for both the continuous and finite cases.

Classical Fourier theory over $\mathbb{R}$ or the circle $\mathbb{T}=\mathbb{R}/\mathbb{Z}$ decomposes functions into additive characters$x\mapsto e^{-2\pi i\xi x}$, $\xi \in \mathbb{R}$ [18,19]. Its finite analog on a prime field ${\mathbb{F}}_p$ uses the discrete additive characters ${\chi }_a\left(x\right)=e^{-2\pi i\mathrm{Tr}\left(ax\right)/p}$, $a\in {\mathbb{F}}_p$ [2,20]. Although the two theories are usually presented separately, they share a common algebraic skeleton: every cyclic group is Pontryagin self-dual. In this section we show how the constants $i_p,{\pi }_p,e_p$ constructed earlier provide an explicit bridge between the continuous and finite cases.

4.1. Additive Characters: Continuous and Finite

• Continuous. On $(\mathbb{R},+)$ the dual group is again $\mathbb{R}$; the Fourier kernel is

  $$K_{\infty }(x,\xi )=e^{-2\pi i\xi x}.$$
• Finite. On $({\mathbb{F}}_p,+)$ the dual group is $\widehat{{\mathbb{F}}_p}\cong {\mathbb{F}}_p$ via

  $${\chi }_a\left(x\right):=e^{-2\pi i\mathrm{Tr}\left(ax\right)/p}.$$
  The discrete Fourier transform

  $${\mathcal{F}}_{{\mathbb{F}}_p}\left[f\right]\left(a\right)=\sum _{x\in {\mathbb{F}}_p}f\left(x\right){\chi }_a\left(x\right)$$

  satisfies the finite Plancherel identity [20]

  $$\sum _x{\left|f\left(x\right)\right|}^2=p^{-1}\sum _a{\left|{\mathcal{F}}_{{\mathbb{F}}_p}f\left(a\right)\right|}^2.$$

The analytic and arithmetic kernels differ only by the ambient field in which the additive characters live.

4.2. Primitive Roots as Infinitesimal Rotations

Inside the pseudo-real completion ${\mathbb{R}}_p$ (Definition 4) the primitive root $e_p\in \iota \left({\mathbb{F}}_p\right)\subset {\mathbb{R}}_p$ acts like an infinitesimal rotation:

$$\underset{\mathrm{continuous}\mathrm{generator}}{\underbrace{e^{-2\pi i\delta }}}⟷\underset{\mathrm{finite}\mathrm{generator}}{\underbrace{e_p}},\delta \in {­}^{*}\mathbb{R}\mathrm{infinitesimal}.$$

Repeated multiplication by $e_p$ generates the cyclic subgroup $\langle e_p\rangle$ of order $p-1$; its logarithm ${log}_{e_p}:{\mathbb{F}}_p^{\times }\to \mathbb{Z}/(p-1)\mathbb{Z}$ linearizes multiplicative structure (Section 3.2).

4.3. Kernel Correspondence

Embed ${\mathbb{F}}_p$ diagonally: $\iota :{\mathbb{F}}_p\hookrightarrow {\mathbb{R}}_p,a\mapsto \left[(a,a,a,\dots )\right].$ For each $a\in {\mathbb{F}}_p$ define the pseudo-continuous character

$${\tilde{\chi }}_a\left(x\right):=exp\left(-2\pi i\iota \left(a\right)x/p\right),x\in {\mathbb{R}}_p.$$

Sampling ${\tilde{\chi }}_a$ at $x\in \iota \left({\mathbb{F}}_p\right)$ recovers the finite character ${\chi }_a$; sampling at infinitesimal increments $x=\delta k$ with $\delta \in {­}^{*}\mathbb{R}$ yields the continuous kernel. Thus, a single analytic expression lives simultaneously in the finite and continuous worlds.

$$e^{-2\pi iax/p}={\chi }_a\left(x\right)\mathrm{for}x\in {\mathbb{F}}_p,e^{-2\pi i\xi x}\mathrm{for}\xi ={\displaystyle \frac{a}{p}}\in \mathbb{R}$$

(2)

Equation (2) realizes the heuristic identifications

$$e^{-2\pi i/N}⟷e_p^{(p-1)/N},N\mid (p-1),$$

promised in the introduction.

5. Lie Groups in the Finite Ring Continuum

Lemma 5.1

(Smooth-pullback lift). Let p be an odd prime, let ${\mathbb{R}}_p$ be the pseudo-real ultrapower [1,5], and regard ${\mathbb{F}}_p^{\times }\subset {\mathbb{R}}_p^{\times }$ through the diagonal embedding ι. Everyinternalgroup homomorphism

$$f:\left({\mathbb{R}}_p,+\right)⟶\left({\mathbb{F}}_p^{\times },·\right)$$

is internally $C^{\infty }$. Concretely,

$$f\left(x\right)=a^x\mathrm{with}\mathrm{the}\mathrm{unique}\mathrm{unit}a:=f\left(1\right)\in {\mathbb{F}}_p^{\times },$$

and for each $k\ge 1$

$$f^{\left(k\right)}\left(x\right)={(lna)}^k{a}^x\mathrm{in}{\mathbb{R}}_p,$$

where $lna$ is the internal logarithm with base $e_p$.

Proof. 

Represent f by a sequence ${\langle f_n\rangle }_U$ with $f_n:{\mathbb{F}}_p\to {\mathbb{F}}_p^{\times }$. For every n the additive-to-multiplicative homomorphism is necessarily exponential: $f_n\left(x\right)=a_n^x$ with $a_n:=f_n\left(1\right)\in {\mathbb{F}}_p^{\times }$. Passing to the ultrapower yields $f\left(x\right)=a^x$ with $a={\langle a_n\rangle }_U\in {\mathbb{F}}_p^{\times }$. The real identity $\frac{d^k}{d{x}^k}{a}^x={(lna)}^k{a}^x$ is first-order, hence transfers to ${\mathbb{R}}_p$; therefore all higher internal derivatives exist with the stated form, so f is $C^{\infty }$. □

5.1. FRC Recap

Fix an odd prime $p\equiv 1(mod4)$. FRC enlarges the prime field ${\mathbb{F}}_p$ to a pseudo-real completion

$${\mathbb{R}}_p=\overline{{\mathbb{Q}}_p^{\le H}\left({\mathbb{F}}_p\right)}$$

that is compact2, totally bounded, and internally $C^{\infty }$ by the Transfer Principle [5]. Its one-dimensional framed circle is

$${\mathcal{S}}_p^1:={\mathbb{R}}_p/2{\pi }_p\mathbb{Z},{\pi }_p=\frac{p-1}{2},$$

and the canonical finite-field analogues of $i,\pi ,e$ are the units $i_p$, ${\pi }_p$, $e_p$ singled out by the cyclic order of ${\mathbb{F}}_p^{\times }$ as defined in Section 3. Every internal group homomorphism ${\mathbb{R}}_p\to {\mathbb{F}}_p^{\times }$ is automatically $C^{\infty }$ because ${\mathbb{R}}_p$ is an internal differentiable manifold and derivations transfer verbatim from $\mathbb{R}$ to ${\mathbb{R}}_p$ (Lemma 5.1)—this fulfils the smooth-calculus requirement.

5.2. Framed Rounding Map and Its Additivity

Set $N:=p-1=2{\pi }_p$. Define the rounding map

$$\rho :[0,2{\pi }_p)⟶{\mathbb{Z}}_N,\rho \left(\theta \right):=⌊\theta +\frac{1}{2}⌋.$$

Lemma 5.2

(Additivity of $\rho$). For all ${\theta }_1,{\theta }_2\in {\mathcal{S}}_p^1$ one has $\rho ({\theta }_1+{\theta }_2)\equiv \rho \left({\theta }_1\right)+\rho \left({\theta }_2\right)(modN)$.

Proof. 

Write ${\theta }_i={\alpha }_i+2{\pi }_p{m}_i$ with ${\alpha }_i\in [0,2{\pi }_p)$ and $m_i\in \mathbb{Z}$. Since $N=2{\pi }_p$ we have $\rho \left({\theta }_i\right)=\lfloor {\alpha }_i+\frac{1}{2}\rfloor +m_{i}N$. Add and take the floor again:

$$\rho ({\theta }_1+{\theta }_2)=⌊{\alpha }_1+{\alpha }_2+\frac{1}{2}⌋+(m_1+m_2)N\equiv \rho \left({\theta }_1\right)+\rho \left({\theta }_2\right)(modN).$$

□

5.3. Exact Framed Exponential and the Circle Group

Fix the minimum-action base $e_p\in {\mathbb{F}}_p^{\times }$ (the nearest primitive root) as in Section 3.2, and set the framed exponential

$$e_p:{\mathbb{Z}}_N⟶U_p:=\langle e_p\rangle ,e_p\left(k\right):=e_p^k.$$

Proposition 3

(Exact $U\left(1\right)$ over ${\mathbb{F}}_p$). The composite ${\Phi }_p:=e_p\circ \rho :{\mathcal{S}}_p^1\to U_p$ is a surjective group homomorphism with kernel $\mathbb{Z}\subset {\mathcal{S}}_p^1$. Hence

$$U_p\cong {\mathcal{S}}_p^1/\mathbb{Z},$$

realising $U_p$ as the exact FRC analogue of the classical circle.

Proof. 

Lemma 5.2 gives the group law, surjectivity is obvious, and $ker{\Phi }_p=\{\theta :\rho \left(\theta \right)\equiv 0\}=\mathbb{Z}$. □

5.4. Higher-Rank Tori and the Diagonal Embedding

Choose n commuting primitive roots $e_{p,1},\dots ,e_{p,n}\in {\mathbb{F}}_p^{\times }$ and write

$$T_p^{\left(n\right)}:=\left\{\mathrm{diag}\left(e_{p,1}^{k_1},\dots ,e_{p,n}^{k_n}\right)\in {\mathrm{GL}}_{\mathrm{n}}\left({\mathbb{F}}_{\mathrm{p}}\right):{\mathrm{k}}_1+\dots +{\mathrm{k}}_{\mathrm{n}}\equiv 0(mod\mathrm{N})\right\}.$$

Lemma 5.3

(Determinant-one constraint).

$$det\left(\mathrm{diag}(e_{p,1}^{k_1},\dots ,e_{p,n}^{k_n})\right)=e_{p,1}^{k_1}\dots e_{p,n}^{k_n}=1$$

iff $k_1+\dots +k_n\equiv 0(modN);$ hence $T_p^{\left(n\right)}\subset \mathrm{SU}(n,{\mathbb{F}}_p).$

Proof. 

Each $e_{p,j}$ has order N, so $e_{p,1}^{k_1}\dots e_{p,n}^{k_n}=e_p^{k_1+\dots +k_n}$. This equals 1 iff the sum of exponents is a multiple of N. □

Proposition 4

(Exact finite torus). Let $L:=\{(k_1,\dots ,k_n)\in {\mathbb{Z}}^n:k_1+\dots +k_n=0\}$. Then the product map

$${\Phi }_p^{\left(n\right)}:{\left({\mathcal{S}}_p^1\right)}^n⟶T_p^{\left(n\right)},({\theta }_1,\dots ,{\theta }_n)⟼\mathrm{diag}\left(e_{p,1}^{\rho \left({\theta }_1\right)},\dots ,e_{p,n}^{\rho \left({\theta }_n\right)}\right)$$

is a group epimorphism with kernel L. Consequently ${\left({\mathcal{S}}_p^1\right)}^n/L\cong T_p^{\left(n\right)}\subset \mathrm{SU}(n,{\mathbb{F}}_p)$, yielding an exact FRC analogue of the maximal torus in both $\mathrm{SU}\left(n\right)$ and $\mathrm{SO}\left(2n\right)$.

Proof. 

Lemma 5.2 gives homomorphism, surjectivity is component-wise. If ${\Phi }_p^{\left(n\right)}\left(\overrightarrow{\theta }\right)=I$ then each exponent $\rho \left({\theta }_j\right)=k_j$ satisfies $k_1+\dots +k_n\equiv 0$ by Lemma 5.3; hence $\overrightarrow{\theta }\in L$. The converse is immediate. □

Smooth structure inherited. Because ${\Phi }_p$ and ${\Phi }_p^{\left(n\right)}$ are internal group homomorphisms between internal $C^{\infty }$ manifolds, they are themselves $C^{\infty }$ (Lemma 5.1). Thus, the finite tori $U_p$ and $T_p^{\left(n\right)}$ carry an exact Lie-group calculus within the FRC, requiring no limit $p\to \infty$.

6. Conclusions

We have shown that every odd-prime finite field ${\mathbb{F}}_p$ already contains—in purely arithmetic guise— all the structural ingredients needed for a faithful analog of classical smooth geometry and harmonic analysis.

• Discrete-to-smooth passage. Starting from the translation-scaling orbit of ${\mathbb{F}}_p$ we constructed a regular CW complex $N_p$ that is combinatorially $S^2$. Using the pseudo-real completion $R_p$ we lifted $N_p$ to an internal $C^{\infty }$ surface $S_p\subset {\left(R_p\right)}^4$ whose hyperfinite trace is $\epsilon$-dense for every infinitesimal $\epsilon$ and whose Gaussian curvature satisfies $K\equiv 1$.
• Canonical constants. The cyclic order of ${\mathbb{F}}_p$ picks out three frame-invariant elements— the quarter-turn $i_p$, the half-period ${\pi }_p=\frac{p-1}{2}$, and the minimal-deviation base $e_p$. Together they reproduce inside ${\mathbb{F}}_p$ the algebraic rôles played by $i,\pi ,e$ in $\mathbb{C}$ and endow ${\mathcal{S}}_p$ with a built-in complex-analytic flavor.
• Unified harmonic analysis. Embedding ${\mathbb{F}}_p$ into $Rp$ and identifying $e_p$ with an infinitesimal rotation yields a single kernel that specializes both to the classical Fourier kernel on $\mathbb{R}$ and to the discrete characters on ${\mathbb{F}}_p$. Hence Fourier, convolution, Plancherel and Poisson-summation identities coexist in one frame-relative formalism.
• Gauge covariance. Every affine relabelling of the framed field extends to a diffeomorphism of ${\mathcal{S}}_p$ and permutes $i_p,{\pi }_p,e_p$ in a way that preserves their defining extremal properties; the geometry is therefore fully compatible with the relativistic-algebra principle introduced in the companion papers.
• Lie group. Inside FRC, the rounding-exponential map identifies the framed circle ${\mathcal{S}}_p^1={\mathbb{R}}_p/2{\pi }_p\mathbb{Z}$ with the cyclic unit group $U_p=\langle e_p\rangle \subset {\mathbb{F}}_p^{\times }$ up to an integral kernel, giving an exact finite analogue of the Lie group $U\left(1\right)$. Extending component-wise, ${\left({\mathcal{S}}_p^1\right)}^n/{\mathbb{Z}}^n$ realises a maximal torus in $\mathrm{SU}(n,{\mathbb{F}}_p)$, so the resultant Lie group is exact and smooth within the finite-ring continuum.

Outlook. The techniques developed here scale naturally to composite moduli q, where the orbit complex grows from the Hopf-fibered $S^3\to S^2$ picture of the prime case [21] into a full three-manifold. Perelman’s theorem [22,23] and discrete Ricci flow [24,25] then point to a canonical round metric in which the ordinary fibres remain Hopf circles, but surgery along the zero-divisor cores inserts Seifert multiplicities. In this metric the composite-modulus orbit complex of ${\mathbb{Z}}_q$ becomes a Seifert-fibered 3-orbifold [26]: its regular fibres link pairwise exactly once, as in the classical Hopf fibration, while each prime factor of q contributes an exceptional fibre whose DNA-like helix of regular fibres winds around it a number of times equal to the complementary factor; the zero-divisor seams are the axial loops of these helices. Finally, the 2-sphere base of this fibration exhibits the complete set of properties of a Bloch sphere [27,28]. These developments are the explicit subject of our companion paper [29].

By exhibiting a differential, analytic, and symmetry-rich structure generated solely from finite arithmetic data, the present article supports the thesis that finite relativistic algebra and the corresponding finite ring continuum framework can serve as a common foundation for discrete mathematics, classical analysis, and physical modelling within a single, gauge-covariant, finite universe.