Submitted:
22 May 2025
Posted:
23 May 2025
You are already at the latest version
Abstract
Keywords:
1. Motivation
2. Brief Introduction to Information Theory
2.1. Shannon Entropy
My greatest concern was what to call it. I thought of calling it ‘information’, but the word was overly used, so I decided to call it ‘uncertainty’. When I discussed it with John von Neumann, he had a better idea. Von Neumann told me, “You should call it entropy, for two reasons. In the first place your uncertainty function has been used in statistical mechanics under that name, so it already has a name. In the second place, and more important, nobody knows what entropy really is, so in a debate you will always have an advantage [63].
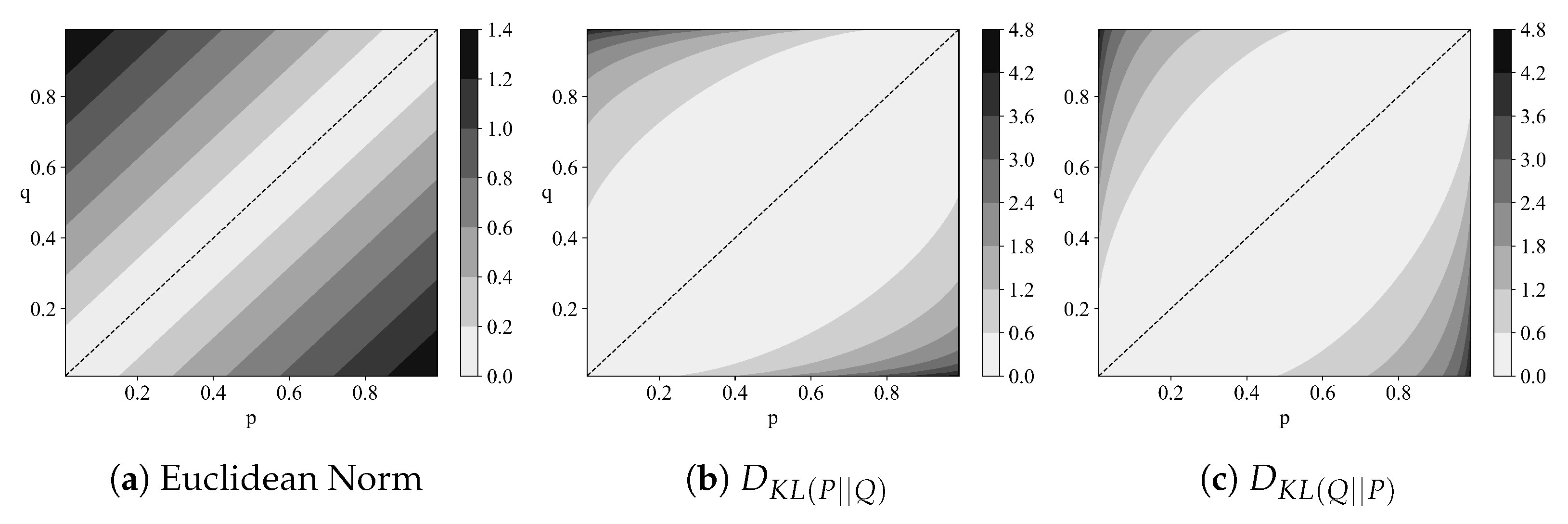
2.2. Relative Entropy
- Non-negativity:
- Identity of indiscernibles:
- Symmetry:
- Triangle inequality:
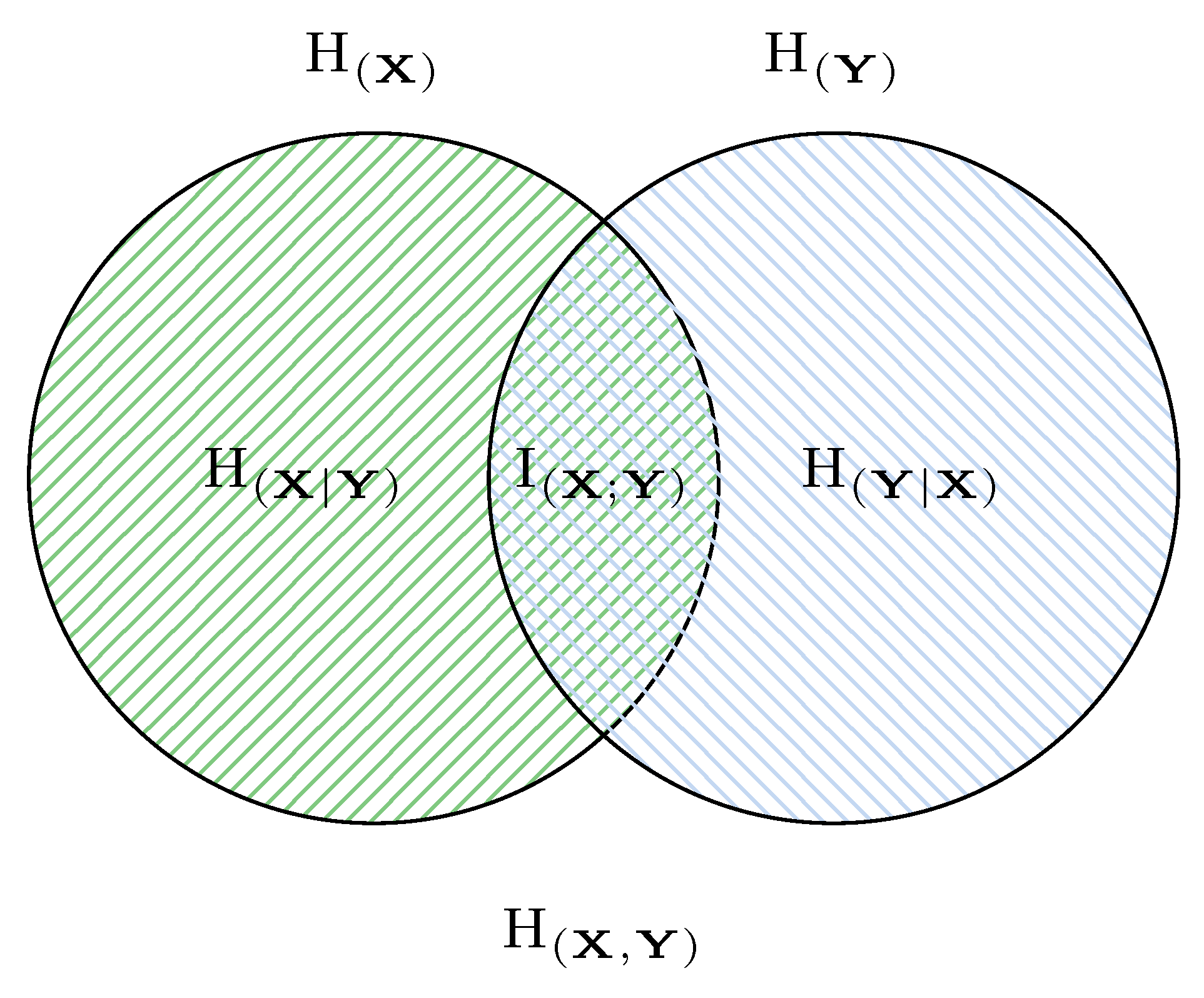
2.3. Bivariate Entropy
- The chain rule.
- Subadditivity.
- The relationship between different bivariate entropy,
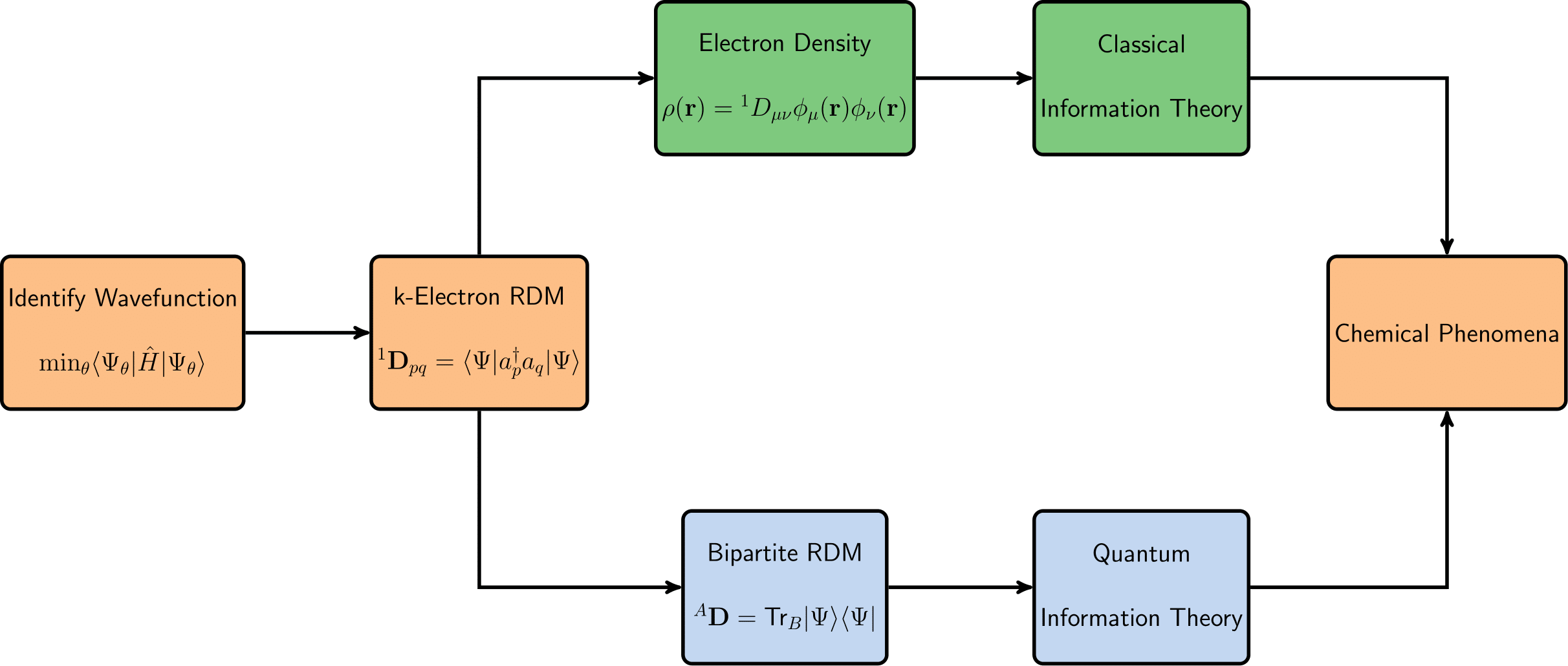
3. Basic Ingredients of Information Theory in Quantum Chemistry: Reduced Density Matrix
3.1. Density Matrix and Reduced Density Matrix
3.2. 1-RDM and 2-RDM
3.3. 3-RDM and 4-RDM
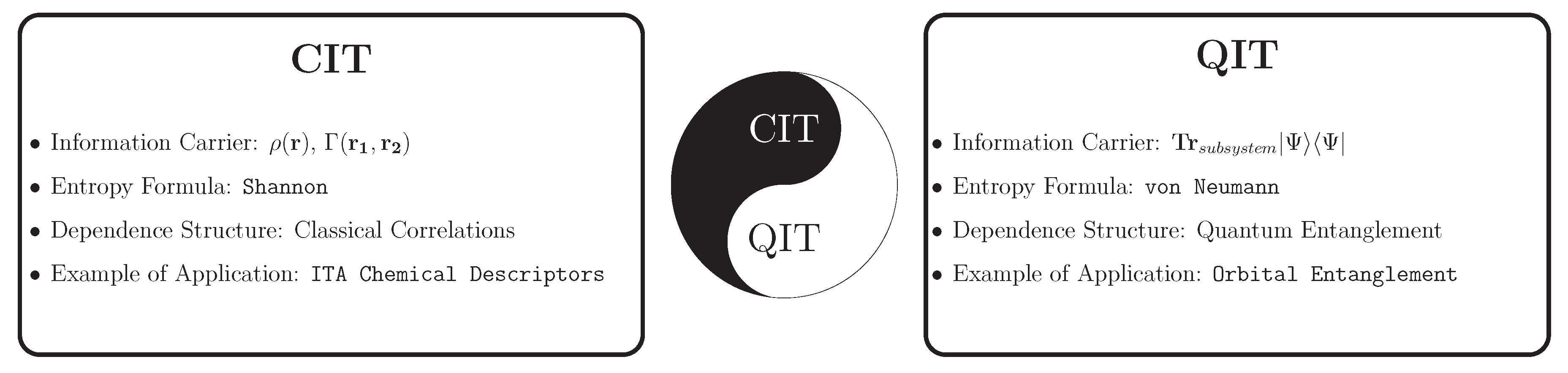
4. Classical Information Theory in Quantum Chemistry
4.1. Electron Density in Position Space
4.2. Information-Theoretic Approach Chemical Descriptors
4.2.1. Examples and Illustrations
- Global Descriptors: Assign a value to the entire system.
- Local Descriptors: Assign a value to each position in the system.
- Nonlocal Descriptors: Assign a value to each pair of positions in the system.
5. Quantum Information Theory in Quantum Chemistry
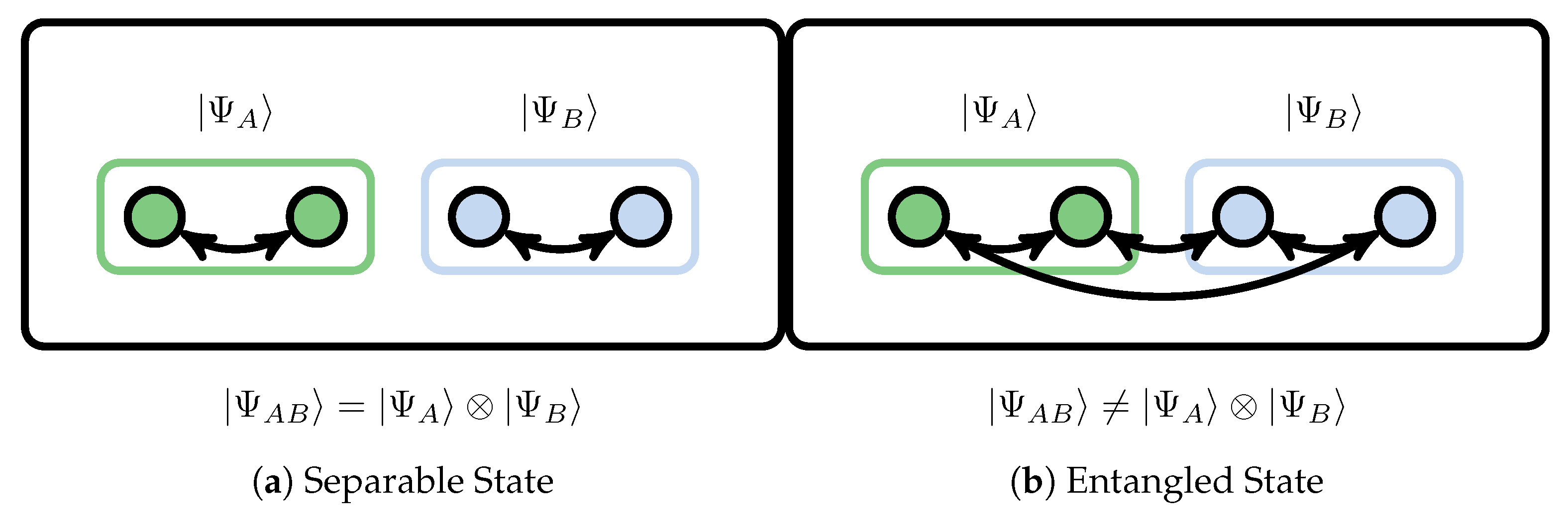
5.1. Bipartite Entanglement
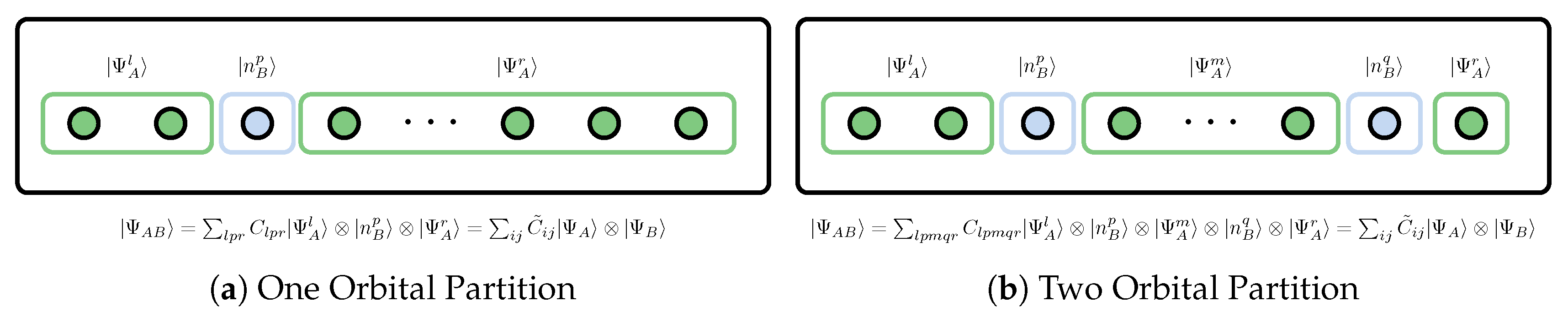
5.2. Orbital Reduced Density Matrix
5.3. Orbital Entanglement
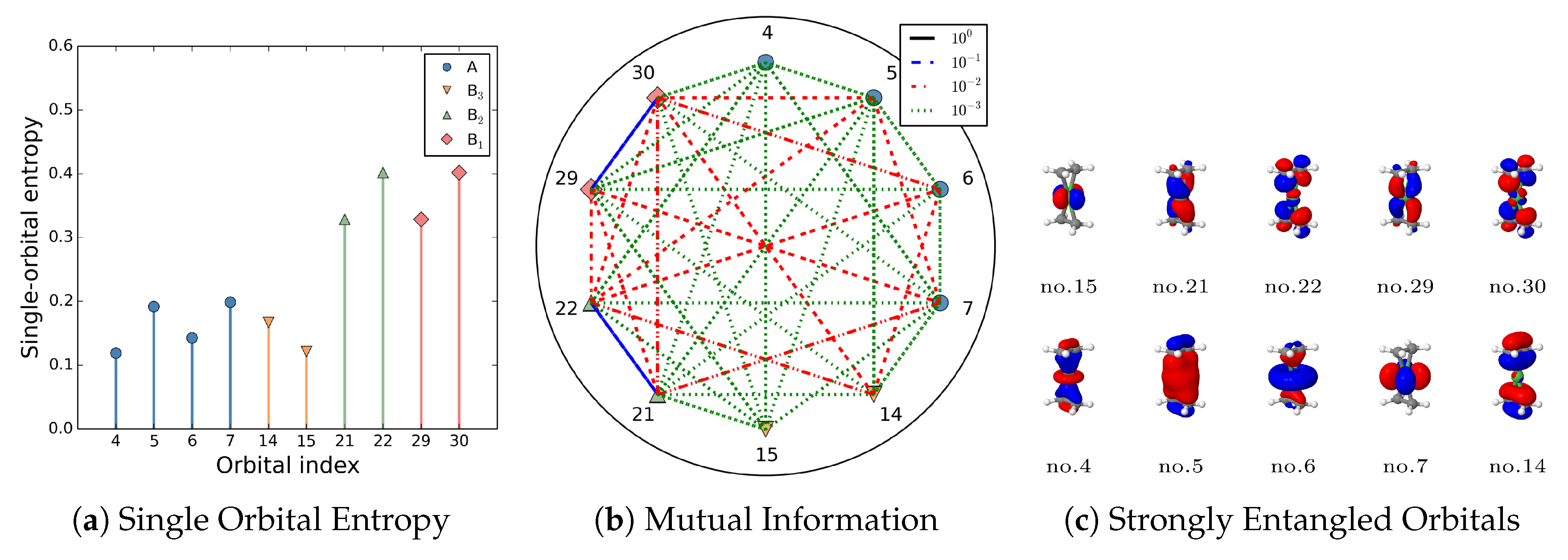
5.3.1. Examples and Illustrations
- Blue lines: Nondynamic correlated orbital pairs.
- Red lines: Static correlated orbitals.
- Green: Dynamic correlated orbitals.
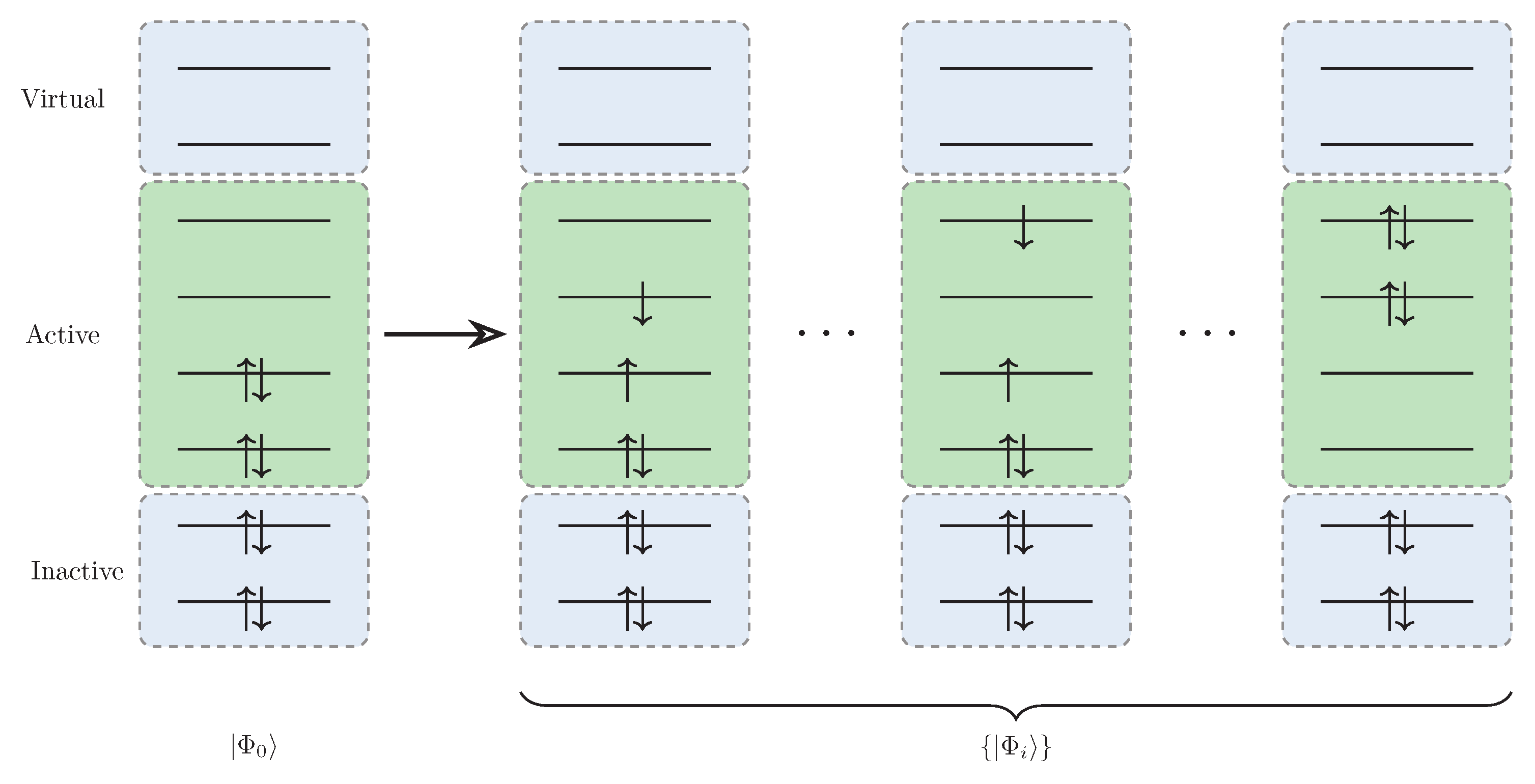
- Inactive space: Always doubly occupied.
- Active space: All the possible configurations are allowed.
- Virtual space: Always empty.
6. Summary and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Shannon entropy | |
| Relative entropy, Kullback-Leibler divergence | |
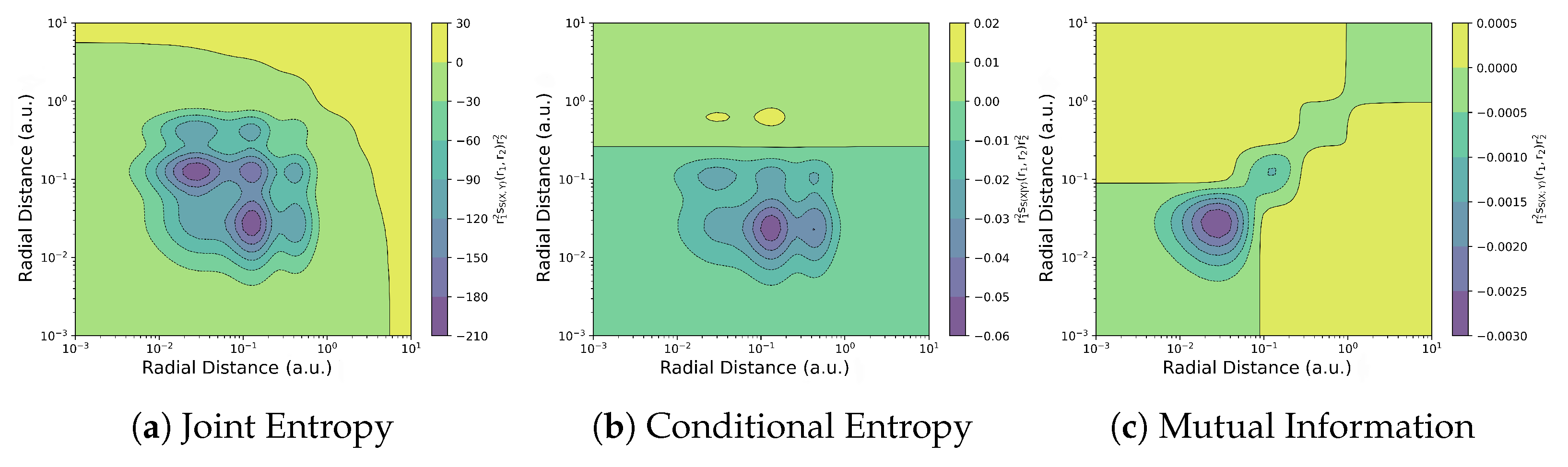
| Joint entropy | |
| Conditional entropy | |
| Mutual information | |
| Density matrix, Density operator | |
| k-Electron reduced density matrix with spin and spatial orbital | |
| Electron density at position | |
| Unit-normalized electron density (shape function) at position | |
| Pair-electron density at position and | |
| Unit-normalized pair-electron density at position and | |
| Shannon entropy with electron density | |
| Relative entropy with electron density | |
| Joint entropy with electron density | |
| Conditional entropy with electron density | |
| Mutual information with electron density | |
| k-Orbital Reduced Density Matrix | |
| One-orbital entropy | |
| Orbital relative entropy | |
| Two-orbital entropy | |
| Orbital conditional entropy | |
| Orbital mutual information |
References
- Hartley, R.V.L. Transmission of information. Bell Syst. Tech. J. 1928, 7, 535–563. [CrossRef]
- Nyquist, H. Certain factors affecting telegraph speed. Bell Syst. Tech. J. 1924, 3, 324–346. [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory, 2nd ed.; John Wiley & Sons, Ltd: New York, 2005. [CrossRef]
- Witten, E. A mini-introduction to information theory. Riv. Nuovo Cim. 2020, 43, 187–227. [CrossRef]
- Parr, R.G.; Yang, W. Density-Functional Theory of Atoms and Molecules; Oxford University Press, 1995. [CrossRef]
- Helgaker, T.; Jørgensen, P.; Olsen, J. Molecular Electronic-Structure Theory; John Wiley & Sons, Ltd, 2000. [CrossRef]
- Liu, S. Information-Theoretic Approach in Density Functional Reactivity Theory. Acta Phys. -Chim. Sin. 2016, 32, 98–118. [CrossRef]
- Wang, B.; Zhao, D.; Lu, T.; Liu, S.; Rong, C. Quantifications and Applications of Relative Fisher Information in Density Functional Theory. J. Phys. Chem. A 2021, 125, 3802–3811. [CrossRef]
- Zhao, D.; Zhao, Y.; He, X.; Li, Y.; Ayers, P.W.; Liu, S. Accurate and Efficient Prediction of Post-Hartree–Fock Polarizabilities of Condensed-Phase Systems. J. Chem. Theory Comput. 2023, 19, 6461–6470. [CrossRef]
- Zhao, D.; Zhao, Y.; He, X.; Ayers, P.W.; Liu, S. Efficient and accurate density-based prediction of macromolecular polarizabilities. Phys. Chem. Chem. Phys. 2023, 25, 2131–2141. [CrossRef]
- Zhao, D.; Zhao, Y.; Xu, E.; Liu, W.; Ayers, P.W.; Liu, S.; Chen, D. Fragment-Based Deep Learning for Simultaneous Prediction of Polarizabilities and NMR Shieldings of Macromolecules and Their Aggregates. J. Chem. Theory Comput. 2024, pp. 2655–2665. [CrossRef]
- Zhao, Y.; Zhao, D.; Liu, S.; Rong, C.; Ayers, P.W. Why are information-theoretic descriptors powerful predictors of atomic and molecular polarizabilities. J. Mol. Model. 2024, 30, 361. [CrossRef]
- Ayers, P.W.; Fias, S.; Heidar-Zadeh, F. The Axiomatic Approach to Chemical Concepts. Comput. Theor. Chem. 2018, 1142, 83–87. [CrossRef]
- Rong, C.; Zhao, D.; He, X.; Liu, S. Development and Applications of the Density-Based Theory of Chemical Reactivity. J. Phys. Chem. Lett. 2022, 13, 11191–11200. [CrossRef]
- Liu, S. Identity for Kullback-Leibler divergence in density functional reactivity theory. J. Chem. Phys. 2019, 151, 141103. [CrossRef]
- Wu, W.; Scholes, G.D. Foundations of Quantum Information for Physical Chemistry. J. Phys. Chem. Lett. 2024, 15, 4056–4069. [CrossRef]
- Materia, D.; Ratini, L.; Angeli, C.; Guidoni, L. Quantum Information reveals that orbital-wise correlation is essentially classical in Natural Orbitals, 2024. [CrossRef]
- Aliverti-Piuri, D.; Chatterjee, K.; Ding, L.; Liao, K.; Liebert, J.; Schilling, C. What can quantum information theory offer to quantum chemistry? Faraday Discuss. 2024, 254, 76–106. [CrossRef]
- Nowak, A.; Legeza, O.; Boguslawski, K. Orbital entanglement and correlation from pCCD-tailored coupled cluster wave functions. J. Chem Phys. 2021, 154, 084111. [CrossRef]
- Ding, L.; Mardazad, S.; Das, S.; Szalay, S.; Schollwöck, U.; Zimborás, Z.; Schilling, C. Concept of Orbital Entanglement and Correlation in Quantum Chemistry. J. Chem. Theory Comput. 2021, 17, 79–95. [CrossRef]
- Ratini, L.; Capecci, C.; Guidoni, L. Natural Orbitals and Sparsity of Quantum Mutual Information. J. Chem. Theory Comput. 2024, 20, 3535–3542. [CrossRef]
- Legeza, O.; Sòlyom, J. Optimizing the density-matrix renormalization group method using quantum information entropy. Phys. Rev. B 2003, 68, 195116. [CrossRef]
- Convy, I.; Huggins, W.; Liao, H.; Birgitta Whaley, K. Mutual information scaling for tensor network machine learning. Mach. Learn. Sci. Technol. 2022, 3, 015017. [CrossRef]
- Legeza, O.; Sólyom, J. Two-Site Entropy and Quantum Phase Transitions in Low-Dimensional Models. Phys. Rev. Lett. 2006, 96, 116401. [CrossRef]
- Szalay, S.; Pfeffer, M.; Murg, V.; Barcza, G.; Verstraete, F.; Schneider, R.; Legeza, O. Tensor product methods and entanglement optimization for ab initio quantum chemistry. Int. J. Quantum Chem. 2015, 115, 1342–1391. [CrossRef]
- Sears, S.B.; Parr, R.G.; Dinur, U. On the Quantum-Mechanical Kinetic Energy as a Measure of the Information in a Distribution. Isr. J. Chem. 1980, 19, 165–173. [CrossRef]
- Nalewajski, R.F.; Parr, R.G. Information theory, atoms in molecules, and molecular similarity. Proc. Natl. Acad. Sci. U.S.A. 2000, 97, 8879–8882. [CrossRef]
- Nalewajski, R.F.; Parr, R.G. Information Theory Thermodynamics of Molecules and Their Hirshfeld Fragments. J. Phys. Chem. A 2001, 105, 7391–7400. [CrossRef]
- Levine, R.D.; Bernstein, R.B. Energy disposal and energy consumption in elementary chemical reactions. Information theoretic approach. Acc. Chem. Res. 1974, 7, 393–400. [CrossRef]
- Procaccia, I.; Levine, R.D. The populations time evolution in vibrational disequilibrium: An information theoretic approach with application to HF. J. Chem Phys. 1975, 62, 3819–3820. [CrossRef]
- Dinur, U.; Kosloff, R.; Levine, R.; Berry, M. Analysis of electronically nonadiabatic chemical reactions: An information theoretic approach. Chem. Phys. Lett. 1975, 34, 199–205. [CrossRef]
- Procaccia, I.; Levine, R.D. Vibrational energy transfer in molecular collisions: An information theoretic analysis and synthesis. J. Chem Phys. 1975, 63, 4261–4279. [CrossRef]
- Levine, R.D.; Manz, J. The effect of reagent energy on chemical reaction rates: An information theoretic analysis. J. Chem Phys. 1975, 63, 4280–4303. [CrossRef]
- Levine, R.D. Entropy and macroscopic disequilibrium. II. The information theoretic characterization of Markovian relaxation processes. J. Chem Phys. 1976, 65, 3302–3315. [CrossRef]
- Levine, R.D. Information Theory Approach to Molecular Reaction Dynamics. Ann. Rev. Phys. Chem. 1978, 29, 59–92. [CrossRef]
- Slater, J.C. The Theory of Complex Spectra. Phys. Rev. 1929, 34, 1293–1322. [CrossRef]
- Hartree, D.R. Some Relations between the Optical Spectra of Different Atoms of the same Electronic Structure. II. Aluminium-like and Copper-like Atoms. Math. Proc. Camb. Phil. Soc. 1926, 23, 304–326. [CrossRef]
- Fock, V.A.Z. Näherungsmethode zur Lösung des quantenmechanischen Mehrkörperproblems. Z. Phys. 1930, 61, 126–148.
- Roothaan, C.C.J. New Developments in Molecular Orbital Theory. Rev. Mod. Phys. 1951, 23, 69–89. [CrossRef]
- Koga, T.; Tatewaki, H.; Thakkar, A.J. Roothaan-Hartree-Fock wave functions for atoms with Z≤54. Phys. Rev. A 1993, 47, 4510–4512. [CrossRef]
- Purvis, G.D.; Bartlett, R.J. A full coupled-cluster singles and doubles model: The inclusion of disconnected triples. J. Chem. Phys. 1982, 76, 1910–1918. [CrossRef]
- Shavitt, I. The history and evolution of configuration interaction. Mol. Phys. 1998, 94, 3–17. [CrossRef]
- Shavitt, I.; Bartlett, R.J. Many-Body Methods in Chemistry and Physics: Theory and Applications. Cambridge University Press 2009. [CrossRef]
- Cooper, N.R.; Leese, M.R. Configuration interaction methods in molecular quantum chemistry. J. Mol. Struct.-THEOCHEM 2000, 94, 71–78.
- Coester, F.; Kümmel, H. Short-range correlations in nuclear wave functions. Nucl. Phys. 1960, 17, 477–485. [CrossRef]
- Ahlrichs, R. Many body perturbation calculations and coupled electron pair models. Comput. Phys. Commun. 1979, 17, 31–45. [CrossRef]
- Bartlett, R.J. Many-body perturbation-theory and coupled cluster theory for electron correlation in molecules. Annu. Rev. Phys. Chem. 1981, 32, 359–401. [CrossRef]
- Bartlett, R.J.; Musiał, M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 2007, 79, 291–352. [CrossRef]
- Asadchev, A.; Gordon, M.S. Fast and Flexible Coupled Cluster Implementation. J. Chem. Theory Comput. 2013, 9, 3385–3392. [CrossRef]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618–622. [CrossRef]
- Cremer, D. Møller–Plesset perturbation theory: from small molecule methods to methods for thousands of atoms. WIREs Comput. Mol. Sci. 2011, 1, 509–530. [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [CrossRef]
- Perdew, J.P.; Schmidt, K. Jacob’s ladder of density functional approximations for the exchange-correlation energy. AIP Conf. Proc. 2001, 577, 1–20. [CrossRef]
- Engel, E.; Dreizler, R.M. Density Functional Theory: An Advanced Course; Theoretical and Mathematical Physics, Springer Berlin Heidelberg: Berlin, Heidelberg, 2011. [CrossRef]
- He, X.; Li, M.; Rong, C.; Zhao, D.; Liu, W.; Ayers, P.W.; Liu, S. Some Recent Advances in Density-Based Reactivity Theory. J. Phys. Chem. A 2024, 128, 1183–1196. [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [CrossRef]
- Onicescu, O. Theorie de l’information energie informationelle. Comptes rendus de l’Academie des Sciences Series AB 1966, 263, 841–842.
- Rényi, A. Probability theory; North-Holland: Amsterdam, 1970.
- Fisher, R.A. Theory of Statistical Estimation. Math. Proc. Cambridge Philos. Soc. 1925, 22, 700–725. [CrossRef]
- Clausius, R. The Mechanical Theory of Heat - Scholar’s Choice Edition; Creative Media Partners, LLC, 2015.
- Accardi, L. Topics in quantum probability. Physics Reports 1981, 77, 169–192. [CrossRef]
- Bengtsson, I.; Zyczkowski, K. Geometry of Quantum States: An Introduction to Quantum Entanglement; Cambridge University Press, 2006.
- Bregman, L.M. The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming. USSR Comput. Math. and Math. Phys. 1967, 7, 200–217. [CrossRef]
- Banerjee, A.; Merugu, S.; Dhillon, I.S.; Ghosh, J. Clustering with Bregman divergences. J. Mach. Learn. Res. 2005, 6, 1705–1749.
- Ali, S.M.; Silvey, S.D. A general class of coefficients of divergence of one distribution from another. J. R. Stat. Soc. Ser. B Methodol. 1966, 28, 131–142.
- Csiszár, I. Information-type measures of difference of probability distributions and indirect observations. Stud. Sci. Math. Hung. 1967, 2, 299–318.
- Liese, F.; Vajda, I. On divergences and informations in statistics and information theory. IEEE Trans. Inform. Theory 2006, 52, 4394–4412. [CrossRef]
- Kullback, S.; Leibler, R.A. On Information and Sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [CrossRef]
- Burago, D.; Burago, J.D.; Ivanov, S. A Course in Metric Geometry; American mathematical society, 2001.
- Dirac, P.A.M. Note on Exchange Phenomena in the Thomas Atom. Mathematical Proceedings of the Cambridge Philosophical Society 1930, 26, 376–385. [CrossRef]
- Mazziotti, D.A., Ed. Reduced-Density-Matrix Mechanics: With Application to Many-Electron Atoms and Molecules, 1 ed.; Vol. 134, Advances in Chemical Physics, Wiley, 2007. [CrossRef]
- Gidopoulos, N.I.; Wilson, S.; Lipscomb, W.N.; Maruani, J.; Wilson, S., Eds. The Fundamentals of Electron Density, Density Matrix and Density Functional Theory in Atoms, Molecules and the Solid State; Vol. 14, Progress in Theoretical Chemistry and Physics, Springer Netherlands: Dordrecht, 2003. [CrossRef]
- Absar, I. Reduced hamiltonian orbitals. II. Optimal orbital basis sets for the many-electron problem. Int. J. Quantum Chem. 1978, 13, 777–790. [CrossRef]
- Absar, I.; Coleman, A.J. Reduced hamiltonian orbitals. I. a new approach to the many-electron problem. Int. J. Quantum Chem. 2009, 10, 319–330. [CrossRef]
- Coleman, A.J.; Absar, I. Reduced hamiltonian orbitals. III. Unitarily invariant decomposition of hermitian operators. Int. J. Quantum Chem. 1980, 18, 1279–1307. [CrossRef]
- Mazziotti, D.A. Two-Electron Reduced Density Matrix as the Basic Variable in Many-Electron Quantum Chemistry and Physics. Chem. Rev. 2012, 112, 244–262. [CrossRef]
- Mazziotti, D.A. Parametrization of the two-electron reduced density matrix for its direct calculation without the many-electron wave function: Generalizations and applications. Phys. Rev. A 2010, 81, 062515. [CrossRef]
- Verstichel, B.; van Aggelen, H.; Van Neck, D.; Ayers, P.W.; Bultinck, P. Variational Density Matrix Optimization Using Semidefinite Programming. Comput. Phys. Commun. 2011, 182, 2025–2028. [CrossRef]
- Verstichel, B.; van Aggelen, H.; Van Neck, D.; Ayers, P.W.; Bultinck, P. Variational Determination of the Second-Order Density Matrix for the Isoelectronic Series of Beryllium, Neon, and Silicon. Phys. Rev. A 2009, 80, 032508. [CrossRef]
- Eugene DePrince III, A. Variational determination of the two-electron reduced density matrix: A tutorial review. WIREs Comput. Mol. Sci. 2024, 14, e1702. [CrossRef]
- Barcza, G.; Legeza, O.; Marti, K.H.; Reiher, M. Quantum-Information Analysis of Electronic States of Different Molecular Structures. Phys. Rev. A 2011, 83, 012508. [CrossRef]
- Szalay, S.; Barcza, G.; Szilvasi, T.; Veis, L.; Legeza, O. The Correlation Theory of the Chemical Bond. Sci. Rep. 2017, 7, 2237. [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information: 10th Anniversary Edition; Cambridge University Press, 2010. [CrossRef]
- Kubo, R. Generalized Cumulant Expansion Method. Journal of the Physical Society of Japan 1962, 17, 1100–1120. [CrossRef]
- Ziesche, P. Cumulant Expansions of Reduced Densities, Reduced Density Matrices, and Green’s Functions. In Many-Electron Densities and Reduced Density Matrices; Cioslowski, J., Ed.; Kluwer: New York, 2000; pp. 33–56.
- Alcoba, D.R.; Valdemoro, C. Family of modified-contracted Schrödinger equations. Phys. Rev. A 2001, 64, 062105. [CrossRef]
- Valdemoro, C.; Alcoba, D.R.; Tel, L.M.; Perez-Romero, E. Imposing Bounds on the High-Order Reduced Density Matrices Elements. Int. J. Quantum Chem. 2001, 85, 214–224. [CrossRef]
- Valdemoro, C. Spin-Adapted Reduced Hamiltonians 2. Total Energy and Reduced Density Matrices. Phys. Rev. A 1985, 31, 2123–2128. [CrossRef]
- Valdemoro, C. Spin-Adapted Reduced Hamiltonians. 1. Elementary Excitations. Phys. Rev. A 1985, 31, 2114–2122. [CrossRef]
- Mazziotti, D.A. Contracted Schrödinger equation: Determining quantum energies and two-particle density matrices without wave functions. Phys. Rev. A 1998, 57, 4219–4234. [CrossRef]
- Kutzelnigg, W.; Mukherjee, D. Cumulant expansion of the reduced density matrices. J. Chem Phys. 1999, 110, 2800–2809. [CrossRef]
- Kutzelnigg, W.; Mukherjee, D. Irreducible Brillouin conditions and contracted Schrödinger equations for n-electron systems. II. Spin-free formulation. J. Chem Phys. 2002, 116, 4787–4801. [CrossRef]
- Kutzelnigg, W.; Mukherjee, D. Irreducible Brillouin conditions and contracted Schrödinger equations for n-electron systems. III. Systems of noninteracting electrons. J. Chem Phys. 2004, 120, 7340–7349. [CrossRef]
- Mukherjee, D.; Kutzelnigg, W. Irreducible Brillouin conditions and contracted Schrödinger equations for n-electron systems. I. The equations satisfied by the density cumulants. J. Chem Phys. 2001, 114, 2047–2061. [CrossRef]
- Nooijen, M.; Wladyslawski, M.; Hazra, A. Cumulant approach to the direct calculation of reduced density matrices: A critical analysis. J. Chem. Phys. 2003, 118, 4832–4848. [CrossRef]
- Levy, M. Universal Variational Functionals of Electron-Densities, 1st- Order Density-Matrices, and Natural Spin-Orbitals and Solution of the V-Representability Problem. Proc. Natl. Acad. Sci. U.S.A. 1979, 76, 6062–6065. [CrossRef]
- Kohn, W.; Becke, A.D.; Parr, R.G. Density Functional Theory of Electronic Structure. J. Phys. Chem. 1996, 100, 12974–12980. [CrossRef]
- Ayers, PW. Axiomatic Formulations of the Hohenberg-Kohn Functional. Phys. Rev. A 2006, 73. [CrossRef]
- Ayers, P.W. Using classical many-body structure to determine electronic structure: An approach using k-electron distribution functions. Phys. Rev. A 2006, 74, 042502. [CrossRef]
- Ziesche, P. Attempts toward a pair density functional theory. International Journal of Quantum Chemistry 1996, 60, 1361–1374. [CrossRef]
- Ziesche, P. Pair density functional theory — a generalized density functional theory. Physics Letters A 1994, 195, 213–220. [CrossRef]
- Nagy, Á. Pair Density Functional Theory. In Proceedings of the The Fundamentals of Electron Density, Density Matrix and Density Functional Theory in Atoms, Molecules and the Solid State; Gidopoulos, N.I.; Wilson, S., Eds., Dordrecht, 2003; pp. 79–87. [CrossRef]
- Nagy, Á. Spherically and system-averaged pair density functional theory. J. Phys. Chem. 2006, 125, 184104. [CrossRef]
- Nagy, Á. Time-Dependent Pair Density from the Principle of Minimum Fisher Information. J. Mol. Model. 2018, 24, 234. [CrossRef]
- Levy, M.; Ziesche, P. The pair density functional of the kinetic energy and its simple scaling property. J. Chem. Phys. 2001, 115, 9110–9112. [CrossRef]
- Ayers, P.W.; Levy, M. Generalized Density-Functional Theory: Conquering the N-representability Problem with Exact Functionals for the Electron Pair Density and the Second-Order Reduced Density Matrix. J. Chem. Sci. 2005, 117, 507–514. [CrossRef]
- Chakraborty, D.; Ayers, P.W. Derivation of Generalized von Weizsäcker Kinetic Energies from Quasiprobability Distribution Functions. In Statistical Complexity: Applications in Electronic Structure; Sen, K.D., Ed.; Springer: New York, 2011; pp. 35–48. [CrossRef]
- Cuevas-Saavedra, R.; Ayers, P.W. Coordinate scaling of the kinetic energy in pair density functional theory: A Legendre transform approach. Int. J. Quantum Chem. 2009, 109, 1699–1705. [CrossRef]
- Ayers, P.W. Generalized Density Functional Theories Using the K-Electron Densities: Development of Kinetic Energy Functionals. J. Math. Phys. 2005, 46, 062107. [CrossRef]
- Ayers, P.W.; Golden, S.; Levy, M. Generalizations of the Hohenberg-Kohn Theorem: I. Legendre Transform Constructions of Variational Principles for Density Matrices and Electron Distribution Functions. J. Chem. Phys. 2006, 124, 054101. [CrossRef]
- Ayers, P.W.; Davidson, E.R., Linear Inequalities for Diagonal Elements of Density Matrices. In Reduced-Density-Matrix Mechanics: With Application to Many-Electron Atoms and Molecules; John Wiley & Sons, Ltd, 2007; chapter 16, pp. 443–483. [CrossRef]
- Keyvani, Z.A.; Shahbazian, S.; Zahedi, M. To What Extent are “Atoms in Molecules” Structures of Hydrocarbons Reproducible from the Promolecule Electron Densities? Chem. Eur. J. 2016, 22, 5003–5009. [CrossRef]
- Spackman, M.A.; Maslen, E.N. Chemical properties from the promolecule. J. Phys. Chem. 1986, 90, 2020–2027. [CrossRef]
- Hirshfeld, F.L. Bonded-Atom Fragments for Describing Molecular Charge Densities. Theor. Chim. Act. 1977, 44, 129–138. [CrossRef]
- Hirshfeld, F.L. XVII. Spatial Partitioning of Charge Density. Isr. J. Chem. 1977, 16, 198–201. [CrossRef]
- Heidar-Zadeh, F.; Ayers, P.W. Generalized Hirshfeld Partitioning with Oriented and Promoted Proatoms. Acta Phys. -Chim. Sin. 2018, 34, 514–518. [CrossRef]
- Nalewajski, R.F.; Switka, E. Information Theoretic Approach to Molecular and Reactive Systems. Phys. Chem. Chem. Phys. 2002, 4, 4952–4958. [CrossRef]
- Nalewajski, R.F. Information Principles in the Theory of Electronic Structure. Chem. Phys. Lett. 2003, 372, 28–34. [CrossRef]
- Nagy, A.; Romera, E. Relative Rényi entropy and fidelity susceptibility. Europhys. Lett. 2015, 109, 60002. [CrossRef]
- Nagy, A. Relative information in excited-state orbital-free density functional theory. Int. J. Quantum Chem. 2020, 120, e26405. [CrossRef]
- Laguna, H.G.; Salazar, S.J.C.; Sagar, R.P. Entropic Kullback-Leibler Type Distance Measures for Quantum Distributions. Int. J. Quantum Chem. 2019, 119, e25984. [CrossRef]
- Borgoo, A.; Jaque, P.; Toro-Labbe, A.; Van Alsenoy, C.; Geerlings, P. Analyzing Kullback-Leibler Information Profiles: An Indication of Their Chemical Relevance. Phys. Chem. Chem. Phys. 2009, 11, 476–482. [CrossRef]
- Parr, R.G.; Bartolotti, L.J. Some remarks on the density functional theory of few-electron systems. J. Phys. Chem. 1983, 87, 2810–2815. [CrossRef]
- Ayers, P.W. Density per particle as a descriptor of Coulombic systems. Proc. Natl. Acad. Sci. U.S.A. 2000, 97, 1959–1964. [CrossRef]
- Ayers, P.W. Information Theory, the Shape Function, and the Hirshfeld Atom. Theor. Chem. Acc. 2006, 115, 370–378. [CrossRef]
- Ayers, P.W.; Cedillo, A. The Shape Function. In Chemical Reactivity Theory: A Density Functional View; Chattaraj, P.K., Ed.; Taylor and Francis: Boca Raton, 2009; chapter 19, p. 269. [CrossRef]
- Noorizadeh, S.; Shakerzadeh, E. Shannon entropy as a new measure of aromaticity, Shannon aromaticity. Phys. Chem. Chem. Phys. 2010, 12, 4742–4749. [CrossRef]
- Donghai, Y. Studying on Aromaticity using Information-Theoretic Approach in Density Functional Reactivity Theory. PhD thesis, Hunan Normal University, 2019.
- Li, M.; Wan, X.; Rong, C.; Zhao, D.; Liu, S. Directionality and additivity effects of molecular acidity and aromaticity for substituted benzoic acids under external electric fields. Phys. Chem. Chem. Phys. 2023, 25, 27805–27816. [CrossRef]
- Cao, X.; Rong, C.; Zhong, A.; Lu, T.; Liu, S. Molecular acidity: An accurate description with information-theoretic approach in density functional reactivity theory. J. Comput. Chem. 2018, 39, 117–129. [CrossRef]
- Yu, D.; Rong, C.; Lu, T.; De Proft, F.; Liu, S. Baird’s Rule in Substituted Fulvene Derivatives: An Information-Theoretic Study on Triplet-State Aromaticity and Antiaromaticity. ACS Omega 2018, 3, 18370–18379. [CrossRef]
- Yu, D.; Stuyver, T.; Rong, C.; Alonso, M.; Lu, T.; De Proft, F.; Geerlings, P.; Liu, S. Global and local aromaticity of acenes from the information-theoretic approach in density functional reactivity theory. Phys. Chem. Chem. Phys. 2019, 21, 18195–18210. [CrossRef]
- Rong, C.; Wang, B.; Zhao, D.; Liu, S. Information-theoretic approach in density functional theory and its recent applications to chemical problems. WIREs Comput. Mol. Sci. 2020, 10, e1461. [CrossRef]
- Liu, S. On the relationship between densities of Shannon entropy and Fisher information for atoms and molecules. J. Chem. Phys. 2007, 126, 191107. [CrossRef]
- Heidar Zadeh, F.; Fuentealba, P.; Cárdenas, C.; Ayers, P.W. An information-theoretic resolution of the ambiguity in the local hardness. Phys. Chem. Chem. Phys. 2014, 16, 6019–6026. [CrossRef]
- Heidar-Zadeh, F.; Ayers, P.W.; Verstraelen, T.; Vinogradov, I.; Vöhringer-Martinez, E.; Bultinck, P. Information-Theoretic Approaches to Atoms-in-Molecules: Hirshfeld Family of Partitioning Schemes. J. Phys. Chem. A 2018, 122, 4219–4245. [CrossRef]
- Tehrani, A.; Anderson, J.S.M.; Chakraborty, D.; Rodriguez-Hernandez, J.I.; Thompson, D.C.; Verstraelen, T.; Ayers, P.W.; Heidar-Zadeh, F. An information-theoretic approach to basis-set fitting of electron densities and other non-negative functions. J. Comput. Chem. 2023, 44, 1998–2015. [CrossRef]
- and, R.F.N. On phase/current components of entropy/information descriptors of molecular states. Mol. Phys. 2014, 112, 2587–2601. [CrossRef]
- Nalewajski, R. Phase/current information descriptors and equilibrium states in molecules. Int. J. Quantum Chem. 2014, 115, 1274–1288. [CrossRef]
- Nalewajski, R.F. Resultant Information Description of Electronic States and Chemical Processes. J. Phys. Chem. A 2019, 123, 9737–9752. [CrossRef]
- Nalewajski, R.F. Information-Theoretic Descriptors of Molecular States and Electronic Communications between Reactants. Entropy 2020, 22. [CrossRef]
- Nalewajski, R.F. Information origins of the chemical bond: Bond descriptors from molecular communication channels in orbital resolution. Int. J. Quantum Chem. 2009, 109, 2495–2506. [CrossRef]
- Wang, B.; Rong, C.; Chattaraj, P.K.; Liu, S. A comparative study to predict regioselectivity, electrophilicity and nucleophilicity with Fukui function and Hirshfeld charge. Theor Chem Acc 2019, 138. [CrossRef]
- Liu, S.; Rong, C.; Lu, T. Information Conservation Principle Determines Electrophilicity, Nucleophilicity, and Regioselectivity. J. Phys. Chem. A 2014, 118, 3698–3704. [CrossRef]
- Liu, S. Quantifying Reactivity for Electrophilic Aromatic Substitution Reactions with Hirshfeld Charge. J. Phys. Chem. A 2015, 119, 3107–3111. [CrossRef]
- Zou, X.; Rong, C.; Lu, T.; Liu, S. Hirshfeld Charge as a Quantitative Measure of Electrophilicity and Nucleophilicity: Nitrogen-Containing Systems. Acta Phys. -Chim. Sin. 2014, 30, 2055–2062. [CrossRef]
- Zhou, X.Y.; Rong, C.; Lu, T.; Zhou, P.; Liu, S. Information Functional Theory: Electronic Properties as Functionals of Information for Atoms and Molecules. J. Phys. Chem. A 2016, 120, 3634–3642. [CrossRef]
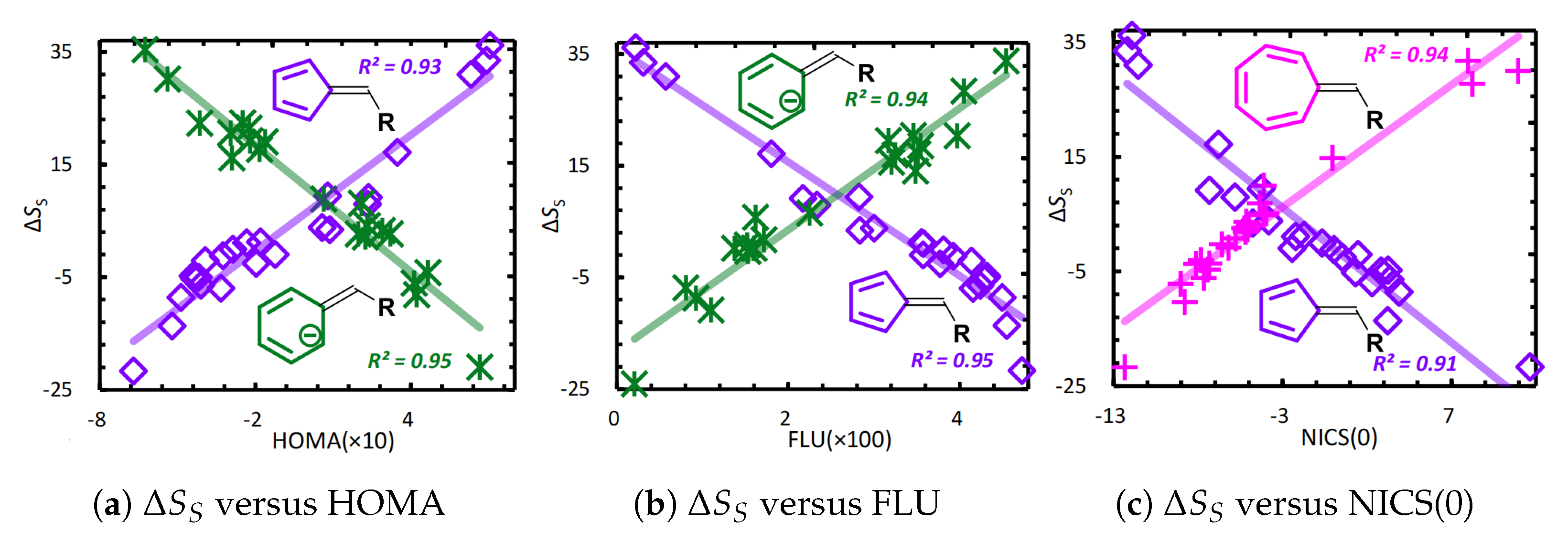
- Kruszewski, J.; Krygowski, T. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett. 1972, 13, 3839–3842. [CrossRef]
- Krygowski, T.M. Crystallographic studies of inter- and intramolecular interactions reflected in aromatic character of .pi.-electron systems. J. Chem. Inf. Comput. Sci. 1993, 33, 70–78. [CrossRef]
- Matito, E.; Duran, M.; Sola , M. The aromatic fluctuation index (FLU): A new aromaticity index based on electron delocalization. J. Chem Phys. 2004, 122, 014109. [CrossRef]
- Schleyer, P.v.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-Independent Chemical Shifts: A Simple and Efficient Aromaticity Probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [CrossRef]
- Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.v.R. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. [CrossRef]
- Zhao, Y.; Zhao, D.; Liu, S.; Rong, C.; Ayers, P.W. Extending the information-theoretic approach from the (one) electron density to the pair density. J. Chem Phys. 2025. Accepted for publication.
- Sagar, R.P.; Guevara, N.L. Mutual information and correlation measures in atomic systems. J. Chem Phys. 2005, 123, 044108. [CrossRef]
- Heinosaari, T.; Ziman, M. The Mathematical Language of Quantum Theory: From Uncertainty to Entanglement, 1 ed.; Cambridge University Press, 2011. [CrossRef]
- Bengtsson, I.; Życzkowski, K. Geometry of Quantum States: An Introduction to Quantum Entanglement, 2 ed.; Cambridge University Press: Cambridge, 2017. [CrossRef]
- Ciarlet, P.G.; Lions, J.L. In Computational Chemistry: Reviews of Current Trends. In Computational Chemistry: Reviews of Current Trends; North-Holland, 2003.
- Reed, M.; Simon, B. Methods of Modern Mathematical Physics. IV, Analysis of Operators; Academic Press: London, 1978.
- Yserentant, H. On the regularity of the electronic Schrödinger equation in Hilbert spaces of mixed derivatives. Numer. Math. 2004, 98, 731–759. [CrossRef]
- Islam, R.; Ma, R.; Preiss, P.M.; Eric Tai, M.; Lukin, A.; Rispoli, M.; Greiner, M. Measuring entanglement entropy in a quantum many-body system. Nature 2015, 528, 77–83. [CrossRef]
- Rissler, J.; Noack, R.M.; White, S.R. Measuring orbital interaction using quantum information theory. Chem. Phys. 2006, 323, 519–531. [CrossRef]
- Mazziotti, D.A. Entanglement, Electron Correlation, and Density Matrices, 1 ed.; Vol. 134, Wiley, 2007; pp. 493–535. [CrossRef]
- Boguslawski, K.; Tecmer, P.; Legeza, O.; Reiher, M. Entanglement Measures for Single- and Multireference Correlation Effects. J. Phys. Chem. Lett. 2012, 3, 3129–3135. [CrossRef]
- Boguslawski, K.; Tecmer, P. Orbital entanglement in quantum chemistry. Int. J. Quantum Chem. 2015, 115, 1289–1295. [CrossRef]
- Zhao, Y.; Boguslawski, K.; Tecmer, P.; Duperrouzel, C.; Barcza, G.; Legeza, O.; Ayers, P.W. Dissecting the bond-formation process of d 10-metal–ethene complexes with multireference approaches. Theor. Chem. Acc. 2015, 134, 120. [CrossRef]
- Duperrouzel, C.; Tecmer, P.; Boguslawski, K.; Barcza, G.; Örs Legeza.; Ayers, P.W. A quantum informational approach for dissecting chemical reactions. Chem. Phys. Lett. 2015, 621, 160–164. [CrossRef]
- Boguslawski, K.; Tecmer, P.; Legeza, O. Analysis of two-orbital correlations in wave functions restricted to electron-pair states. Phys. Rev. B 2016, 94, 155126. [CrossRef]
- Boguslawski, K.; Réal, F.; Tecmer, P.; Duperrouzel, C.; Pereira Gomes, A.S.; Legeza, Ö.; W. Ayers, P.; Vallet, V. On the multi-reference nature of plutonium oxides: PuO22+, PuO2, PuO3 and PuO2(OH)2. Phys. Chem. Chem. Phys. 2017, 19, 4317–4329. [CrossRef]
- Brandejs, J.; Veis, L.; Szalay, S.; Barcza, G.; Pittner, J.; Legeza, Ö. Quantum information-based analysis of electron-deficient bonds. J. Chem. Phys. 2019, 150, 204117. [CrossRef]
- White, S.R. Density matrix formulation for quantum renormalization groups. Phys. Rev. Lett. 1992, 69, 2863–2866. [CrossRef]
- White, S.R. Density-matrix algorithms for quantum renormalization groups. Phys. Rev. B 1993, 48, 10345–10356. [CrossRef]
- White, S.R.; Martin, R.L. Ab initio quantum chemistry using the density matrix renormalization group. J. Chem. Phys. 1999, 110, 4127–4130. [CrossRef]
- Fiedler, M. Algebraic connectivity of graphs. Czech. Math. J. 1973, 23, 298–305.
- Fiedler, M. A property of eigenvectors of nonnegative symmetric matrices and its application to graph theory. Czech. Math. J. 1975, 25, 619–633.
- Levine, B.G.; Durden, A.S.; Esch, M.P.; Liang, F.; Shu, Y. CAS without SCF—Why to use CASCI and where to get the orbitals. J. Chem Phys. 2021, 154, 090902. [CrossRef]
| - | ||||
|---|---|---|---|---|
| – | 0 | 0 | 0 | |
| 0 | 0 | 0 | ||
| 0 | 0 | 0 | ||
| 0 | 0 | 0 |
| – |
|
|
|
|
|
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| – | 1,1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 2,2 | 2,3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 3,2 | 3,3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 4,4 | 4,5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 5,4 | 5,5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
|
|
0 | 0 | 0 | 0 | 0 | 6,6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
|
|
0 | 0 | 0 | 0 | 0 | 0 | 7,7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 8,8 | 8,9 | 8,10 | 8,11 | 0 | 0 | 0 | 0 | 0 | |
|
|
0 | 0 | 0 | 0 | 0 | 0 | 0 | 9,8 | 9,9 | 9,10 | 9,11 | 0 | 0 | 0 | 0 | 0 |
|
|
0 | 0 | 0 | 0 | 0 | 0 | 0 | 10,8 | 10,9 | 10,10 | 10,11 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 11,8 | 11,9 | 11,10 | 11,11 | 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 12,12 | 12,13 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 13,12 | 13,13 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 14,14 | 14,15 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15,14 | 15,15 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 16,16 |
| Correlation Effects | Intensity | ||
|---|---|---|---|
| Nondynamic | Strong | >0.5 | |
| Static | Medium | 0.5-0.1 | |
| Dynamic | Weak | <0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





