Epistemic Gauge Theory: Emergence of U(1) Interactions from Agent Based Inference Dynamics

1. Introduction

Agent-based models have proven to be powerful tools across diverse domains, from economics and social dynamics to machine learning, cognition, and artificial intelligence [1,4,10,19,22]. In these contexts, agents are typically endowed with beliefs, preferences, and decision-making capabilities, allowing researchers to model systems where cognition, learning, and adaptation play central roles. In contrast, the study of physical systems has traditionally eschewed such subjective elements, focusing instead on the dynamics of inanimate matter governed by fundamental laws. Meanwhile, cognitive scientists, philosophers, and others have found that human perception is largely an evolutionarily constructed subjective perception aimed at maintaining organism stability and survival [1,2,3,5]. In this view space, time, and physical properties are not fundamental to our universe but instead comprise useful constructions for adaptability and survival.

Thus there exists a great, but largely unspoken, tension between the field of physics and the field of cognition, philosophy, and neuroscience. Despite remarkable advances in both domains, efforts to place the observer within the formalism of physical theory — especially in the context of quantum mechanics — remain fraught with ambiguity. The measurement problem, the role of the observer in quantum theory, and many more challenges remain unresolved after more than a century of scrutiny [7,8,9,11,20].

In this work, our aim is to bridge this divide by proposing a minimal agent-based framework in which cognition is not an emergent afterthought but a central and generative component. We formulate this theory by modeling agents as local sections of associated bundles whose fibers encode beliefs and generative models. By introducing a generalized variational energy functional that governs agent interactions, we show that the resulting epistemic dynamics naturally give rise to an emergent global $U\left(1\right)$ gauge structure. Agents pull back geometric structures such as the Fisher information metric, variational energy gradients, and observational data from the recognition bundle onto the base manifold, thereby encoding subjective inference in a manner grounded in objective structure.

2. Materials and Methods

We take the following as axioms of our framework:

1. Let $\pi :\mathcal{N}\to \mathcal{C}$ be a smooth principal G-bundle where $\mathcal{C}$ is a smooth manifold, G is a Lie group acting freely and transitively on the right on $\mathcal{N}$. The projection satisfies $\pi (n·g)=\pi \left(n\right)$ for all $g\in G,n\in \mathcal{N}$.

2. Let $\rho :G\to \mathrm{Aut}\left({\mathcal{B}}_q\right)$ be a representation of G on a smooth manifold or vector space ${\mathcal{B}}_q$ called the recognition or belief fiber. Then the associated recognition bundle to $\mathcal{N}$ is defined as:

$${\mathcal{E}}_q:=\mathcal{N}{\times }_{\rho }{\mathcal{B}}_q=(\mathcal{N}\times {\mathcal{B}}_q)/\sim ,$$

where

$$(n·g,v)\sim (n,\rho (g\left)v\right).$$

This gives a fiber bundle ${\pi }_{{\mathcal{E}}_q}:{\mathcal{E}}_q\to \mathcal{C}$ with fiber ${\mathcal{B}}_q$.

3. We define a second associated bundle ${\mathcal{E}}_p$ in the same manner we call the "model bundle" with fiber ${\mathcal{B}}_p$. ${\mathcal{B}}_q$ and ${\mathcal{B}}_p$ are manifolds of probability distributions or model parameters and do not necessarily comprise a vector space.

4. An agent is a pair of local sections ${\mathcal{A}}^i=({\sigma }_q^i\left(c\right),{\sigma }_p^i\left(c\right))$ over $\mathcal{C}$

$${\sigma }_q^i:{\mathcal{U}}_i\subset \mathcal{C}\to {\mathcal{B}}_q,$$

$${\sigma }_p^i:{\mathcal{U}}_i\subset \mathcal{C}\to {\mathcal{B}}_p.$$

6. There exists a generalized functional on the sections we call variational energy such that

$${\displaystyle \frac{\partial q}{\partial t}}=-{\displaystyle \frac{\delta V}{\delta t}},$$

determines the dynamics of agents.

7. A multi-agent ($\mathcal{M}$) over $\mathcal{C}$ is a tuple of agents (where $\mathcal{I}$ is an index set)

$$\mathcal{M}={\{A^i=({\sigma }_q^i\left(c\right),{\sigma }_p^i\left(c\right))\}}_{i\in \mathcal{I}}.$$

8. A scale-dependent agent is a multi-agent whose agents share the same generative models.

9. An observation/observable is a local section of ${\mathcal{B}}_q$

$${\mathcal{O}}_q:\mathcal{U}\subset \mathcal{C}\to {\mathcal{B}}_q.$$

This is similar to an agent, but does not require a section over ${\mathcal{B}}_p$.

Next, in the standard way [13], via horizontal lifting from $\mathcal{N}$ to ${\mathcal{E}}_i$, we may construct a variety of morphisms and induced connections across scales $(i,j)$:

• ${\mathrm{\Omega }}^i:\mathrm{\Gamma }\left({\mathcal{B}}_q\right)\to \mathrm{\Gamma }\left({\mathcal{B}}_q\right)$ ;
• ${\tilde{\mathrm{\Omega }}}^i:\mathrm{\Gamma }\left({\mathcal{B}}_p\right)\to \mathrm{\Gamma }\left({\mathcal{B}}_p\right)$ ;
• ${\Lambda }_j^i:\mathrm{\Gamma }\left({\mathcal{B}}_q\right)\to \mathrm{\Gamma }\left({\mathcal{B}}_q\right)$ ;
• ${\tilde{\Lambda }}_j^i:\mathrm{\Gamma }\left({\mathcal{B}}_p\right)\to \mathrm{\Gamma }\left({\mathcal{B}}_p\right)$;
• ${\Theta }_j^i:\mathrm{\Gamma }\left({\mathcal{B}}_q\right)\to \mathrm{\Gamma }\left({\mathcal{B}}_p\right)$;
• ${\tilde{\Theta }}_j^i:\mathrm{\Gamma }\left({\mathcal{B}}_p\right)\to \mathrm{\Gamma }\left({\mathcal{B}}_q\right)$;
• $\mathrm{\Phi }:{\mathcal{E}}_p\to {\mathcal{E}}_q$;
• $\tilde{\mathrm{\Phi }}:{\mathcal{E}}_q\to {\mathcal{E}}_p$.

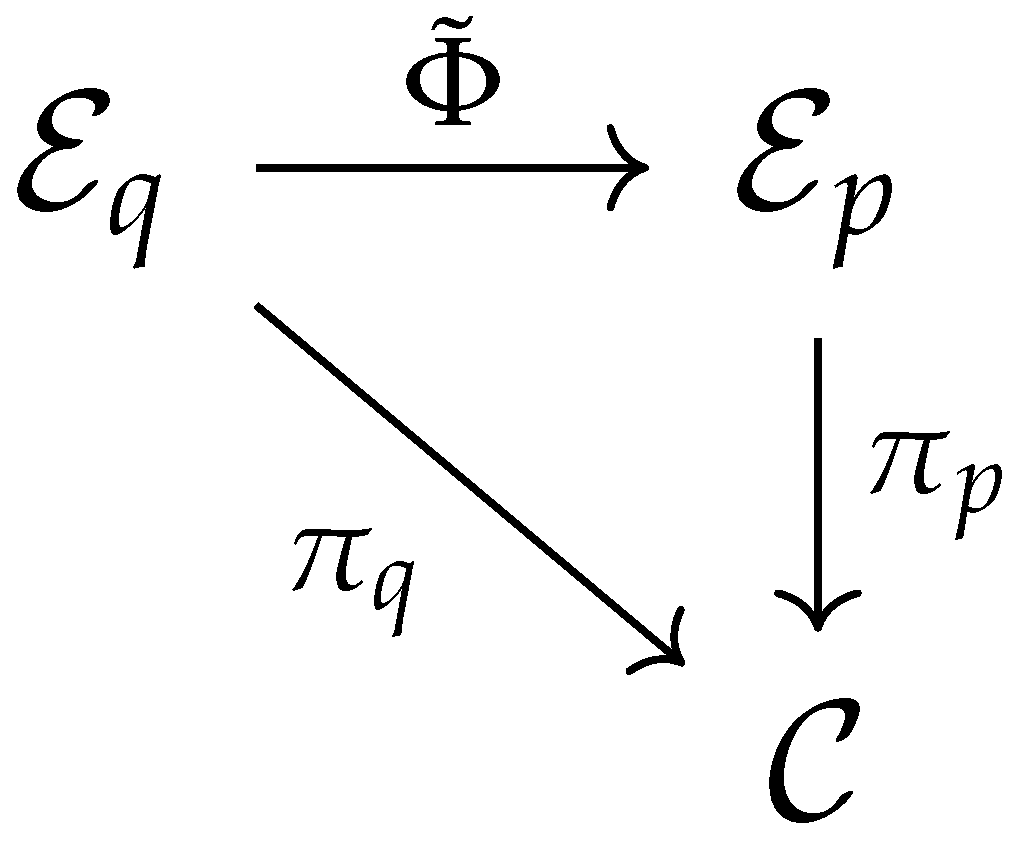
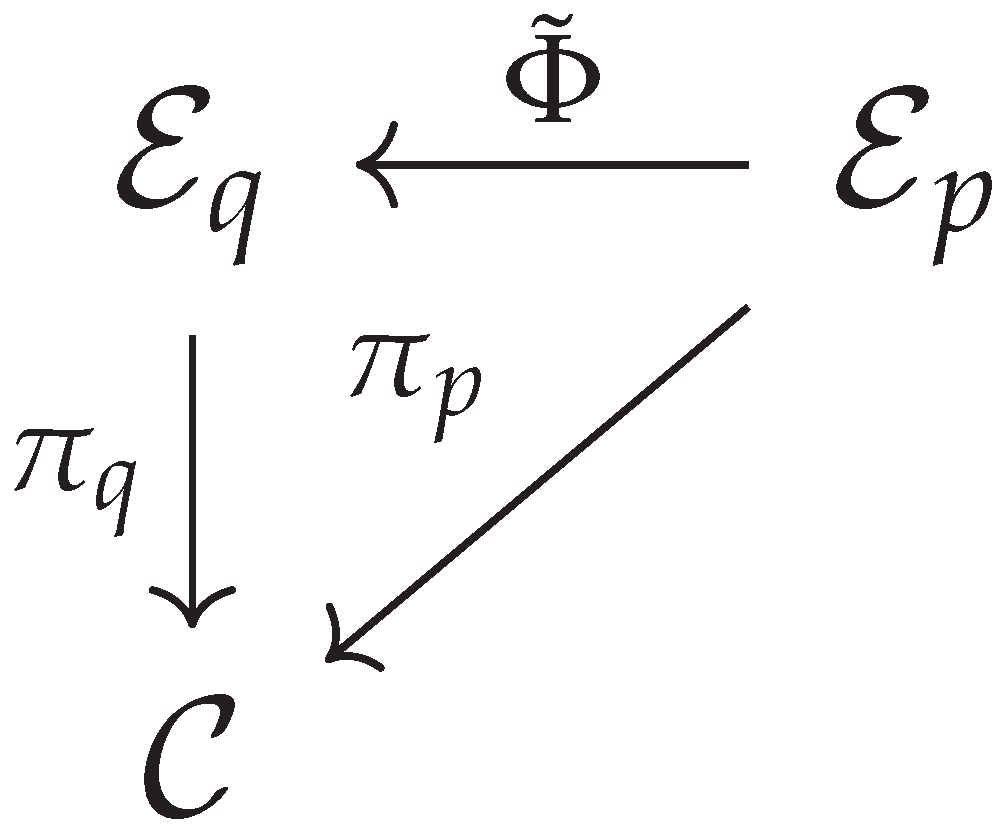
The two bundle morphisms are $\mathrm{\Phi }:{\mathcal{E}}_p\to {\mathcal{E}}_q$ Figure 1 and $\tilde{\mathrm{\Phi }}:{\mathcal{E}}_q\to {\mathcal{E}}_p$ Figure 2. When these diagrams commute (that is when ${\pi }_q\circ \mathrm{\Phi }={\pi }_p\circ \tilde{\mathrm{\Phi }}$, where ${\pi }_i$ are the bundle projection maps), we say that we have an "experimentally verified prediction of an agent’s model". In general, however, these bundle morphisms need not commute.

These connections lead to terms in the generalized variational energy representing possible agent/agent and agent/multi-agent interactions. In our current study we will only focus on the induced connection $\mathrm{\Omega }$ such that agents can compare beliefs between different sections of ${\mathcal{B}}_q$ where

$$\mathrm{\Omega }:\mathrm{\Gamma }\left({\mathcal{B}}_q\right)\to \mathrm{\Gamma }\left({\mathcal{B}}_q\right).$$

The induced connection provides a notion of parallel transport of beliefs which in turn defines the coordination structure used in our generalized variational energy term. This construction is well defined even when the fibers are not vector spaces so long as it carries a smooth G-action[34].

Following Friston [1], we define a variational free energy as

$$\mathcal{F}\left[q\right]=D_{KL}\left[q\left(c\right)\right|\mathrm{\Phi }p\left(c\right)]-{\mathbb{E}}_{q\left(c\right)}[logp\left(o\right|c)].$$

In our more general framework, agent beliefs and models occupy distinct associated bundles, and the comparison between them is only possible via $\mathrm{\Phi }$, $\tilde{\mathrm{\Phi }}$ morphisms. This leads to a more flexible and scalable framework, particularly amenable to multi-agent and multi-scale settings with gauge structure.

Here, we consider that agents share information via parallel transport of beliefs and models. We define a generalized variational energy for an agent A as

$${\mathcal{V}}_A=D_{KL}[q_A\left(c\right)\left|\right|\mathrm{\Phi }{p}_A\left(c\right)]-{\mathbb{E}}_{q_A}[log{p}_A\left(o\right|c)]+\sum _i{\mathcal{V}}_{{\Lambda }_i},$$

where ${\mathcal{V}}_{{\Lambda }_i}$ represents possible interactions between other agents mediated by gauge connections. In the present work we shall consider only one term which couples recognitions between two agents as

$${\mathcal{V}}_T\left[q_A\left(c\right)\right]=D_{\mathrm{KL}}\left[\left(q_A\left(c\right)\right|\mathrm{\Phi }{p}_A\left(c\right))\right]-{\mathbb{E}}_{q_A}[log{p}_A\left(o_A\right|c)]$$

$$+\mu D_{\mathrm{KL}}\left[q_A\left(c\right)\right|\mathrm{\Omega }{q}_B\left(c\right)],$$

where $\mu \in \mathbb{R}$ represents a general coupling. For multiple agents, we sum over terms between each pair of agents. We note in passing that this expression bears remarkable similarities with the Grand potential $\Psi =U-TS+\mu {\sum }_i{n}_i$ in standard thermodynamics.

Importantly, a local non-equilibrium steady state can be approximated by $\delta \mathcal{V}=0$ locally. Then, during some discrete computational update step, we have $q\to q+\Delta q$ such that the change in information is given by

$$\Delta I=D_{KL}\left[q\right|q+\Delta q]=D_{KL}\left[q\right|g^{-1}q],$$

where $g^{-1}$ represents a local gauge transformation acting by left action on an agent’s belief fiber.

3. Results

3.1. Agent Pullbacks to $\mathcal{C}$

Since agents do not perceive $\mathcal{C}$ directly (as consistent with modern neuroscience and cognition) [17], we define their base manifold perceptions as pullbacks of geometric quantities from ${\mathcal{E}}_q$ to the base manifold $\mathcal{C}$. For example, the Fisher information metric may be defined on the agent’s fibers as

$$f_{ij}\left(c\right)={\mathbb{E}}_{q\left(c\right)}{\displaystyle \frac{\partial logq\left(c\right)}{\partial {\theta }^i}}{\displaystyle \frac{\partial logq\left(c\right)}{\partial {\theta }^j}},$$

allowing us to locally expand around $c\in \mathcal{C}$ under pullback ${\sigma }^{*}\left(f_{ij}\left(c\right)\right)$ as

$${\mathcal{G}}_{ij}\left(c\right)={\sigma }^{*}\left(f_{ij}\left(c\right)\right)={\displaystyle \frac{{\partial }^2}{\partial \delta c^i\partial \delta c^j}}{D}_{\mathrm{KL}}\left[q\left(c\right)\right|\left|q(c+\delta c)\right].$$

This perceived metric on $\mathcal{C}$ governs the agent’s experience of a geometry on $\mathcal{C}$. Since belief dynamics vary between agents, their perceived geometries differ unless a subset of their beliefs over $\mathcal{C}$ are in agreement.

Consistent with cognitive science, we propose that the standard Euclidean spacetime emerges as an evolutionary flow in the belief space of human-scale agents. We therefore assume that we have the freedom to choose a particular decomposition such that

$${\mathcal{G}}_{ij}=g_{\mu \nu }\oplus {\mathcal{D}}_{\alpha \beta }.$$

Specifically, since $f_{ij}\left(c\right)$ is G-invariant any subgroup $H\subset G$ defines an invariant subspace of ${\mathcal{B}}_q$. Then the Lie algebra decomposes under the adjoint action of H. In this manner, we can block diagonalize the metric for subgroups of G.

As an example, consider $G=SO\left(10\right)$, $H=SO\left(3\right)$, and $dim{\mathcal{B}}_q=10$. Then

$$\mathfrak{so}\left(10\right)=\mathfrak{so}\left(3\right)\oplus {\mathfrak{h}}^{\perp }.$$

In which case

$${\mathcal{G}}_{ij}={\delta }_{\mu \nu }\oplus {\mathcal{D}}_{\alpha \beta }.$$

Here, ${\delta }_{\mu \nu }$ represents the perceived Euclidean space metric and ${\mathcal{D}}_{\alpha \beta }$ represents an unobservable 7-dimensional "dark" component. This dark component reflects the fact that there generally are aspects of the geometry that are not directly accessible or observable within the agent’s belief space, though they influence the agent’s perceptual experience indirectly. Importantly, perturbations to the agent’s Fischer metric manifest as perturbations on both the perceived and dark pullback metrics.

In this manner, an agent’s $3D$ perception is an emergent and subjective block and not a unique decomposition. Furthermore, the dimension of ${\mathcal{B}}_q$ can be flexible as allowed by the representations of G.

Taking human agents as an example, we point out that this procedure is compatible with reports of observations and perceptions which violate standard physical assumptions (particularly under the effects of hallucinogens, trauma, stroke, etc) [4]. In our framework this directly corresponds to mixing the pullback metric under perturbed belief states about $\mathcal{C}$ with respect to the Euclidean metric. In this sense our framework is cognitively consistent and offers a path towards a more unified model of physical systems in which the observer and observed are modeled together.

Similarly, we can pull back other dimensionless geometric objects from an agent’s sections. For example, with respect to human agents, we conjecture that Plank’s constant is represented as the pullback of the minimum update step to the variational energy. That is, if $\Delta q=1$ bit, then

$${\sigma }^{*}\left(\Delta {\mathcal{V}}_0\right)=\hslash .$$

3.2. Emergence of a $U\left(1\right)$ Gauge Structure

Given the possibility of block-diagonalizing the pullback metric into a standard physical metric $g_{\mu \nu }$ we can show that a $U\left(1\right)$ gauge theory naturally emerges from the agents coordinating and adjusting their beliefs in response to one another.

We consider two overlapping agents under pullback metric coordinates. Agent A has a belief $q_A\left(c\right)$ about $c\in \mathcal{C}$ and agent B has belief $q_B\left(c\right)$. Agents interact via the $\mathrm{\Omega }$ connection of their beliefs

$$\mathrm{\Omega }=e^{ie\theta }\in U\left(1\right),$$

where e represents the "strength" of the disagreement in their beliefs and $\theta$ a general element of the Lie algebra.

Next, we write our agents’ beliefs as a pair $(q_i,{\varphi }_i)$ where $q_i$ is the belief magnitude and ${\varphi }_i$ is the canonically conjugate phase to $q_i$ representing dynamic information on ${\mathcal{B}}_q$. We can encode both coordinates into a complex variable $\psi$ as

$${\psi }_i=\sqrt{q_i}{e}^{i{\varphi }_i}.$$

Their interaction term is then

$$D_{\mathrm{KL}}[{\psi }_A\left(c\right)\left|\right|\mathrm{\Omega }{\psi }_B\left(c\right)].$$

Given $dc\ll 1$, $\sqrt{q_A}=\sqrt{q_B}$, and $log(1+x)\approx x$ allows us to expand

$$D_{\mathrm{KL}}[{\psi }_A\left(c\right)\left|\right|\mathrm{\Omega }{\psi }_B\left(c\right)]\approx \int i{\psi }_A[{\varphi }_A-{\varphi }_B-e\theta \left(c\right)]d^{4}c,$$

$${\mathcal{V}}_{int}=\mu \int i{\psi }_A[{\varphi }_A-{\varphi }_B-e\theta \left(c\right)]d^{4}c.$$

If the phase mismatches are small then we have

$${\mathcal{V}}_{int}=\mu \int q_A({\partial }_{\mu }{\varphi }_A-{\partial }_{\mu }{\varphi }_B-e{A}_{\mu })d^{4}c.$$

Here $A_{\mu }$ is the local Yang-Mills field associated to $\mathrm{\Omega }$ on $\mathcal{C}$.

Minimizing the interaction potential $\delta {\mathcal{V}}_{int}=0$ leads to the condition that the phases of the agents must align, resulting in

$${\partial }_{\mu }{\varphi }_A-{\partial }_{\mu }{\varphi }_B-e{A}_{\mu }=0,$$

$$A_{\mu }={\displaystyle \frac{1}{e}}({\partial }_{\mu }{\varphi }_A-{\partial }_{\mu }{\varphi }_B).$$

Thus, $A_{\mu }$ arises as a gauge field that compensates for the phase mismatch between the agents. In this framework $A_{\mu }$ is not ontological, but instead an epistemic necessity invented by the agents to resolve prediction errors due to their limited knowledge of $\mathcal{C}$. The local gauge field $A_{\mu }$ facilitates the alignment of beliefs, allowing the agents to share consistent beliefs and coordinate their perceptions of the world.

4. Discussion

Our framework represents a novel multi-agent based model that allows agents to coordinate beliefs via rich geometric structures. If we take this model as a serious representation of reality then physics is not a description of an external, observer-independent reality but rather a description of belief coordination among agents embedded within a shared epistemic landscape. This echoes the views of Kant, Helmholtz, and modern cognitive researchers that perception is a manifestation of agent inference [1,2,3,4,5,6,17].

In this view, we cannot take our observations as elements of an underlying reality but rather as constructions our minds utilize to maximize survival under evolutionary pressures. The philosophy of science in this sense is largely about what perceptions are shared among typical agents. Traditionally reports of perceptual perturbations of our generative models (hallucinations) are discounted as subjectively spurious, yet here they offer deep insight into the underlying geometric structure itself.

In the most general framework each agent perceives a world of correlations (via the agent’s sensory data) and builds models with which to represent patterns in those correlations [5]. Our minimal geometric model allows subjective experience and differing perceptions based on the pullback of geometric objects from an agent’s fibers down to the hidden base manifold $\mathcal{C}$. This represents an exciting avenue with which to study subjective aspects of reality such as consciousness and qualia. Every observation and perception, even the pathological, then become valuable data.

The model we have proposed naturally bears similarities to standard field theories in physics. For example, we propose an experimental program by which coupling coefficients in $\mathcal{V}$ are phenomenologically determined across multiple scales and via renormalization procedures ($\Lambda$ and $\tilde{\Lambda }$ connections) predict new configurations of agents which may not otherwise be discerned.

Furthermore, if the pullback of the minimal variational energy update is related to ℏ and/or we assume that information is conserved then researchers may be able to experimentally apply this framework as a novel path in fundamental physics. For example, Landauer’s principle, in our view, becomes a fundamental reflection between information at the associated bundle level and energy/entropy at the perceptual level. If so, then this suggests that belief updates may leak into unobservable sections of perceptual reality.

These claims are falsifiable and experimentally tractable given the recent trends and experiments in computational biology and molecular chemistry [25]. Constraints on our model and interaction couplings may be elucidated by firm experiments. For example, neural synchronicity between agents presents a natural arena in which to study epistemic gauge interactions.

Our model has further applications in linguistics where human language might best be studied as a gauge theory. If so, then evolutionary pressures have fixed useful models that humans share and align as multi-agents under gauge connection. These features can be probed by historical data, anthropology, and other tools that study the dynamics of language over time and space. In this view, language is a concrete biologically instantiated epistemic gauge field: language is a gauge theory.

Still further, our work resonates with, and extends, ideas from quantum Bayesianism (QBism) [23], the Free Energy Principle[1], and relational interpretations of quantum theory [24]. However, our framework differs in that it offers a precise geometric and gauge-theoretic formalism for belief coordination and perception via pullback geometries. It unifies the subjective and objective: agents and observations are not separate but unified, joined by the mathematical language of differential geometry.

Remarkably, our framework reveals a subtle but significant duality in the interpretation of dynamics. We regard the base manifold $\mathcal{C}$ as either:

1. A dynamic base space under right action of G such that agents and observables dynamically evolve as elements of $\mathcal{C}$, or

2. A fixed base space $\mathcal{C}$ where the beliefs of agents evolve within their associated bundles via the left action of G, representing the internal dynamics of agents updating their beliefs about a local patch of a fixed $\mathcal{C}$ over time.

This distinction is not merely mathematical — it also becomes a choice of philosophical stance: as agents embedded within a universe of fixed hidden states, our beliefs of those states are in constant flux. Or we view a dynamically evolving universe with stationary observers whose beliefs reflect that motion. Either stance yields equivalent observable content, but reflects different assumptions about what is taken to be ontological and what is epistemic as well as possibly offering unique perspectives on intelligence, consciousness, and free will [5,6].

Our framework raises many more questions and suggests many future directions of exploration. We have only scratched the surface of an incredibly rich geometric framework of agents and their coordination. The principal bundle, while abstractly postulated, is not yet explicitly modeled. However, via the duality mentioned above this is not necessarily a limit our framework. Furthermore, the full implications of agent coordination as parallel transport of beliefs and models remain to be explored.

Nevertheless, the central insight remains: physics, at its deepest level, is a study of how agents construct, refine, and align structured beliefs about an underlying reality which they can never directly access. In this sense, it is not merely a study of physical properties, but a refined language for organizing perception, grounded in geometry, inference, and communication.

We have proposed a radical but principled synthesis of observation, inference, cognition, and science. Our results suggest that our current understanding of physical law is not necessarily inscribed in nature as we perceive, but instead arises from the alignment of structured beliefs (recognition and model fibers) across agents constrained by geometry. The underlying manifold may be out of reach, but by considering cognitive agents and their patterns of belief updates (including subjective experience and qualia) we hope to glean new information about our shared, fundamental reality.

5. Conclusions

By considering an agent-based model where agents are pairs of local sections of associated bundles to a principal G-bundle $\pi :\mathcal{N}\to \mathcal{C}$ which evolve via a Fristonian variational energy minimization we have shown that a $U\left(1\right)$ gauge structure emerges naturally from the act of communication, specifically, from agents’ attempts to align beliefs about the base manifold. Gauge fields need not be fundamental ontological entities, but instead are understood as epistemic structures required for coherence between interacting observers with limited information. Language, then, is a gauge theory coordinating agents.

This framework offers a fertile ground for unifying traditionally opposed dualities: subject and object, observer and observation, epistemic and ontological. It provides a geometric and information-theoretic language for discussing the emergence of spacetime, interactions, and dynamics from the internal structure of belief and inference echoing Wheeler’s "it from bit" [12,14,15,16,18,21]

Our approach opens new avenues for the study of collective cognition, distributed intelligence, and hierarchical inference, with possible applications to machine learning, multi-agent systems, and socio-physical models. By grounding communication, coordination, and belief-updating in a differential-geometric setting, we offer a path toward a general theory of epistemic interaction, where physical and cognitive processes co-emerge from a shared inferential geometry.