Submitted:
19 May 2025
Posted:
20 May 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. Study Designs
2.3. Collection of Plant Samples and Sensor Data
2.4. Data Wrangling
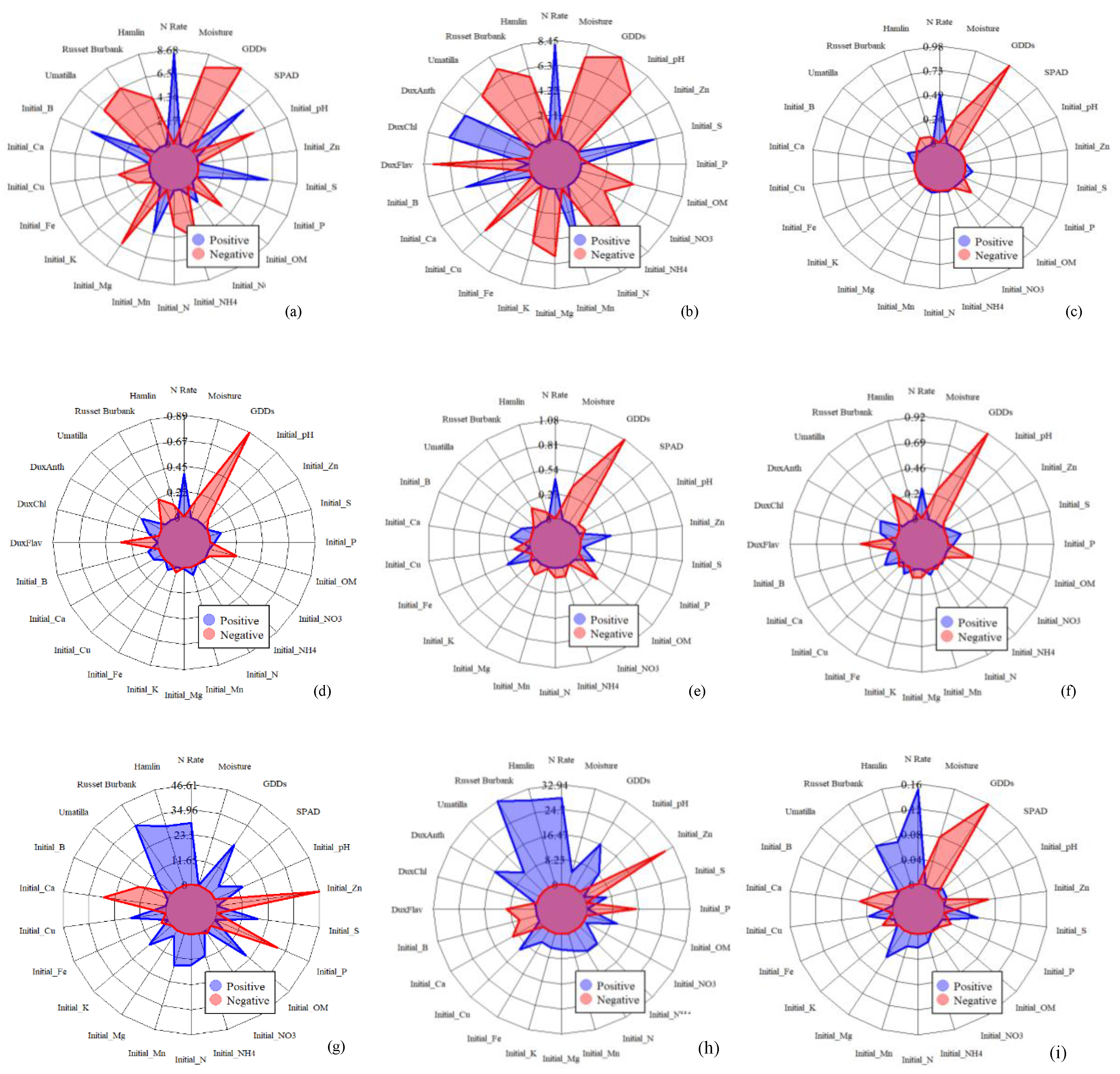
2.5. Statistical Analysis
3. Results
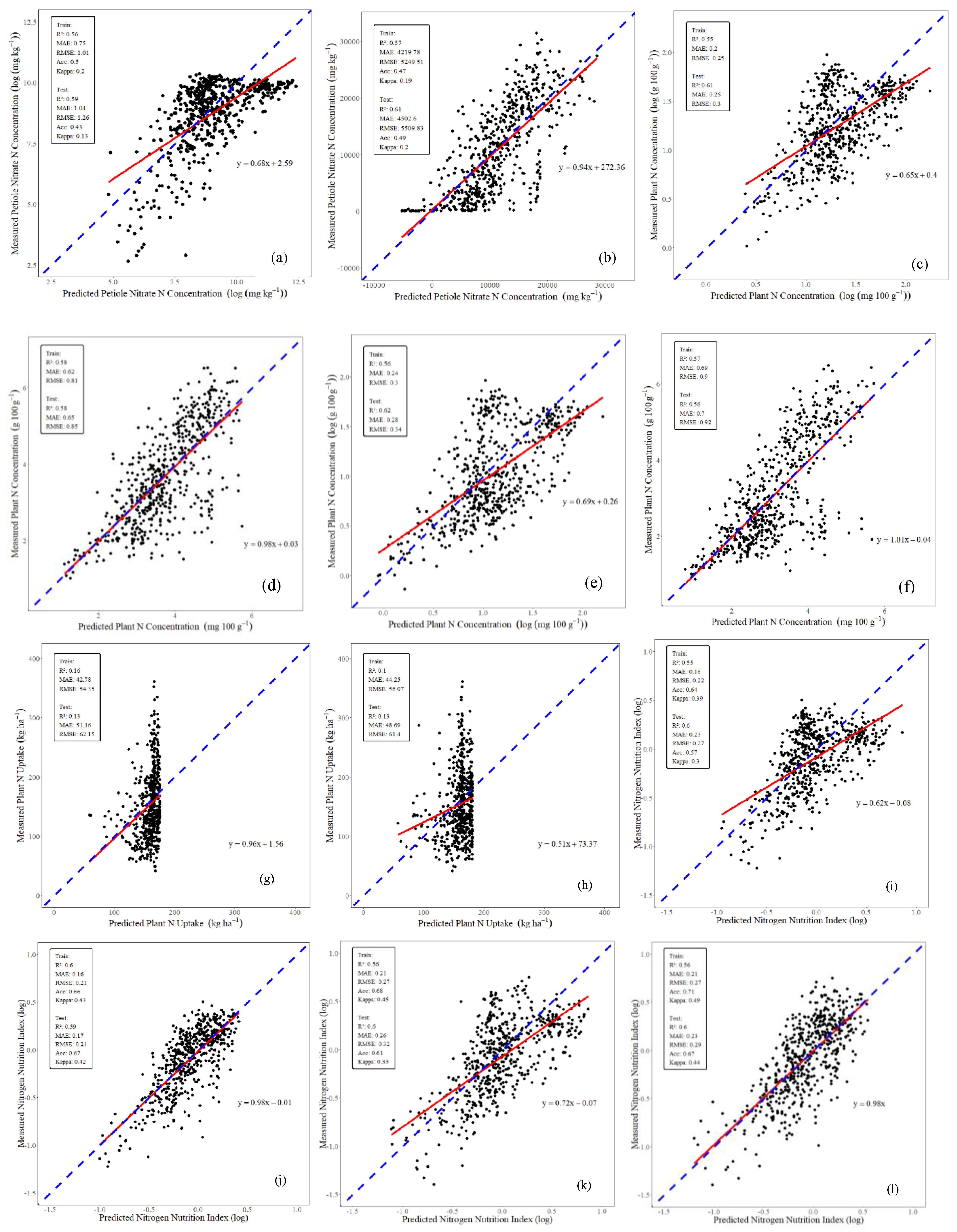
3.1. Scenario 1: Leaf Sensor Data Only
| Year | N indicator | SPAD | DuxChl | DuxNBI | Year | N indicator | SPAD | DuxChl | DuxNBI |
|---|---|---|---|---|---|---|---|---|---|
| 2018 | PNNC | 0.66 | 0.60 | 0.69 | 2021 | PNNC | 0.70 | 0.79 | 0.84 |
| VNC | 0.57 | 0.58 | 0.74 | VNC | 0.87 | 0.86 | 0.67 | ||
| WPNC | 0.53 | 0.55 | 0.72 | WPNC | 0.90 | 0.87 | 0.62 | ||
| PNU | 0.06 | 0.06 | 0.15 | PNU | 0.14 | 0.12 | 0.23 | ||
| Vine NNI | 0.48 | 0.51 | 0.69 | Vine NNI | 0.83 | 0.86 | 0.73 | ||
| NNI | 0.40 | 0.43 | 0.61 | NNI | 0.83 | 0.84 | 0.69 | ||
| 2019 | PNNC | 0.43 | 0.47 | 0.53 | 2023 | PNNC | 0.71 | 0.34 | 0.50 |
| VNC | 0.38 | 0.71 | 0.76 | VNC | 0.69 | 0.33 | 0.47 | ||
| WPNC | 0.38 | 0.71 | 0.76 | WPNC | 0.74 | 0.30 | 0.46 | ||
| PNU | 0.04 | 0.29 | 0.22 | PNU | 0.34 | 0.03 | 0.07 | ||
| Vine NNI | 0.39 | 0.37 | 0.53 | Vine NNI | 0.58 | 0.33 | 0.45 | ||
| NNI | 0.43 | 0.48 | 0.66 | NNI | 0.65 | 0.34 | 0.45 |
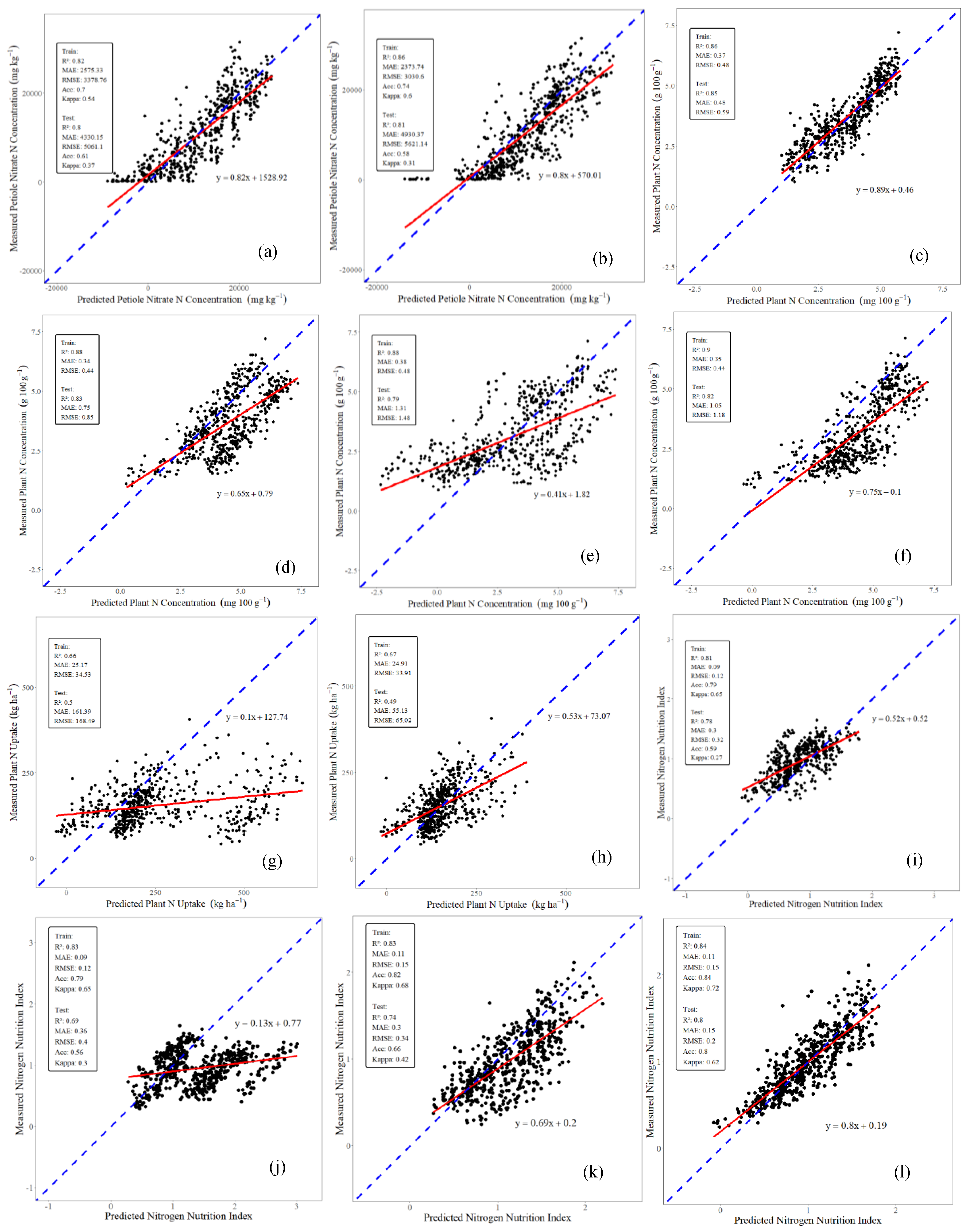
3.2. Scenario 2: Leaf Sensor Data and GxExM Data
| (a) | |||||||
| N Indicator | Dataset | Model | R2 | MAE | RMSE | Acc | Kappa |
| PNNC | Training | SVR L | 0.81 | 2625.87 | 3513.96 | 0.71 | 0.56 |
| Testing | SVR L | 0.79 | 4189.66 | 5285.45 | 0.64 | 0.42 | |
| VNC | Training | SVR L | 0.84 | 0.39 | 0.50 | - | - |
| Testing | SVR L | 0.85 | 0.56 | 0.68 | - | - | |
| WPNC | Training | SVR R | 0.94 | 0.25 | 0.34 | - | - |
| Testing | SVR R | 0.90 | 0.40 | 0.50 | - | - | |
| PNU | Training | SVR L | 0.62 | 26.43 | 36.54 | - | - |
| Testing | SVR L | 0.55 | 34.57 | 45.39 | - | - | |
| Vine NNI | Training | SVR L | 0.80 | 0.09 | 0.12 | 0.79 | 0.65 |
| Testing | SVR L | 0.80 | 0.11 | 0.14 | 0.75 | 0.57 | |
| NNI | Training | SVR L | 0.81 | 0.12 | 0.16 | 0.82 | 0.68 |
| Testing | SVR L | 0.82 | 0.16 | 0.20 | 0.77 | 0.58 | |
| (b) | |||||||
| N Indicator | Dataset | Model | R2 | MAE | RMSE | Acc | Kappa |
| PNNC | Training | RFR | 0.99 | 653.64 | 891.39 | 0.91 | 0.86 |
| Testing | RFR | 0.75 | 3399.62 | 4266.46 | 0.63 | 0.43 | |
| VNC | Training | SVR L | 0.87 | 0.36 | 0.46 | - | - |
| Testing | SVR L | 0.85 | 0.51 | 0.63 | - | - | |
| WPNC | Training | SVR L | 0.90 | 0.35 | 0.45 | - | - |
| Testing | SVR L | 0.87 | 0.47 | 0.58 | - | - | |
| PNU | Training | SVR L | 0.64 | 25.70 | 35.32 | - | - |
| Testing | SVR L | 0.57 | 32.74 | 43.21 | - | - | |
| Vine NNI | Training | SVR L | 0.81 | 0.09 | 0.12 | 0.80 | 0.65 |
| Testing | SVR L | 0.80 | 0.12 | 0.15 | 0.75 | 0.57 | |
| NNI | Training | SVR L | 0.83 | 0.11 | 0.15 | 0.84 | 0.71 |
| Testing | SVR L | 0.81 | 0.17 | 0.22 | 0.75 | 0.54 | |
4. Discussion
4.1. Comparing the Ability of SPAD and Dualex to Predict Potato N Status Indicators
4.2. Improvements of Potato N Status Indicator Prediction Using Multi-Source Data Fusion
4.3. Practical Strategy for in-Season Potato N Status Diagnosis Using a Leaf Sensor and Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AGB | Above ground biomass |
| Anth | Anthocyanin |
| BMP | Best management practice |
| Chl | Chlorophyll |
| DAP | Diammonium phosphate |
| DAS | Days after sowing |
| DM | Dry matter |
| Dualex | Dualex Scientific+ |
| ebf_sigma | RBF kernel parameter sigma |
| ESN | Environmentally Smart Nitrogen |
| Flav | Flavonol |
| FN | False negatives |
| FP | False positives |
| GDD | Growing degree days |
| GxExM | Genetic × environmental × management |
| IRR | Irrigation |
| lambda | L2 regularization term |
| LASSO | Least absolute shrinkage and selection operator |
| learn_rate | Learning rate |
| LNC | Leaf nitrogen concentration |
| MAE | Mean absolute error |
| margin | SVR epsilon margin |
| min_n | Minimum samples per node |
| ML | Machine learning |
| mtry | Number of variables randomly selected at each split |
| MLR | Multiple linear regression |
| n | Number of observations |
| N | Nitrogen |
| NBI | Nitrogen balance index |
| Nc | Critical nitrogen concentration |
| NNI | Nitrogen nutrition index |
| NSI | Nitrogen sufficiency index |
| NUE | Nitrogen use efficiency |
| NPNC | Petiole nitrate-nitrogen concentration |
| OM | Organic matter |
| P | Precipitation |
| penalty | L1 regularization term |
| PNC | Plant nitrogen concentration |
| PNNC | Petiole nitrate-N concentration |
| PNR | Percent nitrogen release |
| PNU | Plant nitrogen uptake |
| Pₑ | Expected agreement by chance |
| Pₒ | Observed agreement |
| PS | Proximal sensing |
| R2 | Coefficient of determination |
| RFR | Random forest regression |
| RMSE | Root mean square error |
| RS | Remote sensing |
| sample_size | Proportion of data sampled per tree |
| scale_factor | Scaling factor |
| SHAP | Shapley additive explanation |
| SPAD | Soil plant analysis development |
| SR | Simple regression |
| SVR | Support vector regression |
| TN | True negatives |
| Tmax | Daily maximum temperature |
| Tmin | Daily minimum temperature |
| TP | True positives |
| TNC | Tuber nitrogen concentration |
| trees | Number of trees in the forest |
| UAN | Urea-ammonium nitrate |
| UV | Ultraviolet |
| VIF | Variance information factor |
| VNC | Vine nitrogen concentration |
| VRA | Variable rate application |
| VRN | Variable rate nitrogen |
| W | Plant dry biomass |
| Wt | Dry tuber biomass |
| Wv | Dry vine biomass |
| WPNC | Whole plant nitrogen concentration |
| XGBoost | Extreme gradient boosting |
| yᵢ | Observed value of the i-th observation |
| ŷᵢ | Predicted value of the i-th observation |
| ȳ | Mean of observed values |
Appendix A
Appendix A.1
| PNNC | |||
| Sensor | Type | Equation | R2 |
| SPAD | power | y = 4.32 × 10- 10 x8.11 | 0.55 |
| DuxChl | power | y = 8.52 × 10- 5 x5.46 | 0.38 |
| DuxFlav | quadratic | y = - 10342.21 x2 - 129710.52 x + 10896.26 | 0.41 |
| DuxAnth | quadratic | y = - 29994.25 x2 - 73319.01 x + 10896.26 | 0.15 |
| DuxNBI | quadratic | y = - 6568.29 x2 - 149803.83 x + 10896.26 | 0.55 |
|
VNC |
|||
| Sensor | Type | Equation | R2 |
| SPAD | power | y = 4.15 × 10- 3 x1.81 | 0.48 |
| DuxChl | power | y = 7.65 × 10- 2 x1.16 | 0.31 |
| DuxFlav | quadratic | y = - 0.47 x2 - 23.40 x + 3.77 | 0.51 |
| DuxAnth | quadratic | y = - 3.29 x2 - 13.68 x + 3.77 | 0.19 |
| DuxNBI | quadratic | y = - 0.08 x2 + 25.33 x + 3.77 | 0.60 |
|
WPNC |
|||
| Sensor | Type | Equation | R2 |
| SPAD | power | y = 5.84 × 10- 4 x2.28 | 0.52 |
| DuxChl | power | y = 1.98 × 10- 2 x1.50 | 0.35 |
| DuxFlav | exponential | y = 21.26 e- 1.34 x | 0.45 |
| DuxAnth | quadratic | y = - 5.52 x2 - 13.24 x + 3.16 | 0.16 |
| DuxNBI | quadratic | y = 3.37 x2 + 27.71 x + 3.16 | 0.61 |
|
PNU |
|||
| Sensor | Type | Equation | R2 |
| SPAD | quadratic | y = - 488.13 x2 - 247.01 x + 155.02 | 0.11 |
| DuxChl | quadratic | y = - 127.65 x2 - 71.00 x + 155.02 | 0.01 |
| DuxFlav | quadratic | y = - 213.96 x2 + 80.41 x + 155.02 | 0.02 |
| DuxAnth | quadratic | y = 306.50 x2 + 76.48 x + 155.02 | 0.04 |
| DuxNBI | quadratic | y = - 411.87 x2 - 154.86 x + 155.02 | 0.08 |
|
Vine NNI |
|||
| Sensor | Type | Equation | R2 |
| SPAD | power | y = 1.89 × 10- 3 x1.65 | 0.49 |
| DuxChl | quadratic | y = - 2.00 x2 + 3.39 x + 0.941 | 0.31 |
| DuxFlav | quadratic | y = - 0.791 x2 - 5.20 x + 0.941 | 0.55 |
| DuxAnth | quadratic | y = - 1.06 x2 - 1.83 x + 0.941 | 0.09 |
| DuxNBI | power | y = 5.24 × 10- 2 x0.967 | 0.60 |
|
NNI |
|||
| Sensor | Type | Equation | R2 |
| SPAD | power | y = 3.21 × 10- 4 x2.12 | 0.52 |
| DuxChl | power | y = 8.95 × 10- 3 x1.39 | 0.34 |
| DuxFlav | exp | y = 5.42 e- 1.21 x | 0.42 |
| DuxAnth | quadratic | y = - 2.43 x2 - 1.18 x + 0.96 | 0.08 |
| DuxNBI | power | y = 2.99 × 10- 2 x1.16 | 0.54 |
References
- Havlin, J.L.; Tisdale, S.L.; Nelson, W.L.; Beaton, J.D. Nitrogen. In Soil fertility and fertilizers: an introduction to nutrient management; Upper Saddle River, N.J.: Pearson, 2013; pp. 117–184 ISBN 978-0-13-503373-9.
- Errebhi, M.; Rosen, C.J.; Gupta, S.C.; Birong, D.E. Potato Yield Response and Nitrate Leaching as Influenced by Nitrogen Management. Agron. J. 1998, 90, 10–15. [Google Scholar] [CrossRef]
- Lesczynski, D.B.; Tanner, C.B. Seasonal Variation of Root Distribution of Irrigated, Field-Grown Russet Burbank Potato. Am. Potato J. 1976, 53, 69–78. [Google Scholar] [CrossRef]
- Westermann, D.T.; Kleinkopf, G.E.; Porter, L.K. Nitrogen Fertilizer Efficiencies on Potatoes. Am. Potato J. 1988, 65, 377–386. [Google Scholar] [CrossRef]
- Rosen, C.J.; Bierman, P.M. Best Management Practices for Nitrogen Use: Irrigated Potatoes. 2008.
- Errebhi, M.; Rosen, C.J.; Birong, D.E. Calibration of a Petiole Sap Nitrate Test for Irrigated ‘Russet Burbank’ Potato. Commun. Soil Sci. Plant Anal. 1998, 29, 23–35. [Google Scholar] [CrossRef]
- Zhang, H.; Smeal, D.; Arnold, R.N.; Gregory, E.J. Potato Nitrogen Management by Monitoring Petiole Nitrate Level. J. Plant Nutr. 1996, 19, 1405–1412. [Google Scholar] [CrossRef]
- Roberts, S.; Cheng, H.H.; Farrow, F.O. Nitrate Concentration in Potato Petioles from Periodic Applications of 15N-Labeled Ammonium Nitrate Fertilizer. Agron. J. 1989, 81, 271–274. [Google Scholar] [CrossRef]
- Wu, J.; Wang, D.; Rosen, C.J.; Bauer, M.E. Comparison of Petiole Nitrate Concentrations, SPAD Chlorophyll Readings, and QuickBird Satellite Imagery in Detecting Nitrogen Status of Potato Canopies. Field Crops Res. 2007, 101, 96–103. [Google Scholar] [CrossRef]
- Greenwood, D.J.; Lemaire, G.; Gosse, G.; Cruz, P.; Draycott, A.; Neeteson, J.J. Decline in Percentage N of C3 and C4 Crops with Increasing Plant Mass. Ann. Bot. 1990, 66, 425–436. [Google Scholar] [CrossRef]
- Lemaire, G.; Gastal, F. N Uptake and Distribution in Plant Canopies. In Diagnosis of the Nitrogen Status in Crops; Lemaire, G., Ed.; Springer: Berlin, Heidelberg, 1997; pp. 3–43. ISBN 978-3-642-60684-7. [Google Scholar]
- Bélanger, G.; Walsh, J.R.; Richards, J.E.; Milburn, P.H.; Ziadi, N. Critical Nitrogen Curve and Nitrogen Nutrition Index for Potato in Eastern Canada. Am. J. Potato Res. 2001, 78, 355–364. [Google Scholar] [CrossRef]
- Bohman, B.J.; Culshaw-Maurer, M.J.; Ben Abdallah, F.; Giletto, C.; Bélanger, G.; Fernández, F.G.; Miao, Y.; Mulla, D.J.; Rosen, C.J. Quantifying Critical N Dilution Curves across G × E × M Effects for Potato Using a Partially-Pooled Bayesian Hierarchical Method. Eur. J. Agron. 2023, 144, 126744. [Google Scholar] [CrossRef]
- Giletto, C.M.; Reussi Calvo, N.I.; Sandaña, P.; Echeverría, H.E.; Bélanger, G. Shoot- and Tuber-Based Critical Nitrogen Dilution Curves for the Prediction of the N Status in Potato. Eur. J. Agron. 2020, 119, 126114. [Google Scholar] [CrossRef]
- Lu, J.; Dai, E.; Miao, Y.; Kusnierek, K. Improving Active Canopy Sensor-Based in-Season Rice Nitrogen Status Diagnosis and Recommendation Using Multi-Source Data Fusion with Machine Learning. J. Clean. Prod. 2022, 380, 134926. [Google Scholar] [CrossRef]
- Mulla, D.J. Twenty Five Years of Remote Sensing in Precision Agriculture: Key Advances and Remaining Knowledge Gaps. Biosyst. Eng. 2013, 114, 358–371. [Google Scholar] [CrossRef]
- Gianquinto, G.; Goffart, J.P.; Olivier, M.; Guarda, G.; Colauzzi, M.; Dalla Costa, L.; Delle Vedove, G.; Vos, J.; Mackerron, D.K.L. The Use of Hand-Held Chlorophyll Meters as a Tool to Assess the Nitrogen Status and to Guide Nitrogen Fertilization of Potato Crop. Potato Res. 2004, 47, 35–80. [Google Scholar] [CrossRef]
- Vos, J.; Bom, M. Hand-Held Chlorophyll Meter: A Promising Tool to Assess the Nitrogen Status of Potato Foliage. Potato Res. 1993, 36, 301–308. [Google Scholar] [CrossRef]
- Wakahara, S.; Miao, Y.; McNearney, M.; Rosen, C.J. Non-Destructive Potato Petiole Nitrate-Nitrogen Prediction Using Chlorophyll Meter and Multi-Source Data Fusion with Machine Learning. Eur. J. Agron. 2025, 164, 127483. [Google Scholar] [CrossRef]
- Nigon, T.J.; Mulla, D.J.; Rosen, C.J.; Cohen, Y.; Alchanatis, V.; Rud, R. Evaluation of the Nitrogen Sufficiency Index for Use with High Resolution, Broadband Aerial Imagery in a Commercial Potato Field. Precis. Agric. 2014, 15, 202–226. [Google Scholar] [CrossRef]
- Giletto, C.M.; Echeverría, H.E. Chlorophyll Meter for the Evaluation of Potato N Status. Am. J. Potato Res. 2013, 90, 313–323. [Google Scholar] [CrossRef]
- Zheng, H.; Liu, Y.; Qin, Y.; Chen, Y.; Fan, M. Establishing Dynamic Thresholds for Potato Nitrogen Status Diagnosis with the SPAD Chlorophyll Meter. J. Integr. Agric. 2015, 14, 190–195. [Google Scholar] [CrossRef]
- Fernandes, F.M.; Soratto, R.P.; Fernandes, A.M.; Souza, E.F.C. Chlorophyll Meter-Based Leaf Nitrogen Status to Manage Nitrogen in Tropical Potato Production. Agron. J. 2021, 113, 1733–1746. [Google Scholar] [CrossRef]
- Goffart, J.P.; Olivier, M.; Frankinet, M. Potato Crop Nitrogen Status Assessment to Improve N Fertilization Management and Efficiency: Past–Present–Future. Potato Res. 2008, 51, 355–383. [Google Scholar] [CrossRef]
- Mohammed, G.H.; Colombo, R.; Middleton, E.M.; Rascher, U.; van der Tol, C.; Nedbal, L.; Goulas, Y.; Pérez-Priego, O.; Damm, A.; Meroni, M.; et al. Remote Sensing of Solar-Induced Chlorophyll Fluorescence (SIF) in Vegetation: 50 years of Progress. Remote Sens. Environ. 2019, 231, 111177. [Google Scholar] [CrossRef]
- Tremblay, N.; Wang, Z.; Cerovic, Z.G. Sensing Crop Nitrogen Status with Fluorescence Indicators. A Review. Agron. Sustain. Dev. 2012, 32, 451–464. [Google Scholar] [CrossRef]
- Cerovic, Z.G.; Masdoumier, G.; Ghozlen, N.B.; Latouche, G. A New Optical Leaf-clip Meter for Simultaneous Non-destructive Assessment of Leaf Chlorophyll and Epidermal Flavonoids. Physiol. Plant. 2012, 146, 251–260. [Google Scholar] [CrossRef] [PubMed]
- Feng, W.; He, L.; Zhang, H.-Y.; Guo, B.-B.; Zhu, Y.-J.; Wang, C.-Y.; Guo, T.-C. Assessment of Plant Nitrogen Status Using Chlorophyll Fluorescence Parameters of the Upper Leaves in Winter Wheat. Eur. J. Agron. 2015, 64, 78–87. [Google Scholar] [CrossRef]
- Ben Abdallah, F.; Philippe, W.; Goffart, J.P. Comparison of Optical Indicators for Potato Crop Nitrogen Status Assessment Including Novel Approaches Based on Leaf Fluorescence and Flavonoid Content. J. Plant Nutr. 2018, 41, 2705–2728. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, C.; Jiang, J.; Wu, J.; Wang, X.; Cao, Q.; Tian, Y.; Zhu, Y.; Cao, W.; Liu, X. Multi-Source Data Fusion Improved the Potential of Proximal Fluorescence Sensors in Predicting Nitrogen Nutrition Status across Winter Wheat Growth Stages. Comput. Electron. Agric. 2024, 219, 108786. [Google Scholar] [CrossRef]
- Dong, R.; Miao, Y.; Wang, X.; Chen, Z.; Yuan, F.; Zhang, W.; Li, H. Estimating Plant Nitrogen Concentration of Maize Using a Leaf Fluorescence Sensor across Growth Stages. Remote Sens. 2020, 12, 1139. [Google Scholar] [CrossRef]
- Dong, R.; Miao, Y.; Wang, X.; Yuan, F.; Kusnierek, K. Combining Leaf Fluorescence and Active Canopy Reflectance Sensing Technologies to Diagnose Maize Nitrogen Status across Growth Stages. Precis. Agric. 2022, 23, 939–960. [Google Scholar] [CrossRef]
- Padilla, F.M.; Peña-Fleitas, M.T.; Gallardo, M.; Thompson, R.B. Proximal Optical Sensing of Cucumber Crop N Status Using Chlorophyll Fluorescence Indices. Eur. J. Agron. 2016, 73, 83–97. [Google Scholar] [CrossRef]
- Huang, S.; Miao, Y.; Yuan, F.; Cao, Q.; Ye, H.; Lenz-Wiedemann, V.I.S.; Bareth, G. In-Season Diagnosis of Rice Nitrogen Status Using Proximal Fluorescence Canopy Sensor at Different Growth Stages. Remote Sens. 2019, 11, 1847. [Google Scholar] [CrossRef]
- Li, J.W.; Zhang, J.X.; Zhao, Z.; Lei, X.D.; Xu, X.L.; Lu, X.X.; Weng, D.L.; Gao, Y.; Cao, L.K. Use of Fluorescence-Based Sensors to Determine the Nitrogen Status of Paddy Rice. J. Agric. Sci. 2013, 151, 862–871. [Google Scholar] [CrossRef]
- Chlingaryan, A.; Sukkarieh, S.; Whelan, B. Machine Learning Approaches for Crop Yield Prediction and Nitrogen Status Estimation in Precision Agriculture: A Review. Comput. Electron. Agric. 2018, 151, 61–69. [Google Scholar] [CrossRef]
- Dong, R.; Miao, Y.; Wang, X.; Chen, Z.; Yuan, F. Improving Maize Nitrogen Nutrition Index Prediction Using Leaf Fluorescence Sensor Combined with Environmental and Management Variables. Field Crops Res. 2021, 269, 108180. [Google Scholar] [CrossRef]
- Li, D.; Miao, Y.; Ransom, C.J.; Bean, G.M.; Kitchen, N.R.; Fernández, F.G.; Sawyer, J.E.; Camberato, J.J.; Carter, P.R.; Ferguson, R.B.; et al. Corn Nitrogen Nutrition Index Prediction Improved by Integrating Genetic, Environmental, and Management Factors with Active Canopy Sensing Using Machine Learning. Remote Sens. 2022, 14, 394. [Google Scholar] [CrossRef]
- Li, D.; Miao, Y.; Gupta, S.K.; Rosen, C.J.; Yuan, F.; Wang, C.; Wang, L.; Huang, Y. Improving Potato Yield Prediction by Combining Cultivar Information and UAV Remote Sensing Data Using Machine Learning. Remote Sens. 2021, 13, 3322. [Google Scholar] [CrossRef]
- Wang, X.; Miao, Y.; Dong, R.; Kusnierek, K. Minimizing Active Canopy Sensor Differences in Nitrogen Status Diagnosis and In-Season Nitrogen Recommendation for Maize with Multi-Source Data Fusion and Machine Learning. Precis. Agric. 2023, 24, 2549–2565. [Google Scholar] [CrossRef]
- Wang, X.; Miao, Y.; Dong, R.; Zha, H.; Xia, T.; Chen, Z.; Kusnierek, K.; Mi, G.; Sun, H.; Li, M. Machine Learning-Based in-Season Nitrogen Status Diagnosis and Side-Dress Nitrogen Recommendation for Corn. Eur. J. Agron. 2021, 123, 126193. [Google Scholar] [CrossRef]
- Zha, H.; Miao, Y.; Wang, T.; Li, Y.; Zhang, J.; Sun, W.; Feng, Z.; Kusnierek, K. Improving Unmanned Aerial Vehicle Remote Sensing-Based Rice Nitrogen Nutrition Index Prediction with Machine Learning. Remote Sens. 2020, 12, 215. [Google Scholar] [CrossRef]
- Gupta, S. Nitrogen Fertilization Rate and Cold-Induced Sweetening in Potato Tubers during Storage.; 2018; pp. 12–19;.
- Gupta, S.; Rosen, C. Nitrogen Fertilization Rate and Cold-Induced Sweetening in Potato Tubers During Storage; 2019; pp. 13–20;.
- Miao, Y.; Wakahara, S.; Rosen, C.; Gupta, S. Proximal Sensing-Based Non-Destructive Diagnosis of Potato Nitrogen Status; 2022; pp. 4–14;.
- Miao, Y.; Wakahara, S.; Sharma, V.; McNearney, M.; Crants, J.; Rosen, C. Developing Variable Rate Nitrogen and Water Management Strategies for Sustainable Potato Production; 2024; pp. 148–166;.
- Egal, D. Midwest Vegetable Production Guide for Commercial Growers 2024. Available online: https://edustore.purdue.edu/ (accessed on 11 January 2025).
- Carlson, R.M.; Cabrera, R.I.; Paul, J.L.; Quick, J.; Evans, R.Y. Rapid Direct Determination of Ammonium and Nitrate in Soil and Plant Tissue Extracts. Commun. Soil Sci. Plant Anal. 1990, 21, 1519–1529. [Google Scholar] [CrossRef]
- Worthington, C.; Hutchinson, C. Accumulated Growing Degree Days as a Model to Determine Key Developmental Stages and Evaluate Yield and Quality of Potato in Northeast Florida. 2006.
- Steele, D.; Scherer, T.; Hopkins, D.; Tuscherer, S.; Wright, J. Spreadsheet Implementation of Irrigation Scheduling by the Checkbook Method for North Dakota and Minnesota. Appl. Eng. Agric. 2010, 26. [Google Scholar] [CrossRef]
- Wilson, M.L.; Rosen, C.J.; Moncrief, J.F. Potato Response to a Polymer-Coated Urea on an Irrigated, Coarse-Textured Soil. Agron. J. 2009, 101, 897–905. [Google Scholar] [CrossRef]
- Kursa, M.B.; Rudnicki, W.R. Feature Selection with the Boruta Package. J. Stat. Softw. 2010, 36, 1–13. [Google Scholar] [CrossRef]
- Kuhn, M.; Wickham, H. Tidymodels: A Collection of Packages for Modeling and Machine Learning Using Tidyverse Principles. 2020.
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T.; et al. Xgboost: Extreme Gradient Boosting 2024.
- Friedman, J.H.; Hastie, T.; Tibshirani, R. Regularization Paths for Generalized Linear Models via Coordinate Descent. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
- Karatzoglou, A.; Smola, A.; Hornik, K.; Australia (NICTA), N.I.; Maniscalco, M.A.; Teo, C.H. Kernlab: Kernel-Based Machine Learning Lab 2024.
- Wright, M.N.; Ziegler, A. Ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R. J. Stat. Softw. 2017, 77, 1–17. [Google Scholar] [CrossRef]
- Landis, J.R.; Koch, G.G. The Measurement of Observer Agreement for Categorical Data. Biometrics 1977, 33, 159–174. [Google Scholar] [CrossRef]
- Lundberg, S.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions 2017.
- Molnar, C.; Casalicchio, G.; Bischl, B. Iml: An R Package for Interpretable Machine Learning. J. Open Source Softw. 2018, 3, 786. [Google Scholar] [CrossRef]
- Mayer, M.; Stando, A. Shapviz: SHAP Visualizations 2025.
- R Core Team R: A Language and Environment for Statistical Computing 2024.
- Thornton, M. Potato Growth and Development. In Potato Production Systems; Stark, J.C., Thornton, M., Nolte, P., Eds.; Springer International Publishing: Cham, 2020; pp. 19–33. ISBN 978-3-030-39157-7. [Google Scholar]
- Cao, Q.; Miao, Y.; Feng, G.; Gao, X.; Li, F.; Liu, B.; Yue, S.; Cheng, S.; Ustin, S.L.; Khosla, R. Active Canopy Sensing of Winter Wheat Nitrogen Status: An Evaluation of Two Sensor Systems. Comput. Electron. Agric. 2015, 112, 54–67. [Google Scholar] [CrossRef]
- Lu, J.; Miao, Y.; Shi, W.; Li, J.; Yuan, F. Evaluating Different Approaches to Non-Destructive Nitrogen Status Diagnosis of Rice Using Portable RapidSCAN Active Canopy Sensor. Sci. Rep. 2017, 7, 14073. [Google Scholar] [CrossRef]
- Gastal, F.; Lemaire, G. N Uptake and Distribution in Crops: An Agronomical and Ecophysiological Perspective. J. Exp. Bot. 2002, 53, 789–799. [Google Scholar] [CrossRef]
- Errecart, P.M.; Agnusdei, M.G.; Lattanzi, F.A.; Marino, M.A.; Berone, G.D. Critical Nitrogen Concentration Declines with Soil Water Availability in Tall Fescue. Crop Sci. 2014, 54, 318–330. [Google Scholar] [CrossRef]
- Kunrath, T.R.; Lemaire, G.; Sadras, V.O.; Gastal, F. Water Use Efficiency in Perennial Forage Species: Interactions between Nitrogen Nutrition and Water Deficit. Field Crops Res. 2018, 222, 1–11. [Google Scholar] [CrossRef]
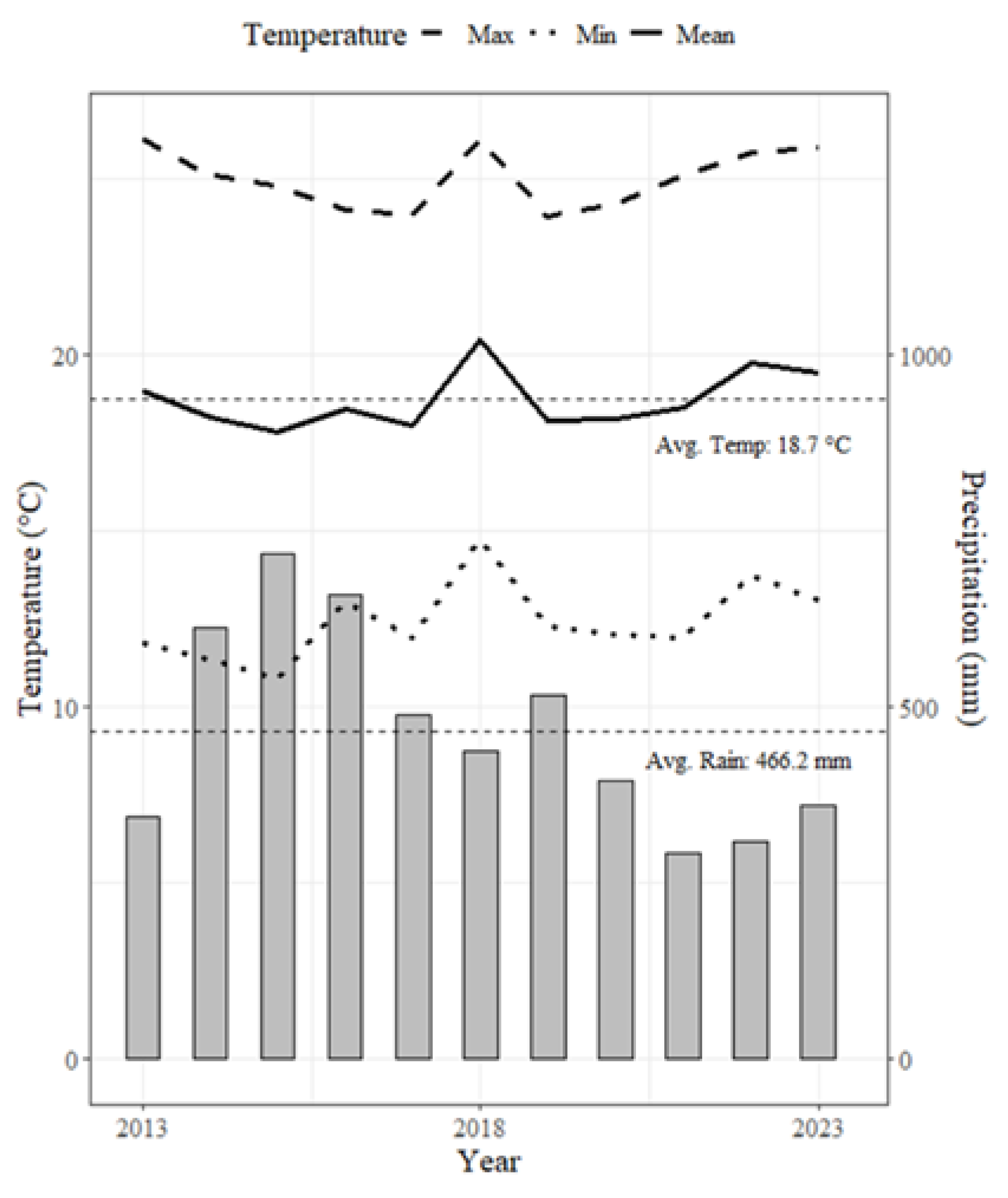
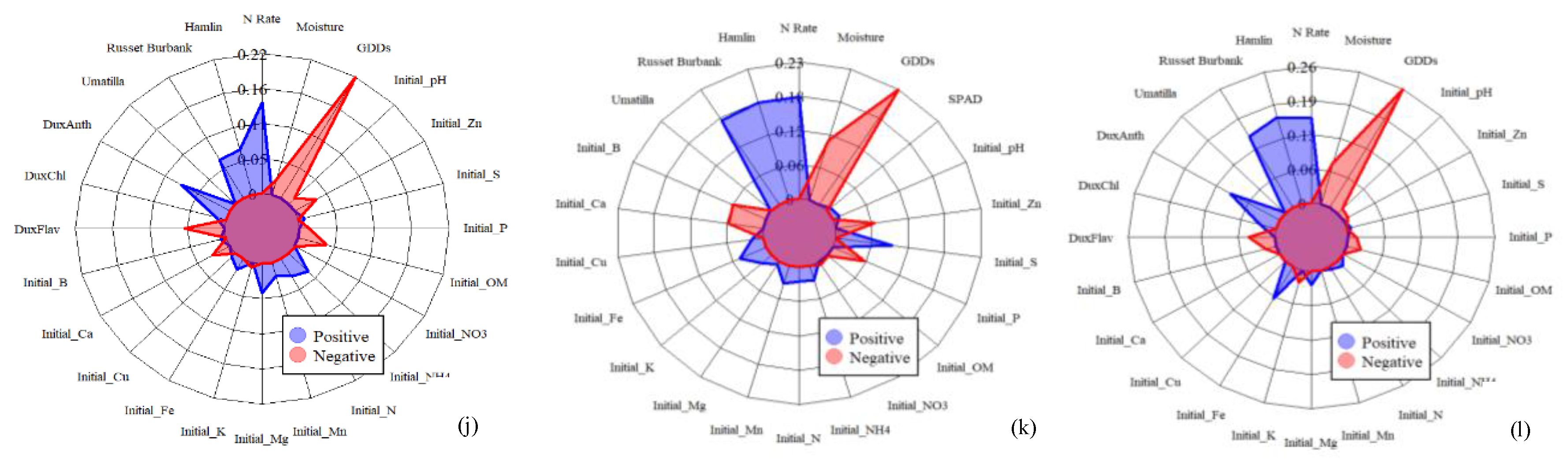
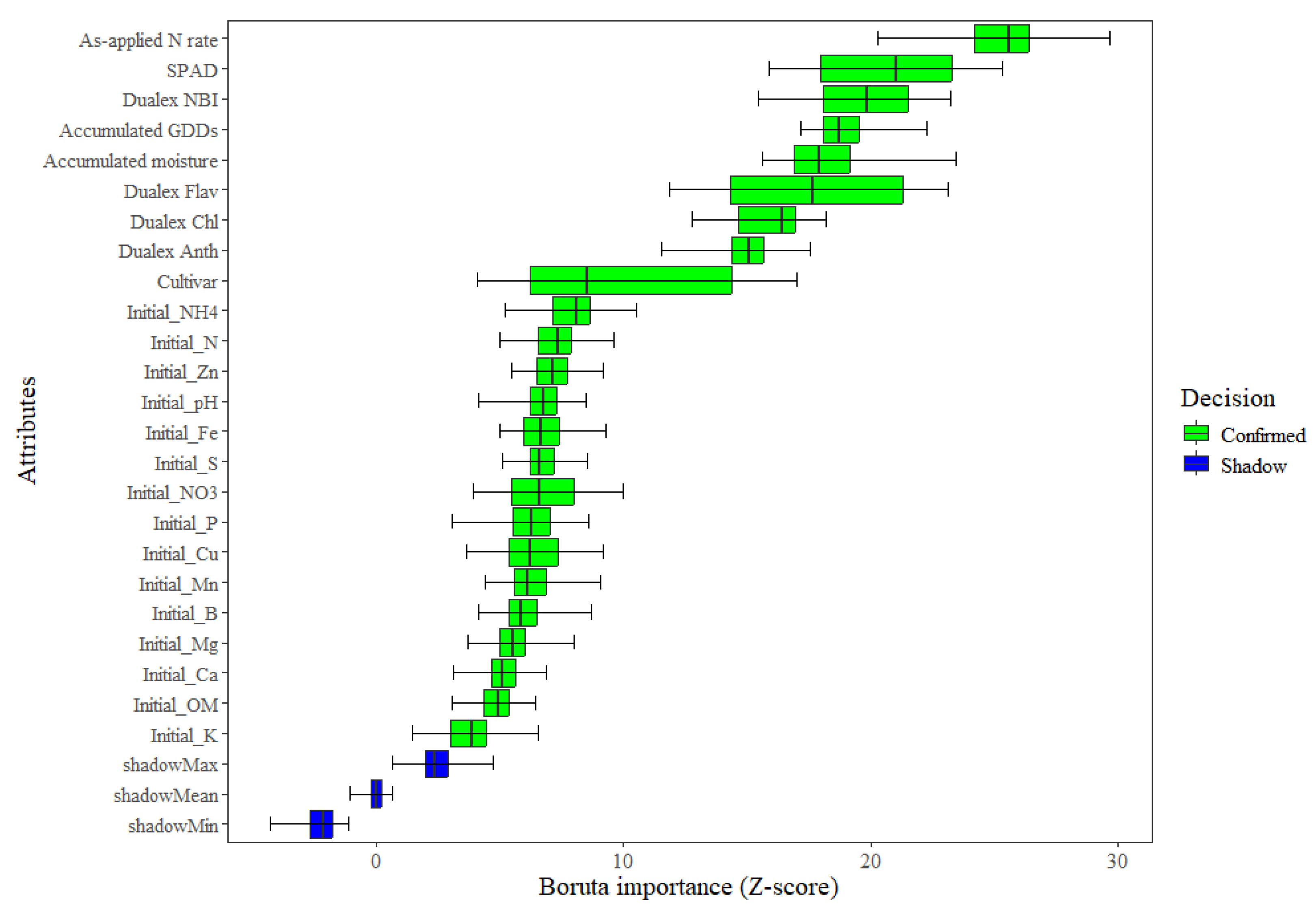
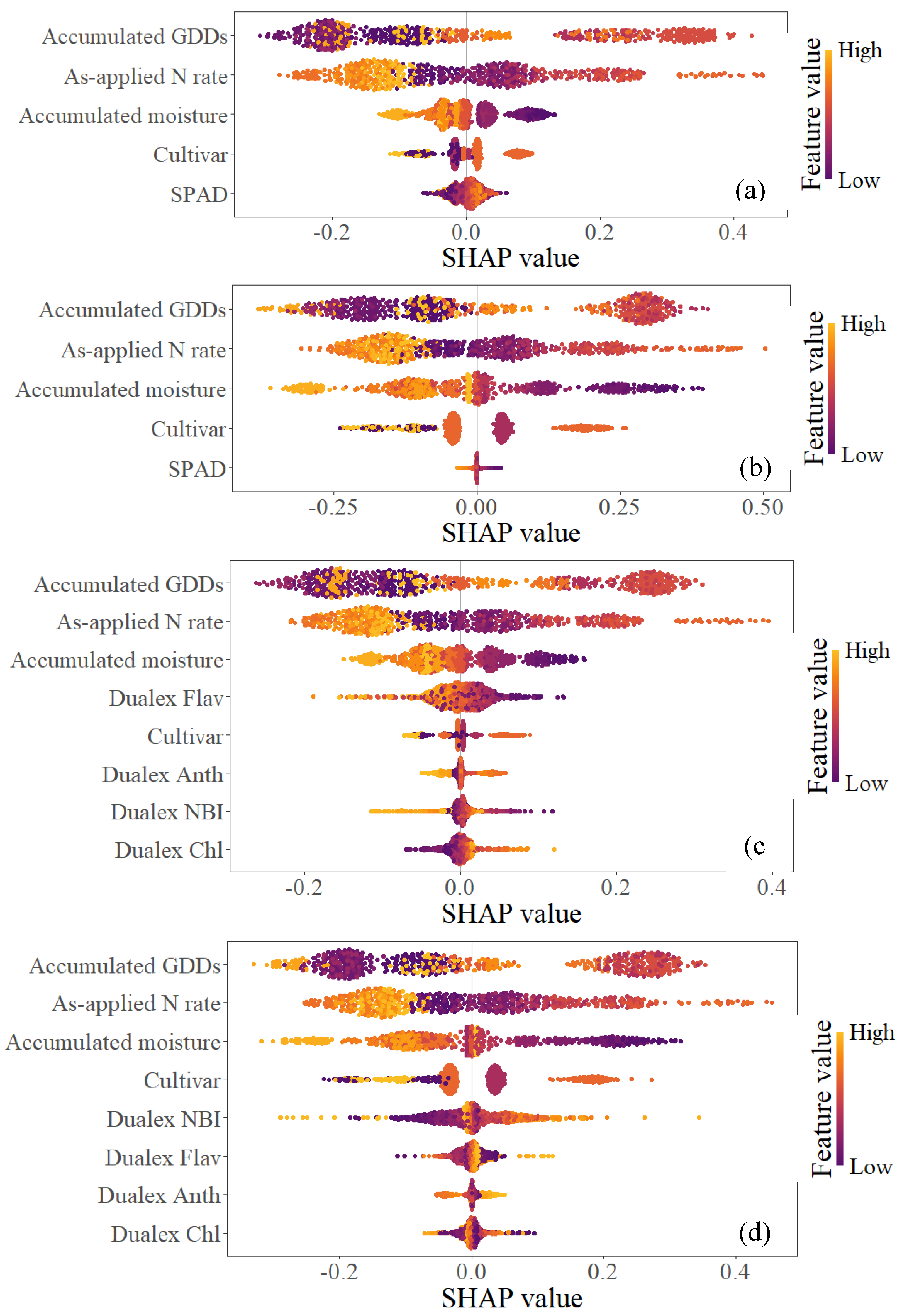
| Max | Min | Mean | Median | |
| OM | 22.0 | 10.0 | 14.7 | 14.0 |
| pH | 7.4 | 6.0 | 6.7 | 6.8 |
| N | 11.7 | 1.7 | 5.9 | 5.9 |
| P | 69.0 | 18.0 | 46.2 | 55.0 |
| K | 157.0 | 74.0 | 100.5 | 94.0 |
| S | 12.2 | 4.4 | 8.0 | 7.0 |
| Ca | 958.8 | 620.2 | 781.2 | 731.7 |
| Mg | 185.1 | 115.2 | 150.6 | 154.6 |
| B | 0.3 | 0.1 | 0.2 | 0.2 |
| Fe | 33.4 | 10.4 | 20.5 | 17.5 |
| Mn | 25.7 | 3.9 | 11.1 | 7.9 |
| Zn | 11.9 | 1.1 | 5.6 | 3.4 |
| Cu | 1.2 | 0.5 | 0.8 | 0.8 |
| Cultivar | Vine a | Vine b | WP a | WP b |
|---|---|---|---|---|
| Russet Burbank Hamlin Russet | 5.08 | 0.28 | 4.57 | 0.42 |
| Umatilla Russet Clearwater Russet Lamoka | 5.44 | 0.27 | 5.04 | 0.42 |
| Ivory Russet MN13142 | 5.17 | 0.18 | 5.19 | 0.25 |
| PNNC | VNC | WPNC | PNU | Vine NNI | NNI | |
| (mg kg-1) | (g 100g-1) | (g 100g-1) | (kg ha-1) | |||
| Min | 5 | 1.02 | 0.87 | 41.05 | 0.29 | 0.25 |
| Mean | 10896 | 3.77 | 3.16 | 155.02 | 0.94 | 0.96 |
| Median | 9984 | 3.65 | 2.73 | 143.84 | 0.96 | 0.93 |
| Max | 31410 | 7.22 | 7.12 | 405.37 | 1.65 | 2.11 |
| SD | 7898 | 1.28 | 1.4 | 59.37 | 0.28 | 0.37 |
| CV | 1 | 0.34 | 0.44 | 0.38 | 0.3 | 0.39 |
| N Indicator | Dataset | Model | R2 | MAE | RMSE | Acc | Kappa |
|---|---|---|---|---|---|---|---|
| PNNC | Training | RFR | 0.94 | 1600.58 | 2052.82 | 0.77 | 0.65 |
| Testing | RFR | 0.66 | 3898.12 | 4864.5 | 0.56 | 0.32 | |
| VNC | Training | SVR L | 0.65 | 0.6 | 0.75 | - | - |
| Testing | SVR L | 0.57 | 0.69 | 0.88 | - | - | |
| WPNC | Training | RFR | 0.95 | 0.24 | 0.32 | - | - |
| Testing | RFR | 0.62 | 0.72 | 1 | - | - | |
| PNU | Training | SVR L | 0.09 | 44.11 | 56.31 | - | - |
| Testing | SVR L | 0.11 | 54.14 | 69.72 | - | - | |
| Vine NNI | Training | SVR L | 0.62 | 0.14 | 0.17 | 0.71 | 0.51 |
| Testing | SVR L | 0.55 | 0.16 | 0.2 | 0.69 | 0.45 | |
| NNI | Training | SVR P | 0.53 | 0.2 | 0.26 | 0.7 | 0.5 |
| Testing | SVR P | 0.54 | 0.26 | 0.32 | 0.64 | 0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





