A Six-Dimensional Symmetry and Density Oscillation Model for Unifying Relativity and Quantum Mechanics and Compressed Quantum Information Transfer via Riemann Prime Distribution

1. General Concepts:

Based on homogeneity, isotropy, and the structural nature of a rigid body, density in four-dimensional space behaves as a length rotating around the mass field. This rotation is accompanied by an additional rotation around a second field in five-dimensional space. The expansion of space in the sixth dimension is made possible through the repetition of wave function states for matter. The arrow of time emerges from geometric potential differences caused by density variations and elliptical eccentricity, indicating that objects approaching the speed of light undergo oscillatory motion along the real time dimension. Motion through space results in a reduction of motion along the time dimension, and the preservation of special and general relativity laws in a symmetric six-dimensional space arises from the existence of three orthogonal time dimensions, which balance the informational field with physical laws. Accordingly, every object contains information about its past, present, and future, which are real from the perspective of higher dimensions. Therefore, both reality and locality act as generators of temporal symmetry and general equivalence. In this framework, the type of mass resulting from motion through space and time unifies relativistic principles with quantum mechanics. The core problem in reconciling quantum mechanics with general relativity is addressed through the distribution of prime numbers based on the Riemann zeta function at the critical line Re(s) = 0.5. The final framework establishes a fundamental connection between prime numbers, geometry, and the fundamental forces of nature, grounded in the three natural constants π, φ, and the golden constant. Domains such as neuroscience and philosophy are also analyzable within this model. This unified model of mathematical, geometric, and physical foundations can account for the origin and mechanism of general entanglement in space-time structure through the overlap of the Taylor expansion and the Riemann zeta function in a geometric formulation of entanglement. Each local coordinate possesses a distinct quantum state, but five dimensions are allocated to three-dimensional matter. A rigid body, based on homogeneity and isotropy, acquires spin as a function of density through hyper geometry mass distribution in five dimensions. This structure emerges from the correlation among five groups of prime numbers. Entanglement occurs through the sixth group corresponding to the second time dimension which unifies space-time oscillations and heterogeneities. This entanglement is facilitated via wormhole laws within Möbius space.

2. Foundations

From the perspective of extrinsic geometry, complex spaces are subsets of Euclidean space. The six-dimensional metric is extendable with respect to the observer’s frame. The six orthogonal basis states define the structure of matter across extended quantum states.

$$\sin \left({cos}^{-1}\left({\displaystyle \frac{\partial x_i}{c}}\right)\right)=\sqrt{1-{\left(\partial \rho \right)}^2} i=\mathrm{1,2},3$$

$$g_{\mu \upsilon }=r{a}^2{cos}^2\theta {cos}^2\varphi d{\kappa }^2+r^2{a}^2{cos}^2\theta d{\varphi }^2+r^2{a}^{2}d{\theta }^2+a^2{r}^{2}d{\theta }^2+a^2{r}^2{sin}^2\theta d{\varphi }^2$$

The absence of matter in the real dimensions defines the necessity of negative density in constructing the arrow of time. The wave function consists of small packets dependent on density. The wavelength corresponds to the density length across time.

$${\int }_{-\rho }^{+\rho }{\int }_{-t}^{+t}{\int }_{-\infty }^{+\infty }{\left|\psi (\rho ,t,x)\right|}^{2}d\rho dtdx=1 , \left|\mathsf{\Psi }⟩=b_1\left|{\tilde{\psi }}_1⟩+b_2\left|{\tilde{\psi }}_2⟩+\dots +b_n\left|{\tilde{\psi }}_n⟩\right.\right.\right.\right.$$

$$\left|\tilde{\psi }⟩={\alpha }_1\left|A_1⟩+{\alpha }_2\left|A_2⟩+{\alpha }_3\left|A_3⟩+{\alpha }_4\left|A_4⟩+\right.\right.\right.\right.\right.{\alpha }_5\left|A_5⟩+{\alpha }_6\left|A_6⟩\right.\right.$$

$$\mathsf{\Psi }\left(\rho ,x,t\right)=\sum _{n=1}^4\sum _{m=1}^4\sum _{k=1}^4{C}_{nmk}cos\left({\displaystyle \frac{2\pi n}{L_{\rho }}}\right)+sin\left({\displaystyle \frac{2\pi m}{L_x}}\right)-isec\left({\displaystyle \frac{2\pi k}{T}}\right)$$

The energy-momentum tensor in Möbius space.

$$T_{\mu \nu }=\left[\begin{array}{cccccc}-{\rho }^{†}& 0& 0& 0& 0& 0\\ 0& -\rho & 0& 0& 0& 0\\ 0& 0& \rho & 0& 0& 0\\ 0& 0& 0& P& 0& 0\\ 0& 0& 0& 0& P& 0\\ 0& 0& 0& 0& 0& P\end{array}\right]$$

Pairing in mass, energy, spin, density, and time generates symmetry along time and defines equivalence and conservation laws. The equivalence between information and energy is based on the principle that two types of information compressed and ongoing over time are symmetrically and inversely equivalent to potential and kinetic forms of energy. Compressed and ongoing information correspond to kinetic and potential energy, defining spacetime curvature through informational fields.

$$I_{c }{\approx E}_k{I}_{o }{\approx E}_{p}E=m{c}^2$$

$$E+F\approx I{c}^2\left|\Psi ⟩\right.$$

$$E_p=U\approx I_{o }{c}^2$$

$$E_k={\displaystyle \frac{1}{2}}{m{v}^2\approx I}_{c }\rho c$$

where $I_{c }$​ represents compressed information and $I_{o }$​ represents ongoing information. Information possesses a temporal nature; accordingly, all physical laws including entanglement are defined within informational fields:

$$I_t=I_{o }+I_{c }$$

$$\left|\Psi ⟩=\right.{\displaystyle \frac{1}{\sqrt{2}}}(\left|I_{c }\right.⟩\left|E_k\right.⟩+\left|I_{o }\right.⟩\left|E_p\right.⟩)$$

$$⟨ \left.I_m\right|={\displaystyle \frac{1}{\sqrt{2}}}(⟨ \left.I_{c }\right|⟨ \left.E_k\right|+⟨ \left.I_{o }\right|⟨ \left.E_p\right|)$$

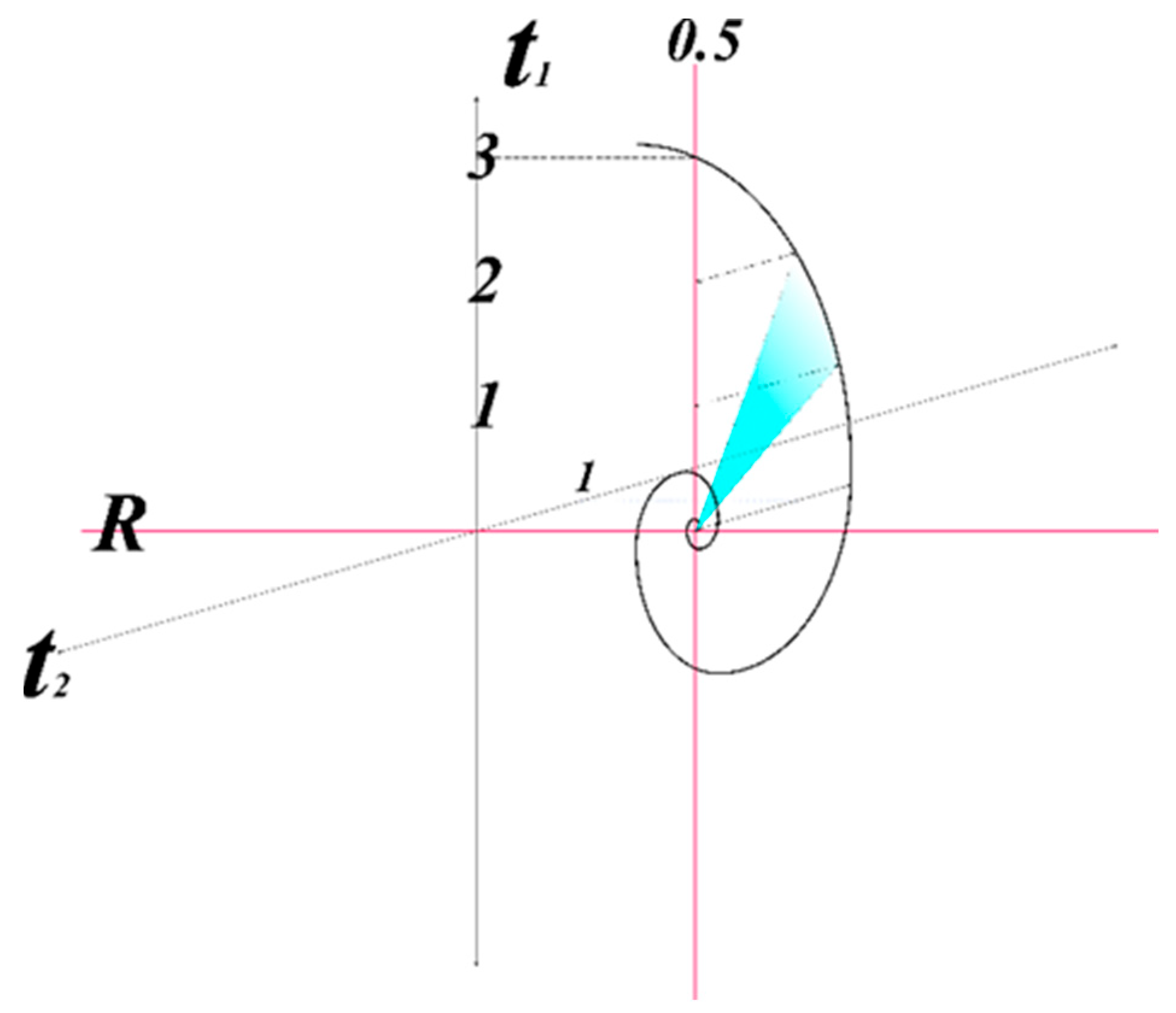
The structure of information is based on numbers; accordingly, the role of prime numbers in preserving the structure of compressed and ongoing information over time is governed by their distribution through the zeta function. The golden spiral, which contains three constant and invariant components, becomes significant across the two time dimensions along the critical strip. (Figure 1)

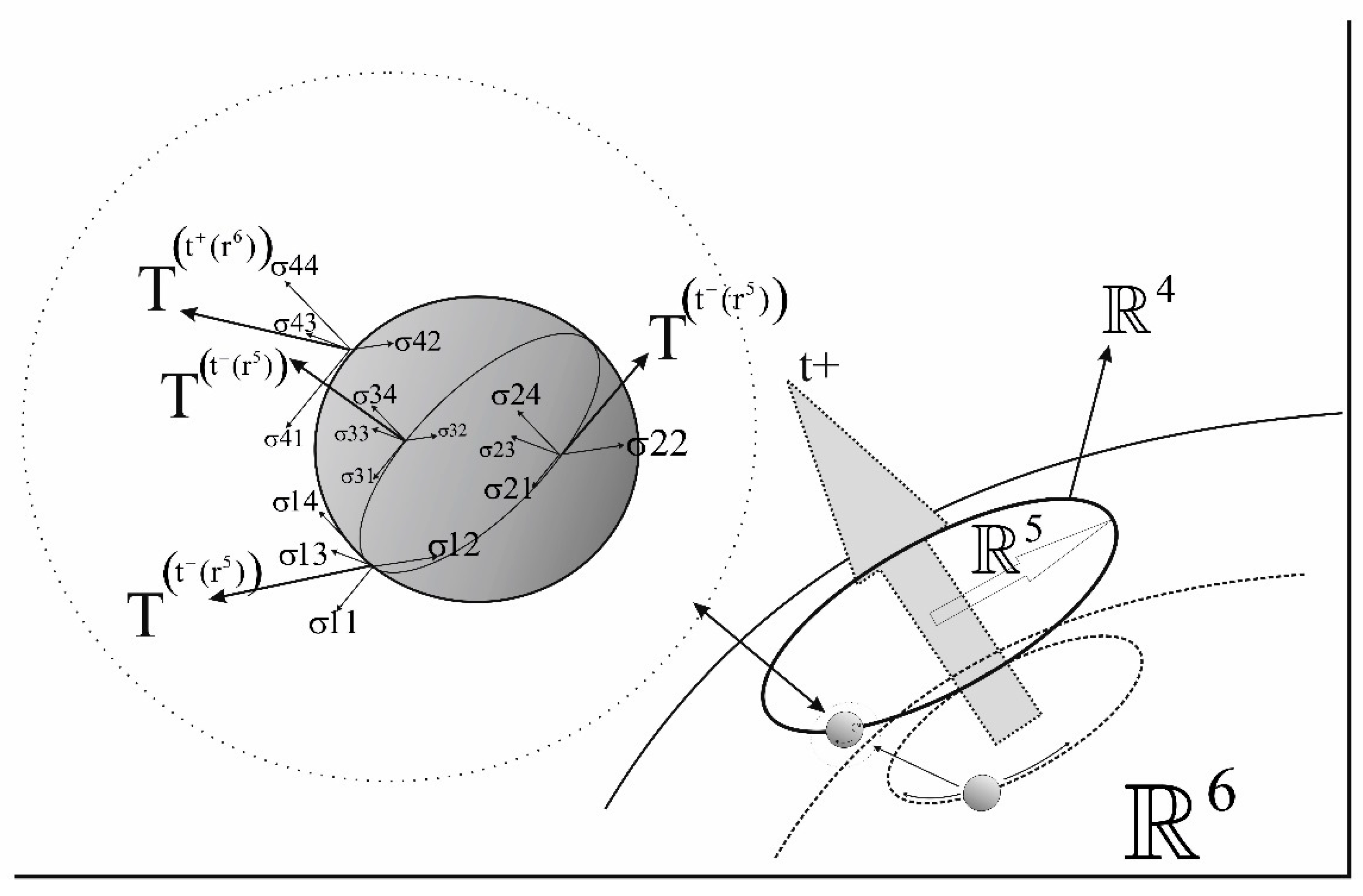
The zeta function contains a complex conjugate pair. Bounded functions defined on the five-dimensional curved surface include subsets with zeros based on trigonometric ratio preservation.

$$\xi {\xi }^{*}={sin}^2\left(\theta \right)$$

The constancy of the rigid body's length, within the metric dependent on elliptical eccentricity, establishes a relationship between trigonometric functions and prime number groups based on the inner digit sums associated with the logarithmic spiral. Figure 2

The reduction of inner digit sums to a single-digit number defines the group regularity and oscillatory gaps in modular structures.

$$NDS\left(P_{\mu }\right)=\lambda ϵG_{\upsilon } \upsilon =\mathrm{1,2},\mathrm{4,5},\mathrm{7,8}{G}_{\mathrm{3,6},9}=\varnothing$$

$$\left(INDS(\alpha \beta \gamma \dots \eta )\right)\Rightarrow {INDS}_n\left(n\right)=IDNS\left({INDS}_{n-1}\left(n\right)\right) until {INDS}_n\left(n\right)\in \left\{\mathrm{1,2},,\mathrm{4,5},\mathrm{7,8}\right\}$$

$${sec}^{-1}\left(2^{\alpha }{2}^{\beta }\dots 2^{\eta }\right)={\theta }_{\mu }$$

$$`P_{52}=233\Rightarrow 2+3+3=8\Rightarrow \left({\displaystyle \frac{1}{2^2}}+{\displaystyle \frac{1}{2^3}}+{\displaystyle \frac{1}{2^3}}\right)=0.5\Rightarrow {cos}^{-1}\left(0.5\right)=60 \sin \left(60\right)=\sqrt{{\displaystyle \frac{3}{2}}}$$

The rows of the six-scale table define the overlap of oscillation periods within each group, corresponding to the hypergeometry of mass distribution in Möbius space dependent on density variations.

$$N{\alpha }_1\left|A_1⟩=\right.P_{G_1}=\left(n\sqrt{m}+\left(z{z}^{*}\right)i\right)\left(n\sqrt{m}-\left(z{z}^{*}\right)i\right)$$

$$⟨\widetilde{{\psi }_n}|\widetilde{{\psi }_n}⟩\to P_{G_1},P_{G_2},P_{G_3},P_{G_4},P_{G_5},P_{G_6}$$

$$pf\left(X,u\right)= \left\{\begin{array}{c}0 u<0\\ 0 3<u\\ \left({\displaystyle \frac{1}{6}}\right)\left(\right(binomial\left(3, u\right)\left)\right(\left(binomial\left(3, 5-u\right)\right) other\end{array}\right.$$

$$pf\left(X,2\right); {\displaystyle \frac{1}{2}}$$

$$\overline{X} ={\displaystyle \frac{5}{2}}$$

$$w=\left({\displaystyle \frac{\sin \left(\theta \right)c+{\cos \left(\theta \right)t}_0}{\sin \left(\theta \right)c+\acute{{ct}_0}}}\right)\Rightarrow \left({\displaystyle \frac{2\sin \left(60\right)+1}{2\cos \left(60\right)+2i}}\right)\left({\displaystyle \frac{2\sin \left(60\right)-1}{2\cos \left(60\right)-2i}}\right)=2/5$$

$$\left({\displaystyle \frac{2\mathit{sin}\left(30\right)+1}{2\mathit{cos}\left(60\right)+2i}}\right)\left({\displaystyle \frac{2\mathit{sin}\left(30\right)-1}{2\mathit{cos}\left(60\right)-2i}}\right)=0$$

Density rotates around the mass field along the real time dimensions. The geometric potential difference, derived from the generalization of the rigid body to higher dimensions, defines the rotation. Figure 3

$$w_2={\displaystyle \frac{a_2\left(z_2+t_1\right)+b_2\left(t_1\right)}{c_2\left(z_2+t_1\right)+d_2\left(t_2\right)}}$$

$${w_2={\displaystyle \frac{a_2\left(z_2\right)+b_2}{c_2\left(z_2\right)+b_2}} w}_2={\displaystyle \frac{a_2\left(z_2+sin\theta \right)+b_2\left(sin\theta \right)}{c_2\left(z_2+sin\theta \right)+d_2\left(sin\varphi \right)}}$$

$$w_3={\displaystyle \frac{a_3\left(w_2\right)+b_3}{c_3\left(w_2\right)+b_3}}{ w}_5={\displaystyle \frac{a_5\left(w_4\right)+b_4}{c_5\left(w_4\right)+b_4}}$$

$${\displaystyle \frac{{\left(\frac{1}{2\pi }\right)}^3{\left(\frac{1}{2}\right)}^6{\pi }^3+\Delta x}{2{\pi }^2{\left(\frac{1}{2}\right)}^6{\pi }^3+\Delta \acute{x}}}={\displaystyle \frac{m}{\sqrt{1-\frac{v^2}{c^2}}}}=\Delta \rho \Rightarrow ∆\rho =w_5.f\left(z_4\right)$$

The golden ratio depends on the hypergeometric distribution of mass across two time dimensions, based on the Taylor expansion at the differentiable point of the critical strip of the zeta function.

$$1+\sum _{x=1}^n\left(\left({\displaystyle \frac{x!+2x!}{2}}\right)\right)=1+{\displaystyle \frac{3}{2}}HG\left(\left[\mathrm{1,2}\right],\left[ \right],1\right)-{\displaystyle \frac{3}{2}}\Gamma \left(n+2\right)HG(\left[1,n+2\right],\left[ \right],1)$$

$$\mathsf{\Psi }\left(x\right)~\mathsf{{\rm Y}}\left(k\right)=\sum _{n=0}^{\infty }{\displaystyle \frac{{\gamma }^n\left(k\right)a}{n!}}{\left(x-a\right)}^n\Rightarrow$$

$$\left(\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(\frac{1+\sqrt{5}}{2}\right)}^n\left(\frac{1}{2}\right)}{n!e^{\frac{1+\sqrt{5}}{2}}}}\right(x-0.5\left)\right(\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(\frac{1+\sqrt{5}}{2}\right)}^n\left(\frac{1}{2}\right)}{n!e^{\frac{1+\sqrt{5}}{2}}}}\left(x+0.5\right)$$

Geometric tensions in the expanding sixth dimension correspond to the fundamental forces on three-dimensional matter.

$$\left({\displaystyle \frac{{\left(\frac{1}{2\pi }\right)}^3+{\left(\frac{1}{2}\right)}^6{\pi }^3\left(\frac{1}{6}\right){\pi }^3\left(\frac{\left(\frac{3\pi -6}{2\pi }\right) }{360}\right){\phi }^3}{c}}\right)\cong 6.6765834\times {10}^{-11}\cong G\left({\displaystyle \frac{{\left(\frac{{\mathit{tan}}^{-1}\left(\phi \right)-\left(\frac{180}{\pi }\right)}{2\pi }\right)}^3\left(\frac{1}{6}\right){\pi }^3}{c}}\right)=G$$

$${\left({\displaystyle \frac{{\left(\frac{1}{2\pi }\right)}^3+{\left(\frac{1}{2}\right)}^6{\pi }^3{e}^{\tan \left(\frac{180}{\pi }\right)}}{c^2}}\right)}^2=6.5693903027\times {10}^{-34}\cong h$$

$$\ln \left(\phi \right)\approx {\left({\displaystyle \frac{1}{2}}\right)}^6{\pi }^3$$

Accordingly, the cosmological constant depends on the geometric structure of time and three natural numbers.

$$h^2{G}^2{e}^{{\left(\phi \right)}^2{\pi }^3}=\mathsf{\Lambda }$$

This phenomenon defines the geometric K-tensor based on the force generating the wave.

$$K_{\mu \nu }=\left[\begin{array}{cccccc}{\displaystyle \frac{r_t}{\pi c}}& 0& 0& 0& 0& 0\\ 0& {\displaystyle \frac{{r_{t}he}^{{\pi }^3}}{c}}& 0& 0& 0& 0\\ 0& 0& {\displaystyle \frac{r_t\sqrt{G}h{e}^{{\phi }^2}}{c}}& 0& 0& 0\\ 0& 0& 0& {\displaystyle \frac{\sqrt{G}}{r_x}}& 0& 0\\ 0& 0& 0& 0& {\displaystyle \frac{\sqrt{G}}{r_x}}& 0\\ 0& 0& 0& 0& 0& {\displaystyle \frac{\sqrt{G}}{r_x}}\end{array}\right]$$

Parallel transport in the sixth dimension and the relation between the wave function and density define the two tensors of field and wave based on the metric structure.

$${\mathsf{\Psi }}_{\mu \nu }=\left[\begin{array}{cccccc}{cos}^2\theta {cos}^2\varphi & A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }\\ A_{\iota }& {cos}^2\varphi & A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }\\ A_{\iota }& A_{\iota }& e^{-i\pi \phi }& A_{\iota }& A_{\iota }& A_{\iota }\\ A_{\iota }& A_{\iota }& A_{\iota }& e^{i\pi \phi }& A_{\iota }& A_{\iota }\\ A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }& {sin}^2\theta & A_{\iota }\\ A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }& A_{\iota }& {sin}^2\theta {sin}^2\varphi \end{array}\right]$$

$$A_{\sigma }=\pm \left({\displaystyle \frac{\pi }{3}}\right)+iz,A_2=\pm \left({\displaystyle \frac{2\pi }{3}}\right)+iz,{ A}_3=\pm \left(\pi \right)+iz , A_4=\pm \left({\displaystyle \frac{4\pi }{3}}\right)+iz, A_5=\pm \left({\displaystyle \frac{5\pi }{3}}\right)+iz,A_6=\pm \left(2\pi \right)+iz$$

$$\sigma =\mathrm{1,2},\mathrm{3,4},\mathrm{5,6}$$

$$G_{\mu \nu }=\left[\begin{array}{cccccc}{\displaystyle \frac{10}{r^2}}& 0& 0& 0& 0& 0\\ 0& {\displaystyle \frac{4}{{r cos}^2\varphi }}& 0& 0& 0& 0\\ 0& 0& {\displaystyle \frac{4}{r {{cos}^2\theta cos}^2\varphi }}& 0& 0& 0\\ 0& 0& 0& {\displaystyle \frac{4}{r {{cos}^2\theta cos}^2\varphi }}& 0& 0\\ 0& 0& 0& 0& {\displaystyle \frac{4{\mathit{sin}}^2\theta }{{{r cos}^2\theta cos}^2\varphi }}& 0\\ 0& 0& 0& 0& 0& {\displaystyle \frac{4{\mathit{sin}}^2\mathit{\theta }{\mathit{sin}}^2\varphi }{{{ r a cos}^2\theta cos}^2\varphi }}\end{array}\right]$$

Accordingly, the final equation balances symmetric equilibrium across two metric spaces using Planck’s constant with relativistic and quantum scales.

$$\mathsf{\mu },\nu =\mathrm{1,2},\mathrm{3,4},\mathrm{5,6}$$

$${\mathsf{\Psi }}_{\mu \nu }+R_{\mu \nu }-{\displaystyle \frac{1}{2}}R{g}_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\left({\displaystyle \frac{\pi -2}{2}}\right)}^6\left({\displaystyle \frac{he}{c}}\right)T_{\mu \nu }+K_{\mu \nu }$$

Bottlenecks and constrictions in Möbius space create gaps in prime number groups and natural eccentricities within the spacetime structure, defined by the Möbius ODE and Bernoulli’s geometric principle.

$$d{s}^2=r{a}^2{cos}^2\theta {cos}^2\varphi d{\kappa }^2+r^2{a}^2{cos}^2\theta d{\varphi }^2+{\displaystyle \frac{r{a}^2}{1+\frac{b\left(\acute{r}\right)}{r}}}+{\displaystyle \frac{r^{2}a}{1+\frac{b\left(\acute{r}\right)}{r}}}+a^2{r}^2{sin}^2\theta d{\varphi }^2+a{r}^2{sin}^2\theta {sin}^2\varphi d{\kappa }^2$$

$$u \left(t\right)=c+c\left(t-t_0\right)+{\displaystyle \frac{1}{2}}c{(t-t_0)}^2$$

$$u\left(t\right)=c+c(t-t_0)+{\displaystyle \frac{1}{2}}c{(t-t_0)}^2+{\displaystyle \frac{1}{6}}c{(t-t_0)}^3+{\displaystyle \frac{1}{24}}c{(t-t_0)}^4+{\displaystyle \frac{1}{120}}c{(t-t_0)}^5$$

$$P+{\displaystyle \frac{1}{2}}\rho v^2+\rho gh⟹({{\displaystyle \frac{1}{2}})}^6{\pi }^3\rho c^2+\rho \sqrt{1-{\left(\partial \rho \right)}^2} \left({\displaystyle \frac{{\left(\frac{{\mathit{tan}}^{-1}\left(\phi \right)-\left(\frac{180}{\pi }\right)}{2\pi }\right)}^3\left(\frac{1}{6}\right){\pi }^3}{c}}\right)$$

The intrinsic eccentricity of spacetime geometry in the domain of information dependent on numbers between two time dimensions can be related to the metric phase difference across the two time dimensions.

$${\displaystyle \frac{\mathrm{t}\mathrm{a}\mathrm{n}\left(\theta \right)}{tan\left(\varphi \right)}}={\displaystyle \frac{\mathrm{s}\mathrm{i}\mathrm{n}\left(\theta \right)cos\left(\varphi \right)}{sin\left(\varphi \right)cos\left(\theta \right)}}={\displaystyle \frac{t_1}{t_2}}$$

$$x\propto {\displaystyle \frac{1}{t_2}} v={\displaystyle \frac{\Delta x2m}{\Delta \left(t_1,t_2\right)}} \left(m_{t_1}.m_{t_2}\right)={\displaystyle \frac{1}{\frac{\Delta x}{\Delta \left(t_1,t_2\right)} }}$$

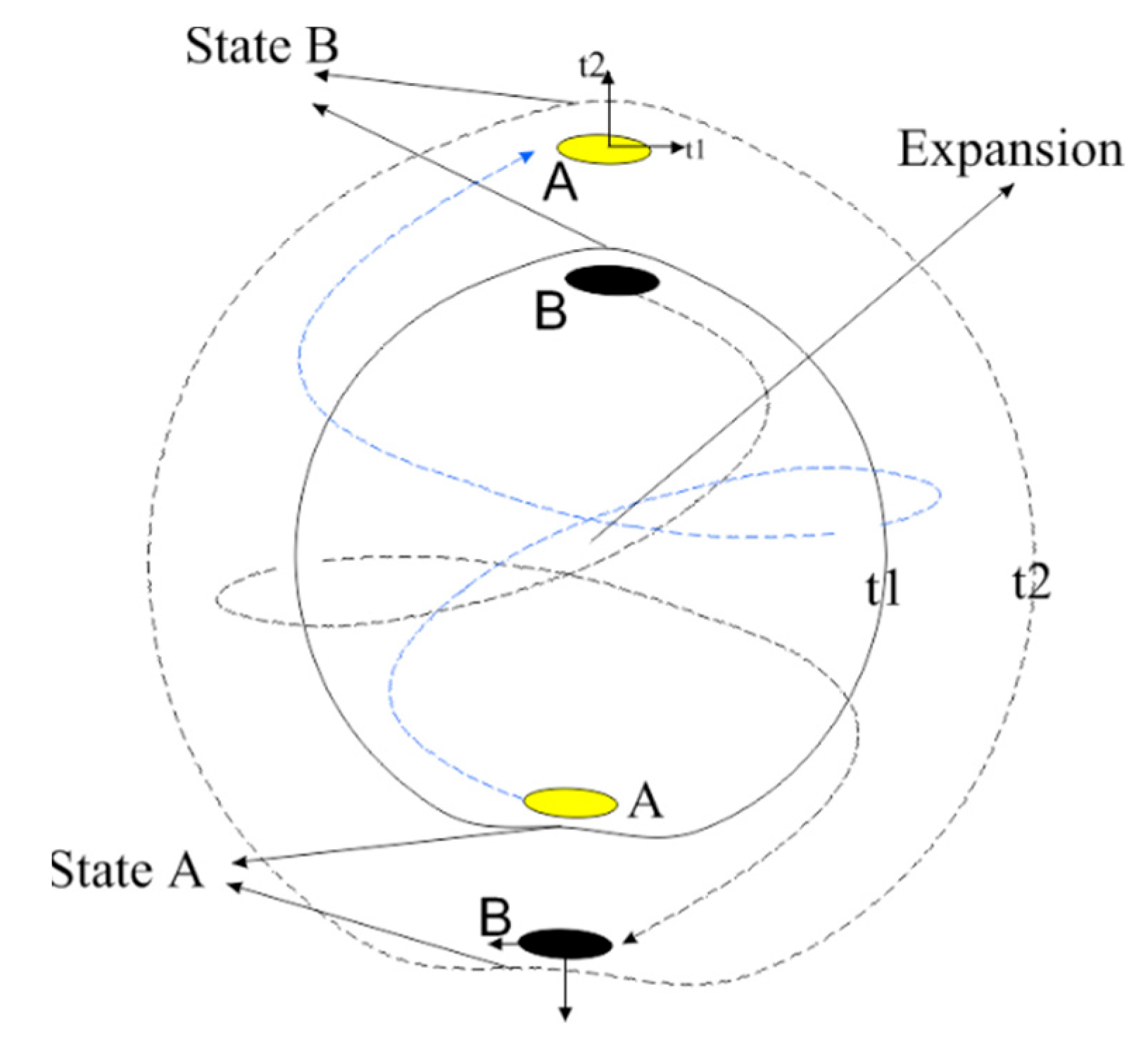
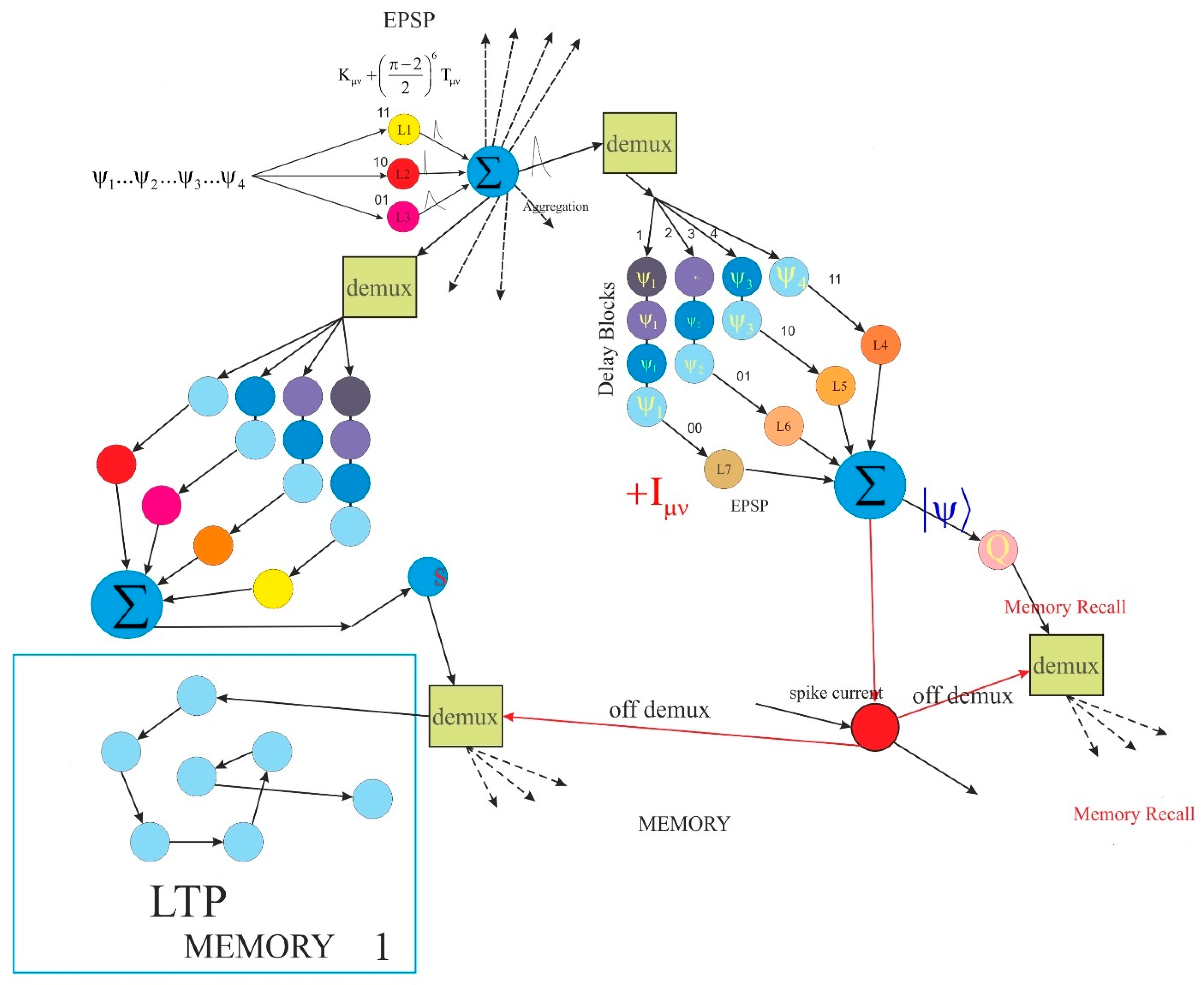
The correlation between wave function packets and the density-dependent wave function arises from continuous variations of intrinsic geometric density emerging from two of the time dimensions. Based on the six prime number groups and the five spacetime dimensions, the seesaw function establishes a shared continuity between two entangled particles within one of the groups.

$$E\left(a,b\right)={\int }_{-\rho }^{+\rho }{\int }_{-t}^{+t}{\int }_{-\infty }^{+\infty }{\left|\psi \left(\rho ,t,x\right)\right|}^{2}d\rho dtdx\tilde{\psi }\left(t_1,a\rho \right){\tilde{\psi }}^{-1}\left(t_2,b\rho \right)$$

Accordingly, the Möbius ODE links the gaps and regular variations of the shared group in a mirrored form to density changes and continuity in the time dimension through the geometric structure of spacetime. Based on this, multiple types of entanglement with distinct properties exist.

$$\tan \left({\displaystyle \frac{u\left(t\right)}{2}}\right)={\displaystyle \frac{\sqrt{1+\sqrt{1-\frac{a^2}{b^2}}}}{\sqrt{1-\sqrt{1-\frac{a^2}{b^2}}}}}.\mathit{tan}\left({\displaystyle \frac{E}{2}}\right)={\displaystyle \frac{\sqrt{1+sin\left({cos}^{-1}\left(\frac{a}{b}\right)\right)}}{\sqrt{1-sin\left({cos}^{-1}\left(\frac{a}{b}\right)\right)}}} . tan\left({\displaystyle \frac{E}{2}}\right)$$

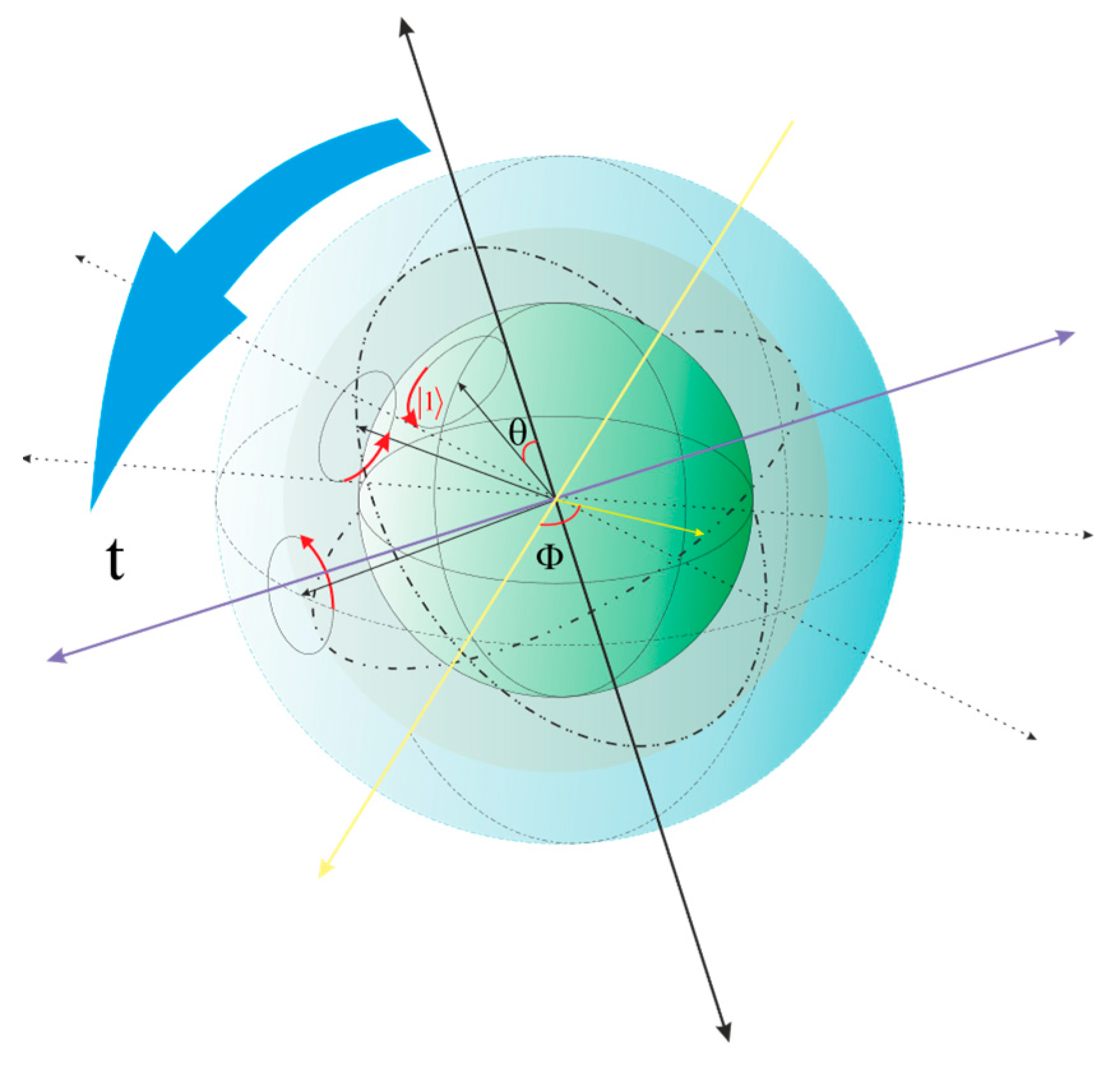
Therefore, the measurements of Alice and Bob are related to the two time dimensions and extend a long time. Figure 4

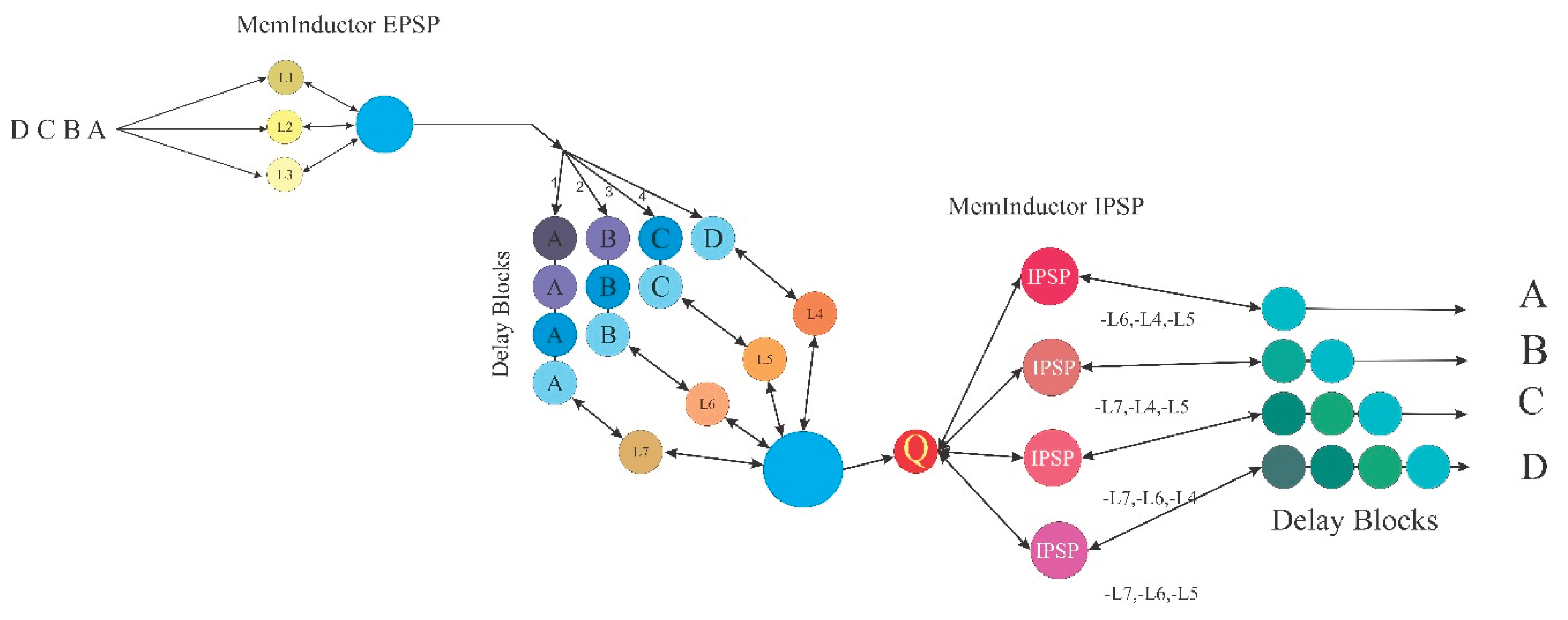
The effects of geometric potential on rotation, spin, and motion in the time dimensions depend on Bernoulli’s geometric principle in six-dimensional space. The generalized Pauli matrices define how geometric influences in six dimensions determine instantaneous entanglement. Based on the Möbius ODE and the seesaw function, the role of symmetric numbers within the groups and the mirror structure in Möbius space is defined across the gaps between each group. Figure 5

$$M=\left[\begin{array}{cc}{\sigma }_x.\rho & {\sigma }_y.\gamma \\ {\sigma }_y.\gamma & {\sigma }_z.P\end{array}\right]k\in \left(\mathrm{1,2},\dots ,6\right)$$

$${\sigma }_k=\left[\begin{array}{cc}0& {\sum }_k \\ {\sum }_k^{†} & 0\end{array}\right]$$

$${\sigma }_k\mathsf{\Psi }=\lambda \Psi$$

λ corresponds to spin–geometric coupling. Ψ is the state vector of the wave function in six-dimensional space.

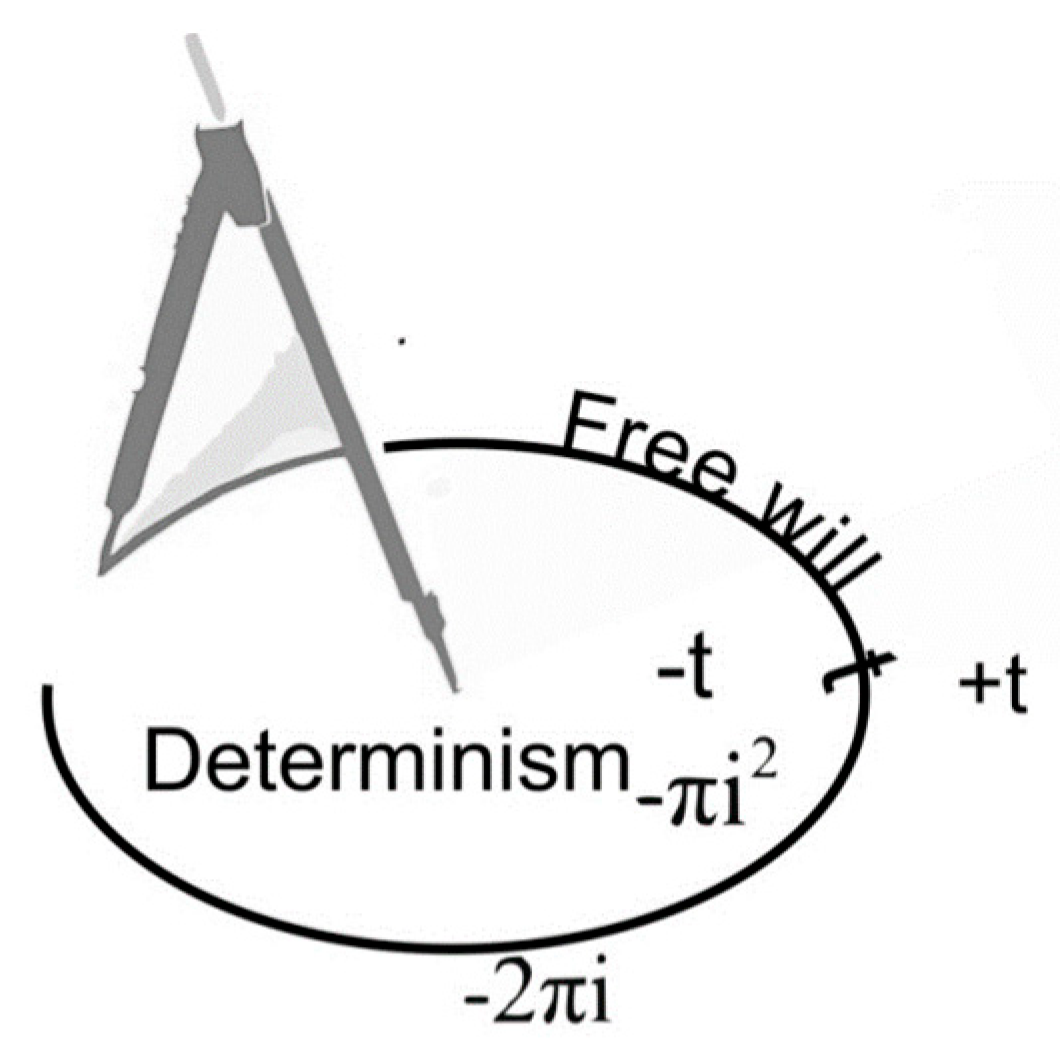
Reversal with preserved isotropy and homogeneity in the information domain leads to symmetric displacement of information over time.

$$∆n=\left|n-rev\left(n\right)\right|$$

Given the shared informational field and the equivalence principle between information and energy, and the presence of intrinsic geometric eccentricity in the Möbius structure, two clocks one with 100 minutes and one with 60 minutes are used for studying information in the temporal domain based on geometric and algebraic concepts over time, enabling precise prediction of outcomes.

$$h_{\acute{60}}\Rightarrow \left(h_n\times 60\right)+\left((h_n-1)\times 40\right)+m_{\acute{60}}=h_{\acute{100}} h_n\in 24:00$$

$$S={\int }_{-\rho }^{+\rho }{\int }_{-t}^{+t}{\int }_{-\infty }^{+\infty }{\left|\psi (I,t)\right|}^2 ln(sec({sin}^{-1}\left({\displaystyle \frac{{\log }_{\frac{40}{6}}\left(\frac{h_{\acute{60}}}{360}\right)}{{\mathit{log}}_{\frac{40}{6}}\left(\frac{h_{\acute{100}}}{360}\right)}}\right))d\rho dtdx=1$$

As a result, the significance of the Riemann zeta function and the intersection of five groups of prime numbers within the sixth group becomes evident in the phenomenon of entanglement.

$$\zeta {\zeta }^{*}\equiv A\left(1+{\displaystyle \frac{1}{2^s}}+{\displaystyle \frac{1}{3^s}}+{\displaystyle \frac{1}{5^s}}+{\displaystyle \frac{1}{7^s}}\right)\equiv 1$$

And likewise, in the SHCH test, the duration of time linked to two inhomogeneous geometric dimensions and the 60-minute and 100-minute clocks is crucial for accurately predicting outcomes.

$$sec({sin}^{-1}\left(\left|\left({\log }_2\left({\displaystyle \frac{\mathsf{\Delta }n\left(h_{60}\right)}{360}}\right)\right)\left({\mathit{log}}_2\left({\displaystyle \frac{\Delta n\left(h_{100}\right)}{360}}\right)\right)\right|\right)={\displaystyle \frac{1}{\sqrt{1+\frac{{\left(\ln \left(\frac{\Delta n\left(h_{60}\right)}{360}\right)\right)}^2{\left(\mathit{ln}\left(\frac{\Delta n\left(h_{60}\right)}{360}\right)\right)}^2}{\left(\mathit{ln}\left(2\right)\right)}}}}=R$$

$${\theta ,\varphi ϵ tan}^{-1}\left(R\sqrt{1-{\displaystyle \frac{{\left(\mathit{ln}\left(\frac{\Delta n\left(h_{60}\right)}{360}\right)\right)}^2{\left(\mathit{ln}\left(\frac{\Delta n\left(h_{60}\right)}{360}\right)\right)}^2}{\left(\mathit{ln}\left(2\right)\right)}}}\right)$$

$${\beta }_{CHSH}\left(S\right)={\left({\displaystyle \frac{1}{2}}\right)}^2{\sum _{x,y\in \mathrm{0,1}}(-1)}^{x^y}.⟨\left.\psi \right|A_z⨂B_y\left|\psi ⟩\right.$$

$$\left|\left({\tilde{\psi }}^2,\rho a\right)+\left({\tilde{\psi }}^2,\rho b\right)+\left({\tilde{\psi }}^2,-\rho a\right)+\left({\tilde{\psi }}^2,-\rho b\right)+\left({\tilde{\psi }}^2,-{\rho }^{†}b\right)+\left({\tilde{\psi }}^2,-{\rho }^{†}a\right)\right|=2\sqrt{2}\pm iP$$

$$⟨\tilde{\psi }|\tilde{\psi }⟩={\tilde{\psi }}^2{{\alpha }_1}^{*}=\sec \left(\arcsin \left({\log }_c\left({\displaystyle \frac{\partial x}{\partial t}}\right)\right)\right)={\displaystyle \frac{1}{\sqrt{1-\frac{{\left(ln\left(\frac{\partial x}{\partial t}\right)\right)}^2}{{\left(ln\left(c\right)\right)}^2}} }}{A}_{P_{G_i}} \cap B_{P_{G_i}}=P_{G_{6-5}}$$

$${\alpha }_1={\displaystyle \frac{1}{\sqrt{1+\frac{{\left(ln\left(\frac{\partial x}{\partial t}\right)\right)}^2}{{\left(ln\left(c\right)\right)}^2}} }}{{\alpha }_1}^{*}{\alpha }_1=\left(t,\rho \right),(t,-\rho )$$

The tensor E defines the relationship between the two operators E and K over time, as well as the role of past and future states in the entanglement phenomenon within Möbius space.

$${\left|\left(\left|1⟩\right.⨂\left|a_1⟩\right.\right)⟨\left.\acute{\phi }\right|\right|}^2=E {\left|\left(⟨\left.1\right|⨂⟨\left.b_1\right|\right)\left|\acute{\phi }⟩\right.\right|}^2=K$$

$$E_{\mu \nu }=\left[\begin{array}{cccccc}r{a}^2{\left|\left(⟨\left.0\right|⨂⟨\left.a_0\right|\right)\left|\phi ⟩\right.\right|}^{2}K& 0& 0& 0& 0& 0\\ 0& r^2{a}^2{\left|\left(⟨\left.1\right|⨂⟨\left.a_1\right|\right)\left|\acute{\phi }⟩\right.\right|}^2& 0& 0& 0& 0\\ 0& 0& r^2{a}^2⟨\acute{\phi }|\phi ⟩& 0& 0& 0\\ 0& 0& 0& {a^{2}r}^2⟨\phi |\acute{\phi }⟩& 0& 0\\ 0& 0& 0& 0& a^2{r}^2{\left|\left(\left|1⟩\right.⨂\left|b_1⟩\right.\right)⟨\left.\acute{\phi }\right|\right|}^2& 0\\ 0& 0& 0& 0& 0& {a r}^2{\left|\left(\left|0⟩\right.⨂\left|b_0⟩\right.\right)⟨\left.\phi \right|\right|}^{2}E\end{array}\right]$$

$$M\left\{1,-1,-\mathrm{1,0},-\mathrm{1,1}\right\}$$

$${cos}^2\left({cos}^{-1}\left({\displaystyle \frac{p_n}{p_{n+1}}}\right)\right)=P_{diff}$$

$${\left|\left(⟨\left.0\right|⨂⟨\left.a_0\right|\right)\left|\phi ⟩\right.\right|}^2={\displaystyle \frac{1}{2}}{cos}^2{\displaystyle \frac{\pi }{8}}{\left|\left(⟨\left.1\right|⨂⟨\left.a_1\right|\right)\left|\phi ⟩\right.\right|}^2={\displaystyle \frac{1}{2}}{cos}^2{\displaystyle \frac{\pi }{8}}$$

The entanglement equation over time, based on information fields, density variations, and wave functions, is expressed as a generalization of the general relativity equation in six dimensions.

$$\mathsf{\mu },\nu =\mathrm{1,2},\mathrm{3,4},\mathrm{5,6}$$

$${\mathsf{\Psi }}_{\mu \nu }+E_{\mu \nu }+\mathsf{\Lambda }{g}_{\mu \nu }={\left({\displaystyle \frac{\pi -2}{2}}\right)}^6\left({\displaystyle \frac{he}{c}}\right)T_{\mu \nu }+K_{\mu \nu }$$

The cosmological constant acts as a deterrent against violation of causality in the macroscopic world. It also describes the backward butterfly effect over time. The reversed butterfly effect equation: a past fluctuation $\delta \rho$over time lag $\mathsf{\Delta }t$is proportional to the cosmological constant$\mathsf{\Lambda }$ times the spacetime Laplacian of the potential $\varphi \left(x^{\upsilon }\right)$.

$${\displaystyle \frac{dx}{dt}}=\sigma \left(x-y\right) {\displaystyle \frac{dy}{dt}}=x\left(\rho -z\right)-y {\displaystyle \frac{dz}{dt}}=xy-\beta z$$

$$sin\left(\theta \right)cos\left(\theta \right)sin\left(\varphi \right)cos\left(\varphi \right)=t_1{t}_2$$

$$sin\left(\theta \right)cos\left(\theta \right)sin\left(\varphi \right)cos\left(\varphi \right)=\partial t$$

$$\left(\partial t\right)\sigma \left(x-y\right)=dx \left(\partial t\right)x\left(\rho -z\right)-y=dy \left(\partial t\right)xy-\beta z=dz$$

$$\partial t_{-}={\displaystyle \frac{x{y}^2}{1+\frac{z\left(\partial t\right)}{x}}}+{\displaystyle \frac{x^{2}y}{1+\frac{z\left(\partial t\right)}{x}}}$$

$$\phi +{INDS\left(G_8\right)}^s{x}^{\mu }\left({\displaystyle \frac{1}{{INDS\left(G_1\right)}^s}}+{\displaystyle \frac{1}{{INDS\left(G_2\right)}^s}}+{\displaystyle \frac{1}{{INDS\left(G_4\right)}^s}}+{\displaystyle \frac{1}{{INDS\left(G_5\right)}^s}}+{\displaystyle \frac{1}{{INDS\left(G_7\right)}^s}}-{\displaystyle \frac{1}{{INDS\left(G_8\right)}^{s}B}}\right)=\varphi \left(x^{\upsilon }\right){\Delta }_{\mu }{∆}^{\mu }.\mathsf{\Lambda }.\delta \rho (t-\Delta t)$$

This equation expresses the role of prime numbers in creating an algebraic environment over time. It means the butterfly’s path may be influenced by a weakened reverse butterfly effect from the future, while the flight itself is the chaotic cause of a larger phenomenon in the future. Figure 6

Based on density variations, quantization, and wave packets, as well as the relation between temperature and radiation, and defining physical concepts in the information domain through equivalence of information and energy, information transfer between spatial points can occur instantly faster than light via continuity of time-dimensional structures. Figure 7 and Figure 8

$${\displaystyle \frac{ \lambda \left(t\right) }{c}}~{\displaystyle \frac{1}{{cos}^2\theta {cos}^2\varphi }}.{\displaystyle \frac{1}{\omega }} ~L_{\tilde{\psi }} ,{\displaystyle \frac{h}{mv}}=\lambda$$

$$\Rightarrow \left|{\tilde{\psi }}_1\right.⟩={\displaystyle \frac{h}{r {cos}^2\theta {cos}^2\varphi }} \chi ={sin}^2\theta {sin}^2\varphi {sin}^2\theta$$

$$\left|\mathsf{\Psi }⟩\right.={\displaystyle \frac{h\upsilon {(e}^{-ik{r}^2\chi })}{{a^{4}r}^3{cos}^2\theta {cos}^2\varphi { cos}^2\varphi \pi }} T_{\left(\rho \right)}\equiv {\displaystyle \frac{\hslash c}{k_b}}{.\left({\displaystyle \frac{{\partial }^2\sqrt{1+{\left(\partial \rho \right)}^2}}{\partial {\left(sec\right({sin}^{-1}({\mathit{log}}_n\left(\frac{\partial \rho }{\partial x}\right)\left)\right)}^2}}\right)}^{{\displaystyle \frac{1}{4}}}$$

$$\lambda \approx {\displaystyle \frac{h}{{\left(\rho c\right)}^{\frac{1}{2}}}}.e^{i\pi \phi }$$