Submitted:
16 May 2025
Posted:
17 May 2025
You are already at the latest version
Abstract
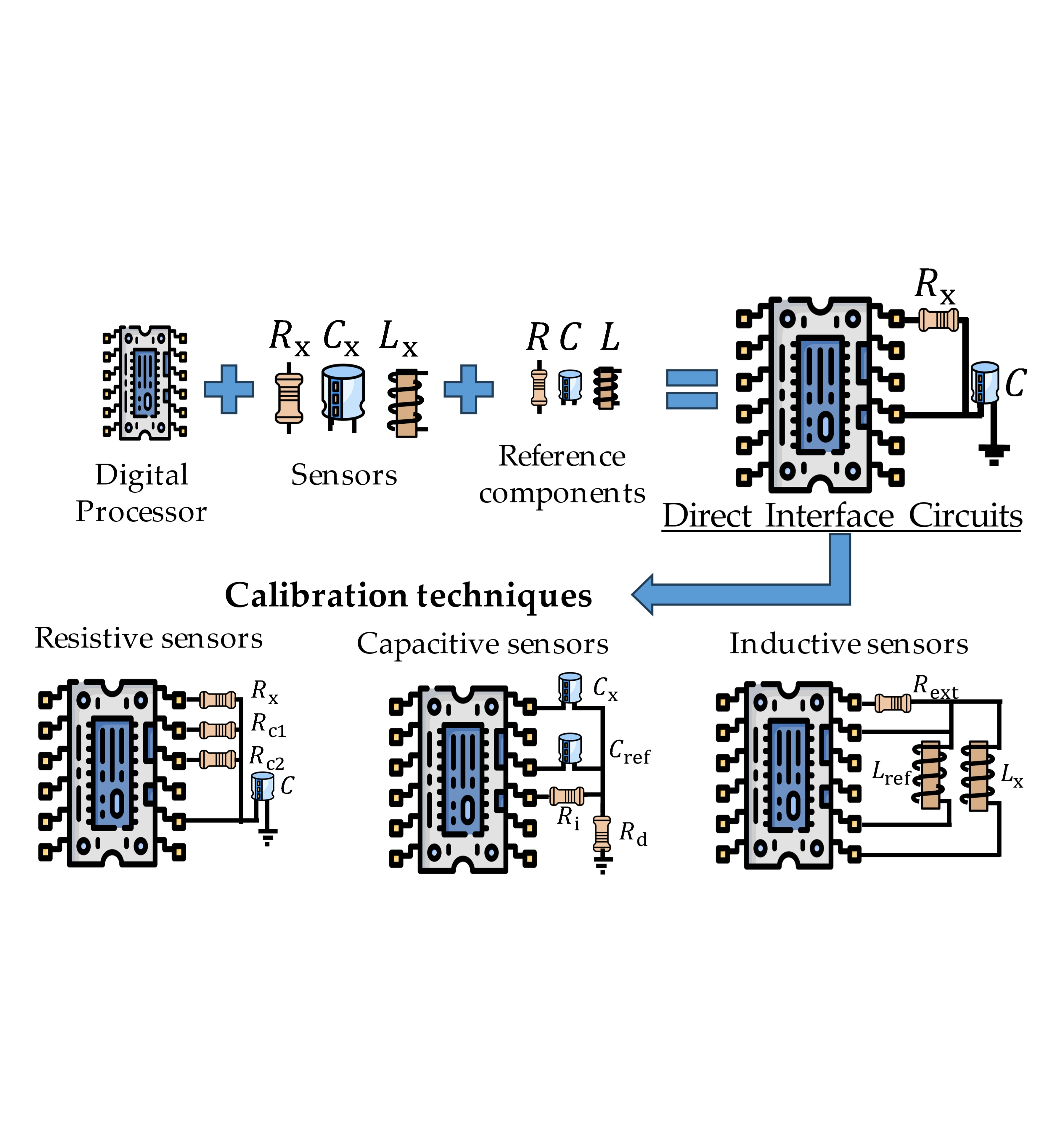
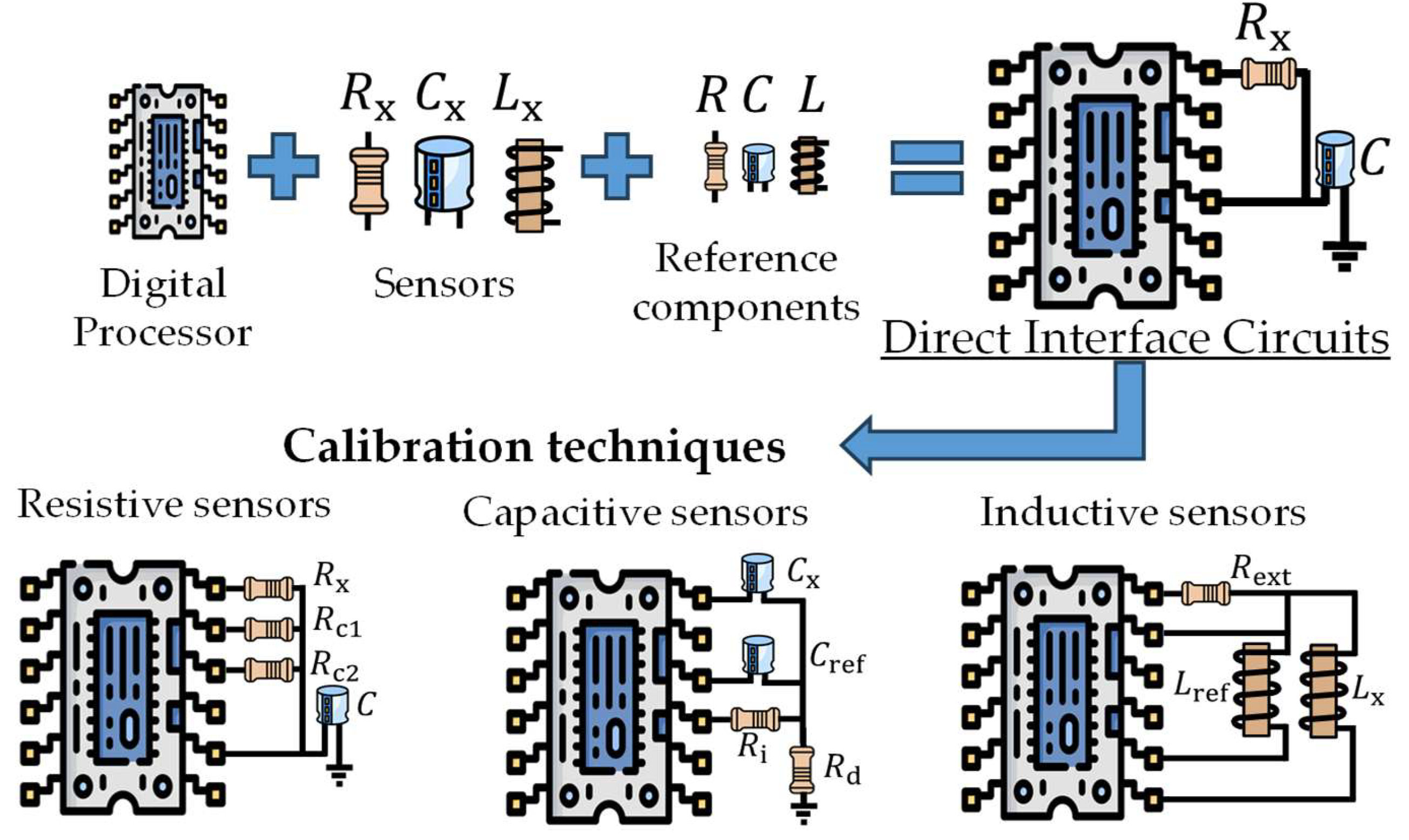
Keywords:
1. Introduction
1.1. Related Works
- A comprehensive overview of the operating principles, core components, and implementation techniques of DICs for resistive, capacitive, and inductive sensors.
- A critical analysis of recent publications proposing improved methods to enhance measurement accuracy, resolution, acquisition time, and uncertainty management in DIC-based systems.
- An assessment of current application domains for DICs and strategic recommendations for future research efforts.
- A discussion of the most significant advances to date and the remaining technical challenges that must be addressed for broader adoption of DICs in future instrumentation systems.
1.2. Paper Organization
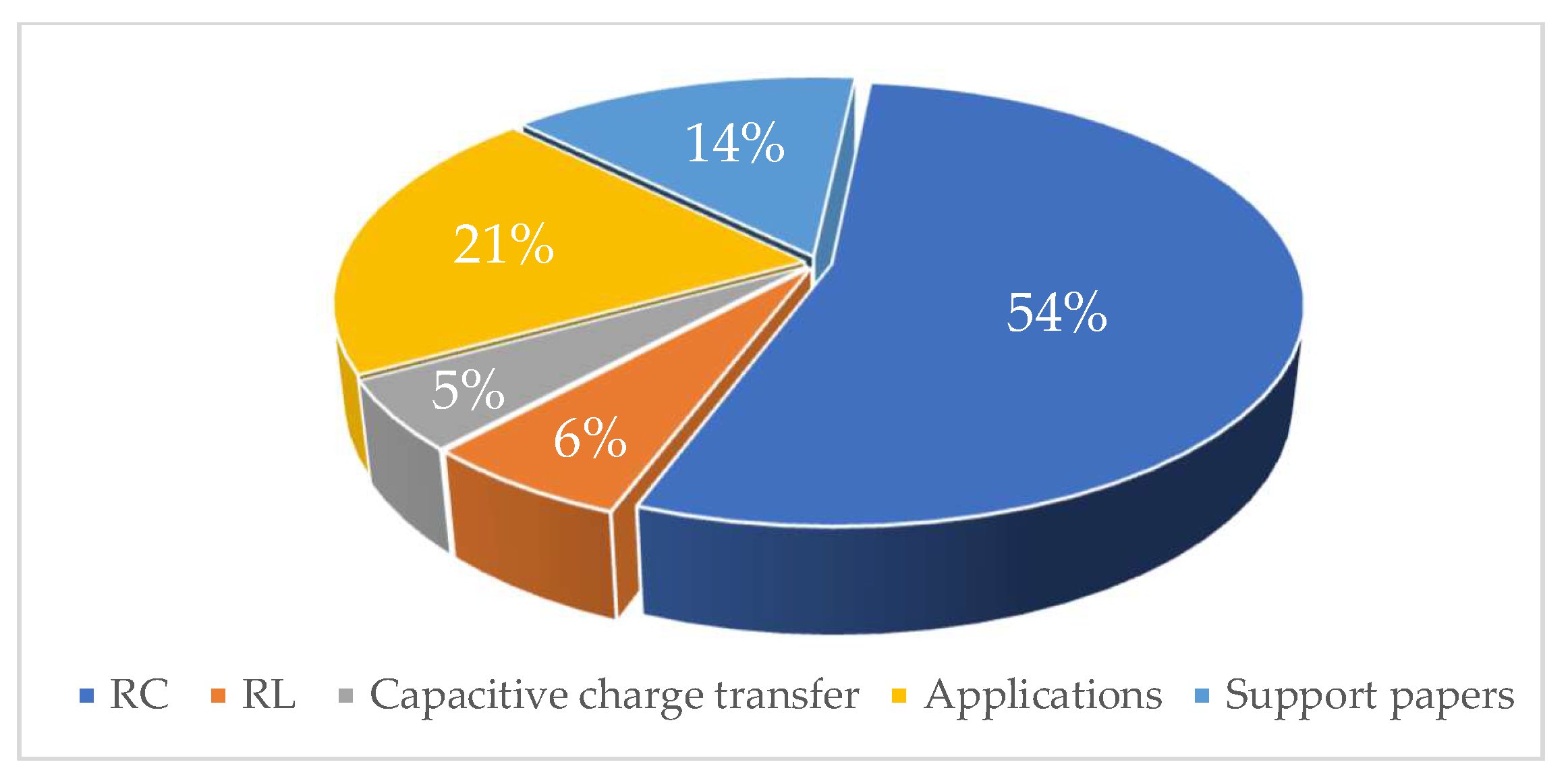
1.3. Review Methodology
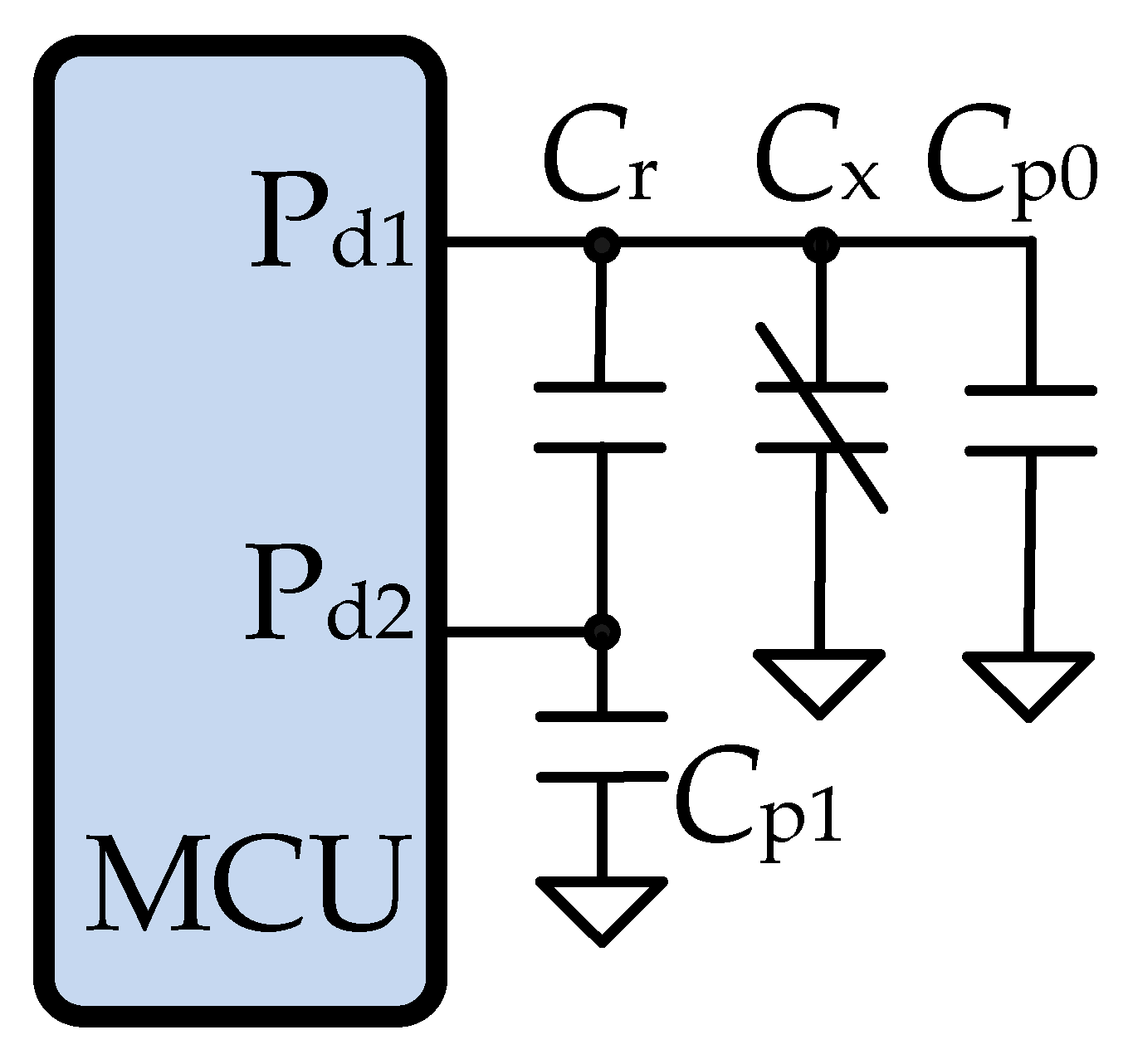
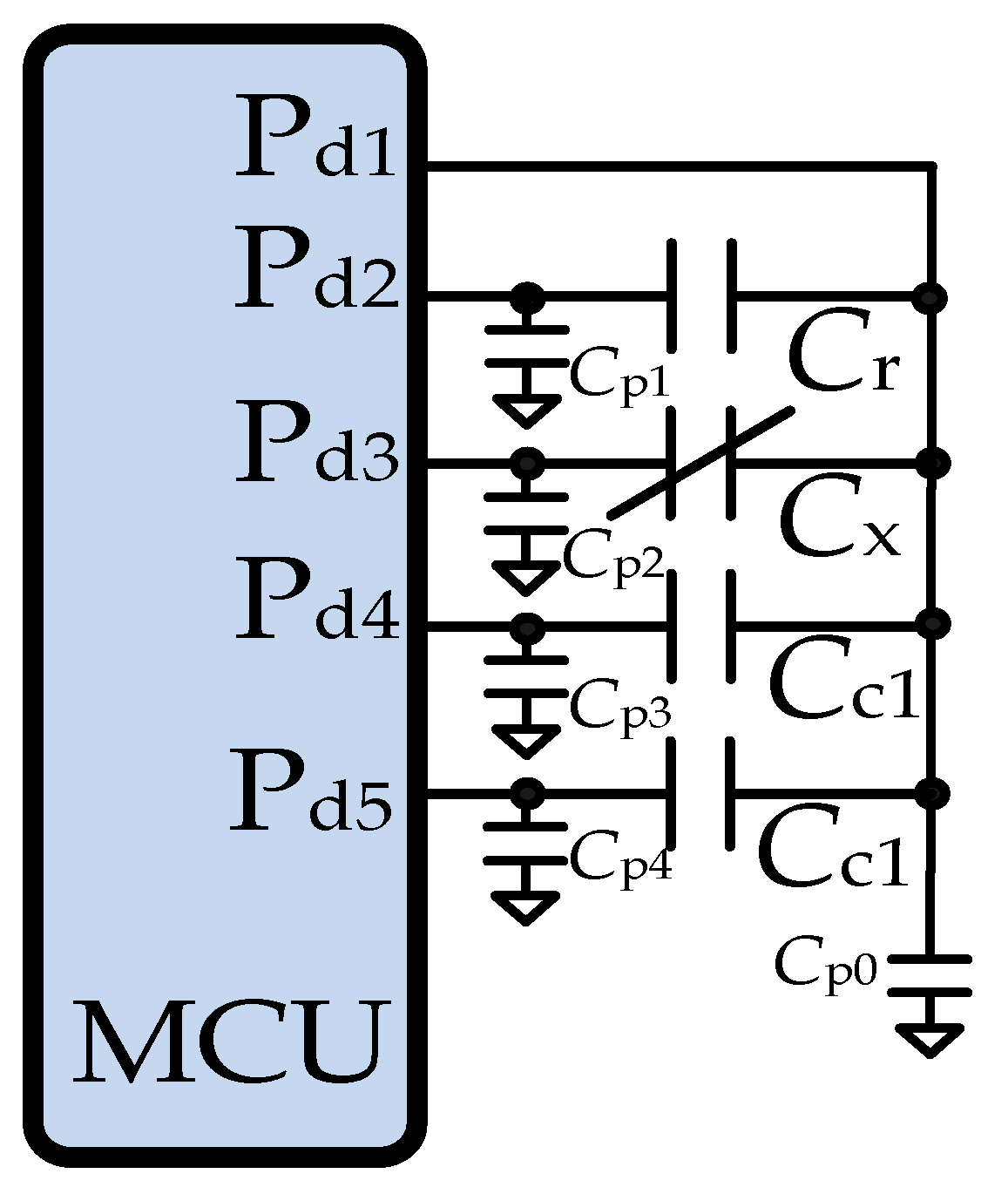
2. Elements of a DIC
2.1. Sensors
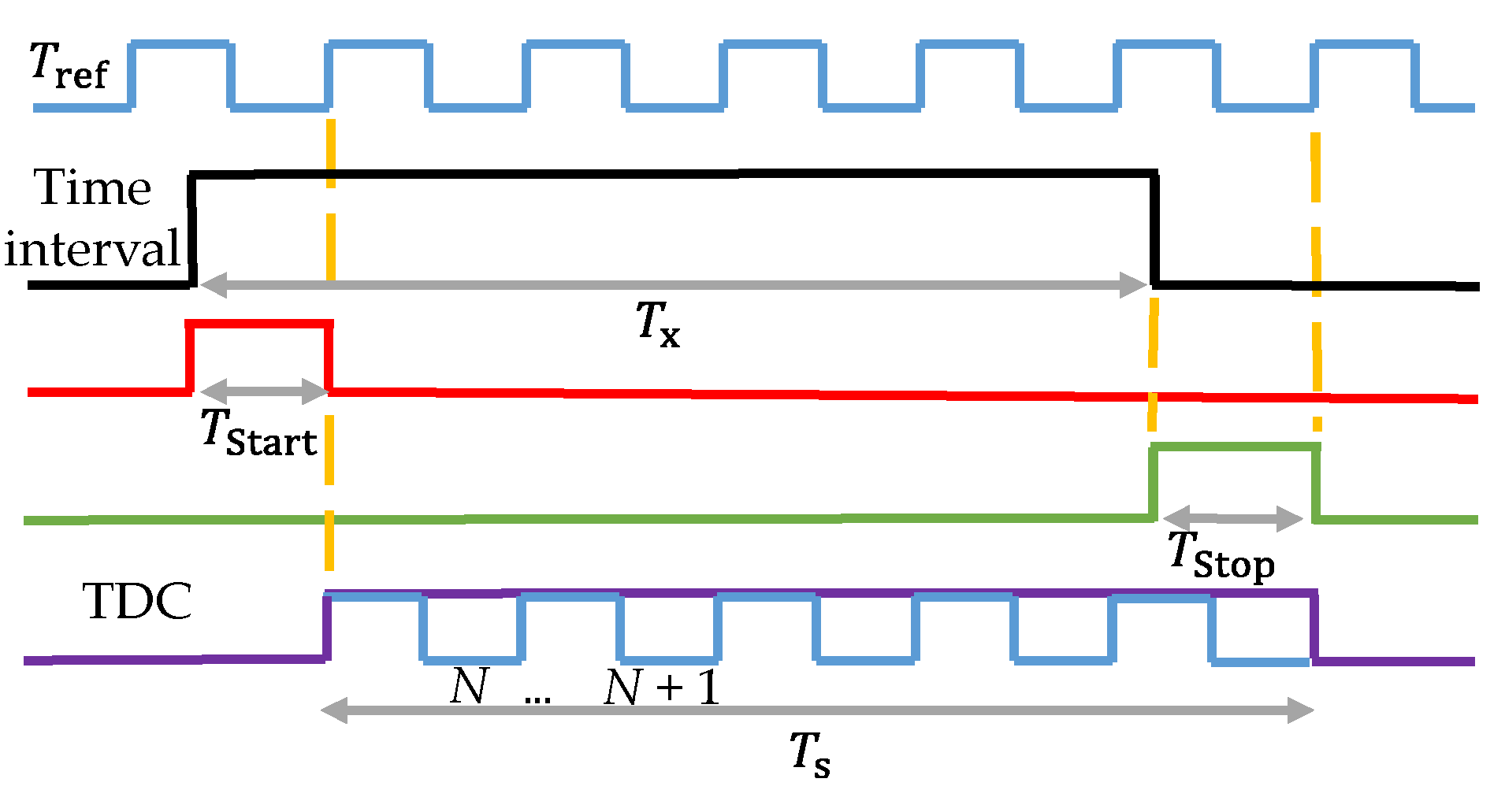
2.2. Time-to-Digital Converter
2.3. Digital Processor
3. Direct Interface Techniques
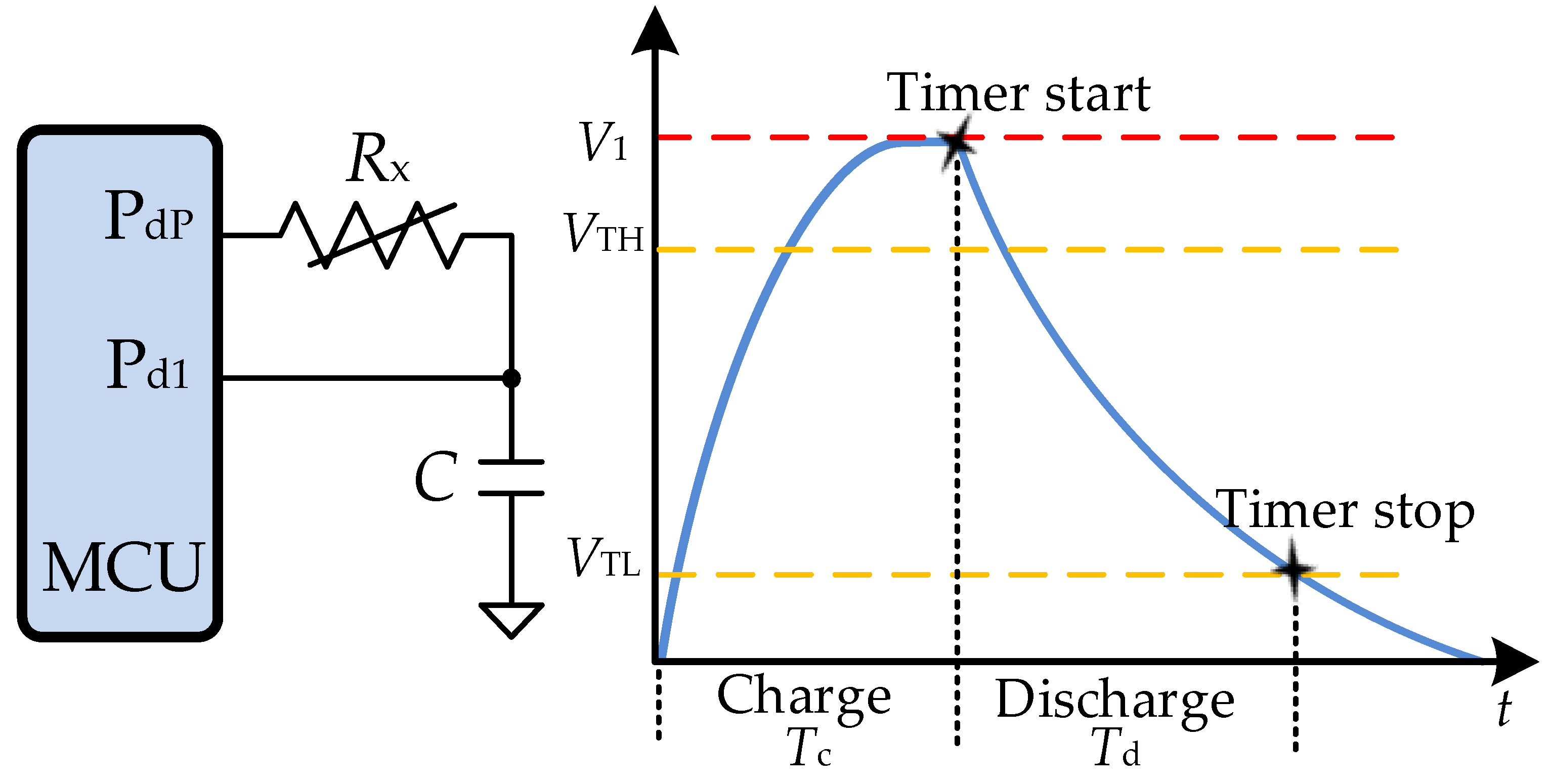
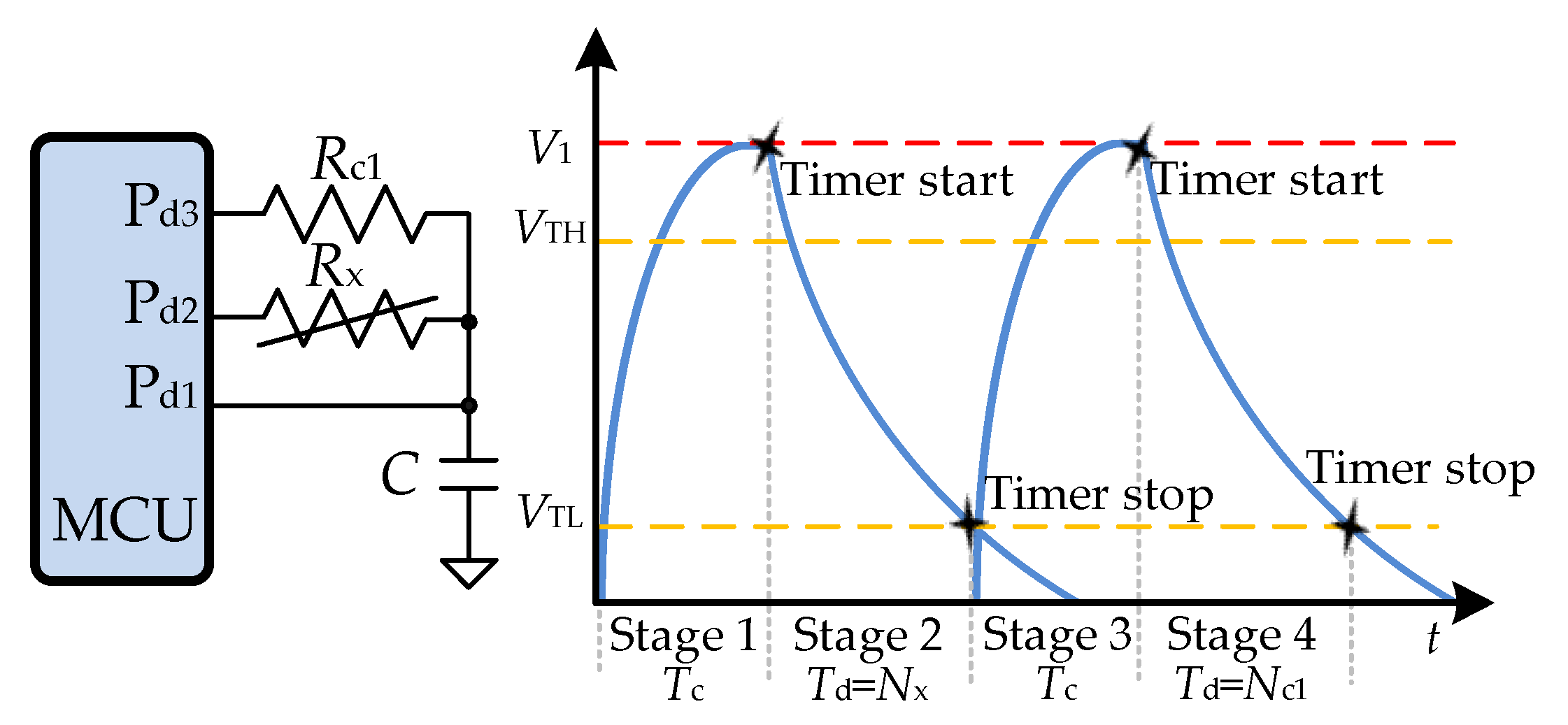
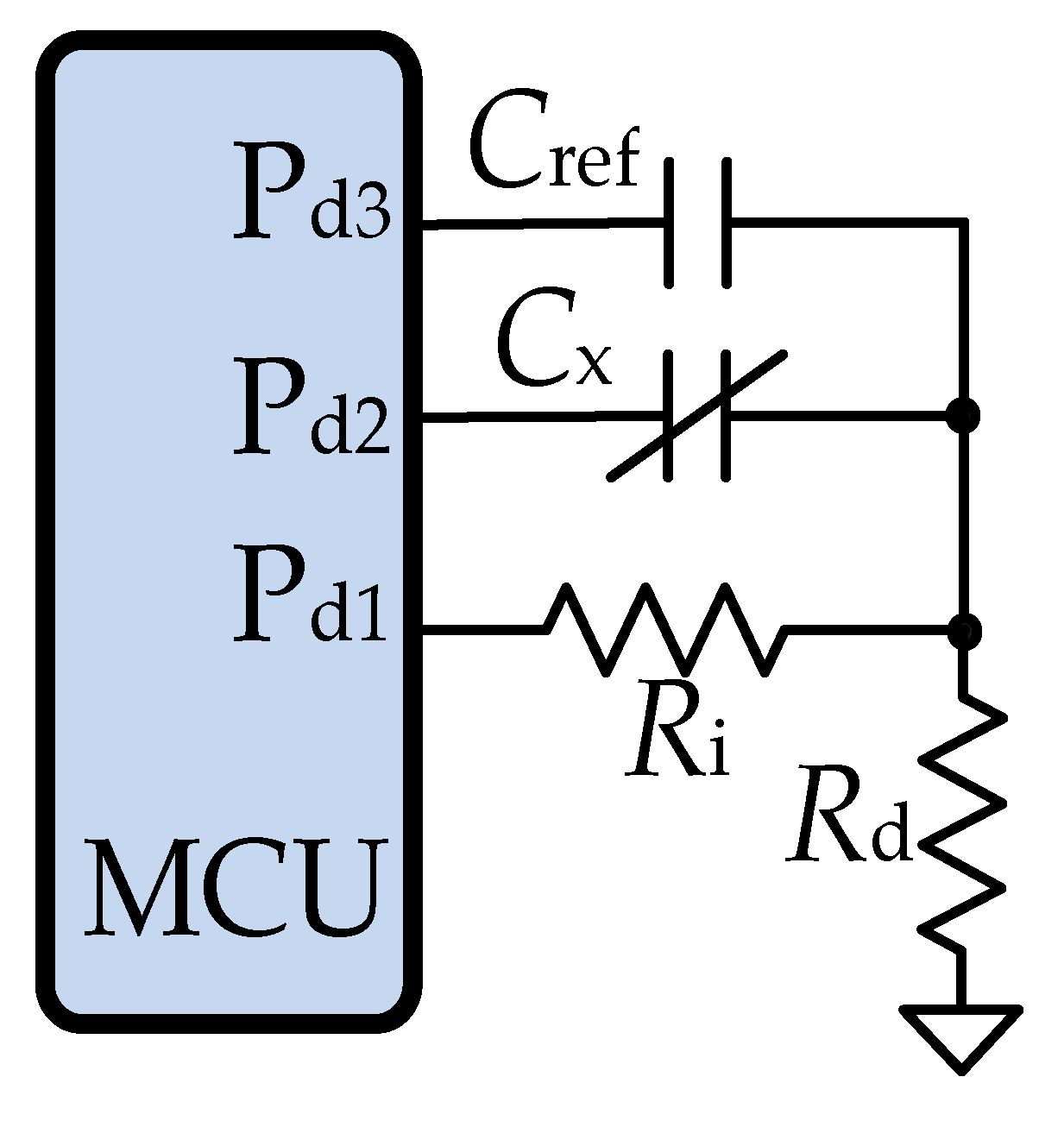
3.1. Circuits with RC Components
3.2. Circuits with RL Components
3.3. Circuits with Capacitive Charge Transfer
4. Analysis
4.1. Initial Scope of a DIC
4.2. Implemented Digital Processors
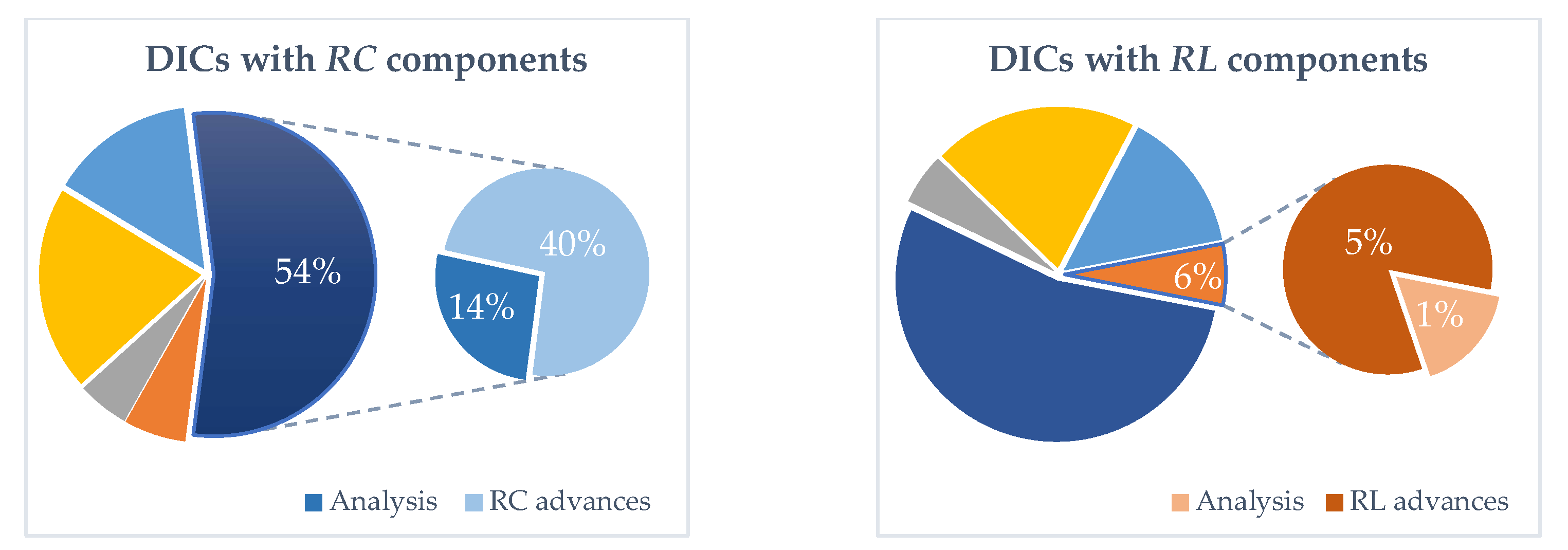
4.3. DIC with RC Components
4.4. DIC with RL Components
4.5. DIC with Capacitive Charge Transfer
4.6. Summary of DIC Applications
5. Discussion
6. Conclusion
Author Contributions
Funding
Conflicts of Interest
References
- Sehrawat, D.; Gill, N.S. Smart Sensors: Analysis of Different Types of IoT Sensors. In Proceedings of the 3rd International Conference on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India; 2019. [Google Scholar]
- Mohammadzadeh, N.; Gholamzadeh, M.; Saeedi, S.; Rezayi, S. The application of wearable smart sensors for monitoring the vital signs of patients in epidemics: a systematic literature review. J. Ambient Intell. Humaniz. Comput. 2023, 14, 6027–6041. [Google Scholar] [CrossRef] [PubMed]
- Ramírez-Moreno, M.A.; Keshtkar, S.; Padilla-Reyes, D.A.; Ramos-López, E.; García-Martínez, M.; Hernández-Luna, M.C.; Mogro, A.E.; Mahlknecht, J.; Huertas, J.I.; Peimbert-García, R.E.; Ramírez-Mendoza, R.A.; et al. Sensors for Sustainable Smart Cities: A Review. Appl. Sci. 2021, 11, 29. [Google Scholar] [CrossRef]
- Daugherty, K.M. Analog-to-digital conversion. A practical Approach; McGraw Hill: New York, NY, USA, 1995. [Google Scholar]
- Webster, J.G.; Eren, H. Characteristics of instrumentation. In Measurement, Instrumentation, and Sensors Handbook; CRC Press: N.W. (Florida), USA, 1999. [Google Scholar]
- Reverter, F.; Pallás-Areny, R. Direct Sensor-to-Microcontroller Interface Circuits; Marcombo: Barcelona, Spain, 2005. [Google Scholar]
- Reverter, F. The art of directly interfacing sensors to microcontrollers. J. Low Power Electron. 2012, 2, 265–281. [Google Scholar] [CrossRef]
- Sherman, D. Measure resistance and capacitance without an A/D: AN449. Philips Semiconductors Microcontrollers Products 1993. [Google Scholar]
- Webjör, Å. Simple A/D for MCUs without built-in A/D converters: AN477. Motorola Semiconductors 1993. [Google Scholar]
- Cox, D. Implementing Ohmmeter/Temperature Sensor: AN512. Microchip Technology: Chandler, AZ, USA, 1994.
- Richey, R. Resistance and Capacitance Meter Using a PIC16C622: AN611. Microchip Technology: Chandler, AZ, USA, 1997.
- Bierl, L. Precise Measurements with the MSP430; Texas Instruments: Dallas, TX, USA, 1996. [Google Scholar]
- Merritt, B. MSP430 based digital thermometer. Application Report 1999; Texas Instruments.
- Hauptmann, P. Resonant sensors and applications. Sens. Actuators 1991, 371–377. [Google Scholar] [CrossRef]
- Reverter, F.; Jordana, J.; Gasulla, M.; Pallàs-Areny, R. Accuracy and resolution of direct resistive sensor-to-microcontroller interfaces. Sens. Actuators 2005, 121, 78–87. [Google Scholar] [CrossRef]
- Reverter, F.; Casas, O. Interfacing differential resistive sensors to microcontrollers: a direct approach. IEEE Trans. Instrum. Meas. 2009, 3405–3410. [Google Scholar] [CrossRef]
- Sifuentes, E.; Casas, O.; Reverter, F.; Pallàs-Areny, R. Direct interface circuit to linearise resistive sensor bridges. Sens. Actuators 2008, 147, 210–215. [Google Scholar] [CrossRef]
- Reverter, F.; Casas, O. Direct interface circuit for capacitive humidity sensors. Sens. Actuators A Phys. 2008, 143, 315–322. [Google Scholar] [CrossRef]
- Reverter, F.; Casas, O. Interfacing differential capacitive sensors to microcontrollers: a direct approach. IEEE Trans. Instrum. Meas. 2010, 59, 2763–2769. [Google Scholar] [CrossRef]
- Reverter, F.; Casas, O. A microcontroller-based interface circuit for lossy capacitive sensors. Meas. Sci. Technol. 2010, 21. [Google Scholar] [CrossRef]
- Kokolanski, Z.; Jordana, J.; Gasulla, M.; Dimcev, V.; Reverter, F. Direct inductive sensor-to-microcontroller interface circuit. Sens. Actuators A Phys. 2015, 224, 185–191. [Google Scholar] [CrossRef]
- Ramadoss, N.; Boby, G. A simple microcontroller based digitizer for differential inductive sensors. In Proceedings of the 2015 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Pisa, Italy; 2015. [Google Scholar]
- Peatman, J. Design with PIC Microcontrollers; Pearson Education: Upper Saddle River, NJ, USA, 1997. [Google Scholar]
- Hall, S.; Hall, G.; McCal, J. High-speed digital system design. A handbook of interconnect theory and design practices; Wiley-IEEE Press: New York, NY, USA, 2000. [Google Scholar]
- Pallàs-Areny, R.; Webster, J.G. Sensors and Signal Conditioning, 2nd ed.; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Bakhoum, E.G.; Cheng, M.H.M. High-Sensitivity Inductive Pressure Sensor. IEEE Trans. Instrum. Meas. 2011, 60, 2960–2966. [Google Scholar] [CrossRef]
- Henzler, S. Time-To-Digital Converters; Springer Series in Advanced Microelectronics 29; Springer: Berlin, Germany, 2010.
- Bannatyne, R.; Viot, G. Introduction to microcontrollers. In WESCON/97 Conference Proceedings, Santa Clara, CA, USA, 1997.
- Boutros, A.; Betz, V. FPGA Architecture: Principles and Progression. IEEE Circuits Syst. Mag. 2021, 21, 4–29. [Google Scholar] [CrossRef]
- Reverter F.; Vidal-Verdú, F.; Hidalgo-Lopez, J.A. Advanced techniques for directly interfacing resistive sensors to digital systems, In Advanced Interfacing Techniques for Sensors: Measurement Circuits and Systems for Intelligent Sensors, Boby, G.; Roy, J. K.; Kumar, V. J.; Mukhopadhyay, S. C.; Eds.; Springer International Publishing, Cham, Switzerland, 2017, 139–165.
- Reverter, F.; Gasulla, M.; Pallàs-Areny, R. A Low-Cost Microcontroller Interface for Low-Value Capacitive Sensors. In Proceedings of the 21st IEEE Instrumentation and Measurement Technology Conference (IEEE Cat. No.04CH37510), 2004.
- Van Der Goes, F.M.; Meijer, G.C. A novel low-cost capacitive-sensor interface. IEEE Trans. Instrum. Meas. 1996, 45, 536–540. [Google Scholar] [CrossRef]
- Gaitán-Pitre, J.E.; Gasulla, M.; Pallàs-Areny, R. Direct interface for capacitive sensors based on the charge transfer method. In 2007 IEEE Instrumentation & Measurement Technology Conference IMTC 2007, Warsaw, Poland, 2007.
- Dietz, P.H.; Leigh, D.; Yerazunis, W.S. Wireless Liquid Level Sensing for Restaurant Applications. In SENSORS, 2002 IEEE, Orlando, FL, USA, 2002.
- Gaitán-Pitre, J.E.; Gasulla, M.; Pallàs-Areny, R. Analysis of a direct interface circuit for capacitive sensors. IEEE Trans. Instrum. Meas. 2009, 58, 2931–2937. [Google Scholar] [CrossRef]
- Hidalgo-Lopez, J.A. A Simple Digital Readout Circuit for Differential Resistive or Capacitive Sensors. Meas. Sci. Technol. 2023. [Google Scholar] [CrossRef]
- Hidalgo-Lopez, J.A.; Castellanos-Ramos, J. Two proposals to simplify resistive sensor readout based on Resistance-to-Time-to-Digital conversion. Measurement 2023, 213. [Google Scholar] [CrossRef]
- Hidalgo-López, J.A.; Castellanos-Ramos, J. Simplifying Capacitive Sensor Readout Using a New Direct Interface Circuit. IEEE Trans. Instrum. Meas. 2023, 72, 1–10. [Google Scholar] [CrossRef]
- Hidalgo-López, J.A.; Oballe-Peinado, Ó.; Castellanos-Ramos, J.; Sánchez-Durán, J.A. Two-Capacitor Direct Interface Circuit for Resistive Sensor Measurements. Sensors 2021, 21. [Google Scholar] [CrossRef] [PubMed]
- Hidalgo-López, J.A.; Sánchez-Durán, J.A.; Oballe-Peinado, Ó. Method to Reduce Quantization Error in Direct Interface Circuits for Resistive Sensors. IEEE Sens. J. 2020, 20, 13910–13918. [Google Scholar] [CrossRef]
- Hidalgo-López, J.A.; Sánchez-Durán, J.A.; Oballe-Peinado, Ó. Reducing Measurement Time in Direct Interface Circuits for Resistive Sensor Readout. Sensors 2020, 20, 1–13. [Google Scholar] [CrossRef]
- Hidalgo-López, J.A.; Botín-Córdoba, J.A.; Sánchez-Durán, J.A.; Tejero-Calado, J.C.; Oballe-Peinado, Ó. Improved Calibration Method for Resistive Sensors using Direct Interface Circuits. IEEE Trans. Instrum. Meas. 2019, 69. [Google Scholar] [CrossRef]
- Hidalgo-López, J.A.; Botín-Córdoba, J.A.; Sánchez-Durán, J.A. Fast Calibration Methods for Resistive Sensor Readout Based on Direct Interface Circuits. Sensors 2019, 19. [Google Scholar] [CrossRef]
- Oballe-Peinado, Ó.; Vidal-Verdú, F.; Sánchez-Durán, J.A.; Castellanos-Ramos, J.; Hidalgo-López, J.A. Smart Capture Modules for Direct Sensor-to-FPGA Interfaces. Sensors 2015, 15, 31762–31780. [Google Scholar] [CrossRef]
- Czaja, Z. Time-domain measurement methods for R, L and C sensors based on a versatile direct sensor-to-microcontroller interface circuit. Sens. Actuators A Phys. 2018, 274, 199–210. [Google Scholar] [CrossRef]
- Czaja, Z. A measurement method for capacitive sensors based on a versatile direct sensor-to-microcontroller interface circuit. Measurement 2020, 155, 1–11. [Google Scholar] [CrossRef]
- Nagarajan, P.R.; Boby, G.; Kumar, V.J. Improved Single-Element Resistive Sensor-to-Microcontroller Interface. IEEE Trans. Instrum. Meas. 2017, 66, 2736–2744. [Google Scholar] [CrossRef]
- Asif, A.; Ali, A.; Ul Abdin, M.Z. Resolution Enhancement in Directly Interfaced System for Inductive Sensors. IEEE Trans. Instrum. Meas. 2019, 68, 4104–4111. [Google Scholar] [CrossRef]
- Kokolanski, Z.; Gasulla, M.; Reverter, F. Differential Inductive Sensor-to-Microcontroller Interface Circuit. In 2019 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Auckland, New Zealand, 2019.
- Anarghya, A.; Rao, S.S.; Herbert, M.A.; Karanth, P.N.; Rao, N. Investigation of errors in microcontroller interface circuit for mutual inductance sensor. Eng. Sci. Technol. Int. J. 2019, 22, 578–591. [Google Scholar] [CrossRef]
- Sifuentes, E.; González-Landaeta, R.; Cota-Ruiz, J.; Reverter, F. Measuring Dynamic Signals with Direct Sensor-to-Microcontroller Interfaces Applied to a Magnetoresistive Sensor. Sensors 2017, 17, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Reverter, F. Power Consumption in Direct Interface Circuits. IEEE Trans. Instrum. Meas. 2013, 62, 503–509. [Google Scholar] [CrossRef]
- Reverter, F.; Pallàs-Areny, R. Effective number of resolution bits in direct sensor-to-microcontroller interfaces. Meas. Sci. Technol. 2004, 15, 2157–2162. [Google Scholar] [CrossRef]
- Reverter, F.; Pallàs-Areny, R. Uncertainty reduction techniques in microcontroller-based time measurements. Sens. Actuators A Phys. 2006, 127, 74–79. [Google Scholar] [CrossRef]
- Yurish, S.Y.; Reverter, F.; Pallàs-Areny, R. Measurement error analysis and uncertainty reduction for period- and time-interval-to-digital converters based on microcontrollers. Meas. Sci. Technol. 2005, 16, 1160–1166. [Google Scholar] [CrossRef]
- Jordana, J.; Pallàs-Areny, R. A simple, efficient interface circuit for piezoresistive pressure sensors. Sens. Actuators A Phys. 2006, 127, 69–73. [Google Scholar] [CrossRef]
- Reverter, F.; Gasulla, M.; Pallàs-Areny, R. Analysis of Power-Supply Interference Effects on Direct Sensor-to-Microcontroller Interfaces. In 2005 IEEE Instrumentation and Measurement Technology Conference Proceedings, Ottawa, ON, Canada, 2005.
- Gaitán-Pitre, J.E.; Pallàs-Areny, R. Interferencias capacitivas en circuitos de interfaz directa entre sensores capacitivos and microcontrolador. In Seminario Anual de Automática, Electrónica Industrial e Instrumentación, Guimarães, Portugal, 2012.
- Reverter, F.; Li, X.; Meijer, G.C. Liquid-level measurement system based on a remote grounded capacitive sensor. Sens. Actuators A Phys. 2007, 138, 1–8. [Google Scholar] [CrossRef]
- Kokolanski, Z.; Reverter, F.; Gavrovski, C.; Dimcev, V. Improving the Resolution in Direct Inductive Sensor-to-Microcontroller Interface. Annu. J. Electron. 2015, 135–138. [Google Scholar]
- Dutta, L.; Hazarika, A.; Bhuyan, M. Microcontroller Based E-Nose for Gas Classification without Using ADC. Sens. Transducers 2016, 202, 38–45. [Google Scholar]
- Gaitán-Pitre, J.E.; Pallàs-Areny, R. Charge-transfer-based signal interface for differential capacitive sensors. In XXI IMEKO World Congress “Measurement in Research and Industry”, Prague, Czech Republic, 2015.
- Gaitán-Pitre, J.E.; Pallàs-Areny, R. Charge-transfer-based signal interface for resistive sensors. In XXI IMEKO World Congress, Prague, Czech Republic, 2015.
- López-Lapeña, O.; Serrano-Finetti, E.; Casas, O. Low-Power Direct Resistive Sensor-to-Microcontroller Interfaces. IEEE Trans. Instrum. Meas. 2016, 65, 222–230. [Google Scholar] [CrossRef]
- López-Lapeña, O.; Serrano-Finetti, E.; Casas, O. Calibration-less direct capacitor-to-microcontroller interface. Instrum. Meas. 2016, 52, 289–291. [Google Scholar] [CrossRef]
- Sifuentes, E.; Gasulla, M.; Casas, O.; Reverter, F. Improving the performance of direct interface circuits using the Vernier technique. In 2009 IEEE Instrumentation and Measurement Technology Conference, Singapore, 2009.
- Sifuentes, E.; González-Landaeta, R.; Cota-Ruiz, J.; Reverter, F. Seat Occupancy Detection Based on a Low-Power Microcontroller and a Single FSR. Sensors 2019, 19, 699. [Google Scholar] [CrossRef]
- Sifuentes, E.; Cota-Ruiz, J.; González-Landaeta, R. Respiratory Rate Detection by a Time-Based Measurement System. Rev. Mex. Ing. Bioméd. 2016, 37, 91–99. [Google Scholar]
- Sifuentes, E.; Casas, O.; Pallàs-Areny, R. Wireless Magnetic Sensor Node for Vehicle Detection With Optical Wake-Up. IEEE Sens. J. 2011, 11, 1669–1675. [Google Scholar] [CrossRef]
- Ortiz-Alvarado, J.; Gómez-Quintero, E.; Rodríguez-Sierra, J.; García-Isáis, C.A. Photocapacitance discharge of LEDs applied in remote sensing detectors. J. Phys. Conf. Ser. 2024, 2804. [Google Scholar] [CrossRef]
- Bravo, G.; Silva, J.M.; Noriega, S.A.; Martinez, E.A.; Enriquez, F.J.; Sifuentes, E. A Power-Efficient Sensing Approach for Pulse Wave Palpation-Based Heart Rate Measurement. Sensors 2021, 21, 7549. [Google Scholar] [CrossRef]
- Jin, B.; Zhang, Z.; Zhang, H. Structure design and performance analysis of a coaxial cylindrical capacitive sensor for liquid-level measurement. Meas. Sci. Technol. 2015, 30. [Google Scholar] [CrossRef]
- Stojanovic, R.; Karadaglic, D. Design of an Oximeter Based on LED-LED Configuration and FPGA Technology. Sensors 2013, 13, 574–586. [Google Scholar] [CrossRef]
- Pallàs-Areny, R.; Bragos, R.; Custodio, A. Procedure to connect a variable resistor sensor bridge to a microcontroller. Spain Patent ES2172407, 12 November 2003.
- Van Der Goes, F.M. Low-Cost Smart Sensor Interface; PhD Thesis, Delft University of Technology: Delft, Netherlands, 1996. [Google Scholar]
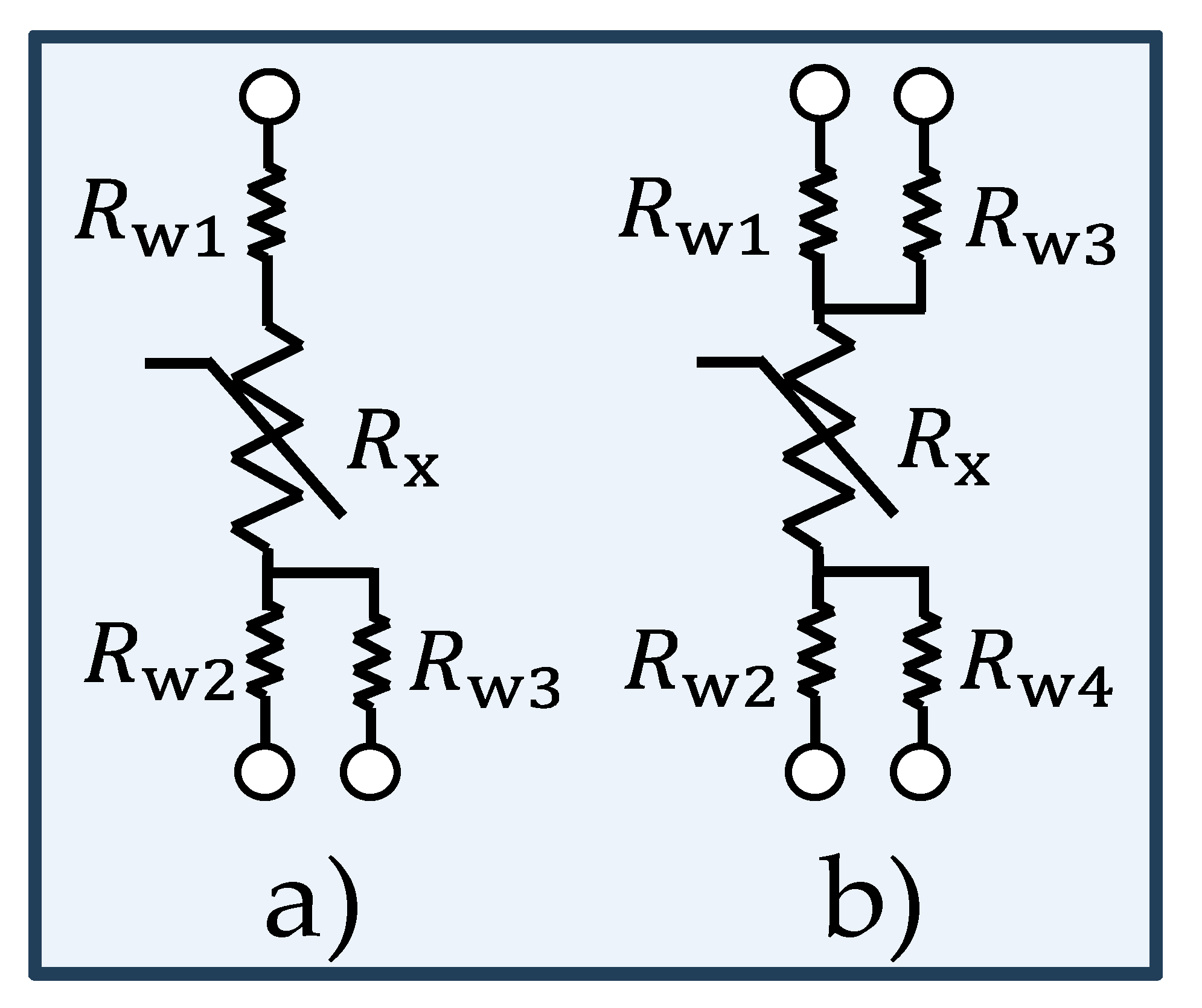
- Reverter, F. A direct approach for interfacing four-wire resistive sensors to microcontrollers. Meas. Sci. Technol. 2023, 34, 037001. [Google Scholar] [CrossRef]
- Philip V N. Direct microcontroller interface-based digital readout circuit for single-element resistive sensors. Proc. IEEE Int. Conf. Power, Control. Signals Instrum. Eng. 2017, 2480–3.
- Reverter, F. A Microcontroller-Based Interface Circuit for Three-Wire Connected Resistive Sensors. IEEE Trans. Instrum. Meas. 2022, 71, 1–4. [Google Scholar] [CrossRef]
- Elangovan, K.; Antony, A. Simplified digitizing interface-architectures for three-wire connected resistive sensors: Design and comprehensive evaluation. IEEE Trans. Instrum. Meas 2022, 71, 1–9. [Google Scholar] [CrossRef]
- Elangovan, K.; Sreekantan A., C. Evaluation of new digital signal conditioning techniques for resistive sensors in some practically relevant scenarios. IEEE Trans. Instrum. Meas. 2021, 70, 1–9. [Google Scholar] [CrossRef]
- Hidalgo-López, J.A. Direct interface circuits for resistive sensors affected by lead wire resistances. Measurement, 2023, 218, 113250. [Google Scholar] [CrossRef]
- Reverter, F. A microcontroller-based interface circuit for non-linear resistive sensors. Meas. Sci. Technol. 2020, 32, 027001. [Google Scholar] [CrossRef]
- Areekath, L.; Boby, G.; Reverter, F. Analysis of a direct microcontroller interface for capacitively coupled resistive sensors. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Hidalgo-López, J.A. Direct interface circuit for capacitive sensors affected by parasitic series resistances. IEEE Trans. Instrum. Meas 2023, 72, 1–8. [Google Scholar] [CrossRef]
- Botín-Córdoba, J.A.; Oballe-Peinado, Ó.; Sánchez-Durán, J.A.; Hidalgo-López, J.A. Quasi single point calibration method for high-speed measurements of resistive sensors. Micromachines 2019, 10, 664. [Google Scholar] [CrossRef]
- Reverter, F. Direct interface circuits for sensors. In Smart Sensors and Mems; Nihtianov, S., Luque A.; Eds.; Woodhead Publishing, 2014, 27-62.
- Courbat, J.; Briand, D.; Yue, L.; Raible, S.; Rooij, N.F. Drop-coated metal-oxide gas sensor on polyimide foil with reduced power consumption for wireless applications. Sensors and Actuators B: Chemical 2012, 161, 862–868. [Google Scholar] [CrossRef]
- Kokolanski, Z.; Gavrovski, C.; Dimcev, V. Continual One Point Auto-Calibration Technique in Simple Sensor-Microcontroller Interface. Electronics 2011, 31, 72–77. [Google Scholar]
- Vidal-Verdú, F.; Oballe-Peinado, Ó.; Sánchez-Durán, J.A.; Castellanos-Ramos, J.; Navas-González, R. Three realizations and comparison of hardware for piezoresistive tactile sensors. Sensors 2011, 11, 3249–3266. [Google Scholar] [CrossRef]
- Pelegrí-Sebastiá, J.; García-Breijo, E.; Ibáñez, J.; Sogorb, T.; Laguarda-Miro, N.; Garrigues, J. Low-cost capacitive humidity sensor for application within flexible rfid labels based on microcontroller systems. IEEE Trans. Instrum. Meas. 2012, 61, 545–553. [Google Scholar] [CrossRef]
- Oballe-Peinado, Ó.; Vidal-Verdú, F.; Sánchez-Durán, J.A.; Castellanos-Ramos, J.; Hidalgo-López, J.A. Accuracy and Resolution Analysis of a Direct Resistive Sensor Array to FPGA Interface. Sensors 2016, 16, 181. [Google Scholar] [CrossRef] [PubMed]
- Oballe-Peinado, Ó.; Vidal-Verdú, F.; Sánchez-Durán, J.A.; Castellanos-Ramos, J.; Hidalgo-López, J.A. Improved Circuits with Capacitive Feedback for Readout Resistive Sensor Arrays. Sensors 2016, 16, 149. [Google Scholar] [CrossRef] [PubMed]
- Yurish, S.Y. Universal resistance-to-digital converter. In Proceedings CENICS 2009, Sliema, Malta, 2009.
- Yurish, S.Y. Universal capacitive sensors and transducers interface, in Proceedings Eurosensors XXIII, Lausanne, Switzerland, 2009.
- Yurish, S.Y. A simple and universal resistive-bridge sensors interface. Sensors & Transducers Journal 2011, 10, 46–59. [Google Scholar]
- Yurish, S.Y. Distance measurement system based on ultrasonic smart sensors and universal sensors and transducers interface (USTI). Sensors & Transducers Journal 2020, 243, 24–30. [Google Scholar]
- Ponnalagu, R.N.; Boby, G.; Jagadeesh Kumar, V. A microcontroller sensor interface suitable for resistive sensors with large lead resistance. International Journal on Smart Sensing and Intelligent Systems 2014, 7, 1–5. [Google Scholar] [CrossRef]
- Hidalgo-López, J. A. Sigma-Delta approach in direct interface circuits for readout of resistive sensors. IEEE Trans. Instrum. Meas. 2021, 71, 1–9. [Google Scholar] [CrossRef]
- Reverter, F.; Sreekantan, A.Ch.; Boby, G. Circuits for the Measurement of Remote Resistive Sensors: A Review. IEEE Trans. Instrum. Meas. 2025, 74, 2002213. [Google Scholar] [CrossRef]



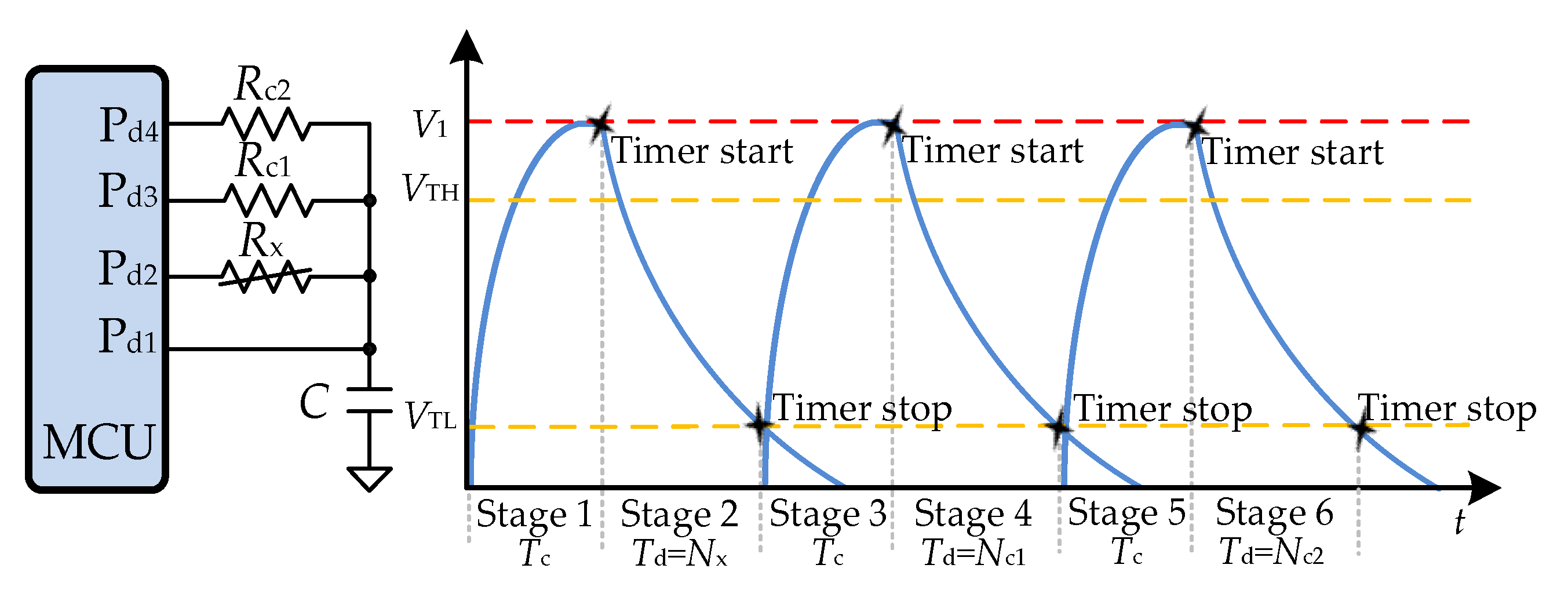
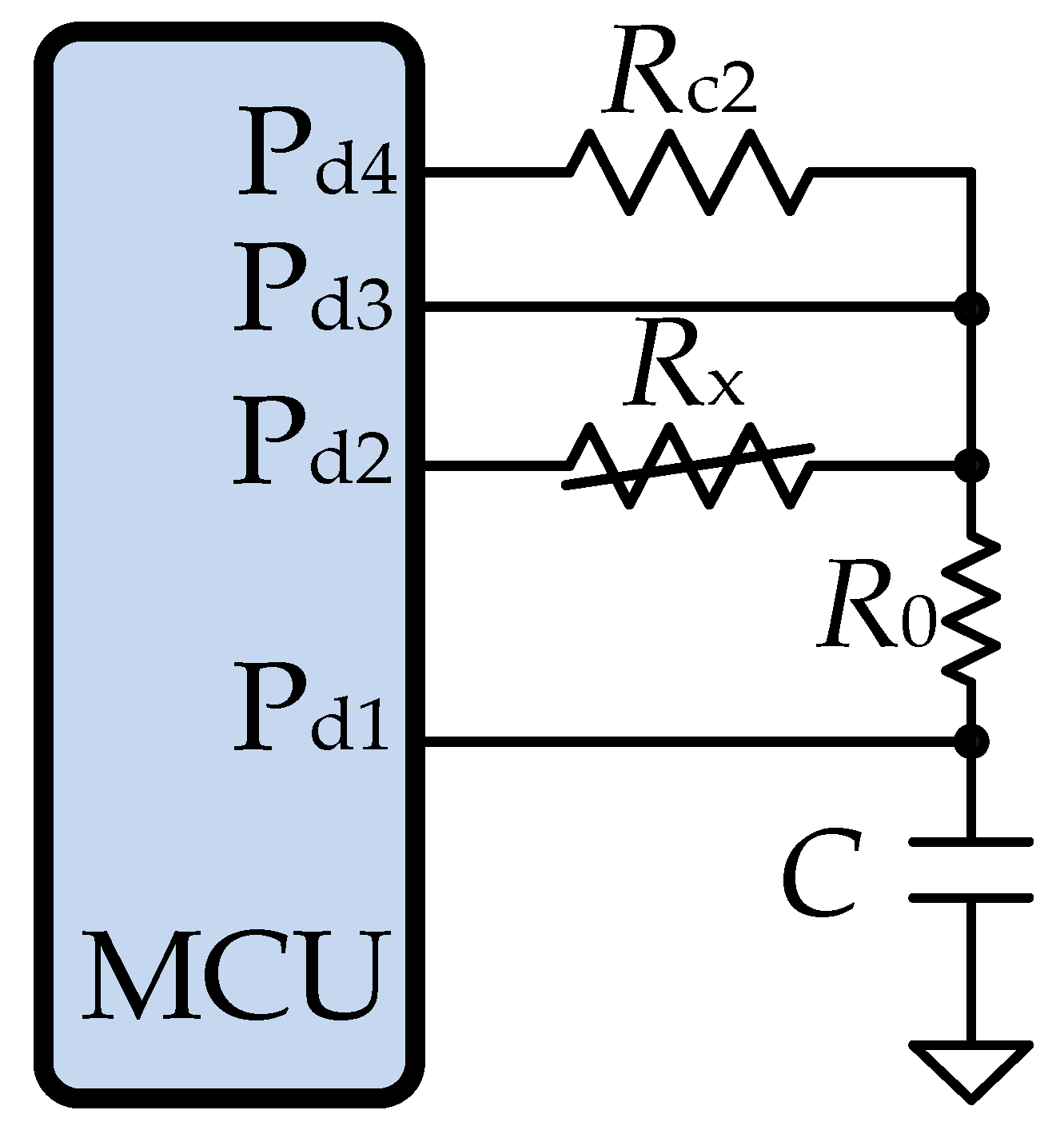
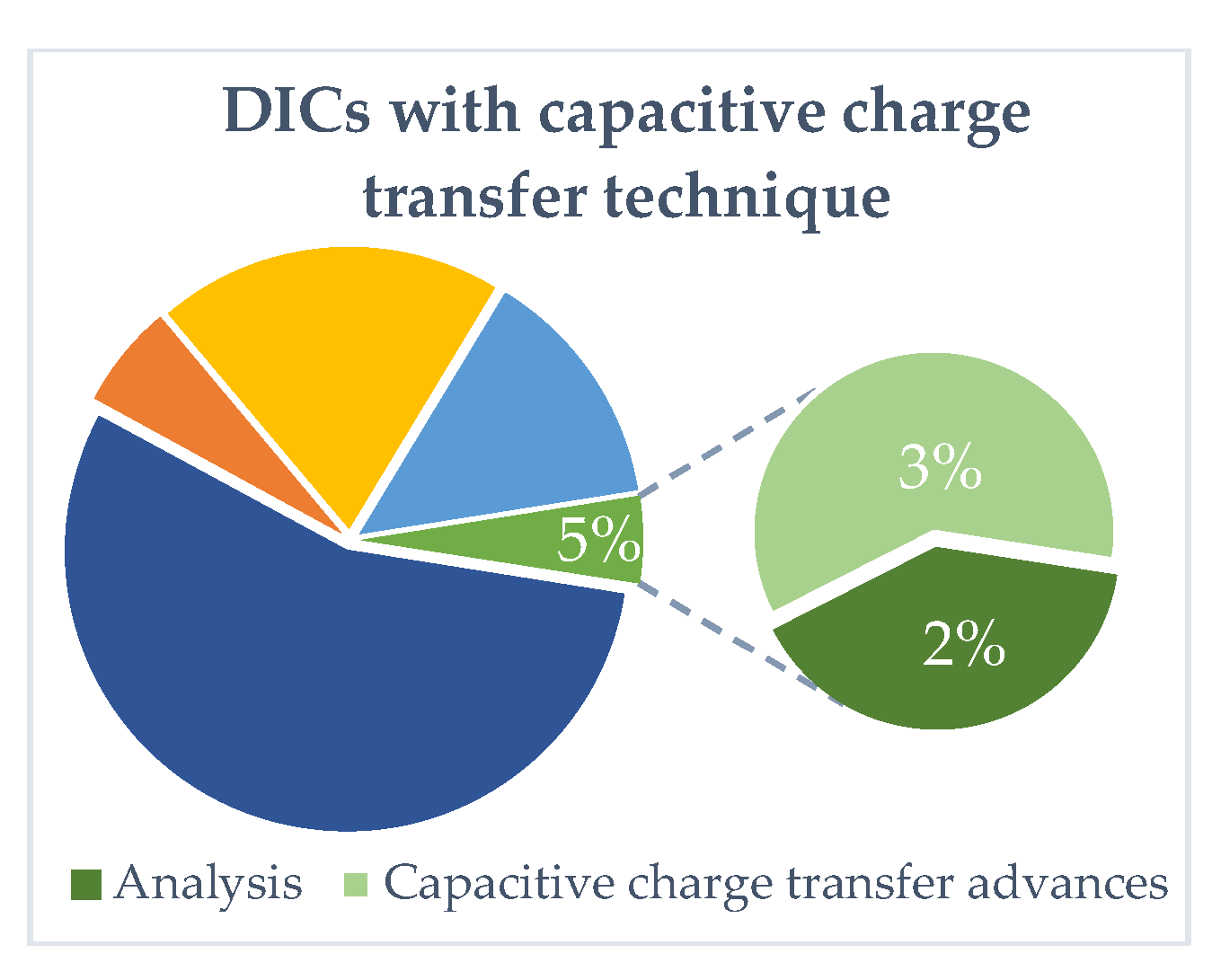
| Stage | Process | ||
|---|---|---|---|
| 1 | '1' | 'HZ' | |
| 2 | 'HZ', and capture time | '0' |
| Stage | Process | |||
|---|---|---|---|---|
| 1 | '1' | 'HZ' | 'HZ' | |
| 2 | 'HZ', and capture | '0' | 'HZ' | |
| 3 | '1' | 'HZ' | 'HZ' | |
| 4 | 'HZ', and capture | 'HZ' | '0' |
| Stage | Process | |||
|---|---|---|---|---|
| 1 | '1' | '0' | 'HZ' | |
| 2 | 'HZ', and capture | '0' | 'HZ' | |
| 3 | '1' | 'HZ' | '0' | |
| 4 | 'HZ', and capture | 'HZ' | '0' |
| Stage | Process | ||||
|---|---|---|---|---|---|
| 1 | '1' | 'HZ' | 'HZ' | 'HZ' | |
| 2 | 'HZ', and capture | '0' | 'HZ' | 'HZ' | |
| 3 | '1' | 'HZ' | 'HZ' | 'HZ' | |
| 4 | 'HZ', and capture | 'HZ' | '0' | 'HZ' | |
| 5 | '1' | 'HZ' | 'HZ' | 'HZ' | |
| 6 | 'HZ', and capture | 'HZ' | 'HZ' | '0' |
| Stage | Process | |||
|---|---|---|---|---|
| 1 | '1' | '0' | 'HZ' | |
| 2 | 'HZ', and capture | '0' | 'HZ' | |
| 3 | '1' | 'HZ' | '0' | |
| 4 | 'HZ', and capture | 'HZ' | '0' | |
| 5 | '1' | 'HZ' | '0' | |
| 6 | 'HZ', and capture | 'HZ' | 'HZ' |
| Stage | Process | ||||
|---|---|---|---|---|---|
| 1 | '1' | 'HZ' | 'HZ' | 'HZ' | |
| 2 | 'HZ', and capture | '0' | 'HZ' | 'HZ' | |
| 3 | '1' | 'HZ' | 'HZ' | 'HZ' | |
| 4 | 'HZ', and capture | 'HZ' | '0' | 'HZ' | |
| 5 | '1' | 'HZ' | 'HZ' | 'HZ' | |
| 6 | 'HZ', Capture | 'HZ' | 'HZ' | '0' |
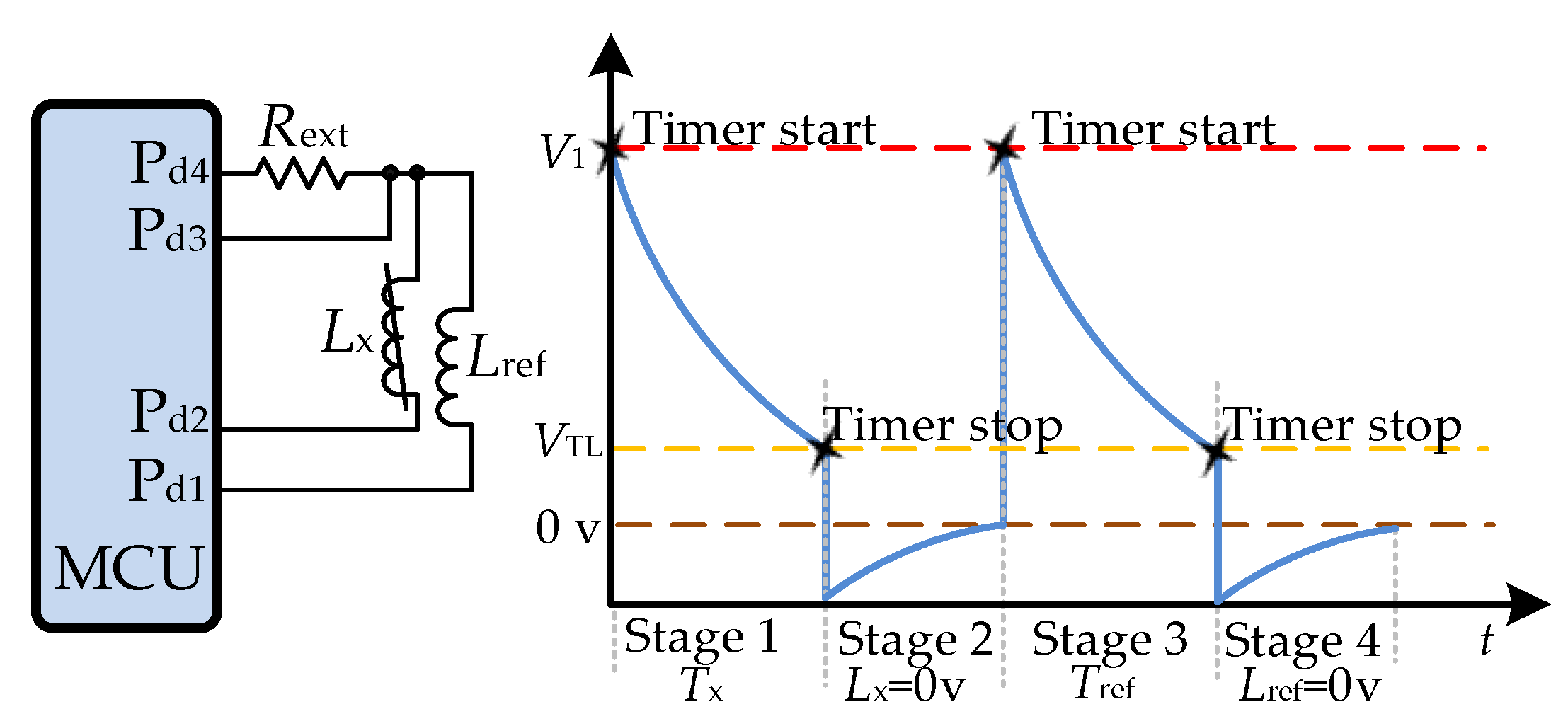
| Stage | Process | ||||
|---|---|---|---|---|---|
| 1 | '1' | 'HZ', and capture | '0' | 'HZ' | |
| 2 | '0' | 'HZ' | '0' | 'HZ' | during |
| 3 | '1' | 'HZ', Capture | 'HZ' | '0' | |
| 4 | '0' | 'HZ' | 'HZ' | '0' | during |
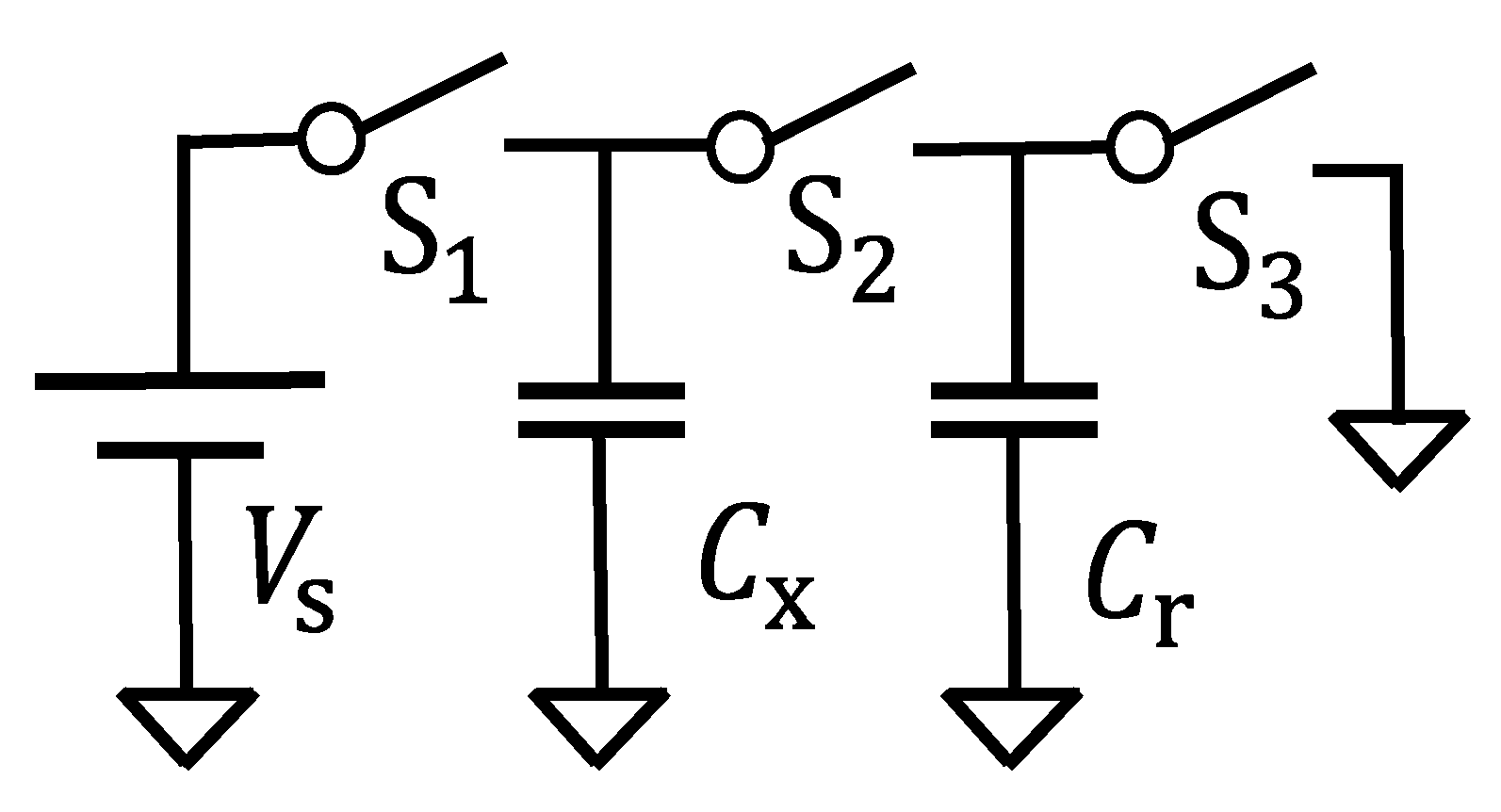
| Stage | Process | |||
|---|---|---|---|---|
| 1 | open | open | close | discharge |
| 2 | close | open | open | |
| 3 | open | close | open | charge transfer |
| Stage | Process | ||
|---|---|---|---|
| 1 | '0' | '0' | Discharge to |
| 2 | '1' | 'HZ' | |
| 3 | 'HZ', Capture | '0' | Capture of charge cycles |
| Ref. | Digital processor | Manufacturer | Clock Reference | Timer-counter bits | Time resolution | Supply Voltage (v) | |
|---|---|---|---|---|---|---|---|
| [36,37,38,81,84] | FPGA | Artix 7 XC7A35T | Xilinx | 50 MHz | 18 bits | 20 ns | 3.3 |
| [39,40,41] | FPGA | Spartan 6 (XC6SLX25-3FTG256) | Xilinx | 50 MHz | 14 bits | 20 ns | 3.3 |
| [42,43,44] | FPGA | Spartan 3 (XC3S50AN-4TQG144C) | Xilinx | 50 MHz | 14 bits | 20 ns | 1.2 - 3.3 |
| [45,46] | MCU | ATXmega32A4 | Atmel | 16 MHz | 16 bits | 62.5 ns | 3.3 |
| [21,47,51,83] | MCU | ATmega328P | Atmel | 16 MHz | 16 bits | 62.5 ns | 3.3 – 5 |
| [16,18,19,20,52,76,78,82] | MCU | AVR ATtiny2313 | Atmel | 20 MHz | 16 bits | 50 ns | 5 |
| [15,53,54,55] | MCU | AVR AT90S2313 | Atmel | 4 MHz | 16 bits | 250 ns | 5 |
| [22] | MCU | SAM3X8E ARM Cortex-M3 | Atmel | 84 MHz | 32 bits | Prescaler (11.9 ns × 2) = 23.8 ns | 3.3 |
| [15,31,56,57,58] | MCU | PIC16F873 | Microchip | 20 MHz | 16 bits | 200 ns | 5 |
| [42] | MCU | PIC16LF1559 | Microchip | 32 MHz | 16 bits | 125 ns | 3.3 |
| [59] | MCU | PIC16F876 | Microchip | 20 MHz | 16 bits | 200 ns | 5 |
| [21] | MCU | PIC16F877A | Microchip | 5 MHz | 16 bits | 800 ns | 5 |
| [60,90] | MCU | PIC16F877A | Microchip | 20 MHz | 16 bits | 200 ns | 5 |
| [61] | MCU | PIC18F45K22 | Microchip | 20 MHz | 16 bits | 200 ns | 5 |
| [34] | MCU | PIC12C508 | Microchip | not specified | 8 bits | not specified | 5 |
| [33,35,62,63] | MCU | PIC16F84A | Microchip | 4 MHz | 16 bits | 1 µs | 5 |
| [89] | MCU | PIC18F4680 | Microchip | 8 MHz | 16 bits | 125 ns | 5 |
| [64] | MCU | MSP430F1471 | Texas Instruments | 32 KHz | 16 bits | 7 MHz (DCO) =142 ns | 3.3 |
| [65] | MCU | MSP430F1471 | Texas Instruments | 8 MHz | 16 bits | 125 ns | 3.3 |
| [66,67,68] | MCU | MSP430F123 | Texas Instruments | 8 MHz | 16 bits | 125 ns | 3.3 |
| [17] | MCU | MSP430F123 | Texas Instruments | 4 MHz | 16 bits | 250 ns | 3.3v |
| [69] | MCU | MSP430F2274 | Texas Instruments | 8 MHz | 16 bits | 125 ns | 3.3 |
| [70] | MCU | STM32F401CBU6 | ST Micro | 48 MHz | 16 bits | 20.83 ns | 2.7 - 3.6 |
| [71] | MCU | D1 mini ESP32 | Espressif Systems | 80 MHz | 64 bits | 12.5 ns | 3.3 |
| [72] | MCU | C8051F040 | Silicon Labs | 25 MHz | 16 bits | 40 ns | 2.7 - 5.6 |
| [73] | FPGA | Cyclone III EP3C10 | Intel | 48 MHz | 16 bits | 20 ns | 3.3 |
| Ref. | Sensor type | DIC components | Keywords | Operative parameters reported |
|---|---|---|---|---|
| [76] | Four-wire resistive sensors | Three resistors, a capacitor, a switch, a sensor, and MCU. | A direct approach for interfacing four-wire resistive sensors. |
|
| [78] | Three-wire resistive sensors | Three resistors, a capacitor, a sensor, and MCU. | A DIC for Three-Wire connected resistive sensors |
|
| [81] | Simple resistive sensors | Two resistors, a capacitor, a sensor, and FPGA. | Two-Measurement Method (TMM) for resistive sensors affected by lead-wire resistances. |
|
| Three resistors, a capacitor, a sensor, and FPGA. | Improved Method (IM) for resistive sensors affected by lead-wire resistances. |
|
||
| [82] | Non-linear resistive sensors, such as thermistor B57164K from TDK | Three resistors, a capacitor, a sensor, and MCU. | DIC for non-linear resistive sensors. |
|
| [36] | Differential resistive sensors | Two capacitors, a resistor, a sensor, and FPGA. | Proposal of a simple digital readout DIC for differential resistive sensors. |
|
| Differential capacitive sensors | Two resistors, a capacitor, a sensor, and FPGA. | Proposal of a simple digital readout DIC for differential capacitive sensors. |
|
|
| [16] | Differential resistive sensors for linear position, angular position, pressure sensors, or level sensors. | Two resistors, a capacitor, a sensor, and MCU. | Interfacing differential resistive sensors with DIC. |
|
| [19] | Differential capacitive sensors, as the accelerometer SCG10Z-G001CC from VTI Technologies. | Two resistors, a sensor, and MCU. | Interfacing differential capacitive sensors with DIC. |
|
| [37] | Simple resistive sensors include resistance temperature detectors (RTD), gas, force, or humidity sensors. | Two capacitors, a sensor, and FPGA. | Proposal of a Two-Capacitor Interface (TCI) to simplify resistive sensor readout |
|
| Two resistors, a sensor, and FPGA. | Proposal of a Single-Capacitor Interface (SCI) to simplify resistive sensor readout |
|
||
| [38] | Simple capacitive sensors, such as liquid level, pressure, strain, and humidity sensors. | Two resistors, a sensor, and MCU. | Proposal of a new DIC to simplify the capacitive sensor |
|
| [84] | Capacitive sensors | Two resistors, an operational amplifier, a sensor, and FPGA. | DIC for capacitive sensors affected by parasitic series resistances. |
|
| [15] | Simple resistive sensors, as Pt1000 RTD sensors. | Two resistors, a capacitor, a sensor, and MCU. | Study of the accuracy and resolution of a DIC for resistive sensors. |
|
| [39] | Simple resistive sensors, focused on tactile sensors. | Four resistors, two capacitors, a sensor, and FPGA. | Proposal of a Two-Capacitor Direct Interface Circuit (TCDIC) to enhance the measurement of resistive sensors |
|
| [40] | Simple resistive sensors include thermistors, strain gauges, pressure sensors, and biomedical sensors. | Three resistors, two capacitors, a sensor, and FPGA. | Proposal of a Quantization Error Reduction Method (QERM) to reduce quantization errors when measuring low resistance values. |
|
| [41] | Simple resistive sensors. | Three resistors, a capacitor, a sensor, and FPGA. | Proposal to reduce time measurement in DIC for resistive sensors. |
|
| [46] | Simple capacitive sensors, as capacitive relative humidity (RH) sensors. | A resistor, an analog comparator, a DAC, a sensor, and MCU. | Proposal a measurement method based on a versatile DIC with internal MCU peripherals. |
|
| [42] | Simple resistive sensors include temperature, gas, anemometers, and tactile sensors. | Four resistors, a capacitor, a sensor, and MCU. | MCU proposes an Improved Calibration Method (ICM) to provide more accurate measurements and reduce relative errors. |
|
| Four resistors, a capacitor, a sensor, and FPGA. | FPGA proposes an Improved Calibration Method (ICM) to provide more accurate measurements and reduce relative errors. |
|
||
| [83] | Capacitively-coupled resistive sensors. | A reference resistor, a capacitor, an operational amplifier, a capacitively-coupled resistive sensors, and a MCU. | A first approach of a DIC for Capacitively-Coupled Resistive Sensors. |
|
| [43] | Simple resistive sensors include thermistors, gas detection, magneto-resistive, and tactile sensors. | Two resistors, a capacitor, a sensor, and FPGA. | Proposal of two fast calibration methods to improve faster, more efficient, and more accurate sensor data acquisition. |
|
| [85] | Resistive sensors | Three resistors, a capacitor, a sensor, and FPGA. | Quasi single point calibration method for high-speed measurements. |
|
| [45] | Simple resistive sensors, as thermistors or strain gauges. | A resistor, a capacitor, an ADC, an analog comparator, two MOSFETs, a sensor, and MCU. | The time-domain measurement method for resistive sensors is based on a versatile DIC with external components. |
|
| Simple capacitive sensors, such as touch sensing, pressure sensing, liquid level measurement, or proximity sensors. | The time-domain measurement method for capacitive sensors is based on a versatile DIC with external components. |
|
||
| [47] | Simple resistive sensors include RTD, thermistors, LDRs, strain gauges, gas sensors, and piezoresistive sensors. | Two resistors, a capacitor, an analog comparator, 2 diodes, a sensor, and MCU. | Propose a DIC that minimizes measurement errors due to lead wire resistance variations and temperature compensation. |
|
| [64] | Simple resistive sensors | Two resistors, a capacitor, a sensor, and MCU. | Proposal for a low-power consumption DIC through a design guide for the selection of optimal parameters related to the measurement setup for resistive sensors |
|
| [65] | Simple capacitive sensors | A resistor, a sensor, and MCU. | Proposal of calibration-less DIC |
|
| [52] | Simple resistive sensors | A resistor, a capacitor, a sensor, and MCU. | Analysis for optimizing DICs to enhance their power consumption, particularly for battery-operated applications. |
|
| Simple capacitive sensors | Two resistors, a sensor, and MCU. |
|
||
| [20] | Lossy capacitors, as P14–Rapid capacitive humidity sensor. | Two resistors, a capacitor, a sensor, and MCU. | Proposal DIC for lossy capacitance sensors. |
|
| [66] | Simple resistive sensors, such as Pt1000 temperature sensors or magneto-resistive sensors. | Two resistors, a capacitor, a sensor, and MCU. | Proposal to improve traditional DIC performance using a Vernier technique. |
|
| [17] | Bridge type resistive sensors, as the full-bridge HMC1052 sensor, an Anisotropic Magneto-resistive (AMR) sensor or the half-bridge AAH002 sensor, a Giant Magneto-resistive (GMR). | A resistor, a capacitor, a sensor, and MCU. | A DIC proposal to linearize resistive sensor bridges. |
|
| [56] | Bridge type resistive sensors, as MPXV53GC7U piezoresistive pressure sensors. | A resistor, a capacitor, a Schmitt trigger, a sensor, and MCU. | A simple and efficient DIC proposal for piezoresistive pressure sensors |
|
| [18] | Simple capacitive sensors, like Philips H1 Sensor and Humirel HS1101 Sensor. | Two resistors, a capacitor, a sensor, and MCU. | A DIC proposal for capacitive humidity sensors. |
|
| [31] | Simple capacitive sensors. | A resistor, a capacitor, a sensor, and MCU. | A low-cost DIC proposal for low-value capacitive sensors. |
|
| [88] | Simple resistive sensors | Two resistors, a capacitor, a sensor, and MCU. | One point auto-calibration technique sensor interface |
|
| [91] | Resistive sensor arrays | A sensor array, a capacitor, and a FPGA | DIC for resistive sensor arrays: resolution analysis. |
|
| [57] | Analysis of power-supply interference effects on DIC sensor-MCU. | |||
| [53] | Effective number of resolution bits in direct sensor-to-microcontroller interfaces. | |||
| [54] | Uncertainty reduction techniques in microcontroller-based time measurements. | |||
| [44] | Innovative capture modules for DIC sensor-FPGA. | |||
| [55] | Measurement error analysis and uncertainty reduction for period and time interval-to-digital converters based on MCU. | |||
| Ref. | Sensor type | DIC components | Keywords | Operative parameters reported |
|---|---|---|---|---|
| [21] | Simple inductive sensors for displacement or position measurement, and inductive pressure or temperature sensors. | A resistor, an inductor, a sensor, and MCU. | A DIC proposal for low-pass filter (LPF) inductive sensors. |
|
| [60] | Simple inductive sensors. | A resistor, an inductor, four MOSFETs, a sensor, and MCU. | Improving the resolution in a DIC for LPF and high-pass filter (HPF) inductive sensors. |
|
| [22] | Differential inductive sensors include linear variable differential transformer (LVDT) and differential variable reluctance transducer (DVRT). | A resistor, an analog comparator, an inductor, two diodes, a sensor, and MCU. | A simple and effective digitizer designed for differential variable inductive and reluctance sensors. |
|
| [45] | Simple inductive sensors | A resistor, a capacitor, an ADC, an analog comparator, two MOSFET, a sensor, and MCU. | Time-domain measurement method for inductive sensors based on a versatile DIC with external components |
|
| [48] | Simple inductive sensors | A resistor, an inductor, an analog comparator, a sensor, and MCU. | DIC proposal for resolution enhancement for inductive sensors. |
|
| [49] | Differential inductive sensors, like the SM260.100.2 inductive sensor from Schreibe, for linear displacement. | A resistor, a sensor, and MCU. | DIC proposal for differential inductive sensors. |
|
| [50] | Investigation of errors in the microcontroller interface circuit for the mutual inductance sensor. | |||
| Ref. | Sensor type | DIC components | Keywords | Operative parameters reported |
|---|---|---|---|---|
| [34] | Simple capacitive sensors, fluid levels monitoring. | A capacitor, a diode, an inductor, a sensor, and MCU. | Wireless liquid level sensing for restaurant applications with charge transfer technique. |
|
| [33,35] | Simple capacitive sensors. | Two capacitors, a sensor, and MCU. | DIC proposal for simple capacitive sensors with charge transfer technique. |
|
| [62] | Differential capacitive sensors measure various physical quantities, such as linear or angular position, displacement, pressure, and force. | Two capacitors, a sensor, and MCU. | DIC proposal for differential capacitive sensors with charge transfer technique. |
|
| [63] | Simple resistive sensors, such as NTC Thermistors or LDR. | Three resistors, two capacitors, a sensor, and MCU. | DIC proposal for simple resistive sensors with charge transfer technique. |
|
| [58] | Analysis of capacitive interferences in DIC with the transfer charge technique. | |||
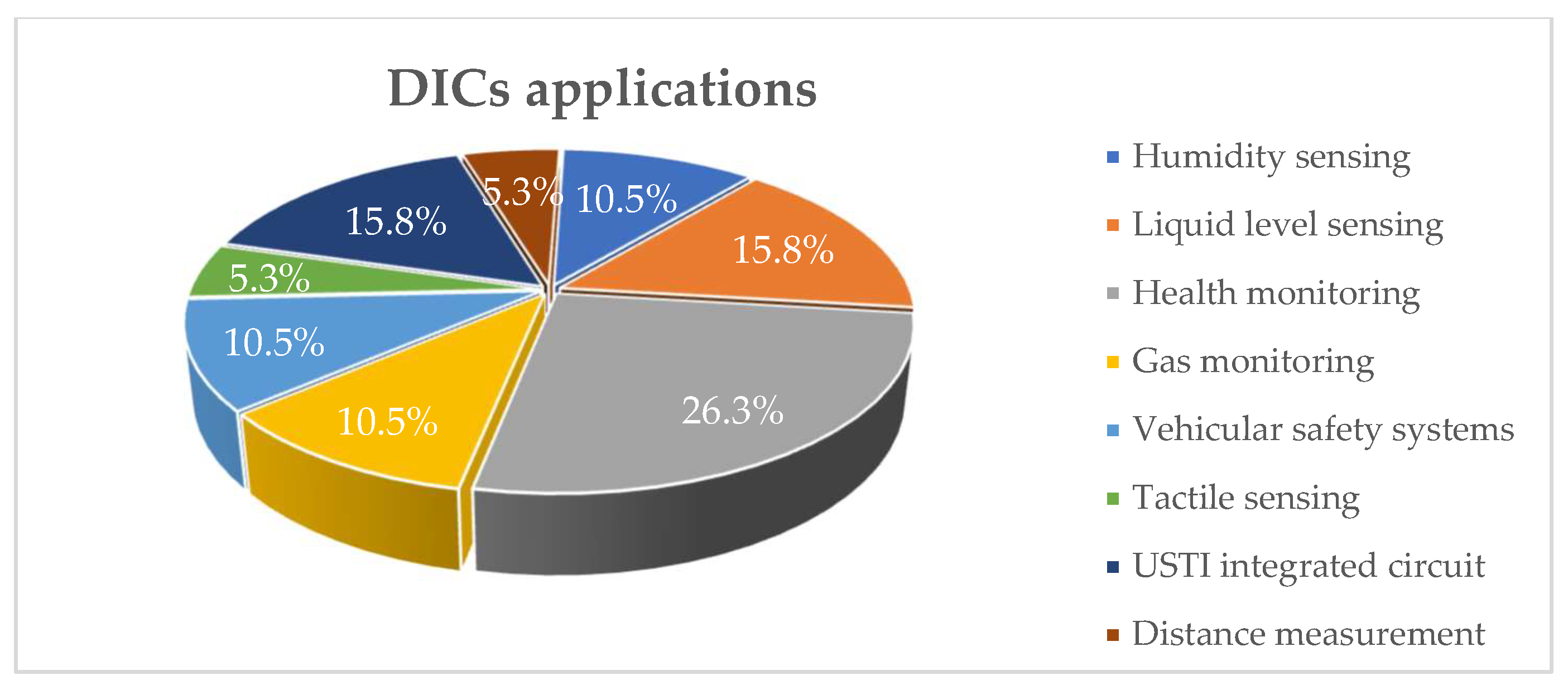
| Ref. | Sensor type | Application |
|---|---|---|
| [70] | Light emitting diodes (LEDs) for light sensing. | Monitoring vegetation health and density |
| [71] | Force sensing resistor | Heart rate measurement. |
| [67] | Force sensing resistor | Seat occupancy detection system |
| [51] | Magneto-resistive sensor | Measuring dynamic signals such as Electrocardiogram (ECG) signals |
| [61] | Metal oxide semiconductor (MOS) gas sensor | Gas sensors are used to monitor and discriminate between different gases. |
| [87] | Chemoresistive gas sensor | Gas sensor to estimate CO and NO2. |
| [68] | Nasal thermistor and piezoresistive sensor | Application in clinical and home settings for respiratory rate detection systems for health monitoring. |
| [72] | Grounded cylindrical capacitive sensor | Water level monitoring for tanks |
| [73] | LEDs for a photoplethysmography (PPG) sensor | Oximeter for blood oxygen saturation monitoring |
| [69] | Giant Magneto-resistive (GMR) sensor and an LDR | Wireless magnetic sensor node for vehicle detection |
| [18] | Capacitive humidity sensor | Humidity sensing for industrial automation |
| [59] | Grounded capacitive sensor | Liquid-level measurement for industrial processes |
| [34] | Capacitive sensor | Wireless liquid level sensing |
| [21] | Inductive sensor | Displacement and position measurement. |
| [22] | Differential inductive sensors | Linear variable differential transformer (LVDT), and differential variable reluctance transducer (DVRT). |
| [89] | Piezoresistive tactile sensors | Humanoid robots, industrial robotics, medical prosthetics and rehabilitation devices |
| [90] | RFID capacitive humidity sensor | RFID labels for wireless sensing, such as food traceability and industrial monitoring |
| [93,94,95] | Universal Sensors and Transducers Interface circuit (USTI) |
An integrated circuit for resistive, resistive-bridge, and capacitive sensors, such as, measurement of gases, humidity, temperature sensors, pressure sensors, displacement sensors and biomedical devices. |
| [96] | Ultrasonic smart sensors | Distance measurement with a USTI integrated circuit for distance measurements, tank level measurements, object detection and monitoring, garage parking assistance, and motion detection systems. |
| Decade | Percentage | Contribution |
|---|---|---|
| 1990s | 3% | Basic concepts, application notes, and simple DICs; publications specifically focused on detailed interface designs. |
| 2000s | 15.5% | Operative principles of DIC, significant improvement papers, such as calibration techniques to increase accuracy and reduce uncertainty errors, and analysis papers of key parameters. |
| 2010s | 45% | Most advances in compact circuits, error mitigation techniques, improved calibration methods, low-power solutions, and DIC applications. |
| 2020s | 36.5% | Novel sensor interfaces for non-linear sensors, correction of parasitic resistance effects with wire-resistance techniques for resistive, capacitive, and remote sensors. |
| Category | Key elements | Advances | Challenges | Perspectives and recommendations |
|---|---|---|---|---|
| RC circuits | Resistors, capacitors, MCU or FPGA | Low cost, compact design, energy-efficient, and simple implementation. | Enhancing accuracy and resolution, reducing measurement time, and minimizing quantization errors. | Investigate advanced calibration strategies and optimize power consumption. |
| RL circuits | Inductors, resistors, and MCU | Energy efficiency and accurate inductance measurements. | Addressing issues related to noise sensitivity and prolonged measurement time. | Develop strategies for noise immunity, faster measurement processes, and optimized circuit topologies. |
| Capacitive charge transfer | Capacitors, resistors, and MCU | Compact and efficient measurement, robust performance under controlled conditions | Sensitivity to parasitic capacitances and systematic measurement errors | Apply enhanced multi-point calibration methods to increase reliability and reduce systematic errors. |
| Digital processors | MCU or FPGA | Flexible integration, broad commercial availability, and adaptability for various applications. | Resolution variability is dependent on internal timers and power management challenges. | Evaluate trade-offs between energy consumption and performance and adjust operating frequencies according to the application. |
| Calibration techniques | Single-point, two-point, and three-point calibration. | Improved accuracy, compensating for systematic measurement errors and enhancing reliability. | Increased complexity and higher power consumption with advanced techniques. | Explore hybrid and adaptive calibration methods tailored to sensor characteristics and application environments. |
| Differential and bridge-type sensors | Resistive, capacitive, and inductive differential sensors. | Improved precision through reduced common-mode noise and increased reliability. | Higher complexity and cost in design and implementation | Develop innovative DICs with compensation methods to mitigate environmental effects and parasitic influences. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





