Submitted:
23 May 2025
Posted:
26 May 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Entropy in Classical Information Theory
3. Quantum Information: von Neumann Entropy
4. Time Evolution and Dynamics
4.1. Classical Case: Markov Dynamics
4.2. Quantum Case: Lindblad Evolution
5. Entropy as a Spacetime Field
6. Entropy Gradient and Information Flux
7. Conclusion
- -
- Cosmological entropy flows
- -
- Black hole thermodynamics
- -
- Relativistic quantum communication
Figure representations
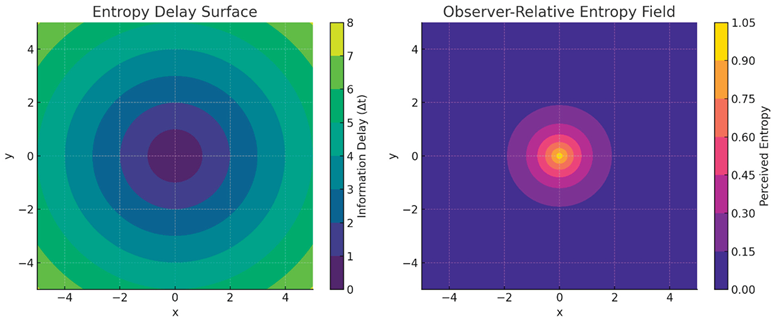
- Entropy Delay Surface: This shows how information delay (Δt) increases with spatial separation from the observer (at the origin). It forms concentric contours, similar to light cones.
- Observer-Relative Entropy Field: This model perceived entropy as decreasing with distance due to the delay, following an exponential decay for illustrative purposes.
References
- Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal, 27(3), 379–423. [CrossRef]
- Nielsen, M. A., & Chuang, I. L. (2010). Quantum Computation and Quantum Information. Cambridge University Press.
- Peres, A., & Terno, D. R. (2004). Quantum Information and Relativity Theory. Rev. Mod. Phys., 76(1), 93–123. [CrossRef]
- Rovelli, C. (1996). Relational Quantum Mechanics. Int. J. Theor. Phys., 35(8), 1637–1678. [CrossRef]
- Sorkin, R. D. (1997). Forks in the Road, on the Way to Quantum Gravity. Int. J. Theor. Phys., 36(12), 2759–2781. [CrossRef]
- Gorini, V., Kossakowski, A., & Sudarshan, E. C. G. (1976). Completely Positive Dynamical Semigroups of N-Level Systems. J. Math. Phys., 17(5), 821–825. [CrossRef]
- Bekenstein, J. D. (1973). Black Holes and Entropy. Phys. Rev. D, 7(8), 2333–2346. [CrossRef]
- Wootters, W. K. (1981). Statistical Distance and Hilbert Space. Phys. Rev. D, 23(2), 357–362. [CrossRef]
- Terno, D. R. (2006). Introduction to Relativistic Quantum Information. In Quantum Information Processing: From Theory to Experiment (pp. 61–86). Springer.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




