Submitted:
13 May 2025
Posted:
14 May 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
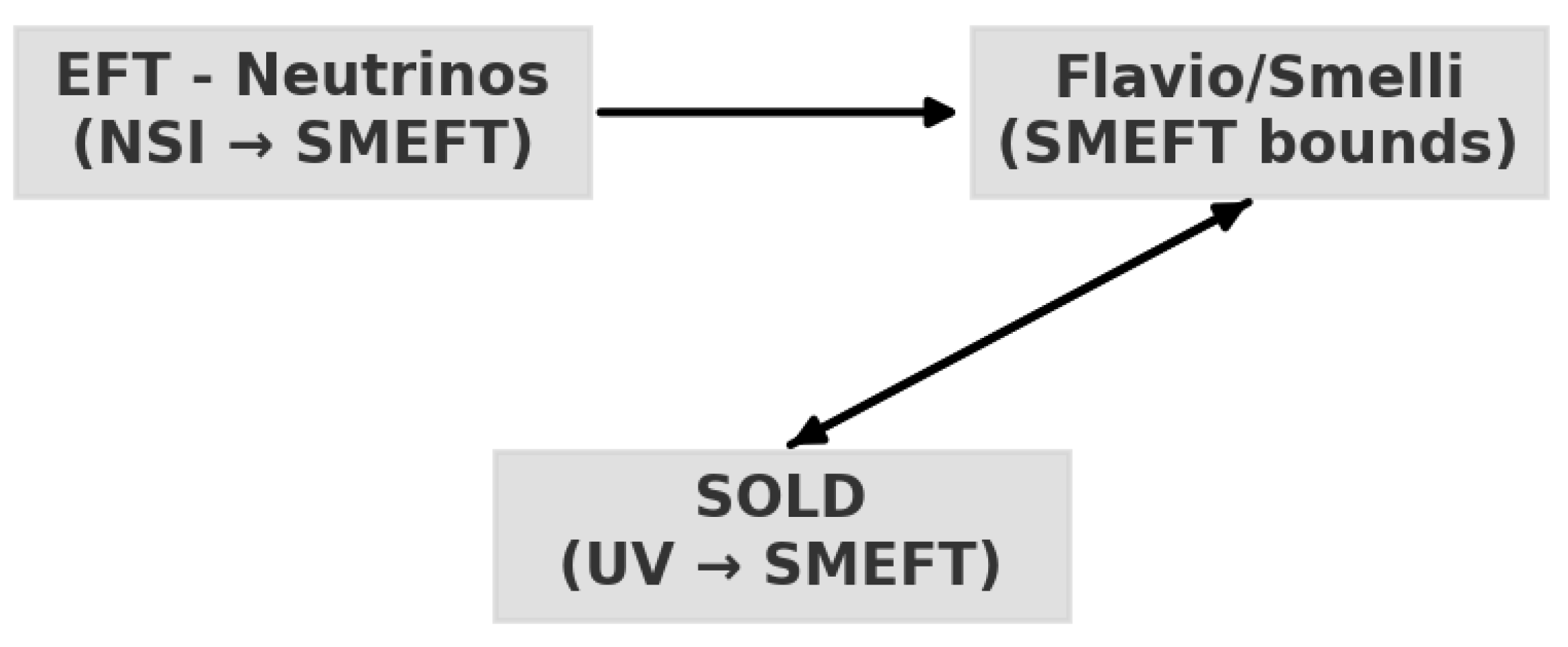
2. Methodology
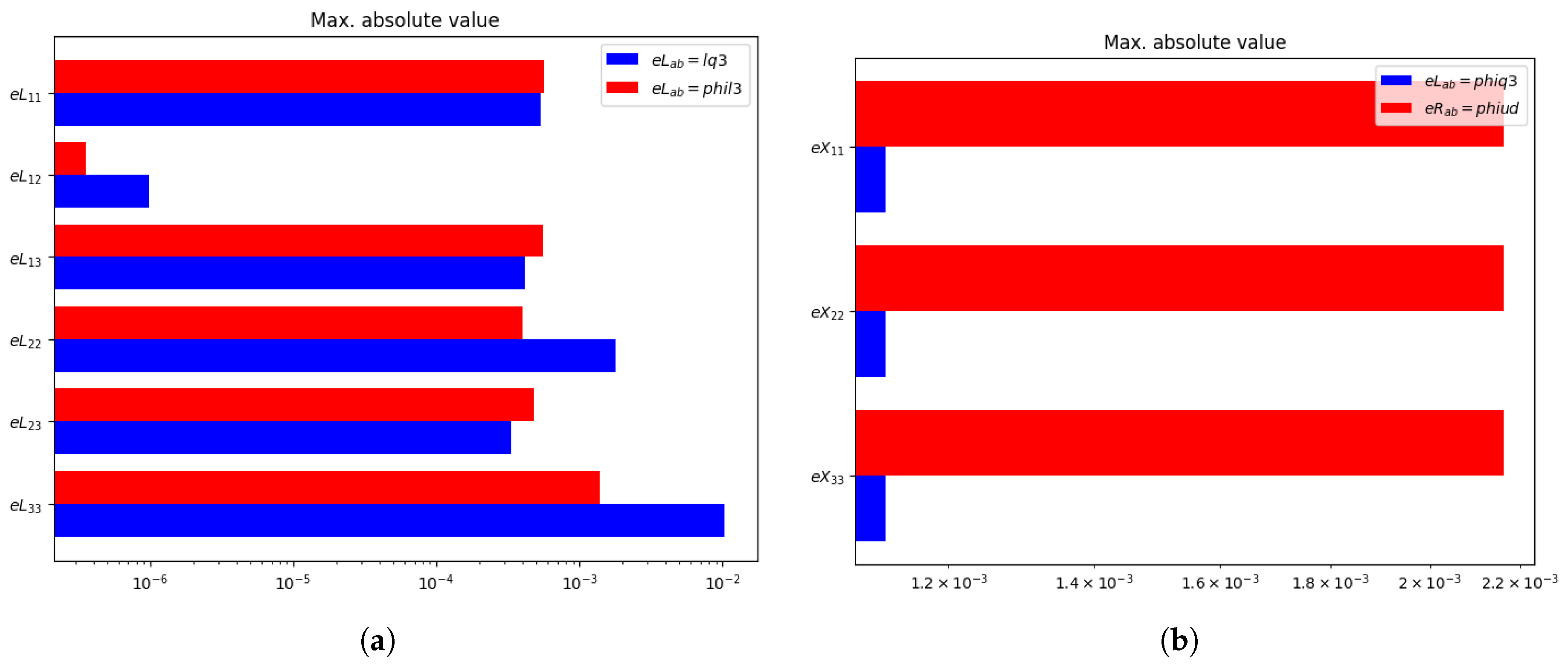
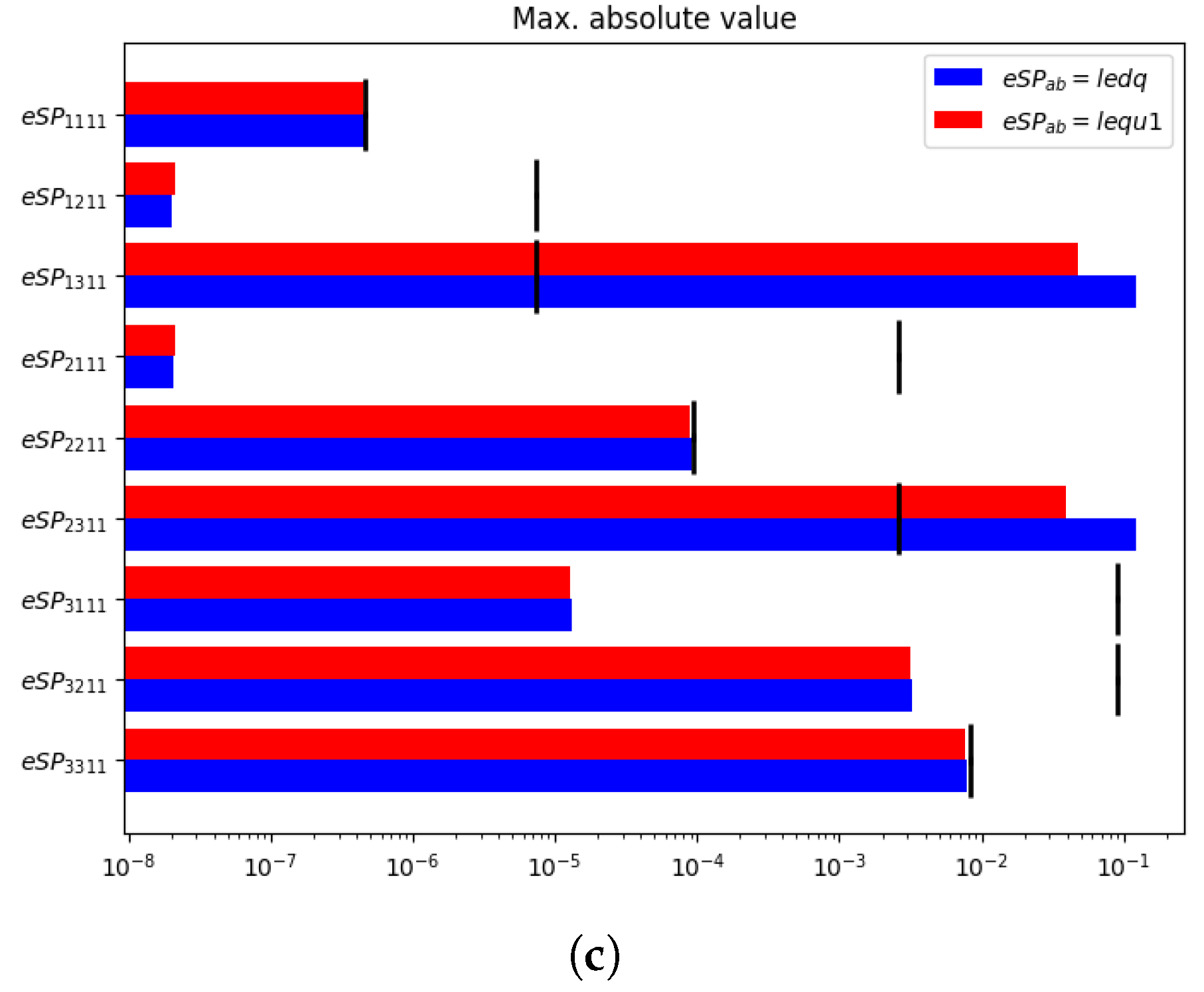
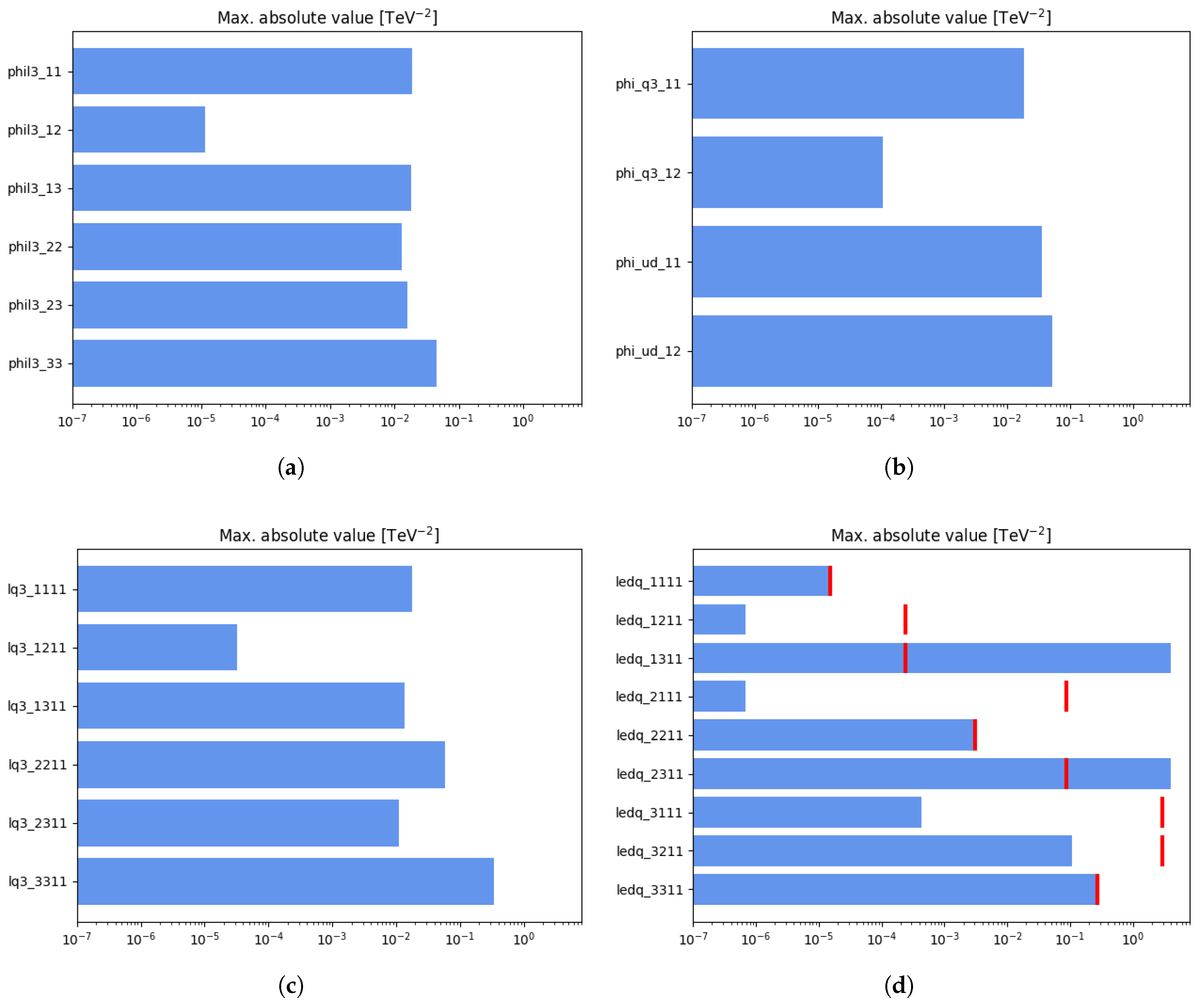
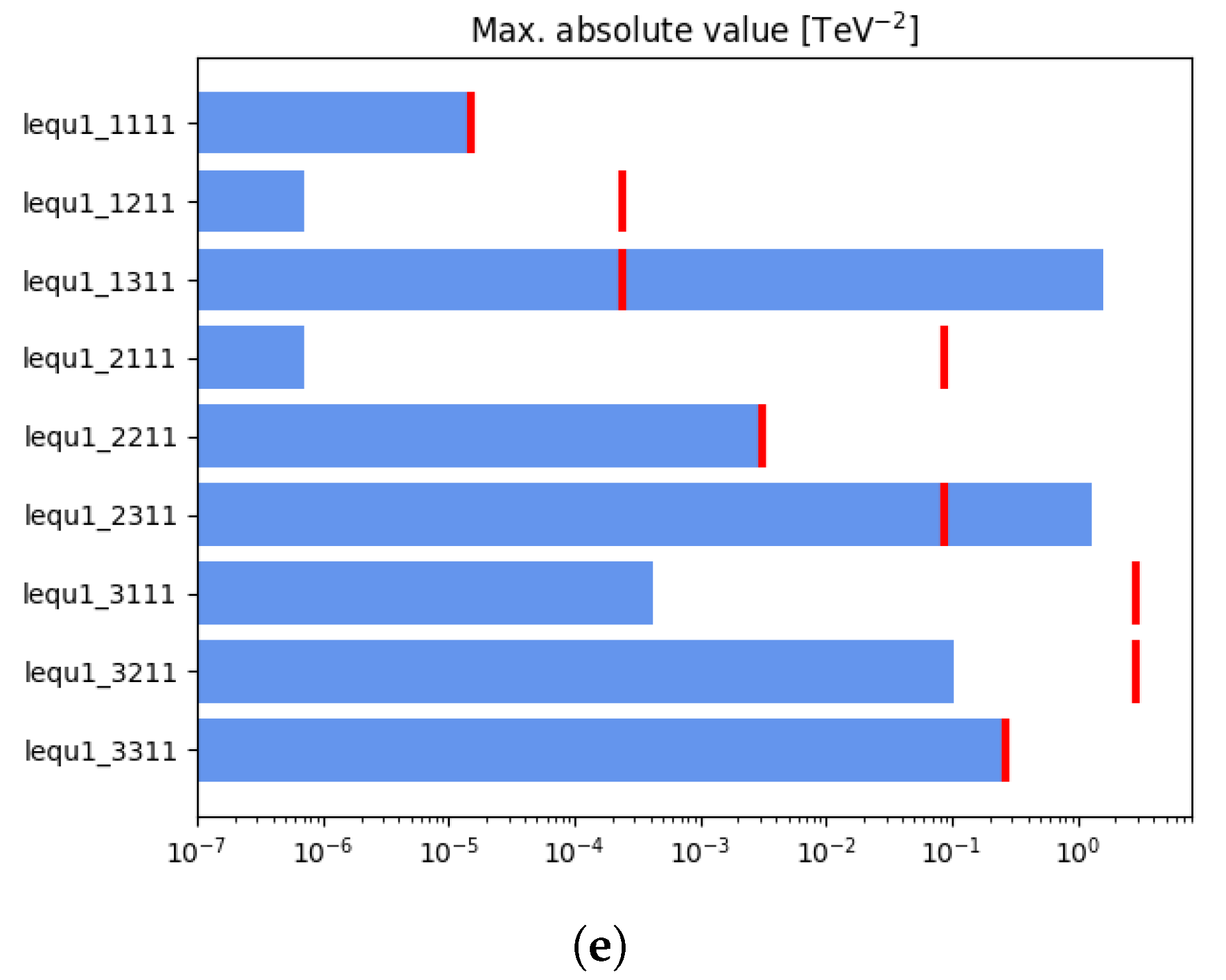
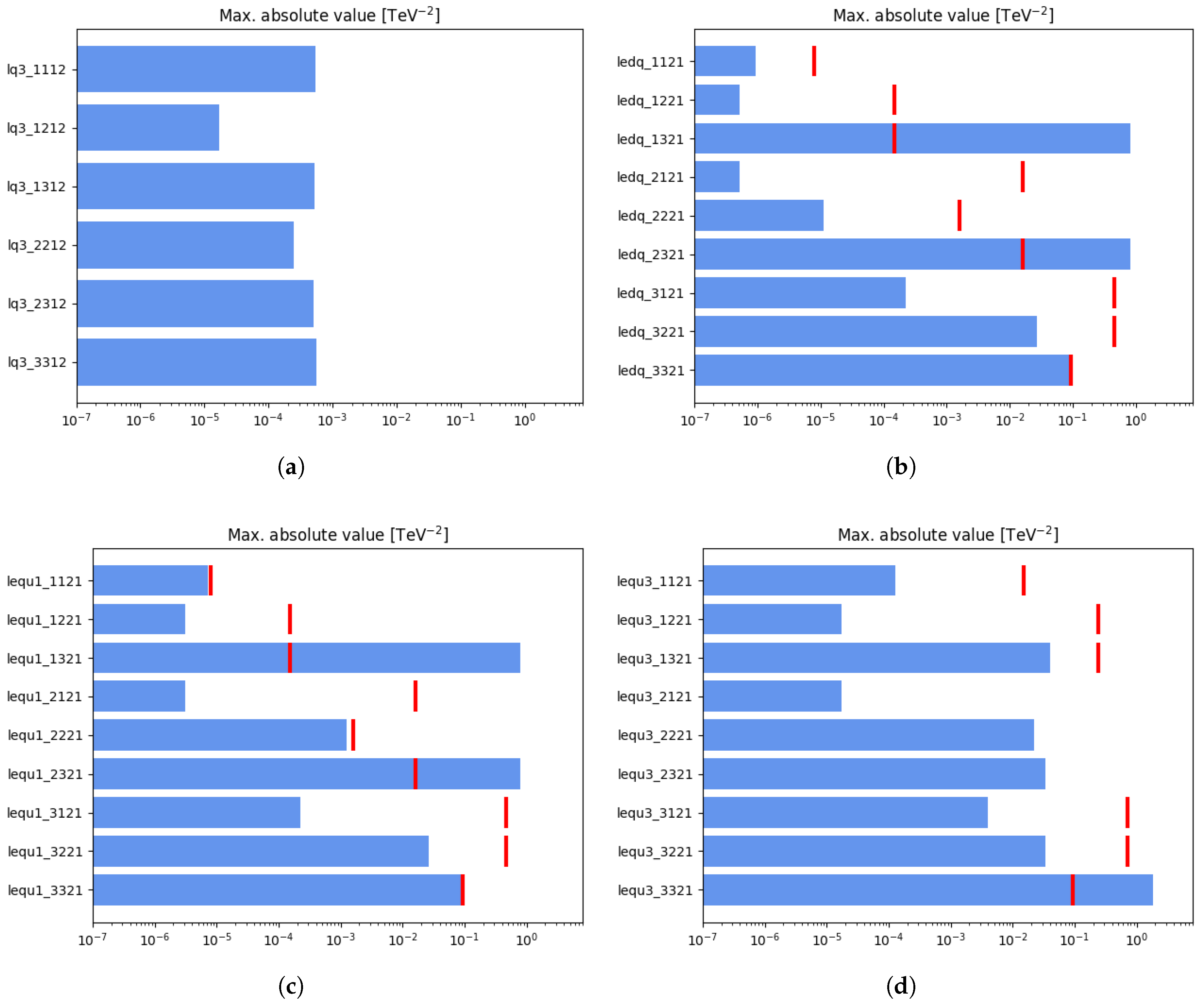
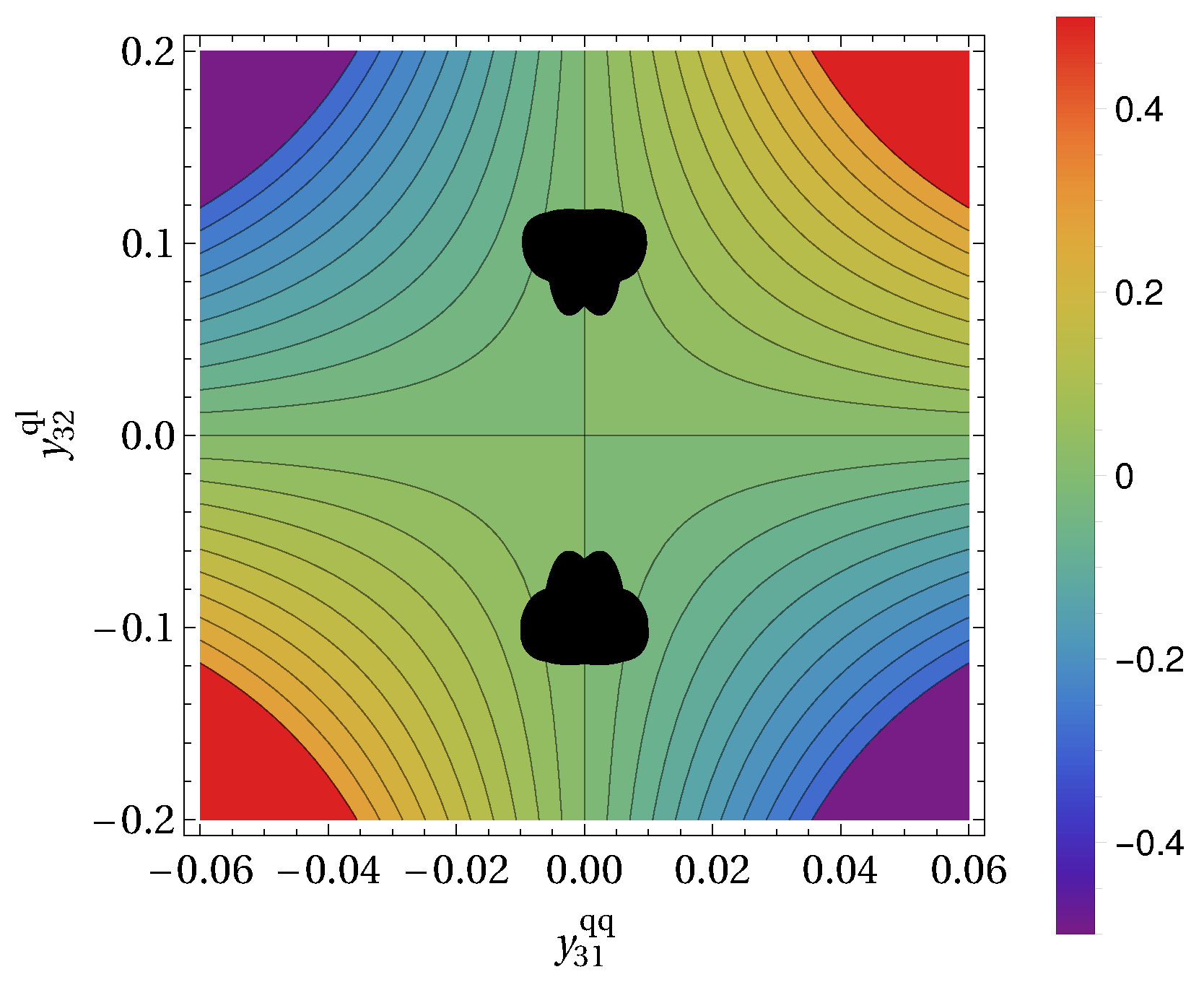
3. Results
4. Discussion
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UV | Ultra-violet |
| IR | Infrared |
| WC | Wilson coefficient |
| BSM | Beyond Standard Model |
| EFT | Effective Field Theory |
| NC-NSI | Neutral non-standard interactions |
| CC-NSI | Charged non-standard interactions |
References
- Abi, B.; et al. Deep Underground Neutrino Experiment (DUNE), Far Detector Technical Design Report, Volume II: DUNE Physics 2020. [arXiv:hep-ex/2002.03005].
- Abi, B.; et al. Prospects for beyond the Standard Model physics searches at the Deep Underground Neutrino Experiment. Eur. Phys. J. C 2021, 81, 322, [arXiv:hep-ex/2008.12769]. [CrossRef]
- Abe, K.; et al. Hyper-Kamiokande Design Report 2018. [arXiv:physics.ins-det/1805.04163].
- Mammen Abraham, R.; et al. First Measurement of νe and νμ Interaction Cross Sections at the LHC with FASER’s Emulsion Detector. Phys. Rev. Lett. 2024, arXiv:hep-ex/2403.12520133, 021802. [Google Scholar] [CrossRef] [PubMed]
- Abreu, H.; et al. First Direct Observation of Collider Neutrinos with FASER at the LHC. Phys. Rev. Lett. 2023, arXiv:hep-ex/2303.14185131, 031801. [Google Scholar] [CrossRef] [PubMed]
- Cortina Gil, E.; et al. Measurement of the very rare K+→π+νν¯ decay. JHEP 2021, arXiv:hep-ex/2103.15389]06, 093. [Google Scholar] [CrossRef]
- Li, T.; Ma, X.D.; Schmidt, M.A. Implication of K→πνν¯ for generic neutrino interactions in effective field theories. Phys. Rev. D 2020, arXiv:hep-ph/1912.10433]101, 055019. [Google Scholar] [CrossRef]
- Gorbahn, M.; Moldanazarova, U.; Sieja, K.H.; Stamou, E.; Tabet, M. The anatomy of K+→π+νν¯ distributions. Eur. Phys. J. C 2024, arXiv:hep-ph/2312.06494]84, 680. [Google Scholar] [CrossRef]
- Deppisch, F.F.; Fridell, K.; Harz, J. Constraining lepton number violating interactions in rare kaon decays. JHEP 2020, arXiv:hep-ph/2009.04494]12, 186. [Google Scholar] [CrossRef]
- Wolfenstein, L. Neutrino Oscillations in Matter. Phys. Rev. D 1978, 17, 2369–2374. [Google Scholar] [CrossRef]
- Ohlsson, T. Status of non-standard neutrino interactions. Rept. Prog. Phys. 2013, arXiv:hep-ph/1209.2710]76, 044201. [Google Scholar] [CrossRef]
- Farzan, Y.; Tortola, M. Neutrino oscillations and Non-Standard Interactions. Front. in Phys. 2018, arXiv:hep-ph/1710.09360]6, 10. [Google Scholar] [CrossRef]
- Coloma, P.; Gonzalez-Garcia, M.C.; Maltoni, M.; Pinheiro, J.a.P.; Urrea, S. Global constraints on non-standard neutrino interactions with quarks and electrons. JHEP 2023, arXiv:hep-ph/2305.07698]08, 032. [Google Scholar] [CrossRef]
- Bergmann, S.; Grossman, Y.; Pierce, D.M. Can lepton flavor violating interactions explain the atmospheric neutrino problem? Phys. Rev. D 2000, 61, 053005. [Google Scholar] [CrossRef]
- Antusch, S.; Baumann, J.P.; Fernandez-Martinez, E. Non-Standard Neutrino Interactions with Matter from Physics Beyond the Standard Model. Nucl. Phys. B 2009, arXiv:hep-ph/0807.1003]810, 369–388. [Google Scholar] [CrossRef]
- Gavela, M.B.; Hernandez, D.; Ota, T.; Winter, W. Large gauge invariant non-standard neutrino interactions. Phys. Rev. D 2009, arXiv:hep-ph/0809.3451]79, 013007. [Google Scholar] [CrossRef]
- Meloni, D.; Ohlsson, T.; Winter, W.; Zhang, H. Non-standard interactions versus non-unitary lepton flavor mixing at a neutrino factory. JHEP 2010, arXiv:hep-ph/0912.2735]04, 041. [Google Scholar] [CrossRef]
- Altmannshofer, W.; Tammaro, M.; Zupan, J. Non-standard neutrino interactions and low energy experiments. JHEP 2019, arXiv:hep-ph/1812.02778]09, 083. [Google Scholar] [CrossRef]
- Babu, K.S.; Dev, P.S.B.; Jana, S.; Thapa, A. Non-Standard Interactions in Radiative Neutrino Mass Models. JHEP 2020, arXiv:hep-ph/1907.09498]03, 006. [Google Scholar] [CrossRef]
- Bischer, I.; Rodejohann, W. General neutrino interactions from an effective field theory perspective. Nucl. Phys. B 2019, arXiv:hep-ph/1905.08699]947, 114746. [Google Scholar] [CrossRef]
- Davidson, S.; Gorbahn, M. Charged lepton flavor change and nonstandard neutrino interactions. Phys. Rev. D 2020, arXiv:hep-ph/1909.07406]101, 015010. [Google Scholar] [CrossRef]
- Terol-Calvo, J.; Tórtola, M.; Vicente, A. High-energy constraints from low-energy neutrino nonstandard interactions. Phys. Rev. D 2020, arXiv:hep-ph/1912.09131]101, 095010. [Google Scholar] [CrossRef]
- Babu, K.S.; Gonçalves, D.; Jana, S.; Machado, P.A.N. Neutrino Non-Standard Interactions: Complementarity Between LHC and Oscillation Experiments. Phys. Lett. B 2021, arXiv:hep-ph/2003.03383]815, 136131. [Google Scholar] [CrossRef]
- Du, Y.; Li, H.L.; Tang, J.; Vihonen, S.; Yu, J.H. Non-standard interactions in SMEFT confronted with terrestrial neutrino experiments. JHEP 2021, arXiv:hep-ph/2011.14292]03, 019. [Google Scholar] [CrossRef]
- Du, Y.; Li, H.L.; Tang, J.; Vihonen, S.; Yu, J.H. Exploring SMEFT induced nonstandard interactions: From COHERENT to neutrino oscillations. Phys. Rev. D 2022, arXiv:hep-ph/2106.15800]105, 075022. [Google Scholar] [CrossRef]
- Jenkins, E.E.; Manohar, A.V.; Stoffer, P. Low-Energy Effective Field Theory below the Electroweak Scale: Operators and Matching. JHEP 2018, arXiv:hep-ph/1709.04486]03, 016. [Google Scholar] [CrossRef]
- Dekens, W.; Stoffer, P. Low-energy effective field theory below the electroweak scale: matching at one loop. JHEP 2019, arXiv:hep-ph/1908.05295]10, 197. [Google Scholar] [CrossRef]
- Straub, D.M. flavio: A Python package for flavour and precision phenomenology in the Standard Model and beyond 2018. [arXiv:hep-ph/1810.08132].
- Aebischer, J.; Kumar, J.; Straub, D.M. Wilson: A Python package for the running and matching of Wilson coefficients above and below the electroweak scale. Eur. Phys. J. C 2018, arXiv:hep-ph/1804.05033]78, 1026. [Google Scholar] [CrossRef]
- Aebischer, J.; Kumar, J.; Stangl, P.; Straub, D.M. A Global Likelihood for Precision Constraints and Flavour Anomalies. Eur. Phys. J. C 2019, arXiv:hep-ph/1810.07698]79, 509. [Google Scholar] [CrossRef]
- Carmona, A.; Lazopoulos, A.; Olgoso, P.; Santiago, J. Matchmakereft: Automated tree-level and one-loop matching. SciPost Phys. 2022, arXiv:hep-ph/2112.10787]12, 198. [Google Scholar] [CrossRef]
- Fuentes-Martín, J.; König, M.; Pagès, J.; Thomsen, A.E.; Wilsch, F. A proof of concept for matchete: An automated tool for matching effective theories. Eur. Phys. J. C 2023, arXiv:hep-ph/2212.04510]83, 662. [Google Scholar] [CrossRef]
- Guedes, G.; Olgoso, P.; Santiago, J. Towards the one loop IR/UV dictionary in the SMEFT: One loop generated operators from new scalars and fermions. SciPost Phys. 2023, arXiv:hep-ph/2303.16965]15, 143. [Google Scholar] [CrossRef]
- Guedes, G.; Olgoso, P. From the EFT to the UV: The complete SMEFT one-loop dictionary 2024. [arXiv:hep-ph/2412.14253].
- de Blas, J.; Criado, J.C.; Perez-Victoria, M.; Santiago, J. Effective description of general extensions of the Standard Model: the complete tree-level dictionary. JHEP 2018, arXiv:hep-ph/1711.10391]03, 109. [Google Scholar] [CrossRef]
- Cherchiglia, A.; Santiago, J. DUNE potential as a new physics probe. JHEP 2024, arXiv:hep-ph/2309.15924]03, 018. [Google Scholar] [CrossRef]
- Cirigliano, V.; Jenkins, J.; Gonzalez-Alonso, M. Semileptonic decays of light quarks beyond the Standard Model. Nucl. Phys. B 2010, arXiv:hep-ph/0908.1754]830, 95–115. [Google Scholar] [CrossRef]
- Giunti, C.; Kim, C.W.; Lee, J.A.; Lee, U.W. On the treatment of neutrino oscillations without resort to weak eigenstates. Phys. Rev. D 1993, 48, 4310–4317. [Google Scholar] [CrossRef]
- Akhmedov, E.K.; Kopp, J. Neutrino Oscillations: Quantum Mechanics vs. Quantum Field Theory. JHEP 2010, arXiv:hep-ph/1001.4815]04, 008. [Google Scholar] [CrossRef]
- Kobach, A.; Manohar, A.V.; McGreevy, J. Neutrino Oscillation Measurements Computed in Quantum Field Theory. Phys. Lett. B 2018, arXiv:hep-ph/1711.07491]783, 59–75. [Google Scholar] [CrossRef]
- Falkowski, A.; González-Alonso, M.; Tabrizi, Z. Consistent QFT description of non-standard neutrino interactions. JHEP 2020, arXiv:hep-ph/1910.02971]11, 048. [Google Scholar] [CrossRef]
- Bresó-Pla, V.; Falkowski, A.; González-Alonso, M.; Monsálvez-Pozo, K. EFT analysis of New Physics at COHERENT. JHEP 2023, arXiv:hep-ph/2301.07036]05, 074. [Google Scholar] [CrossRef]
- Falkowski, A.; González-Alonso, M.; Kopp, J.; Soreq, Y.; Tabrizi, Z. EFT at FASERν. JHEP 2021, arXiv:hep-ph/2105.12136]10, 086. [Google Scholar] [CrossRef]
| 1 | |
| 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



