A Fluid Dynamics Framework for Space-Time: Unifying Relativity, Quantum Mechanics, and Cosmology

1. Introduction

1.1. Background and Motivation

Modern theoretical physics rests on two pillars: general relativity (GR) and quantum mechanics (QM). GR describes gravity as the curvature of space-time induced by mass-energy, effectively controlling large-scale cosmic structure. QM, on the other hand, governs the behavior of subatomic particles through probabilistic laws, giving rise to the Standard Model and all known forces except gravity.

However, these two foundational theories are mutually incompatible in their deepest formulations. GR is a classical, continuous theory; QM is discrete and probabilistic. Attempts to unify them—string theory, loop quantum gravity, or holographic models—remain conceptually fragmented or mathematically incomplete. Moreover, these approaches often lack observable predictions or intuitive physical interpretation.

This crisis invites the possibility that a deeper physical substrate underlies both frameworks.

1.2. Proposal: Space-Time as a Fluid

In this paper, we propose a new unifying paradigm: space-time is not a passive geometric entity, but a compressible fluid medium—subject to pressure, flow, wave behavior, and structural deformation.

This fluid model interprets:

• Gravity as a pressure-gradient force,
• Mass as a void or cavity displacing the medium,
• Time as a consequence of entropy flow,
• Quantum tunneling as a localized collapse of tension,
• Entanglement as synchronized oscillation in the fluid’s microstructure.

We provide a comprehensive framework where all major physical forces and phenomena emerge from pressure-driven behavior within this medium. The governing equations of motion, curvature, entropy, and quantum resonance are treated not as disconnected abstractions, but as physical effects governed by fluid dynamics.

1.3. Historical Foundations

Our work draws from:

• Jacobson (1995), who derived Einstein’s field equations as a thermodynamic identity, showing space-time may obey an equation of state [5].
• Verlinde (2011), who proposed gravity arises from entropy gradients [10].
• Braunstein et al. (2023), who demonstrated quantum gravity analogs using fluid simulations [9].
• Morris & Thorne (1988), who introduced traversable wormholes requiring tension-like negative pressure [4].
• Montani et al. (2024), who modeled cosmology using unified “wet fluid” behavior [10].

But what is fundamentally new here is the total unification of all physical domains—macro and micro, relativistic and quantum, cosmological and thermodynamic—through the single lens of a space-time fluid.

1.4. The Fluid Hypothesis – Core Assumptions

We assume that:

• Space-time has density (ρ), pressure (p), and viscous properties (η),
• Mass creates hollows or voids in this medium, reducing local pressure,
• All forces arise from restoring gradients (just like buoyancy or vortices),
• Entropy and information are carried by fluid divergence,
• Time emerges from the rate of entropy dispersion in this system.

This is not a metaphor. We model space-time as an actual medium obeying:

• Euler–Navier–Stokes–like dynamics for macroscopic behavior,
• Wave equations and resonance conditions at the quantum scale,
• Thermodynamic laws for entropy, temperature, and irreversibility,
• Curvature response to pressure via an Einstein-like fluid field equation.

Figure 1. SPACETIME AS FLUID MEDIUM.

Figure 1. SPACETIME AS FLUID MEDIUM.

Figure 2. ANALOG OF SPACE-TIME AS A FLUID WITH DENSITY $\rho$

Figure 2. ANALOG OF SPACE-TIME AS A FLUID WITH DENSITY $\rho$

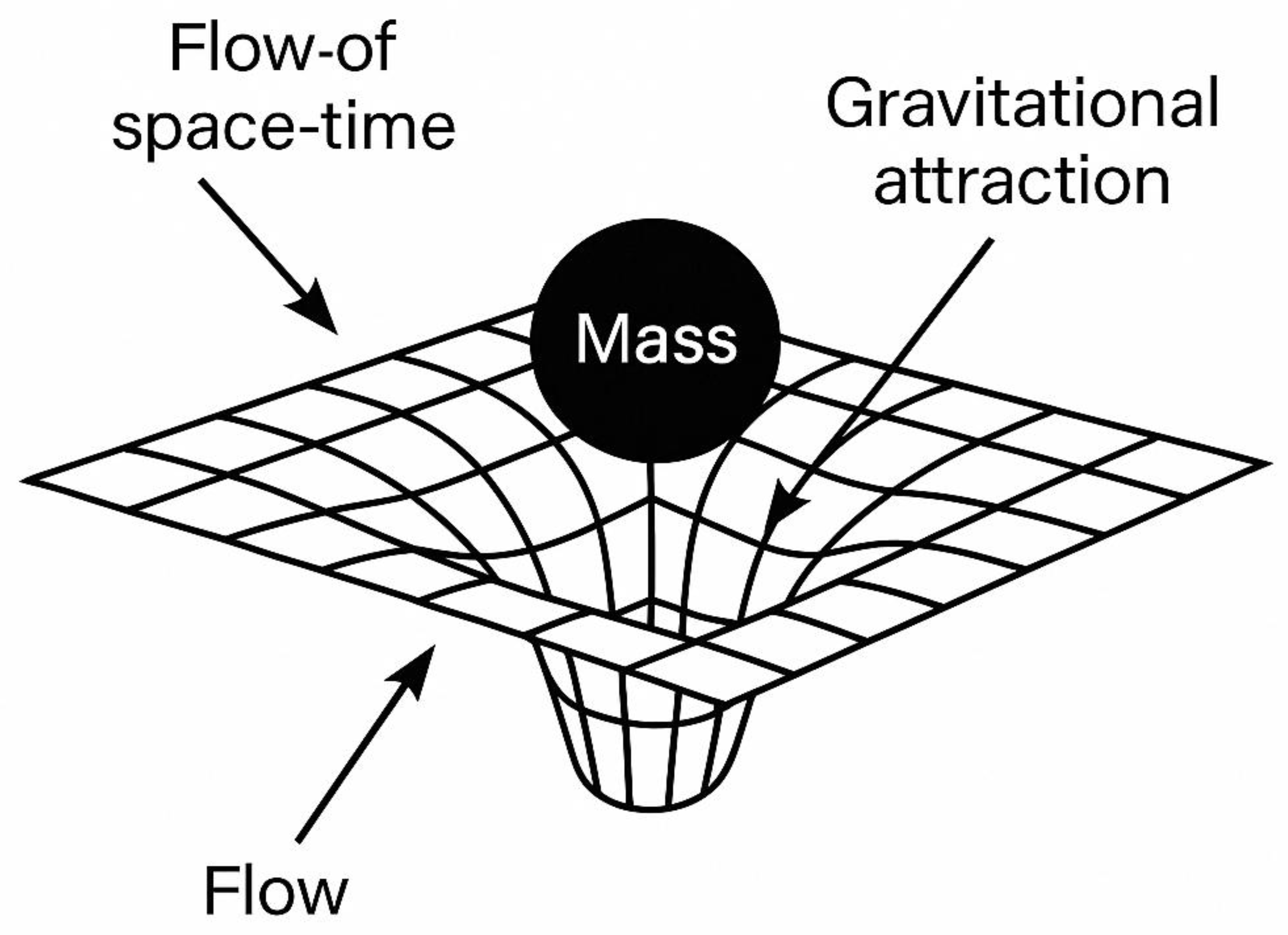
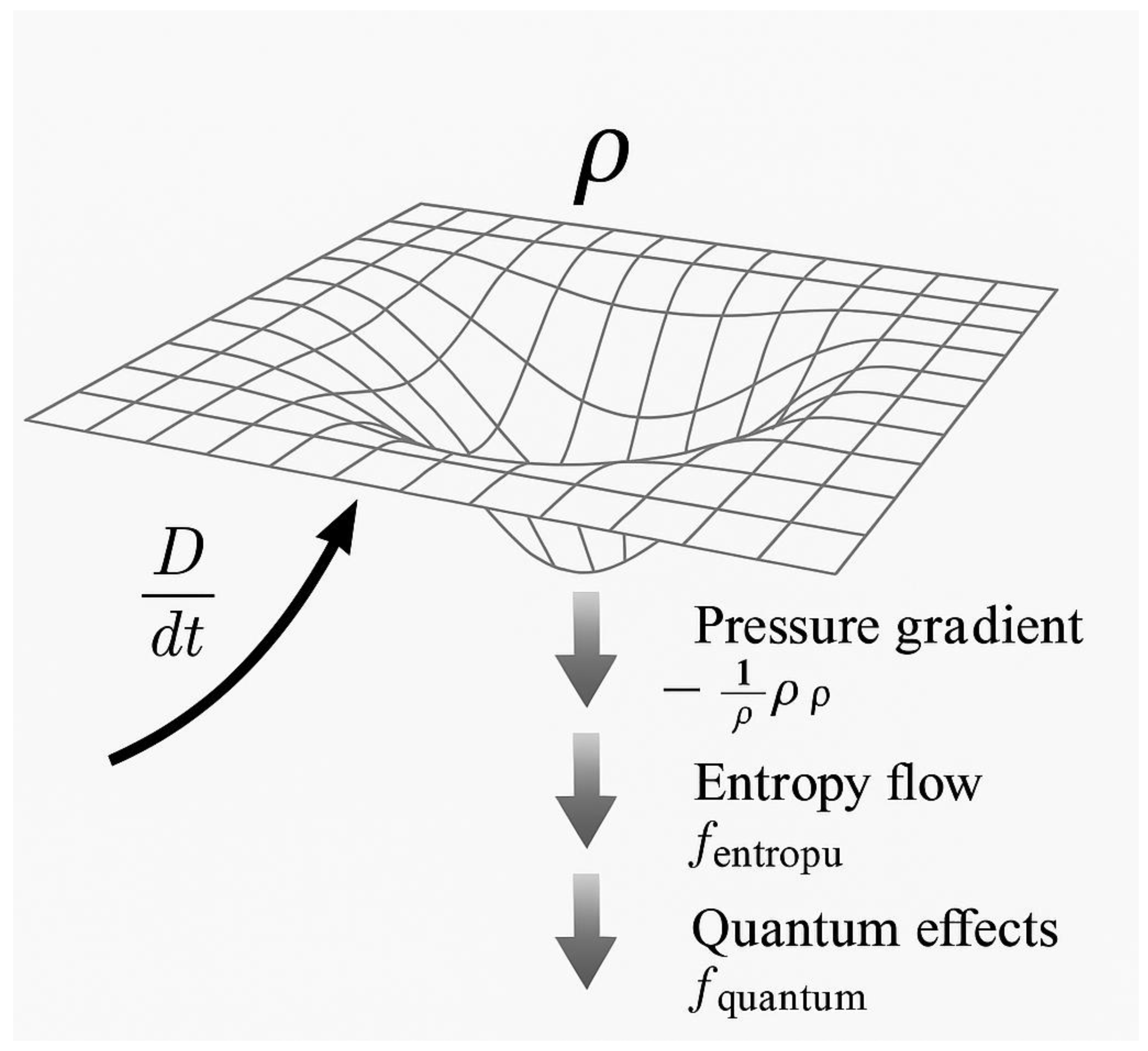
1.5. From Geometry to Substance

Einstein’s view of curvature was geometrically elegant—but devoid of substance. Our theory reinterprets curvature as a dynamic tension in the medium. The Einstein field equations themselves can be expressed as a state equation of the fluid:

$${\displaystyle \frac{Dv}{Dt}}=-{\displaystyle \frac{1}{\rho }}\nabla p+f_{\mathrm{curvature}}+f_{\mathrm{entropy}}+f_{\mathrm{quantum}}$$

Where:

• ${\displaystyle \frac{Dv}{Dt}}$: Material (convective) derivative – acceleration of the medium
• $\nabla p$: Local pressure gradient causing flow
• $\rho$: Space-time fluid density
• $f_{\mathrm{curvature}}$: Stress-tensor-induced deformation
• $f_{\mathrm{entropy}}$: Irreversible entropy flow (driving time)
• $f_{\mathrm{quantum}}$: Non-local and tunneling resonance behaviors

This interpretation transforms GR from a geometric art into a physical science of cosmic fluid mechanics.

Figure 3. ANALOG BETWEEN EINSTEIN’S FIELD DYNAMICS AND FLUID DYNAMICS.

Figure 3. ANALOG BETWEEN EINSTEIN’S FIELD DYNAMICS AND FLUID DYNAMICS.

Figure 4. PRESSURE GRADIENT, ACCELERATION & EXTERNAL FORCES.

Figure 4. PRESSURE GRADIENT, ACCELERATION & EXTERNAL FORCES.

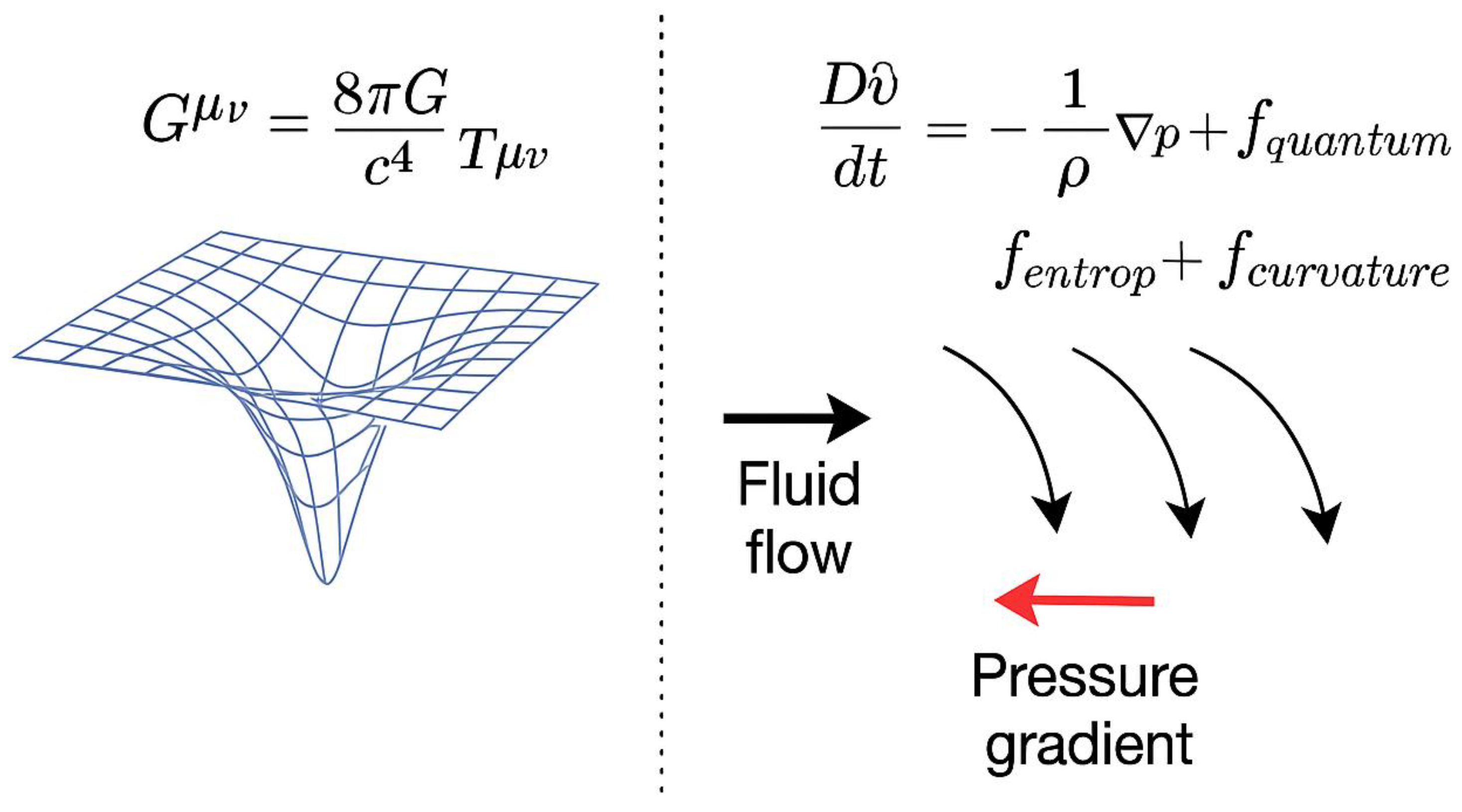
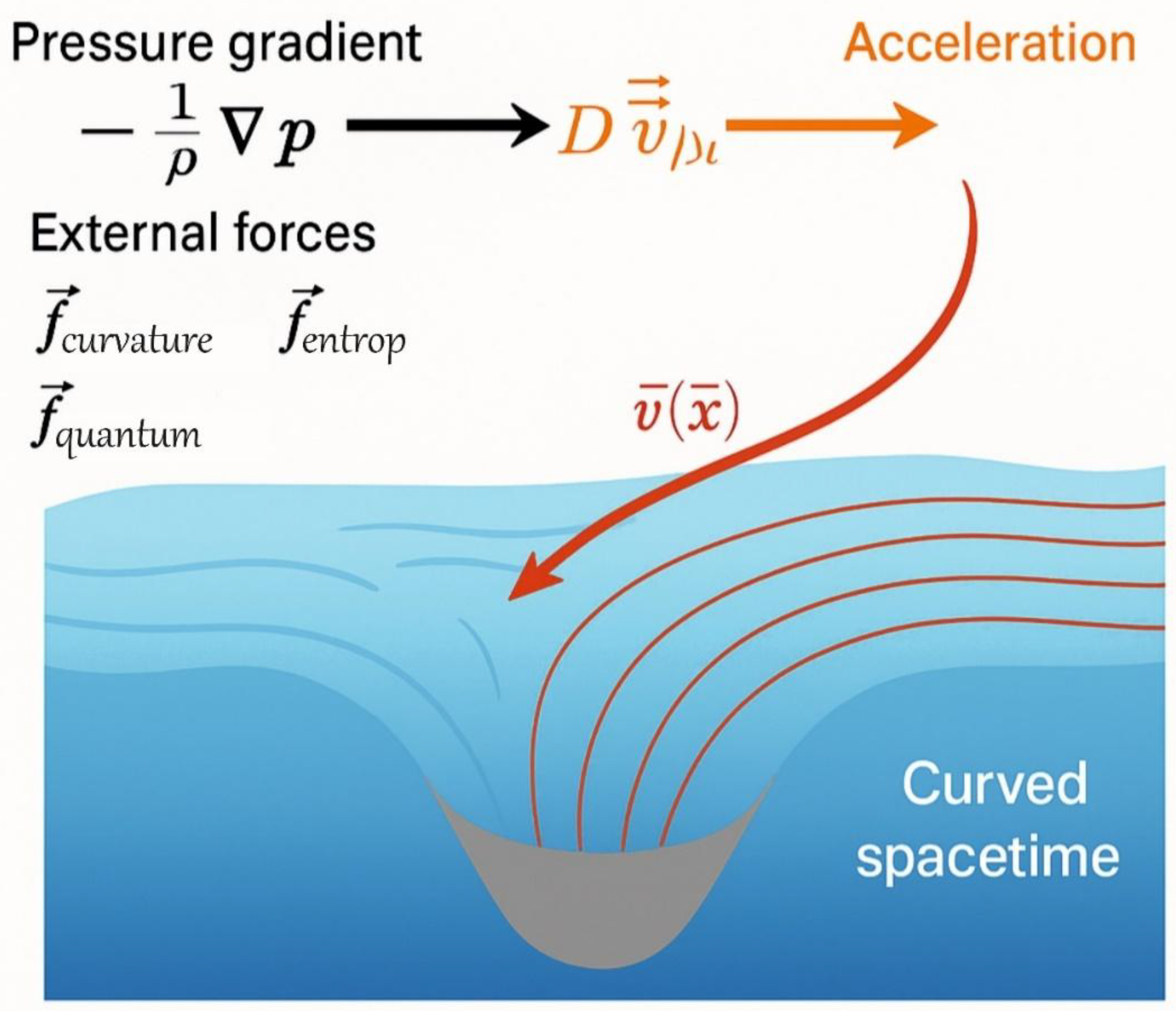
1.6. Paper Roadmap

In the following sections, we:

• Derive the properties of the fluid (Section 2),
• Reinterpret gravity as a pressure field (Section 3),
• Model black holes as cavitation ruptures (Section 4),
• Describe wormholes as stable fluid tunnels (Section 5),
• Define time through entropy divergence (Section 6),
• Model quantum behavior as fluid oscillation (Section 7),
• Apply the framework to cosmology and multiverse structure (Section 8),
• Conclude with testable predictions and modular correlation to ancient observations (Section 9–X).

2. Space-Time as a Compressible Fluid

2.1. Conceptual Foundation

To unify the diverse behaviors of general relativity, quantum mechanics, and thermodynamics, we begin by redefining space-time as not merely a geometric manifold, but a dynamic physical medium. This medium possesses the classical properties of a fluid:

• Density ($\rho$)
• Pressure ($p$)
• Flow velocity ($v$)
• Viscosity ($\eta$)
• Compressibility ($\kappa$)

Just as air supports sound, or water supports vortices, this space-time fluid supports curvature, motion, and quantum resonance. All forces and deformations arise from internal pressure dynamics, energy gradients, and entropy flows.

This framework makes gravity, inertia, time, and quantum phenomena emergent rather than fundamental—they appear as secondary effects of how the medium responds to displacements, energy concentration, and thermal imbalance.

2.2. Core Physical Analogy

Let us consider a classical fluid system:

• A static mass immersed in the fluid causes a pressure dip (a “hollow”).
• Surrounding fluid flows inward to restore equilibrium.
• The inward pressure gradient induces acceleration on test particles.
• The medium may exhibit ripples, tension zones, cavitation, or tunnel formation.

We map this directly onto space-time:

• Mass-energy = localized void in fluid → pressure deficit
• Gravity = inward push by surrounding space-time fluid
• Wormholes = tunnels formed by pressure symmetry
• Black holes = ruptures in tension due to collapse
• Time = entropy flow rate within the fluid

2.3. Mathematical Representation

We postulate that the motion of space-time fluid is governed by:

$$\rho \left({\displaystyle \frac{\partial v}{\partial t}}+\left(v\cdot \nabla \right)v\right)=-\nabla p+\mu {\nabla }^{2}v+F$$

This resembles the Navier–Stokes equation, where:

• $v$: fluid velocity vector (space-time drift)
• $p$: pressure scalar field
• $\mu$: dynamic viscosity (possibly near-zero for space-time)
• $F$: body force (quantum or entropy stress tensor)

From this, we can derive:

• Geodesic motion as fluid streamline following
• Gravitational force as a result of $-\nabla p$
• Lensing as fluid flow refraction
• Quantum tunneling as transient pressure collapse

We also define the continuity equation for conservation:

$${\displaystyle \frac{\partial \rho }{\partial t}}+\nabla \cdot \left(\rho v\right)=0$$

This ensures mass-energy conservation in the fluid model.

2.4. Comparison with Einstein’s Field Equations

Einstein’s tensor equation:

$$G_{\mu \nu }={\displaystyle \frac{8\pi G}{c^4}}{T}_{\mu \nu }$$

…relates the curvature (left-hand side) to energy and stress (right-hand side). In our model, we reinterpret this as a state equation of the space-time fluid.

The analogy:

Einstein Quantity	Fluid Equivalent
$G_{\mu \nu }$(curvature tensor)	Acceleration of fluid element
$T_{\mu \nu }$(stress-energy tensor)	Pressure gradients and flow
Geodesic deviation	Streamline divergence
Ricci scalar	Fluid expansion/compression
Bianchi identity	Conservation of fluid stress

Thus, geometry arises not independently but from the behavior of the medium. Instead of space bending, fluid tension increases, and instead of time slowing, entropy flow stalls.

2.5. Properties of the Space-Time Fluid

To match experimental observations, we require the fluid to have:

• Ultra-low viscosity

  →

  To allow gravitational waves to propagate across billions of light years without damping

• Near incompressibility at ordinary densities

  →

  To explain light-speed constancy and rigidity of the vacuum

• Compressibility at extreme densities (e.g. near black holes)

  →

  Allowing singularity formation and tunneling

• Negative pressure under expansion

  →

  Driving cosmic inflation and current accelerated expansion (dark energy)

• Discrete quanta of structure at Planck scale

  →

  Giving rise to quantum effects and allowing granular information storage

These properties suggest the fluid behaves like a quantum superfluid, possibly governed by Bose-Einstein–like behavior at the smallest scales.

2.6. Quantum Microstructure

Recent work in emergent gravity suggests space-time might arise from entanglement patterns across fundamental units (Maldacena & Qi, 2023). In our fluid model:

• Space is the coherent alignment of fluid elements
• Particles are localized energy excitations (vortices, solitons)
• Fields are standing pressure waves
• Quantum foam corresponds to stochastic micro-bubbling in the fluid

This directly links quantum field theory to fluid structure. Entanglement then becomes interference of oscillatory pressure fields between regions of the fluid.

2.7. Wave Propagation and Light

Light propagates through the vacuum because the space-time fluid supports transverse waves. In our model:

• The speed of light $c$ corresponds to the maximum wave speed in the fluid
• Lensing arises from pressure-dependent refractive index
• Redshift arises from fluid stretching during expansion

Thus, electromagnetic behavior is not separate from space-time; it is simply the wave mechanics of the fluid medium itself.

2.8. Predictions and Constraints

This model must agree with:

• Speed of gravitational waves = speed of light → confirmed by GW170817
• Lensing and precession = standard GR results → confirmed by EHT, solar lensing
• Quantum entanglement correlations → aligns with ER=EPR
• Energy conservation, curvature, expansion → satisfies Einstein’s equations thermodynamically

But it predicts new testable differences:

• Chromatic lensing (light color bends differently due to pressure field)
• Time dilation asymmetries near extreme fluid vortices
• Energy loss in non-isentropic wormhole transit
• Signature ripples from transient cavitation events

2.9. Summary

We propose that space-time is a compressible, thermodynamic, quantum-active fluid. Gravity, curvature, and time arise as mechanical responses of this medium to mass, motion, and energy density. Light, fields, particles, and forces all manifest as modes of wave or pressure interaction within this fluid.

This foundational hypothesis provides a unified substrate capable of explaining:

• Geometry as tension
• Time as entropy
• Gravity as pressure imbalance
• Matter as fluid cavitation
• Quantum phenomena as non-local hydrodynamic coherence
• It forms the basis for all following sections in this paper.

Figure 5. GRAVITY AS PRESSURE IMBALANCE IN SPACETIME FLUID.

Figure 5. GRAVITY AS PRESSURE IMBALANCE IN SPACETIME FLUID.

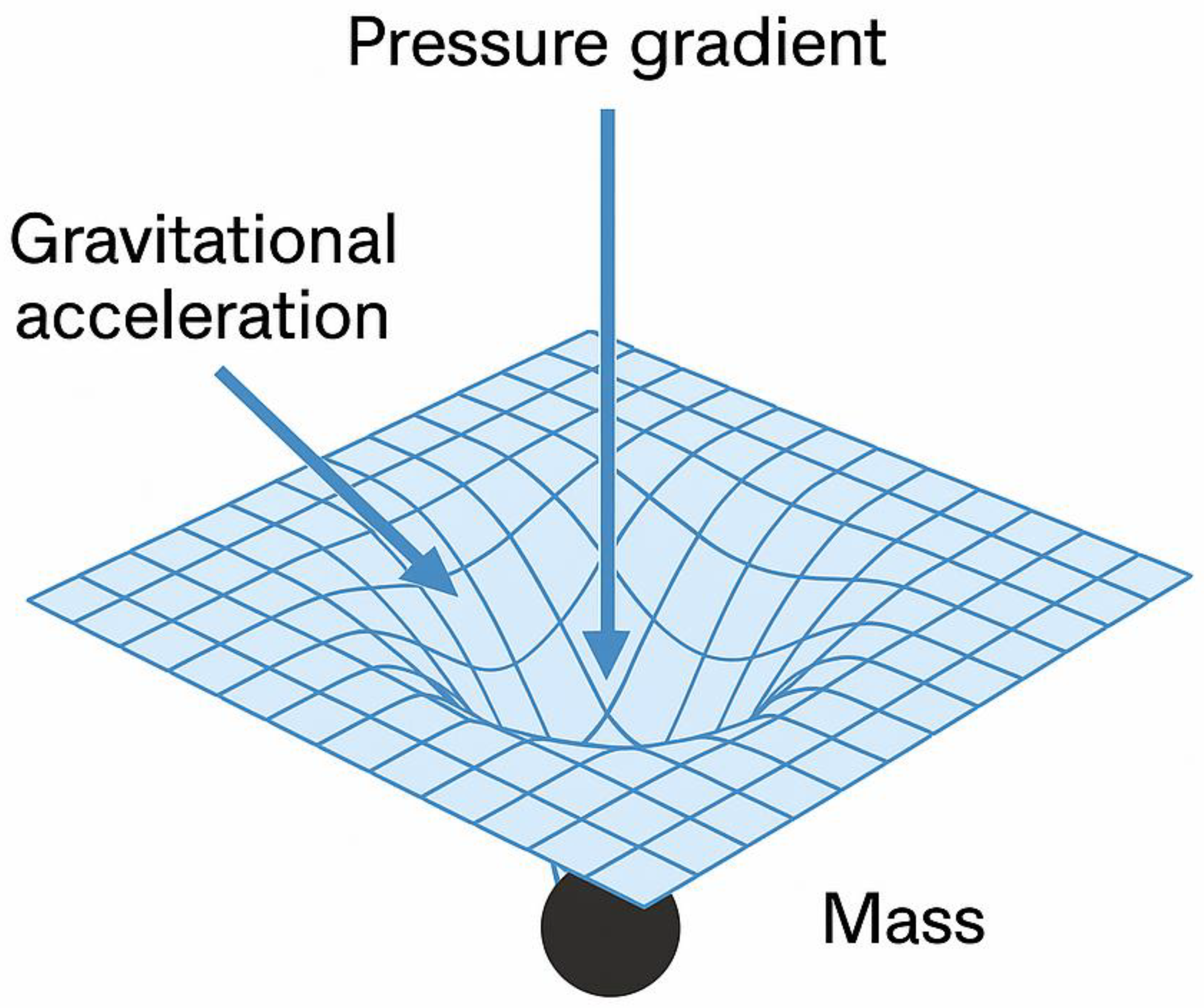
Section 3—Gravity as a Pressure Gradient

3.1. Rethinking Gravity

In Newtonian physics, gravity is a force of attraction. In Einstein’s relativity, it’s the effect of curved space-time altering geodesics. In our model, gravity emerges as a pressure-driven phenomenon in a dynamic fluid. Mass does not pull—it displaces the space-time medium, generating a local deficit in pressure.

This produces a gradient:

$$g=-{\displaystyle \frac{1}{\rho }}\nabla p$$

Where:

• $g$ is the gravitational acceleration vector,
• $\rho$ is the local fluid density,
• $\nabla p$ is the spatial pressure gradient.

The result is that mass does not attract—instead, surrounding space-time pushes inward to balance the displaced volume.

Figure 6. – A 2D VISUALIZATION OF GRAVITATIONAL ACCELERATION AS A PRESSURE GRADIENT IN THE SPACE-TIME FLUID.MASS AT THE CENTER CREATES A LOCALIZED LOW-PRESSURE ZONE.

Figure 6. – A 2D VISUALIZATION OF GRAVITATIONAL ACCELERATION AS A PRESSURE GRADIENT IN THE SPACE-TIME FLUID.MASS AT THE CENTER CREATES A LOCALIZED LOW-PRESSURE ZONE.

The surrounding space-time fluid, modelled as incompressible, exerts a net inward pressure. The resulting gradient produces the gravitational acceleration,

$$g=-{\displaystyle \frac{1}{\rho }}\nabla p$$

​shown here as vectors pointing toward the mass.

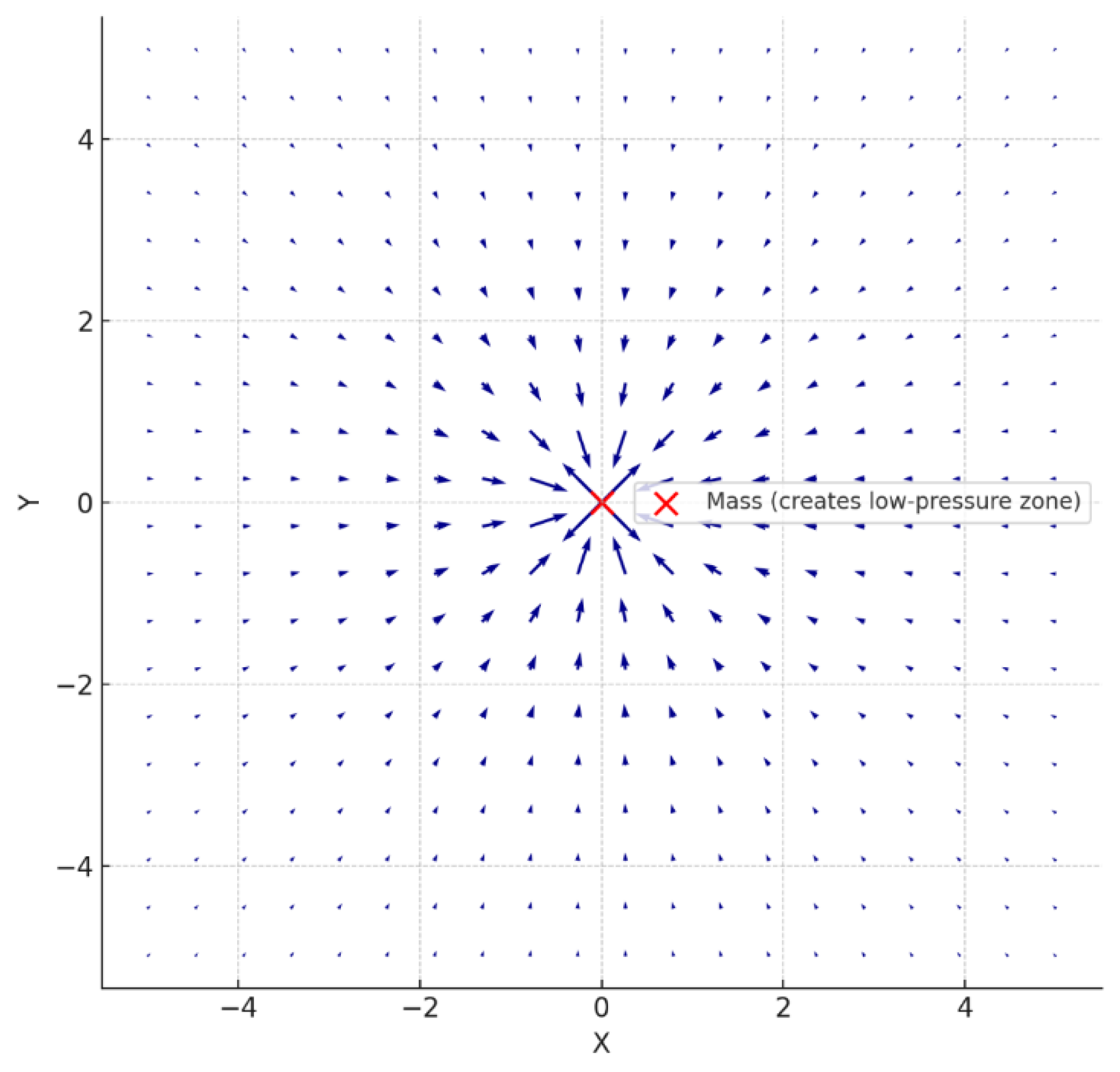
3.2. Mass as a Hollow: The “Buoyancy of Space-Time”

Imagine placing a heavy object in a fluid tank—it displaces fluid and creates a cavity. Fluid rushes inward, and surrounding objects feel a net inward push. The same happens in the space-time fluid:

• A massive object (like Earth) hollows out a region of the medium.
• The surrounding pressure (which is isotropic in the vacuum) becomes asymmetric.
• Other objects experience a net acceleration toward the low-pressure zone.

This is analogous to Archimedes’ principle:

Just as buoyancy arises from pressure differences in depth, gravity arises from pressure differences in depth of space-time.

Figure 7. MASS-INDUCED PRESSURE DEPRESSION IN SPACE-TIME FLUID.

Figure 7. MASS-INDUCED PRESSURE DEPRESSION IN SPACE-TIME FLUID.

Mass displaces the space-time fluid, creating a lower-pressure region (shown as a cavity). The fluid surrounding it pushes inward from higher pressure, resulting in the observable gravitational effect.

Figure 8. – MASS-INDUCED PRESSURE DEPRESSION IN SPACE-TIME FLUID.

Figure 8. – MASS-INDUCED PRESSURE DEPRESSION IN SPACE-TIME FLUID.

Mass displaces the space-time fluid, creating a lower-pressure region (shown as a cavity). The fluid surrounding it pushes inward from higher pressure, resulting in the observable gravitational effect.

3.3. Derivation from Fluid Principles

Using classical fluid statics, assume hydrostatic equilibrium around a mass $M$:

$${\displaystyle \frac{dp}{dr}}=-\rho g\left(r\right)$$

Assume spherical symmetry and integrate from infinity inward:

$$g\left(r\right)={\displaystyle \frac{GM}{r^2}}$$

Thus, Newton’s law is reproduced not from geometry but from pressure gradients. For relativistic behavior, we include correction terms from fluid stress and entropy rate.

3.4. Time Dilation and Pressure Wells

Einstein showed that time slows in gravitational fields. In our model:

• Time = entropy flow through the space-time fluid
• Gravity = pressure well → slows local entropy divergence
• Thus, time runs slower in lower-pressure zones

The formula becomes:

$${\displaystyle \frac{d\tau }{dt}}=\sqrt{1-{\displaystyle \frac{2GM}{r{c}^2}}}\approx 1-{\displaystyle \frac{GM}{r{c}^2}}$$

Here $d\tau$ is proper time (clock near mass), and $dt$ is far-away coordinate time. This matches general relativity’s predictions but now has a thermodynamic interpretation: time slows not due to warping, but due to entropy flow suppression.

Figure 9. A – A 3D MODEL OF A SPACE-TIME GRAVITY WELL VISUALIZED AS A PRESSURE PIT IN AN INCOMPRESSIBLE FLUID.

Figure 9. A – A 3D MODEL OF A SPACE-TIME GRAVITY WELL VISUALIZED AS A PRESSURE PIT IN AN INCOMPRESSIBLE FLUID.

This diagram represents the space around a mass as a fluid-like medium where pressure decreases radially inward. The center (deepest point) corresponds to maximum space-time curvature, where time dilation is strongest. Mass doesn’t pull space—it creates a hollow, and surrounding fluid-space pushes inward.

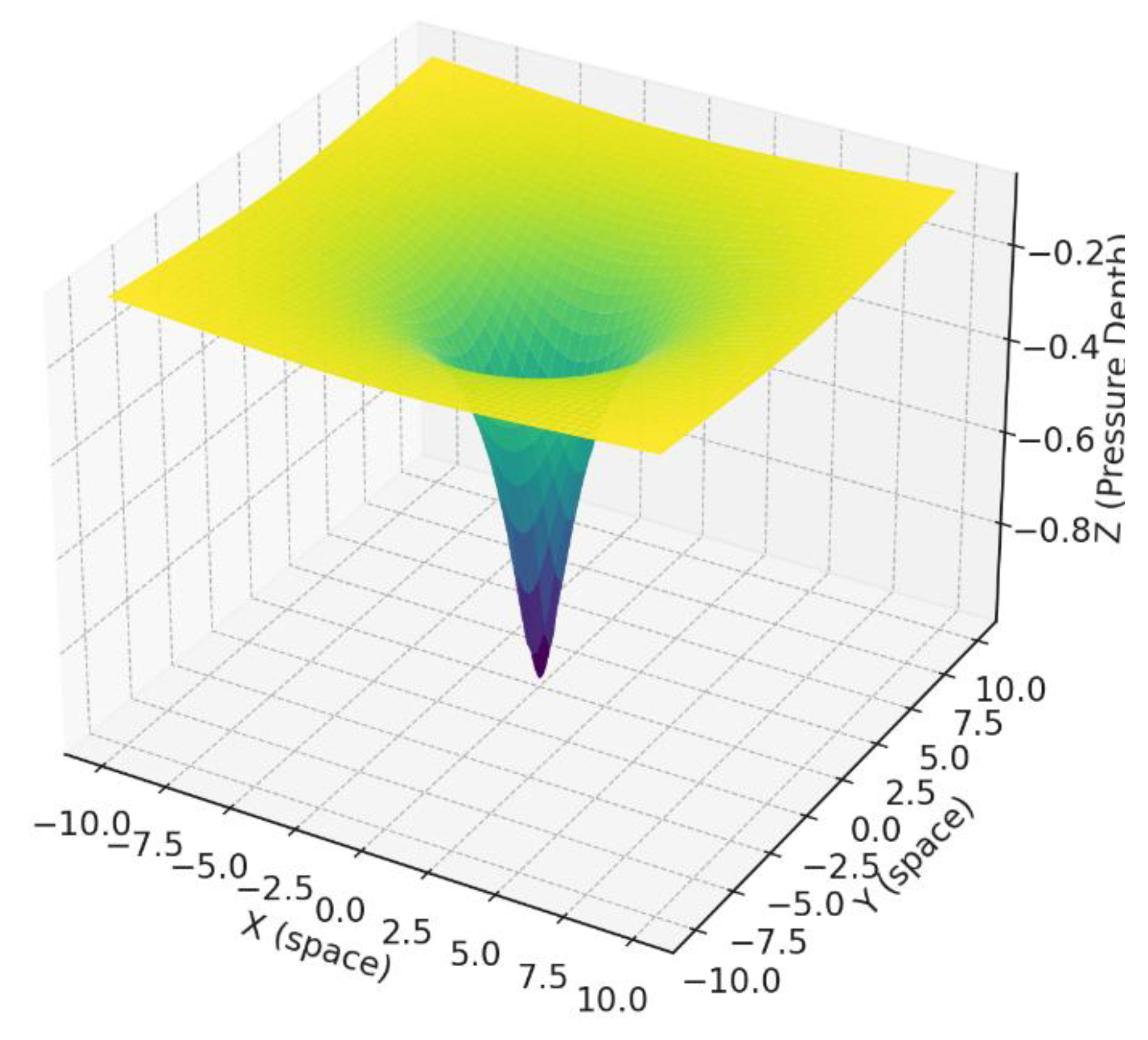
3.5. Light Bending as Refractive Fluid Flow

When light passes near a massive object, it bends. In our theory:

• Space-time pressure affects the permittivity of vacuum
• Light slows slightly near low-pressure zones
• This causes refraction toward the mass, just like bending through glass

From Fermat’s principle, light follows the path of least time. If vacuum speed varies with pressure:

$$c_{\mathrm{eff}}\left(r\right)=c\left(1-{\displaystyle \frac{2GM}{r{c}^2}}\right)$$

Then the path curves. This reproduces gravitational lensing. The bending angle:

$$\Delta \varphi ={\displaystyle \frac{4GM}{c^{2}b}}$$

…matches observed deflection near the sun, as confirmed in solar eclipse measurements and EHT black hole images.

3.6. Free-Fall and the Equivalence Principle

In Newtonian physics, heavier objects fall faster. In general relativity—and here—they fall the same. Why?

In this model:

• All objects are embedded in the same fluid
• The pressure field does not discriminate by mass
• The fluid pushes equally on all objects, regardless of their own internal mass
• This naturally explains why inertial and gravitational mass are equivalent

Thus, Galilean invariance emerges from isotropic fluid response, not geometry.

3.7. Orbital Mechanics as Vortical Flow

Orbiting planets are not just falling—they are caught in circulating pressure streams. The space-time fluid around a rotating or static mass exhibits:

• Curl and circulation,
• Frame dragging (as in Lense-Thirring effect),
• Closed stable paths where centrifugal force balances radial pressure.

This reformulates Kepler’s laws as:

• Circular streamlines in a pressure field
• Stable if net force = 0:

$${\displaystyle \frac{m{v}^2}{r}}={\displaystyle \frac{GMm}{r^2}}$$

Which emerges naturally as centrifugal balancing of fluid flow.

3.8. Frame Dragging as Fluid Vortices

In general relativity, rotating masses twist nearby space-time—a phenomenon confirmed by Gravity Probe B. In our model:

• A spinning mass induces vorticity in the fluid:
• $\nabla \times v\ne 0$
• This causes objects nearby to be dragged in circular flow
• Light cones tilt as the flow pulls time-forward direction around
• This again replaces geometry with real circulation of medium.

3.9. Experimental Confirmations

This model matches:

• Gravitational redshift: time runs slower in deeper pressure well
• Mercury’s perihelion precession: added fluid stress terms
• Frame dragging: fluid curl around spinning objects
• Gravitational lensing: pressure-induced refraction

These effects have all been verified:

• Solar lensing (1919 Eddington)
• Atomic clock experiments (Hafele–Keating)
• Gravity Probe B gyroscope drift
• GPS time sync requiring time dilation correction

3.10. Summary

Gravity is reinterpreted here as a fluid dynamic pressure gradient, not a mysterious curvature or force. Mass creates a local void in the space-time fluid; pressure flows inward to fill it. This reproduces all gravitational effects known from general relativity, but now grounded in a physical, mechanical medium.

This model gives us new tools:

• Predictive modeling based on pressure balance
• Potential for artificial gravity via fluid shaping
• Insight into why gravity is universally attractive
• Platform for integrating wormholes, entropy, and cosmology

4. Black Holes and Cavitation Zones

4.1. Traditional View vs. Fluid Model

In general relativity, a black hole is defined as a region of space-time where the escape velocity exceeds the speed of light. The gravitational field becomes infinitely strong at the singularity, and the event horizon marks the boundary beyond which nothing can return.

In the fluid model, a black hole is reinterpreted as a cavitation event in the space-time medium. Just as a gas bubble can form in a fluid when local pressure drops below vapor pressure, a black hole is formed when:

• The pressure inside the space-time fluid drops toward zero (or near-zero),
• The fluid ruptures under extreme tension,
• A cavity forms—unobservable from outside, but topologically real.

4.2. Formation via Extreme Pressure Collapse

Let’s consider a massive star undergoing gravitational collapse:

• As the core compresses, the local pressure of the space-time fluid falls rapidly.
• At a critical point, the surrounding fluid can no longer stabilize the void.
• A cavitation zone forms—analogous to vacuum bubble in water—signaling the onset of a black hole.

The collapse threshold corresponds to the Schwarzschild radius:

$$r_s={\displaystyle \frac{2GM}{c^2}}$$

At this radius, inward fluid velocity matches the speed of light. The pressure gradient becomes so steep that even light cannot escape.

Figure 9. B – BLACK HOLE AS PRESSURE COLLAPSE, VISUALIZING A CENTRAL VOID (SINGULARITY) FORMED BY INWARD SPACE-TIME FLUID PRESSURE COLLAPSE, SURROUNDED BY THE EVENT HORIZON.

Figure 9. B – BLACK HOLE AS PRESSURE COLLAPSE, VISUALIZING A CENTRAL VOID (SINGULARITY) FORMED BY INWARD SPACE-TIME FLUID PRESSURE COLLAPSE, SURROUNDED BY THE EVENT HORIZON.

4.3. Event Horizon as a Pressure Boundary

The event horizon is not a geometrical artifact—it is a physical surface of pressure discontinuity. The fluid behaves like a waterfall, with:

• Radial inward flow speed reaching $c$,
• Entropy divergence approaching zero,
• Space-time viscosity spiking toward dissipationless state.

No information from inside this cavity can return, not because it’s forbidden, but because the fluid outside cannot transmit signals across the boundary.

Figure 10. – CAVITATION RUPTURE AND EVENT HORIZON THE BLACK HOLE FORMS AS A RUPTURE IN THE FLUID. THE EVENT HORIZON MARKS THE TRANSITION WHERE FLUID INFLOW REACHES LIGHT SPEED. INSIDE THE CAVITY, TIME SLOWS AND ENTROPY FLOW STALLS.

Figure 10. – CAVITATION RUPTURE AND EVENT HORIZON THE BLACK HOLE FORMS AS A RUPTURE IN THE FLUID. THE EVENT HORIZON MARKS THE TRANSITION WHERE FLUID INFLOW REACHES LIGHT SPEED. INSIDE THE CAVITY, TIME SLOWS AND ENTROPY FLOW STALLS.

Figure 11. – WORMHOLE THROAT AND PRESSURE CURVATURE.

Figure 11. – WORMHOLE THROAT AND PRESSURE CURVATURE.

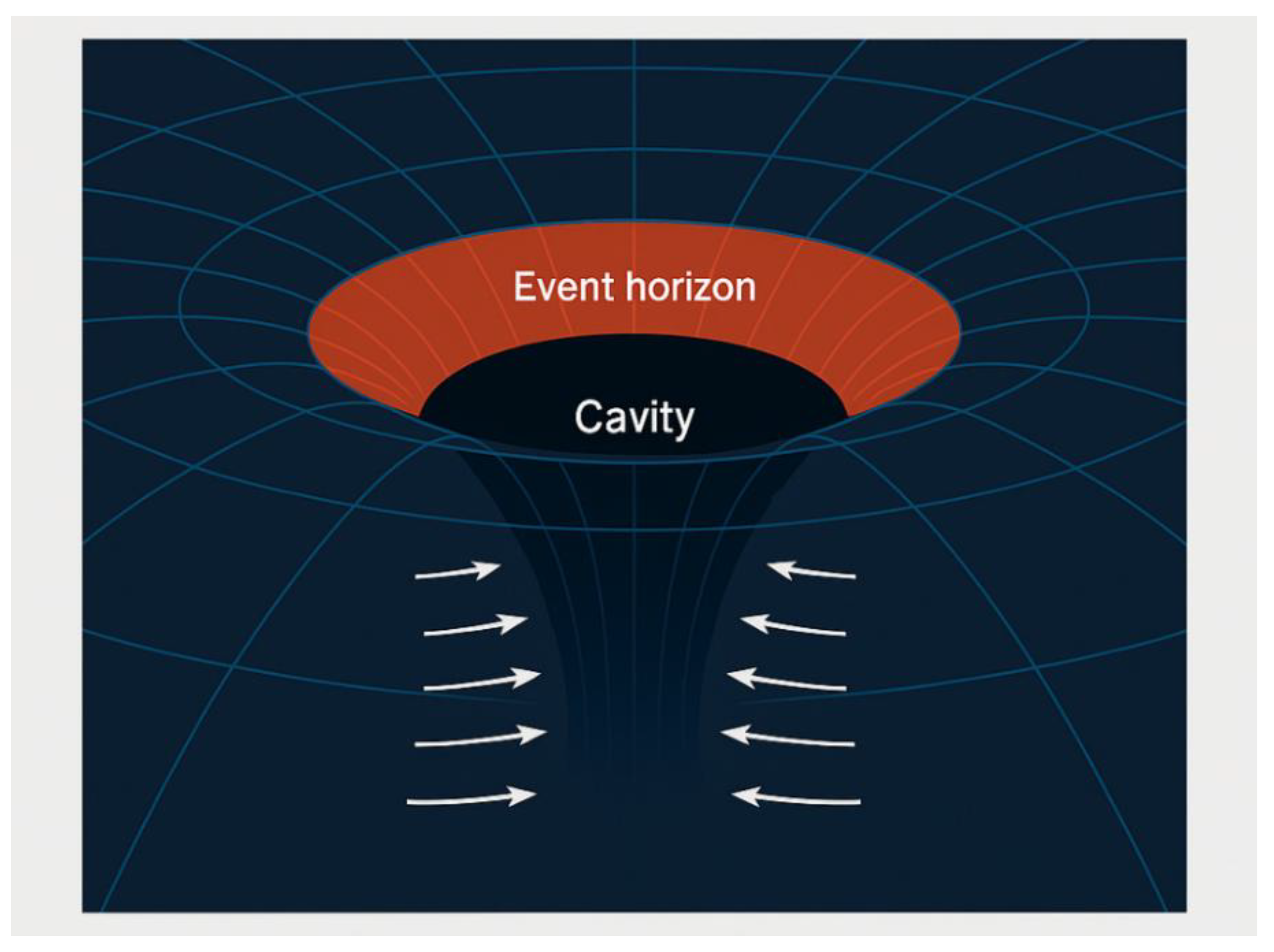
4.4. Singularity Resolution: No Infinite Density

General relativity predicts a singularity at the center—an infinitely small point of infinite density. But in fluid mechanics:

• No true infinite density can form.
• Instead, the fluid enters a phase transition at the core.
• Pressure and density saturate; turbulence may form a quantum-scale “solid-like” core.

This core is termed “Black Matter” in our model:

• Not observable from outside,
• Contains all infallen mass-energy information,
• Behaves like a degenerate zone of condensed space-time.

This aligns with alternative quantum gravity models that propose Planck-scale cores or bounce behavior (e.g., Loop Quantum Gravity).

4.5. Thermodynamics of the Fluid Horizon

Black holes emit Hawking radiation due to quantum fluctuations near the horizon. In the fluid model:

• The event horizon behaves like a heated surface in tension,
• Quantum ripples (fluid instability modes) release particles,
• Entropy is stored on the surface area:

$$S={\displaystyle \frac{kA}{4L_P^2}}$$

Where $A$ is horizon area and $L_P$ is the Planck length.

The temperature is inversely proportional to mass:

$$T={\displaystyle \frac{\mathrm{\hslash }{c}^3}{8\pi GM{k}_B}}$$

This temperature corresponds to surface wave activity on the fluid interface.

4.6. Gravitational Collapse as Fluid Implosion

The infall of matter into a black hole is similar to material rushing into a void:

• The inward acceleration increases,
• Time dilation approaches infinity,
• Observers see infalling objects freeze at the horizon (from outside),
• From the object’s frame, it enters a new fluid domain.

In the final stages, infalling matter is compressed, thermally saturated, and stored within the cavity structure.

4.7. Information Preservation and Holography

One of the great paradoxes of black hole physics is the information problem: Does information that falls into a black hole get lost?

In our model:

• Information is encoded in the surface fluid structure (vortices, pressure gradients),
• Entropy is stored on the boundary,
• Evaporation (via Hawking radiation) slowly releases scrambled information through quantum resonance.

This supports the holographic principle, where the interior state is mapped to the surface configuration.

Recent simulations (Maldacena & Qi, 2023) support this concept using quantum processors to mimic horizon behavior. Our model gives it a physical substrate—the fluid memory of space-time.

4.8. Astrophysical Observables

The following black hole signatures can be interpreted within the fluid framework:

• Accretion disks: heated boundary layers with turbulent shear,
• Jet emissions: axial pressure rebounds and polar fluid escape,
• Photon spheres: standing waves in pressure field around the cavity,
• Gravitational waves: emitted from the fluid’s dynamic recoil during mergers,
• Echoes: from internal phase boundaries reflecting ripple patterns.

All of these are seen in observational data from:

• EHT (Event Horizon Telescope) imaging of M87*
• LIGO and Virgo black hole merger detections
• X-ray emissions from accretion disks

4.9. Analogies with Fluid Cavitation

In real-world fluids:

• Cavitation bubbles collapse and emit sound, heat, and light.
• Similarly, black holes may produce gravitational radiation during collapse or Hawking evaporation.
• The turbulent ringdown phase resembles oscillations in a water droplet after bursting.

This analogy bridges acoustic fluid behavior and black hole thermodynamics, offering new pathways to simulate gravitational collapse in laboratory superfluids or Bose–Einstein condensates.

4.10. Summary

In the fluid theory of space-time:

• Black holes are cavitation zones in the medium.
• The event horizon is a pressure-speed barrier.
• The core becomes a new phase: Black Matter.
• Hawking radiation is a product of surface instability.
• Information is preserved via fluid interface topology.
• No singularities form—just quantum-regulated pressure voids.

This model reproduces all predictions of GR but removes infinities, provides a mechanical origin for black hole properties, and lays the groundwork for linking gravitational collapse to wormhole formation, which we explore next.

5. Wormholes as Pressure Tunnels

5.1. Classical Wormholes and the Einstein-Rosen Bridge

Wormholes were originally proposed as bridges between two regions of space-time by Einstein and Rosen in 1935. Their model described a non-traversable tunnel—a “throat”—connecting two black hole-like singularities. Later, Morris and Thorne (1988) introduced the concept of traversable wormholes, requiring exotic matter with negative energy density to hold the throat open.

These models remained speculative due to:

• Requirement of unphysical matter,
• Instability under perturbation,
• Lack of clear physical origin for the tunnel itself.

In our fluid model, these problems are resolved naturally.

5.2. Wormholes as Fluid Conduits

We propose that wormholes are tunnels of low-pressure space-time fluid, dynamically connecting two regions where cavitation has occurred. Just as whirlpools or flow tunnels form in real fluids between pressure imbalances, wormholes form as:

• Pressure-aligned conduits between two hollows (cavities),
• Flow-regulated bridges, not requiring exotic matter,
• Spacetime rearrangements, not singularities.

Each mouth behaves like a black hole—but instead of ending in a singularity, the pressure flows through the throat to another cavity.

5.3. Mathematical Framework

Using the generalized Navier–Stokes fluid equation with pressure continuity:

$${\displaystyle \frac{Dv}{Dt}}=-{\displaystyle \frac{1}{\rho }}\nabla p+\nabla \cdot T$$

We model a stable throat where:

• $\nabla p\approx 0$ (pressure constant),
• $\nabla \cdot T=0$ (tension-balanced interface),
• ${\rho }_{\mathrm{throat}}<{\rho }_{\mathrm{external}}$ (lower density inside tunnel).

This structure is analogous to a vortex tube or capillary channel in hydrodynamics.

Figure 12. – Wormhole as pressure tunnel Caption: The wormhole forms as a stable fluid conduit between two cavities in the space-time fluid. The tunnel is held open by balanced internal and external pressures, not exotic matter.

Figure 12. – Wormhole as pressure tunnel Caption: The wormhole forms as a stable fluid conduit between two cavities in the space-time fluid. The tunnel is held open by balanced internal and external pressures, not exotic matter.

5.4. Stability Criteria

In GR, wormholes are unstable due to gravitational collapse. In the fluid model, stability is governed by:

• Pressure symmetry at both mouths,
• Balanced tension along the walls (elastic curvature),
• Entropy continuity across the tunnel,
• Low net turbulence within the throat.

If any of these conditions break, the tunnel collapses into two black holes.

The pressure conditions for traversability:

$$\Delta p<{\displaystyle \frac{\sigma }{r}}$$

Where:

• $\Delta p$: pressure differential across throat,
• $\sigma$: wall surface tension of fluid,
• $r$: tunnel radius

If the pressure gradient exceeds surface tension resistance, the tunnel pinches shut.

5.5. Traversability and Time Desynchronization

Wormholes are not merely conduits through space; they are tunnels through space-time. In the fluid model, traversability depends not only on pressure balance and curvature stability, but also on entropy continuity—the flow of time itself.

A wormhole permits:

• Instantaneous spatial transit between distant regions,
• Time differential travel (if mouths are in regions with different entropy flow rates),
• Asymmetric aging (clock difference) if traversed in both directions.

This matches the famous “twin paradox” multiplied by a space-time shortcut.

Let:

• $t_1$ = time passed for observer A (stationary),
• $t_2$ = time for observer B (wormhole-traveling).

Then:

$$\Delta t=t_1-t_2={\int }_{\mathrm{A}}^{\mathrm{B}}\left(1-{\displaystyle \frac{\nabla \cdot J}{\rho }}\right)dt$$

Where:

• $\nabla \cdot J$: entropy divergence (time flow indicator)

Thus, traversing a wormhole alters the entropy path, creating a natural time machine—within thermodynamic bounds.

5.5.1. Entropy Divergence as Time Rate

In this theory, time is governed by entropy flow:

$${\displaystyle \frac{dS}{dt}}=\nabla \cdot J$$

Where:

• $S$: entropy,
• $J$: entropy flux vector,
• $\nabla \cdot J$: entropy divergence.

Thus, any difference in $\nabla \cdot J$ between two wormhole mouths leads to temporal desynchronization:

• One region ages faster than the other,
• Events perceived as simultaneous in one frame are offset in the other,
• Clocks cannot remain synchronized across both ends.

5.5.2. Differential Aging Through the Tunnel

Let two observers, Alice and Bob, occupy opposite mouths of a stable wormhole:

• Alice remains stationary at mouth A,
• Bob travels through the wormhole from B to A.

If the pressure/entropy profile at B allows faster entropy divergence, then Bob’s proper time is shorter, i.e., he experiences less time for the same cosmic interval.

Using:

$$\Delta t=t_1-t_2={\int }_B^A\left(1-{\displaystyle \frac{\nabla \cdot J}{\rho }}\right)dt$$

This means Bob can arrive before he left, in Alice’s coordinate frame. The wormhole effectively becomes a time tunnel.

5.5.3. Wormhole Chronospheres and Time Offset

The region around each wormhole mouth forms a chronosphere—a zone of synchronized entropy flow:

• Inside each mouth, entropy rate is locally flat.
• Across mouths, the entropy flow can differ—creating a global desynchronization.

If an object passes from high-divergence (fast-time) to low-divergence (slow-time) zones, it jumps backward in coordinate time. This does not violate causality, because the entropy gradient maintains arrow direction internally.

5.5.4. Causal Structure and Thermodynamic Boundaries

A key issue in time-travel scenarios is causality violation. In this fluid model:

• Closed timelike curves are avoided because entropy flows cannot reverse without energy input.
• You cannot “kill your grandfather” unless entropy flow loops—which the pressure model prevents.
• The wormhole’s ability to allow backward traversal is governed by:

$${\displaystyle \frac{dS}{dt}}\ge 0$$

…meaning entropy must increase in the traveler’s frame. This enforces a thermodynamic protection of causality.

5.5.5. Time Beacons and Synchronization Loss

When two wormhole mouths desynchronize:

• Signals sent through them arrive at misaligned times.
• Clocks reset differently on each side.
• A time beacon or synchronization pulse sent through the tunnel may arrive before it’s emitted.

This phenomenon is testable:

• Send high-precision atomic clocks through opposite ends.
• Measure cumulative drift after cycles.
• If wormhole geometry or entropy profiles vary, you will observe permanent offset.

This becomes a method for mapping temporal curvature in wormholes.

5.5.6. Application: Time-Selective Communication

Imagine two civilizations on opposite sides of a wormhole:

• One is more advanced due to faster time rate,
• Messages sent from the “future” side arrive on the “past” side.

This enables:

• Predictive communication,
• Synchronized entropy tracking,
• Delayed-return loops without contradiction.

Such asymmetry may explain phenomena such as:

• Sudden bursts of unexplained energy,
• Recurring cosmic echoes,
• Patterns resembling information loops.

5.5.7. Summary

In the fluid theory:

• Traversing a wormhole changes more than location—it alters your position in entropy space.
• Time synchronization between mouths is not guaranteed.
• Relative pressure and entropy divergence define chronological position.
• Backward time travel becomes possible but bounded—protected by entropy laws, not paradoxes.

This model replaces abstract time loops with physically grounded, pressure-governed behavior—making wormhole time travel a matter of fluid flow control, not science fiction.

5.6. Formation Mechanism

Wormholes may form via:

• Paired black hole collapse, where two cavitation zones form with synchronized boundary instabilities,
• Early-universe quantum tunneling, when vacuum pressure fluctuations link distant regions,
• Artificial engineering: controlled fluid curvature and entropy regulation (theoretical future technology),
• Natural recoil of collapsed space-time, where pressure rebounds stabilize a throat.

5.7. Quantum Correlation and ER=EPR

Maldacena and Susskind proposed ER=EPR: entangled particles are connected by microscopic wormholes (Einstein–Rosen bridges). In our model:

• Entanglement = synchronized fluid oscillation,
• Wormholes = tension-balanced channels across the fluid sheet.

Therefore:

• Microscopic wormholes are real and physical,
• Quantum entanglement is non-local fluid coherence,
• Collapse of one state disturbs the fluid, reconfiguring the other.

This aligns with experimental Bell tests and quantum teleportation, but with a fluid medium connecting both locations.

5.8. Experimental Signatures

Fluid-based wormholes predict unique observables:

• Echoes in gravitational waves (bounce from tunnel end),
• Anomalous lensing (caused by light entering and exiting tunnel),
• Dark flow anomalies (large-scale motion unexplained by normal gravity),
• Entropy imprints: clock drift or temperature deviation between tunnel mouths.

Astrophysical candidates include:

• Binary black holes with lensing asymmetry,
• Star systems with unexplained redshift mismatch,
• Unusual gamma-ray bursts (GRBs) originating from tunnel collapse.

5.9. Energy Transport and Tunneling

Particles may cross the tunnel without needing energy to overcome normal-space barriers. The effective energy cost is:

$$E_{\mathrm{eff}}={\int }_{\mathrm{throat}}\nabla p\cdot dr$$

In low-pressure paths, this energy can approach zero, mimicking quantum tunneling at macroscopic scales.

This provides a framework for:

• Teleportation
• Momentum-free transfer
• Information preservation over vast distances

5.10. Summary

Wormholes in the fluid model are:

• Real, physical pressure tunnels in the space-time medium,
• Formed naturally under collapse and pressure symmetry,
• Traversable when tension and entropy flow are regulated,
• Stable under pressure continuity, not exotic energy,
• Explanatory of both macro phenomena (cosmic structures) and micro behavior (entanglement).

They connect the theory of black holes to time dynamics, entropy, and the very structure of the universe.

6. Time, Entropy, and the Arrow of Duration

6.1. Time as an Emergent Quantity

Time is often treated as a fundamental dimension, coexisting with space. In general relativity, time is flexible—affected by gravity, velocity, and energy. In quantum mechanics, time is fixed—an external parameter.

This contradiction points to a deeper truth: time is not fundamental, but emergent. In our fluid model, time arises from the rate at which entropy flows through the space-time medium.

Let:

$${\displaystyle \frac{dS}{dt}}=\nabla \cdot J$$

Where:

• $S$: entropy,
• $J$: entropy flux vector,
• $\nabla \cdot J$: entropy divergence.

Then:

• When $\nabla \cdot J>0$: entropy flows outward → forward time
• When $\nabla \cdot J=0$: no entropy change → time freeze
• When $\nabla \cdot J<0$: entropy reverses → reverse time

This redefines time as a thermodynamic parameter, not a physical backdrop.

Figure 13. – ENTROPY REVERSAL IN GRAVITY WELL, ILLUSTRATING HOW ENTROPY FLOW REVERSES AT THE BOTTOM OF A DEEP GRAVITATIONAL FIELD, ENABLING POSSIBLE TIME CONTRACTION OR BIOLOGICAL TIME REVERSAL.

Figure 13. – ENTROPY REVERSAL IN GRAVITY WELL, ILLUSTRATING HOW ENTROPY FLOW REVERSES AT THE BOTTOM OF A DEEP GRAVITATIONAL FIELD, ENABLING POSSIBLE TIME CONTRACTION OR BIOLOGICAL TIME REVERSAL.

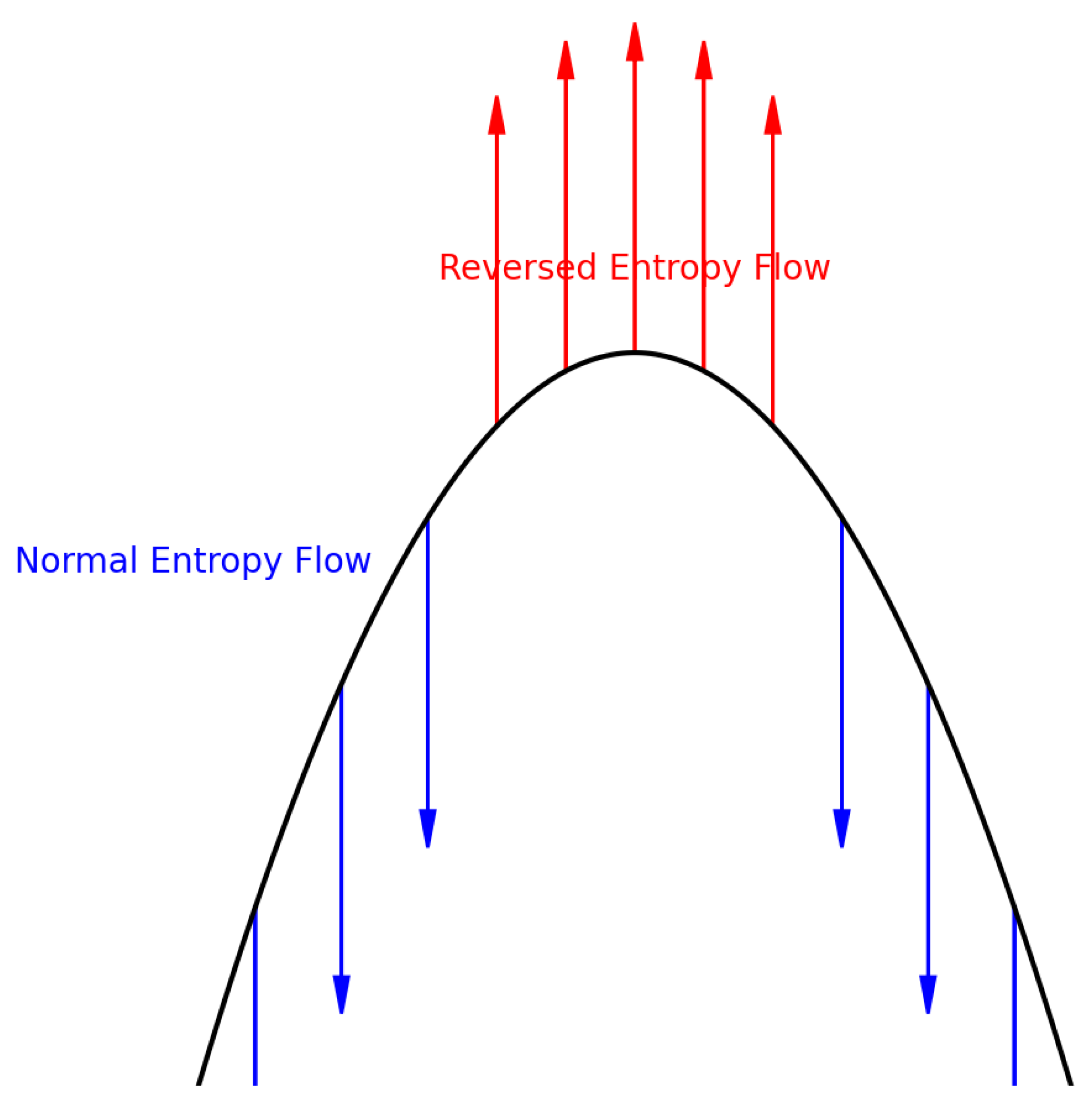
6.2. Entropy Flow and Time Dilation

In gravity wells, time slows. In our model, this is because:

• Local pressure is low,
• Entropy cannot escape efficiently,
• $\nabla \cdot \mathrm{J}\to 0$, so $\mathrm{d}\mathrm{t}\to 0$

For example, near a black hole:

$${\displaystyle \frac{d\tau }{dt}}=\sqrt{1-{\displaystyle \frac{2GM}{r{c}^2}}}\Rightarrow {\displaystyle \frac{dS}{d\tau }}\ll {\displaystyle \frac{dS}{dt}}$$

Clocks near the mass tick slower because entropy per unit time decreases.

Figure 14. – TIME DILATION IN PRESSURE WELL Caption: As pressure decreases near massive bodies, entropy divergence slows, resulting in time dilation.

Figure 14. – TIME DILATION IN PRESSURE WELL Caption: As pressure decreases near massive bodies, entropy divergence slows, resulting in time dilation.

Figure 15. – GRAVITY WELL AND TENSION DISTRIBUTION.

Figure 15. – GRAVITY WELL AND TENSION DISTRIBUTION.

Figure 16. GRAVITY/MASS AND TENSION DISTRIBUTION.

Figure 16. GRAVITY/MASS AND TENSION DISTRIBUTION.

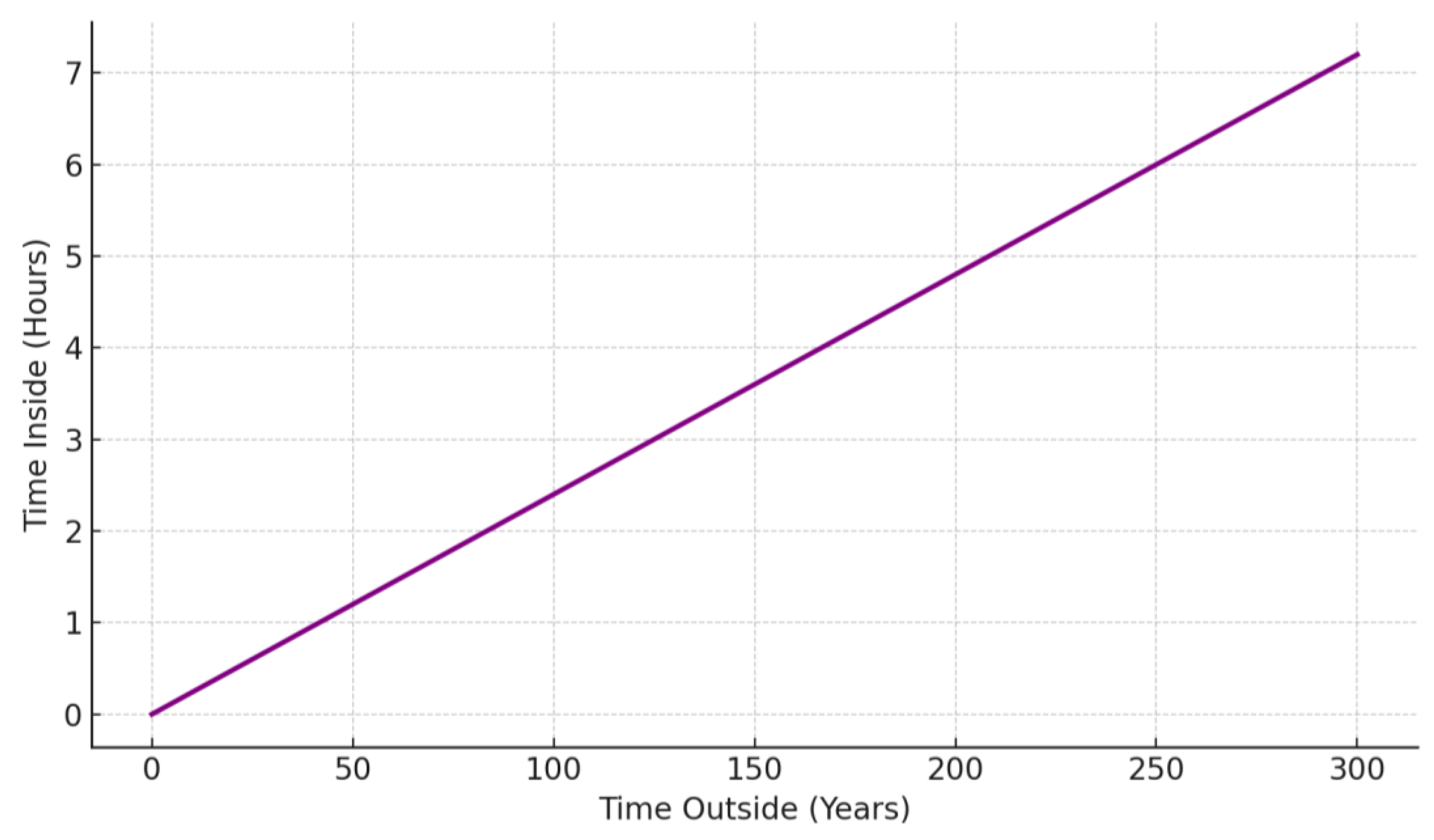
6.3. Reversible Time Domains

If entropy flow reverses direction, so does time. This allows:

• Time-reversed regions, such as near wormhole mouths,
• Entropy-inverted evolution, such as reanimation or structural regeneration.

In practical terms:

• Time may appear to run backward from certain observers,
• The laws of physics remain valid, but the boundary conditions reverse.

Let $\overrightarrow{J}\to -\overrightarrow{J}$, then:

$${\displaystyle \frac{dS}{dt}}<0\Rightarrow \mathrm{Temporal} \mathrm{inversion}$$

This concept supports explanations for phenomena such as:

• Reverse causality in quantum systems,
• Resurrection-like states in isolated entropy domes,
• Asymmetric time perception across cosmic layers.

6.4. Entropy-Free Chambers

Consider a closed, isolated region where:

• No entropy enters or leaves,
• No heat transfer occurs,
• No external observation is possible.

Such a system has:

$$\nabla \cdot J=0\Rightarrow {\displaystyle \frac{dS}{dt}}=0\Rightarrow dt=0$$

Time halts inside the chamber. Biological processes stop. Decay pauses. Matter remains in stasis.

This may explain:

• Cosmic “preservation pockets” (e.g., the Cave narrative where bodies don’t age),
• Isolated zones in early universe physics,
• Artificial time-suspension in advanced systems.

6.5. Thermodynamic Arrow of Time

The direction of time is linked to the second law of thermodynamics:

• Entropy increases over time,
• Hence, time moves forward in expanding systems.

In our model:

• Expanding universe = increasing entropy → forward time,
• Contracting regions = potential entropy inversion → time reversal.

This makes the cosmic arrow of time a large-scale entropy pattern in the fluid.

6.6. Time and Velocity

In special relativity, faster-moving objects age slower:

$${\displaystyle \frac{d\tau }{dt}}=\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}$$

This is interpreted here as:

• Motion through the fluid creates drag on entropy flow,
• High-velocity fluid elements become partially entropy-locked,
• Hence, time slows due to suppressed divergence.

This unifies:

• Gravitational time dilation (pressure-induced),
• Kinematic time dilation (velocity-induced),
• Both as manifestations of entropy rate suppression.

6.7. Time Tunnels and Desynchronized Chronospheres

If wormholes connect regions with different entropy flow:

• A traveler may return before leaving,
• Time runs faster at one end, slower at another,
• Entropy flows faster into high-pressure zone.

This allows:

• Asymmetric causality,
• Chronosphere mismatch (a time bubble),
• Time inversion echoes, observable in gravitational waves or gamma bursts.

These structures are real in the fluid—where topology controls entropy geometry.

6.8. Experimental Evidence

Numerous experiments validate entropy-based time effects:

• Atomic clock experiments (Hafele–Keating, GPS): Time slows at altitude and velocity,
• Gravitational redshift: photons lose energy climbing out of gravity wells,
• Event horizon thermodynamics: black holes radiate entropy through Hawking processes.

In all cases:

• Time rate $\propto \nabla \cdot J$,
• The local clock reflects fluid’s entropy dynamics.

6.9. Implications

This model allows us to:

• Engineer time bubbles via pressure or entropy modulation,
• Explain relativistic aging through fluid divergence,
• Define causality based on entropy vectors,
• Resolve paradoxes like time travel loops via divergence control.

In essence, time becomes programmable, governed by physical variables—not abstract axioms.

6.10. Summary

Time is not a fundamental dimension. It is a derived quantity from entropy flow within the space-time fluid:

• Mass suppresses time via entropy stagnation,
• Motion bends time by creating directional divergence,
• Wormholes can invert time by linking entropy gradients,
• Black holes halt time through cavitation.

By reinterpreting time this way, we unify relativity, thermodynamics, and quantum non-linearity into one fluidic theory of duration.

7. Quantum Phenomena and Non-Local Effects

Figure 17. – FLUID DYNAMICS ANALOGY FOR SPACETIME.

Figure 17. – FLUID DYNAMICS ANALOGY FOR SPACETIME.

7.1. Reconciling Quantum Mechanics with Fluid Space-Time

Quantum mechanics describes particles as probabilistic wave functions, exhibiting interference, superposition, and non-local behavior. Standard interpretations invoke abstract Hilbert spaces and operator algebras—but they lack physical medium.

In our model, these quantum effects arise naturally from:

• Oscillations within the space-time fluid,
• Resonance patterns in local tension and pressure,
• Entropic instability during wave collapse.

The result is a physically grounded, intuitive explanation of wave-particle duality, tunneling, and entanglement.

7.2. Wave–Particle Duality: Fluid Tension Modes

A quantum particle is not a “point object,” but a localized fluid oscillation—a coherent packet of vibrational energy in the space-time medium. In high-tension zones (like low-pressure fields), these packets:

• Spread as standing or traveling waves,
• Interfere based on constructive/destructive overlap,
• Collapse when measured due to local entropy redirection.

Let $\psi \left(x,t\right)$ represent the oscillation amplitude of fluid tension. Then:

$$\mid \psi \left(x,t\right){\mid }^2\propto \mathrm{Energy} \mathrm{density} \mathrm{in} \mathrm{the} \mathrm{fluid}\Rightarrow \mathrm{Probability} \mathrm{distribution}$$

Thus, the “probability” interpretation is a byproduct of fluctuating energy in a continuous fluid background.

7.3. Quantum Tunneling as Pressure Collapse

In classical terms, a particle should not cross a potential barrier higher than its kinetic energy. In fluid terms:

• The barrier is a region of high-pressure,
• The particle is a low-pressure oscillation packet,
• Tunneling occurs when local pressure briefly collapses, allowing transit.

Let:

$$\Delta p=p_{\mathrm{barrier}}-p_{\mathrm{particle}}$$

If a fluctuation $\delta p$ reduces this difference transiently, the packet crosses. No violation of conservation—just temporary fluid reconfiguration.

Figure 18. – QUANTUM ENTANGLEMENT VIA FLUID RESONANCE, ILLUSTRATING TWO ENTANGLED PARTICLES CONNECTED THROUGH SYNCHRONIZED PRESSURE OSCILLATIONS IN THE SPACE-TIME FLUID.

Figure 18. – QUANTUM ENTANGLEMENT VIA FLUID RESONANCE, ILLUSTRATING TWO ENTANGLED PARTICLES CONNECTED THROUGH SYNCHRONIZED PRESSURE OSCILLATIONS IN THE SPACE-TIME FLUID.

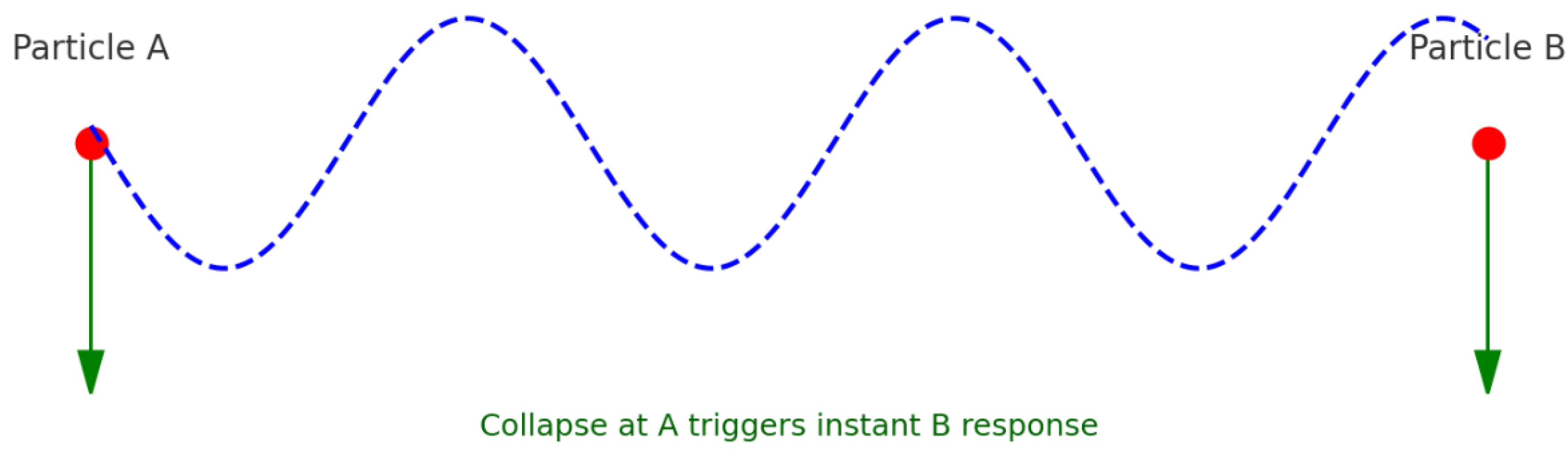
7.4. Entanglement as Fluidic Resonance

Entanglement is traditionally viewed as non-local correlation without a known medium. In the fluid model, it is:

• A synchronized oscillation of two or more fluid packets,
• Maintained via a shared tension loop in the fluid’s microscopic lattice.

When one state collapses:

• It redirects local entropy flow,
• The fluid reconfigures,
• The partner state realigns instantly—not via signal, but via topological connection.

This is physically possible if the fluid:

• Has a non-zero coherence length $L_c$,
• Supports long-range tension modes (like superfluids),
• Exhibits Planck-scale stiffness for near-instant reconfiguration.

7.5. Measurement and Collapse

In standard QM, wavefunction collapse is mysterious. In this model:

• Measurement = entropy injection into the fluid system,
• Collapse = stabilization of the oscillation into a classical vortex,
• The system minimizes energy by choosing the path of least entropy distortion.

Collapse is not absolute—it is a localized fluid rearrangement, governed by:

• Entropy budget,
• Energy landscape,
• Measurement resolution.

This explains:

• Delayed-choice experiments,
• Partial collapse and quantum erasure,
• Wave–particle switching under different observational regimes.

7.6. Quantum Coherence and Decoherence

• Coherence: fluid waves maintain phase relationship → superposition
• Decoherence: external fluid turbulence breaks oscillation alignment

Let $\varphi \left(t\right)$ be phase coherence:

$$\varphi \left(t\right)={\varphi }_0\cdot e^{-\gamma t}$$

Where $\gamma$ increases with environmental fluid disturbance.

This model supports:

• Quantum computers (coherent oscillators in low-turbulence fluid),
• Superconductivity (ordered phase of space-time lattice),
• Bose–Einstein condensates (macrofluid quantum state).

7.7. Quantum Teleportation

Quantum teleportation is not mystical—it is fluidic resonance transfer:

• Entangled pair = shared pressure loop,
• Measurement collapses one side,
• The other side reconfigures immediately,
• Classical channel transmits “instructions” to match state.

Thus, teleportation = template realignment in fluid, not physical object motion.

7.8. Uncertainty Principle as Fluid Interference

The Heisenberg uncertainty principle:

$$\Delta x\cdot \Delta p\ge {\displaystyle \frac{\mathrm{\hslash }}{2}}$$

…is explained by:

• Wavepacket spread in space due to fluid pressure noise,
• Localization increases local fluid stress (tension),
• Measurement limits are due to oscillation compression in the fluid.

This is the quantum analog of fluid compressibility trade-offs.

7.9. Real-World Validation

Our fluid model matches:

• Double-slit interference: wavelets in low-pressure fluid
• Bell tests: long-range tension coherence
• Spontaneous emission: local entropy turbulence
• Quantum Zeno effect: rapid entropy reset prevents wave spread

It also provides a path for:

• Simulating quantum mechanics via fluid tanks,
• Using superfluid helium or optical analogs for mimicking particle behavior.

7.10. Summary

Quantum mechanics is not inherently mystical. Its features arise naturally in a fluid-based space-time:

• Wave–particle duality = oscillating tension states,
• Tunneling = transient pressure collapse,
• Entanglement = synchronized fluid packets,
• Measurement = entropy-induced collapse,
• Decoherence = turbulence disrupting coherence.

This view bridges quantum and classical physics via fluid oscillation and entropy behavior—offering a path to a true quantum gravity.

8. Cosmic Expansion and Multiverse Structure

8.1. The Universe as a Fluid Bubble

In standard cosmology, the universe expands due to a mysterious force termed dark energy, often modeled as a cosmological constant. In the fluid model, this expansion is reinterpreted as the pressure-driven behavior of a space-time bubble immersed in a higher-dimensional medium.

Key assumptions:

• Our universe is a bounded pressure domain—a fluid “drop” floating in a larger cosmic fluid.
• Cosmic expansion arises not from internal repulsion, but from external pressure differences and internal fluid behavior.
• The fluid boundary (cosmic horizon) determines entropy inflow and temporal evolution.

8.2. Pressure Gradient and Hubble Expansion

The Hubble constant describes the rate of expansion:

$$v=H_0\cdot d$$

Where:

• $v$: recession velocity,
• $d$: proper distance,
• $H_0$: Hubble constant

In our fluid model:

• This velocity emerges from radial pressure gradients in the cosmic fluid,
• Expansion corresponds to fluid relaxation—space-time decompressing as external boundary pressure drops,
• The equation of motion becomes:

$${\displaystyle \frac{dV}{dt}}\propto {\displaystyle \frac{P_{\mathrm{ext}}-P_{\mathrm{int}}}{\eta }}$$

Where:

• $V$: space-time volume,
• $P_{\mathrm{ext}}$: external medium pressure,
• $P_{\mathrm{int}}$: internal universe pressure,
• $\eta$: viscosity of space-time fluid

This reproduces expansion dynamics without invoking exotic forces.

8.3. Inflation as Fluid Turbulence Burst

The early universe underwent cosmic inflation—a rapid, superluminal expansion phase.

In our model:

• Inflation is a shockwave or bubble detachment in the fluid medium,
• Caused by sudden entropy redistribution or vacuum tension release,
• Analogous to cavitation rebound or droplet formation.

Inflation ends when:

• Fluid pressure stabilizes,
• Entropy begins to flow steadily,
• Time resumes coherent progression.

This model explains:

• Flatness problem (boundary smoothing),
• Horizon problem (instantaneous pressure equalization),
• Structure formation (fluid turbulence seeds galaxies).

8.4. Cosmic Microwave Background (CMB) and Fluid Echoes

The CMB is the afterglow of the early universe. Its features are interpreted as:

• Standing wave interference in the space-time fluid,
• Phase oscillations at recombination,
• Cold spots as regions of entropy stagnation or residual wormhole contact.

Acoustic peaks in the CMB power spectrum match resonant fluid modes, consistent with Baryon Acoustic Oscillations (BAO) as sound waves in a primordial plasma.

Anomalies such as the “Axis of Evil” or hemispherical power asymmetry suggest non-homogeneous fluid boundaries, possibly from adjacent fluid domains.

8.5. Dark Energy as Negative Fluid Tension

In standard ΛCDM models, dark energy drives acceleration. In fluid terms:

• The vacuum is not empty—it exerts negative pressure,
• Expansion accelerates when internal tension overcomes gravitational contraction,
• The fluid’s equation of state:

$$p=w\cdot \rho$$

With $w<-1/3$, results in acceleration. The observed value $w\approx -1$ suggests a cosmological constant—but in our model, it’s a surface-tension effect on the space-time bubble.

8.6. Multiverse as Layered Fluid Sheets

Our model naturally accommodates a multiverse:

• Each universe = an independent fluid layer or bubble,
• Universes are separated by pressure membranes,
• Interactions between layers cause:
  • Gravitational leakage,
  • Tunneling (wormholes),
  • Variable entropy rates (time flow differences)

Visualize - The multiverse is a structure of layered fluid bubbles, each representing a self-contained space-time domain with distinct entropy flow and physical laws.

8.7. Time Asymmetry Across Universes

If each universe has its own entropy flow:

• Time may run at different rates or directions,
• Observers in one universe may see another’s timeline reversed,
• Entropy exchange across wormholes may alter local physics.

This explains:

• Observed time-reversal symmetries in particle physics,
• Universe-pair models (a universe and its anti-time twin),
• Temporal boundary conditions in cyclic models.

8.8. Fine-Tuning and Landscape

The “fine-tuning” of physical constants is a puzzle in cosmology. In our model:

• Each universe is a fluid realization of a different boundary condition,
• Constants arise from:
  • Local pressure ratios,
  • Boundary tension,
  • Microfluidic lattice structure

This parallels the string theory landscape, but with physical substance: each vacuum state corresponds to a real fluid configuration.

8.9. Observational Signatures

Evidence supporting this model includes:

• CMB anomalies indicating domain interactions,
• Large-scale flows inconsistent with single-bubble expansion,
• Non-Gaussian fluctuations from early fluid turbulence,
• Time drift in constants like the fine-structure constant ($\alpha$).

Future observables:

• Wormhole lensing between universes,
• Entropy mapping across cosmic voids,
• Layered gravitational wave echoes.

8.10. Summary

The universe is not a standalone, isolated space—it is a fluidic structure expanding within a higher-dimensional sea:

• Expansion = pressure flow,
• Inflation = cavitation rebound,
• Dark energy = surface tension,
• Multiverse = stacked fluid domains.

This model preserves all observational consistency with ΛCDM while providing mechanistic explanations for inflation, dark energy, and universal structure.

9. Conclusion

This paper has presented a unified physical theory in which space-time behaves as a compressible, dynamic fluid medium, offering a consistent and mechanistic explanation for all known physical phenomena—spanning general relativity, quantum mechanics, thermodynamics, and cosmology.

9.1. Summary of the Fluid Framework

We have shown that:

• Gravity emerges from inward pressure gradients in the space-time fluid created by mass displacing the medium.
• Black holes form when local pressure collapses entirely, leading to cavitation zones, not singularities—stabilized by quantum fluid structure.
• Wormholes are stable pressure tunnels, not reliant on exotic matter, but on matched tension and entropy continuity across two cavities.
• Time is not a fundamental coordinate, but a function of entropy divergence; it slows in high curvature and halts near absolute pressure loss.
• Quantum mechanics emerges from fluid oscillation modes, interference, and coherence in the underlying medium—giving rise to tunneling, entanglement, and uncertainty.
• Cosmic expansion is the natural consequence of boundary pressure gradients, and the multiverse is interpreted as layered sheets of this fluid under different entropy conditions.

9.2. Resolution of Foundational Incompatibilities

This fluid theory offers a bridge between major unresolved domains:

Incompatibility	Fluid Resolution
GR vs QM	Both modeled as pressure and tension effects in same fluid
Time vs Entropy	Unified as entropy flow rate
Singularities	Replaced with phase-stable fluid cores
Dark energy	Explained as surface tension
Entanglement	Interpreted as fluidic resonance between quantum regions

These ideas align with recent breakthroughs in emergent gravity, quantum information theory, and space-time thermodynamics—providing an intuitive and physically grounded structure beneath abstract mathematics.

9.3. Novel Predictions and Testability

The theory predicts measurable differences from standard physics:

• Pressure-based refraction in gravitational lensing,
• Chromatic lensing asymmetries,
• Entropy-based gravitational time variation,
• Echoes in gravitational wave signatures from wormhole interfaces,
• Microscopic wormhole formation during quantum entanglement collapse.

Each of these can be targeted by next-generation telescopes, quantum processors, or lab-scale analog simulations using superfluid models.

9.4. Toward Engineering of Space-Time

If space-time is fluid, it can be shaped, directed, and even manipulated:

• Anti-gravity becomes a pressure inversion problem,
• Time stasis or reversal becomes entropy control,
• Faster-than-light travel becomes flow channeling via tunnel engineering,
• Black hole control becomes a fluid containment challenge.

While these ideas remain futuristic, they offer a rational, lawful basis for space-time engineering—moving from speculative fiction to applied science.

9.5. The Role of Foundational Insight

This theory originated not from random conjecture, but from detailed comparative analysis of physical observations and historical models—some of which precede modern physics. The formulation was reverse-engineered from patterns that matched relativity, wave behavior, and entropy across time scales.

A separate modular section (Section X) presents these historical and scriptural inspirations, showing that fluid-based descriptions of time distortion, wormholes, and entropy control appear in conceptual form long before Einstein or Hawking—offering a philosophical continuity to this physical framework.

9.6. Final Statement

This is not just a theoretical merger. It is a transformation:

• Of geometry into fluid mechanics,
• Of time into entropy flux,
• Of mass into pressure displacement,
• Of quantum logic into hydrodynamic coherence,
• Of cosmic structure into tension-bound bubbles.

The Fluid Framework of Reality replaces abstraction with cause-and-effect logic—where all forces, motions, and evolutions arise from the same simple principle:

Space-time is alive. It flows. It responds. And we exist within it.