4.1. Simulation Design Results
Figure 4 and
Figure 5 are the simulation results of A-type transducer.
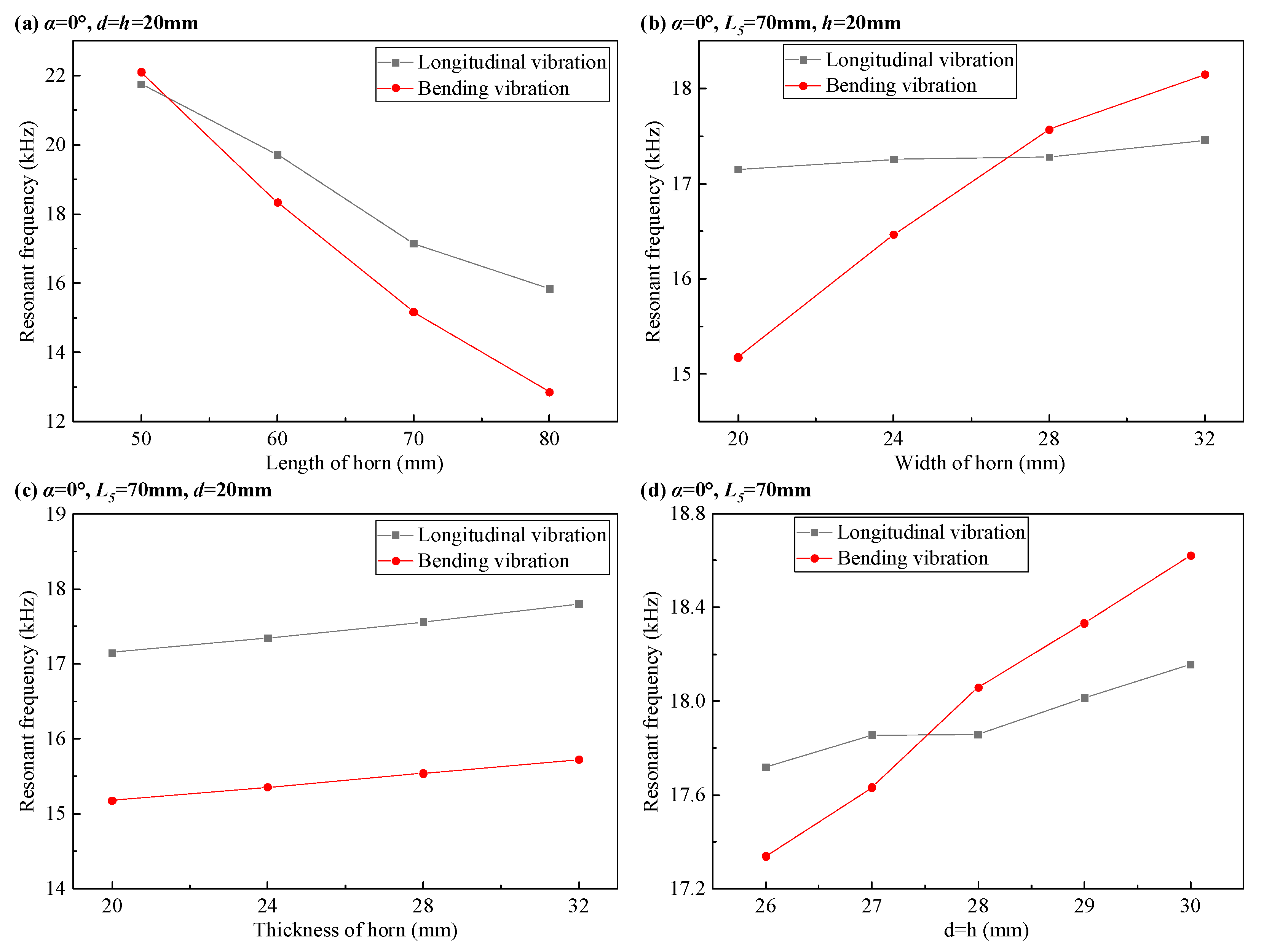
Figure 4 shows influence of structural dimensions of A-type transducer on resonance frequency. The initial section size is estimated to be
according to the required stiffness and size requirements of the horn, and then the influence of the length of horn
on the resonance frequency of longitudinal vibration and bending vibration is analyzed. As can be seen from
Figure 4a, with the shortening of the length of horn, the resonant frequencies of bending vibration and longitudinal vibration increases, and the frequency of bending vibration increases faster so that the resonant frequencies of bending vibration and longitudinal vibration can be equal. In order to ensure that the horn can extend out of the side of the transducer after bending, and at the same time consider the influence of the length of horn on the stiffness,
is determined.
On the basis of obtaining the length of the horn, the influence of the width of horn d on the resonance frequency of longitudinal vibration and bending vibration is studied. As can be seen from
Figure 4b, with the increase of the width of horn, the resonant frequency of bending vibration increases obviously, while the resonant frequency of longitudinal vibration increases slightly. Therefore, the resonant frequencies of bending vibration and longitudinal vibration can be close by changing the width of horn.
On the basis of obtaining the length of horn, the influence of the thickness of horn h on the resonance frequency of longitudinal vibration and bending vibration is studied. It can be found from
Figure 4c that with the increase of thickness of horn, the resonant frequencies of bending vibration and longitudinal vibration have the same changing trend, so it is impossible to make the resonant frequencies of bending vibration and longitudinal vibration close by changing thickness of horn. The thickness of horn has little influence on the resonant frequency, but it has great influence on the stiffness of the horn, so that the thickness and width of the horn are equal to meet the requirements of frequency matching and stiffness at the same time. In
Figure 4d, with the increase of the section size d and h of the horn, the resonance frequencies of bending vibration and longitudinal vibration increase, and the resonance frequencies of bending vibration increases faster so that the resonance frequencies of bending vibration and longitudinal vibration can be equal.
The influence of the length, width and thickness of the horn in
Figure 4 on the resonant frequency of the bending vibration and longitudinal vibration corresponds to equation (9) and equation (10). Equations (9) and (10) are obtained under the condition of pure bending beam. From equation (9) and equation (10), it can be seen that the angular frequency of longitudinal vibration is inversely proportional to the length of the horn, and the angular frequency of bending vibration is inversely proportional to the square of the length of the horn. In
Figure 4a, as the length of the horn decreases, the resonant frequency of bending vibration increases faster than that of longitudinal vibration. Equation (9) is independent of the width of the horn, and the angular frequency of bending vibration in equation (10) is proportional to the width of the horn. In
Figure 4b, the resonant frequency of longitudinal vibration does not change much with the increase of the width of the horn, while the resonant frequency of bending vibration increases with the increase of the width of the horn. Equations (9) and (10) are independent of the thickness of the horn. In
Figure 4c, the resonant frequencies of longitudinal vibration and bending vibration do not change much with the increase of the thickness of the horn.
The transducer with and is selected as an elliptical vibration ultrasonic transducer with a straight horn. The resonance frequencies of longitudinal vibration and bending vibration are 17.858kHz and 18.058kHz, respectively. After bending the horn for a certain angle, an elliptical vibration ultrasonic transducer with a bending horn can be obtained. Considering that the difference between 17.858kHz and 18.058kHz is only 0.2kHz, and the resonant frequency of the transducer will change after the horn is bent to a certain angle, it is only required that the resonant frequencies of longitudinal vibration and bending vibration are close, but not equal.
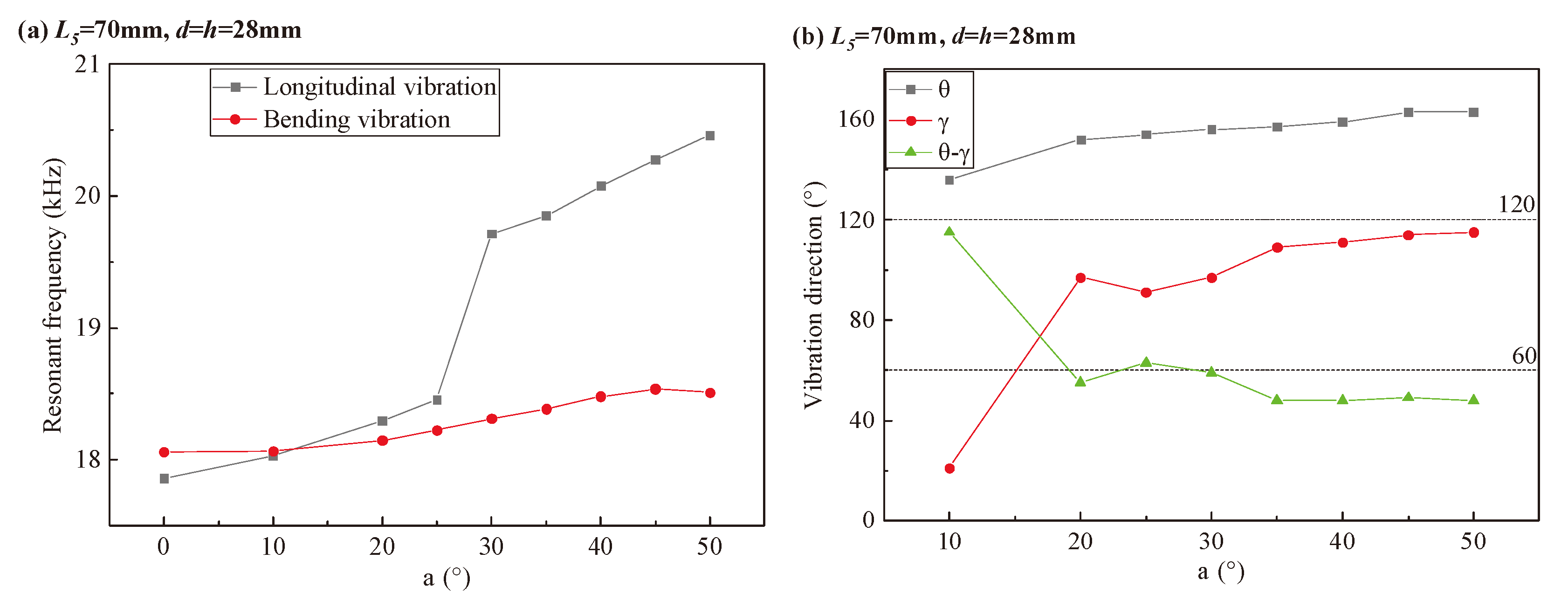
Figure 5 shows the influence of the bending angle α of the horn on the resonance characteristics of the transducer.
Figure 5a studies the influence of bending angle α on resonance frequency. In
Figure 5a, when α increases from 0° to 50°, the resonant frequency of bending vibration increases slowly. The resonant frequency of longitudinal vibration increases slowly with α increasing from 0° to 25°, and increases rapidly with α increasing from 25° to 50°. In the case of small α, the influence of the bending angle α of the horn on the frequency matching can be ignored, and in the case of large α, it is not conducive to the frequency matching.
As shown in
Figure 2a, θ and γ are the included angles between the vibration direction of point A and the axis of the transducer in bending vibration and longitudinal vibration, respectively.
Figure 5b studies the influence of bending angle α on vibration direction. In
Figure 5b, when α increases from 10° to 50°, the angle θ of the vibration direction of bending vibration slowly increases. The angle γ of the vibration direction of longitudinal vibration increases rapidly with α increasing from 10° to 20°, and slowly increases with α increasing from 20° to 50°.
The bending of the horn causes the asymmetry of the structure, which makes the vibration directions of bending vibration and longitudinal vibration incline to the bending direction of the horn. Because of the different inclination degrees of the vibration directions of bending vibration and longitudinal vibration, the vibration directions of bending vibration and longitudinal vibration are not vertical. Considering the influence of the bending angle α of the horn on the resonant frequency and vibration direction of the transducer,
is determined as the appropriate bending angle of the horn. After the optimization design, the structural parameters of the A-type transducer satisfying
Figure 3a are shown in
Table 4.
Figure 6 is the simulation results of B-type transducer.
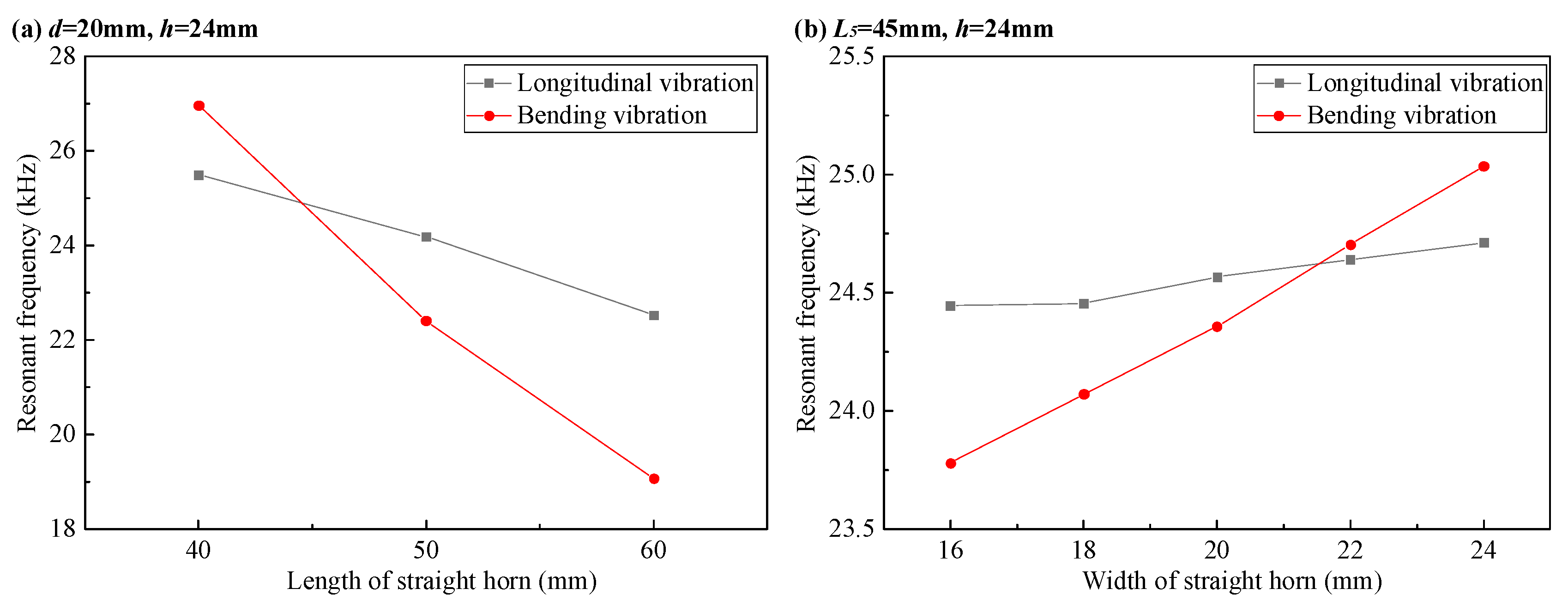
Figure 6 shows influence of structural dimensions of B-type transducer on resonance frequency. The initial width of straight horn is estimated to be
according to the required stiffness and size requirements of the horn, and then the influence of the length of straight horn
on the resonance frequency of longitudinal vibration and bending vibration is analyzed. As can be seen from
Figure 6a, with the shortening of the length of straight horn, the resonant frequencies of bending vibration and longitudinal vibration increases, and the frequency of bending vibration increases faster so that the resonant frequencies of bending vibration and longitudinal vibration can be equal.
On the basis of obtaining the length of the horn, the influence of the width of horn d on the resonance frequency of longitudinal vibration and bending vibration is studied. As can be seen from
Figure 6b, with the increase of the width of horn, the resonant frequency of bending vibration increases obviously, while the resonant frequency of longitudinal vibration increases slightly. Therefore, the resonant frequencies of bending vibration and longitudinal vibration can be close by changing the width of horn. The influence of the length and width of the straight horn in
Figure 6 on the resonant frequency of the bending vibration and longitudinal vibration corresponds to equation (9) and equation (10). The front structure of the horn of B-type transducer is too thin, which will amplify the local vibration, it is difficult to judge the direction of the vibration, so the influence of the structural size of the horn on the direction of the vibration is not discussed here. After the optimization design, the structural parameters of the B-type transducer satisfying
Figure 3b are shown in
Table 5.
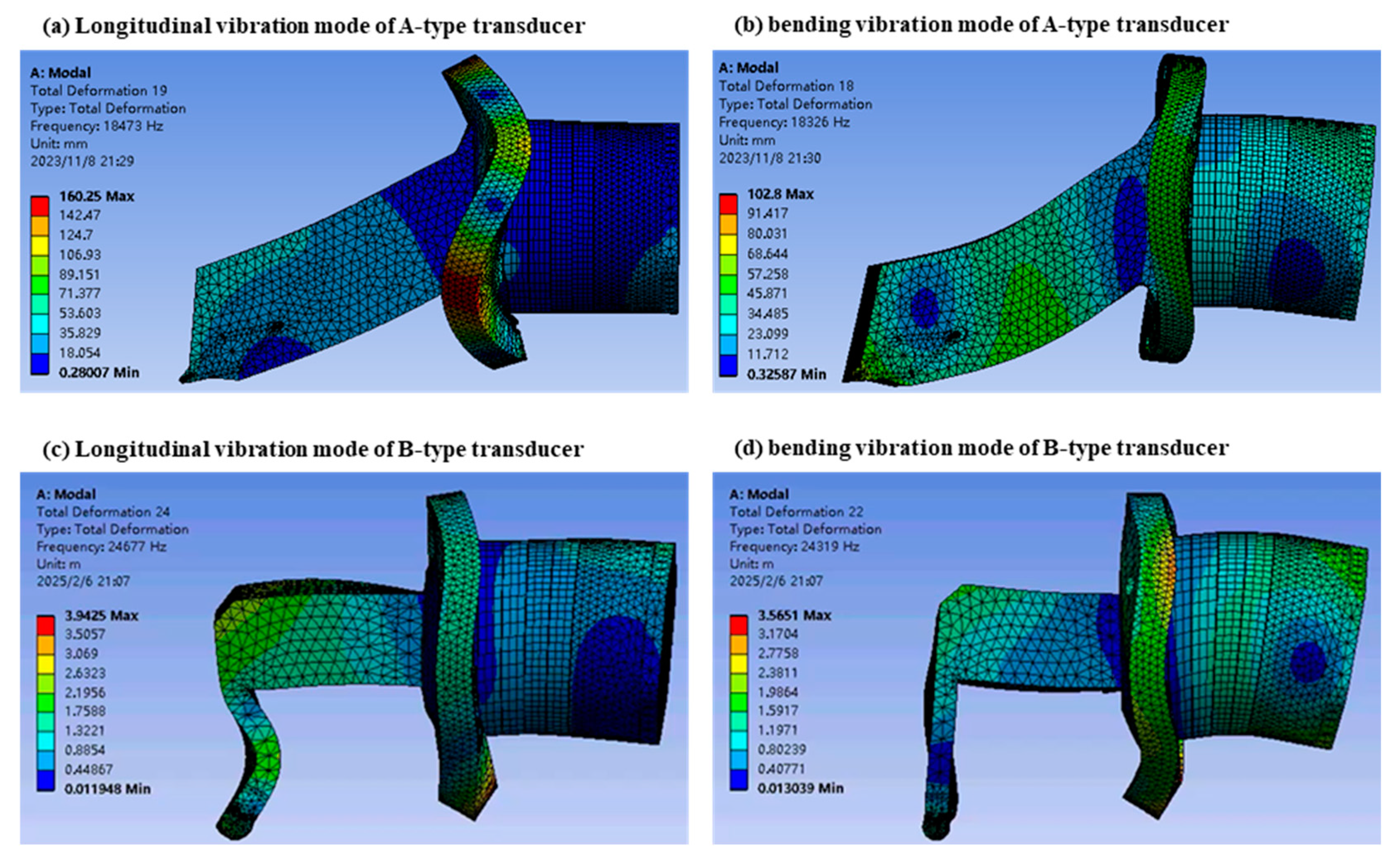
The modal analysis results of the optimized longitudinal-bending elliptical vibration ultrasonic transducer with bending horn are shown in
Figure 7.
Figure 7a,c show the first longitudinal vibration mode, and the node is located in the flange. The mode shows that the vibration of the end cap is small, and it can also be used as a clamping point. In practice, clamping the end cap has little effect on the resonance characteristics.
Figure 7b,d show the second bending vibration mode, and the nodes are located in the flange and the end cap. Therefore, the transducer can be fixed by the flange and the end cap.
4.2. Vibration Test
The transducers corresponding to the structural parameters in
Table 4 and
Table 5 are manufactured and assembled together according to the assembly relationship in
Figure 2. The resonant frequency of the transducer is measured by PV520A impedance analyzer developed by Tsinghua University. The resonant frequencies of longitudinal vibration and bending vibration of A-type transducer are 18.332kHz and 18.290kHz, respectively, and the difference between the designed and measured resonant frequencies of longitudinal vibration and bending vibration is 0.76% and 0.19%, respectively. The resonance frequencies of longitudinal vibration and bending vibration of B-type transducer are 22.328kHz and 22.678kHz respectively, and the difference between the designed and measured resonance frequencies of longitudinal vibration and bending vibration is 9.51% and 6.74% respectively.
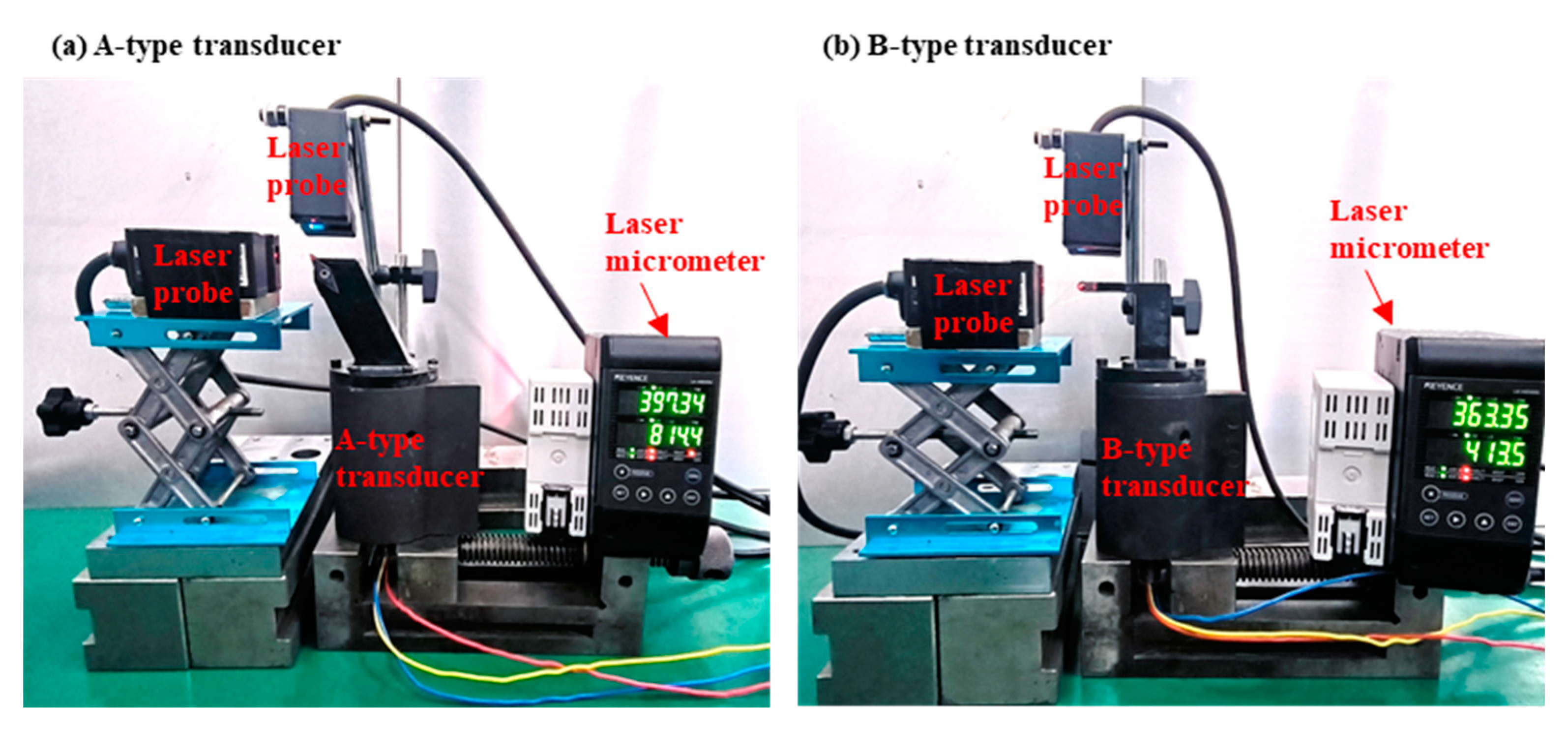
Figure 8 shows measuring device for vibration amplitude and vibration direction. The transducer is excited by applying voltage from ultrasonic power supply, and the vibration amplitude is measured simultaneously in horizontal and vertical directions by a laser micrometer. When the vibration in a single direction is excited (exciting longitudinal vibration or bending vibration), the vibration amplitude and vibration direction can be obtained by synthesizing the amplitude measured in the horizontal and vertical directions. When longitudinal vibration and bending vibration are excited at the same time, the elliptical vibration trajectory of the tool tip can be obtained by synthesizing the amplitudes measured in the horizontal and vertical directions.
For A-type transducer, the direction angle of longitudinal vibration is , the direction angle of bending vibration is , and the included angle between the directions of longitudinal vibration and bending vibration is . The difference between the designed and the measured included angle between the directions of longitudinal vibration and bending vibration is 7.93%. For B-type transducer, the direction angle of longitudinal vibration is , the direction angle of bending vibration is , and the included angle between the directions of longitudinal vibration and bending vibration is . The difference between the designed and the measured included angle between the directions of longitudinal vibration and bending vibration is 9.72%.
The transducer is capacitive, which requires matching inductance to make the circuit resonate and thus increase the amplitude of the transducer. The appropriate matching inductance can be determined by debugging the transducer.
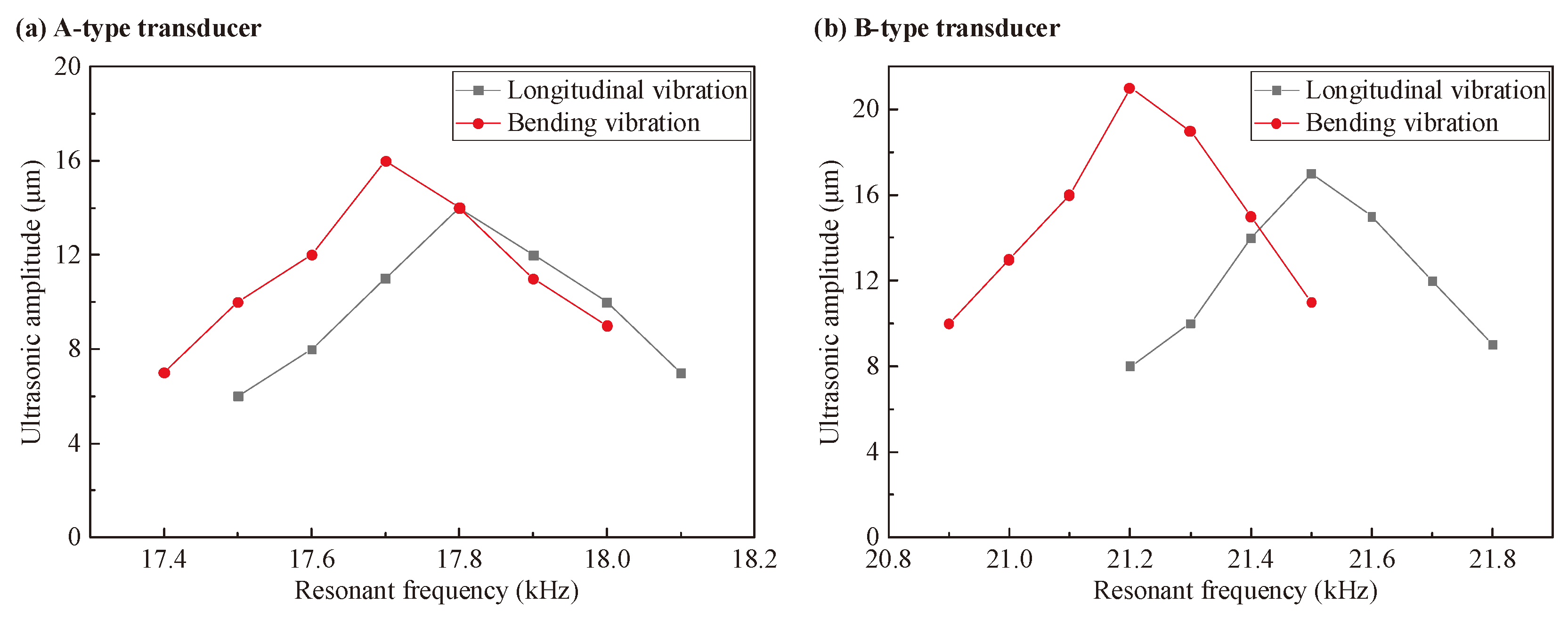
Figure 9 shows the Peak-peak amplitudes of transducer at different resonant frequencies with inductance
. As can be seen from
Figure 9, there is a resonance frequency with the largest amplitude for both longitudinal vibration and bending vibration, which is lower than the mechanical resonance frequency measured by the impedance analyzer. The maximum peak-peak amplitudes of longitudinal vibration and bending vibration for A-type transducer are 14μm and 16μm, respectively. The maximum peak-peak amplitudes of longitudinal vibration and bending vibration for B-type transducer are 17μm and 21μm, respectively. In order to make the resonance frequencies of longitudinal vibration and bending vibration equal and their amplitudes as large as possible, 17.8kHz is selected as the resonance frequency of elliptical vibration ultrasonic transducer for A-type transducer and 21.4kHz is selected as the resonance frequency of elliptical vibration ultrasonic transducer for B-type transducer.
Let the longitudinal vibration of the elliptical vibration ultrasonic transducer vibrate along the x axis, and its bending vibration vibrates in the xOy plane, so the vibration equation of the tool tip can be obtained as follows:
where, B is the amplitude of longitudinal vibration, μm; C is the amplitude of bending vibration, μm; F is the frequency of longitudinal vibration and bending vibration, Hz; t is time, s;
is the phase difference of bending vibration compared with longitudinal vibration,
;
Figure 10a shows the vibration trajectories of the tool tip under different phase differences for A-type transducer at
and
. Because there is an included angle of
between the directions of longitudinal vibration and bending vibration, the trajectory of the tool tip is an oblique oblate ellipse when the phase difference
is
, but it is approximately circular when the phase difference
is
.
Figure 10b shows the vibration trajectories of the tool tip under different phase differences for B-type transducer at
and
. Because there is an included angle of
between the directions of longitudinal vibration and bending vibration, the trajectory of the tool tip is an oblique oblate ellipse when the phase difference
is
, but it is approximately circular when the phase difference
is
.
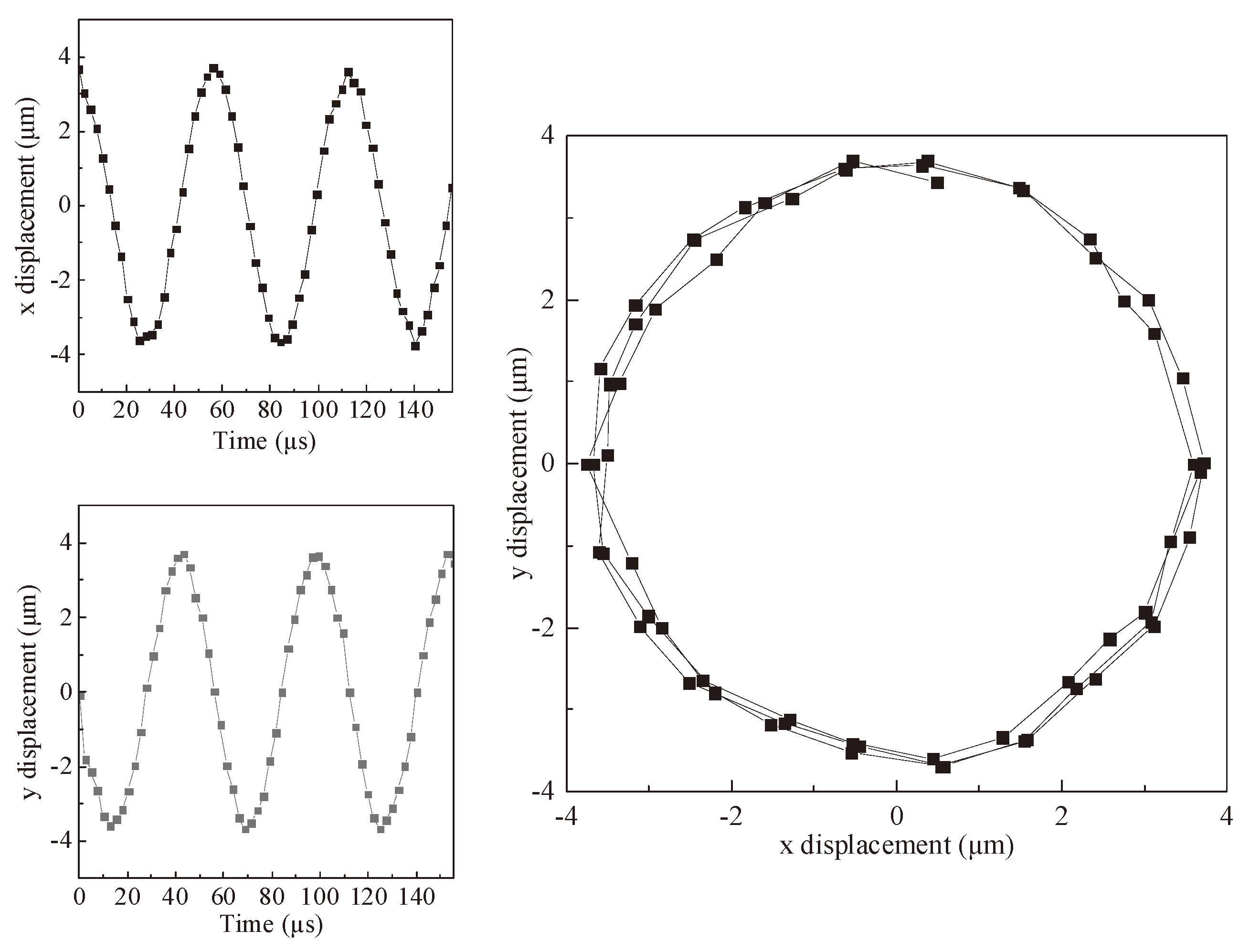
Figure 11 shows the measured vibration trajectory of the tool tip for A-type transducer at
and
.
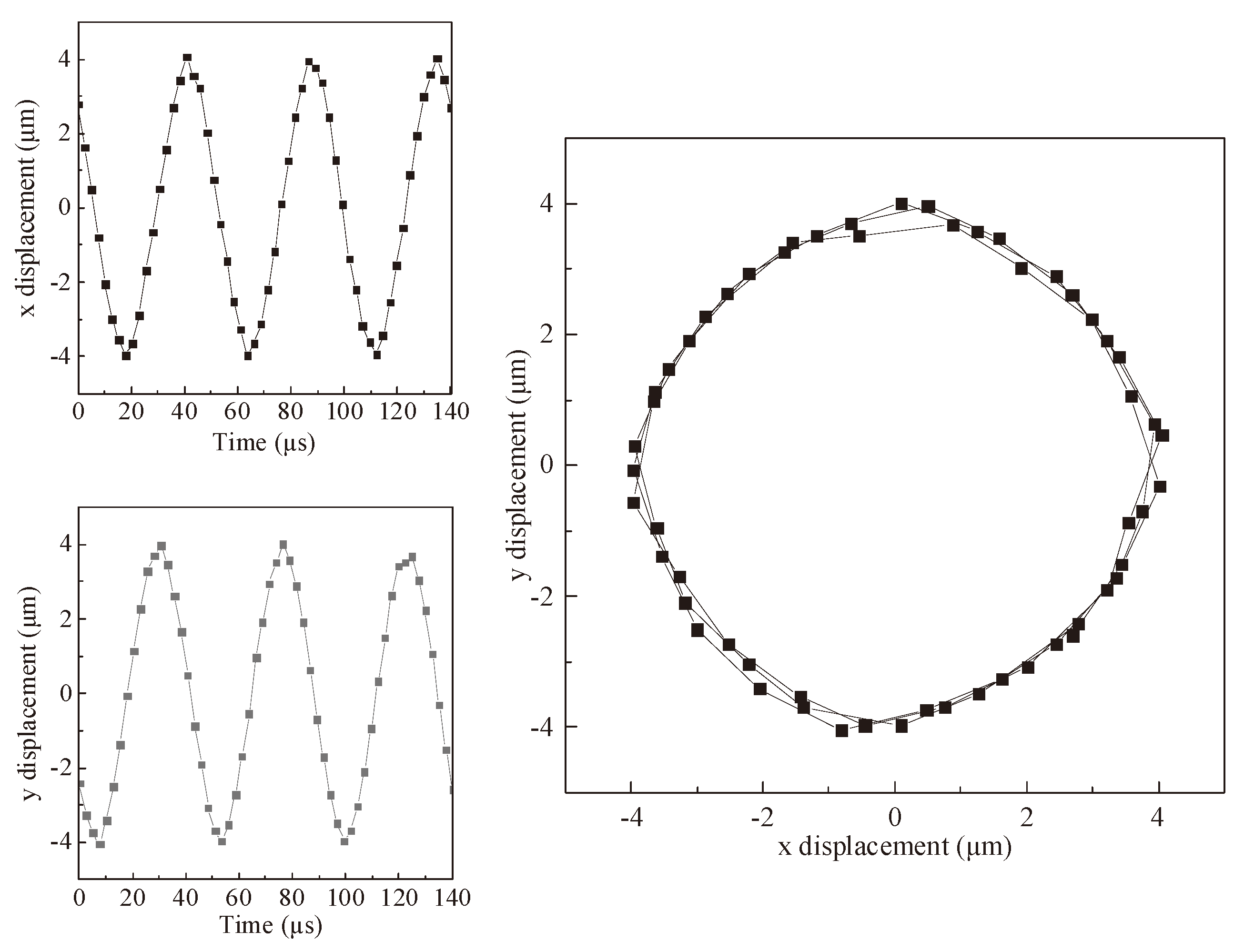
Figure 12 shows the measured vibration trajectory of the tool tip for B-type transducer at
and
. The elliptical trajectories in
Figure 11 and
Figure 12 are all approximately circular.
4.3. Machining Test
It is difficult to open the cutting zone in continuous cutting, so high cutting temperature and cutting force limit the tool life when cutting difficult-to-machine materials. Intermittent UVAC can reduce the cutting temperature and cutting force by opening the cutting area to improve the tool life, so it is widely used in cutting difficult-to-machine materials. However, intermittent cutting makes the MRR of UVAC low. Zhang et al. [
10] put forward the partial separation continuous high-speed ultrasonic vibration cutting method, which can open the cutting area while cutting continuously, greatly improving the tool life and MRR. In this paper, an elliptical vibration ultrasonic transducer with bending horn is used to study the partial separation continuous high-speed elliptical ultrasonic vibration cutting Inconel 718.
Figure 13 shows experimental setup in HEUVC. In
Figure 13a, a rhombic-type AlTiN-coated cemented carbide insert from Iscar (VCMT 160408-SM IC804) was mounted on the A-type transducer. The tool tip of A-type transducer vibrates elliptically at the frequency of 17.8kHz in the tool base. In
Figure 13b, a TiAlN+AlTiN+TiN-coated cemented carbide insert from Iscar (TAGB 630Y IC808) was mounted on the B-type transducer. The tool tip of B-type transducer vibrates elliptically at the frequency of 21.4kHz in the tool base. A water-soluble emulsion is applied as a coolant on the rake face.
The comparative experiments of HEUVC and CC were carried out on CNC lathe.
Table 6 contains all the machining parameters. In this paper, the finishing experiment of Inconel 718 is carried out, and the cutting parameters are set according to the requirements of finishing. When the maximum flank wear VBmax = 0.3 mm, the cutting experiment is stopped. Three experiments were carried out to obtain the average of the experimental results.
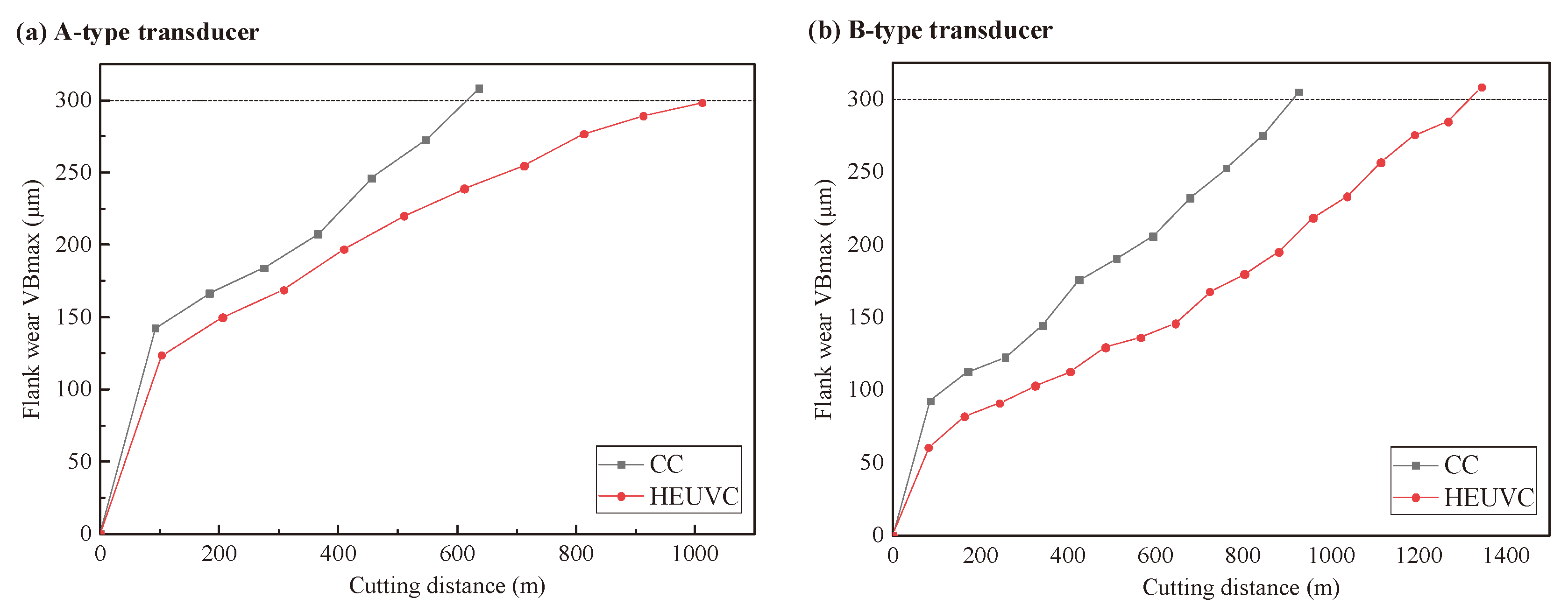
Figure 14 show effect of cutting distance on flank wear when an elliptical vibration ultrasonic transducer with bending horn is used to study the partial separation continuous high-speed elliptical ultrasonic vibration cutting Inconel 718. HEUVC method can partially open the cutting area in the process of continuous cutting, so that the coolant can enter the cutting area to cool and lubricate the tool and workpiece, reduce the cutting temperature and cutting force, and thus prolong the tool life. Compared with CC, HEUVC can improve the tool life by 65.74% when cutting with A-type transducer. Compared with CC, HEUVC can improve the tool life by 44.62% when cutting with B-type transducer.
Figure 15 show topographies of machined surface of Inconel 718.
Figure 15a,b are topographies of machined surface in CC. The existence of chatter marks is not observed in
Figure 15a,b, which indicates that the designed ultrasonic vibration tool holder has sufficient rigidity.
Figure 15c,d are topographies of machined surface in HEUVC. In
Figure 15c,d, the stable ultrasonic vibration trace on the workpiece surface show that the ultrasonic turning tool holder has stable resonance characteristic, which shows that the design of elliptical vibration ultrasonic turning tool holder with bending horn is successful. The wavelength
of ultrasonic vibration in
Figure 15c is 73μm, which is close to the theoretical calculation of 75μm. The wavelength
of ultrasonic vibration in
Figure 15d is 63μm, which is close to the theoretical calculation of 62μm.