1. Introduction
Gas-phase ozonation reaction is the most significant degradation pathway for unsaturated alkenes in the atmosphere[
1]. The reaction is known to generate a key product, Criegee Intermediate (CI), which is a series of positively and negatively charged carbonyl oxidising biradicals with the basic chemical formula (CR
2OO). It is evident that the alkene ozonation reaction produces a significant amount of exotherm, which results in the enrichment of CI molecules and subsequent unimolecular isomerization decomposition. This process is a source of hydroxyl radical (•OH), which is widely recognized as the most significant oxidant within the troposphere[
2]. Furthermore, CI has the capacity to release energy through collisions with surrounding molecules to form Stabilized Criegee Intermediate (SCI), which undergoes a bimolecular reaction with atmospheric species such as H
2O, SO
2, NH
3, CO, CO
2, O
3, RO
2, alcohol, aldehyde, ketone, alkene and so on[
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13].
Organic acid is an essential component of the tropospheric atmosphere, and its bimolecular reaction with SCI has the potential to be a substantial source of secondary organic aerosol (SOA) [
14]. A substantial number of studies have documented elevated reaction rates for the bimolecular reactions between organic acids (HCOOH and CH
3COOH) and SCI. For instance, Neeb[
15] calculated the rate coefficient for the reaction of CH
2OO with formic acid to be 14,000 times higher than that of the reaction with water. Similarly, Tobias[
16] determined the rate coefficient for the reaction of C
13-SCI with formic acid to be 7,000 times higher than that of the reaction with water. Sipilä[
17] calculated the ratio of the rate coefficients for the reaction of (CH
3)
2COO with organic acids and sulfur dioxide to be 2.8-3.4. Welz[
18] reported a kinetic study on the reaction of SCI with HCOOH and CH
3COOH, and the measured reaction rate coefficients were all greater than 10
-10 cm
3 s
-1, which is several orders of magnitude larger than the earlier results of Johnson[
19] (1×10
-14 cm
3 s
-1) and Vereecken[
20] (5×10
-12 cm
3 s
-1). These findings suggest that the bimolecular reaction with organic acids is an important decay process for SCI and far more important than previously predicted. This result was subsequently corroborated in Peltola's UV absorption spectroscopy experiment, wherein the coefficient exhibited a linear negative correlation with temperature, independent of pressure changes[
21]. The global atmospheric model demonstrated that the bimolecular reaction of SCI and organic acid exerted a substantial influence on ambient SCI and acid concentration in regions of the equator and northern latitudes where human activities were prevalent[
18]. The reaction of SCI with organic acids can provide a pathway for the conversion of alkene to low volatile compounds, thus promoting the formation of SOA.
Despite the fact that SCI reacts with organic acids at rates that are close to the collision limit and the reaction products may contribute significantly to SOA, related studies are scarce, and the results of the reaction mechanism, reaction products, and reaction rate coefficients are still controversial. In this paper, a high-precision theoretical study of the bimolecular reaction of SCI with organic acid was investigated at CCSD(T)/CBS//M06-2X/def2-TZVP level[
22]. The reaction system consists of the bimolecular reaction between CH
2OO and formic acid, syn-CH
3CHOO and formic acid, anti-CH
3CHOO and formic acid, (CH
3)
2COO and formic acid, CH
2OO and acetic acid, CH
2OO and oxalic acid. The study of reactants with different conformations and numbers of carbon atoms will provide a reference point for the future management of complex molecular reaction systems.
2. Computational Methods
All theoretical calculations in this paper were performed using the Gaussian 09 program. Geometry optimisation, vibrational analysis and intrinsic reaction coordinate calculations (IRC) were performed using the M06-2X method, which was developed by the University of Minnesota in combination with the Ahlrichs def2 base set of def2-TZVP[
23]. CCSD(T) coupled cluster methods, in combination with cc-pVTZ and cc-pVDZ base set extrapolation, have been demonstrated to reach the complete basis set (CBS) limit for single point energy[
24,
25]. It is evident that the single reference method is not applicable to systems characterized by strong static correlation. The two radical systems are paradigmatic examples of such systems. T1 diagnostics[
26] (Eq. 1) were conducted for CH
2OO, syn-CH
3CHOO, anti-CH
3CHOO, and C
2H
6COO at the CCSD(T)/cc-pVDZ level prior to calculation, yielding 0.043, 0.039, 0.040, and 0.034, respectively. The results obtained from the study indicate that the single-reference method utilized is indeed feasible. This conclusion is supported by the consistent value for CH
2OO that was observed in the literature[
27]. Furthermore, Nguyen[
28] optimised the geometry of SCI by means of a complete active space self-consistent field (CASSCF). The results obtained demonstrated that both the bipartite and amphipathic contributions of SCI are negligible.
As the biradical is found within the open-shell layer system, characterized by varying numbers of α and β electrons, the issue was resolved through the implementation of unrestricted open-shell layer Hartee-Fock (UHF) or Kohn-Sham (UKS) calculations in the present study[
29]. The calculations employed the Pople-Nesbet equation to solve α and β orbitals separately; however, the spin contamination that occurred during the calculations may lead to inaccurate predictions. It has been previously observed that spin contamination in UHF-based coupled clusters is a relatively minor issue that does not require significant consideration. The KS-DFT method introduces the wavefunction solely for the purpose of obtaining the exact electron kinetic energy, not the HF approximation to the real wavefunction. Consequently, spin contamination does not possess exact physical significance for the DFT, and the problem of spin contamination can be disregarded[
30].
Geometrical optimization is employed to ascertain the force required to obtain the smallest point of the potential energy surface of the system. Subsequent to convergence, the structure of the lowest energy point of the system is obtained. Vibrational analysis is a method by which the thermodynamic parameters of a reaction system can be obtained, and the frequency calculated thereby can determine the transition state structure. It is evident that the transition state possesses a single imaginary frequency, whilst the lowest energy structures of other compounds manifest as positive frequencies. In the frequency calculation process, the frequency correction factor is considered to eliminate the systematic error, and the base group of different methods varies numerically, usually between 0.9-1.0[
31,
32]. The term 'IRC' refers to the path of the lowest energy of the two minimal points adjacent to the continuous potential energy surface in the mass-weighted coordinates. IRC calculations facilitate the observation of changes in the structure of the substance during the reaction, thereby ensuring that the transition state is relevant to the reactants and products.
It is evident that the limited size of the base group employed in practice gives rise to the base group incompleteness error during the calculation process. In general, the incompleteness error is known to decrease with an increase in the size of the base group, eventually converging. Consequently, it is possible to extrapolate the results of smaller basis groups to larger or even CBS by obtaining the mathematical form of the convergence trend. In this paper, the SCF energy and the correlation energy are extrapolated by a three-point formula and a two-point formula, respectively, to finally obtain the post-HF electron energy close to the CBS.
The rate coefficients of the reaction system are calculated using the Gibbs free energy, with calculations based on transition state theory (TST) and a correction for the tunnelling effect.
3. Results and Discussion
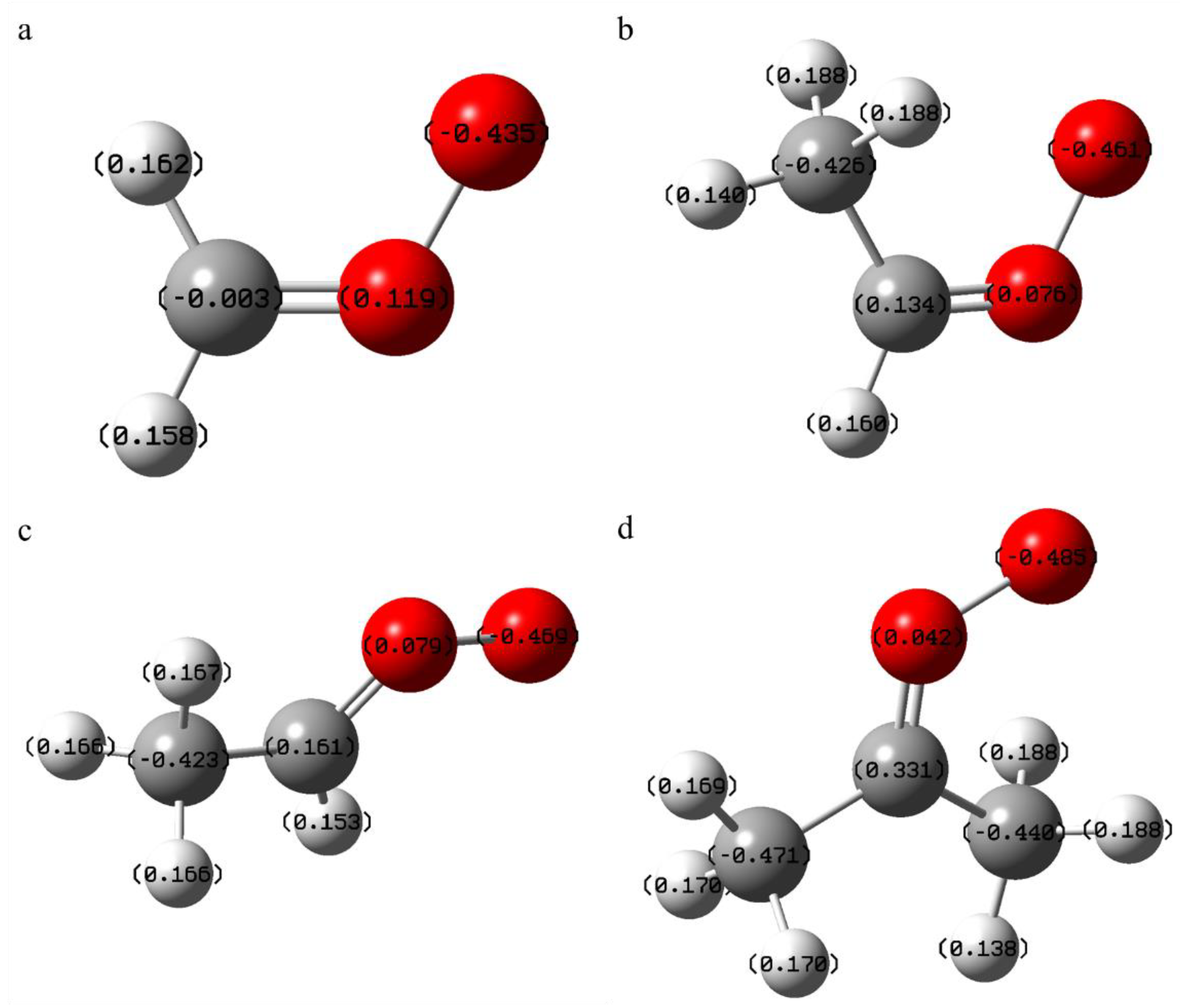
In the present study, the reaction of four conformational isomers of SCI with organic acids was considered, and their optimized structures at M06-2X/def2-TZVP level are shown in
Figure 1. It has been established that the molecules under consideration contain the same COO functional group. Furthermore, the substituents on the C atom are considered to be two hydrogen atoms, one hydrogen atom, one CH
3 and two CH
3. In consideration of the relative orientation of the O-O bond in relation to the C-CH
3 bond, two distinct conformational isomers of cis and trans were taken into account. For cis-SCI, hydrogen transfer reactions are more likely to occur due to the orientation of the C-CH
3 bond towards the O-O bond. Conversely, for trans-SCI, the terminal oxygen is farther away from the hydrogen atom on the β-carbon, and it is relatively difficult to carry out the isomerization reaction.
By comparing the parameters with those in the literature, we confirm that the geometrically optimized results represent the real SCI structure. To illustrate this, consider the example of CH
2OO. The detailed bond length and bond angle information is shown in
Table 1. The differences are primarily manifested in the fact that different methods correspond to different potential energy surfaces, and the energies of molecules on different potential energy surfaces are different. Consequently, the steady state structures corresponding to the ground state energies are not exactly the same. When evaluated in comparison to extant literature, the outcomes of this study are found to be within the margin of error. Consequently, the results of optimizing the biradical system at the M06-2X/def2-TZVP level are deemed reliable.
3.1. Electron Energy and Thermodynamic Parameters
In order to eliminate the base group incompleteness error to the greatest extent possible, this study obtained post-HF electron energies (including SCF energies and electron correlation energies) close to CBS by base group extrapolation. It is demonstrated that, for the Dunning's correlation-consistent basis group cc-PVnZ, the SCF energy satisfies the following equation:
In this equation, L denotes the highest angular momentum of the basic functions. The parameters A and α are to be determined, and ESC_(F(∞)) is the desired SCF energy under CBS. The functions cc-pVDZ and ccpVTZ are 2 and 3, respectively. A related study has shown that α is equal to 4.42 for L of 2 and 3, meaning that the actual extrapolation only needs to calculate the cc-pVDZ and cc-pVTZ energies twice[
34].
The abovementioned quantities are designated as ESCF(M) and ESCF(N), respectively, where M and N correspond to the highest angular momentum of the two calculations, with M > N.
As the correlation energy converges slowly with the basis group, extrapolation is necessary. The equation is expressed as follows:
The parameter β, which is pre-fitted, has a value of 2.46 when L is 2 and 3. The two-point formula for calculating the CBS correlation energy can be expressed as:
As illustrated in
Table S1, the electron energy of the CBS electron energy, E
CBS, which is the sum of E
SCF(∞) and E
corr(∞), is shown. The table lists the electron energies of the reactant (R), the pre-reaction complex (PRC), the transition state (TS), and the product (P) in the reaction system, respectively.
Upon completion of the vibrational analysis, the thermodynamic quantities are outputted in accordance with the standard RRHO (rigid rotor/harmonic oscillator) model. In the context of finite temperatures, the thermodynamic data can be expressed as a sum of the electron ground state energy and thermal contributions, i.e.
In this equation, ε
ele denotes the electron energy, ZPE represents the zero-point vibrational energy, and ∆U(0
→T), ∆H(0
→T), and ∆G(0
→T) are the thermal contributions to the internal enthalpy, enthalpy, and free energies, respectively. The thermodynamic data have been calculated based on the resonance approximation model; therefore, the frequency correction factor must be considered. According to the literature, the correction factor employed in this paper is 0.9754[
32]. In order to ensure the statistical convenience of the data, the output thermodynamic data were obtained and analyzed by Shermo software[
35]. The detailed parameters are shown in
Table S2.
3.2. Reaction Path
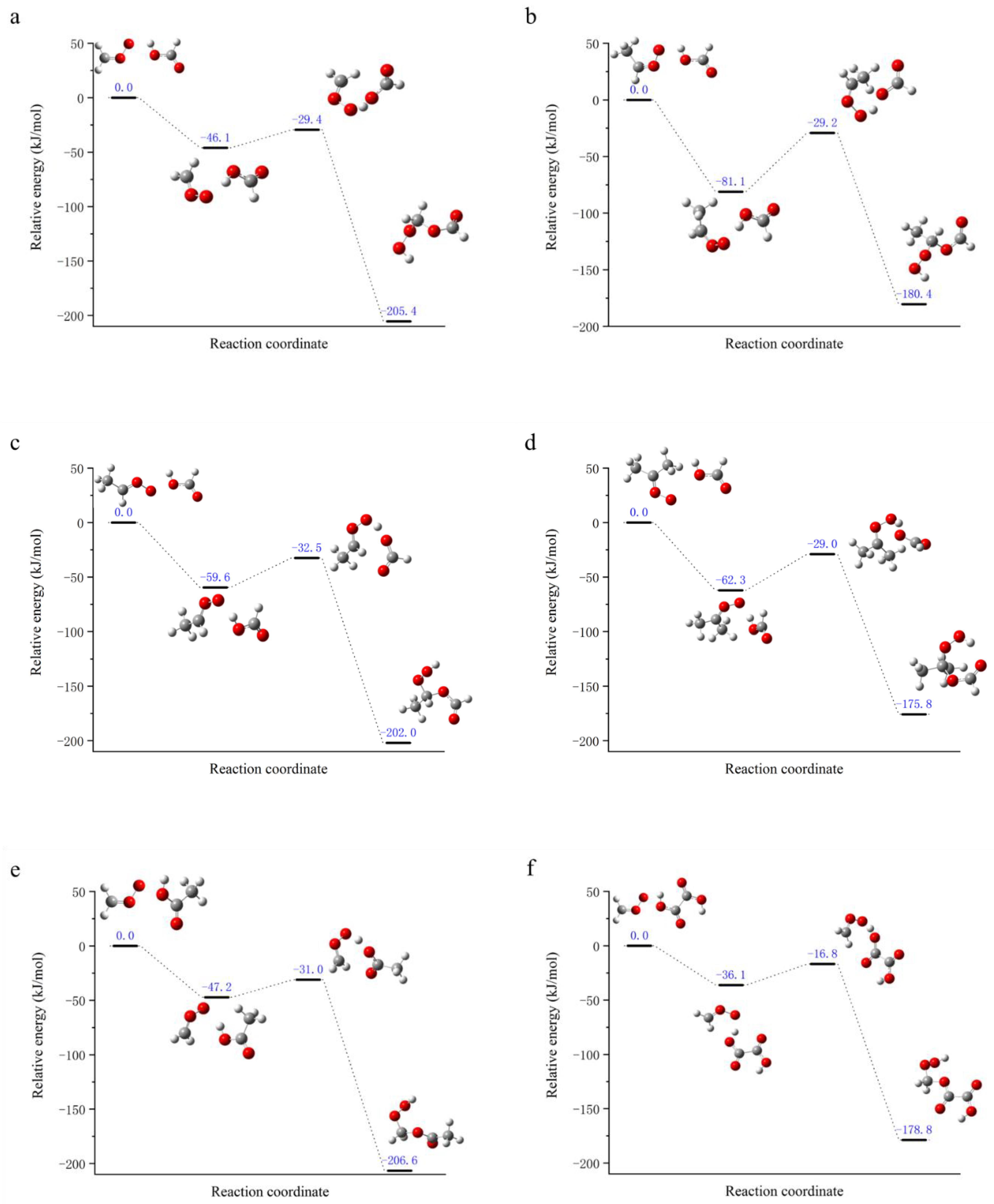
Assuming that the standing point energy of the separated reactants is zero, the energy distribution of the bimolecular reaction system of SCI and organic acid at 298 K along any reaction coordinate direction is shown in
Figure 2. As demonstrated by the figure, the bimolecular reaction of SCI and organic acid can be spontaneous at room temperature. Initially, a stable hydrogen bond is formed between the terminal oxygen atoms of SCI and the hydrogen atoms on the carboxyl group of organic acid, resulting in a reaction complex. During the reaction, the structure of organic acid undergoes a flipping process, whereby the oxygen atoms bonded to the hydrogen atoms move towards the carbon atoms of SCI, thereby forming a transition state structure. Following the crossing of the reaction potential barrier, the hydroxide bond on the carboxyl group of the organic acid is broken. At this point, the hydrogen atom forms a new hydroxide bond with the terminal oxygen atom of the SCI, and the oxygen atom is added to the carbon atom of the SCI. This process results in the generation of product hydroperoxide ester compounds.
Welz[
18] utilised multiplexed photoionization mass spectrometry to ascertain the rate coefficients of the bimolecular reaction of syn- and anti-CH
3CHOO with CHOOH. indicated that the rapid reaction of SCI with HCOOH could make a significant contribution to global atmospheric chemistry. However, the reaction products were not identified. Liu[
36] employed the technique of photoionization mass spectrometry in order to detect the occurrence of a single-molecule heterogeneous reaction of CH
3CHOO, the result of which was the production of VHP, and to do so he used formic acid as the catalyst. In this paper, quantitative calculations were performed, revealing that hydroperoxides are the most stable products of the bimolecular reaction between SCI and organic acids. This finding is in accordance with the results reported by Cabezas, which lends further credence to the stability of hydroperoxides over VHP, both kinetically and thermodynamically[
37].
It has been established that the reaction between CH
2OO and formic acid yields hydroperoxymethyl formate (HPMF), which subsequently undergoes dehydration to formic acid anhydride (FAA)[
38]. The findings of the present study demonstrate that HPMF is more stable at room temperature. This suggests that the bimolecular reaction products of SCI and organic acids are not short-lived as originally thought, but are more condensable than the reactants and have lower vapor pressures. This property is more conducive to SOA formation.
The internal energy changes in the reaction pathway were quantified, with the following definitions: stabilization energy (E
stab), representing the energy difference between the pre-reaction complex and the reactant; activation potential (E
a), representing the energy difference between the transition state and the pre-reaction complex; and reaction energy (ΔE), representing the energy difference between the product and the reactant, as shown in
Table 2. It has been demonstrated that the bimolecular reaction between SCI and organic acids can be carried out spontaneously at room temperature. Furthermore, the activation potential for the reaction of cis-SCI is higher than that of trans-SCI, and the change in reaction energy tends to decrease with the increase in the number of methyl substituents in the reactants. In addition, the reaction energy of cis-SCI is lower than that of the trans-structure. This is attributable to the increased stability provided by the presence of methyl substituents, while the cis structure exhibits greater stability in comparison to the trans structure due to ring tension.
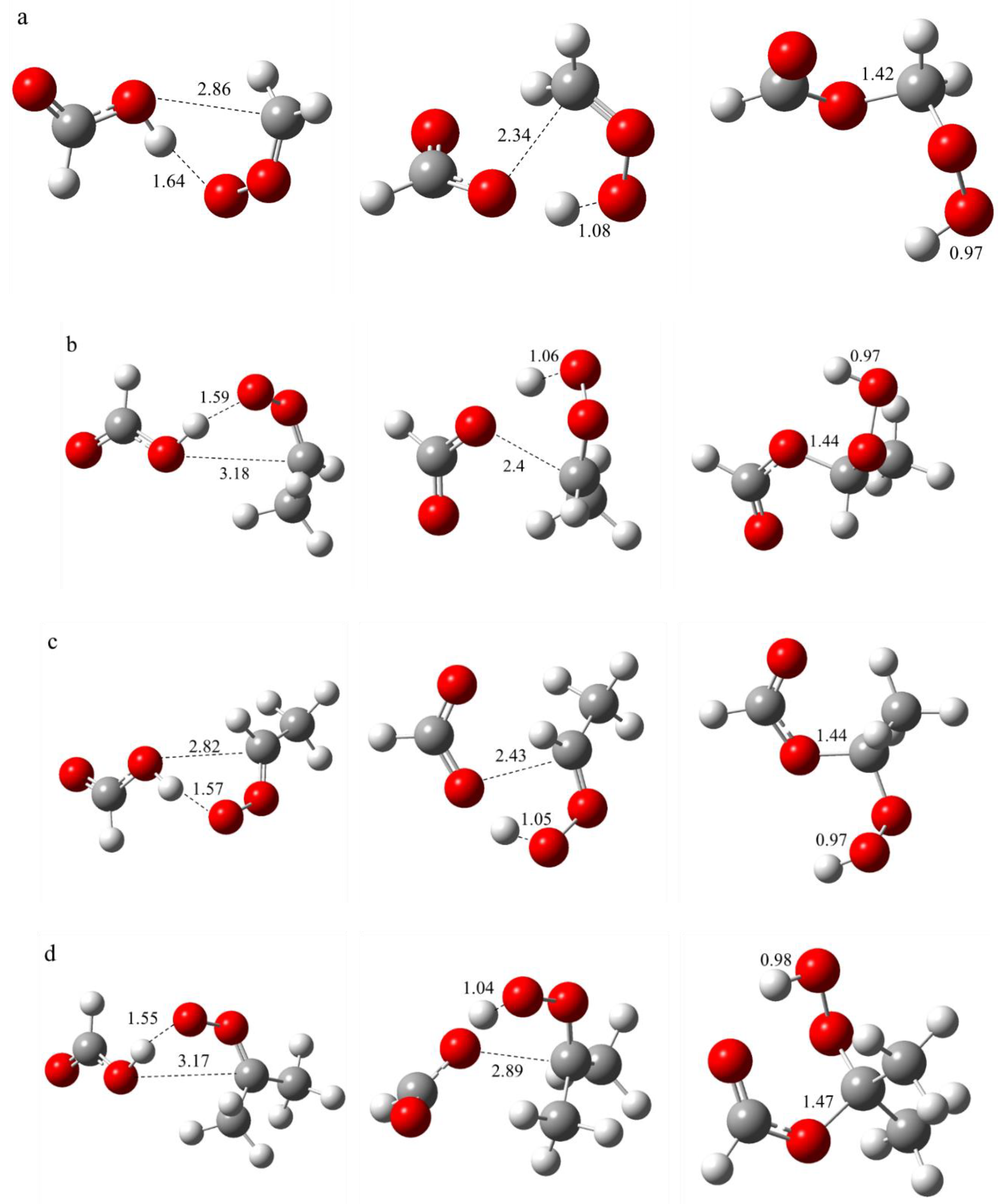
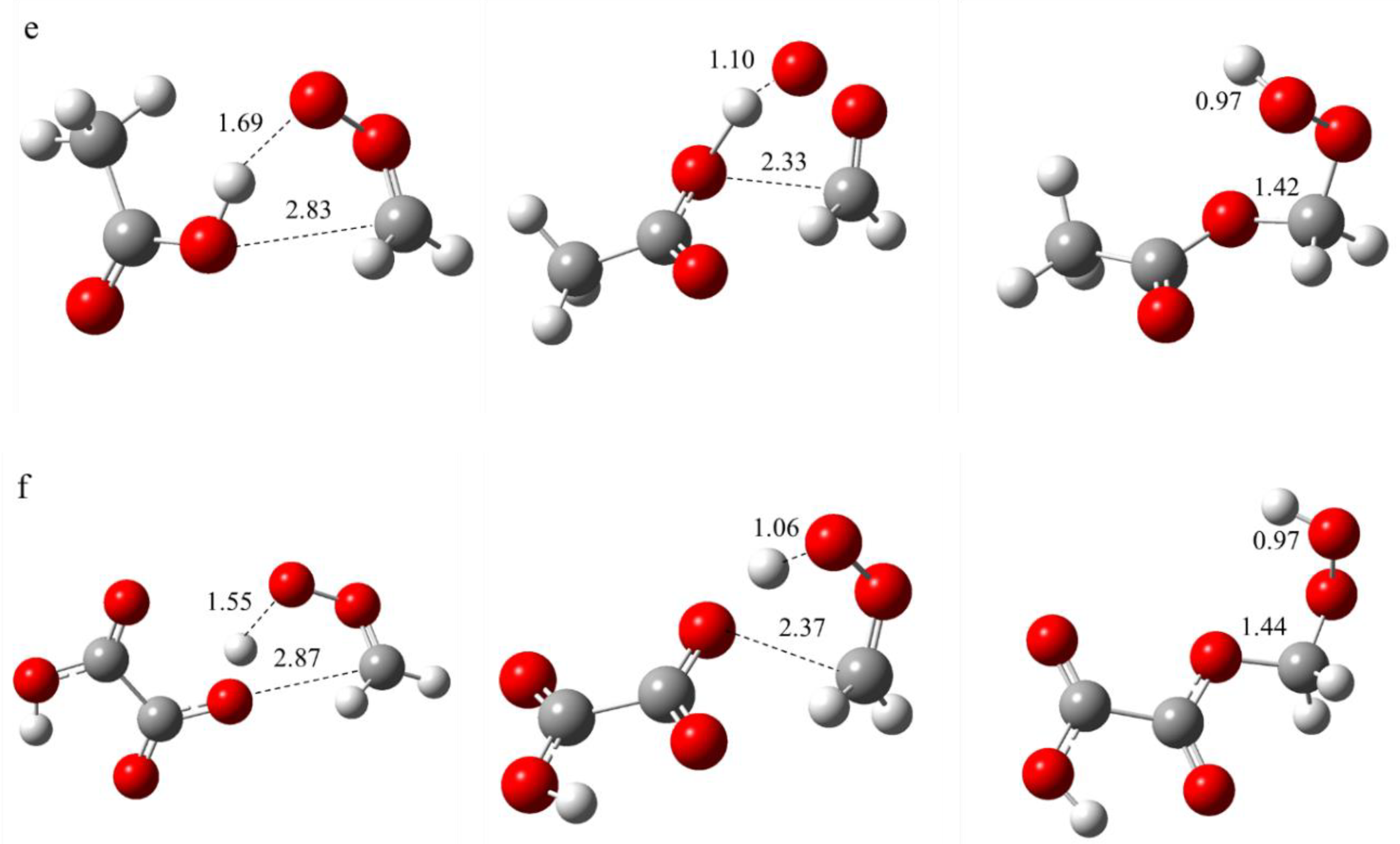
The structural changes of SCI with organic acids during the reaction are shown in
Figure 3, from a-f representing the reactions CH
2OO + CHOOH, syn-CH
3CHOO + CHOOH, anti-CH
3CHOO + CHOOH, (CH
3)
2COO + CHOOH, CH
2OO + CH
3COOH and CH
2OO + C
2H
4O
4, respectively. As illustrated in
Figure 1, during the reaction, the distances of the hydrogen and oxygen atoms on the carboxyl group of the organic acid from the oxygen and carbon atoms at the end of the SCI change, respectively. In contrast, the other atoms primarily undergo changes in bond angles and dihedral angles. The distances between the hydrogen atoms on the carboxyl groups of the organic acids and the SCI-terminal oxygen atoms in the reaction complexes ranged from 1.59-1.69 Å, forming more stable hydrogen bonds. The distances of oxygen and carbon atoms were found to be closer to the trans SCI, with values ranging from 2.82 to 2.87 Å. In contrast, the interatomic distances between the two atoms of the cis SCI were determined to be 3.18 and 3.17 Å. These findings suggest that the trans SCI is more likely to form a reactive complex with the organic acid. In comparison with the reactants, the bond lengths within the two fragments of the reactive complexes remain relatively constant, with hydrogen bonding primarily responsible for maintaining structural stability.
As the reaction occurs, the reaction structure reaches the transition state, which is defined as the highest energy point on the reaction path. The interaction of the two molecules in the transition state becomes closer, and the hydrogen and oxygen atoms on the carboxyl group of the organic acid are further distanced from the oxygen and carbon atoms at the end of the SCI, respectively. It is evident that the distances between the hydrogen and oxygen atoms decrease in proportion to the increase in the number of carbon atoms. Concurrently, the distances between the oxygen and carbon atoms increase in proportion to the increase in the number of carbon atoms. Furthermore, the cis isomerization is closer to the interatomic distances than the trans isomerization.
The formation of new bonds is indicative of the creation of the reaction product, as illustrated in the figure. The formation of new H-O and O-C bonds is evident in the product. The H-O bond length is measured at 0.97 Å, which is considered the standard H-O chemical bond length. The O-C bond length increases with the complexity of the product.
3.3. Reaction Rate Calculations
Transition state theory (TST) posits that thermodynamic equilibrium is established between the reactants and the activated complexes, and that the system undergoes partitioning into products without reverting to the reactants[
39,
40]. The fundamental expression is predicated on the partition function Q, which predicts the reaction rate coefficient at a specified temperature and infinite pressure. In the case of bimolecular reactions, the following equation can be used:
In this equation, kB denotes Boltzmann's constant, h represents Planck's constant, and QTS, QA, and QB are the coordination functions of the transition state and the two reactants, respectively. NA signifies Avogadro's constant, V denotes the volume, and represents the height of the potential barriers. The difference in U(0) of the TS and the reactants is indicative of the reaction path simplicity, denoted by σ. This is defined as the ratio of the number of rotational symmetries of the reactants to the transition state, and is determined by the molecular point group of the structure.
The quantum effect is responsible for the occurrence of the tunnelling effect, which is defined as the transmission of particles through a potential barrier, when the particle's kinetic energy is less than the barrier's potential energy. The effect is more pronounced for lighter particles, particularly in reactions involving hydrogen transfer, which are not negligible. The tunnelling effect enables the particle to react without passing through the potential barrier, thereby reducing the reaction activation energy. This results in an increased reaction rate coefficient. The effect of tunnelling on the reaction is quantified by calculating the transmission coefficient κ (transmission coefficient) in the TST calculation, and the result corrected for tunnelling can be obtained by multiplying κ with the reaction rate coefficient obtained by TST.
In this paper, the Skodje-Truhlar method is employed to obtain the transmission coefficient[
41]. The method delineates two parameters, α and β:
In this theoretical framework, is defined as the transition state imaginary frequency rate, is expressed as the transition state minus the U(0) of the reactants, and V is assigned a value of 0 in exothermic reactions and is defined as the product minus the U(0) of the reactants in absorptive reactions.
The TST formula, based on the partition function, can be converted to a form based on the free energy barriers. This alternative form is more convenient to use and has a clearer physical meaning.
In the context of an n-molecule reaction, the change in the number of moles is represented by the symbol ∆n, which is equivalent to n–1. The difference in the standard free energy of the transition state and the reactant free energy barrier is denoted by . The gas-phase standard state pressure, denoted P0, is defined as 1 bar.
The reaction rate coefficients for the bimolecular reactions of SCI with organic acids were calculated by transition state theory and then compared with the literature values, as shown in
Table 3. It is evident that, in general, the rate of reaction of SCI with organic acids is rapid, with all reactions exhibiting a rate greater than 10
-10 cm
3 s
-1. For CHOOH, the fastest reaction is with anti-CH
3CHOO, followed by CH
2OO and cis SCI. Of the six reactions studied in this paper, CH
2OO has been found to exhibit the highest rate of reaction with oxalic acid. It is important to note that, since oxalic acid possesses two carboxyl groups, and since the reaction can be carried out on any of these groups, the calculations should be made by multiplying the obtained reaction rate results by a factor of two.
4. Conclusion
Organic acids represent a significant component of the atmospheric troposphere, and their bimolecular reaction with SCI has been identified as a potential catalyst for the formation of atmospheric SOA. The global atmospheric modelling suggests that the bimolecular reaction between SCI and organic acids exerts a significant effect on the ambient SCI and acid concentrations in the regions near the equator and at northern latitudes where human activities are intensive.
In this chapter, a theoretical study of the bimolecular reaction between SCI and organic acids is carried out by Gaussian 09 quantitative calculations with high accuracy at the CCSD(T)/CBS//M06-2X/def2-TZVP level. The reactions encompass the bimolecular reactions of CH2OO and formic acid, syn-CH3CHOO and formic acid, anti-CH3CHOO and formic acid, (CH3)2COO and formic acid, CH2OO and acetic acid, and CH2OO and oxalic acid. The structures of these reaction transition states were found, and the structures of the reaction complexes and products were obtained by means of reaction coordinate IRC calculations.
Organic acids represent a significant component of the atmospheric troposphere, and their bimolecular reaction with SCI has been identified as a potential catalyst for the formation of atmospheric SOA. The global atmospheric modelling suggests that the bimolecular reaction between SCI and organic acids exerts a significant effect on the ambient SCI and acid concentrations in the regions near the equator and at northern latitudes where human activities are intensive.
In this chapter, a theoretical study of the bimolecular reaction between SCI and organic acids is carried out by Gaussian 09 quantitative calculations with high accuracy at the CCSD(T)/CBS//M06-2X/def2-TZVP level. The reactions encompass the bimolecular reactions of CH2OO and formic acid, syn-CH3CHOO and formic acid, anti-CH3CHOO and formic acid, (CH3)2COO and formic acid, CH2OO and acetic acid, and CH2OO and oxalic acid. The structures of these reaction transition states were found, and the structures of the reaction complexes and products were obtained by means of reaction coordinate IRC calculations.
The single-point energies were calculated at the CCSD(T)/cc-pVDZ and CCSD(T)/cc-pVTZ levels and extrapolated to the results under the complete basis group by the two-point formula. The thermodynamic quantities were output based on the standard RRHO model, and the thermodynamic parameters were corrected with a frequency correction factor. The path of the bimolecular reaction of SCI with organic acids along arbitrary reaction coordinates was obtained by using the variation of the internal energy of the standing point structure. Analysis of the stabilization energy, activation potential and reaction energy revealed that the reaction can proceed spontaneously at room temperature accompanied by a large amount of exotherm. It has been established that the activation potential barrier for the reaction occurring in cis-SCI is higher than that in trans-SCI, and that the reaction energy change tends to decrease with the increase of the number of methyl substituents of the reactants. In addition, the reaction energy of cis-SCI is lower than that of the trans-structure. The increase in the number of methyl substituents in the substance is indicative of enhanced stability. Conversely, the cis structure is more stable than the trans structure due to reduced ring tension.
The alterations in the reaction structure of SCI and organic acid bilayers are predominantly manifested in the oxygen and carbon atoms at the terminus of SCI and the hydrogen and oxygen atoms on the carboxyl group of the organic acid. As the reaction progresses, the H-O bond of the organic acid is broken, the hydrogen atom forms a new hydrogen bond with the terminal oxygen atom of SCI, and the oxygen atom forms a new C-O bond with the carbon atom of SCI, ultimately forming hydroperoxyl esters. It is evident that, due to their high degree of stability, hydroperoxides are capable of playing a significant role in the formation of SOA.
The article also calculates the rate coefficients of the bimolecular reactions of SCI and organic acids by transition state theory for CH2OO and formic acid, syn-CH3CHOO and formic acid, anti-CH3CHOO and formic acid, (CH3)2COO and formic acid, CH2OO and acetic acid, and CH2OO and oxalic acid, respectively, with rate coefficients of 1.87 × 10-10, 1.59 × 10-10, 5.30 × 10-10, 1.26 × 10-10, 2.09× 10-10 and 7.16 × 10-10 cm3 s-1, respectively. All reactions were found to occur at extremely rapid rates. In the case of reaction with CHOOH, anti-CH3CHOO was found to be the most rapid, followed by CH2OO and cis-SCI. In the present study, the rate of reaction of CH2OO with oxalic acid was found to be the fastest among the six reactions examined.
Supplementary Materials
The following supporting information can be downloaded at the website of this paper posted on Preprints.org.
References
- Atkinson, R.; Arey, J. Atmospheric Degradation of Volatile Organic Compounds. Chemical Reviews. 2003, 103, 4605–4638. [Google Scholar] [CrossRef] [PubMed]
- Fang, Y.; et al. Communication: Real time observation of unimolecular decay of Criegee intermediates to OH radical products. J Chem Phys. 2016, 144, 061102. [Google Scholar] [CrossRef]
- Taatjes, C. A.; et al. Direct Measurements of Conformer-Dependent Reactivity of the Criegee Intermediate CH3CHOO. Science. 2013, 340, 177–180. [Google Scholar] [CrossRef] [PubMed]
- Chao, W.; et al. Direct kinetic measurement of the reaction of the simplest Criegee intermediate with water vapor. Science. 2015, 347, 751–754. [Google Scholar] [CrossRef] [PubMed]
- Mauldin Iii, R. L.; et al. A new atmospherically relevant oxidant of sulphur dioxide. Nature. 2012, 488, 193–196. [Google Scholar] [CrossRef]
- Misiewicz, J. P.; et al. Re-examining ammonia addition to the Criegee intermediate: converging to chemical accuracy. Phys Chem Chem Phys. 2018, 20, 7479–7491. [Google Scholar] [CrossRef]
- Kumar, M.; et al. Criegee Intermediate Reaction with CO: Mechanism, Barriers, Conformer-Dependence, and Implications for Ozonolysis Chemistry. The Journal of Physical Chemistry A. 2014, 118, 1887–1894. [Google Scholar] [CrossRef]
- Lin, Y.-H.; et al. Reactivity of Criegee Intermediates toward Carbon Dioxide. The Journal of Physical Chemistry Letters. 2018, 9, 184–188. [Google Scholar] [CrossRef]
- Chang, Y.-P.; et al. Kinetics of the simplest Criegee intermediate reaction with ozone studied using a mid-infrared quantum cascade laser spectrometer. Physical Chemistry Chemical Physics. 2018, 20, 97–102. [Google Scholar] [CrossRef]
- Zhao, Y.; et al. Role of the reaction of stabilized Criegee intermediates with peroxy radicals in particle formation and growth in air. Physical Chemistry Chemical Physics. 2015, 17, 12500–12514. [Google Scholar] [CrossRef]
- Tadayon, S. V.; et al. Kinetics of the Reactions between the Criegee Intermediate CH2OO and Alcohols. The Journal of Physical Chemistry A. 2018, 122, 258–268. [Google Scholar] [CrossRef] [PubMed]
- Jalan, A.; et al. Chemically activated formation of organic acids in reactions of the Criegee intermediate with aldehydes and ketones. Physical Chemistry Chemical Physics. 2013, 15, 16841–16852. [Google Scholar] [CrossRef] [PubMed]
- Decker, Z. C. J.; et al. Direct experimental probing and theoretical analysis of the reaction between the simplest Criegee intermediate CH2OO and isoprene. Physical Chemistry Chemical Physics. 2017, 19, 8541–8551. [Google Scholar] [CrossRef] [PubMed]
- Sakamoto, Y.; et al. Oligomerization Reaction of the Criegee Intermediate Leads to Secondary Organic Aerosol Formation in Ethylene Ozonolysis. The Journal of Physical Chemistry A. 2013, 117, 12912–12921. [Google Scholar] [CrossRef]
- Neeb, P.; et al. Formation of hydroxymethyl hydroperoxide and formic acid in alkene ozonolysis in the presence of water vapour. Atmospheric Environment. 1997, 31, 1417–1423. [Google Scholar] [CrossRef]
- Tobias, H. J.; Ziemann, P. J. Kinetics of the Gas-Phase Reactions of Alcohols, Aldehydes, Carboxylic Acids, and Water with the C13 Stabilized Criegee Intermediate Formed from Ozonolysis of 1-Tetradecene. The Journal of Physical Chemistry A. 2001, 105, 6129–6135. [Google Scholar] [CrossRef]
- Sipilä, M.; et al. Reactivity of stabilized Criegee intermediates (sCIs) from isoprene and monoterpene ozonolysis toward SO<sub>2</sub> and organic acids. Atmos. Chem. Phys. 2014, 14, 12143–12153. [Google Scholar] [CrossRef]
- Welz, O.; et al. Rate coefficients of C(1) and C(2) Criegee intermediate reactions with formic and acetic Acid near the collision limit: direct kinetics measurements and atmospheric implications. Angew Chem Int Ed Engl. 2014, 53, 4547–4550. [Google Scholar] [CrossRef]
- Johnson, D.; et al. The Effect of Criegee-Intermediate Scavengers on the OH Yield from the Reaction of Ozone with 2-methylbut-2-ene. The Journal of Physical Chemistry A. 2001, 105, 2933–2935. [Google Scholar] [CrossRef]
- Vereecken, L.; et al. The reaction of Criegee intermediates with NO, RO2, and SO2, and their fate in the atmosphere. Physical Chemistry Chemical Physics. 2012, 14, 14682–14695. [Google Scholar] [CrossRef]
- Peltola, J.; et al. Time-resolved, broadband UV-absorption spectrometry measurements of Criegee intermediate kinetics using a new photolytic precursor: unimolecular decomposition of CH2OO and its reaction with formic acid. Physical Chemistry Chemical Physics. 2020, 22, 11797–11808. [Google Scholar] [CrossRef] [PubMed]
- Gaussian, R.; et al. Gaussian, Gaussian, Inc., Wallingford, CT. Gaussian, Inc., Wallingford CT. 2004.
- Zhao, Y.; Truhlar, D. G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theoretical Chemistry Accounts. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Neese, F. Software update: the ORCA program system, version 4.0. WIREs Computational Molecular Science. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system—Version 5.0. WIREs Computational Molecular Science. 2022, 12, e1606. [Google Scholar] [CrossRef]
- Lee, T. J. Comparison of the T1 and D1 diagnostics for electronic structure theory: a new definition for the open-shell D1 diagnostic. Chemical Physics Letters. 2003, 372, 362–367. [Google Scholar] [CrossRef]
- Rienstra-Kiracofe, J. C.; et al. The C2H5 + O2 Reaction Mechanism: High-Level ab Initio Characterizations. The Journal of Physical Chemistry A. 2000, 104, 9823–9840. [Google Scholar] [CrossRef]
- Nguyen, M. T.; et al. Heats of formation of the Criegee formaldehyde oxide and dioxirane. Chemical Physics Letters. 2007, 448, 183–188. [Google Scholar] [CrossRef]
- Vereecken, L.; et al. Theoretical Chemical Kinetics in Tropospheric Chemistry: Methodologies and Applications. Chemical Reviews. 2015, 115, 4063–4114. [Google Scholar] [CrossRef]
- Pople, J. A.; et al. Spin-unrestricted character of Kohn-Sham orbitals for open-shell systems. International Journal of Quantum Chemistry. 1995, 56, 303–305. [Google Scholar] [CrossRef]
- Scott, A. P.; Radom, L. Harmonic Vibrational Frequencies: An Evaluation of Hartree−Fock, Møller−Plesset, Quadratic Configuration Interaction, Density Functional Theory, and Semiempirical Scale Factors. The Journal of Physical Chemistry. 1996, 100, 16502–16513. [Google Scholar] [CrossRef]
- Kesharwani, M. K.; et al. Frequency and Zero-Point Vibrational Energy Scale Factors for Double-Hybrid Density Functionals (and Other Selected Methods): Can Anharmonic Force Fields Be Avoided? The Journal of Physical Chemistry A. 2015, 119, 1701–1714. [Google Scholar] [CrossRef] [PubMed]
- Nakajima, M.; Endo, Y. Communication: Determination of the molecular structure of the simplest Criegee intermediate CH2OO. J Chem Phys. 2013, 139, 101103. [Google Scholar] [CrossRef]
- Aroeira, G. J. R.; et al. The addition of methanol to Criegee intermediates. Physical Chemistry Chemical Physics. 2019, 21, 17760–17771. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.; Chen, Q. Shermo: A general code for calculating molecular thermochemistry properties. Computational and Theoretical Chemistry. 2021, 1200, 113249. [Google Scholar] [CrossRef]
- Liu, F.; et al. Direct observation of vinyl hydroperoxide. Physical Chemistry Chemical Physics. 2015, 17, 20490–20494. [Google Scholar] [CrossRef]
- Cabezas, C.; Endo, Y. Observation of hydroperoxyethyl formate from the reaction between the methyl Criegee intermediate and formic acid. Physical Chemistry Chemical Physics. 2020, 22, 446–454. [Google Scholar] [CrossRef]
- Aplincourt, P.; Ruiz-López, M. F. Theoretical Study of Formic Acid Anhydride Formation from Carbonyl Oxide in the Atmosphere. The Journal of Physical Chemistry A. 2000, 104, 380–388. [Google Scholar] [CrossRef]
- Fernández-Ramos, A.; et al. Modeling the Kinetics of Bimolecular Reactions. Chemical Reviews. 2006, 106, 4518–4584. [Google Scholar] [CrossRef]
- Bao, J. L.; Truhlar, D. G. Variational transition state theory: theoretical framework and recent developments. Chemical Society Reviews. 2017, 46, 7548–7596. [Google Scholar] [CrossRef]
- Skodje, R. T.; et al. A general small-curvature approximation for transition-state-theory transmission coefficients. The Journal of Physical Chemistry. 1981, 85, 3019–3023. [Google Scholar] [CrossRef]
- Chhantyal-Pun, R.; et al. (2018). Criegee Intermediate-Carboxylic Acid Reactions, A Potential Source for Secondary Organic Aerosols in the Atmosphere.
- Berndt, T.; et al. Direct Probing of Criegee Intermediates from Gas-Phase Ozonolysis Using Chemical Ionization Mass Spectrometry. Journal of the American Chemical Society. 2017, 139, 13387–13392. [Google Scholar] [CrossRef] [PubMed]
- Behera, B.; et al. Mechanism and kinetics of the reaction of the Criegee intermediate CH2OO with acetic acid studied using a step-scan Fourier-transform IR spectrometer. Physical Chemistry Chemical Physics. 2022, 24, 18568–18581. [Google Scholar] [CrossRef] [PubMed]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).