Tidal Forces Around Black-Bounce-Reissner–Nordstrom Black Hole

1. Introduction

Gravity itself seems to be one of the greatest puzzles of all time and Einstein’s General Relativity (GR) [1,2,3] is still believed to give its most precise description till date. Few theoretical solutions of the fundamental field equations of GR have been identified as some mysterious astrophysical objects such as Black Holes (BHs). But these BH spacetimes themselves pose some practical limits on the underlying theory itself. Many attempts have been made in order to avoid the naturally occurring central singularities in recent past. In the similar line of action, some models have been proposed which modify and regularize the Riemannian metric behavior near singularity while almost preserve the geometry in the regions of weak or moderate curvature. One of the pioneering work in this field was by J. Bardeen [4], who probably first time used a regular BH metric rather than the Schwarzschild metric. A metric which is singular at the center (i.e. Riemannian curvature there is infinite) can be converted to a regular metric by removing the singularity alongwith its close neighborhood from space-time and then smoothly joining its remaining part to one more copy of this part. In this way, the Schwarzschild metric can be converted into a wormhole throat or BH depending on the region in which it resides.

Simpson and Visser applied the coordinate transformation r to $\sqrt{r^2+a^2}$ to modify the Schwarzschild metric to avoid central singularity. Modified metric is known as the Simpson-Visser (SV) spacetime or the Schwarzschild spacetime with black bounce [5]. Afterwards, the electrically charged counterpart of this SV spacetime was also derived in similar manner [6,7,8] followed by the rotating extension presented in [9].

Regular BH models typically introduce nonlinear modifications to the classical Maxwell equations or GR itself to circumvent the central singularity. SV spacetime can have a range of features depending on the value of the length scale parameter a, such as for $a<2$ it describes a regular BH,at $a=2$ it represents a one-way wormhole or BH with a null throat and for $a>2$ it describes a traversable wormholes [10,11,12].

In this article we study the tidal forces and their effect in the background of a black-bounce-Reissner–Nordström BH (black-bounce-RNBH) spacetime. Generalized geodesic deviation equations are derived and solved to observe the possible difference due to the presence of length scale parameters a and charge parameter Q involved here.

The article is arranged as follows, in Section 2 the horizon structure of black-bounce-RNBH spacetime is reviewed. In Section 3, we discussed about the first integrals of geodesic equations and effective potential for neutral massive test particles.

In Section 4, the Newtonian acceleration for radially infalling neutral test particle is discussed in detail along with the tidal forces.

Generalised geodesic deviation equations and their generalised and specific solutions are discussed in Section 5. Conclusions and future directions are presented in Section 6.

2. Black-Bounce-Reissner–Nordström Spacetime

A black-bounce-RNBH spacetime is considered as a black-bounce extension of general Reissner–Nordström spacetime [1]. The metric for black-bounce-RNBH spacetime is given as,

$${ds}^2=-f\left(r\right){dt}^2+f^{-1}\left(r\right){dr}^2+h^2\left(r\right)\left(d{\theta }^2+{sin}^2\theta d{\varphi }^2\right),$$

(1)

where,

$$\begin{array}{c}\hfill f\left(r\right)=1-{\displaystyle \frac{2M}{\sqrt{r^2+a^2}}}+{\displaystyle \frac{Q^2}{r^2+a^2}}\end{array}$$

(2)

$$\begin{array}{c}\hfill h^2\left(r\right)=\left(r^2+a^2\right),\end{array}$$

(3)

where M and Q respectively represent the mass and charge of the black-bounce-RNBH. Here a is known as length-scale parameter which is related to the Planck length, it is also known as bounce parameter.

The RNBH metric describes a charged, non-rotating BH and is derived from the Einstein–Maxwell field equations [1]. The black-bounce-RNBH spacetime arises when the standard Maxwell electromagnetism is coupled with an anisotropic fluid. It is a theoretical construct in GR that modifies the traditional RNBH solution to eliminate its singularity, resulting in a globally regular and traversable spacetime [13,14,15,16]. The black-bounce-RN spacetime reduces to the RN spacetime in absence of length-scale parameter, the black-bounce-Schwarzschild spacetime in absence of charge parameter and to the Schwarzschild BH in the absence of both length-scale and charge parameter i.e. $a=0$ and $Q=0$ simultaneously [2]. Further it reduces to the Ellis wormhole [17] with $M=0$ and $Q=0$.

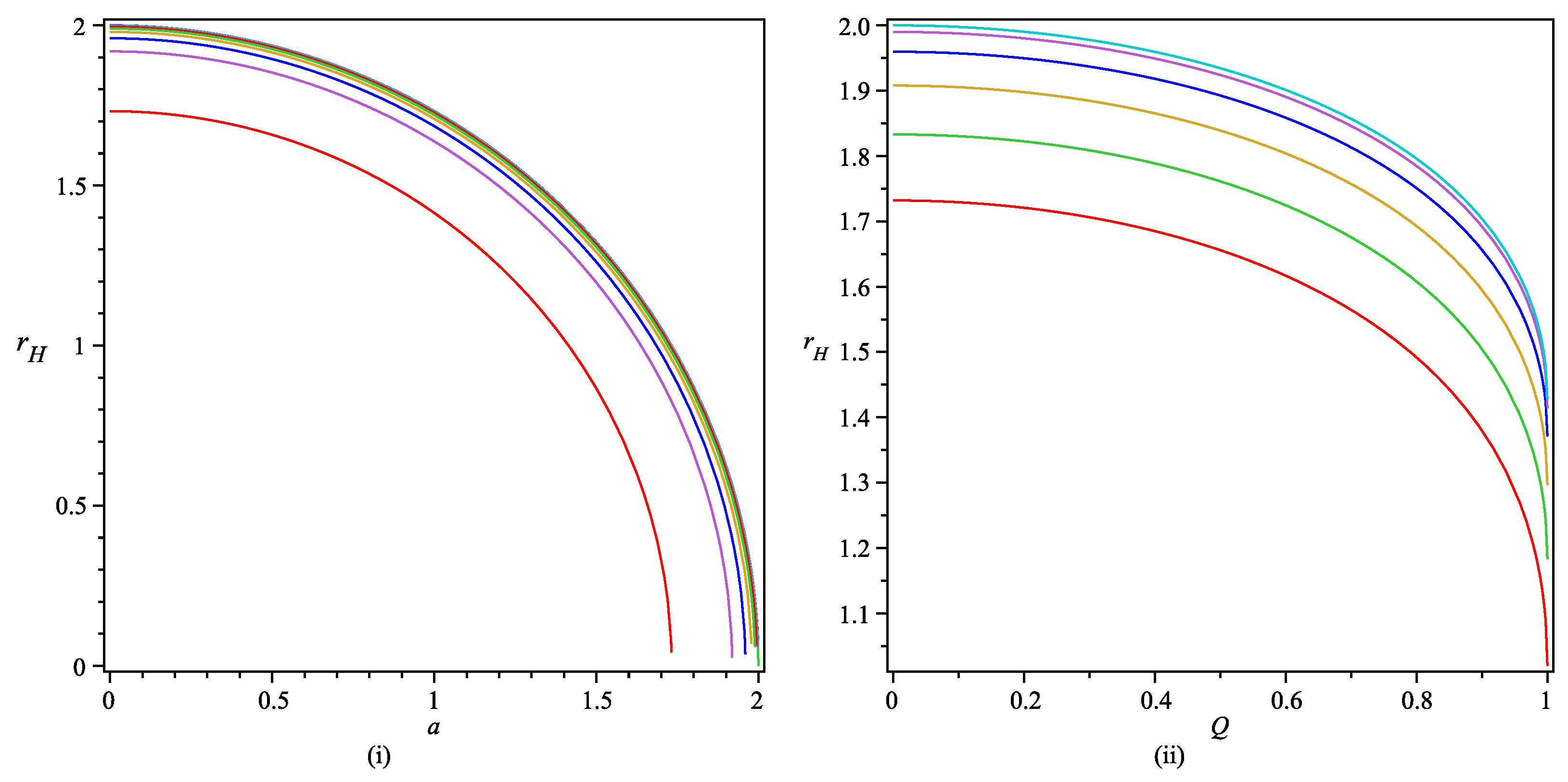
2.1. Event Horizon of Black-Bounce-RNBH Spacetime

Two horizons of the spacetime given in Equation (1) are represented as,

$$r_{\pm }=\sqrt{{\left(m\pm \sqrt{m^2-Q^2}\right)}^2-a^2},$$

(4)

where $r_{+}$ shows the distance of outer horizon while $r_{-}$ shows the inner horizon of the same [1]. For black-bounce-RNBH spacetime 1 to represent a BH spacetime the event horizon obtained from Equation (4) must have non-zero values and thus must satisfy $Q^2<m^2$ and $a^2\le {\left(m\pm \sqrt{m^2-Q^2}\right)}^2$ simultaneously. In the present study we are limiting our discussions to only the black-bounce-RNBH spacetime having inner and outer horizons both.

As the presence of length-scale or bounce parameter removes the singularity present at the center in RN BH arising in GR and replaces it with a bounce [13,14,15,16], the horizon structure also gets modified accordingly. In order to visualize this modification and specific the characteristics of the event horizon we have plotted the event horizon radius of BH with length scale parameter a and BH charge Q depicted in Figure 1.

It can be inferred from Figure 1 that at as $Q⟶0$, the event horizon also tends zero as a approaches its limiting value i.e. 2. Physically, it can be described as the transformation of the BH spacetime into a wormhole spacetime [13,15]. While as Q approaches its upper limit i.e. $Q=1$, this limiting value for a reduces to 1. Similarly, as the parameter a increases, the maximum allowed value of Q correspondingly decreases.

3. First Integrals of Geodesic Equations

The generalized set up of geodesic equations and their constraint equations [1,2,3,18,19] are given by,

$${\ddot{x}}^{\mu }+{\Gamma }_{\nu \lambda }^{\mu }{\dot{x}}^{\nu }{\dot{x}}^{\lambda }=0,$$

(5)

$$g_{\mu \nu }{\dot{x}}^{\mu }{\dot{x}}^{\nu }=e.$$

(6)

Where $x^{\mu }$ represents the spacetime coordinates and ${\ddot{x}}^{\mu }$ represents the differentiation of $x^{\mu }$ with respect to the affine parameter $\tau$. Constant e in Equation (6) takes values 0 and 1 for null and timelike geodesics respectively . For neutral timelike geodesics Equation (5) reduces to the following set of equations,

$$\ddot{t}-{\displaystyle \frac{2r}{(r^2+a^2)}}\left({\displaystyle \frac{m\sqrt{r^2+a^2}-Q^2}{2m\sqrt{r^2+a^2}-Q^2-\left(r^2+a^2\right)}}\right)\dot{r}\dot{t}=0,$$

(7)

$$\ddot{r}-{\displaystyle \frac{r\left(r^2+a^2+Q^2-2m\sqrt{r^2+a^2}\right)\left(-m\sqrt{r^2+a^2}+Q^2\right)}{{\left(r^2+a^2\right)}^3}}{\dot{t}}^2$$

$$+{\displaystyle \frac{r\left(-m\sqrt{r^2+a^2}+Q^2\right)}{\left(r^2+a^2\right)\left(r^2+a^2+Q^2-2m\sqrt{r^2+a^2}\right)}}{\dot{r}}^2-{\displaystyle \frac{r\left(r^2+a^2+Q^2-2m\sqrt{r^2+a^2}\right)}{\left(r^2+a^2\right)}}{\dot{\theta }}^2$$

$$-{\displaystyle \frac{r\left(r^2+a^2+Q^2-2m\sqrt{r^2+a^2}\right)}{\left(r^2+a^2\right)}}{sin}^2\theta {\dot{\varphi }}^2=0,$$

(8)

$$\ddot{\theta }+{\displaystyle \frac{2r}{r^2+a^2}}\dot{r}\dot{\theta }-cos\theta sin\theta {\dot{\varphi }}^2=0,$$

(9)

$$\ddot{\varphi }+{\displaystyle \frac{2r}{r^2+a^2}}\dot{r}\dot{\varphi }+2cot\theta \dot{\theta }\dot{\varphi }=0,$$

(10)

with time-like constraint,

$$\left(1-{\displaystyle \frac{2M}{\sqrt{r^2+a^2}}}-{\displaystyle \frac{Q^2}{r^2+a^2}}\right){\dot{t}}^2-{\left(1-{\displaystyle \frac{2M}{\sqrt{r^2+a^2}}}-{\displaystyle \frac{Q^2}{r^2+a^2}}\right)}^{-1}{\dot{r}}^2$$

$$-\left(r^2+a^2\right)({\dot{\theta }}^2+{sin}^2\theta {\dot{\varphi }}^2)=1.$$

(11)

This set of equations from Equation (7) to Equation (11) is the basic initial requisite to the study various phenomenon related to timelike geodesics around black-bounce-RNBH spacetime.

3.1. Effective Potential for Black-Bounce-RNBH Spacetime

Now we restrict ourselves for the study of neutral test particles moving in equatorial plane only. For this one has to fix $\theta =\pi /2$. Thus integration of Equation (7) and Equation (10) results into,

$$\dot{t}={\displaystyle \frac{{\kappa }_1}{f\left(r\right)}},$$

(12)

$$\dot{\varphi }={\displaystyle \frac{{\kappa }_2}{r^2+a^2}},$$

(13)

where the integrating constants ${\kappa }_1$ corresponds to the conserved total energy E and ${\kappa }_2$ corresponds to the conserved angular momentum L of the neutral test particle respectively [1,2,3,18,19]. Using Equation (12) and Equation (13) with $\theta =\pi /2$ in the constraint Equation (11), the energy conservation equation for the time-like geodesics [1,2,3,18,19] takes following form,

$${\displaystyle \frac{{\dot{r}}^2}{2}}={\displaystyle \frac{E^2-V_{eff}}{2}},$$

(14)

where $V_{eff}$ is defined as an effective potential and can be expressed as,

$$V_{eff}\left(r\right)=f\left(r\right)\left({\displaystyle \frac{L^2}{r^2+a^2}}+1\right)$$

$$\Rightarrow V_{eff}\left(r\right)=\left(1-{\displaystyle \frac{2M}{\sqrt{r^2+a^2}}}\right)+{\displaystyle \frac{L^2}{r^2+a^2}}-{\displaystyle \frac{2m{L}^2}{{\left(r^2+a^2\right)}^{3/2}}}+{\displaystyle \frac{Q^2}{r^2+a^2}}\left(1+{\displaystyle \frac{L^2}{r^2+a^2}}\right).$$

(15)

The effective potential of black-bounce-RNBH spacetime is modified than that of SBH [1,2] due to the presence of bounce and charge parameters here. If one compares termwise, the first term aises due to the Newtonian gravitational potential, the second term shows the presence of a repulsive centrifugal potential and the third term represents the relativistic correction of GR which is proportional to $1/{\left(r^2+a^2\right)}^{3/2}$ [19,20]. The extra term ${\displaystyle \frac{Q^2}{r^2+a^2}}\left(1+{\displaystyle \frac{L^2}{r^2+a^2}}\right)$ in Equation (15) is due to the presence of bounce and charge parameters both.

4. Newtonian Radial Acceleration

On substituting $V_{eff}\left(r\right)$ for radial geodesics i.e. where $L=0$, the Equation (14) reduces to,

$${\dot{r}}^2=E^2-f\left(r\right).$$

(16)

A test particle which is initially at rest and starts falling freely from a fixed position b will have initial energy $E=\sqrt{f(r=b)}$ [19,20,21,22]. Newtonian acceleration for test particles falling freely along such radial geodesics is known as “Newtonian radial acceleration” and is defined as [19,20,21,22,23],

$$A^{\left(R\right)}\equiv \ddot{r},$$

(17)

For black-bounce-RNBH spacetime, using Equation (16), the Newtonian radial acceleration takes the following form,

$$A^{\left(R\right)}=-{\displaystyle \frac{Mr}{{\left(r^2+a^2\right)}^{3/2}}}-{\displaystyle \frac{Qr}{{\left(r^2+a^2\right)}^2}}.$$

(18)

The analysis of this radial force plays an important role to understand the possible difference in the effect of gravitational field than that of SBH and RNBH qualitatively.

• To study the effect of the gravitational field of the black-bounce-RNBH spacetime on the orbiting neutral test particle one may be interested to look for the possible distance from where a neutral test particle bounces back as happened in standard RNBH [20]. To derive expression for this distance,one will have to look for the real root of equation $E^2(r=b)-f\left(r\right)=0$. After solving such relation for black-bounce-RNBH, the expression for such distance comes out as,

  $$R_{back-bounce-radius}=-\sqrt{{\displaystyle \frac{-4a^2{M}^2{b}^2+Q^4{b}^2-4a^4{M}^2+4a^{2}M{Q}^2\sqrt{b^2+a^2}}{4M^2{b}^2+Q^4-4M{Q}^2\sqrt{b^2+a^2}+4a^2{M}^2}}}$$

  (19)

4.1. Analysis of Tidal Forces Acting in Black-Bounce-RNBH Spacetime

For any arbitrary object or test particles moving in a strong gravitational field, the study of geodesic deviation explains the effect of spacetime curvature on their relative motion [1,2,3,24]. It gives a quantitative analysis of the divergence or convergence present for neighboring geodesics as an effect of underlying gravitational field. In the present work, the methodology used in [18,19,20,22,24] is adopted to derive the corresponding geodesic deviation equation or Jacobi field equation,

$${\displaystyle \frac{D^2{\eta }^a}{D{\tau }^2}}-{R^a}_{bcd}{v}^b{v}^c{\eta }^d=0,$$

(20)

here ${\eta }^a$ represent the connection normal vectors to infinitesimally close geodesics while $v^a$ represents the tangent vector to the geodesics.

The tetrad basis for radial free-fall reference frames in given spacetime background is,

$$e_0^a=\left({\displaystyle \frac{E}{f}},\sqrt{E^2-f},0,1\right);e_1^a=\left(-{\displaystyle \frac{E^2-f}{f}},-E,0,1\right);$$

$$e_2^a=\left(0,0,{\displaystyle \frac{1}{h\left(r\right)}},0\right);e_3^a=\left(0,0,0,{\displaystyle \frac{1}{h\left(r\right)sin\theta }}\right).$$

(21)

where the normalization condition $e_{\alpha }^{\mu }{e}_{\beta }^{\mu }{g}_{\mu \nu }={\eta }_{\alpha \beta }$ is satisfied by $e_{\alpha }^{\mu }$. ${\eta }_{\alpha \beta }$ being a Minkowski metric. Hence the geodesic deviation vector can be devised as,

$$\tilde{\eta }=e_{\nu }^{\mu }{\eta }^{\nu }$$

(22)

The expressions for radial and angular tidal forces can be obtained by substituting Equation (22) into Equation (20) as,

$${\ddot{\eta }}^{\widehat{1}}=\left[{\displaystyle \frac{M(2r^2-a^2)}{{(r^2+a^2)}^{5/2}}}+{\displaystyle \frac{Q^2(a^2-3r^2)}{{(r^2+a^2)}^3}}\right]{\eta }^{\widehat{1}},$$

(23)

$${\ddot{\eta }}^{\widehat{i}}=-\left[{\displaystyle \frac{r{f}^{\prime }\left(r\right)}{2(r^2+a^2)}}+a^2{\displaystyle \frac{f\left(r\right)-E^2}{{(r^2+a^2)}^2}}\right]{\eta }^{\widehat{i}}.$$

(24)

where $i=2,3$, correspond to $\theta$ and $\varphi$ directions respectively. Tidal force corresponding to time coordinate can be ignored as ${\ddot{\eta }}^{\widehat{t}}=0$ gives no physically important information as such. Explicit expressions for tidal forces along radial and angular directions are given in Equation (23) and Equation (24). Following one can observe the variation of tidal forces with radial parameter r for different settings of all other BH parameters.

One can infer from Equation (23) that tidal force in radial direction becomes zero at,

$$R_{rtf}=\pm {\left[{\displaystyle \frac{2M^2}{y}}+Q^2-a^2\mp 2M\sqrt{M^2+y{Q}^2}\right]}^{1/2},$$

(25)

where,

$$y=-{\displaystyle \frac{2M}{\sqrt{b^2+a^2}}}+{\displaystyle \frac{Q^2}{b^2+a^2}}.$$

Figure 2i represents the comparative plots of radial tidal force around SBH, RNBH spacetime and a black-bounce-RNBH with different possible values of the BH parameters involved therein. As seen in the figure, the radial tidal force for SBH is always positive and diverges near singularity, which represents the infinite radial stretching[19,20,21] as object reaches near center. As charge parameter Q comes into play, tidal force curve now has a maxima and diverges in opposite direction than that of SBH. While for black-bounce-RNBH, the radial tidal force is finite everywhere, hence no infinite radial stretching is present. Figure 2ii depicts the tidal force $F_{rad}$ in radial direction, for fixed value of charge parameter i.e. $Q=0.5$ and different values of bounce parameter a, as shown in the figure. As the value of a is increased, the curve for $F_{rad}$ becomes flatter and maxima of curve shifts towards larger value of r. Now Figure 2iii represents $F_{rad}$, for fixed value of bounce parameter i.e. $a=0.5$ and different values of charge parameter Q, as shown in the figure. Again curves for $F_{rad}$ become flatter with increasing Q values but interestingly it flips on the limiting value of Q i.e. 1.

Figure 3i represents the comparative plots of angular tidal force around SBH, RNBH spacetime and a black-bounce-RNBH with different possible values of the BH parameters involved therein. The curve corresponding to SBH diverges to negative infinity as one approaches to singularity, representing the infinite angular compressing present there[19,20,21], while this divergence is absent incase of black-bounce-RNBH again assuring the finite value tidal force present everywhere.

Figure 3ii depicts the tidal force $F_{ang}$ in angular direction, for fixed value of charge parameter i.e. $Q=0.5$ and different values of bounce parameter a, as shown in the figure. As the value of a is increased, the curve for $F_{ang}$ also becomes flatter. Now Figure 3iii represents $F_{ang}$, for fixed value of bounce parameter i.e. $a=0.5$ and different values of charge parameter Q, as shown in the figure. It is noticed that as the value of charge Q reaches near its upper limiting value i.e., 1, the qualitative nature of radial as well as angular tidal force changes near the center as depicted in Figure 2iii and Figure 3iii.

In the next section the geodesic deviation equations for black-bounce-RNBH spacetime is solved in order know more about the relative acceleration of freely falling particles in this geometry.

5. Revisiting the Geodesic Deviation Equations and Their Solutions

Using Equation (14) for particles falling freely along radial geodesics i.e. having $L=0$, the radial coordinate r can be written as,

$${\displaystyle \frac{dr}{d\tau }}=-\sqrt{E^2-f\left(r\right)}.$$

(26)

Now lets re-frame the set of geodesics deviation equations given in eqs.(23-24), as function of radial coordinate itself,

$$\left(E^2-f\left(r\right)\right){\displaystyle \frac{d^2{\widehat{\eta }}^1}{d{r}^2}}-{\displaystyle \frac{f^{\prime }}{2}}{\displaystyle \frac{d{\widehat{\eta }}^1}{dr}}=-{\displaystyle \frac{f^{″}}{2}}{\widehat{\eta }}^1,$$

(27)

$$\left(E^2-f\left(r\right)\right){\displaystyle \frac{d^2{\widehat{\eta }}^i}{d{r}^2}}-{\displaystyle \frac{f^{\prime }}{2}}{\displaystyle \frac{d{\widehat{\eta }}^i}{dr}}=-\left({\displaystyle \frac{r{f}^{\prime }}{2(r^2+a^2)}}+{\displaystyle \frac{a^2(f\left(r\right)-E^2)}{{(r^2+a^2)}^2}}\right){\widehat{\eta }}^i$$

(28)

The analytic solutions [20] of Equation (27) and Equation (28) can be written in standard form using elliptical integrals as,

$${\widehat{\eta }}^1=\left[A_1+B_1\int {\displaystyle \frac{dr}{{\left(f\left(r\right)\right)}^{3/2}}}\right]\sqrt{f\left(r\right)},$$

(29)

$${\widehat{\eta }}^i=\left[A_i+B_i\int {\displaystyle \frac{dr}{(r^2+a^2)\sqrt{f\left(r\right)}}}\right]r.$$

(30)

here $A_1$, $B_1$, $A_i$ and $B_i$ are constants of integration.

For numerical solutions of Equation (27) and Equation (28) we have opted the boundary conditions used in [19,20,23,24]. A particle falling from its initial position outside the event horizon $r=b>r_H$ is considered in above boundary conditions. Specifically, the first initial condition ICI is,

$${\eta }^{\widehat{\alpha }}\left(b\right)=1,{\dot{\eta }}^{\widehat{\alpha }}\left(b\right)=0,$$

(31)

According to this condition the 4-velocity component of infalling particle is taken as zero i.e. $\dot{r}=0$ which further fixes the energy of the particles $E=f\left(b\right)$. Similarly the second initial condition ICII mathematically reads,

$${\eta }^{\widehat{\alpha }}\left(b\right)=0,{\dot{\eta }}^{\widehat{\alpha }}\left(b\right)=1.$$

(32)

which pysically corresponds to the particle ‘exploding’ at $r=b>r_H$. Now,

$${\eta }^{\widehat{\mu }\prime }\left(b\right)={\displaystyle \frac{1}{\sqrt{\frac{E^2}{f\left(b\right)}-1}}},$$

(33)

thus energy E of the infalling test particle is not a fixed parameter. One can say that the energy of the particle also affects the kinematical evolution of the geodesic deviation vectors in this condition.

It can be observed from Figure (4), Figure (5), Figure (6) and Figure (7) that for large values of r, the variation of geodesic deviation vector with radial distance is similar while near singularity, the relative compression or stretching becomes weaker as both a and Q become non-zero. Further increment in both of these parameters show further decrement in the corresponding geodesic deviation vector magnitude showing the presence of comparatively weak gravitational field.

As radial parameter varies beyond event horizon radius, relative separation between geodesics increases first, reaches a maximum value and then decreases. Although the qualitative behaviour shown in Figure 4i and Figure 4ii is similar, but one can observe the difference due to the presence of scale and charge parameters a and Q. As a and Q have non-zero values and either of the parameters increases, the steepness of the curve obtained on both sides of maxima decreases. It is worth to note that the position of maxima is unaffected due to change in the values of a and Q.

Under IC-II the initially diverging geodesics keep on diverging and divergence is stronger in presence of a and Q as depicted in Figure 5.

In contrast to radial geodesic deviation vector, the corresponding vector in angular direction decreases up to a certain distance and then increases further under IC-I. Qualitative behavior is similar but magnitude of vector becomes smaller with increasing values of either a or Q. It again depicts correspondingly weaker gravitational field around given BH.

6. Conclusions

In the present work, we focused on black-bounce-RNBH spacetime and discussed about the evolution of tidal forces in its vicinity. The discussion was carried forward with the help of equations of motion for tidal forces in radial and angular directions. For better understanding of the gravitational field and its effect the geodesic deviation equations were derived and solved analytically as well as numerically. Few key results of this study are outlined as below,

(i)

The presence or absence of horizons defines whether it’s a black bounce (with event horizon) or a wormhole-like structure (without horizon). The event horizon is present only for moderate charge Q and bounce parameter a satisfying the conditions $Q^2<m^2$ and $a^2\le {\left(M\pm \sqrt{M^2-Q^2}\right)}^2$.

(ii)

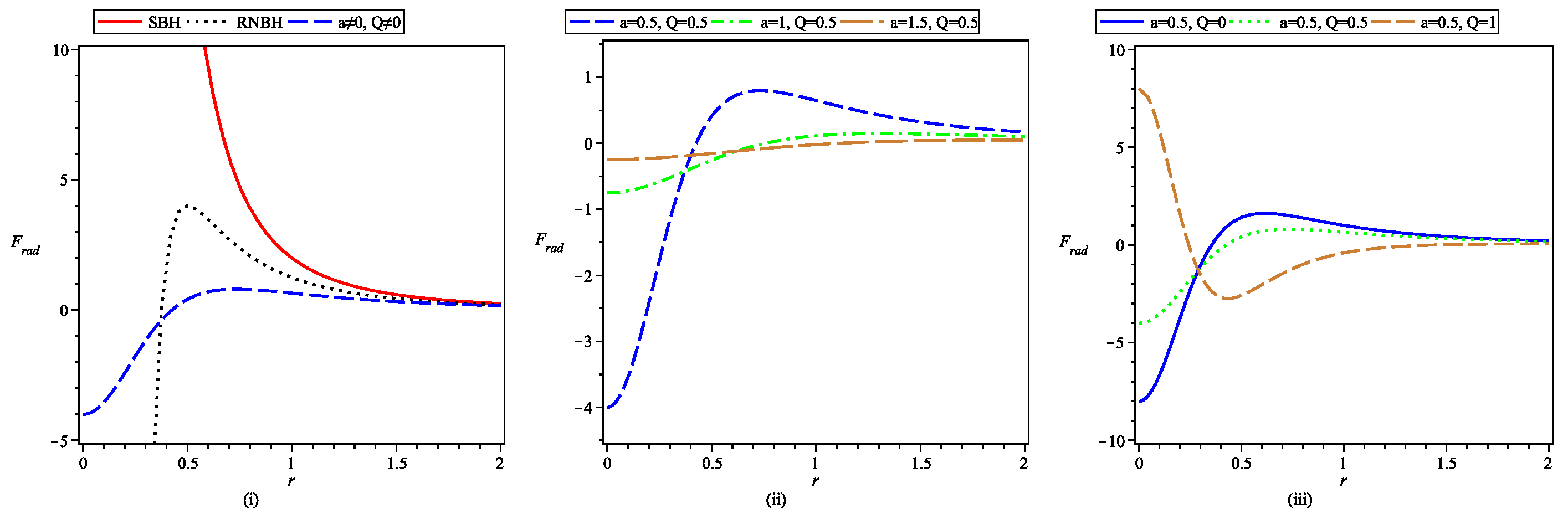
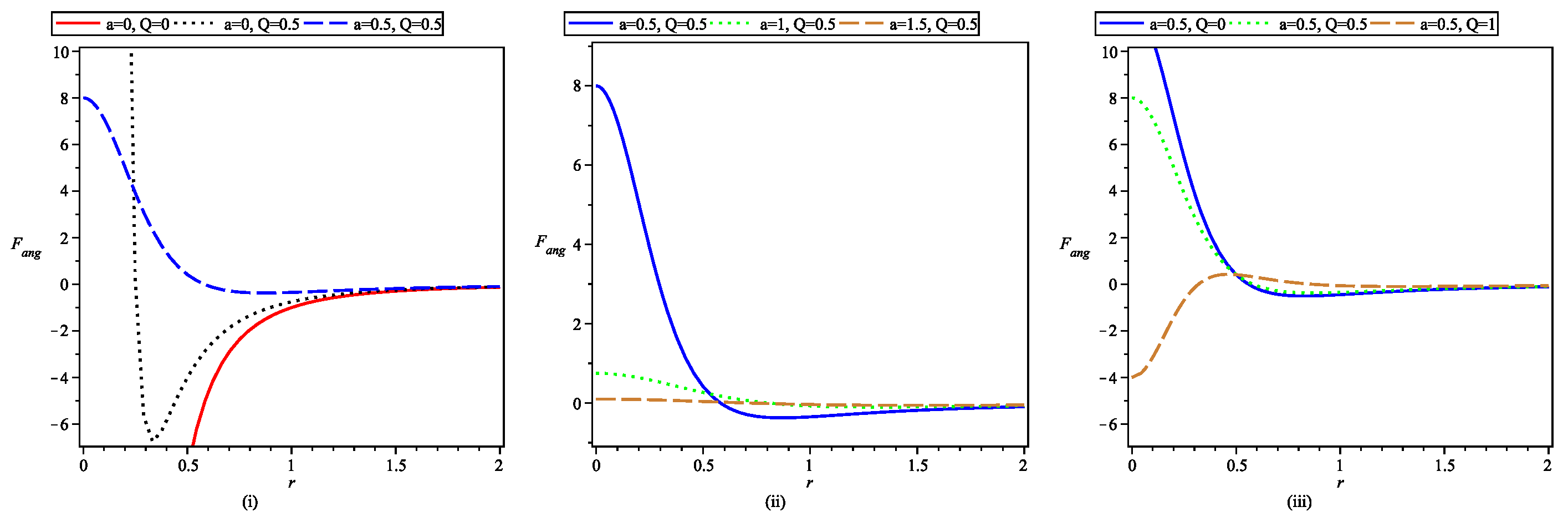
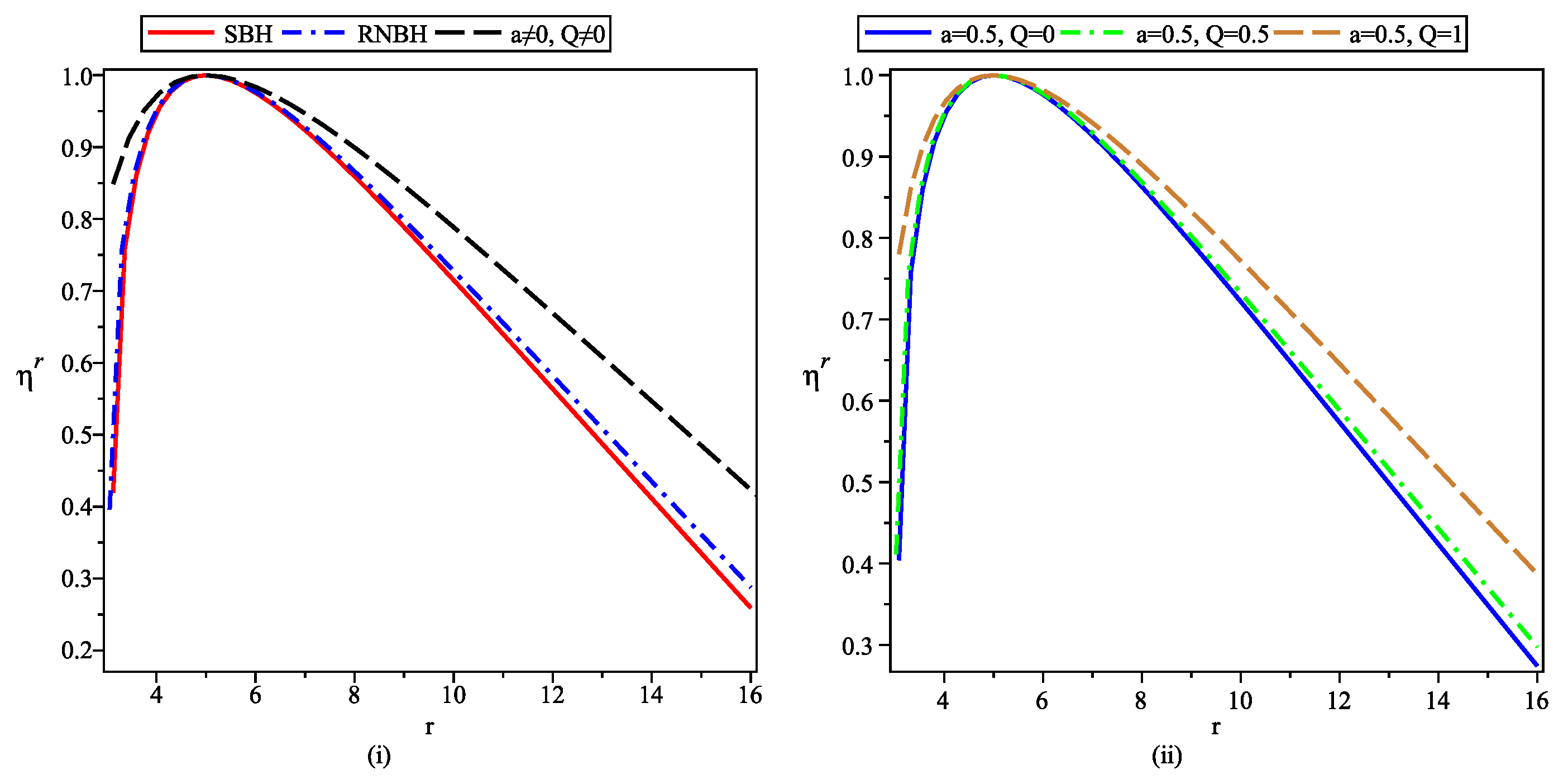
The expression for Newtonian radial acceleration is obtained for black-bounce-RNBH spacetime and further the tidal forces in radial and angular directions are analyzed in detail.

(iii)

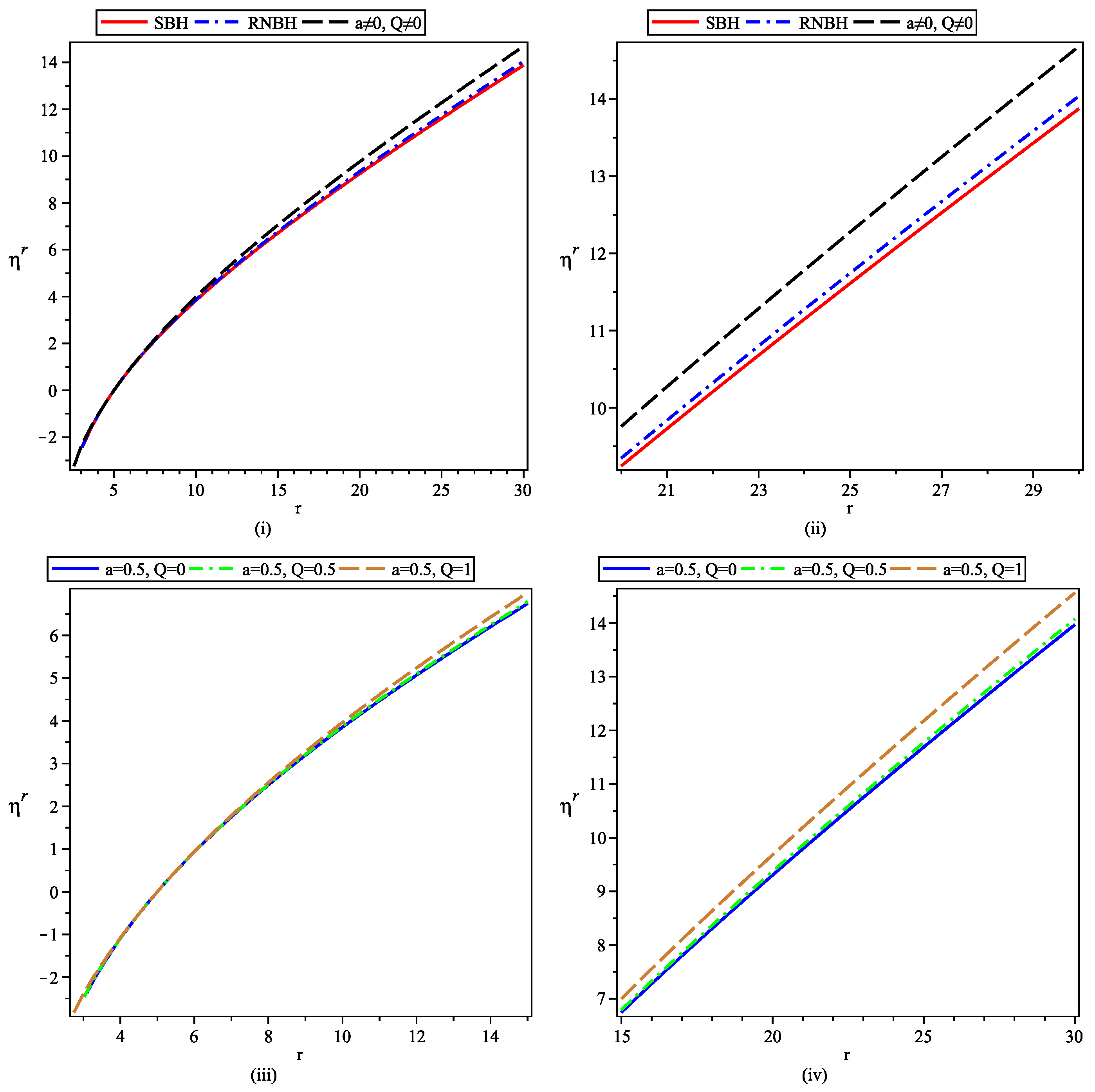
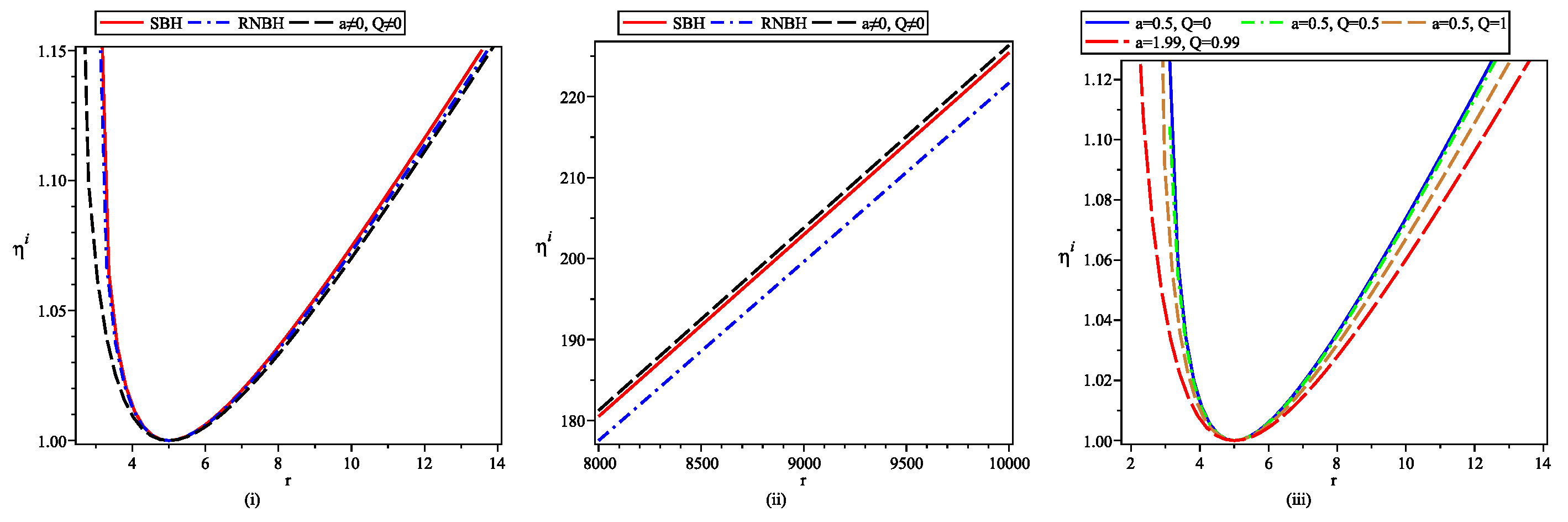
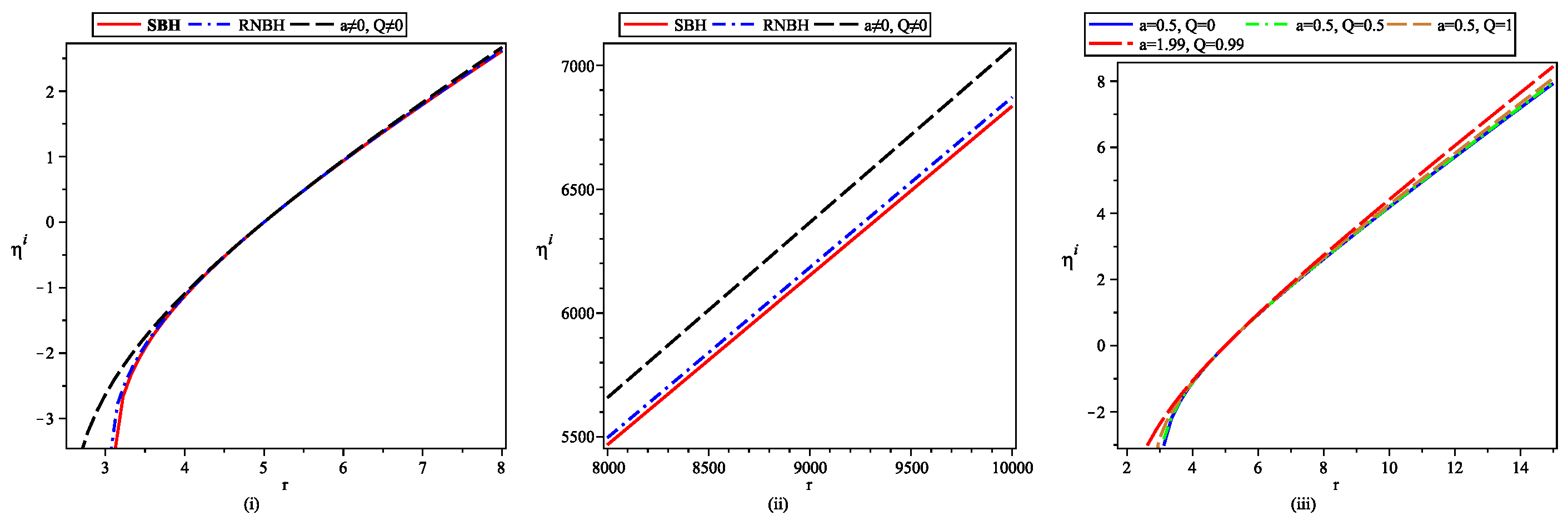
Comparative plots for tidal forces show the absence of infinite radial stretching and infinite angular compression incase of black-bounce-RNBH spacetime for any object approaching central singularity. As particle reaches near central region, now its not turned apart by infinite forces as incase of SBH but the magnitude of tidal forces reaches their respective maxima and decrease afterwards.

(iv)

The generalised set up of geodesic deviation equations around black-bounce-RNBH spacetime are derived and solved analytically in terms of elliptical integrals.

(v)

The geodesic deviation equations are also solved numerically using two initial conditions, first corresponding to the particle starting from rest and having fixed energy while second corresponding to an exploding particle with varying energy value along its path. The numerical plots are shown in Figure (4), Figure (5), Figure (6) and Figure (7). If one observes that under IC-I, radial divergence between neighboring geodesics starts at a fixed r and it increases for far distances from center, while near central region the behaviour is opposite. The strength of relative separation reduces for black-bounce-RNBH spacetime in comparison to SBH and RNBH. In contrast, the initially diverging geodesics keep on diverging in radial as well as angular directions under IC-II.

(vi)

In angular direction, the initially converging geodesics for SBH become diverging under IC-I. Now if one observes the far field behavior, the non-zero and increasing values of both Q and a result in larger magnitude of separation vector, thus helping the relative divergence of geodesics. Similar pattern is seen under IC-II in angular direction.

This work presented in this article is important to have a better understanding of the gravitational field of black-bounce-RNBH spacetime. It can be extended further to discuss the tidal force transition through the bounce can be studied in order to understand the gravitating effects of a wormhole-like or bounce passage to another region.