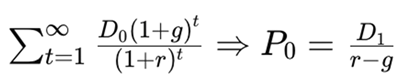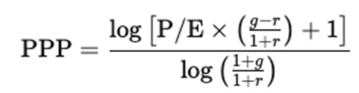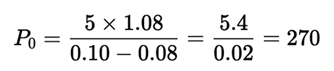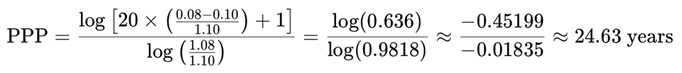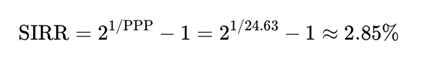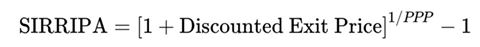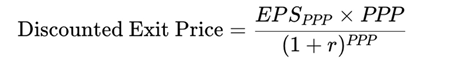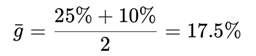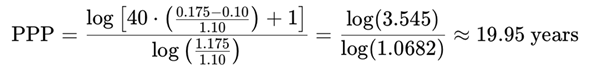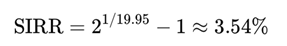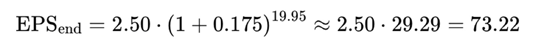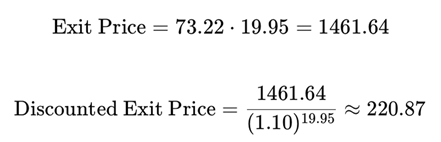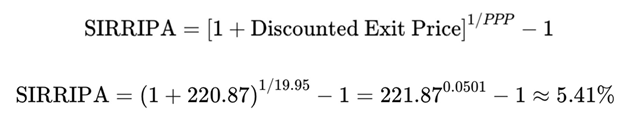1. Introduction
Stock valuation is a cornerstone of investment finance, guiding decisions on whether to buy, hold, or sell securities based on their expected returns and underlying fundamentals. Over time, various models have shaped our understanding of what constitutes fair value in the market.
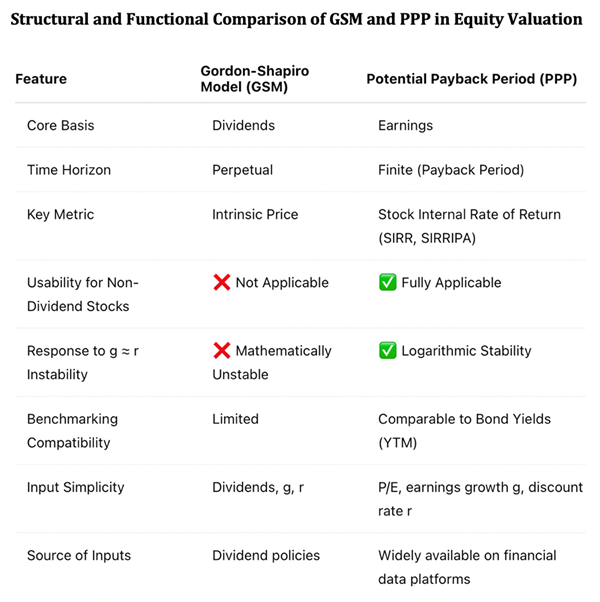
One of the most influential frameworks is the Gordon-Shapiro model, known for its mathematical rigor and simplicity. Traditionally, it links dividend growth—not earnings growth—to stock valuation, assuming that dividend payments grow at a constant rate and represent the actual cash flows received by shareholders. The model rests on the premise that a stock’s value derives from the present value of this perpetual dividend stream, discounted appropriately for risk and time.
Despite its elegance, the Gordon-Shapiro model has clear limitations. When the dividend growth rate g approaches the discount rate r, the denominator of the formula shrinks, leading to mathematical instability and inflated valuations. Moreover, the assumption of perpetual dividend growth fails to account for real-world economic cycles, firm-specific changes, and modern reinvestment strategies. Most notably, it offers no clear investment horizon, limiting its usefulness for performance benchmarking or return planning.
To address these challenges, the author introduces the Potential Payback Period (PPP)—a valuation framework that retains the spirit of Gordon-Shapiro but replaces perpetual dividend assumptions with finite, earnings-based payback logic. The PPP establishes a defined time horizon and supports the calculation of two key return metrics: the Stock Internal Rate of Return (SIRR), which reflects the compounded return from cumulative earnings, and the Stock Internal Rate of Return Including Price Appreciation (SIRRIPA), which adds capital gains at exit. These metrics enable realistic, risk-adjusted comparisons with fixed-income instruments such as bonds.
This paper begins by revisiting the Gordon-Shapiro model in its original form, highlighting its contributions and limitations, and then shows how the PPP builds upon and extends this classic framework to better align with contemporary valuation needs.
2. The Original Gordon-Shapiro Dividend Discount Model
Originally formulated in 1956, the Gordon-Shapiro model is a specific case of the Dividend Discount Model (DDM). It determines the intrinsic value of a stock as the present value of an infinite series of future dividends, assuming these dividends grow at a constant rate. The formula is:
This formulation is derived from an infinite geometric series
For the model to produce meaningful results, it must satisfy g < r, ensuring that the present value of future dividends converges. When these conditions hold, the model offers a clean, single-equation solution for stock valuation.
However, its practical relevance is increasingly limited. The model is best suited for mature, dividend-paying firms with stable payout policies—yet today, many of the market’s most valuable companies retain earnings to fund growth rather than issue dividends. This disconnect creates a conceptual and practical gap: while the model depends on dividends to estimate value, investors often price stocks based on future earnings potential, not immediate cash distributions.
This highlights a broader limitation in the model’s applicability to modern finance. Valuing a stock purely on dividends can overlook the economic substance of retained earnings, especially when reinvestment drives future profitability.
To modernize valuation practice, the PPP replaces dividends with earnings as the core input and introduces a finite horizon. Before transitioning to the PPP framework, it is important to clarify a fundamental distinction: the Gordon-Shapiro model assumes growth in dividends, while the PPP evaluates growth in earnings. Since many growth-oriented firms pay little or no dividends, their valuation must rely on projected earnings rather than payout policy. By anchoring valuation to earnings growth and allowing for flexible reinvestment and risk adjustments, the PPP provides a more comprehensive, adaptable approach for today’s market conditions.
3. The Potential Payback Period (PPP): Formula and Rationale
The Potential Payback Period (PPP) is a forward-looking valuation metric that measures how long it takes for a company’s cumulative earnings—adjusted for growth and discounting—to repay the initial investment. It addresses key weaknesses of traditional models by introducing a time-bound, risk-adjusted framework.
The PPP formula is:
where:
P/E: price-to-earnings ratio,
g: expected annual earnings growth rate,
r: discount rate (e.g., using CAPM).
This logarithmic formulation ensures mathematical stability even when g ≈ r, a scenario where the Gordon-Shapiro model breaks down.
- Special Case: When g = r, applying L’Hôpital’s Rule to resolve the indeterminate form in the logarithmic expression simplifies the formula to: PPP =P/E.
This emphasizes that the PPP formula remains mathematically coherent even at the limit case where growth equals discount rate—a point at which the traditional Gordon-Shapiro formula becomes undefined due to division by zero. Using L’Hôpital’s Rule in this context not only validates the PPP’s internal logic but also reinforces its superiority in edge-case valuation scenarios.
- No-Growth World: When g = 0 and r = 0, the formula also reduces to PPP = P/E, demonstrating that PPP unifies various valuation frameworks into a single, dynamic model.
4. Numerical Example: PPP vs. Gordon-Shapiro
Consider a stock with the following parameters:
Price: $100
EPS: $5
P/E = 20
g = 8%, r = 10%.
4.1. Gordon-Shapiro Estimate
This valuation is highly inflated due to the small denominator.
Note: In order to allow comparison with the PPP, which is based on earnings, we adapt the Gordon-Shapiro model here by replacing dividends with earnings—effectively assuming full earnings distribution as dividends.
4.2. PPP Estimate
Consider a stock with the following parameters:
We calculate the PPP using:
Then the Stock Internal Rate of Return (SIRR) is computed using the doubling formula:
This reflects a stable and interpretable return, unlike the Gordon-Shapiro model, which fails when g > r due to a near-zero or negative denominator, and becomes inapplicable when dividends are absent.
While the Gordon-Shapiro model suggests a supposedly objective and absolute fair price for a stock, the PPP-derived SIRR corresponds to a continuous return metric. This metric enables direct comparisons across stocks and can be benchmarked against bond yields, reflecting how stock and bond markets are interrelated in practice.
5. SIRRIPA and Investment Return with Exit Price
5.1. Formula and Rationale
In addition to cumulative earnings, PPP also supports calculating a more comprehensive return that includes the terminal stock price (SIRRIPA). Using the “doubling formula” to approximate the sum of discounted future earnings over the PPP period, the formula for SIRRIPA is as follows:
where
where
The SIRRIPA allows direct comparison with a bond’s yield to maturity (YTM). This is because both SIRRIPA and YTM represent annualized internal rates of return that incorporate not only periodic cash flows (earnings for stocks or coupons for bonds) but also the terminal value (exit price for stocks or face value for bonds). As such, SIRRIPA provides a yield-like metric for equities, fully accounting for both income and capital appreciation, just as YTM does for bonds.
5.2. Practical Example of a High-Growth Stock Inapplicable to GSM
Consider a stock with the following parameters:
Since the company pays no dividends the Gordon-Shapiro model becomes mathematically unstable and practically inapplicable. However, PPP remains fully operational.
We approximate the average growth rate over the investment horizon:
Applying the PPP formula:
Using the doubling formula:
Assume EPS0 = 2.50:
(This figure, combined with the P/E ratio of 40, implies a stock price of $100. This makes subsequent return metrics directly comparable to a bond’s par value structure.)
Assuming Exit P/E = PPP = 19.95:
SIRRIPA (with standardized price = 1)
By the very definition of PPP, the sum of discounted EPS over the PPP horizon equals the standardized initial stock price (1). This is reflected in the SIRRIPA formula below, where the “1” represents full recovery of the initial investment through earnings alone.
This example illustrates that the PPP can compute realistic, risk-adjusted return metrics (SIRR and SIRRIPA) even for high-growth, zero-dividend companies—precisely where the Gordon-Shapiro model breaks down.
Moreover, the SIRRIPA of 5.41%—derived from real-world valuation inputs—can be meaningfully benchmarked against a risk-free rate of approximately 4.00%. This demonstrates a higher degree of realism, consistency, and comparability across the financial universe, making SIRRIPA a powerful and actionable metric for both absolute and relative return analysis.
6. Conclusions
The PPP provides a unified, time-based framework for equity valuation that modernizes the Gordon-Shapiro model. It replaces perpetual assumptions with finite horizons and enables both SIRR and SIRRIPA computations, thereby aligning stock and bond return assessments. By refocusing on earnings rather than dividends, the PPP redefines valuation through a more realistic and operational lens.
In doing so, the PPP and its derivatives not only complement the Gordon-Shapiro model—it revitalizes it for the complexities of contemporary markets.
This innovative approach, built on classical models, allows investors, analysts, and portfolio managers to rigorously compute the total annualized return of any stock using just three basic inputs—readily available from most financial data platforms: the P/E ratio, the expected earnings growth rate, and the discount rate derived from the CAPM. The result is a unified, forward-looking return metric—directly comparable to a bond’s Yield to Maturity (YTM)—that supports more coherent portfolio construction and risk-adjusted allocation across asset classes.
References
- Bodie, Z., Kane, A., & Marcus, A. J. (2013). Investments (10th ed.). McGraw-Hil.
- Comprehensive coverage of investment theory, useful for contrasting traditional valuation methods with the PPP-derived SIRR and SIRRIPA.
- Damodaran, A. (2002). Investment valuation: Tools and techniques for determining the value of any asset. Wiley Finance.
- Provides insights into valuation techniques for various asset classes, highlighting why traditional methods can fall short in capturing long-term earning power as reflected by PPP-derived SIRR and SIRRIPA.
- Fama, E. F., & French, K. R. (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics, 33(1), 3–56.
- Examines risk factors influencing stock and bond returns, underscoring the importance of risk-adjusted metrics in investment evaluation such as PPP-derived SIRR and SIRRIPA.
- Graham, B., & Dodd, D. (1934). Security analysis. McGraw-Hill.
- Classic work on value investing emphasizing intrinsic value, a concept central to the PPP-derived SIRR and SIRRIPA’s focus on earning power.
- Modigliani, F., & Miller, M. H. (1958). The cost of capital, corporation finance, and the theory of investment. The American Economic Review, 48(3), 261–297.
- Foundational paper in financial theory, highlighting the role of capital costs in investment decisions, relevant to discount rate discussions in PPP, SIRR, and SIRRIPA.
- Sam, R. (1984). Le PER, un instrument mal adapté à la gestion mondiale des portefeuilles. Comment remédier à ses lacunes. Revue Analyse Financière, 2e trimestre 1984.
- Critiques the limitations of the P/E ratio for global portfolio management and proposes the DR (Payback Period) as a more robust evaluation tool, paving the way for PPP-derived metrics such as SIRR and SIRRIPA.
- Sam, R. (1985). Le Délai de Recouvrement (DR). Revue Analyse Financière, 3e trimestre 1985.
- Refines the DR concept (early form of the PPP), setting theoretical groundwork for dynamic valuastion metrics like SIRR and SIRRIPA.
- Sam, R. (1988). Le DR confronté à la réalité des marchés financiers. Revue Analyse Financière, 4e trimestre 1988.
- Applies the DR concept in real-world financial markets, validating its relevance and laying further foundations for the PPP and its derivatives such as SIRR and SIRRIPA.
- Sam, R. (2024). Stock evaluation: Discovering the Potential Payback Period (PPP) as a dynamic P/E ratio.
- Dedicated platform focusing on the Potential Payback Period (PPP) and its innovative use in deriving both the Stock Internal Rate of Return (SIRR) and the Stock Internal Rate of Return Including Price Appreciation (SIRRIPA).
- Sam, R. (2025). Le Potential Payback Period (PPP) : Une généralisation utile du Price Earnings Ratio (PER) pour l’évaluation des actions. Revue Française d’Économie et de Gestion, 1(2), 621–632.
- Explores how the PPP generalizes and extends the traditional P/E ratio by integrating earnings growth, interest rates, and risk, leading to evaluation metrics such as SIRR and SIRRIPA.
- Sam, R. (2025). Le Potential Payback Period (PPP) : La septième révolution financière. Revue Française d’Économie et de Gestion, 6(2), 594–620.
- Positions the PPP as a major evolution in financial analysis, comparable to earlier pivotal innovations, and highlights the significance of metrics such as SIRR and SIRRIPA.
- Sam, R. (2025). Anatomy of a looming bear market: How to assess the impact of Donald Trump’s chaotic measures on Wall Street. Revue Française d’Économie et de Gestion, 6(3), 550–560.
- Analyzes potential bear market scenarios linked to political instability, applying PPP-derived methods, including SIRR and SIRRIPA, to assess market risks.
- Sam, R. (2025). Comparing global stock markets using risk-premiums derived from the Potential Payback Period (PPP). Revue Française d’Économie et de Gestion, 6(3), 541–549.
- Applies PPP-derived risk premiums and related return metrics such as SIRR and SIRRIPA to compare and rank different global stock markets.
- Sam, R. (2025). Analyse financière: Le Potential Payback Period (PPP), une alternative au Price Earnings Ratio pour évaluer les entreprises temporairement déficitaires—Étude de cas : Intel Corp. Revue Française d’Économie et de Gestion, 6(3), 561–576.
- Demonstrates how the PPP, through metrics such as SIRR and SIRRIPA, can be effectively applied to companies with temporary losses, where the traditional P/E ratio fails, using Intel Corp. as a case study.
- Sharpe, W. F. (1964). Capital asset prices: A theory of market equilibrium under conditions of risk. The Journal of Finance, 19(3), 425–442.
- Introduces the Capital Asset Pricing Model (CAPM), forming the basis for adjusting returns for risk, crucial for calculating PPP-derived SIRR and SIRRIPA.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).