Extending the P/E and PEG Ratios: The Role of the Potential Payback Period (PPP) in Modern Equity Valuation

1. Introduction: Revisiting Traditional Valuation Metrics

In financial analysis, the Price-to-Earnings (P/E) ratio and the Price-to-Earnings to Growth (PEG) ratio have been longstanding reference points. The P/E ratio provides a snapshot of how much investors are willing to pay for one unit of current earnings, while the PEG attempts to adjust this by accounting for future earnings growth. These metrics are widely appreciated for their simplicity and accessibility.

Yet in today’s fast-changing economic landscape — marked by fluctuating interest rates, technological disruptions, and shifting investor expectations — the static nature of these tools can lead to oversimplification. They often fail to incorporate critical elements such as the time value of money, earnings volatility, and risk-adjusted discounting.

This article explores how the Potential Payback Period (PPP) offers a more dynamic valuation approach by extending and refining these traditional tools. Rather than dismissing the P/E and PEG ratios, the PPP builds upon them to reflect a fuller picture of corporate value creation over time.

Crucially, it introduces the concept of a Hidden Value Zone (HVZ) — a region in the P/E–growth space where high-growth companies with high P/E ratios are shown to offer compelling value when analyzed through the lens of PPP. This zone exposes the limitations of PEG’s simplistic structure and highlights the greater analytical depth provided by the PPP.

2. Understanding the Limitations of P/E and PEG

2.1. The P/E Ratio

The P/E ratio is calculated as:

It is interpreted as the number of years it would take to recover the price paid for a stock if earnings remain constant. However, it inherently assumes:

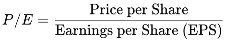
• Zero earnings growth
• No discounting of future earnings
• Static and risk-free operating conditions.

Thus, two companies with identical P/E ratios may have vastly different investment potentials if one is growing rapidly and the other is not. The ratio gives no sense of the time frame for value recovery under realistic conditions.

2.2. The PEG Ratio

The PEG ratio is defined as:

Where g is the expected earnings growth rate.

While the PEG ratio attempts to correct the P/E by factoring in growth, it suffers from key limitations:

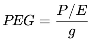
• Linear treatment of growth, ignoring compounding and the time value of money. This linear structure is an oversimplification of financial reality, where growth is exponential in nature and must be discounted over time.
• No consideration of interest rates or risk.
• Arbitrary “PEG = 1” threshold, with no theoretical foundation.
• Over-reliance on analyst projections for growth estimates.

In contrast, the PPP uses a logarithmic structure, which captures the compounding effects of earnings growth and the discounting of future returns. This makes it mathematically more aligned with real-world investment dynamics.

3. The Potential Payback Period (PPP): A Dynamic Adjustment

The PPP offers a time-based valuation framework that integrates earnings growth (g), interest rates (r), and risk — captured through an appropriate discount rate. It answers a more comprehensive question: How many years of discounted future earnings are needed to recover the current stock price?

3.1. PPP Formula

Where:

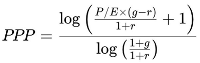
• P/E is the price-to-earnings ratio
• g is the average earnings growth rate
• r is the discount rate, calculated as the risk-free rate plus a market risk premium adjusted for the stock’s specific risk, in accordance with the CAPM framework.

This formula shows that the P/E ratio is a special case of the PPP when both g and r equal zero. In other words, the PPP extends the P/E ratio to reflect real-world financial conditions.

4. From PPP to SIRR: A New Return-Based Metric

From the PPP, one can derive a Stock Internal Rate of Return (SIRR) using the Doubling Formula:

The SIRR provides a return-based interpretation of stock attractiveness, comparable to yield on bonds but adjusted for growth and risk. A stock with a SIRR exceeding the risk-free rate offers a positive expected excess return.

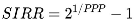
5. Case Study: Applied Materials vs. Broadcom

Data as of January 24, 2025, with discount rate r = 4.62%

Traditional metrics might imply Broadcom is overvalued due to its high P/E and PEG. However, PPP and SIRR reveal that both stocks offer similar return potential once growth and discounting are integrated.

This shows how the PPP adds dimensionality and provides context to traditional metrics, offering a more complete and actionable assessment.

6. The Hidden Value Zone (HVZ): Where the PPP Reveals What PEG Misses

A striking difference between the PPP and PEG approaches emerges when plotting P/E ratios against earnings growth rates (g). The Hidden Value Zone (HVZ), shown in the figure below, highlights an area where traditional PEG-based analysis fails to recognize undervalued stocks—particularly high-growth ones with high P/E ratios.

In this graph:

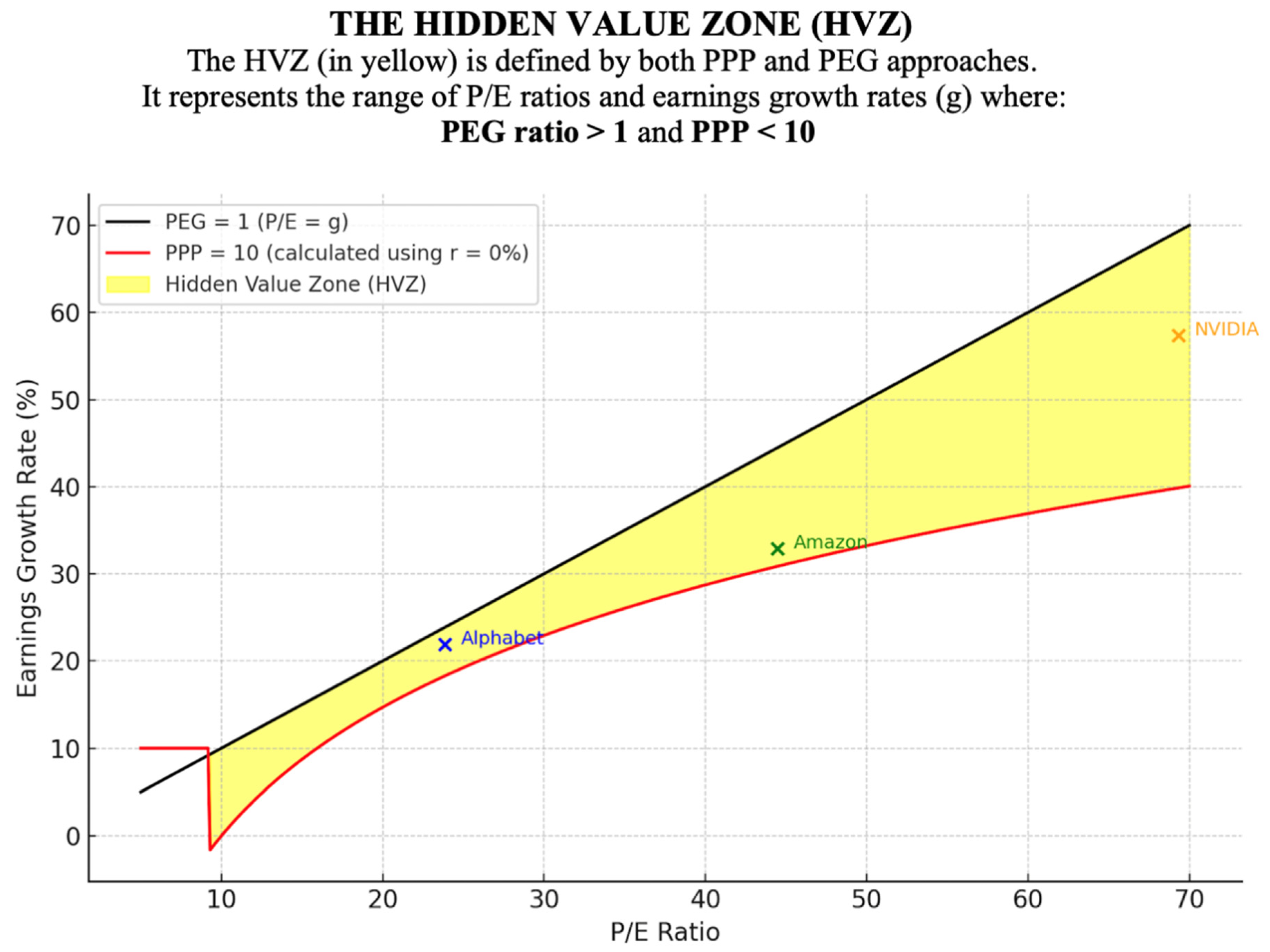
• The black line represents the traditional PEG = 1 boundary (i.e., P/E = g), often used as an arbitrary threshold to judge overvaluation. It is also the bisector of the graph, representing points where the P/E ratio is numerically equal to the earnings growth rate (g). Stocks below this line have a PEG ratio above 1 and are therefore considered overvalued according to the PEG approach.
• The red curve represents PPP = 10 years, assuming a 0% discount rate (r = 0), focusing purely on the relationship between price and compounded growth. As earnings growth accelerates, the PPP decreases, reducing the time needed to recover the investment through future discounted earnings.Stocks positioned above this curve have a PPP below 10 years and are therefore considered to offer attractive intrinsic value according to the PPP approach.
• The yellow shaded area between the two curves is the Hidden Value Zone (HVZ) — a region where high-growth stocks appear overvalued by PEG standards but are revealed as undervalued under the PPP framework. The HVZ essentially results from a clash between the linear logic of the PEG ratio and the logarithmic structure of the PPP formula, with the latter offering a more realistic representation of earnings growth and value recovery over time.

Key Interpretation:

Stocks above the red PPP = 10 line have PPP values below 10 years, suggesting high intrinsic earning power and quicker payback, even if their P/E ratios appear high. This is because the PPP decreases as earnings growth accelerates, reducing the time needed for future profits — once discounted — to recoup the stock price.

A PPP of 10 years can serve as an intuitive yet justified lower threshold for identifying stock undervaluation, grounded in both financial logic and investor expectations.

Specifically, a PPP of 10 years corresponds to a Stock Internal Rate of Return (SIRR) of approximately 7.18%, based on the Doubling Formula:

This is well above the current risk-free rate of 4.62%, indicating a meaningful intrinsic return premium. Such a spread signals that the stock is likely undervalued, offering strong earning power relative to its price. While the PEG ratio might misclassify these high-growth, high-P/E stocks as overvalued, the PPP approach correctly reclassifies them as attractive opportunities, thanks to its incorporation of compounding growth and time-based valuation.

Recent Examples from the Hidden Value Zone (HVZ)

As of November 8, 2024, using data from Yahoo Finance, several prominent U.S. technology companies — part of the so-called “Magnificent Seven” — were positioned in the Hidden Value Zone. Despite having high P/E ratios and PEG ratios above 1, their strong earnings growth rates and relatively low PPP values reveal intrinsic value overlooked by the PEG model. For example:

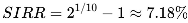
• NVIDIA: P/E = 69.31; growth rate = 57.38%; PPP = 8.18; PEG = 1.21.
• Alphabet: P/E = 23.85; growth rate = 21.91%; PPP = 9.23; PEG = 1.09.
• Amazon: P/E = 44.48; growth rate = 32.90%; PPP = 9.67; PEG = 1.35.

All three companies fall above the red PPP = 10 line yet below the black PEG = 1 line, placing them firmly in the HVZ. This positioning confirms that high-growth stocks can still be fundamentally undervalued, even when dismissed by simplistic PEG thresholds.

7. Application to Market Indices: The S&P 500

As of January 2025:

• P/E = 30
• g = 18%
• r = 4.62% (risk-free rate represented by the 10-year U.S. Treasury yield).

Applying the PPP and SIRR:

• PPP = 13.10 years
• SIRR = 5.43%

Although the S&P 500 exhibits a historically elevated P/E ratio, the PPP model suggests that it remains fairly valued, as the SIRR clearly exceeds the risk-free rate. By integrating growth and discounting, the PPP offers a more nuanced assessment than traditional metrics, which might otherwise label the market as prematurely overvalued.

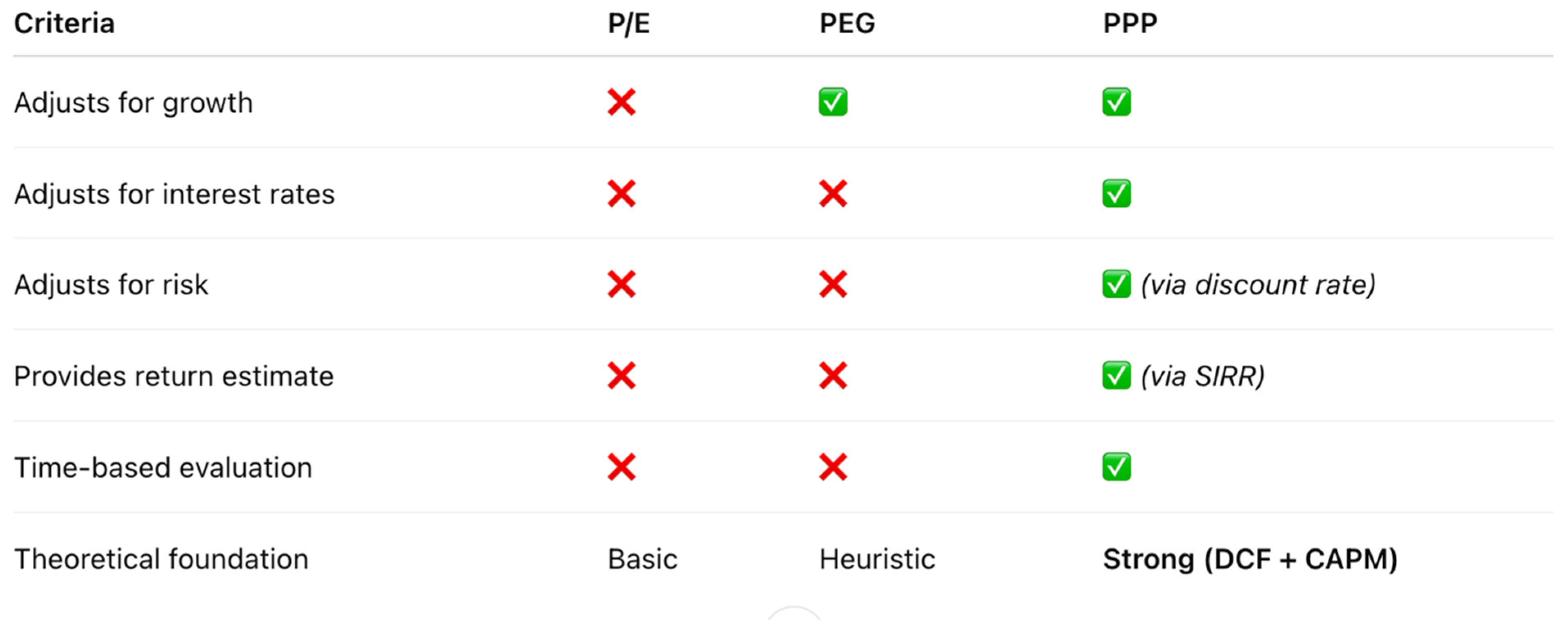
8. Comparing PPP to Traditional Metrics

Another fundamental distinction lies in their mathematical architecture: the PEG ratio’s linear structure provides only a heuristic shortcut, whereas the PPP’s logarithmic formula is rooted in the mathematics of compound growth and present value discounting. This structural difference makes PPP a more rigorous and reliable valuation model.

Rather than rendering older tools useless, the PPP extends and refines them, offering a richer analytical framework.

9. Conclusion

The Potential Payback Period (PPP) and its derivative, the Stock Internal Rate of Return (SIRR), provide a meaningful evolution in stock valuation. These tools:

• Incorporate growth, risk, and the time value of money
• Extend the traditional P/E and PEG ratios into dynamic metrics
• Offer investors a time-based and return-based framework
• Reveal valuation clarity for both individual stocks and broad indices.

One of the most compelling contributions of this model is the identification of the Hidden Value Zone (HVZ) — a conceptual and visual breakthrough where PPP reveals investment opportunities missed by linear PEG analysis. The HVZ illustrates how high-growth stocks with high P/E ratios, often dismissed by PEG thresholds, may in fact offer superior value based on their rapid payback potential.

By adopting PPP, investors and analysts gain access to more forward-looking, risk-aware, and mathematically grounded metrics that better reflect modern market realities. The PPP doesn’t discard the P/E or PEG ratios — it subsumes and enhances them, making them more useful and relevant in today’s complex financial landscape.