Submitted:
06 May 2025
Posted:
09 May 2025
You are already at the latest version
Abstract
Keywords:
2. Materials and Methods
2.1. Materials and Technique
2.2. Thermodynamic Methods
2.2.1. Surface Energy Parameters of Modified Copolymers
2.2.2. Surface Energy and Work of Adhesion
3. Results
3.1. London Dispersive Surface Energy of Modified Copolymers
3.2. Polar (Lewis Acid–Base) Surface Energy of Modified Copolymers
3.3. Polar Surface Energy of Organic Solvents
3.4. Work of Adhesion of Organic Solvents on Modified Copolymer
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, S. Polymer Interface and Adhesion. Marcel Dekker, New York, USA, 1982. [CrossRef]
- Mittal, K.L. Polymer Surface Modification: Relevance to Adhesion, Volume 5 (1st ed.). CRC Press. 2009. [Google Scholar] [CrossRef]
- Venkatakrishnan, A.; Kuppa, V.K. Polymer adsorption on rough surfaces, Current Opinion in Chemical Engineering, 2018, 19, 170-177. [CrossRef]
- Zdziennicka, A.; Krawczyk, J.; Jańczuk, B. Wettability and Adhesion Work Prediction in the Polymer–Aqueous Solution of Surface Active Agent Systems. Colloids Interfaces 2018, 2, 21. [Google Scholar] [CrossRef]
- Harkins, W.D. Surface energy and the orientation of molecules in surfaces as revealed by surface energy relations. Z Phys Chem, 1928, 139, 647_691.
- Young, T. An essay on the cohesion of fluids. Philosophical Transactions of the Royal Society of London, 1805, 95, 65–87. [Google Scholar] [CrossRef]
- Dupré, A. Théorie mécanique de la chaleur. Paris, Gauthier-Villars, France, 1869.
- Fowkes, F. M. Attractive forces at interfaces. Industrial & Engineering Chemistry, 1964, 56, 40–52. [Google Scholar]
- Owens, D. K.; Wendt, R. C. (1969). Estimation of the surface free energy of polymers. Journal of Applied Polymer Science, 1969, 13, 1741–1747. [Google Scholar] [CrossRef]
- van Oss, C. J.; Chaudhury, M. K.; Good, R. J. Interfacial Lifshitz–van der Waals and polar interactions in macroscopic systems. Chemical Reviews, 1988, 88, 927–941. [Google Scholar] [CrossRef]
- Van Oss, C.J.; Good, R.J.; Chaudhury, M.K. Additive and nonadditive surface tension components and the interpretation of contact angles. Langmuir. 1988, 4, 884–891. [Google Scholar] [CrossRef]
- Voelkel, A. IGC as a tool for surface characterization of polymers. Journal of Chromatography A, 2004, 1037, 467–478. [Google Scholar]
- Hansen, C. M. (2007). <italic>Hansen Solubility Parameters: A User’s Handbook</italic> (2nd ed.). CRC Press.
- Packham, D.E. Surface energy, surface topography and adhesion, International Journal of Adhesion and Adhesives, 2003, 23(6), 437-448. [CrossRef]
- Nikkhah, S.J.; Moghbeli, M.R.; Hashemianzadeh, S.M. Investigation of the interface between polyethylene and functionalized graphene: A computer simulation study, Current Applied Physics, 2015, 15(10), 1188-1199. A. [CrossRef]
- Hamieh, T. Study of the temperature effect on the surface area of model organic molecules, the dispersive surface energy and the surface properties of solids by inverse gas chromatography. J. Chromatogr. A 2020, 1627, 461372. [Google Scholar] [CrossRef]
- Hamieh, T. New methodology to study the dispersive component of the surface energy and acid–base properties of silica particles by inverse gas chromatography at infinite dilution. J. Chromatogr. Sci. 2022, 60, 126–142. [Google Scholar] [CrossRef]
- Hamieh, T. Inverse Gas Chromatography to Characterize the Surface Properties of Solid Materials. Chem. Mater. 2024, 36, 2231–2244. [Google Scholar] [CrossRef]
- Hamieh, T. Some Irregularities in the Evaluation of Surface Parameters of Solid Materials by Inverse Gas Chromatography. Langmuir 2023, 39, 17059–17070. [Google Scholar] [CrossRef] [PubMed]
- Hamieh, T. Serious irregularities and errors in the determination of the surface free energy and acido-basicity of MXene materials, Carbon, 2025, 120209. [CrossRef]
- Hamieh, T. New Physicochemical Methodology for the Determination of the Surface Thermodynamic Properties of Solid Particles. AppliedChem 2023, 3, 229–255. [Google Scholar] [CrossRef]
- Hamieh, T. New Progress on London Dispersive Energy, Polar Surface Interactions, and Lewis’s Acid–Base Properties of Solid Surfaces. Molecules 2024, 29, 949. [Google Scholar] [CrossRef]
- Hamieh, T. London Dispersive and Lewis Acid-Base Surface Energy of 2D Single-Crystalline and Polycrystalline Covalent Organic Frameworks. Crystals 2024, 14, 148. [Google Scholar] [CrossRef]
- Conder, J.R.; Locke, D.C.; Purnell, J.H. Concurrent solution and adsorption phenomena in chromatography. I. J. Phys. Chem. 1969, 73, 700–708. [Google Scholar] [CrossRef]
- Conder, J.R.; Purnell, J.H. Gas chromatography at finite concentrations. Part 2.—A generalized retention theory. Trans. Faraday Soc. 1968, 64, 3100–3011. [Google Scholar] [CrossRef]
- Conder, J.R.; Purnell, J.H. Gas chromatography at finite concentrations. Part 1.—Effect of gas imperfection on calculation of the activity coefficient in solution from experimental data. Trans. Faraday Soc. 1968, 64, 1505–1512. [Google Scholar] [CrossRef]
- Sawyer, D.T.; Brookman, D.J. Thermodynamically based gas chromatographic retention index for organic molecules using salt-modified aluminas and porous silica beads. Anal. Chem. 1968, 40, 1847–1850. [Google Scholar] [CrossRef]
- Saint-Flour, C.; Papirer, E. Gas-solid chromatography. A method of measuring surface free energy characteristics of short carbon fibers. 1. Through adsorption isotherms. Ind. Eng. Chem. Prod. Res. Dev. 1982, 21, 337–341. [Google Scholar] [CrossRef]
- Saint-Flour, C.; Papirer, E. Gas-solid chromatography: Method of measuring surface free energy characteristics of short fibers. 2. Through retention volumes measured near zero surface coverage. Ind. Eng. Chem. Prod. Res. Dev. 1982, 21, 666–669. [Google Scholar] [CrossRef]
- Donnet, J.-B.; Park, S.; Balard, H. Evaluation of specific interactions of solid surfaces by inverse gas chromatography. Chromatographia 1991, 31, 434–440. [Google Scholar] [CrossRef]
- Brendlé, E.; Papirer, E. A new topological index for molecular probes used in inverse gas chromatography for the surface nanorugosity evaluation, 2. Application for the Evaluation of the Solid Surface Specific Interaction Potential. J. Colloid Interface Sci. 1997, 194, 217–224. [Google Scholar] [CrossRef] [PubMed]
- Brendlé, E.; Papirer, E. A new topological index for molecular probes used in inverse gas chromatography for the surface nanorugosity evaluation, 1. Method of Evaluation. J. Colloid Interface Sci. 1997, 194, 207–216. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Gu, Y.; Wang, S.; Li, M. Optimization for testing conditions of inverse gas chromatography and surface energies of various carbon fiber bundles. Carbon Lett. 2023, 33, 909–920. [Google Scholar] [CrossRef]
- Pal, A.; Kondor, A.; Mitra, S.; Thua, K.; Harish, S.; Saha, B.B. On surface energy and acid–base properties of highly porous parent and surface treated activated carbons using inverse gas chromatography. J. Ind. Eng. Chem. 2019, 69, 432–443. [Google Scholar] [CrossRef]
- Hamieh, T.; Gus'kov, V.Y. Surface Thermodynamic Properties of Styrene–Divinylbenzene Copolymer Modified by Supramolecular Structure of Melamine Using Inverse Gas Chromatography. Chemistry 2024, 6, 830–851. [Google Scholar] [CrossRef]
- Hamieh, T.; Gus’kov, V.Y. London Dispersive and Polar Surface Properties of Styrene–Divinylbenzene Copolymer Modified by 5-Hydroxy-6-Methyluracil Using Inverse Gas Chromatography. Crystals 2025, 15, 438. [Google Scholar] [CrossRef]
- Hamieh, T.; Gus’kov, V. Y. Determination of Surface Physicochemical Parameters of Styrene–Divinylbenzene Copolymer Modified by 5-Fluouracil Using Inverse Gas Chromatography. Preprints 2025, 2025041864. [Google Scholar] [CrossRef]
- Young, T. Miscellaneous works of the late Thomas Young. London: John Murray; 1855.
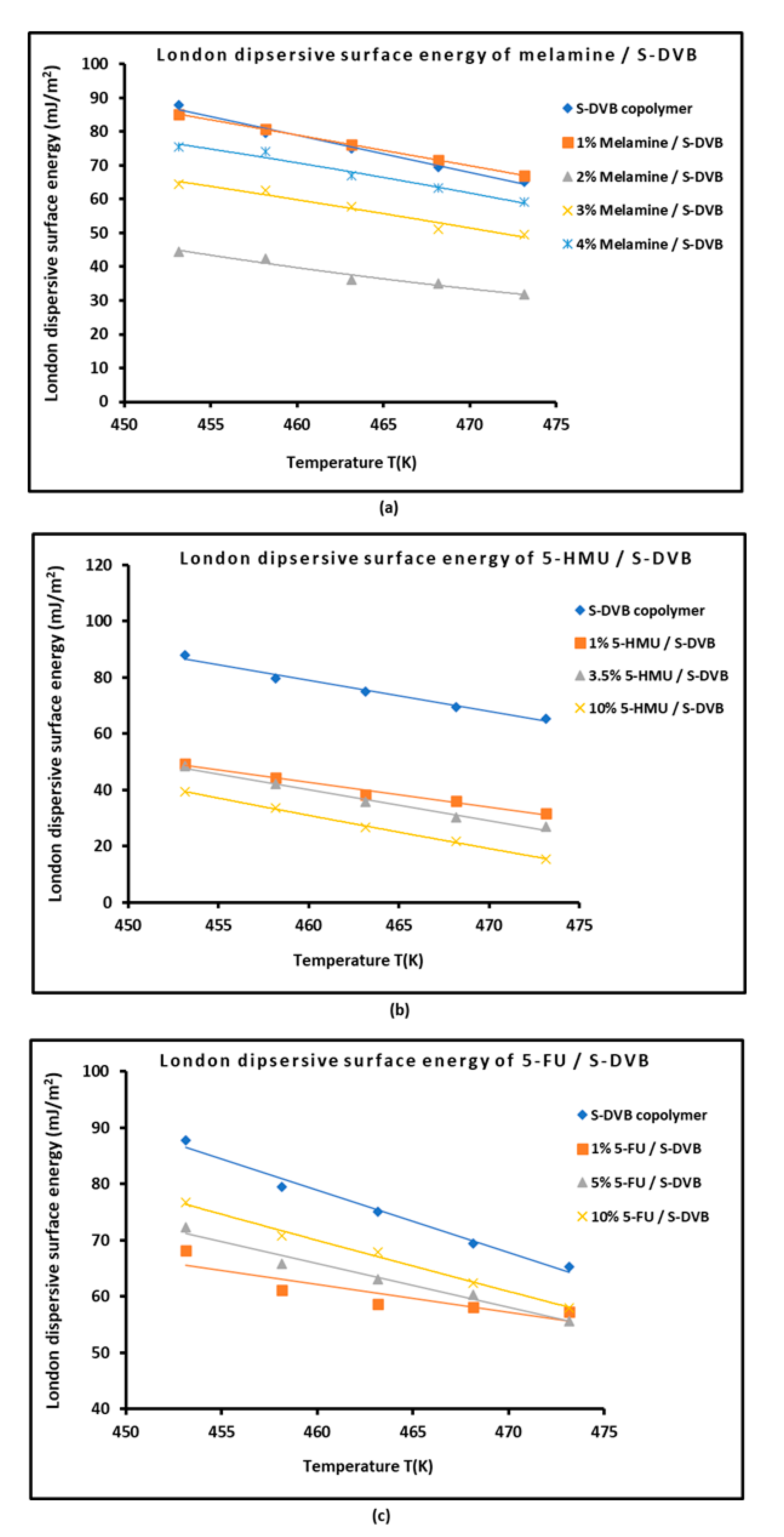
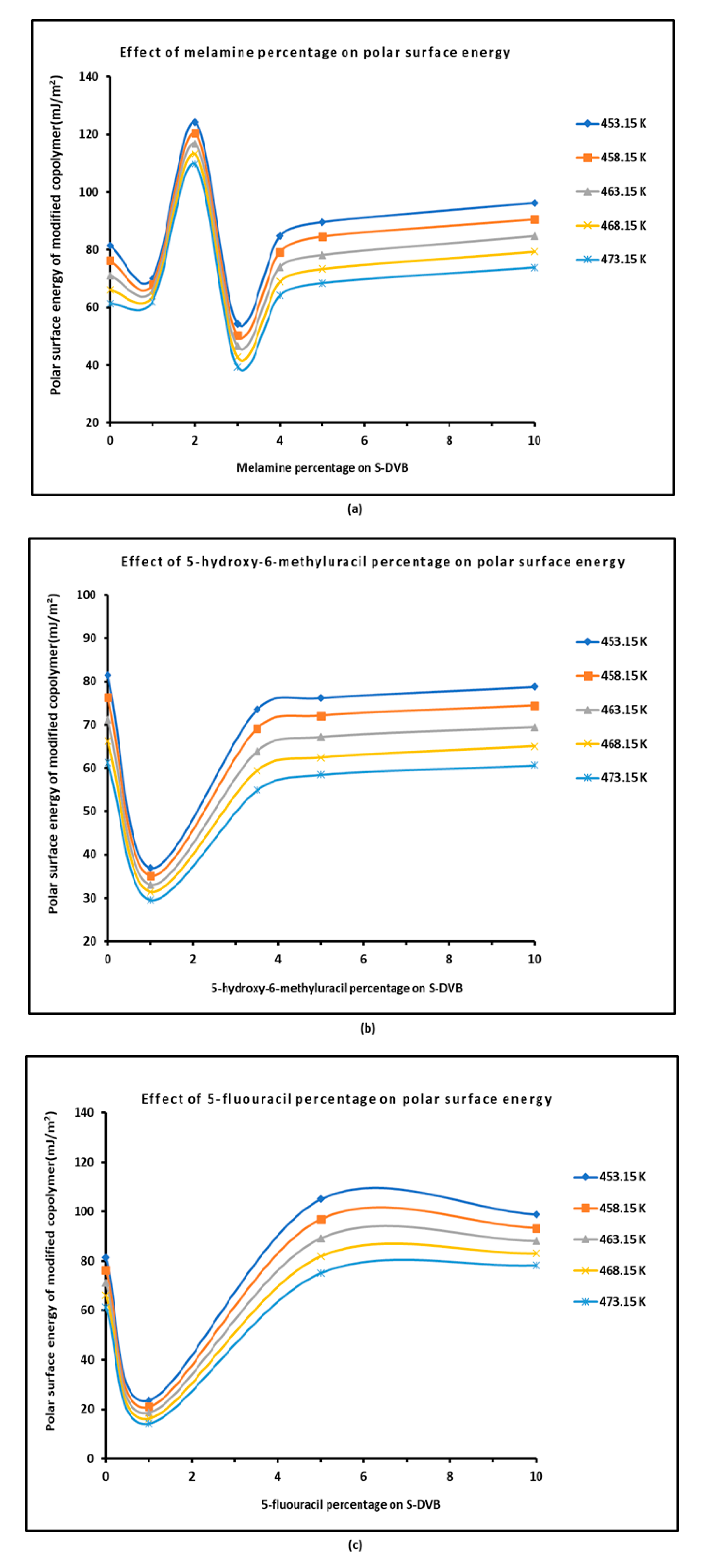
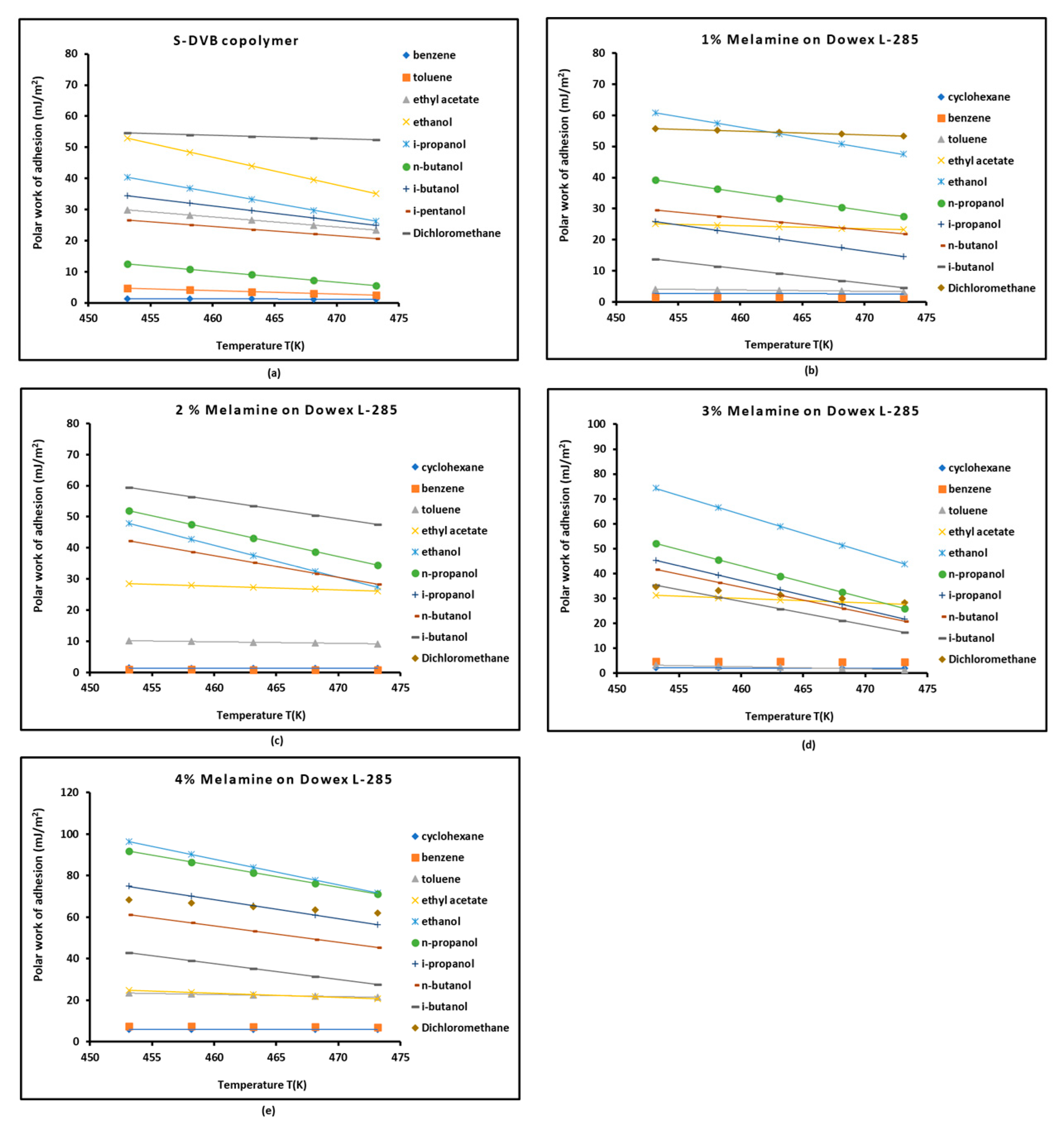
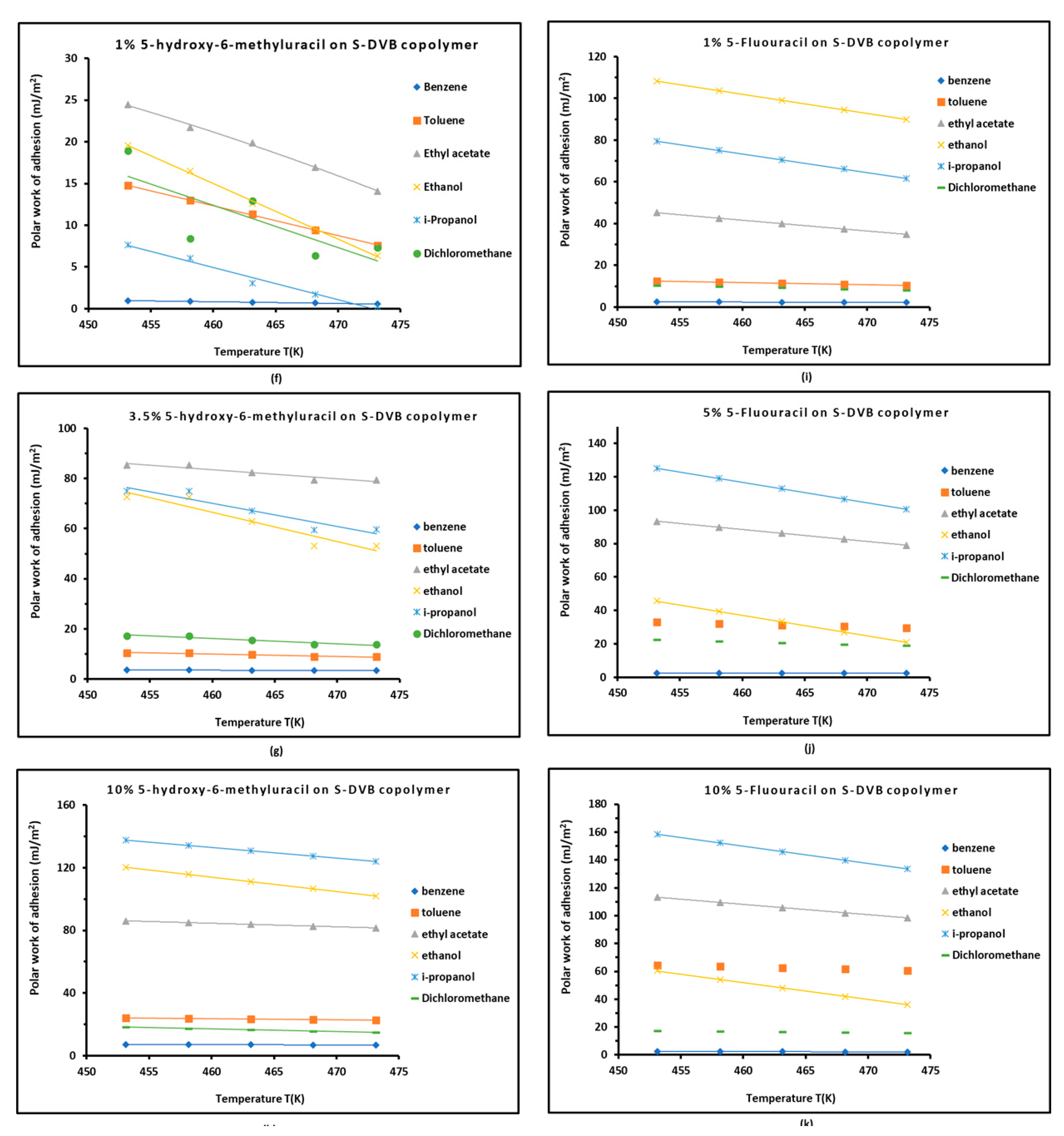
| Copolymer | (mJ/m2) | (mJ m−2 K−1) | (mJ/m2) | (mJ/m2) | (K) | |
|---|---|---|---|---|---|---|
| S+DVB | = −1.105 T + 587.13 | 0.9980 | 0.835 | 587.13 | 257.7 | 531.4 |
| 1% Melamine/ S-DVB | = −0.907 T + 496.21 | 0.9972 | 0.907 | 496.21 | 225.79 | 547.1 |
| 2% Melamine/ S-DVB | = −0.656 T + 341.59 | 0.9590 | 0.656 | 341.59 | 146.12 | 521.0 |
| 3% Melamine/ S-DVB | = −0.827 T + 439.96 | 0.9608 | 0.827 | 439.96 | 193.51 | 532.3 |
| 4% Melamine/ S-DVB | = −0.876 T + 473.64 | 0.975 | 0.876 | 473.64 | 212.40 | 540.6 |
| 5% Melamine/ S-DVB | = −0.935 T + 501.23 | 0.9825 | 0.935 | 501.23 | 222.46 | 536.07 |
| 10% Melamine/ S-DVB | = −1.220 T + 584.42 | 0.9915 | 1.220 | 584.42 | 220.68 | 479.03 |
| Copolymer | Equation of (mJ/m2) | (mJ m−2 K−1) | (mJ/m2) | (mJ/m2) | (K) | |
| 1% HMU/ S-DVB | = -0.874 T + 444.68 | 0.9837 | 0.874 | 444.68 | 184.16 | 508.9 |
| 3.5% HMU/ S-DVB | = -1.096 T + 544.23 | 0.9886 | 1.096 | 544.23 | 217.52 | 496.7 |
| 5% HMU/ S-DVB | = -1.120 T + 552.77 | 0.9973 | 1.198 | 552.77 | 218.84 | 493.6 |
| 10% HMU/ S-DVB | = -1.198 T + 582.13 | 0.9973 | 1.198 | 582.13 | 224.95 | 485.9 |
| Copolymer | Equation of (mJ/m2) | (mJ m−2 K−1) | (mJ/m2) | (mJ/m2) | (K) | |
| 1% 5-FU / S-DVB | = -0.497 T + 290.95 | 0.8900 | 0.497 | 290.95 | 142.77 | 585.4 |
| 5% 5-FU / S-DVB | = -0.780 T + 424.67 | 0.9800 | 0.780 | 424.67 | 192.11 | 544.4 |
| 10% 5-FU / S-DVB | = -0.913 T + 490.08 | 0.9900 | 0.913 | 490.08 | 217.87 | 536.8 |
| Temperature T(K) | 453.15 | 458.15 | 463.15 | 468.15 | 473.15 | R² | |
|---|---|---|---|---|---|---|---|
| S-DVB copolymer | 81.54 | 76.29 | 71.17 | 66.19 | 61.33 | = -1.0104 T + 539.27 | 0.9998 |
| 1% Melamine / S-DVB | 70.11 | 68.03 | 65.99 | 64 | 62.07 | = -0.4022 T + 252.32 | 0.9998 |
| 2% Melamine / S-DVB | 124.35 | 120.53 | 116.81 | 113.18 | 109.63 | = -0.7358 T + 457.69 | 0.9998 |
| 3% Melamine / S-DVB | 54.36 | 50.34 | 46.51 | 42.87 | 39.41 | = -0.7474 T + 392.86 | 0.9991 |
| 4% Melamine / S-DVB | 84.71 | 79.24 | 73.99 | 68.97 | 64.16 | = -1.0274 T + 550.05 | 0.9994 |
| Temperature T(K) | 453.15 | 458.15 | 463.15 | 468.15 | 473.15 | Equation | R² |
| 1% 5-HMU / S-DVB | 36.89 | 35.08 | 33.04 | 31.34 | 29.61 | = -0.366 T + 202.7 | 0.9990 |
| 3.5% 5-HMU / S-DVB | 73.56 | 69.12 | 63.85 | 59.40 | 54.90 | = -0.9408 T + 499.9 | 0.9992 |
| 10% 5-HMU / S-DVB | 78.82 | 74.47 | 69.42 | 65.06 | 60.66 | = -0.9146 T + 493.28 | 0.9994 |
| Temperature T(K) | 453.15 | 458.15 | 463.15 | 468.15 | 473.15 | Equation | R² |
| 1% 5-FU / S-DVB | 23.61 | 21.01 | 18.60 | 16.35 | 14.28 | = -0.4664 T + 234.78 | 0.9980 |
| 5% 5-FU / S-DVB | 105.08 | 96.96 | 89.26 | 81.96 | 75.06 | = -1.5008 T + 784.76 | 0.9990 |
| 10% 5-FU / S-DVB | 98.84 | 93.37 | 88.12 | 83.08 | 78.23 | = -1.0302 T + 565.47 | 0.9994 |
| S-DVB | ||||
| Solvents | Equation | R² | ||
| cyclohexane | = 4×10-4 T - 0.116 | 0.9909 | ||
| benzene | = 3×10-5 T - 0.010 | 0.9911 | ||
| toluene | = -0.0022 T + 1.048 | 0.9984 | ||
| ethyl acetate | = -0.0251 T + 14.11 | 0.9999 | ||
| ethanol | = -0.180 T + 90.12 | 0.9999 | ||
| n-propanol | = -0.063 T + 30.01 | 0.9905 | ||
| i-propanol | = -0.111 T + 55.49 | 0.9999 | ||
| n-butanol | = -0.019 T + 9.124 | 0.9958 | ||
| i-butanol | = -0.054 T + 28.21 | 0.9999 | ||
| n-pentanol | = -0.0032 T + 1.766 | 0.9995 | ||
| i-pentanol | = -0.020 T + 11.360 | 0.9994 | ||
| Pyridine | = -0.065 T + 33.38 | 1 | ||
| Dichloromethane | = 0.094 T - 33.51 | 0.9906 | ||
| 1% melamine/S-DVB | ||||
| Solvents | Equation | R² | ||
| cyclohexane | = 6×10-5 T - 0.003 | 0.9999 | ||
| benzene | = -6×10-5 T + 0.035 | 1 | ||
| toluene | = -8×10-4 T + 0.437 | 0.9999 | ||
| ethyl acetate | = -0.004 T + 4.024 | 0.9999 | ||
| ethanol | = -0.205 T + 105.85 | 0.9998 | ||
| n-propanol | = -0.122 T + 60.84 | 0.9992 | ||
| i-propanol | = -0.076 T + 36.61 | 0.9966 | ||
| n-butanol | = -0.059 T + 29.78 | 0.9997 | ||
| i-butanol | = -0.030 T + 14.080 | 0.9846 | ||
| Dichloromethane | = 0.020 T + 2.037 | 0.9995 | ||
| 2% melamine/S-DVB | ||||
| Solvents | Equation | R² | ||
| cyclohexane | = -2×10-5 T + 0.013 | 0.9999 | ||
| benzene | = -3×10-5 T + 0.016 | 0.9999 | ||
| toluene | = -8×10-4 T + 0.561 | 0.9999 | ||
| ethyl acetate | = -0.004 T + 3.351 | 0.9999 | ||
| ethanol | = -0.145 T + 70.16 | 0.9966 | ||
| n-propanol | = -0.136 T + 66.86 | 0.9987 | ||
| i-propanol | = -0.147 T + 99.70 | 0.9999 | ||
| n-butanol | = -0.088 T + 43.58 | 0.9989 | ||
| i-butanol | = -0.097 T + 50.92 | 1 | ||
| Dichloromethane | = 0.037 T - 1.415 | 0.9995 | ||
| 3% melamine/S-DVB | ||||
| Solvents | Equation | R² | ||
| cyclohexane | = 2×10-4 T - 0.050 | 0.9977 | ||
| benzene | = 0.0012 T - 0.452 | 0.9969 | ||
| toluene | = -0.0017 T + 0.825 | 0.9978 | ||
| ethyl acetate | = 0.020 T - 4.373 | 0.9979 | ||
| ethanol | = -0.662 T + 325.2 | 0.9999 | ||
| n-propanol | = -0.409 T + 197.56 | 0.999 | ||
| i-propanol | = -0.325 T + 156.67 | 0.9985 | ||
| n-butanol | = -0.263 T + 126.86 | 0.9991 | ||
| i-butanol | = -0.201 T + 96.57 | 0.9984 | ||
| Dichloromethane | = -0.022 T + 15.682 | 0.9996 | ||
| 4% melamine/S-DVB | ||||
| Solvents | Equation | R² | ||
| cyclohexane | = 0.002 T - 0.587 | 0.9971 | ||
| benzene | = 0.002 T - 0.497 | 0.9978 | ||
| toluene | = 0.008 T - 2.192 | 0.9983 | ||
| ethyl acetate | = -0.007 T + 4.91 | 0.9992 | ||
| ethanol | = -0.371 T + 195.72 | 0.9998 | ||
| n-propanol | = -0.253 T + 139.54 | 0.9995 | ||
| i-propanol | = -0.210 T + 111.55 | 0.9997 | ||
| n-butanol | = -0.154 T + 80.89 | 0.9997 | ||
| i-butanol | = -0.124 T + 61.62 | 1 | ||
| Dichloromethane | = 0.057 T - 11.874 | 0.9973 | ||
| 1% 5-HMU/S-DVB | ||||
| Solvents | Equation | R² | ||
| benzene | = 3×10-5 T + 0.008 | 0.9914 | ||
| toluene | = -0.043 T + 24.09 | 0.9891 | ||
| ethyl acetate | = 0.036 T - 3.586 | 0.9981 | ||
| ethanol | = -0.292 T + 140.76 | 0.9961 | ||
| i-propanol | = -0.090 T + 42.2 | 0.9287 | ||
| n-butanol | = -0.210 T + 103.05 | 0.9992 | ||
| i-butanol | = -0.124 T + 60.03 | 0.9973 | ||
| i-pentanol | = -0.121 T + 60.29 | 0.9998 | ||
| Dichloromethane | = -0.005 T + 4.348 | 0.9983 | ||
| 3.5% 5-HMU/S-DVB | ||||
| Solvents | Equation | R² | ||
| benzene | = 4×10-4 T - 0.156 | 0.9935 | ||
| toluene | = -4×10-4 T + 0.542 | 0.9988 | ||
| ethyl acetate | = 0.183 T - 58.14 | 0.9938 | ||
| ethanol | = -0.248 T + 130.23 | 0.9997 | ||
| i-propanol | = -0.139 T + 82.08 | 0.9985 | ||
| n-butanol | = -0.1274 T + 72.60 | 0.9983 | ||
| i-butanol | = -0.105 T + 62.56 | 0.998 | ||
| i-pentanol | = 0.047 T + 14.09 | 0.9983 | ||
| Dichloromethane | = -0.0070 T + 4.119 | 0.9998 | ||
| 10% 5-HMU/S-DVB | ||||
| Solvents | Equation | R² | ||
| benzene | = 0.0017 T - 0.588 | 0.9942 | ||
| toluene | = 0.013 T - 3.856 | 0.9949 | ||
| ethyl acetate | = 0.183 T - 59.09 | 0.9945 | ||
| ethanol | = -0.150 T + 113.86 | 0.9995 | ||
| i-propanol | = 0.154 T - 9.398 | 0.995 | ||
| n-butanol | = -0.097 T + 52.92 | 0.9993 | ||
| i-butanol | = 0.162 T - 21.42 | 0.996 | ||
| i-pentanol | = -0.074 T + 37.042 | 1 | ||
| Dichloromethane | = -0.008 T + 4.491 | 0.9999 | ||
| 1% 5-FU/S-DVB | ||||
| Solvents | Equation | R² | ||
| benzene | = 0.0016 T - 0.668 | 0.9905 | ||
| toluene | = 0.015 T - 5.243 | 0.9945 | ||
| ethyl acetate | = -0.020 T + 30.52 | 0.987 | ||
| ethanol | = 0.882 T - 276.34 | 0.9948 | ||
| i-propanol | = -0.021 T + 76.68 | 0.8954 | ||
| n-butanol | = 0.862 T - 304.64 | 0.9947 | ||
| i-butanol | = 0.965 T - 334.37 | 0.995 | ||
| i-pentanol | = -0.520 T + 259.83 | 0.9995 | ||
| Dichloromethane | = 0.001 T + 0.671 | 0.9858 | ||
| 5% 5-FU/S-DVB | ||||
| Solvents | Equation | R² | ||
| benzene | = 2×10-4 T - 0.074 | 0.9967 | ||
| toluene | = 0.016 T - 4.833 | 0.9979 | ||
| ethyl acetate | = 0.003 T + 19.418 | 0.9717 | ||
| ethanol | = -0.175 T + 84.021 | 0.9983 | ||
| i-propanol | = -0.175 T + 116.52 | 0.9974 | ||
| n-butanol | = -0.219 T + 121.67 | 0.9985 | ||
| i-butanol | = 0.160 T - 9.321 | 0.9997 | ||
| i-pentanol | = -0.003 T + 31.15 | 0.9386 | ||
| Dichloromethane | = -0.0002 T + 1.280 | 0.9714 | ||
| 10% 5-FU/S-DVB | ||||
| Solvents | Equation | R² | ||
| benzene | = 1×10-4 T - 0.036 | 0.9986 | ||
| toluene | = 0.063 T - 17.82 | 0.9988 | ||
| ethyl acetate | = -0.073 T + 65.639 | 0.9991 | ||
| ethanol | = -0.2547 T + 124.57 | 0.9992 | ||
| i-propanol | = -0.326 T + 211.43 | 0.9992 | ||
| n-butanol | = -0.318 T + 176.42 | 0.9996 | ||
| i-butanol | = -0.192 T + 93.24 | 0.9989 | ||
| i-pentanol | = -0.347 T + 213.6 | 0.9999 | ||
| Dichloromethane | = 0.002 T - 0.057 | 0.9981 | ||
| S-DVB Copolymer | |||||
| Solvents | (K) | R² | |||
| n-hexane | = -1.07 T + 513.05 | 1.07 | 513.05 | 477.57 | 0.9972 |
| n-heptane | = -0.92 T + 454.45 | 0.92 | 454.45 | 495.64 | 0.9858 |
| n-octane | = -0.95 T + 475.17 | 0.95 | 475.17 | 502.61 | 0.9804 |
| n-nonane | = -0.99 T + 498.93 | 0.99 | 498.93 | 506.17 | 0.9778 |
| Benzene | = -1.10 T + 550.93 | 1.10 | 550.93 | 502.67 | 0.9812 |
| Toluene | = -1.29 T + 664.32 | 1.29 | 664.32 | 514.42 | 0.9754 |
| Ethyl acetate | = -1.29 T + 669.43 | 1.29 | 669.43 | 518.38 | 0.9859 |
| Ethanol | = -1.85 T + 945.32 | 1.85 | 945.32 | 510.21 | 0.9932 |
| i-Propanol | = -1.74 T + 891.1 | 1.74 | 891.1 | 511.04 | 0.9905 |
| Dichloromethane | = -1.23 T + 654.39 | 1.23 | 654.39 | 531.03 | 0.9921 |
| 1% Melamine / S-DVB Copolymer | |||||
| Solvents | R² | ||||
| n-hexane | = -1.00 T + 480.8 | 1.00 | 480.8 | 479.55 | 0.9967 |
| n-heptane | = -0.66 T + 335.68 | 0.65 | 335.68 | 512.65 | 0.9999 |
| n-octane | = -0.59 T + 317.85 | 0.60 | 317.85 | 531.17 | 0.9999 |
| n-nonane | = -0.58 T + 316.17 | 0.58 | 316.17 | 542.69 | 0.9999 |
| Benzene | = -0.71 T + 375.92 | 0.71 | 375.92 | 531.94 | 0.9999 |
| Toluene | = -0.57 T + 335.24 | 0.57 | 335.24 | 585.37 | 0.9999 |
| Ethyl acetate | = -0.58 T + 319.32 | 0.58 | 319.32 | 554.47 | 0.9999 |
| Ethanol | = -0.64 T + 368.46 | 0.64 | 368.46 | 574.46 | 0.9999 |
| i-Propanol | = -1.21 T + 668.61 | 1.21 | 668.61 | 553.39 | 0.9999 |
| Dichloromethane | = -1.34 T + 662.71 | 1.34 | 662.71 | 494.38 | 0.9997 |
| 2% Melamine / S-DVB Copolymer | |||||
| Solvents | R² | ||||
| n-hexane | = -0.78 T + 372.02 | 0.78 | 372.02 | 477.93 | 0.9946 |
| n-heptane | = -0.52 T + 265.41 | 0.52 | 265.41 | 506.89 | 0.994 |
| n-octane | = -0.50 T + 260.01 | 0.50 | 260.01 | 520.64 | 0.9894 |
| n-nonane | = -0.50 T + 263.73 | 0.50 | 263.73 | 528.73 | 0.9864 |
| Benzene | Wa = -0.59 T + 308.05 | 0.59 | 308.05 | 519.30 | 0.9904 |
| Toluene | = -0.58 T + 324.78 | 0.58 | 324.78 | 563.95 | 0.9789 |
| Ethyl acetate | = -0.59 T + 334.41 | 0.59 | 334.41 | 568.34 | 0.9892 |
| Ethanol | = -1.5 T + 764.61 | 1.50 | 764.61 | 510.52 | 0.9983 |
| i-Propanol | = -1.15 T + 694.21 | 1.15 | 694.21 | 602.30 | 0.9964 |
| Dichloromethane | = -0.85 T + 502.92 | 0.85 | 502.92 | 590.42 | 0.9978 |
| 3% Melamine / S-DVB Copolymer | |||||
| Solvents | R² | ||||
| n-hexane | = -0.88 T + 423.69 | 0.88 | 423.69 | 479.34 | 0.9952 |
| n-heptane | = -0.60 T + 307.28 | 0.60 | 307.28 | 509.75 | 0.9954 |
| n-octane | = -0.56 T + 296.17 | 0.56 | 296.17 | 525.68 | 0.9917 |
| n-nonane | = -0.56 T + 297.66 | 0.56 | 297.66 | 535.36 | 0.9889 |
| Benzene | = -0.67 T + 355.5 | 0.67 | 355.5 | 529.33 | 0.9926 |
| Toluene | = -0.65 T + 363.83 | 0.65 | 363.83 | 557.68 | 0.9822 |
| Ethyl acetate | = -0.69 T + 392.76 | 0.69 | 392.76 | 566.75 | 0.992 |
| Ethanol | = -2.05 T + 1049.6 | 2.05 | 1049.6 | 511.88 | 0.9991 |
| i-Propanol | = -1.72 T + 875.58 | 1.72 | 875.58 | 510.42 | 0.9983 |
| Dichloromethane | = -1.12 T + 577.52 | 1.12 | 577.52 | 516.75 | 0.9985 |
| 4% Melamine / S-DVB Copolymer | |||||
| Solvents | R² | ||||
| n-hexane | = -0.96 T + 460.73 | 0.96 | 460.73 | 479.28 | 0.9952 |
| n-heptane | = -0.63 T + 323.74 | 0.63 | 323.74 | 511.52 | 0.9969 |
| n-octane | = -0.58 T + 308.83 | 0.58 | 308.83 | 528.91 | 0.995 |
| n-nonane | = -0.57 T + 308.54 | 0.57 | 308.54 | 539.59 | 0.9934 |
| Benzene | = -0.71 T + 377.26 | 0.71 | 377.26 | 535.04 | 0.9956 |
| Toluene | = -0.67 T + 394.99 | 0.66 | 394.99 | 594.24 | 0.9896 |
| Ethyl acetate | = -0.73 T + 407.05 | 0.73 | 407.05 | 557.37 | 0.9956 |
| Ethanol | = -1.78 T + 950.98 | 1.78 | 950.98 | 535.58 | 0.9993 |
| i-Propanol | = -1.47 T + 797.06 | 1.47 | 797.06 | 543.18 | 0.9986 |
| Dichloromethane | = -1.17 T + 638 | 1.17 | 638 | 545.21 | 0.9988 |
| 1% 5-HMU / S-DVB Copolymer | |||||
| Solvents | R² | ||||
| n-hexane | = -0.79 T + 377.09 | 0.79 | 377.09 | 478.42 | 0.9996 |
| n-heptane | = -0.59 T + 297.17 | 0.59 | 297.17 | 503.00 | 0.9969 |
| n-octane | = -0.58 T + 298.07 | 0.58 | 298.07 | 514.00 | 0.9949 |
| n-nonane | = -0.59 T + 306.26 | 0.59 | 306.26 | 520.14 | 0.9939 |
| Benzene | = -0.69 T + 355.57 | 0.69 | 355.57 | 512.20 | 0.9956 |
| Toluene | = -1.01 T + 530.27 | 1.01 | 530.27 | 523.16 | 0.9969 |
| Ethyl acetate | = -1.08 T + 552.6 | 1.08 | 552.6 | 514.14 | 0.9991 |
| Ethanol | = -1.23 T + 617.99 | 1.23 | 617.99 | 501.37 | 0.9969 |
| i-Propanol | = -0.98 T + 495.06 | 0.98 | 495.06 | 507.75 | 0.9897 |
| Dichloromethane | = -1.26 T + 619.03 | 1.26 | 619.03 | 490.52 | 0.9023 |
| 3.5% 5-HMU / S-DVB Copolymer | |||||
| Solvents | R² | ||||
| n-hexane | = -0.80 T + 380.26 | 0.80 | 380.26 | 477.77 | 0.999 |
| n-heptane | = -0.66 T + 326.22 | 0.66 | 326.22 | 497.51 | 0.997 |
| n-octane | = -0.67 T + 337.84 | 0.67 | 337.84 | 505.37 | 0.9958 |
| n-nonane | = -0.69 T + 353 | 0.69 | 353 | 509.53 | 0.9954 |
| Benzene | = -0.78 T + 397.1 | 0.78 | 397.1 | 508.39 | 0.996 |
| Toluene | = -0.89 T + 471.28 | 0.89 | 471.28 | 526.98 | 0.9955 |
| Ethyl acetate | = -0.97 T + 567.37 | 0.97 | 567.37 | 582.46 | 0.9976 |
| Ethanol | = -1.66 T + 862.63 | 1.66 | 862.63 | 520.85 | 0.9992 |
| i-Propanol | = -1.49 T + 795.55 | 1.490 | 795.55 | 533.78 | 0.9988 |
| Dichloromethane | = -0.99 T + 495.17 | 0.986 | 495.17 | 502.00 | 0.9989 |
| 10% 5-hydroxy-6-methyluracil / S-DVB Copolymer | |||||
| Solvents | R² | ||||
| n-hexane | = -0.76 T + 361.98 | 0.76 | 361.98 | 476.48 | 0.9998 |
| n-heptane | = -0.70 T + 344.16 | 0.70 | 344.16 | 490.89 | 0.9996 |
| n-octane | = -0.75 T + 371.62 | 0.75 | 371.62 | 495.49 | 0.9993 |
| n-nonane | = -0.80 T + 396.43 | 0.80 | 396.43 | 497.78 | 0.9991 |
| Benzene | = -0.87 T + 438.65 | 0.87 | 438.65 | 502.58 | 0.9994 |
| Toluene | = -1.08 T + 562.98 | 1.08 | 562.98 | 522.63 | 0.9979 |
| Ethyl acetate | = -1.02 T + 585.03 | 1.02 | 585.03 | 573.90 | 0.9992 |
| Ethanol | = -1.71 T + 931.89 | 1.71 | 931.89 | 544.61 | 0.9998 |
| i-Propanol | = -1.54 T + 878.5 | 1.54 | 878.5 | 569.09 | 0.9995 |
| Dichloromethane | = -1.01 T + 503.78 | 1.01 | 503.78 | 499.09 | 0.9998 |
| 1% 5-Fluouracil / S-DVB Copolymer | |||||
| Solvents | R² | ||||
| n-hexane | = -0.85 T + 409.22 | 0.85 | 409.22 | 480.47 | 0.9991 |
| n-heptane | = -0.53 T + 276.42 | 0.53 | 276.42 | 517.25 | 0.9892 |
| n-octane | = -0.47 T + 253.35 | 0.47 | 253.35 | 540.65 | 0.9742 |
| n-nonane | = -0.44 T + 247.09 | 0.44 | 247.09 | 556.26 | 0.9622 |
| Benzene | = -0.56 T + 301.56 | 0.56 | 301.56 | 540.91 | 0.9769 |
| Toluene | = -0.48 T + 295.44 | 0.48 | 295.44 | 614.09 | 0.9325 |
| Ethyl acetate | = -0.92 T + 507.43 | 0.92 | 507.43 | 554.51 | 0.9892 |
| Ethanol | = -1.32 T + 753.74 | 1.32 | 753.74 | 569.94 | 0.9949 |
| i-Propanol | = -1.29 T + 716.03 | 1.29 | 716.03 | 556.01 | 0.9931 |
| Dichloromethane | = -0.85 T + 432.53 | 0.85 | 432.53 | 508.32 | 0.997 |
| 5% 5-Fluouracil / S-DVB Copolymer | |||||
| Solvents | R² | ||||
| n-hexane | = -0.91 T + 438.27 | 0.91 | 438.27 | 479.61 | 0.9983 |
| n-heptane | = -0.60 T + 309.29 | 0.60 | 309.29 | 512.15 | 0.9978 |
| n-octane | = -0.55 T + 293.5 | 0.55 | 293.5 | 530.26 | 0.9956 |
| n-nonane | = -0.54 T + 292.32 | 0.54 | 292.32 | 541.53 | 0.9941 |
| Benzene | = -0.6554 T + 347.96 | 0.6554 | 347.96 | 530.91 | 0.9961 |
| Toluene | = -0.6949 T + 415.71 | 0.6949 | 415.71 | 598.23 | 0.9927 |
| Ethyl acetate | = -1.2143 T + 693.27 | 1.2143 | 693.27 | 570.92 | 0.9986 |
| Ethanol | = -1.7361 T + 880.53 | 1.7361 | 880.53 | 507.19 | 0.9993 |
| i-Propanol | = -1.7287 T + 963.71 | 1.7287 | 963.71 | 557.48 | 0.9991 |
| Dichloromethane | = -0.9861 T + 507.27 | 0.9861 | 507.27 | 514.42 | 0.9991 |
| 10% 5-Fluouracil / S-DVB Copolymer | |||||
| Solvents | R² | ||||
| n-hexane | = -0.94 T + 451.85 | 0.94 | 451.85 | 479.67 | 0.9976 |
| n-heptane | = -0.64 T + 327.09 | 0.64 | 327.09 | 510.76 | 0.9992 |
| n-octane | = -0.59 T + 313.4 | 0.59 | 313.4 | 527.52 | 0.9986 |
| n-nonane | = -0.58 T + 313.9 | 0.58 | 313.9 | 537.68 | 0.9981 |
| Benzene | = -0.70 T+ 369.84 | 0.70 | 369.84 | 528.04 | 0.9987 |
| Toluene | = -0.77 T+ 484.8 | 0.77 | 484.8 | 627.41 | 0.9978 |
| Ethyl acetate | = -1.28 T+ 744.91 | 1.28 | 744.91 | 581.55 | 0.9996 |
| Ethanol | = -1.77T+ 912.74 | 1.77 | 912.74 | 515.38 | 0.9998 |
| i-Propanol | = -1.80 T+ 1031.2 | 1.80 | 1031.2 | 572.89 | 0.9997 |
| Dichloromethane | = -0.93 T+ 478.52 | 0.93 | 478.52 | 514.04 | 0.9993 |
| S-DVB Copolymer | ||||
| Solvents | Equation (in mJ m-2K-1) | R² | Equation (in mJ m-2) | R² |
| n-hexane | = 0.076 q (Mela) + 0.65 | 0.9757 | = 46.92 q (Mela) + 277.19 | 0.9948 |
| n-heptane | = 0.033 q (Mela) + 0.615 | 0.9945 | = 33.70 q (Mela) + 196.20 | 0.9699 |
| n-octane | = 0.024 q (Mela) + 0.485 | 0.9931 | = 24.44 q (Mela) + 215.01 | 0.9701 |
| n-nonane | = 0.016 q (Mela) + 0.51 | 0.9143 | = 22.05 q (Mela) + 223.96 | 0.9647 |
| Benzene | = 0.065 q (Mela) + 0.46 | 0.9837 | = 34.78 q (Mela) + 242.54 | 0.9821 |
| Toluene | = 0.031 q (Mela) + 0.545 | 0.9468 | = 30.83 q (Mela) + 270.14 | 0.9852 |
| Ethyl acetate | = 0.055 q (Mela) + 0.51 | 0.9181 | = 32.15 q (Mela) + 283.00 | 0.9313 |
| Ethanol | = 0.235 q (Mela) + 0.97 | 0.9612 | = 193.26 q (Mela) + 225.28 | 0.9515 |
| i-Propanol | = 0.146 q (Mela) + 1.04 | 0.9769 | = 101.67 q (Mela) + 517.19 | 0.9238 |
| Dichloromethane | = -0.09 q (Mela) + 1.41 | 0.962 | = 60.23 q (Mela) + 394.56 | 0.9885 |
| S-DVB/5-HMU | ||||
| Solvents | Equation (in mJ m-2K-1) | R² | Equation (in mJ m-2) | R² |
| n-hexane | = -0.003 q (5-HMU) + 0.793 | 0.9963 | = 1.15 q (5-HMU) + 376.06 | 0.9992 |
| n-heptane | = 0.011 q (5-HMU) + 0.592 | 0.9106 | = 3.98 q (5-HMU) + 306.11 | 0.9177 |
| n-octane | = 0.018 q (5-HMU) + 0.582 | 0.9209 | = 7.58 q (5-HMU) + 299.23 | 0.9137 |
| n-nonane | = 0.022 q (5-HMU) + 0.589 | 0.9508 | = 9.35 q (5-HMU) + 306.71 | 0.9276 |
| Benzene | = 0.019 q (5-HMU) + 0.689 | 0.9382 | = 8.66 q (5-HMU) + 355.24 | 0.9383 |
| Toluene | = 0.02 q (5-HMU) + 0.88 | 0.9999 | = 3.55 q (5-HMU) + 527.96 | 0.9914 |
| Ethyl acetate | = -0.006 q (5-HMU) + 1.080 | 0.9382 | = 3.43 q (5-HMU) + 551.78 | 0.9606 |
| Ethanol | = 0.050 q (5-HMU) + 1.233 | 0.9261 | = 33.10 q (5-HMU) + 610.84 | 0.9582 |
| i-Propanol | = 0.033 q (5-HMU) + 1.205 | 0.9999 | = 39.70 q (5-HMU) + 497.81 | 0.9249 |
| Dichloromethane | = -0.026 q (5-HMU) + 1.254 | 0.9008 | = -12.08 q (5-HMU) + 620.49 | 0.9479 |
| S-DVB/5-FU | ||||
| Solvents | Equation (in mJ m-2K-1) | R² | Equation (in mJ m-2) | R² |
| n-hexane | = 0.010 q (5-FU) + 0.848 | 0.9368 | = 4.65 q (5-FU) + 408.29 | 0.9286 |
| n-heptane | = 0.012 q (5-FU) + 0.526 | 0.9523 | = 5.55 q (5-FU) + 274.69 | 0.9462 |
| n-octane | = 0.013 q (5-FU) + 0.467 | 0.9368 | = 6.56 q (5-FU) + 251.75 | 0.9357 |
| n-nonane | = 0.015 q (5-FU) + 0.439 | 0.9089 | = 7.30 q (5-FU) + 245.52 | 0.9311 |
| Benzene | = 0.015 q (5-FU) + 0.557 | 0.9286 | = 7.46 q (5-FU) + 300.03 | 0.9296 |
| Toluene | = 0.032 q (5-FU) + 0.478 | 0.9026 | = 20.74 q (5-FU) + 288.02 | 0.9529 |
| Ethyl acetate | = 0.026 q (5-FU) + 1.037 | 0.9126 | = 25.73 q (5-FU) + 511.32 | 0.8628 |
| Ethanol | = 0.049 q (5-FU) + 1.312 | 0.9243 | = 11.00 q (5-FU) + 809.76 | 0.9292 |
| i-Propanol | = 0.056 q (5-FU) + 1.284 | 0.9141 | = 23.48 q (5-FU) + 811.75 | 0.9257 |
| Dichloromethane | = 0.019 q (5-FU) + 0.892 | 0.9999 | = 5.08 q (5-FU) + 428.94 | 0.9898 |
| Copolymer | R² | ||
|---|---|---|---|
| S-DVB Copolymer | = 527.12 - 23.502 | 527.12 | 0.9923 |
| 1% Melamine / S-DVB Copolymer | = 476.71 + 42.251 | 476.71 | 0.9672 |
| 2% Melamine / S-DVB Copolymer | = 543.47 - 1.841 | 543.47 | 0.9596 |
| 3% Melamine / S-DVB Copolymer | = 500.3 + 18.342 | 500.3 | 0.9957 |
| 4% Melamine / S-DVB Copolymer | = 532.74 + 1.972 | 532.74 | 0.9882 |
| 1% 5-HMU / S-DVB Copolymer | = 494.38 + 9.860 | 494.38 | 0.9917 |
| 3.5% 5-HMU / S-DVB Copolymer | = 546.19 - 25.452 | 546.19 | 0.9838 |
| 10% 5-HMU / S-DVB Copolymer | = 609.06 - 86.224 | 609.06 | 0.9884 |
| 1% 5-Fluouracil / S-DVB Copolymer | = 558.33 - 11.407 | 558.33 | 0.9793 |
| 5% 5-Fluouracil / S-DVB Copolymer | = 534.46 - 0.318 | 534.46 | 0.9803 |
| 10% 5-Fluouracil / S-DVB Copolymer | = 556.11 - 14.185 | 556.11 | 0.973 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





