Submitted:
01 May 2025
Posted:
08 May 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction-Early History and Modern Developments
- In the first step, the basic physical/empirical entities are postulated, such as the timelike worldlines for freely falling massive particles, the lightlike wordlines of light rays, and radar echoes between massive particle wordlines. These empirical elements provide enough structure to define a system of coordinates and allow for the construction of a differentiable structure on the spacetime set M, turning it into a smooth manifold.
- The conformal structure is established by requiring that, at each point in spacetime, the set of all possible directions (i.e. tangent vectors) splits into two components when the directions corresponding to massless (lightlike) trajectories are removed. This splitting reflects the causal distinction between future and past. Additionally, in a sufficiently small neighborhood V around the worldline of a massive particle, for any point not lying on the particle’s path, the function that maps p to the product of the radar emission time and reception time , i.e. , must be at least twice differentiable.
- Imposing that through each point in spacetime, and for each timelike direction, there exists one unique timelike (massive) trajectory passing through that point, results in a projective structure. Each of these trajectories must admit a parametrization such that, in local coordinates near the point, the motion satisfies . This expresses the fact that particles move along straight lines in free fall.
- In the final step the compatibility between the conformal and projective structures is demanded. In particular, light rays must be special cases of particle geodesics in the limit of zero mass. This determines the metric up to a conformal factor, which leads to a Weyl structure. Through some technical steps (see .), eliminating the second clock effect leads to a Lorentzian structure, i.e. a pseudo-Riemannian manifold.
2. Fundamentals of Finsler Geometry
- (i)
- is on ,
- (ii)
- is 1-positive homogeneous: , for all and ,
- (iii)
- for each , the Hessian matrix (29) is positive defined in .
3. Osculating Type Cosmological Models
3.1. Mathematical Foundations of the Finslerian Cosmologies
3.1.1. Kropina and Geometries
3.1.2. The Barthel Connection
3.1.3. The Y-Osculating Riemann Geometry
The Case of the Metrics
The Curvature Tensor
3.2. Building Cosmological Models in Geometries
The Universe Is Homogeneous and Isotropic
The Riemannian Metric Is the FLRW Metric
The Finsler Metric Depends on only
The 1-Form b Has Vanishing Space-like Components
Matter Moves Along the Hubble Flow
The Matter Content of the Universe is a Perfect Fluid
Geometric Quantities
- (iii)
- (iv)
- ;
- (v)
- ;
- (vi)
Gravitational Field Equations
Flowchart of the Algorithmic Construction of Osculating Barthel Type Finslerian Gravitational Theories
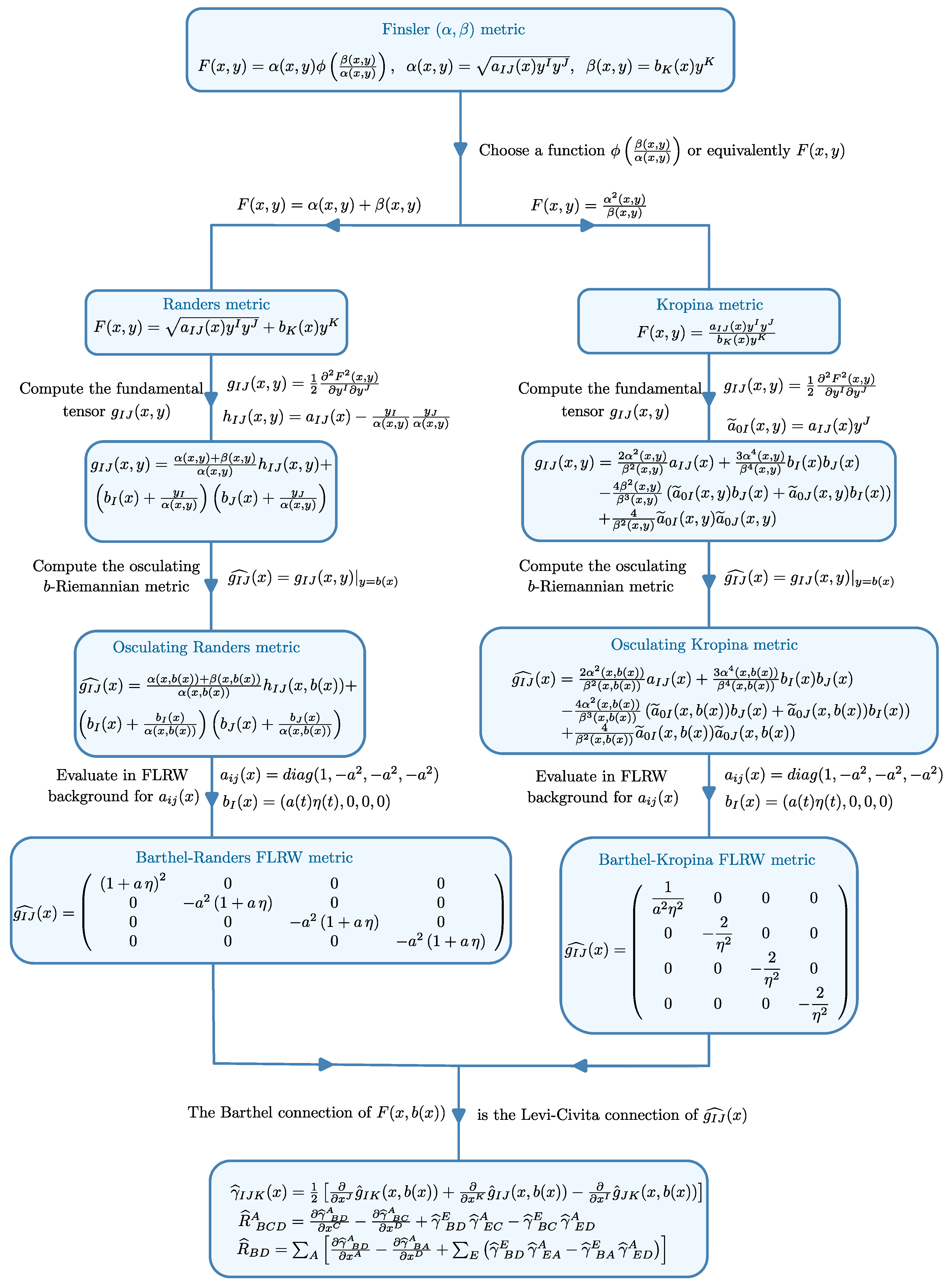
3.3. Barthel-Randers Cosmology
The Energy Conservation Equation
3.4. Barthel-Kropina Cosmology
Energy Balance Equation
The General Relativistic Limit
3.5. Conformal Barthel-Kropina Cosmology
The Generalized Friedmann Equations
3.6. Thermodynamic Interpretation of the Cosmologies
3.6.1. Irreversible Thermodynamics and Matter Creation
Particle Balance Equations
The Entropy Flux
The Creation Pressure
3.6.2. Application: Particle Creation in Barthel-Randers Cosmology
Creation Pressure in Barthel-Randers Cosmology
The Particle Creation Rate
The Matter Temperature
3.6.3. Creation of Exotic Matter
4. Cosmological Implications of Barthel Randers and Barthel-Kropina Models
4.1. Specific Cosmological Models
- Linear model: ,
- Logarithmic model: ,
- Exponential model: .
4.2. Methodology and Datasets
-
Cosmic Chronometers : In this study, we utilize the Hubble measurements extracted based on the differential age approach, as described in [155]. This technique leverages passively evolving massive galaxies, which formed at redshifts around , enabling a direct and model-independent determination of the Hubble parameter using the relationship . This method significantly reduces the reliance on astrophysical assumptions [156,157].For our analysis, we use 15 Hubble measurements selected from the 31 Hubble measurements used in [158], which cover a redshift range from . We define the likelihood function for the CC dataset using the following expression: with . Here, is the theoretical Hubble parameter, calculated at each redshift value using the model parameters , while represents the corresponding observed value of the Hubble parameter at the redshift. Following [159], we use the full covariance matrix , which takes into account both statistical and systematic uncertainties in the observations. The inverse of this covariance matrix, , is employed to incorporate these uncertainties into the likelihood function.
- Type Ia supernova : We also use the Pantheon+ dataset without the SHOES calibration, which consists of light curves from 1701 Type Ia Supernovae (SNe Ia) covering a redshift range of [160]. To analyze this data, we adopt the likelihood function described in [161], which incorporates the total covariance matrix, , that includes both statistical () and systematic () uncertainties [162]. The likelihood function is given by: where represents the residual vector, defined as the difference between the observed and theoretical distance moduli: , where Here, is the inverse of the total covariance matrix. The model-predicted distance modulus is calculated as: where the luminosity distance in a flat FLRW Universe is given by: Here, c is the speed of light, and is the Hubble parameter. This formulation highlights the degeneracy between the nuisance parameter and the Hubble constant .
- Baryon Acoustic Oscillation : In our analysis, we also incorporate the most recent Baryon Acoustic Oscillation (BAO) measurements from the Dark Energy Spectroscopic Instrument (DESI) Data Release 2 (DR2) [163]. The BAO scale is determined by the sound horizon at the drag epoch, , given by: where is a function of the baryon to photon densities ratio, and is the Hubble parameter. In a flat CDM model, Mpc [63]. However, in this study, we treat as a free parameter, allowing late-time observations to constrain the corresponding model parameters [164,165,166,167,168]. For our analysis, we compute the following cosmological distance measures: the Hubble distance, , the comoving angular diameter distance, , and the volume-averaged distance, , given by: Here, c denotes the speed of light in vacuum. To constrain each model parameter, we analyze the following ratios: We also use the ratio , which serves as an additional constraint independent of the sound horizon scale . The likelihood function for the BAO data is given by: where the residuals are defined as: with In our case, the statistical covariance matrix has been considered generally to be diagonal, with elements corresponding to the squared observational uncertainties and defined as : The overall BAO likelihood function is then constructed as the product of the individual likelihoods:
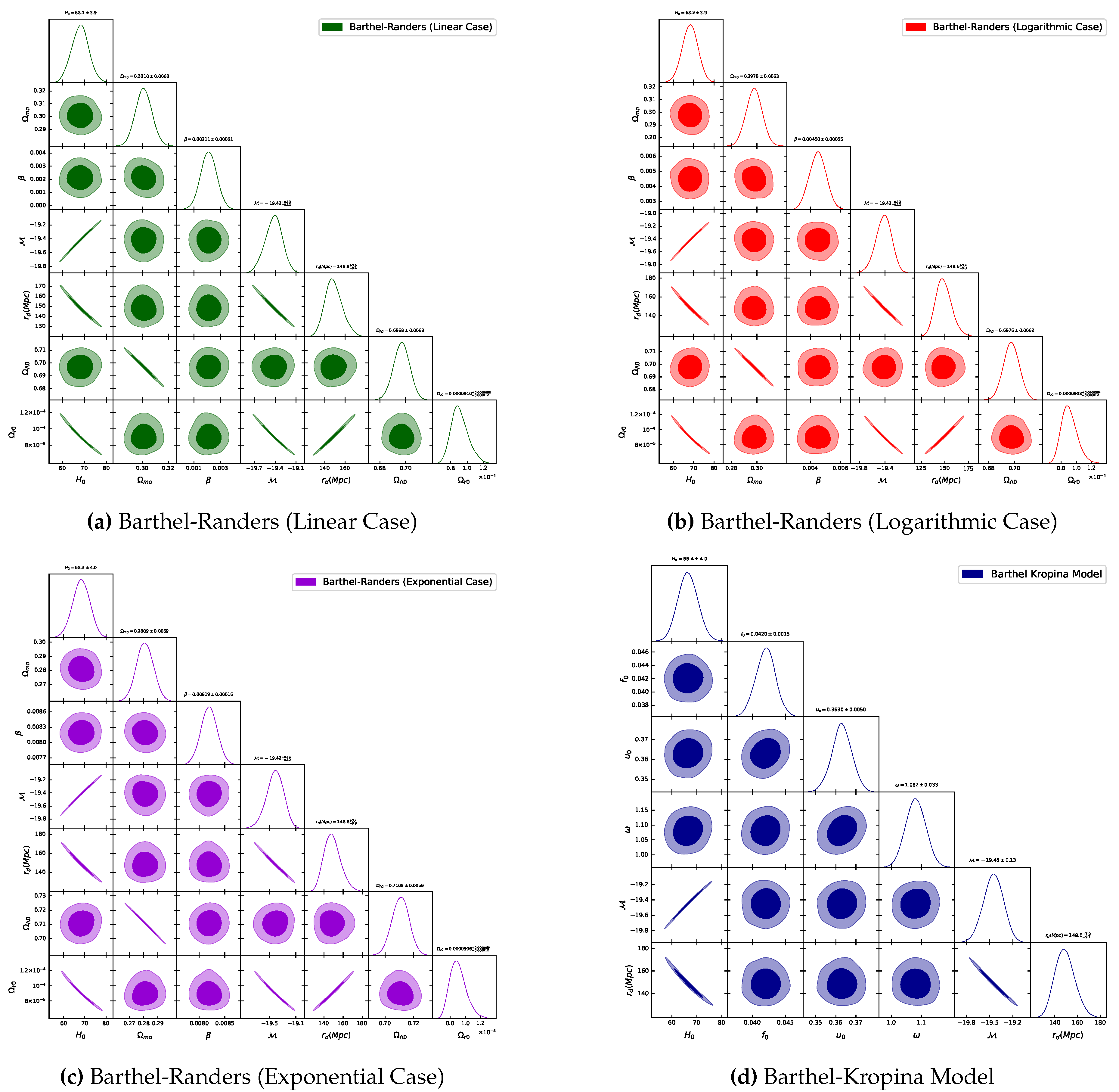
| Cosmological Models | Parameter | JOINT |
|---|---|---|
| CDM Model | ||
| BR (Linear Case) | ||
| BR (Logarithmic Case) | ||
| BR (Exponential Case) | ||
| Barthel-Kropina Model | ||
5. Comparing Barthel-Randers, Barthel-Kropina and CDM Cosmological Models
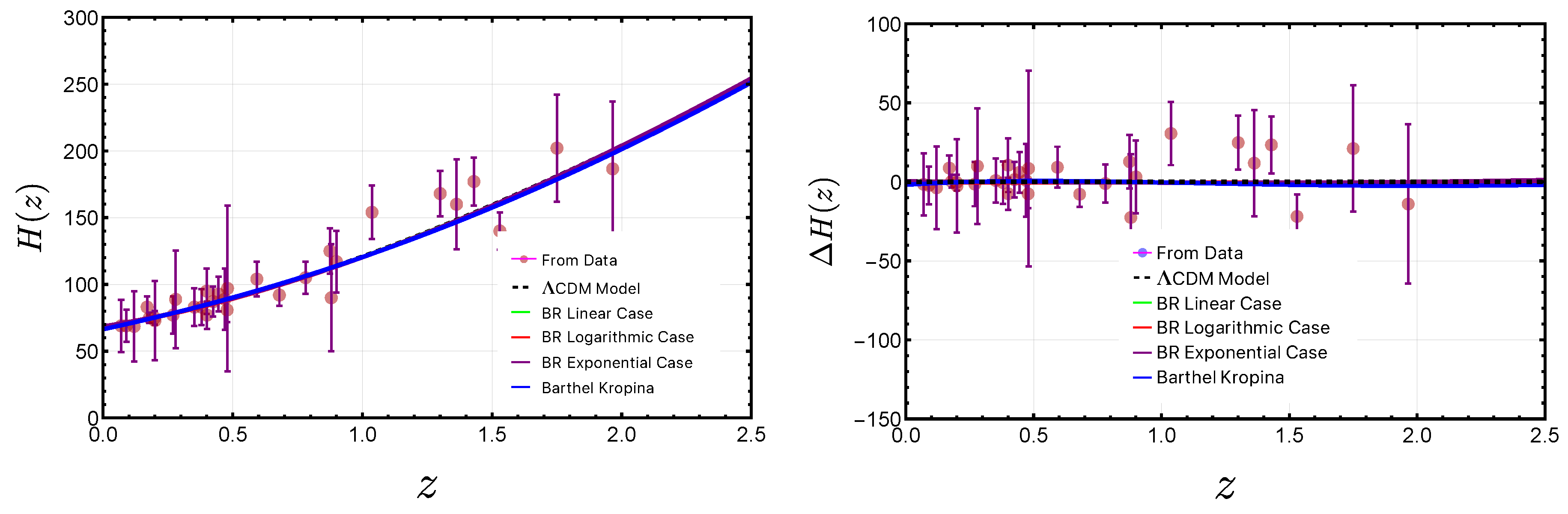
5.1. Evolution of the Hubble Parameter and Hubble Residual
5.2. Cosmographic Analysis of Barthel-Randers and Barthel-Kropina Models
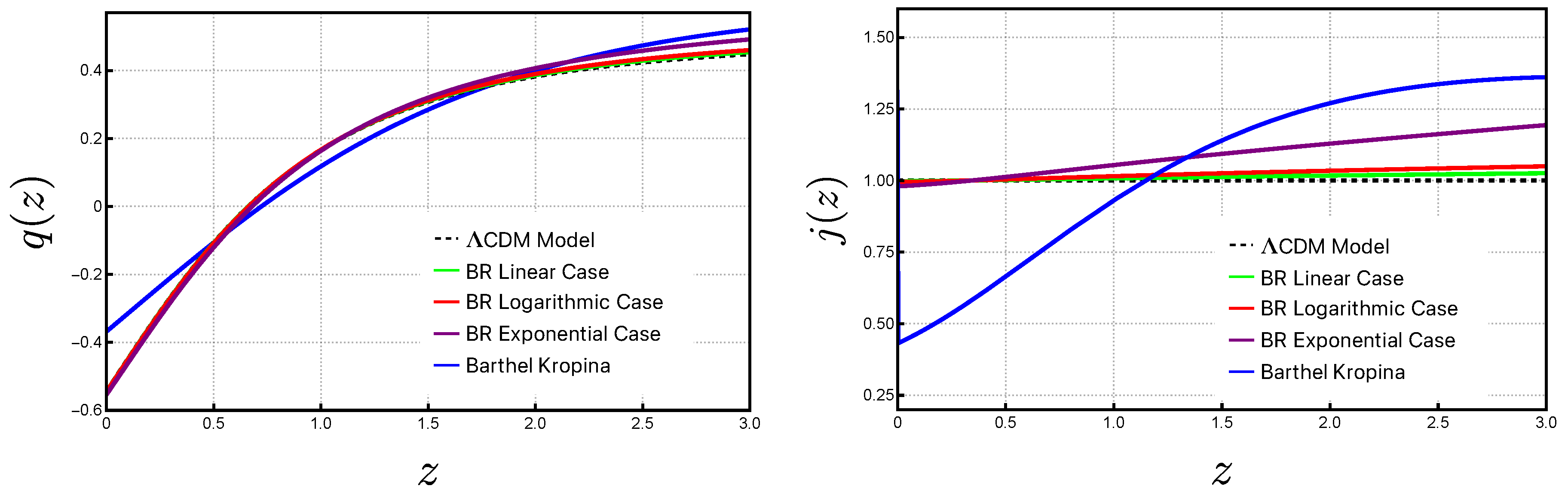
5.2.1. Deceleration Parameter and Jerk Parameter
5.3. Statistical Assessment of Barthel-Randers and Barthel-Kropina Models
5.4. Goodness of Fit: and
5.4.1. Model Comparison Using AIC and BIC
5.4.2. Relative Comparison: AIC and BIC
- : Comparable support.
- : Considerably less support.
- : Strongly disfavored.
- : Weak evidence against the model.
- : Moderate evidence against the model.
- : Strong evidence against the model.
5.4.3. p-Value Statistics
| Model | AIC | AIC | BIC | BIC | p-value | ||
|---|---|---|---|---|---|---|---|
| CDM Model | 1802.34 | 1.032 | 1810.34 | 0.00 | 1832.20 | 0.00 | 0.165 |
| BR (Linear Case) | 1802.54 | 1.033 | 1812.54 | 2.20 | 1839.87 | 7.76 | 0.160 |
| BR (Logarithmic Case) | 1802.89 | 1.033 | 1812.89 | 2.55 | 1840.22 | 8.01 | 0.159 |
| BR (Exponential Case) | 1805.15 | 1.035 | 1815.15 | 4.81 | 1842.48 | 10.27 | 0.150 |
| Barthel-Kropina Model | 1782.19 | 1.022 | 1794.19 | 1826.99 | 0.251 |
6. Synthesis of the Results, and Their Discussion
6.1. MCMC Results
6.2. Hubble parameter and Hubble residual results
6.3. Cosmographic Results
6.4. Statistical Results
7. Discussions and Final Remarks
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Weyl, H. Gravitation und Elektrizität. In Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin, 1918 ed.; Königlich Preussische Akademie: Berlin, Germany, 1918; pp. 465–480. [Google Scholar]
- Weyl, H. Space, Time, Matter; Dover Publications: New York, NY, USA, 1952. [Google Scholar]
- Finsler, P. Über Kurven und Flächen in allgemeinen Räumen. Dissertation, University of Göttingen, Germany, 1918; reprinted by Birkhäuser: Basel, Switzerland, 1951.
- Einstein, A. Die Feldgleichungen der Gravitation. In Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften zu Berlin, 1915 ed.; Königlich Preussische Akademie: Berlin, Germany, 1915; pp. 844–847. [Google Scholar]
- Einstein, A. Die Grundlage der allgemeinen Relativitätstheorie. Annalen der Physik 1916, 49, 769–822. [Google Scholar] [CrossRef]
- Hilbert, D. Die Grundlagen der Physik. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse 1915, 395–407.
- Scholz, E. Weyl Geometry in Late 20th Century Physics. In Beyond Einstein: Perspectives on Geometry, Gravitation, and Cosmology in the Twentieth Century; Rowe, D.E., Sauer, T., Walter, S.A., Eds.; Springer: New York, NY, USA, 2018; pp. 261–360. [Google Scholar]
- Riemann, B. Über die Hypothesen, welche der Geometrie zu Grunde liegen. Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen 1868, 13, 133–150. [Google Scholar]
- Chern, S.S. Finsler Geometry Is Just Riemannian Geometry without the Quadratic Restriction. Notices of the American Mathematical Society 1996, 43, 959–963. [Google Scholar]
- Rund, H. The Differential Geometry of Finsler Spaces; Springer-Verlag: Berlin, Germany, 1959. [Google Scholar]
- Asanov, G.S. Finsler Geometry, Relativity and Gauge Theories; D. Reidel Publishing Company: Dordrecht, The Netherlands, 1985. [Google Scholar]
- Bejancu, A. Finsler Geometry and Applications; Ellis Horwood: New York, NY, USA, 1990. [Google Scholar]
- Bao, D.; Chern, S.-S.; Shen, Z. An Introduction to Riemann-Finsler Geometry; Springer-Verlag: New York, NY, USA, 2000. [Google Scholar]
- Shen, Y.-B.; Shen, Z. Introduction to Modern Finsler Geometry; World Scientific: Singapore, 2016. [Google Scholar]
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Reviews in Relativity 2014, 17, 4. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P. et al. (LIGO Scientific Collaboration and Virgo Collaboration). Observation of Gravitational Waves from a Binary Black Hole Merger. Physical Review Letters 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, R. et al. (LIGO Scientific Collaboration and Virgo Collaboration). GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophysical Journal Letters 2020, 896, L44. [Google Scholar] [CrossRef]
- Cartan, É. Sur les variétés à connexion affine et la théorie de la relativité généralisée. Annales de l’École Normale Supérieure 1924, 41, 1–25. [Google Scholar] [CrossRef]
- Cartan, É. Sur les variétés à connexion affine et la théorie de la relativité généralisée. Annales de l’École Normale Supérieure 1925, 42, 17–88. [Google Scholar] [CrossRef]
- Weitzenböck, R. Invariantentheorie; Noordhoff: Groningen, The Netherlands, 1923. [Google Scholar]
- Ehlers, J.; Pirani, F.A.E.; Schild, A. The Geometry of Free Fall and Light Propagation. General Relativity and Gravitation, 44, 1587 (2012).
- Linnemann, N.; Read, J. Constructive Axiomatics in Spacetime Physics Part I: Walkthrough to the Ehlers-Pirani-Schild Axiomatisation. Preprint, arXiv:2112.14063 [gr-qc], 2021.
- Adlam, E.; Linnemann, N.; Read, J. Constructive Axiomatics in Spacetime Physics Part II: Constructive Axiomatics in Context. Preprint, arXiv:2211.05672 [gr-qc], 2022.
- Adlam, E.; Linnemann, N.; Read, J. Constructive Axiomatics in Spacetime Physics Part III: A Constructive Axiomatic Approach to Quantum Spacetime. Preprint, arXiv:2208.07249 [gr-qc], 2022.
- Pfeifer, C. Finsler Spacetime Geometry in Physics. International Journal of Geometric Methods in Modern Physics, 16 (suppl. 02), 1941004 (2019).
- Randers, G. On an Asymmetrical Metric in the Four-Space of General Relativity. Physical Review, 59, 195 (1941).
- Ingarden, R. On the Geometrically Absolute Optical Representation in the Electron Microscope. Travaux de la Société des Sciences et des Lettres de Wrocław, Série B, 45, 3 (1957).
- Miron, R. The Geometry of Ingarden Spaces. Reports on Mathematical Physics, 54, 131 (2004).
- Tavernelli, I. On the Geometrization of Quantum Mechanics. Annals of Physics, 371, 239 (2016).
- Tavernelli, I. On the Self-Interference in Electron Scattering: Copenhagen, Bohmian and Geometrical Interpretations of Quantum Mechanics. Annals of Physics, 393, 447 (2018).
- Liang, S.-D.; Sabau, S.V.; Harko, T. Finslerian Geometrization of Quantum Mechanics in the Hydrodynamical Representation. Physical Review D, 100, 105012 (2019).
- Tavernelli, I. Gravitational Quantum Dynamics: A Geometrical Perspective. Foundations of Physics, 51, 46 (2021).
- Hohmann, M.; Pfeifer, C.; Voicu, N. The Kinetic Gas Universe. European Physical Journal C, 80, 809 (2020).
- Pfeifer, C.; Voicu, N.; Friedl-Szász, A.; Popovici-Popescu, E. From Kinetic Gases to an Exponentially Expanding Universe. Preprint, arXiv:2504.08062 [gr-qc], 2025.
- Rätzel, D.; Rivera, S.; Schuller, F.P. Geometry of Physical Dispersion Relations. Physical Review D, 83, 044047 (2011).
- Duval, C. Finsler Spinoptics. Communications in Mathematical Physics, 283, 701–727 (2008).
- Schreck, M. Classical Lagrangians and Finsler Structures for the Nonminimal Fermion Sector of the Standard-Model Extension. Physical Review D, 93, 105017 (2016).
- Edwards, B.R.; Kostelecký, V.A. Riemann–Finsler Geometry and Lorentz-Violating Scalar Fields. Physics Letters B, 786, 319–326 (2018).
- Horváth, J.I. A Geometrical Model for the Unified Theory of Physical Fields. Physical Review, 80, 901 (1950).
- Horváth, J.I.; Moór, A. Entwicklung einer einheitlichen Feldtheorie begründet auf die Finslersche Geometrie. Zeitschrift für Physik, 131, 548 (1952).
- Takano, Y. Gravitational Field in Finsler Spaces. Lettere al Nuovo Cimento, 10, 747 (1974).
- Takano, Y. Variation Principle in Finsler Spaces. Lettere al Nuovo Cimento, 11, 486 (1974).
- Asanov, G.S. Finslerian Extension of General Relativity. Foundations of Physics, 11, 137 (1981).
- Asanov, G.S. Finsler Geometry, Relativity and Gauge Theories; D. Reidel: Dordrecht, The Netherlands, 1985. [Google Scholar]
- Asanov, G.S. Finslerian Solution for Static Spherically Symmetric Gravitational Field. Fortschritte der Physik, 39, 185 (1991).
- Asanov, G.S. Finslerian Extension of Schwarzschild Metric. Fortschritte der Physik, 40, 667 (1992).
- Miron, R.; Anastasiei, M. Vector Bundles, Lagrange Spaces, and Applications to the Theory of Relativity; Editura Academiei Române: Bucharest, Romania, 1987. (in Romanian) [Google Scholar]
- Ikeda, S. Advanced Studies in Applied Geometry; Seizansha: Sagamihara, Japan, 1995. [Google Scholar]
- Rutz, S.F. A Finsler Generalisation of Einstein’s Vacuum Field Equations. General Relativity and Gravitation, 25, 1139 (1993).
- Li, X.; Chang, Z. Exact Solution of Vacuum Field Equation in Finsler Spacetime. Chinese Physics C, 34, 28 (2010).
- Hohmann, M.; Pfeifer, C.; Voicu, N. Finsler Gravity Action from Variational Completion. Physical Review D, 100, 064035 (2019).
- Riess, A.G.; et al. (Supernova Search Team). Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astronomical Journal, 116, 1009 (1998).
- Perlmutter, S.; et al. (Supernova Cosmology Project). Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophysical Journal, 517, 565 (1999).
- Knop, R.A.; et al. New Constraints on ΩM, ΩΛ, and w from an Independent Set of Eleven High-Redshift Supernovae Observed with HST. Astrophysical Journal, 598, 102 (2003).
- Amanullah, R.; et al. Spectra and Light Curves of Six Type Ia Supernovae at 0.511 < z < 1.12 and the Union2 Compilation. Astrophysical Journal, 716, 712 (2010).
- Weinberg, D.H.; Mortonson, M.J.; Eisenstein, D.J.; Hirata, C.; Riess, A.G.; Rozo, E. Observational Probes of Cosmic Acceleration. Physics Reports, 530, 87 (2013).
- Einstein, A. Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie. Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften (Berlin), part 1, 142–152 (1917).
- Weinberg, S. The Cosmological Constant Problem. Reviews of Modern Physics, 61, 1 (1989).
- Salucci, P.; Turini, N.; Di Paolo, C. Paradigms and Scenarios for the Dark Matter Phenomenon. Universe, 6, 118 (2020).
- Alam, S.; et al. (BOSS Collaboration). The Clustering of Galaxies in the Completed SDSS-III Baryon Oscillation Spectroscopic Survey: Cosmological Analysis of the DR12 Galaxy Sample. Monthly Notices of the Royal Astronomical Society, 470, 2617 (2017).
- Abbott, T.M.C.; et al. (DES Collaboration). Dark Energy Survey Year 1 Results: Cosmological Constraints from Galaxy Clustering and Weak Lensing. Physical Review D, 98, 043526 (2018).
- Tanabashi, M.; et al. (Particle Data Group). Review of Particle Physics. Physical Review D, 98, 030001 (2018).
- Aghanim, N.; et al. (Planck Collaboration). Planck 2018 Results. VI. Cosmological Parameters. Astronomy & Astrophysics, 641, A6 (2020).
- Martel, H.; Shapiro, P.R.; Weinberg, S. Likely Values of the Cosmological Constant. Astrophysical Journal, 492, 29 (1998).
- Weinberg, S. The Cosmological Constant Problems. In Sources and Detection of Dark Matter and Dark Energy in the Universe; Cline, D.B., Ed.; Springer-Verlag: Berlin, Germany, 2001; p. 18, arXiv:astro-ph/0005265. [Google Scholar]
- Lake, M.J. A New Approach to the Cosmological Constant Problems. SciPost Physics Proceedings, 4, 014 (2021).
- Tanabashi, M.; et al. (Particle Data Group). Review of Particle Physics. Physical Review D, 98, 030001 (2018).
- Aghanim, N.; et al. (Planck Collaboration). Planck 2018 Results. VI. Cosmological Parameters. Astronomy & Astrophysics, 641, A6 (2020).
- Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Scolnic, D. Large Magellanic Cloud Cepheid Standards Provide Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics Beyond LCDM. Astrophysical Journal, 876, 85 (2019).
- Huang, C.D.; Riess, A.G.; Yuan, W.; Macri, L.M.; Zakamska, N.L.; Casertano, S.; Whitelock, P.A.; Hoffmann, S.L.; Filippenko, A.V.; Scolnic, D. Hubble Space Telescope Observations of Mira Variables in the SN Ia Host NGC 1559: An Alternative Candle to Measure the Hubble Constant. Astrophysical Journal, 889, 5 (2020).
- Pesce, D.W.; et al. The Megamaser Cosmology Project. XIII. Combined Hubble Constant Constraints. Astrophysical Journal Letters, 891, L1 (2020).
- Harko, T.; Lobo, F.S.N. Beyond Einstein’s General Relativity: Hybrid Metric-Palatini Gravity and Curvature-Matter Couplings. International Journal of Modern Physics D, 29, 2030008 (2020).
- Haghani, Z.; Harko, T.; Sepangi, H.R.; Shahidi, S. Weyl-Cartan-Weitzenböck Gravity as a Generalization of Teleparallel Gravity. Journal of Cosmology and Astroparticle Physics, 10, 061 (2012).
- Haghani, Z.; Harko, T.; Sepangi, H.R.; Shahidi, S. Weyl-Cartan-Weitzenböck Gravity through Lagrange Multiplier. Physical Review D, 88, 044024 (2013).
- Nester, J.M.; Yo, H.-J. Symmetric Teleparallel General Relativity. Chinese Journal of Physics, 37, 113 (1999).
- Beltrán Jiménez, J.; Heisenberg, L.; Koivisto, T. Coincident General Relativity. Physical Review D, 98, 044048 (2018).
- D’Agostino, R.; Luongo, O. Growth of Matter Perturbations in Nonminimal Teleparallel Dark Energy. Physical Review D, 98, 124013 (2018).
- Fontanini, M.; Huguet, E.; Le Delliou, M. Teleparallel Gravity (TEGR) as a Gauge Theory. Physical Review D, 99, 064006 (2019).
- Koivisto, T.; Tsimperis, G. The Spectrum of Teleparallel Gravity. Universe, 5, 80 (2019).
- Pereira, J.G.; Obukhov, Y.N. Gauge Structure of Teleparallel Gravity. Universe, 5, 139 (2019).
- Blixt, D.; Hohmann, M.; Pfeifer, C. On the Gauge Fixing in the Hamiltonian Analysis of General Teleparallel Theories. Universe, 5, 143 (2019).
- Coley, A.A.; van den Hoogen, R.J.; McNutt, D.D. Symmetry and Equivalence in Teleparallel Gravity. Journal of Mathematical Physics, 61, 072503 (2020).
- Haghani, Z.; Khosravi, N.; Shahidi, S. The Weyl–Cartan Gauss–Bonnet Gravity. Classical and Quantum Gravity, 32, 215016 (2015).
- Sotiriou, T.P.; Faraoni, V. f(R) Theories of Gravity. Reviews of Modern Physics, 82, 451 (2010).
- De Felice, A.; Tsujikawa, S. f(R) Theories. Living Reviews in Relativity, 13, 3 (2010).
- Cai, Y.F.; Capozziello, S.; De Laurentis, M.; Saridakis, E.N. f(T) Teleparallel Gravity and Cosmology. Reports on Progress in Physics, 79, 106901 (2016).
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-Time Evolution. Physics Reports, 692, 1 (2017).
- Odintsov, S.D.; Oikonomou, V.K.; Giannakoudi, I.; Fronimos, F.P.; Lymperiadou, E.C. Recent Advances in Inflation. Symmetry, 15, 1701 (2023).
- Basilakos, S.; Stavrinos, P. Cosmological Equivalence between the Finsler–Randers Space-Time and the DGP Gravity Model. Physical Review D, 87, 043506 (2013).
- Exirifard, Q. Cosmological Implications of Modified Gravity Induced by Quantum Metric Fluctuations. Journal of Cosmology and Astroparticle Physics, 11, 026 (2015).
- Silva, J.E.G.; Maluf, R.V.; Almeida, C.A.S. Effective Gravitational Equations on a Brane in Teleparallel Gravity. Physics Letters B, 766, 263 (2017).
- Papagiannopoulos, G.; Basilakos, S.; Paliathanasis, A.; Savvidou, S.; Stavrinos, P.C. Dynamics and Observational Constraints in Scalar–Tensor Theories in Finsler–Randers Spacetime. Classical and Quantum Gravity, 34, 225008 (2017).
- Papagiannopoulos, G.; Basilakos, S.; Paliathanasis, A.; Pan, S.; Stavrinos, P. Finsler–Randers Cosmology: Dynamical Analysis and Growth of Matter Perturbations. European Physical Journal C, 80, 816 (2020).
- Raushan, R.; Chaubey, S. Finslerian Cosmological Model with Bulk Viscosity in Bianchi Type-I Space-Time. European Physical Journal Plus, 135, 228 (2020).
- Triantafyllopoulos, A.; Basilakos, S.; Kapsabelis, E.; Stavrinos, P.C. Finsler–Randers Cosmology: Dynamical Analysis and Growth of Matter Perturbations. European Physical Journal C, 80, 1200 (2020).
- Kapsabelis, E.; Triantafyllopoulos, A.; Basilakos, S.; Stavrinos, P.C. Dynamical Analysis of a Scalar Field Cosmology in Finsler–Randers Spacetime. European Physical Journal C, 81, 990 (2021).
- Kapsabelis, E.; Kevrekidis, P.G.; Stavrinos, P.C.; Triantafyllopoulos, A. Finsler–Randers Cosmology: Dynamical Analysis and Growth of Matter Perturbations. European Physical Journal C, 82, 1098 (2022).
- Nekouee, Z.; Narasimhamurthy, S.K.; Manjunatha, H.M.; Srivastava, S.K. Finslerian Cosmological Model with Bulk Viscosity in Bianchi Type-I Space-Time. European Physical Journal Plus, 137, 1388 (2022).
- Feng, W.; Yang, W.; Jiang, B.; Wang, Y.; Han, T.; Wu, Y. Observational Constraints on Finslerian Cosmology. International Journal of Modern Physics D, 32, 2350029 (2023).
- Das, P.D.; Debnath, U. Finslerian Cosmological Model with Bulk Viscosity in Bianchi Type-I Space-Time. European Physical Journal C, 83, 821 (2023).
- Triantafyllopoulos, A.; Kapsabelis, E.; Stavrinos, P.C. Finsler–Randers Cosmology: Dynamical Analysis and Growth of Matter Perturbations. Universe, 10, 26 (2024).
- Kapsabelis, E.; Saridakis, E.N.; Stavrinos, P.C. Finsler–Randers Cosmology: Dynamical Analysis and Growth of Matter Perturbations. European Physical Journal C, 84, 538 (2024).
- Praveen, J.; Narasimhamurthy, S.K.; Yashwanth, B.R. Finslerian Cosmological Model with Bulk Viscosity in Bianchi Type-I Space-Time. European Physical Journal C, 84, 597 (2024).
- Liu, J.; Wang, R.; Gao, F. Finsler–Randers Cosmology: Dynamical Analysis and Growth of Matter Perturbations. Universe, 10, 302 (2024).
- Nekouee, Z.; Narasimhamurthy, S.K.; Pourhassan, B.; Pacif, S.K.J. Finslerian Cosmological Model with Bulk Viscosity in Bianchi Type-I Space-Time. Annals of Physics, 470, 169787 (2024).
- Nekouee, Z.; Chaudhary, H.; Narasimhamurthy, S.K.; Pacif, S.K.J.; Malligawad, M. Finsler–Randers Cosmology: Dynamical Analysis and Growth of Matter Perturbations. Journal of High Energy Astrophysics, 44, 19 (2024).
- Praveen, J.; Narasimhamurthy, S.K. Finslerian Cosmological Model with Bulk Viscosity in Bianchi Type-I Space-Time. Journal of High Energy Astrophysics, 44, 300 (2024).
- Yashwanth, B.R.; Narasimhamurthy, S.K.; Praveen, J.; Malligawad, M. Finsler–Randers Cosmology: Dynamical Analysis and Growth of Matter Perturbations. European Physical Journal C, 84, 1272 (2024).
- Praveen, J.; Narasimhamurthy, S.K. Finslerian Cosmological Model with Bulk Viscosity in Bianchi Type-I Space-Time. New Astronomy, 119, 102404 (2025).
- Ikeda, S.; Saridakis, E.N.; Stavrinos, P.C.; Triantafyllopoulos, A. Cosmology of Lorentz Fiber-Bundle Induced Scalar-Tensor Theories. Physical Review D, 100, 124035 (2019).
- Fuster, A.; Pabst, C.; Pfeifer, C. Berwald Spacetimes and Very Special Relativity. Physical Review D, 98, 084062 (2018).
- Hohmann, M.; Pfeifer, C.; Voicu, N. Cosmological Finsler Spacetimes. Universe, 6, 65 (2020).
- Hama, R.; Harko, T.; Sabau, S.V.; Shahidi, S. Cosmological Evolution and Dark Energy in Osculating Barthel–Randers Geometry. European Physical Journal C, 81, 742 (2021).
- Hama, R.; Rattanasak, R.; Harko, T.; Sabau, S.V. Dark Energy and Accelerating Cosmological Evolution from Osculating Barthel–Kropina Geometry. European Physical Journal C, 82, 385 (2022).
- Bouali, A.; Chaudhary, H.; Hama, R.; Harko, T.; Sabau, S.V.; San Martín, M. Cosmological Tests of the Osculating Barthel–Kropina Dark Energy Model. European Physical Journal C, 83, 121 (2023).
- Hama, R.; Harko, T.; Sabau, S.V. Conformal Gravitational Theories in Barthel–Kropina-Type Finslerian Geometry and Their Cosmological Implications. European Physical Journal C, 83, 1030 (2023).
- Tavakol, R.K.; Van den Bergh, N. Finsler Spaces and the Underlying Geometry of Space-Time. Physics Letters A, 112, 23 (1985).
- Tavakol, R.K. Geometry of Spacetime and Finsler Geometry. International Journal of Modern Physics A, 24, 1678 (2009).
- Javaloyes, M.A.; Sánchez, M. On the Definition and Examples of Finsler Metrics. Annali della Scuola Normale Superiore di Pisa, Classe di Scienze, 13, 813 (2014).
- Yoshikawa, R.; Sabau, S.V. Kropina Metrics and Zermelo Navigation on Riemannian Manifolds. Geometriae Dedicata, 171, 119 (2014).
- Kropina, V.K. On Projective Finsler Spaces with a Metric of Special Form. Nauchnye Doklady Vysshei Shkoly, Fiziko-Matematicheskie Nauki, 2, 38 (1959).
- Kropina, V.K. On Projective Finsler Spaces with a Metric of Special Form. Uchenye Zapiski Arkhangelskogo Gosudarstvennogo Pedagogicheskogo Instituta, 4, 111 (1959).
- Matsumoto, M. On C-Reducible Finsler Spaces. Tensor, New Series, 24, 29–37 (1972).
- Matsumoto, M. Theory of Finsler Spaces with (α, β)-Metric. Reports on Mathematical Physics, 31, 43–83 (1992).
- Bácsó, S.; Cheng, X.; Shen, Z. Curvature Properties of (α, β)-Metrics. Advanced Studies in Pure Mathematics, 48, 73–110 (2007).
- Antonelli, P.L.; Ingarden, R.S.; Matsumoto, M. The Theory of Sprays and Finsler Spaces with Applications in Physics and Biology; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Miron, R.; Hrimiuc, D.; Shimada, H.; Sabau, S.V. The Geometry of Hamilton and Lagrange Spaces; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Yoshikawa, R.; Sabau, S.V. Kropina Metrics and Zermelo Navigation on Riemannian Manifolds. Publicationes Mathematicae Debrecen, 84, 483–499 (2014).
- Sabau, S.V.; Shibuya, K.; Yoshikawa, R. Geodesics on Strong Kropina Manifolds. European Journal of Mathematics, 3, 1172–1224 (2017).
- Heefer, S.; Pfeifer, C.; van Voorthuizen, J.; Fuster, A. On the Metrizability of m-Kropina Spaces with Closed Null One-Form. Journal of Mathematical Physics, 64, 022502 (2023).
- Heefer, S. Berwald m-Kropina Spaces of Arbitrary Signature: Metrizability and Ricci-Flatness. Journal of Mathematical Physics, 65, 122502 (2024).
- Barthel, W. Über eine Geometrische Deutung der Automorphen Funktionen. Mathematische Zeitschrift, 58, 358 (1953).
- Barthel, W. Zur Theorie der Automorphen Funktionen. Archiv der Mathematik, 4, 346 (1953).
- Ingarden, R.S.; Tamássy, L. The Point Finsler Spaces and Their Physical Applications in Electron Optics and Thermodynamics. Mathematical and Computer Modelling, 20, 93 (1994).
- Nazim, A. Über Finslersche Räume. Dissertation, München, Germany, 1936.
- Varga, O. Zur Herleitung des Invarianten Differentials in Finslerschen Räumen. Monatshefte für Mathematik und Physik, 50, 165 (1941).
- Harko, T. Thermodynamic Interpretation of the Generalized Gravity Models with Geometry–Matter Coupling. Physical Review D, 90, 044067 (2014).
- Bertolami, O.; Böhmer, C.G.; Harko, T.; Lobo, F.S.N. Extra Force in f(R) Modified Theories of Gravity. Physical Review D, 75, 104016 (2007).
- Harko, T.; Lobo, F.S.N.; Otalora, G.; Saridakis, E.N. Nonminimal Torsion–Matter Coupling Extension of f(T) Gravity. Physical Review D, 89, 124036 (2014).
- Parker, L. Particle Creation in Expanding Universes. Physical Review Letters, 21, 562 (1968).
- Parker, L. Quantized Fields and Particle Creation in Expanding Universes. I. Physical Review, 183, 1057 (1969).
- Zeldovich, Ya.B.; Starobinsky, A.A. Particle Production and Vacuum Polarization in an Anisotropic Gravitational Field. Zhurnal Éksperimental’noĭ i Teoreticheskoĭ Fiziki, 61, 2161 (1971); [Soviet Physics JETP, 34, 1159 (1972)].
- Parker, L. Particle Creation in Isotropic Cosmologies. Physical Review Letters, 28, 705 (1972); Erratum: Physical Review Letters, 28, 1497 (1972).
- Fulling, S.A.; Parker, L.; Hu, B.L. Conformal Energy-Momentum Tensor in Curved Spacetime: Adiabatic Regularization and Renormalization. Physical Review D, 10, 3905 (1974).
- Parker, L. Particle Creation and Particle Number in an Expanding Universe. Journal of Physics A: Mathematical and Theoretical, 45, 374023 (2012).
- Prigogine, I.; Geheniau, J.; Gunzig, E.; Nardone, P. Thermodynamics of Cosmological Matter Creation. Proceedings of the National Academy of Sciences of the USA, 85, 7428 (1988).
- Calvão, M.O.; Lima, J.A.S.; Waga, I. On the Thermodynamics of Matter Creation in Cosmology. Physics Letters A, 162, 223 (1992).
- Su, J.; Harko, T.; Liang, S.-D. Thermodynamics in Modified Gravity Theories with Geometry–Matter Coupling. Advances in High Energy Physics, 2017, 7650238 (2017).
- Lima, J.A.S.; Baranov, I.P. Gravitationally Induced Particle Production: Thermodynamics and Kinetic Theory. Physical Review D, 90, 043515 (2014).
- Saridakis, E.N.; González-Díaz, P.F.; Sigüenza, C.L. Unified Dark Energy Thermodynamics: Varying w and the −1-Crossing. Classical and Quantum Gravity, 26, 165003 (2009).
- Bernardo, J. M. Reference Prior Distributions for Bayesian Inference. J. R. Stat. Soc. B 1979, 41, 113–127. [Google Scholar] [CrossRef]
- Joyce, J. Bayes’ Theorem. In The Stanford Encyclopedia of Philosophy, Fall 2021 ed.; Zalta, E.N., Ed.; Stanford University: Stanford, CA, USA, 2021. [Google Scholar]
- Lewis, A. GetDist: A Python Package for Analysing Monte Carlo Samples. arXiv 2019, arXiv:1910.13970. [Google Scholar]
- Lewis, A. GetDist: A Python Package for Analysing Monte Carlo Samples. arXiv 2019, arXiv:1910.13970. [Google Scholar]
- Jimenez, R.; Loeb, A. Constraining Cosmological Parameters Based on Relative Galaxy Ages. Astrophys. J. 2002, 573, 37–51. [Google Scholar] [CrossRef]
- Moresco, M. Raising the Bar: New Constraints on the Hubble Parameter with Cosmic Chronometers at z ∼2. Mon. Not. R. Astron. Soc. 2015, 450, L16–L20. [Google Scholar] [CrossRef]
- Moresco, M.; Pozzetti, L.; Cimatti, A.; Jimenez, R.; Maraston, C.; Verde, L.; Thomas, D.; Citro, A.; Tojeiro, R.; Wilkinson, D. A 6% Measurement of the Hubble Parameter at z ∼0.45: Direct Evidence of the Epoch of Cosmic Re-acceleration. J. Cosmol. Astropart. Phys. 2016, 2016, 014. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Loeb, A.; Moresco, M. Eppur è Piatto? The Cosmic Chronometers Take on Spatial Curvature and Cosmic Concordance. Astrophys. J. 2021, 908, 84. [Google Scholar] [CrossRef]
- Moresco, M.; Jimenez, R.; Verde, L.; Cimatti, A.; Pozzetti, L. Setting the Stage for Cosmic Chronometers. II. Impact of Stellar Population Synthesis Models Systematics and Full Covariance Matrix. Astrophys. J. 2020, 898, 82. [Google Scholar] [CrossRef]
- Brout, D.; Scolnic, D.; Popovic, B.; Riess, A. G.; Carr, A.; Zuntz, J.; Kessler, R.; Davis, T. M.; Hinton, S.; Jones, D.; et al. The Pantheon+ analysis: Cosmological constraints. Astrophys. J. 2022, 938, 110. [Google Scholar] [CrossRef]
- Astier, P.; Guy, J.; Regnault, N.; Pain, R.; Aubourg, E.; Balam, D.; Basa, S.; Carlberg, R.; Fabbro, S.; Fouchez, D.; et al. The supernova legacy survey: measurement of ω, ω and from the first year data set. Astron. Astrophys. 2006, 447, 31–48. [Google Scholar] [CrossRef]
- Conley, A.; Guy, J.; Sullivan, M.; Regnault, N.; Astier, P.; Balland, C.; Basa, S.; Carlberg, R.; Fouchez, D.; Hardin, D.; et al. Supernova constraints and systematic uncertainties from the first three years of the supernova legacy survey. Astrophys. J. Suppl. Ser. 2010, 192(1), 1.
- Karim, M. A.; Aguilar, J.; Ahlen, S.; Alam, S.; Allen, L.; Prieto, C. A.; Alves, O.; Anand, A.; Andrade, U.; Armengaud, E.; Aviles, A. DESI DR2 Results II: Measurements of Baryon Acoustic Oscillations and Cosmological Constraints. arXiv preprint 2025, arXiv:2503.14738, March 18, 2025.
- Pogosian, L.; Zhao, G.-B.; Jedamzik, K. Recombination-independent determination of the sound horizon and the Hubble constant from BAO. Astrophys. J. Lett. 2020, 904, L17. [Google Scholar] [CrossRef]
- Jedamzik, K.; Pogosian, L.; Zhao, G.-B. Why reducing the cosmic sound horizon alone can not fully resolve the Hubble tension. Commun. Phys. 2021, 4, 123. [Google Scholar] [CrossRef]
- Pogosian, L.; Zhao, G.-B.; Jedamzik, K. A consistency test of the cosmological model at the epoch of recombination using DESI BAO and Planck measurements. Astrophys. J. Lett. 2024, 973, L13. [Google Scholar] [CrossRef]
- Lin, W.; Chen, X.; Mack, K.J. Early universe physics insensitive and uncalibrated cosmic standards: Constraints on Ωm and implications for the Hubble tension. Astrophys. J. 2021, 920, 159. [Google Scholar] [CrossRef]
- Vagnozzi, S. Seven hints that early-time new physics alone is not sufficient to solve the Hubble tension. Universe 2023, 9, 393. [Google Scholar] [CrossRef]
- H. Chaudhary, L. Csillag, and T. Harko, "Semi-Symmetric Metric Gravity: A Brief Overview," Universe 10, 419 (2024).
- Cattoën, C.; Visser, M. Cosmographic Hubble fits to the supernova data. Phys. Rev. D 2008, 78, 063501. [Google Scholar] [CrossRef]
- Visser, M.; Cattoën, C. Cosmographic analysis of dark energy. In Dark Matter In Astrophysics And Particle Physics; Klapdor-Kleingrothaus, H.V., Krivosheina, I.V., Eds.; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2009; pp. 287–300. [Google Scholar]
- Visser, M. Cosmography: Cosmology without the Einstein equations. Gen. Relativ. Gravit. 2005, 37, 1541. [Google Scholar] [CrossRef]
- Luongo, O. Cosmography with the Hubble parameter. Mod. Phys. Lett. A 2011, 26, 1459. [Google Scholar] [CrossRef]
- Visser, M. Jerk, snap and the cosmological equation of state. Class. Quantum Gravity 2004, 21, 2603. [Google Scholar] [CrossRef]
- Andrae, R.; Schulze-Hartung, T.; Melchior, P. Dos and don’ts of reduced chi-squared; arXiv preprint arXiv:1012.3754, 2010.
- Liddle, A.R. Information criteria for astrophysical model selection. Mon. Not. R. Astron. Soc. Lett. 2007, 377, L74. [Google Scholar] [CrossRef]
- Vrieze, S.I. Model selection and psychological theory: A discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). Psychol. Methods 2012, 17, 228. [Google Scholar] [CrossRef]
- Tan, M.Y.J.; Biswas, R. The reliability of the Akaike information criterion method in cosmological model selection. Mon. Not. R. Astron. Soc. 2012, 419, 3292. [Google Scholar] [CrossRef]
- Arevalo, F.; Cid, A.; Moya, J. AIC and BIC for cosmological interacting scenarios. Eur. Phys. J. C 2017, 77, 1. [Google Scholar] [CrossRef]
- Burnham, K.P.; Anderson, D.R. Model Selection and Multimodel Inference, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Jeffreys, H. The Theory of Probability; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Andrade, C. The P value and statistical significance: Misunderstandings, explanations, challenges, and alternatives; Indian Journal of Psychological Medicine, 41(3), 210–215, 2019.
| Name | Finsler Function | Properties |
|---|---|---|
| Semi-Riemannian | Quadratic in y, reversible, i.e. . | |
| Randers | Non-reversible, i.e. ; appears in EM analogs and Lorentz-violating physics. | |
| Kropina | Singular on hypersurfaces; non-reversible. | |
| Matsumoto | Non-reversible; used in irreversible mechanics; singular on hypersurfaces. | |
| Bogoslovsky | Breaks full Lorentz invariance; ; used in very special relativity. | |
| Funk | Defined on unit ball; forward complete; non-reversible. | |
| Locally Minkowskian | General flat case; depends only on y, independent of x. | |
| - metrics | Unifies and generalizes Randers, Kropina, Matsumoto metrics via the scalar function . | |
| General Lagrangian | , L 2-homogeneous in y | More general case; has some applications in mechanics. |
| Optical / Media | Includes anisotropic effects in optics through the direction-dependent refractive index . | |
| Non-reversible Finsler | General F such that | Includes Funk, Randers, and non-reversible geometries. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





