Submitted:
05 May 2025
Posted:
06 May 2025
You are already at the latest version
Abstract
Keywords:
Introduction
1. Literature Review
2. Model
2.1. Cobb-Douglas-Negative Feedback Model
2.1.1. Establishment of a Net Environmental Revenue (NER) Model
- : the investment in the treatment of pollutants
- : the pollutants cost of
- : the coefficient of environmental returns per unit investment of pollutants
- : the deceleration rate of marginal returns of pollutants
- : the hazard coefficient of pollutant emissions
- Based on the shortcomings reflected in equation (5), the following accounting method will be used in the paper:It stands for thirty-one provinces and regions in China and is the year (2015-2023). Relative indicators such as growth rate () rather than absolute indicators are used to reflect the dynamic changes of the economy and the environment, and avoid the limitation of inconsistent dimensions of static indicators.
2.1.2. Establishment of Green GDP (GGDP) Model
- if and , then ;
- If and , then ;
- If and , then .
- Satisfied :
- if , then ;
- If , then ;
- If , then .
- if , which means , then the elasticity to GGDP is greater than the elasticity to GGDP;
- if , which means , then the elasticity to GGDP is less than the elasticity to GGDP;
- if , which means , then the elasticity to GGDP is equal to the elasticity to GGDP.
- if , which means , then the substitution ability of towards is exponentially efficient;
- if , which means , then the substitution ability of towards is decreasingly efficient;
- if , which means , then the substitution ability of and is equally efficient.
2.1.3. Establishment of Green GDP (GGDP) Growth Rate Model
- The formula for calculating the growth rate of GGDP before the correction is as follows:
- if , then ;
- if , then ;
- if , then .
- The formula for calculating the modified GGDP growth rate is:
2.2. The Double Helix Coupling Model (DHCM) Was Established
2.2.1. Establishment of Ecological Supply Capacity (E) Model
- Based on the integrated framework of ecosystem service theory and welfare economics, the paper will construct a Dual Helix Coupling Model (DHCM) to provide theoretical support for the estimation of ecological welfare.
- The ecological supply function is defined as follows:
- the core element of the ecological subsystem
- the element elasticity coefficient
- the correction factor of regional ecological carrying ability
- the weight of the abilities.
- If , then , The marginal revenue of E is increasing;
- If , then , The marginal revenue of E is decreasing;
- If , then , The marginal revenue of E is constant.
2.2.2. Establishment of the Welfare Conversion Capacity (W) Model
- Benefit conversion functionsatisfy:
- the possible ability component ().
- the weight of the abilities ().
- marginal transformation efficiency ().
- the system quality adjustment coefficient ().
- If , then , The marginal revenue of W is increasing;
- If , then , The marginal revenue of W is decreasing;
- If , then , The marginal revenue of W is constant.
2.2.3. Establishment of the Ecological Welfare-Being (EWI) Model
- the ecological self-organization coefficient;
- the welfare self-organization coefficient ;
- the co-gain parameter
- the critical value of ecosystem collapse
- the critical value of social the welfare economic system collapse.
- The hyperbolic tangent function is used to characterize the nonlinear interaction between systems.
2.2.4. The Welfare Analysis
- From equation (26), it can be seen that:
- When :
- If satisfied
- If satisfied
- If satisfied
- If satisfied
- If satisfied
- If satisfied
3. Empirical Analyses12
3.1. The Experience of the Cobb-Douglas-Negative Feedback Model
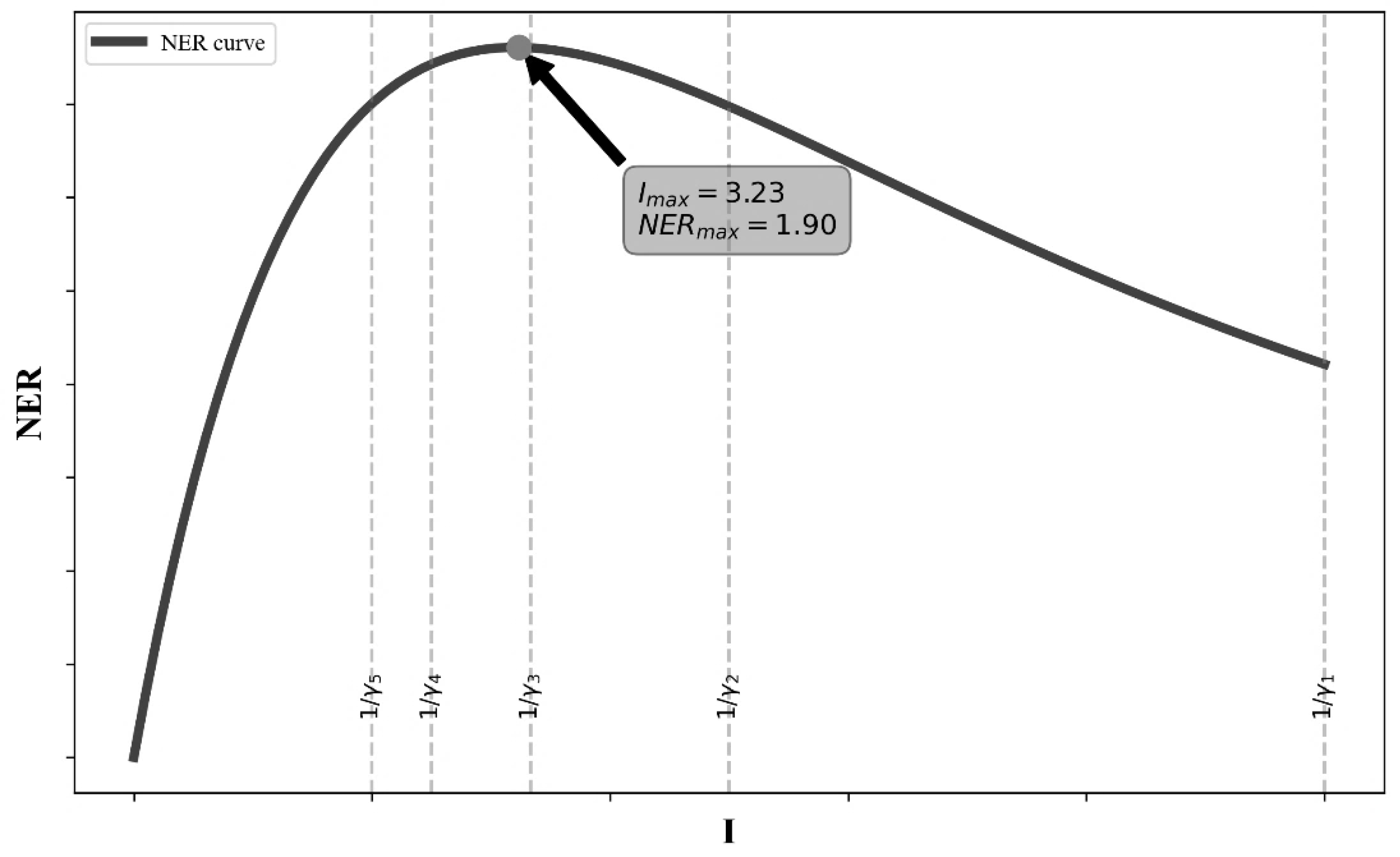
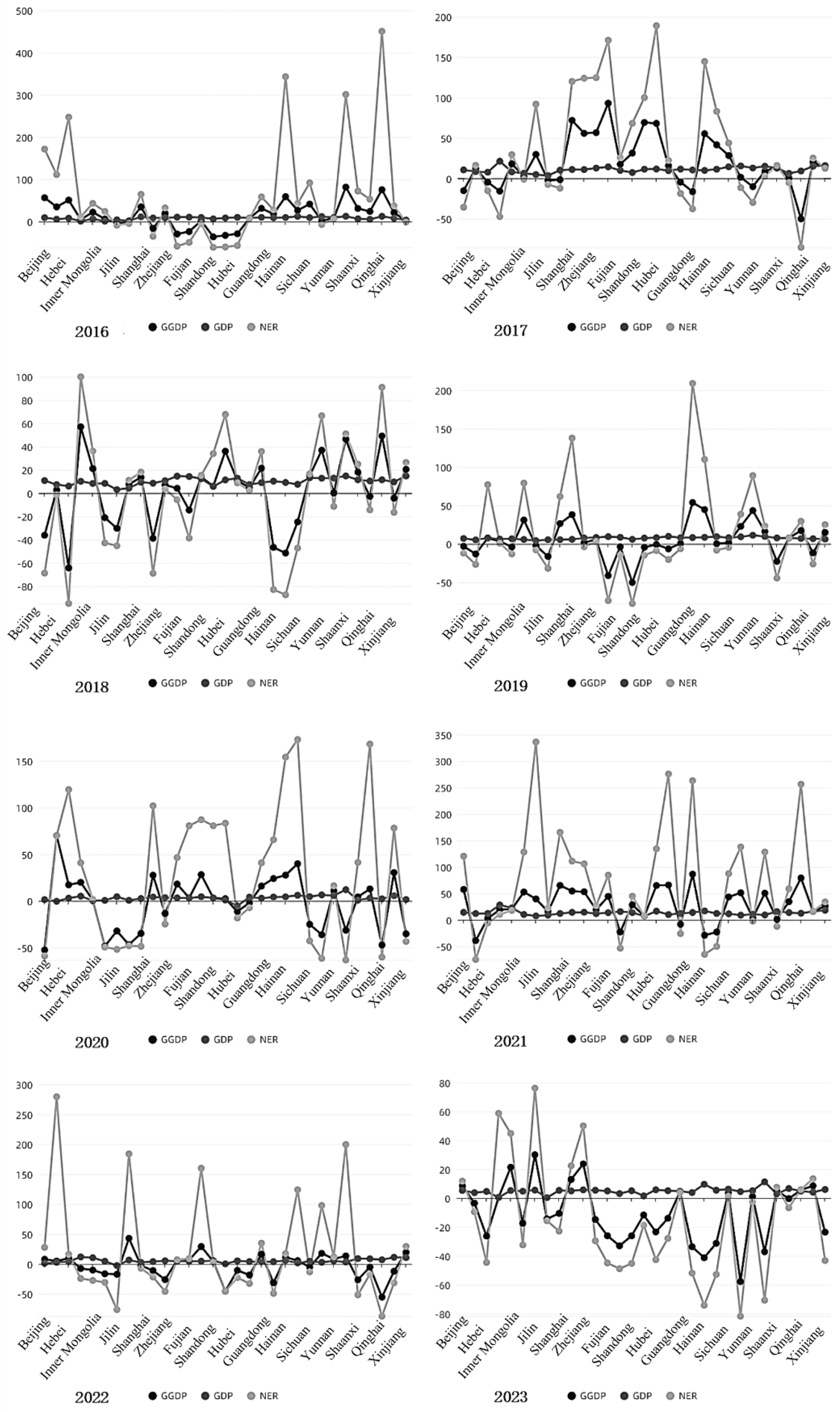
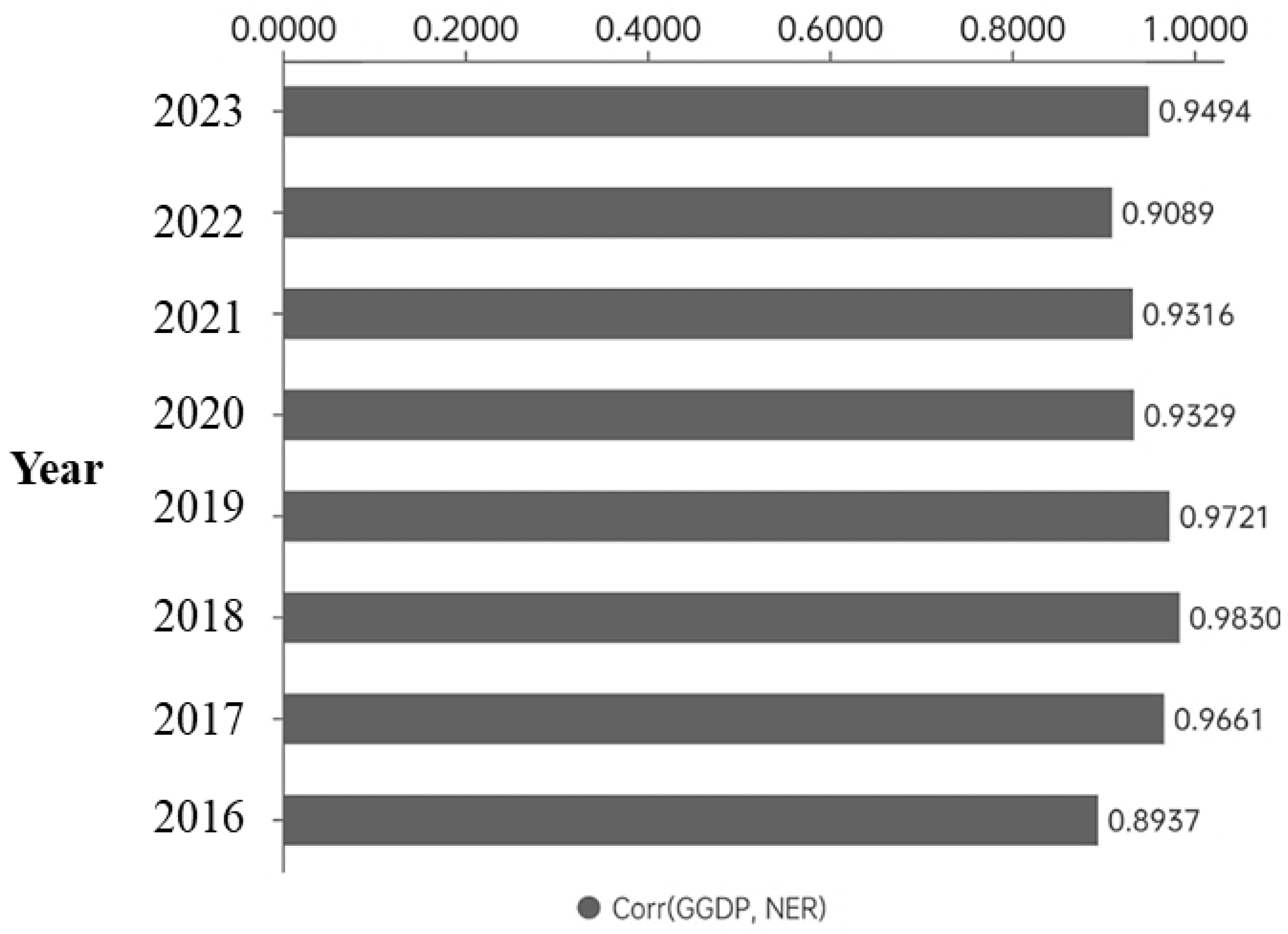
3.1.1. Empirical Evidence of Net Environmental Revenues (NER) Results
| Level 1 indicators | Secondary indicators | Meaning | Data source |
| NER | Investment in industrial waste gas treatment | NBSC | |
| Investment in industrial wastewater treatment | NBSC | ||
| Investment in industrial waste treatment | NBSC | ||
| Investment in industrial noise control | NBSC | ||
| Other governance investments | NBSC | ||
| Nitrogen oxide emissions | NBSC | ||
| Sulphur dioxide emissions | NBSC | ||
| Particulate matter emissions | NBSC | ||
| GDP | GDP | Gross regional product | NBSC |
3.1.2. Empirical Results of the Green GDP (GGDP) Growth Rate Model
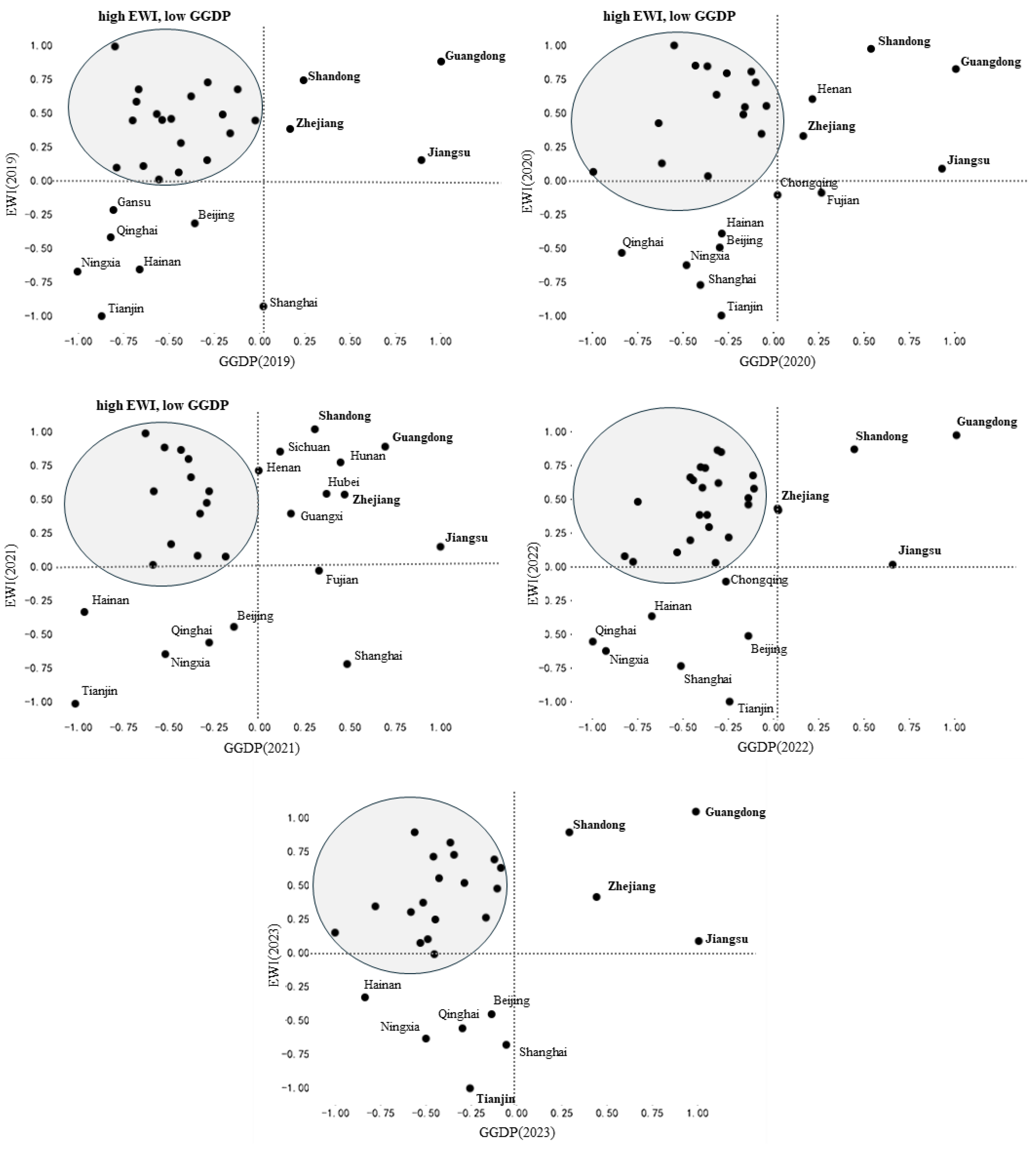
3.1.3. Empirical Results of the Green GDP (GGDP) Model
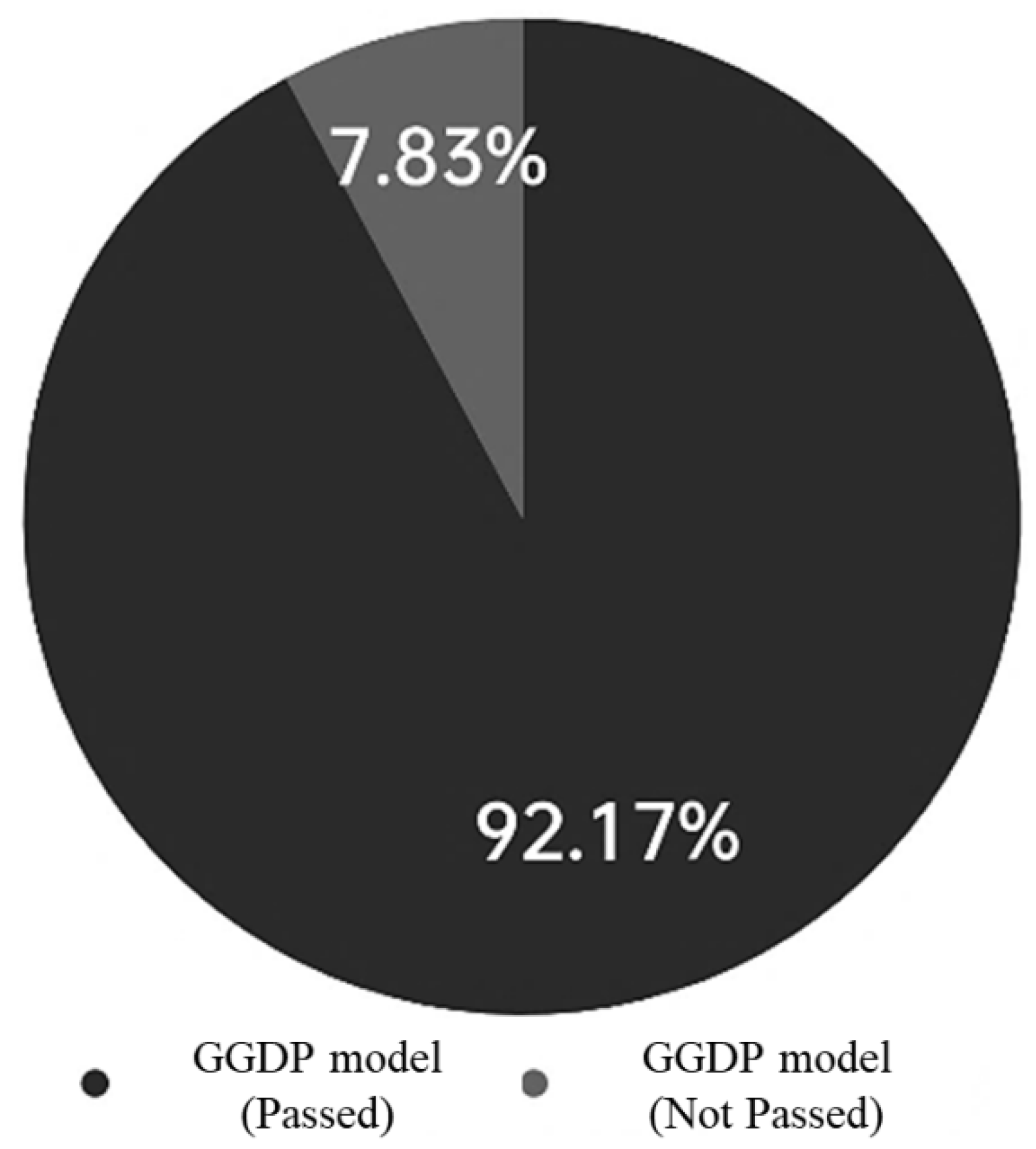
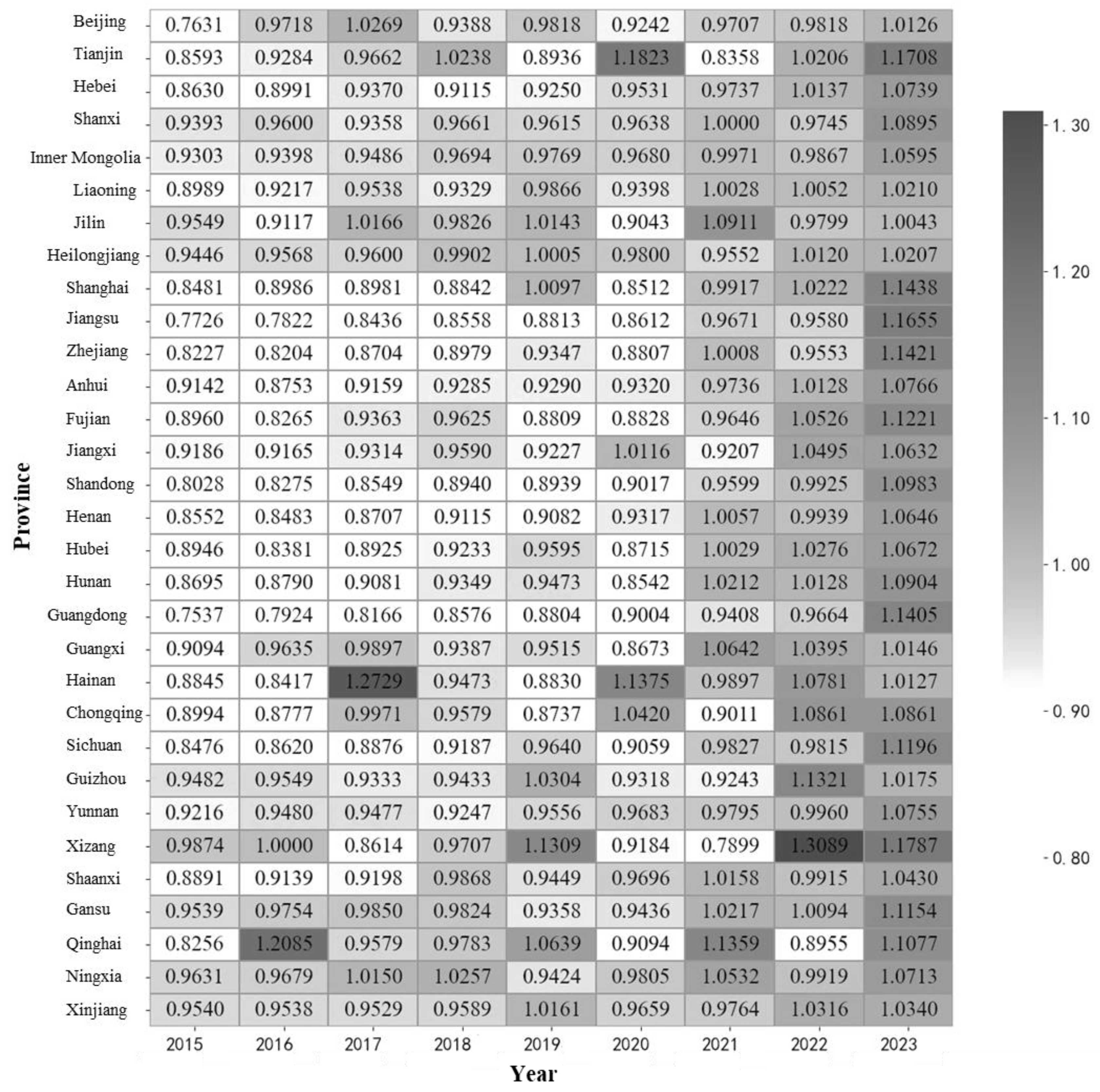
3.1.4. Sustainability Index (SI) Measurement
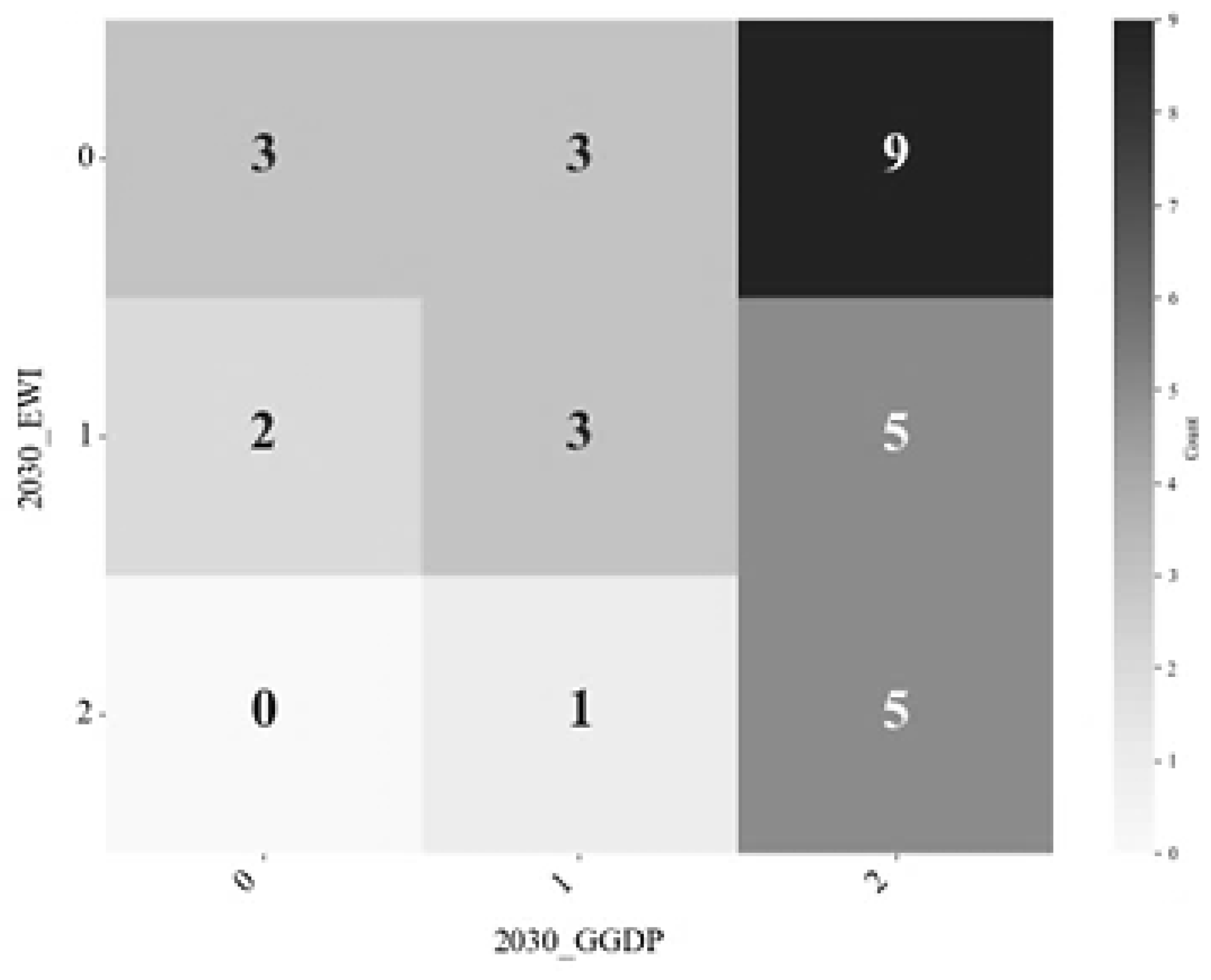
3.1.5. CA-Maekov Predicts the Results of the Sustainability Index (SI)
| SI level | In 2030 | Year 2060 |
|---|---|---|
| Elevated level of status | Xinjiang Uygur Autonomous Region, Qinghai, Heilongjiang, Liaoning, Beijing City, Shanxi, Shaanxi, Chongqing Municipality, Henan, Shandong, Anhui, Jiangsu, Zhejiang, Fujian, Guangdong, Guangxi Zhuang Autonomous Region, Hainan | Xinjiang Uygur Autonomous Region, Qinghai, Yunnan, Guangxi Zhuang Autonomous Region, Guangdong, Hainan, Hunan, Chongqing Municipality, Fujian, Zhejiang, Jiangsu, Anhui, Henan, Hebei, Liaoning, Jilin, Heilongjiang |
| Moderate level of status | Tibet Autonomous Region, Sichuan, Gansu, Ningxia Hui Autonomous Region, Guizhou, Jiangxi, Hebei, Jilin | Sichuan, Hubei. Shanxi, Ningxia Hui Autonomous Region |
| Low-level state | Inner Mongolia Autonomous Region, Hubei, Hunan, Yunnan | Tibet Autonomous Region, Inner Mongolia Autonomous Region, Gansu, Shaanxi, Shandong, Jiangxi, Guizhou |
| SI | 2030/2060 | |||
|---|---|---|---|---|
| 0 | 1 | 2 | ||
| In 2023 | 0 | 0.4516 | 0.1935 | 0.3549 |
| 1 | 0.3448 | 0.4828 | 0.1724 | |
| 2 | 0.0745 | 0.0851 | 0.8404 | |
3.2. Experience of the Double Helix Coupling Model (DHCM)
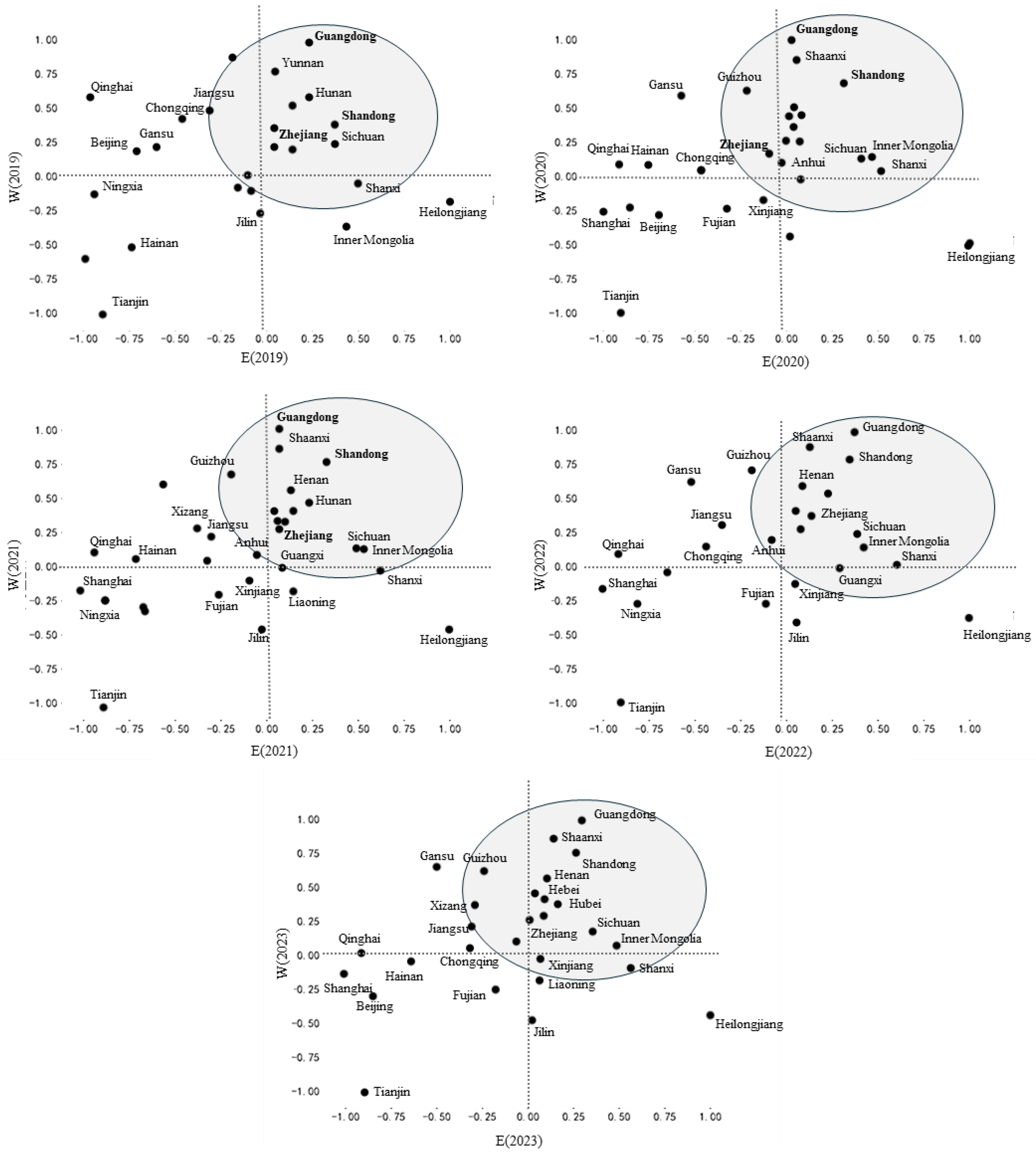
3.2.1. Empirical Results of the Ecological Welfare (EWI) Model
| Dimension | Level 1 indicators | Secondary indicators | Data source |
|---|---|---|---|
| Ecological supply capacity (E) | Resource supply capacity | Total amount of water resources | Water Resources Bulletin |
| Forest cover | Nbs | ||
| Environmental quality level | PM2.5 concentration | China Statistical Yearbook | |
| Proportion of surface water | Water Resources Bulletin | ||
| Ecological regulation capacity | Arable land | International Bureau of Statistics | |
| Carbon emissions | China Carbon Accounting Database | ||
| Level of The welfare Conversion (W) | Basic Coverage | Natural population growth rate | NBSC |
| Number of beds in medical institutions | NBSC | ||
| Development opportunities | Number of undergraduate graduates | NBSC | |
| Expenditure on scientific research | NBSC | ||
| Distributive fairness | Gini coefficient | NBSC | |
| Urban-rural income ratio | NBSC |
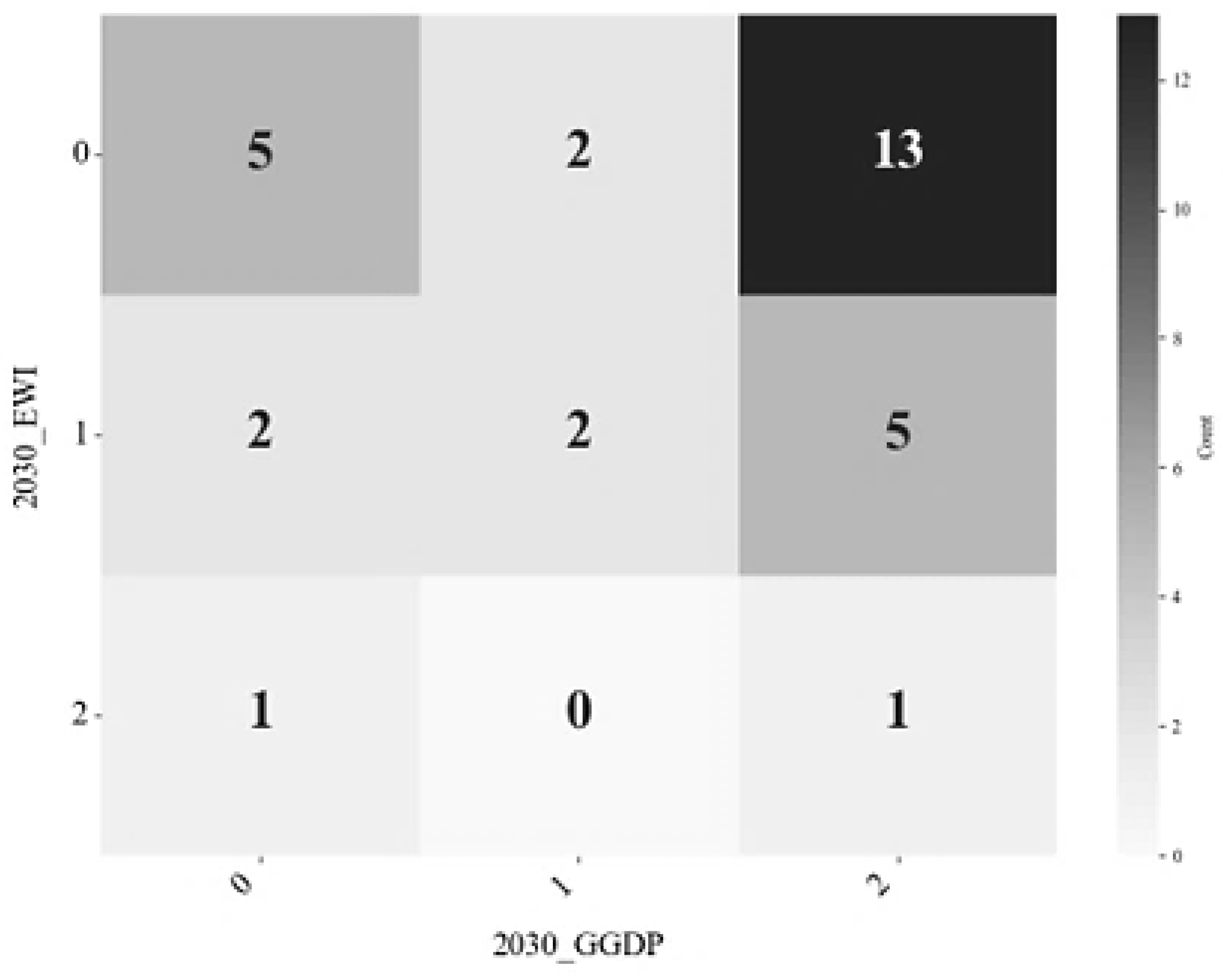
3.2.2. CA-Maekov Predicts the Results of Ecological Welfare-Being (EWI)
4. Robustness Analysis
4.1. Robustness of the Cobb-Douglas-Negative Feedback Model
4.1.1. Robustness Analysis of Green GDP (GGDP) Model
- If , , when increases or decreases, increases;
- If , , when increases or decreases, decreases;
- If , , when increases or decreases, remains constant.
- If ,when increases, increases;
- If ,, when increases, decreases;
- If ,, when increases, remains constant;
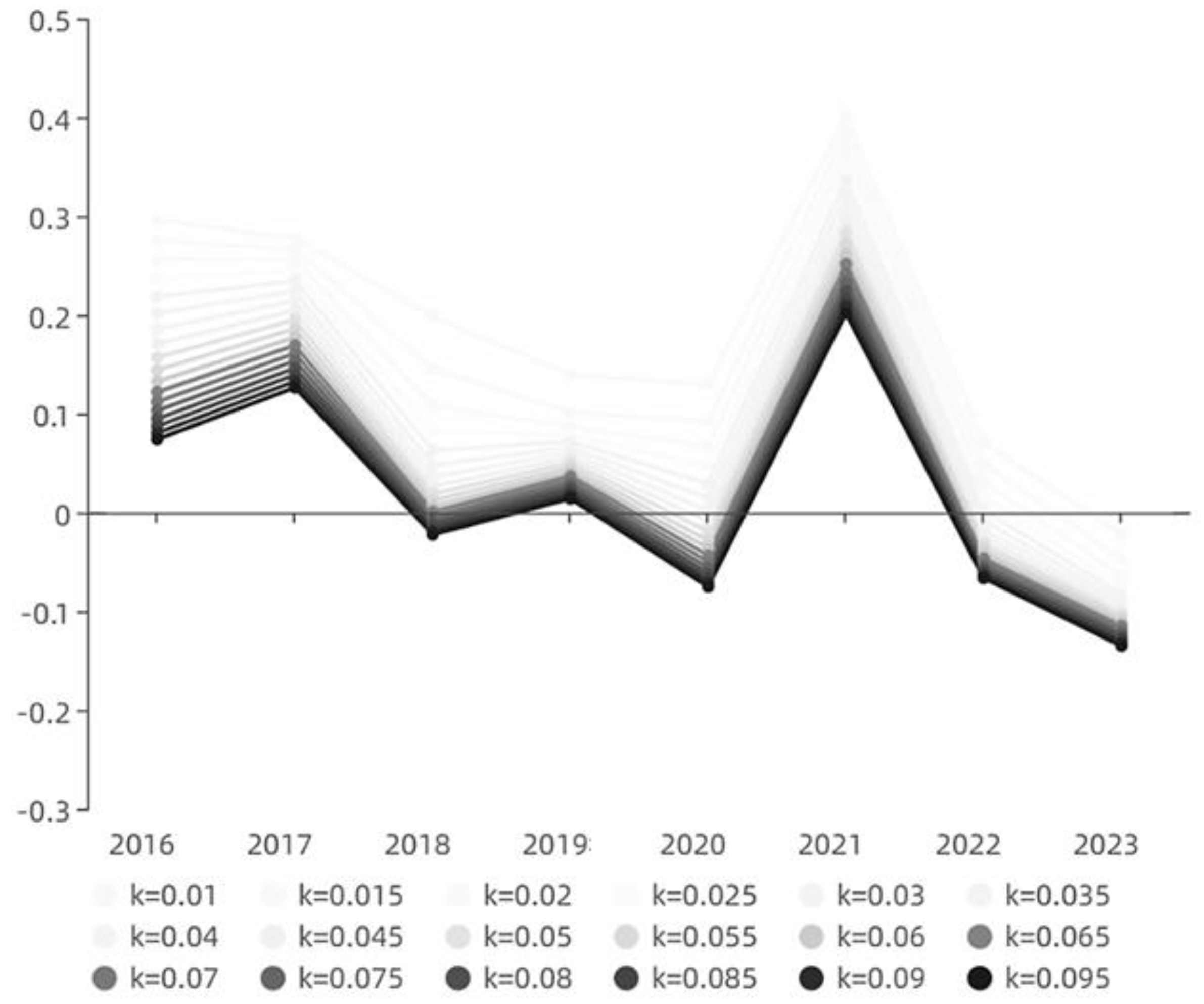
4.1.2. Robustness Analysis of the Green GDP (GGDP) Growth Rate Model
- If the , , ,when increases, increases and decreases;
- If the , , ,when increases, decreases and increases;
- If the , , ,when increases, remains constant. (Fig. 13).
| Model | Target | Time complexity | Spatial complexity |
|---|---|---|---|
| GGDP model | Calculate the GGDP growth rate | ||
| GGDP growth rate correction model | Calculate the GGDP growth rate |
| Condition | Outcome |
|---|---|
| Both GDP and NER growth rates are stable | The growth rate of GGDP is stable |
| GDP and NER growth rates are at least one of them stable | The growth rate of GGDP has plateaued |
4.2. Robustness Analysis of the Double Helix Coupled Model (DHCM)
4.2.1. Robustness Analysis of Ecological Supply Capacity (E)
- From equation (20):
4.2.2. Robustness Analysis of the Welfare Conversion Capacity (W)
5. Conclusions and Recommendations
References
- Talberth J , Bohara A K . Economic openness and green GDP[J]. Ecological Economics, 2006, 58(4):743-758. [CrossRef]
- Boyd J . The Non-Market Benefits of Nature: What Should Be Counted in Green GDP? [J]. Ecological Economics, 2006, 61(4):716-723.
- Li G, Fang C. Global mapping and estimation of ecosystem services values and gross domestic product: A spatially explicit integration of national ‘green GDP’accounting[J]. Ecological Indicators, 2014, 46: 293-314. [CrossRef]
- Sun F , Jia Z , Shen J ,et al. Research on the Accounting and Spatial Effects of Emergy Ecological Footprint and Industrial Green GDP--The Case of Yangtze River Economic Belt[J]. Ecological Indicators, 2024, 163(000):13. [CrossRef]
- Nahman A , Mahumani B K , Lange W J D . Beyond GDP: Towards a Green Economy Index[J]. Development Southern Africa, 2016, 33(2):215-233. [CrossRef]
- Liu Z , Guan D , Moore S ,et al. Climate policy: Steps to China's carbon peak[J]. Nature, 2015, 522(7556):279-281. [CrossRef]
- Yu Y, Yu M, Lin L, et al. National green GDP assessment and prediction for China based on a CA-Markov land use simulation model[J]. Sustainability, 2019, 11(3): 576. [CrossRef]
- Brajer V , Mead R W , Xiao F . Health benefits of tunneling through the Chinese environmental Kuznets curve (EKC)[J]. Ecological Economics, 2008, 66(4):674-686. [CrossRef]
- Wang J . Revive China's green GDP programme[J]. Nature, 2016, 534(7605):37-37. [CrossRef]
- Caviglia-Harris J L , Chambers D , Kahn J R . Taking the "U" out of Kuznets: A comprehensive analysis of the EKC and environmental degradation[J]. Ecological Economics, 2009, 68(4):1149-1159.
- Tang Shaoxiang,Guo Zhi,Zhou Xinmiao. Research on sustainable development of China's economy:green accounting and empirical analysis[M].Shanghai Jiao Tong University Press,2016:63-73.
- FANG Shijiao,XIAO Quan. Study on regional ecological welfare performance level and its spatial effect in China[J].Chinese Population, Resources and Environment, 2019, 29(003):1-10.).
- DONG Ying,SUN Yuhuan,DING Jiao. Acta Geographica Sinica, 2024, 79(5):1337-1354.
- ZANG Mandan,ZHU Dajian,LIU Guoping. Ecological welfare performance: concept, connotation and G20 empirical evidence[J].Chinese Population, Resources and Environment, 2013, 23(5):7.
- Costanza R, d'Arge R, De Groot R, et al. The value of the world's ecosystem services and natural capital[J]. Nature, 1997, 387(6630): 253-260. [CrossRef]
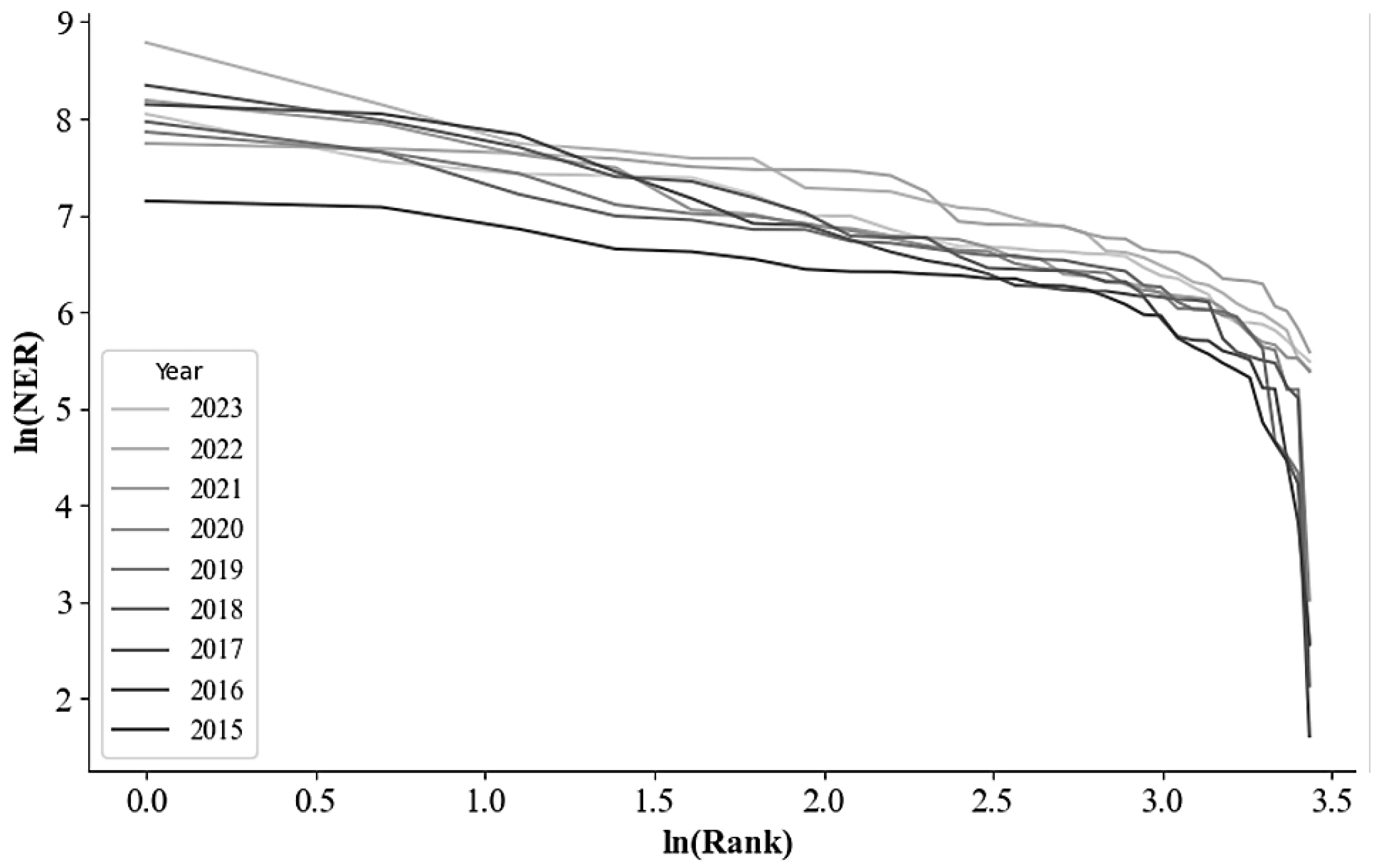
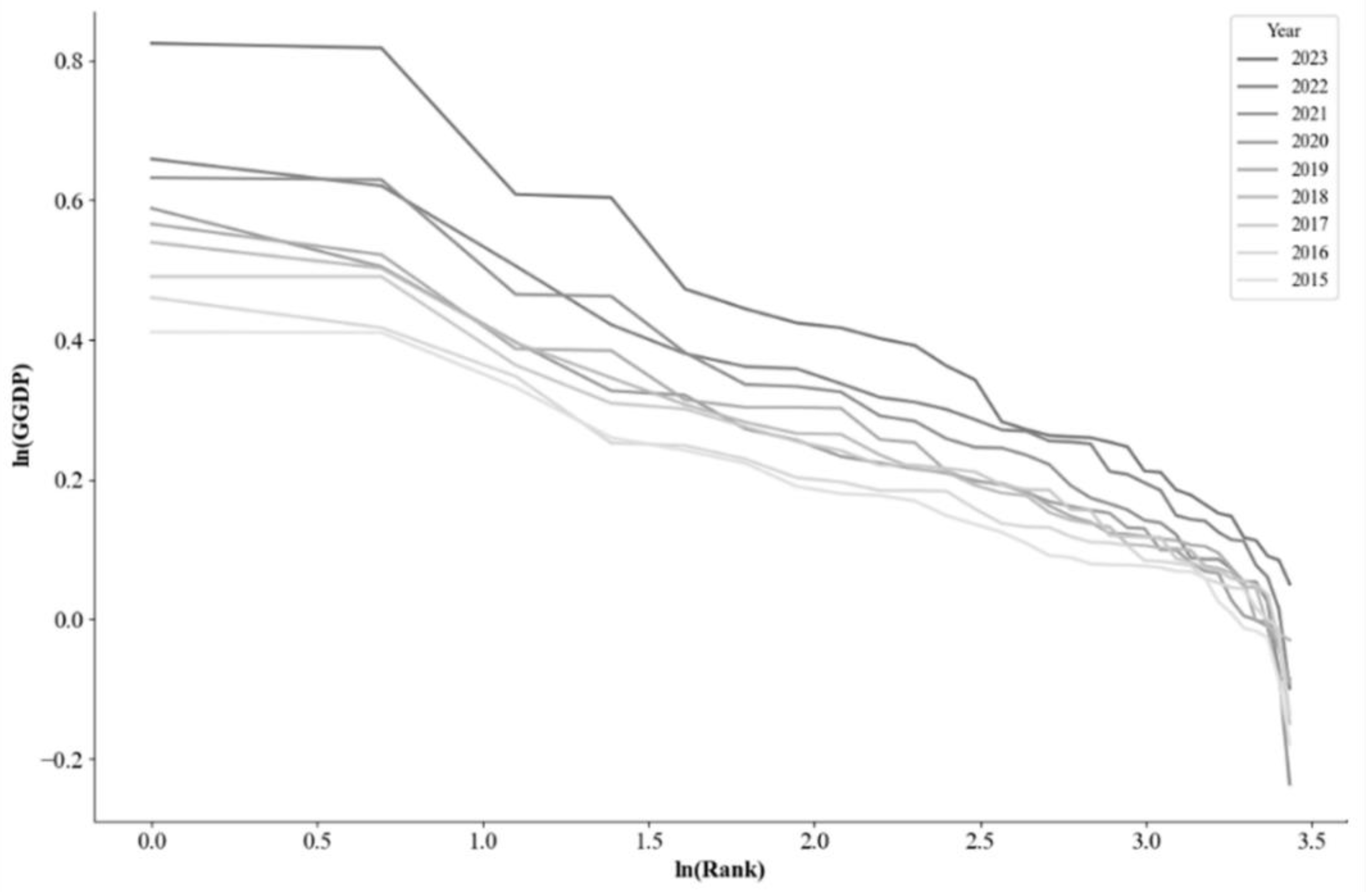
| Argument | Dependent variable | Factors not normalized | Normalization factor | |
| Ln (Rank) | Ln (2015_NER) | -0.850(***) | -0.740(***) | 0.548 |
| Ln (2016_NER) | -1.173(***) | -0.810(***) | 0.656 | |
| Ln (2017_NER) | -1.047(***) | -0.812(***) | 0.659 | |
| Ln (2018_NER) | -0.921(***) | -0.755(***) | 0.570 | |
| Ln (2019_NER) | -0.835(***) | -0.806(***) | 0.650 | |
| Ln (2020_NER) | -0.797(***) | -0.976(***) | 0.952 | |
| Ln (2021_NER) | -0.614(***) | -0.897(***) | 0.805 | |
| Ln (2022_NER) | -0.874(***) | -0.960(***) | 0.921 | |
| Ln (2023_NER) | -0.699(***) | -0.951(***) | 0.903 |
| Yangtze River Delta urban agglomeration | GGDP | GDP | DOWN | |||
|---|---|---|---|---|---|---|
| Shanghai | 1.5285 | -10.55% | 1.3363 | 5.38% | 1.4904 | -22.80% |
| Jiangsu | 2.2659 | 12.96% | 1.9441 | 5.02% | 1.1723 | 22.40% |
| Anhui | 1.4374 | -14.81% | 1.3351 | 5.48% | 1.1780 | -29.54% |
| Zhejiang | 1.8290 | 23.69% | 1.6014 | 5.76% | 1.1930 | 50.05% |
| Beijing-Tianjin-Hebei urban agglomeration | GGDP | GDP | DOWN | |||
|---|---|---|---|---|---|---|
| Beijing | 1.3269 | 8.47% | 1.3104 | 5.34% | 1.1910 | 11.79% |
| Tianjin City | 1.1268 | -3.44% | 1.1076 | 3.75% | 2.0000 | -9.47% |
| Hebei | 1.4087 | -26.24% | 1.3118 | 4.66% | 1.0416 | -44.48% |
| Chengdu-Chongqing urban agglomeration | GGDP | GDP | DOWN | |||
|---|---|---|---|---|---|---|
| Sichuan | 1.6046 | 3.74% | 1.4332 | 6.22% | 1.1786 | 1.36% |
| Chongqing | 1.3122 | -31.21% | 1.2082 | 5.49% | 1.2939 | -52.80% |
| Urban agglomeration in the middle reaches of the Yangtze River | GGDP | GDP | DOWN | |||
|---|---|---|---|---|---|---|
| Hubei | 1.4949 | -23.32% | 1.4007 | 5.81% | 1.1707 | -42.53% |
| Hunan | 1.4800 | -13.96% | 1.3573 | 5.16% | 1.2138 | -27.84% |
| Jiangxi | 1.3009 | -32.95% | 1.2236 | 3.16% | 1.1650 | -48.82% |
| Beibu Gulf urban agglomeration | GGDP | GDP | DOWN | |||
|---|---|---|---|---|---|---|
| Guangxi | 1.2035 | -33.61% | 1.1861 | 3.88% | 1.0835 | -51.89% |
| Guangdong | 2.2809 | 4.35% | 2.0000 | 4.76% | 1.1141 | 3.94% |
| Hainan | 1.0519 | -41.22% | 1.0387 | 9.60% | 1.0204 | -74.09% |
| Argument | Dependent variable | Regression coefficients | Normalization factor | |
| Ln (Rank) | Ln (2015_GGDP) | -0.145*** | -0.951*** | 0.905 |
| Ln (2016_GGDP) | -0.139*** | -0.963*** | 0.928 | |
| Ln (2017_GGDP) | -0.152*** | -0.951*** | 0.904 | |
| Ln (2018_GGDP) | -0.161*** | -0.987*** | 0.974 | |
| Ln (2019_GGDP) | -0.172*** | -0.972*** | 0.944 | |
| Ln (2020_GGDP) | -0.173*** | -0.971*** | 0.942 | |
| Ln (2021_GGDP) | -0.205*** | -0.946*** | 0.894 | |
| Ln (2022_GGDP) | -0.184*** | -0.959*** | 0.920 | |
| Ln (2023_GGDP) | -0.229*** | -0.988*** | 0.976 |
| Classification factor | Classification criteria | Category name |
|---|---|---|
| 0 | Low | |
| 1 | Moderate | |
| 2 | High |
| Classification factor | Classification criteria | Category name |
|---|---|---|
| 0 | Low | |
| 1 | Moderate | |
| 2 | High |
| EWI | 2030/2060 | |||
|---|---|---|---|---|
| 0 | 1 | 2 | ||
| In 2023 | 0 | 0.9500 | 0.0500 | 0.0000 |
| 1 | 0.1429 | 0.8095 | 0.0476 | |
| 2 | 0. 0000 | 0.1190 | 0.8810 | |
| 1 | DONG Han,ZOU Minghua,LI Lu,LI Yan. Correlation and prediction analysis of green GDP accounting based on SEEA[J].Bulletin of Soil and Water Conservation,2024,44(2):187-195,204.) |
| 2 | Kravchenko Maryna,Trofymenko Olena,Kopishynska Kateryna,et al. Ensuring energy security on the basis of intelligent decarbonisation and innovative economic development[J]. E3S THE PAPERB OF CONFERENCES,2024,558. |
| 3 | Renewable Resources and Circular Economy,2021,14(12):43 |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | Gao Yunhong,Zhang Yanshu,Yang Mingjie. 20 Years of Western Development: Northwest vs. Southwest[J]. Regional Economic Review,2020(5):36-51. |
| 10 | Gansu Provincial Forestry and Grassland Bureau 2023 Forestry and Grassland Ecological Protection and Restoration Fund Performance Self-Assessment Report |
| 11 | |
| 12 | In order to eliminate the influence of dimensions, all data in the empirical analysis module are interpolated, with regions ranging from 1 to 2. |
| 13 | |
| 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




