CMB Parity Asymmetry from Unitary Quantum Gravitational Physics

1. Introduction

Understanding and testing the interplay between gravity and quantum mechanics (QM) is the most important key to unraveling the new physics beyond the standard model of particle physics and Einstein’s general relativity (GR). The merge of GR and QM is an essential physics that can be unlocked at the length scales of gravitational horizons. For this, we perhaps need an in-depth understanding of how one can resolve an age-old conundrum in the concept of time between the GR and QM. The success of Quantum field theory (QFT) in Minkowski spacetime ([1]) already teaches us several lessons in this regard. Indeed, QFT is the culmination of special relativity (SR) and QM, where the concept of time already enters into the conflict. In SR, the space and time are on equal footing, but in QM, spatial coordinates are elevated to operators while time is just a parameter due to its anti-unitary nature under the discrete transformation ($\mathcal{T}:t\to -t$). The SR and QM are merged by imposing the commutativity of operators corresponding to space-like distances. The underlying reason is that SR forbids any communication happening in space-like distances, and we respect it and achieve it by formulating new mathematical rules via second quantization. This is exactly the lesson one must keep in mind to understand quantum fields in curved spacetime. That is, we take lessons from classical physics and comply with them according to the rules of quantum physics. The quantum field theory in curved spacetime (QFTCS) is the first step in seeing GR and QM acting together besides the renormalizable ultra-violet complete quantum gravity that may be required at the Planck scales. Furthermore, QFTCS is a necessity in the context of understanding inflationary quantum fluctuations ([2,3,4]).

In this paper, we address crucial questions related to the meaning of time reversal and parity inversions in the context of inflationary background spacetime to place quantum fields on it and uncover their true nature in the cosmic microwave background (CMB). We explain how direct-sum quantum field theory (DQFT), [5,6,7]) is a necessity to solve the unitarity problem of QFTCS. The question of unitarity in QFTCS precedes the question of a completely renormalizable quantum gravity theory of Planck scales. In contrast to the widespread schools of thought that argue unitarity in QFTCS needs to be given up within GR and QM, we propose a new fundamental understanding of this issue and a new observational test using the parity asymmetry in the CMB. We find that the theory of inflationary quantum fluctuations with DQFT (which we call shortly DSI, which stands for "Direct-Sum inflation") fits up to 650 times better than the Standard Inflation (SI). This paper ultimately presents the picture of how a new theory of QFTCS emerged from fundamental questions of quantum gravitational physics that can potentially explain the observed CMB large-scale anomalies. The new results in this paper are further complemented by our more extended companion paper ([8]).

2. DQFT, in a Nutshell ($\hslash =\mathbf{c}=\mathbf{1}$)

DQFT formulation emerges from a simple reconstruction of a quantum state or a quantum field operator through the discrete (a)symmetries (parity $\mathcal{P}$ and time reversal $\mathcal{T}$) of the background spacetime. Here, we summarize the conceptual understanding of DQFT and direct the reader to [5,6,7,8] for more details. Construction of QFT in Minkowski spacetime requires the definition of positive energy state and the arrow of time [9]. Here, we build quantum theory with two arrows of time using the direct-sum Schrödinger equation

$$i{\displaystyle \frac{\partial |\Psi \rangle }{\partial t_p}}=\left(\begin{array}{cc}{\widehat{\mathbb{H}}}_{+}& 0\\ 0& -{\widehat{\mathbb{H}}}_{-}\end{array}\right)|\Psi \rangle$$

(1)

where $\mathbb{H}={\mathbb{H}}_{+}\oplus {\mathbb{H}}_{-}$ is the time-independent Hamiltonian operator (which is Hermitian) that is $\mathcal{P}\mathcal{T}$ symmetric. The quantum state $|\Psi \rangle$ is the direct-sum of two components

$$\begin{array}{ccc}\hfill |\Psi \rangle & =& {\displaystyle \frac{1}{\sqrt{2}}}\left(|{\Psi }_{+}\rangle \oplus |{\Psi }_{-}\rangle \right)={\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{c}|{\Psi }_{+}\rangle \\ |{\Psi }_{-}\rangle \end{array}\right)\hfill \\ \hfill {\int }_{-\infty }^{\infty }\langle \Psi |\Psi \rangle dx& =& {\displaystyle \frac{1}{2}}{\int }_{-\infty }^{\infty }\left[\langle {\Psi }_{+}|{\Psi }_{+}\rangle +\langle {\Psi }_{-}|{\Psi }_{-}\rangle \right]dx=1.\hfill \end{array}$$

(2)

where $|{\Psi }_{+}\rangle ,|{\Psi }_{-}\rangle$ are the two components of the same state at parity conjugate points. The component $|{\Psi }_{+}\rangle$ is a positive energy state that evolves forward in time as $|{\Psi }_{+}{\rangle }_{t_p}=e^{-i\mathbb{E}{t}_p}{|{\Psi }_{+}\rangle }_0$ where the parametric time arrow $t_p:-\infty \to \infty$ while $|{\Psi }_{-}\rangle$ can also be seen as a positive energy state that evolves back in time as $|{\Psi }_{-}{\rangle }_{t_p}=e^{i\mathbb{E}{t}_p}{|{\Psi }_{-}\rangle }_0$ with the parametric time convention $t_p:+\infty \to -\infty$. One can notice here the purely antiunitary character of time associated with the replacement $i\to -i$ ([9]). The direct-sum Schrödinger equation does not have any arrow of time associated with it compared to the conventional Schrödinger equation. The direct-sum splitting of the quantum state as in Eq.2 implies the Hilbert space ($\mathcal{H}$) splitting into a direct-sum of the two (${\mathcal{H}}_{\pm }$) corresponding to parity conjugate points in position space: $\mathcal{H}={\mathcal{H}}_{+}\oplus {\mathcal{H}}_{-}$. Here, the Hilbert spaces ${\mathcal{H}}_{\pm }$ are called the geometric superselection sectors ([5,7]). The position and momentum commutation relations now become double associated with parity conjugate position and momentum space operators denoted by subscripts $+,-$, and their relations are

$$\begin{array}{ccc}\hfill {\widehat{p}}_{+}=-i{\displaystyle \frac{\partial }{\partial x_{+}}}& ;& \left[{\widehat{x}}_{+},{\widehat{p}}_{+}\right]=-\left[{\widehat{x}}_{-},{\widehat{p}}_{-}\right]=i\hfill \\ \hfill {\widehat{p}}_{-}=+i{\displaystyle \frac{\partial }{\partial x_{-}}}& ;& [{\widehat{x}}_{+},{\widehat{x}}_{-}]=[{\widehat{p}}_{+},{\widehat{p}}_{-}]=[{\widehat{x}}_{\pm },{\widehat{p}}_{\mp }]=0.\hfill \end{array}$$

(3)

This framework only makes the wavefunction of the quantum system explicitly $\mathcal{P}\mathcal{T}$ symmetric that resonates with the assumed $\mathcal{P}\mathcal{T}$ symmetry of the physical system, i.e. $[\mathbb{H},\mathcal{P}\mathcal{T}]=0$ and the results of standard quantum mechanics remain the same as shown with the example of harmonic oscillator worked out in [8] (see also further discussions and Fig.1 in [5]). The DQFT in Minkowski spacetime ($d{s}^2=-d{t}_m^2+d{\mathbf{x}}^2$ which is $\mathcal{P}\mathcal{T}$ symmetric) is just built on the direct-sum Schrödinger equation, following how the standard QFT is built on the definition of positive energy state and the causality condition (i.e., commutativity of operators for spacelike distances). See Appendix A for more details.

3. DQFT in de Sitter & Unitarity ($\mathbf{G}=\hslash =\mathbf{c}=\mathbf{1}$)

The de Sitter (dS) spacetime is a perfect testing ground for exploring the theory of QFTCS because of its maximally symmetric aspect, and it is also relevant for unlocking the nature of inflationary quantum fluctuations. Furthermore, a dS spacetime has the closest resemblance with black holes, where the most important conundrums in quantum physics emerge such as the loss of unitarity and the information-loss paradox. We start with the dS metric in the flat Friedman-Lemaître-Robertson-Walker (FLRW) coordinates

$$d{s}^2=-d{t}^2+e^{2Ht}d{\mathbf{x}}^2={\displaystyle \frac{1}{H^2{\tau }^2}}\left(-d{\tau }^2+d{\mathbf{x}}^2\right),$$

(4)

where the scale factor $a=e^{Ht}$ is the clock that determines the expansion of the Universe, $H={\displaystyle \frac{\dot{a}}{a}}$ is the Hubble parameter and $\tau =\int {\displaystyle \frac{dt}{a}}={\displaystyle \frac{1}{aH}}$ is the conformal time. If one has to place quantum theory in dS spacetime Eq.4 the first and foremost things to be understood are the parity and time reversal operations. The usual conception of understanding the expansion of the Universe is to restrict ourselves to $\tau <0$. But the metric carries a symmetry

$$\mathcal{T}:\tau \to -\tau ,\mathcal{P}:\mathbf{x}\to -\mathbf{x}$$

(5)

Restricting to $\tau <0$ before quantization of a classical field (as is usually followed in standard QFTCS) means throwing away the symmetry in Eq.5 by hand. The expanding Universe can be realized in two ways:

$$\begin{array}{cc}\hfill & \Rightarrow \left\{\begin{array}{cc}t:-\infty \to +\infty ,H>0\hfill & (\tau :-\infty \to 0)\hfill \\ t:+\infty \to -\infty ,H<0\hfill & (\tau :\infty \to 0)\hfill \end{array}\right.\hfill \end{array}$$

(6)

This would explain why in the Wheeler-de Witt equation the cosmic time does not explicitly appear, rather the scale factor is the clock that runs with expanding Universe ([10]). Note that $H\to -H$ does not change any properties of the dS space at all. For example, curvature invariants such as the Ricci scalar $R=12H^2$ remain the same under a discrete sign flip of H. Eq.6 illustrates two possible time realizations for an expanding universe. By convention, choosing $\tau >0$ or $\tau <0$ results in loss of information beyond the horizon. In his famous monograph of 1956, Schrodinger [11] rejected the idea of two universes because it would lead to a conundrum of ignorance of information beyond the horizon, which in modern language means pure states evolving into mixed states which leads the violation of unitarity and information-loss ([12,13]).

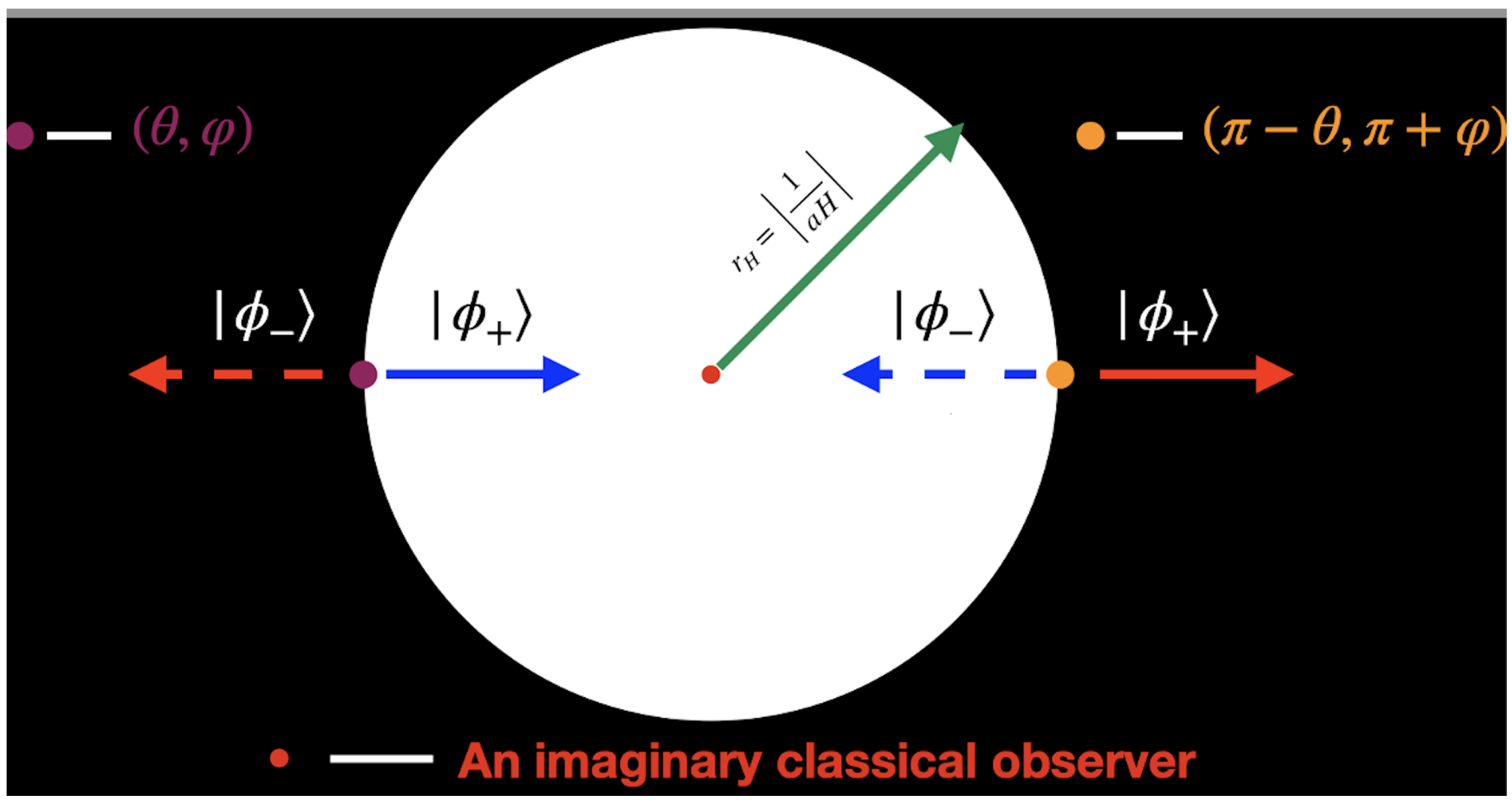
Similar to the Minkowski space (see Appendix A), the quantum fields in the dS space are described through a direct-sum vacuum $|0_T{\rangle }_{\mathrm{dS}}=|0_{+}{\rangle }_{\mathrm{dS}}\oplus {|0_{-}\rangle }_{\mathrm{dS}}$ corresponding to the direct-sum Fock space ${\mathcal{F}}_{\mathrm{dS}}={\mathcal{F}}_{\mathrm{dS}+}\oplus {\mathcal{F}}_{\mathrm{dS}-}$. This implies that everywhere in dS space, a quantum field is tied by time forward and backward evolutions at the parity conjugate points, see Appendix B. At any moment of dS expansion, the parity-conjugate points on the comoving horizon $r_H=\left|{\displaystyle \frac{1}{aH}}\right|$ are space-like separated for an imaginary classical observer as shown in Figure 1.

Note that by DQFT construction, the direct-sum quantum states $|{\varphi }_{\pm }\rangle ={\widehat{d}}_{(\pm )\mathbf{k}}^{†}{|0_{\pm }\rangle }_{\mathrm{dS}}$ that follow from Eq.A6 are the opposite time evolving positive energy states at the parity conjugate points and this holds for any imaginary classical observer. Furthermore, in DQFT the causality and locality are preserved too. A consequence of this is that any state that disappears beyond the horizon happens to be the complimentary direct-sum (component) state that reappears at the antipodal point. This is because all the imaginary classical observers, including those on the horizons of each other, should observe the same direct-sum quantum state $|{\varphi }_{+}\rangle \oplus |{\varphi }_{-}\rangle$.

This means the horizon acts as a $\mathcal{P}\mathcal{T}$ mirror which maps every information outside the horizon to the states inside the horizon. To see this, consider a pure state:

$$|\psi \rangle =\sum _m{d}_m|{\varphi }_m\rangle ,$$

(7)

where $|{\varphi }_m\rangle$ are the eigenvectors, i.e. for any observable (an operator) $\widehat{O}$ we have: $\widehat{O}|{\varphi }_m\rangle ={\lambda }_m|{\varphi }_m\rangle$ where ${\lambda }_m$ are the corresponding eigenvalues. Each ${\lambda }_m$ will be observed in $|\psi \rangle$ with a probability: $P\left({\lambda }_m\right)={\left|d_m\right|}^2$. Consider now the (deSitter) Hubble horizon $r_H=\left|{\displaystyle \frac{1}{aH}}\right|$ around an observer (as illustrated in Figure 1). In the standard approach, information is lost (a pure state becomes a mix state) because communication can not happen for space-like distances (i.e. outside the horizon) as was shown by Gibbons and Hawking in 1977 [12], in analogy to what happens in Hawking radiation and the black hole information loss paradox [6,14]. This also implies the lost of unitarity in QFT on spacetimes with horizons. In the DQFT approach we have:

$$|\psi \rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{c}\sum d_m^{+}|{\varphi }_m^{+}\rangle \\ \sum d_m^{-}|{\varphi }_m^{-}\rangle \end{array}\right)\equiv {\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{c}|{\psi }^{+}\rangle \\ |{\psi }^{-}\rangle \end{array}\right)$$

(8)

where $|{\varphi }_m^{\pm }\rangle$ are the eigenvectors corresponding to each $\mathcal{P}\mathcal{T}$ separated Hilbert space. So that the observable probabilities and operators become:

$$P\left({\lambda }_m^{\pm }\right)={\left|d_m^{\pm }\right|}^2\mathrm{and}\widehat{O}=\left(\begin{array}{cc}{\widehat{O}}_{+}& 0\\ 0& {\widehat{O}}_{-}\end{array}\right)$$

(9)

Information is not lost in this case because there is not entanglement across the horizon. To see this more clearly, consider the case where $|\psi \rangle$ is a pure entangled system $|{\psi }_{AB}\rangle =|{\psi }_A\rangle \otimes |{\psi }_B\rangle$:

$$|{\psi }_{AB}\rangle =\sum _{m,n}{d}_{mn}|{\varphi }_{Am}\rangle \otimes |{\varphi }_{Bn}\rangle ,$$

(10)

where ⊗ represents the tensor product of two Hilbert spaces A and B which are entangled (inseparable or correlated): $d_{mn}\ne d_m{d}_n$ with: $|{\varphi }_A\rangle ={\sum }_m{d}_m|{\varphi }_{Am}\rangle$ and $|{\varphi }_B\rangle ={\sum }_n{d}_n|{\varphi }_{Bn}\rangle$. For example, a pair of particles (across the horizon). In the DQFT approach, we have:

$$|{\psi }_{AB}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{c}\sum d_{mn}^{+}|{\varphi }_{Am}^{+}\rangle \otimes |{\varphi }_{Bn}^{+}\rangle \\ \sum d_{mn}^{-}|{\varphi }_{Am}^{-}\rangle \otimes |{\varphi }_{Bn}^{-}\rangle \end{array}\right)\equiv {\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{c}|{\psi }_{AB}^{+}\rangle \\ |{\psi }_{AB}^{-}\rangle \end{array}\right)$$

(11)

where $|{\varphi }_{Am}^{\pm }\rangle$ and $|{\varphi }_{Bn}^{\pm }\rangle$ are the eigenvectors corresponding to each $\mathcal{P}\mathcal{T}$ separated Hilbert spaces, which remain within the horizon because no information is exchanged across $\mathcal{P}\mathcal{T}$ separated spaces. All information about the entanglement pairs is mapped within the horizon; thus, the pure state will remain pure. In other words, DQFT forbids any entanglement beyond the gravitational horizons. DQFT constructs a direct-sum Hilbert space with the interior and exterior separated by a geometric superselection rule (which is similar to the concept of superselection sectors in QFT [15,16]). Thus, there would be an observer complementarity (see Fig.3 in [5]). We can also understand the same from the point of view of dS space in static coordinates, which reads as

$$\begin{array}{cc}\hfill d{s}^2& =-\left(1-H^2{r}^2\right)d{t}_s^2+{\displaystyle \frac{1}{\left(1-H^2{r}^2\right)}}d{r}^2+r^{2}d{\Omega }^2\hfill \\ \hfill & ={\displaystyle \frac{1}{H^2{\left(1-UV\right)}^2}}\left(-4dUdV+{\left(1+UV\right)}^{2}d{\Omega }^2\right)\hfill \end{array}$$

(12)

where $r=\left|{\displaystyle \frac{1}{H}}\right|{\displaystyle \frac{1+UV}{1-UV}}$ and ${\displaystyle \frac{V}{U}}=-e^{2H{t}_s}$. The relation between the flat FLRW Eq.4 and Eq.12 is just a simple coordinate change ([17,18]). A very practiced view of flat dS spacetime in Eq.4 is that it covers only half of the dS space. However, we must keep in mind the symmetry in Eq.6, which implies that Eq.4 can cover the entire dS space. Thus, the maximally symmetric nature of the dS spacetime sets no difference whether it is expressed in flat, closed, open FLRW coordinates or the static coordinates ([19]). 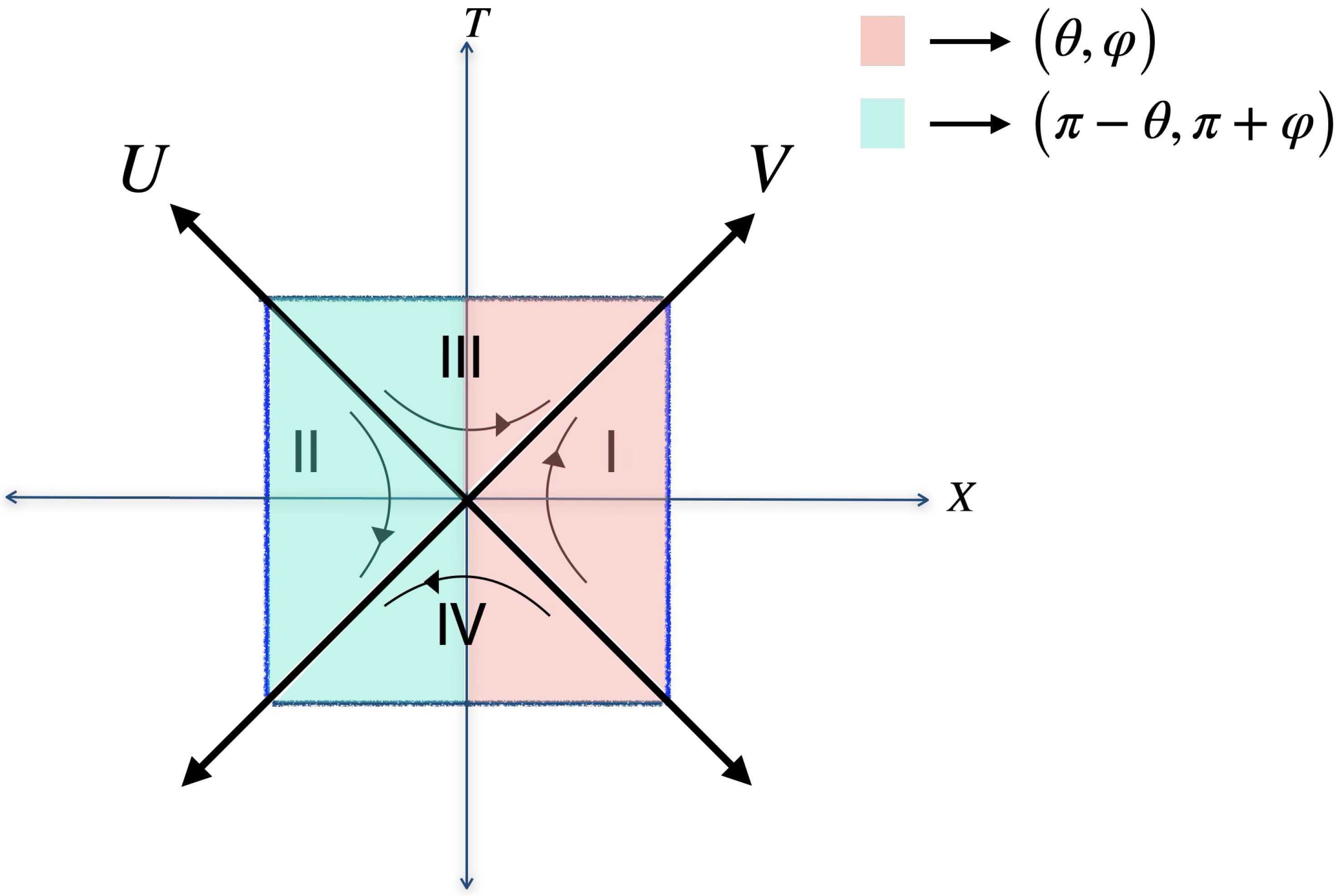The use of mapping flat coordinates to static coordinates here is so that we can realize how unitarity can be achieved with DQFT, whereas it is lost in standard QFT, as was shown by Gibbons and Hawking in 1977 [12]. In Figure 2, we show unitary quantum physics in the static dS space through the (quantum) conformal diagram, where we see the three-dimensional space divided by parity for the interior and exterior of the cosmological event horizon. We can picture here how none of the observers loses any information beyond the horizon. If any state leaves the horizon, it is only the (complimentary) direct-sum component of what is inside the horizon. This means that any observer can perfectly reconstruct the information about what is beyond the horizon. According to DQFT, every density matrix of a maximally entangled pure state is split into direct-sum of 4 components

$$\rho =\left({\rho }_I\oplus {\rho }_{II}\right)\oplus \left({\rho }_{III}\oplus {\rho }_{IV}\right)$$

(13)

Each density matrix ${\rho }_n,n=I,II,III,IV$ is defined by a pure state component in the corresponding (geometric) superselection sector Hilbert space ${\mathcal{H}}_n$. Since Von Neumann entropy of each component of density matrix vanishes $S_n=-Tr{\rho }_{n}ln{\rho }_n=0$, any observer in regions I, II, III, IV (see Figure 2) would witness pure states evolving into pure states. Thus, with DQFT we can have both unitarity and observer complementarity in dS ([5]).

According to DQFT, any state is spread across the horizon by distinct components in geometric superselection sectors. This implies that any information of the entangled state is shared by the sectorial Hilbert space, leading to pure states evolving into pure states. To be precise, the Hilbert spaces of the interior and exterior states cannot be connected by direct product (⊗) but rather should be related by direct-sum (⊕). This has to be like this because beyond-the-horizon time is not the same, so one cannot do the same quantum mechanics everywhere. In other words, the gravitational horizons are special, they separate different spacetimes by a boundary. Thus, they cannot be treated as a standard null surface, where quantum states can be entangled across. Furthermore, we stress that no entanglement across the horizon does not lead to firewalls, which happens in standard QFTCS but not in direct-sum QFTCS. For further analogous discussion on unitarity and no information loss in the context of the Schwarzschild black hole, see [6]. In a nutshell, DQFT offers a new understanding of dS space where any observer’s physics of the universe is complete, and no information is lost outside any observer’s universe. This is exactly what Schrödinger envisioned in 1956 for a quantum theory to achieve [11]. Furthermore, our achievement of DQFT echoes well with the recent classical understanding of dS through the Black Hole Universe (BHU) proposal [20,21,22].

4. CMB Parity Asymmetry

Inflationary quantum fluctuations are the initial seeds for large-scale structure formation. It is important to understand their quantum nature to derive consistent CMB predictions. Inflation is by definition a quasi-dS expansion ([23]) and this means that $\mathcal{P}\mathcal{T}$ in Eq.6 is spontaneously broken by the presence of a non-perturbative scalar field in addition to the GR’s tensor degree of freedom. Our focus here is on single-field inflation. The metric and scalar field matter quantum fluctuations are generated during inflation. The quantity which is a gauge-invariant combination of them is called the curvature perturbation ($\zeta$), and it is an effective (scalar) degree of freedom. It connects the quantum physics of inflation to CMB observations. The action for curvature perturbation at the linear order is

$${\delta }^{\left(2\right)}{S}_s={\displaystyle \frac{1}{2}}\int d\tau d^{3}x{a}^2{\displaystyle \frac{{\dot{\varphi }}^2}{H^2}}\left[{\zeta }^{\prime 2}-{\left(\partial \zeta \right)}^2\right],$$

(14)

where $H={\displaystyle \frac{\dot{a}}{a}}$ which is nearly constant during inflation characterized by the smallness of slow-roll parameters $ϵ=-{\displaystyle \frac{\dot{H}}{H^2}},\eta ={\displaystyle \frac{\dot{ϵ}}{Hϵ}}$ for $N=50-60$ number of e-foldings. The canonical variable which is a redefinition of curvature perturbation that we eventually quantize is

$$v=a\zeta \dot{\varphi }/H$$

(15)

In the framework of Direct-sum Inflation (DSI), the canonical variable is promoted to field operator that is split into direct-sum of two components

$$\begin{array}{cc}\hfill \widehat{v}& ={\displaystyle \frac{1}{\sqrt{2}}}\left(\begin{array}{cc}{\widehat{v}}_{(+)}\left(\tau ,\mathbf{x}\right)& 0\\ 0& {\widehat{v}}_{-}\left(-\tau ,-\mathbf{x}\right)\end{array}\right)\hfill \end{array}$$

(16)

which generate quantum fields in a direct-sum vacuum

$${|0\rangle }_{\mathrm{qdS}}={|0\rangle }_{{\mathrm{qdS}}_{\mathrm{I}}}\oplus {|0\rangle }_{{\mathrm{qdS}}_{\mathrm{II}}}=\left(\begin{array}{c}{|0\rangle }_{{\mathrm{qdS}}_{\mathrm{I}}}\\ {|0\rangle }_{{\mathrm{qdS}}_{\mathrm{II}}}\end{array}\right)$$

(17)

in which they evolve forward and backward in time at the parity conjugate points in physical space. In analogy with Eq.6, the time reversal operation (quantum mechanically) in an expanding quasi-dS Universe is

$$\tau \to -\tau \Rightarrow (t,H,ϵ,\eta )\to (-t,-H,-ϵ-\eta ).$$

(18)

These sign differences in the slow-roll parameters, which break the time-reversal symmetry of de Sitter spacetime, lead to corrections in the evolution of quantum fluctuations ${\widehat{v}}_{(\pm )}$ in the parity-conjugate regions. This results in an asymmetry in the CMB temperature under spatial parity.

In spherical coordinates, the parity transformation maps a point at radial distance r from angular position $(\theta ,\phi )$ to its antipode, $(\pi -\theta ,\pi +\phi )$. This transformation cannot be realized by any rotation, and thus represents a discrete global symmetry distinct from statistical isotropy. It is important to emphasize that this global spatial parity asymmetry is unrelated to the observed birefringence in the CMB polarization, which arises from parity-violating interactions with well-defined transformation properties [24].

The CMB provides temperature fluctuations $\mathcal{T}\left(\widehat{n}\right)\equiv \Delta T\left(\widehat{n}\right)/T_0$ all over the sky $\widehat{n}$:

$$\mathcal{T}\left(\widehat{n}\right)=\sum a_{\ell m}{Y}_{\ell m}\left(\widehat{n}\right);C_{\ell }=\sum _m{\displaystyle \frac{|a_{\ell m}{|}^2}{2\ell +1}}$$

(19)

the Fourier coefficients $a_{\ell m}$ are characterized by the angular power spectrum $C_{\ell }$. Because $\mathcal{T}$ (and $\mathcal{P}\mathcal{T})$ is broken by the slow-roll parameters in Eq.18, we expect the quantum field during inflation to evolve time asymmetrically at parity conjugate points in physical space. This leads to an angular power spectrum $C_{\ell }$ of the CMB exhibiting an excess of power in the odd multipoles compared to the even ones, as described by Eq.A7 in Appendix C.

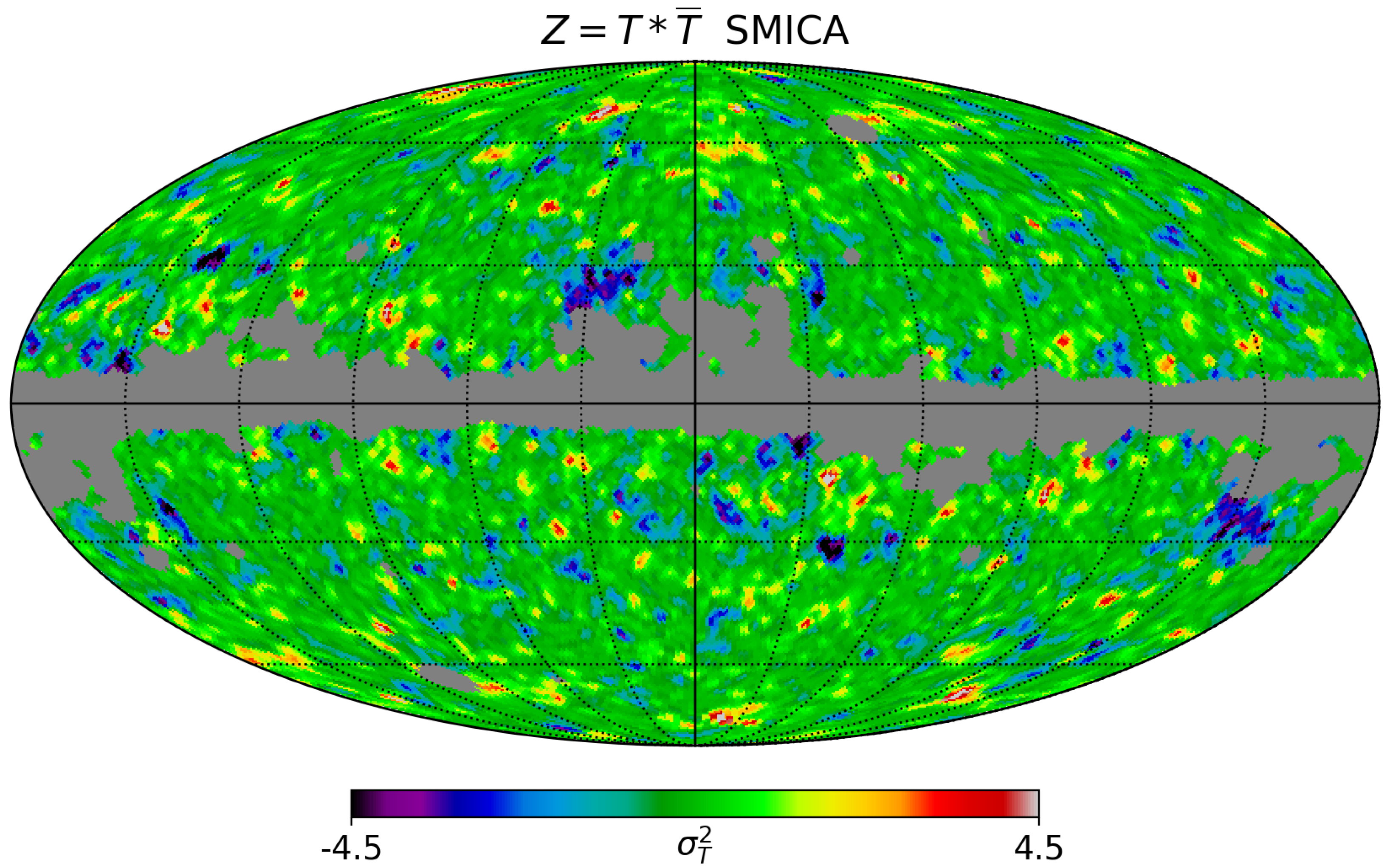
In Figure 3, we can visually see the parity asymmetry by the close resemblance between odd-parity temperature maps and the original CMB maps from Planck data ([25]). This reflects that the CMB temperature maps contain an additional pure odd-parity component. The DSI framework exactly generates this additional odd symmetry, as we can see in Eq.A7. It is worth noticing here that if we take the average of even and odd power spectra, we recover the well-known near-scale invariant power spectrum of Standard Inflation (SI). The benefit of DSI is that there are no additional free parameters. The parity asymmetry only depends on the spectral index $n_s\approx 0.9634\pm 0.0048$ on the pivot scale $k_{*}=0.05{\mathrm{Mpc}}^{-1}$ ($\ell \approx 800$) as measured by Planck data ([26]).

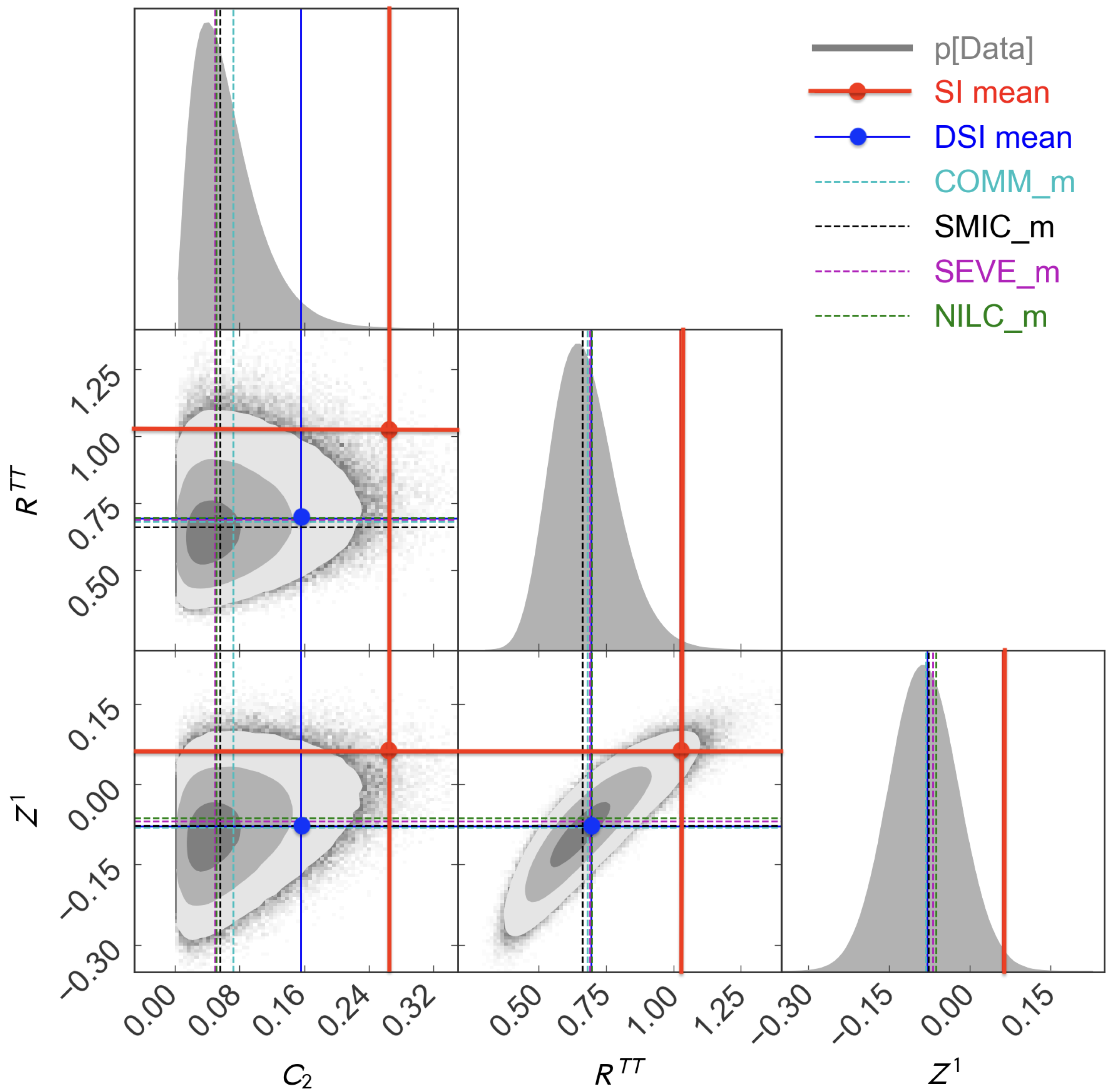
In Figure 5 we present how the observational data significantly prefer DSI over SI. Observed quantities include the observed low quadrupolar amplitude $C_2=C_{\ell =2}$, the even-to-odd multipole ratio of angular power spectra:

$$R^{TT}={\displaystyle \frac{{\sum }_{\ell =even}^{\ell max=20}\ell (\ell +1)C_{\ell }}{{\sum }_{\ell =odd}^{\ell max=20}\ell (\ell +1)C_{\ell }}}$$

(20)

and the mean $Z^1=<Z\left(\widehat{n}\right)>$ of the parity map $Z\left(\widehat{n}\right)\equiv \mathcal{T}\left(\widehat{n}\right)\mathcal{T}(-\widehat{n})$ displayed in Figure 4, where $-\widehat{n}=(\pi -\theta ,\pi +\phi )$ represents the parity conjugate or antipode of the sky position $\widehat{n}=(\theta ,\phi )$. The likelihood probability associated with DSI in these plots is up to 650 times larger than that of SI. DSI favors odd parity, leading to a lower $C_2$. This, in turn, diminishes the significance of other CMB anomalies ([27]), such as the Hemispherical Power Asymmetry, the axis of Evil, and the anomalous 2-point correlation function (see [8] for further details).

5. Conclusions

In this paper, we underscore the pivotal role of unitary Quantum Field Theory in Curved Spacetime (QFTCS) in elucidating the intricacies of early Universe physics. Contrary to prevailing notions, we contend that the issue of unitarity in QFTCS is not inherently tied to quantum gravity at Planck scales, but rather stems from throwing away the $\mathcal{P}\mathcal{T}$ symmetry for quantum fields in curved spacetime.

With the $\mathcal{P}\mathcal{T}$-symmetric formulation of Schrödinger equation Eq.1, the DQFT framework reinstates unitarity, which was previously thought to be lost in curved spacetime. Figure 1and Figure 2 visually represent this concept, illustrating how a hypothetical classical observer consistently experiences pure states without encountering information loss beyond the horizon. Furthermore, the striking correlation illustrated in Figure 3, Figure 4 and Figure 5 between the observed hot and cold mirrored structures of the CMB map at antipodal points strongly supports the unitary treatment of inflationary quantum fluctuations within the framework of DQFT. Our findings indicate that superhorizon fluctuations at antipodes manifest as $\mathcal{P}\mathcal{T}$ conjugates, a prediction derived from direct-sum QFTCS. This prediction is substantially favored with a probability over 650 times greater than that of the standard QTFCS.