Modelling Desorption Rates and Background Concentrations of Heavy Metals Using a One-Dimensional Approach

1. Introduction

Heavy metal pollution poses a global environmental concern due to its severe toxicity [1,2], long-term persistence, and bioaccumulation in food chains [3,4,5]. Harmful heavy metals (HHM) are continuously introduced into the environment [6] through natural and anthropogenic sources [7,8]. In estuarine waters, the presence of HHM is generally observed in two distinct phases: dissolved in the water column and particulate adsorbed on the sediments. The partitioning of HHM between these phases depends on the physical and chemical characteristics of suspended particles [9,10], in conjunction with environmental conditions such as salinity, pH, and dissolved organic matter [10].

Upon entering surface waters, HHM are transported by rivers through wash load transport and eventually accumulate in marine sediments. Hydro-sedimentary processes such as desorption [11], resuspension and dredging can release these contaminants back into the overlying water column [12], affecting water quality, the marine environment, and human health. Although HHM adsorption initially occurs near areas with significant anthropogenic activities, this study emphasizes the downstream consequences, particularly focusing on sediment contamination.

Various researchers rely on predicting interactions between water and sediments as a critical method for understanding HHM pollution [5,13,14,15]. Mathematical models have become powerful tools to address complex research questions related to coastal environments offering reliable, cost-effective, and time-saving approaches [16].

Specifically, reaction-transport models, as described by Boudreau [17], Lynch and Officer [18], and Nicolis [19], have been pivotal in advancing sediment diagenesis and biogeochemical modelling, integrating key processes such as molecular diffusion, advection, and chemical reactions. These frameworks form the theoretical foundation of this study, focused on the vertical distribution and temporal evolution of HHM in sediments.

Previous studies, such as, Wu et al. [10], developed a two-dimensional (2D) transport model, later integrated into a one-dimensional (1D) framework to simulate the movement of dissolved and particulate HHM along estuaries. However, these models did not explicitly address the accumulation of HHM contaminants or their subsequent phase evolution within the substrate, a significant gap in understanding the long-term impacts and interactions of HHM with sediment dynamics.

This study proposes a novel approach that integrates both dissolved and particulate HHM phases. Four critical hydrodynamic processes are quantified and modeled to evaluate their influence on HHM dynamics. This model, in accordance with empirical data, assumes that the dissolved-phase concentration ($C_d$) is considerably lower than the particulate-phase concentration ($C_p$) in the water column ($C_d$<< $C_p$). This assumption aligns with the concept of the infinite dilution diffusion coefficient [17], thereby providing a more realistic representation of HHM in sediments.

To demonstrate the model’s applicability, simulations were referenced against estuarine conditions in the Cartagena Bay, Colombia (CB), a system subject to intense sedimentation and HHM inputs. Results obtained through this model align closely with empirical observations, reinforcing its validity.

A novel 1D mathematical model is developed to investigate HHM dynamics in estuarine sediments and to elucidate the processes HHM governing background concentrations ($C_{bg}$). These concentrations serve as critical indicators for identifying anthropogenic inputs [20] and facilitate the formulation of effective management and remediation strategies [7,21]. This research represents the first attempt to establish$C_{bg}$of HHM in Colombia, highlighting its significance in addressing local and regional environmental concerns.

The model is applicable beyond the specific conditions of the Colombian coastline and could be effectively extended to various aquatic systems, including rivers, estuaries, and lakes worldwide affected by sediment contamination. Model outputs, including dynamic profiles illustrating the temporal drift of $C_{bg}$are presented and critically discussed.

2. Materials and Methods

2.1. Cartagena Bay: A Reference System for Estuarine Conditions

CB is a semi-enclosed estuarine system on Colombia’s Caribbean coast, (10°16′–10°26′ N, 75°30′–75°35′ W), with an average depth of 16 m, a maximum depth of 32 m, and a surface area of 84 km² [22]. The bay receives large amounts of sediments [23], nutrients, wastewater runoff [24], and contaminants from the Dique Channel [25,26], an artificial structure connected to the extensive Magdalena River basin (260,000-km²) [26,27].

The Magdalena River transports a sediment flux of 184 Mt yr⁻¹ and delivers the highest freshwater discharge (6 496 m³ s⁻¹) and sediment load (144 Mt yr⁻¹) to the Caribbean [26,27]. Seasonal rainfall from the Magdalena River, where the Dique Channel diverges, strongly influence the hydrology and sediment quality of CB [28]. Due to wash load transport, HHM adsorption does not occur in CB but rather in distant sources before HHM are transported downstream. This explains the HHM accumulation in precipitated sediments.

2.2. Mathematical Model

2.2.1. Definition of the Physical Problem

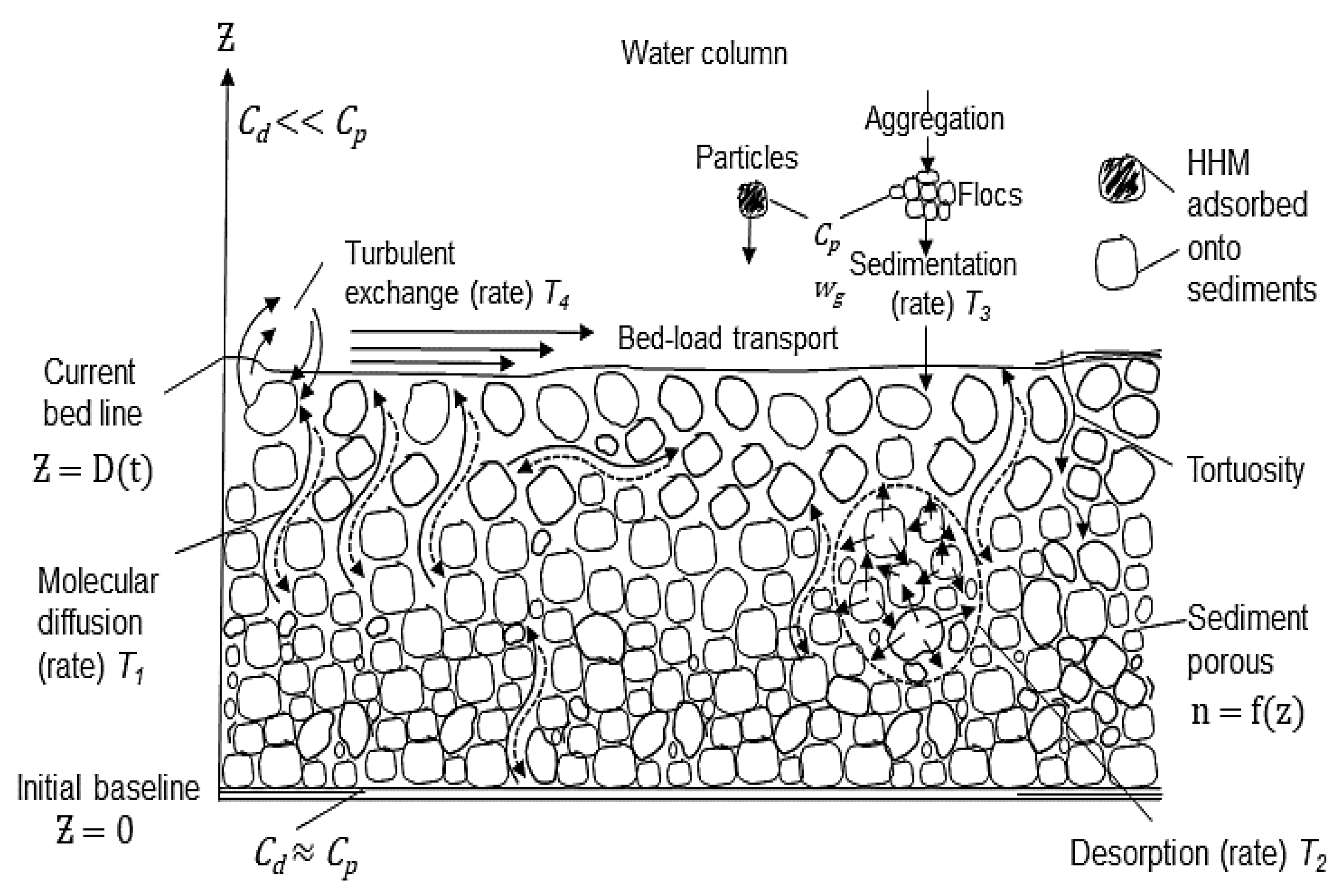
This research considers wash load transport [29] of fine cohesive sediments (silt and clay) loaded with HHM in particulate form. The primary source of HHM is the rapid upstream industrialization in the Magdalena River. Particles are deposited at the bottom in the form of flocs. In the porous medium of precipitated sediments, desorption continues but at a lower rate than that during transport in the water column.

In the water column, HHM exist in colloidal, particulate, and dissolved phases. The concentration of HHM in dissolved form ($C_d$) is generally lower than that in particulate form ($C_p$). Hereafter, we assume that $C_d$ concentrations are multiplied by the constant K_d, which represents the equilibrium distribution coefficient. In the sediment substrate, these concentrations are also assumed to reach equilibrium due to limitations in molecular diffusion, which is partially restricted by porosity (n) and tortuosity ($\theta ).$ Lower porosity and higher tortuosity restrict molecular diffusion, reducing HHM exchange with overlying waters and consequently promoting high accumulation and persistence within the sediment layer.

Tortuosity quantifies the complexity of pore pathways through which water and dissolved substances, such as HHM, move within sediment layers [30]. Porosity, defined as the ratio of pore volume to total sediment volume [17], also plays a critical role in transport dynamics. Lower porosity implies fewer and smaller pores, restricting mobility and facilitating contaminant accumulation. As sediment compacts over time, porosity typically decreases with depth (z), becoming a time-dependent function. This leads to a gradual increase in substrate thickness in the absence of resuspension.

The desorption rate$\left(\gamma \right)$, reflects the release of HHM from $C_p$to $C_d$ and depends on the grain diameter of sediments ($d_{50}$), their porosity (n), salinity (S), and pH. The porosity and tortuosity together influence molecular diffusion, calculated in the model using the Schmidt number (Sc), a dimensionless parameter to characterizes the relationship between the molecular viscosity of water and the diffusion of substances [31].

A 1D vertical model was formulated, neglecting the horizontal dispersion of HHM, with the vertical axis directed upward from z = 0 (the reference level is assumed to be the starting point of sedimentation, as shown in Figure 1). The 1D model can be considered a sufficient approximation, considering that (a) the relationship between the vertical scale of the sediment layer and its horizontal extent along an estuary or river is small, and (b) exchange processes in the substrate in the vertical direction are much faster than the horizontal dynamics.

The domain is defined as $\left\{0\le z\le D\left(t\right);t\ge 0\right\}$, where D = sediment thickness as a function of time (t). At the initial time, D was set as D(t = 0) = 0. To avoid singularities when solving the differential equations of the model, we assumed that ${\displaystyle \frac{\partial D}{\partial t}}>0,\forall t$under the absence of resuspension. The dynamics of the layer D(t) are expressed as follows:

$${\displaystyle \frac{\partial D}{\partial t}}={-w}_g{C}_v{\left(1-n\right)}^{-1}={\displaystyle \frac{{-w}_g{\left(1-n\right)}^{-1}{C}_m}{{\rho }_{S,}}}$$

(1)

where $w_g$is the settling velocity of sediments due to gravity, given by the Stokes formula ($w_g<0$), and $C_v$, $C_m$, and ${\rho }_s$ are the volumetric and mass concentrations of suspended sediments, and their density, respectively. Within the bottom substrate, the molecular diffusion flux of the dissolved fraction $C_d$ is defined as:

$$Q={\alpha }_S\nu {\displaystyle \frac{\partial C_d}{\partial z}},$$

(2)

where $\nu$ is the kinematic molecular viscosity of water (Constant) and ${\alpha }_S$ defines the inverse Schmidt number (${\alpha }_S={Sc}^{-1}$) [31], which generally depends on time and substrate level or porosity n.

To determine the desorption rate $\gamma =f\left(d_{50},n,S,pH\right)$, at least three timescales must be considered: 1) the molecular diffusion rate (T₁) of HHM, 2) the desorption rate (T₂), and 3) the sediment deposition rate (T₃) at the bottom, as follows:

$$T_1={\displaystyle \frac{D_0^{2}Sc}{\nu }},$$

(3)

$$T_2={\displaystyle \frac{1}{2\gamma }},$$

(4)

$$T_3={\displaystyle \frac{D_0}{w_g{C}_v}}$$

(5)

The parameters of the model, particularly sedimentation and desorption rates were calibrated within observed HHM concentrations reported in empirical data from CB [24,25,27,32]. The resulting optimization problem was numerically solved using FORTRAN program, with an implicit time-stepping scheme to ensure numerical stability under varying sediment thicknesses and boundary conditions.

Table 1. State variables and parameters used in this study.

Parameter	Description	Unit	Value	Reference
$C_{bg}$	HHM Background concentration	g L⁻¹, mg kg⁻¹ (dw)*	see Table 2	calculated
$C_D$	Drag coefficient	/	2 × 10⁻³	[33]
$C_d$	Dissolved-phase HHM concentration	g L⁻¹, mg kg⁻¹ (dw)*	/	calculated
Cm	Suspended-sediment mass concentration	g L⁻¹	/	[34]
$C_p$	Particulate-phase HHM concentration	g L⁻¹, mg kg⁻¹ (dw)*	/	calculated
$C_{p0}$	Initial particulate HHM at precipitation	g L⁻¹	/	assumed
$C_v$	Suspended-sediment volumetric concentration	/	10⁻⁴–10⁻⁵	assumed
d50	Median grain diameter of sediment	m	/	measured
D	Sediment thickness	m	0–1.6**	calculated
F	Porosity–tortuosity factor	/	/	calculated
HHM	Harmful heavy metals	g L⁻¹, mg kg⁻¹ (dw)*	varies	measured
$K_d$	Coefficient of equilibrium distribution	/	/	assumed
m	Exponent in the relationship of Sc and n	/	/	literature
N	Number of computational nodes	/	100	assumed
n	Porosity	/	0.4	[35]
Q	Molecular diffusion flux	kg m⁻² s⁻¹	varies	calculated
S	Salinity	/	0.06-35.7	assumed
$S_C$	Schmidt number	/	10–100	[6]
t	Time	s	0–8.64 × 10⁸ s	assumed
T1	Molecular diffusion rate	yr	0.3–3	calculated
T2	Desorption rate	yr	3.15 (for γ=5×10⁻⁸)	calculated
T3	Sediment rate	yr	>31	calculated
T4	Turbulent exchange rate	yr	/	calculated
$u_{*}$	Friction (dynamic) velocity	m s⁻¹	0–0.01	assumed
$w_g$	Settling velocity of sediments due to gravity	m s⁻¹	10⁻⁵	assumed
y	Dimensionless vertical coordinate	/	0–1	calculated
$z$	Vertical level within the substrate	m	0–1.6	calculated
$z_0$	Roughness parameter	m	/	literature
${\alpha }_S$	Inverse Schmidt number $\left({\mathrm{S}\mathrm{c}}^{-1}\right)$	/	0.01–0.1	[31]
γ	Desorption coefficient	s⁻¹	5×10⁻⁸–1×10⁻⁹	[36]
$∆y$	Vertical grid size in dimensionless coordinates	/	1/(N−1)	calculated
θ	Tortuosity	/	/	[30]
$\kappa$	Karman constant	/	0.41	literature
ν	Kinematic molecular viscosity of water	m² s⁻¹	10⁻⁶	constant
${\rho }_s$	Sediment–particle density	kg m⁻³	2 650	[33]
${\chi }_0$	Molecular diffusion coefficient (water only)	m² s⁻¹	/	[17]
${\chi }_S$	Molecular diffusion coefficients (with sediments)	m² s⁻¹	/	calculated

*Cd and Cp represent concentrations expressed in g L⁻¹ or kg m⁻³ in the model for consistency, but in the figures, they are presented in mg kg⁻¹ dry weight (dw) for easier comparison with laboratory data. Laboratories generally measure HHM concentrations in mg kg⁻¹, dw. Note that this difference in units is important when interpreting model results and comparing them with laboratory data or figures. ** D (0–1.6 m) based on 28 yr of sedimentation. “/” means no value.

Table 1. State variables and parameters used in this study.

Parameter	Description	Unit	Value	Reference
$C_{bg}$	HHM Background concentration	g L⁻¹, mg kg⁻¹ (dw)*	see Table 2	calculated
$C_D$	Drag coefficient	/	2 × 10⁻³	[33]
$C_d$	Dissolved-phase HHM concentration	g L⁻¹, mg kg⁻¹ (dw)*	/	calculated
Cm	Suspended-sediment mass concentration	g L⁻¹	/	[34]
$C_p$	Particulate-phase HHM concentration	g L⁻¹, mg kg⁻¹ (dw)*	/	calculated
$C_{p0}$	Initial particulate HHM at precipitation	g L⁻¹	/	assumed
$C_v$	Suspended-sediment volumetric concentration	/	10⁻⁴–10⁻⁵	assumed
d50	Median grain diameter of sediment	m	/	measured
D	Sediment thickness	m	0–1.6**	calculated
F	Porosity–tortuosity factor	/	/	calculated
HHM	Harmful heavy metals	g L⁻¹, mg kg⁻¹ (dw)*	varies	measured
$K_d$	Coefficient of equilibrium distribution	/	/	assumed
m	Exponent in the relationship of Sc and n	/	/	literature
N	Number of computational nodes	/	100	assumed
n	Porosity	/	0.4	[35]
Q	Molecular diffusion flux	kg m⁻² s⁻¹	varies	calculated
S	Salinity	/	0.06-35.7	assumed
$S_C$	Schmidt number	/	10–100	[6]
t	Time	s	0–8.64 × 10⁸ s	assumed
T1	Molecular diffusion rate	yr	0.3–3	calculated
T2	Desorption rate	yr	3.15 (for γ=5×10⁻⁸)	calculated
T3	Sediment rate	yr	>31	calculated
T4	Turbulent exchange rate	yr	/	calculated
$u_{*}$	Friction (dynamic) velocity	m s⁻¹	0–0.01	assumed
$w_g$	Settling velocity of sediments due to gravity	m s⁻¹	10⁻⁵	assumed
y	Dimensionless vertical coordinate	/	0–1	calculated
$z$	Vertical level within the substrate	m	0–1.6	calculated
$z_0$	Roughness parameter	m	/	literature
${\alpha }_S$	Inverse Schmidt number $\left({\mathrm{S}\mathrm{c}}^{-1}\right)$	/	0.01–0.1	[31]
γ	Desorption coefficient	s⁻¹	5×10⁻⁸–1×10⁻⁹	[36]
$∆y$	Vertical grid size in dimensionless coordinates	/	1/(N−1)	calculated
θ	Tortuosity	/	/	[30]
$\kappa$	Karman constant	/	0.41	literature
ν	Kinematic molecular viscosity of water	m² s⁻¹	10⁻⁶	constant
${\rho }_s$	Sediment–particle density	kg m⁻³	2 650	[33]
${\chi }_0$	Molecular diffusion coefficient (water only)	m² s⁻¹	/	[17]
${\chi }_S$	Molecular diffusion coefficients (with sediments)	m² s⁻¹	/	calculated

*Cd and Cp represent concentrations expressed in g L⁻¹ or kg m⁻³ in the model for consistency, but in the figures, they are presented in mg kg⁻¹ dry weight (dw) for easier comparison with laboratory data. Laboratories generally measure HHM concentrations in mg kg⁻¹, dw. Note that this difference in units is important when interpreting model results and comparing them with laboratory data or figures. ** D (0–1.6 m) based on 28 yr of sedimentation. “/” means no value.

2.2.2. Governing equations and boundary conditions

The mathematical formulation of the problem is expressed in Equation (1). The governing equations for $C_p$ and $C_d$ of HHM are defined clearly below (Equations (6)–(7)), including mass balance constraints and desorption processes:

$${\displaystyle \frac{\partial C_p}{\partial t}}=-\gamma \left(C_p-C_d\right)-{\displaystyle \frac{w_g}{D}}{C}_{p0}\delta \left(z-D\right)$$

(6)

$${\displaystyle \frac{\partial C_d}{\partial t}}=\gamma \left(C_p-C_d\right)+{\displaystyle \frac{\partial }{\partial z}}\left({\alpha }_S\nu {\displaystyle \frac{\partial C_d}{\partial z}}\right),$$

(7)

where $w_g<0;C_{p0}$ is the HHM concentration in sediment particles, with the concentration $C_m$ at the time of precipitation [34]; and $\delta \left(z\right)$ is the Dirac delta function. This function in Equation (6) models a localized source of HHM at depth z = D, representing the input of $C_p$concentrations at the top of the sediment layer. Details on the Schmidt number in Equation (7) can be found in Appendix C.

Equations (6) and (7) require initial conditions $C_p\left(z,t=0\right)=C_d\left(z,t=0\right)=0$ and the following boundary conditions:

$${AC}_d+{\alpha }_S\nu {\displaystyle \frac{\partial C_d}{\partial z}}=0,\mathrm{a}\mathrm{t}\mathrm{z}=\mathrm{D}\left(\mathrm{t}\right)$$

(8)

$${\displaystyle \frac{\partial C_d}{\partial z}}=0,\mathrm{a}\mathrm{t}\mathrm{z}=0$$

(9)

In equation (8), A is a constant defined in Appendix B, based on the fact that in the water column, $C_d\ll C_p$due to diffusion in open water systems. As stated by the no-flux condition in Equation (9), an asymptotic equilibrium is assumed at z = 0 between $C_p$and $C_d$, with values equal to the $C_{bg}$to be defined in this study.

This boundary condition assumes equilibrium at lower sediment layers (z = 0), reaching a balance due to decreased porosity and restricted molecular diffusion over time. In equation (9), the molecular flux of $C_d$ at z = 0 is assumed to be zero. The boundary conditions at z = 0 and z = D(t) ensure the mass balance of HHM within the sediment, accurately representing fluxes and the conservation of mass. At z = D(t), the boundary condition models the exchange between the sediment and the overlying water column.

2.2.3. Numerical solution under variable boundary conditions

The equations (6)–(9), with their respective initial conditions of $C_p\left(z,t=0\right)=C_d\left(z,t=0\right)=0$, have a variable boundary at an initial thickness of D(t = 0) = 0. The vertical coordinate (z) was transformed into a non-dimensional coordinate, following Yao et al. [13], to imptove numerical solution robustness. The system herein was reformulated using a new variable:

$$y={\displaystyle \frac{z}{D\left(t\right)}}$$

This becomes $y_j=\left(j-1\right)∆y$ ; j = 1, …, N;$∆y={\displaystyle \frac{1}{N-1}}$, where N is the number of vertical computational nodes. Thus, combining Equations (6) and (7) with Equation (1), we obtain:

$${\displaystyle \frac{\partial C_p}{\partial t}}+{\displaystyle \frac{y}{D}}{\displaystyle \frac{w_g{C}_V}{\left(1-n\right)}}{\displaystyle \frac{\partial C_p}{\partial y}}=-\gamma \left(C_p-C_d\right)-{\displaystyle \frac{w_g}{D}}{C}_{p0}\delta \left(z-D\right),$$

(10)

$${\displaystyle \frac{\partial C_d}{\partial t}}+{\displaystyle \frac{y}{D}}{\displaystyle \frac{w_g{C}_V}{\left(1-n\right)}}{\displaystyle \frac{\partial C_d}{\partial y}}=\gamma \left(C_p-C_d\right)+{\displaystyle \frac{\nu }{D^2}}{\displaystyle \frac{\partial }{\partial y}}\left({\alpha }_S{\displaystyle \frac{\partial C_d}{\partial y}}\right).$$

(11)

These equations were then discretized using an implicit time scheme, ensuring numerical stability regardless of the sediment thickness, D. The first derivatives concerning y were then represented using an "upward" scheme of ${\mathrm{O}(∆\mathrm{y}}^1)$. The solution was obtained using the Thomas factorization algorithm.

3. Results

3.1. Estimation of Molecular Diffusion (T₁), Desorption (T₂), and Sedimentation (T₃)

To estimate the timescales (T₁, T₂, T₃) given by Equations (3)–(5), a characteristic sediment thickness ($D_0$= 1 m), molecular viscosity (v =${10}^{-6}$ m² s⁻¹), and Schmidt number (Sc = 100) were adopted [6]. With these parameters, T₁ was estimated to be 3 years. For Sc = 10, T₁ was approximately 115 days. According to Liu et al. [37], the values of $\gamma$ vary between 10^–8 and 10^–9 s⁻¹. For $\gamma =$ 5 × 10⁻⁸ s⁻¹, the timescale of T₂ was 3.15 years.

Finally, assuming that the volumetric concentration was between 10^–4 and 10^–5 and the settling velocity due to gravity was 10^–5 m/s, the value of T₃ was greater than 31 years. Therefore, T₃ >> max (T₁, T₂) T₃ has the slowest timescale, while the other two timescales were similar to each other.

3.2. In Addition to Previously Defined Timescales (T₁-T₃), a Fourth Timescale (T₄) Representing Turbulent Water-Column Exchange Of Dissolved HHM at the Sediment-Water Interface was Determined. Resuspension Was Not Considered, as Particulate-Bound HHM do not Significantly Participate in this Exchange. Numerical Experiments

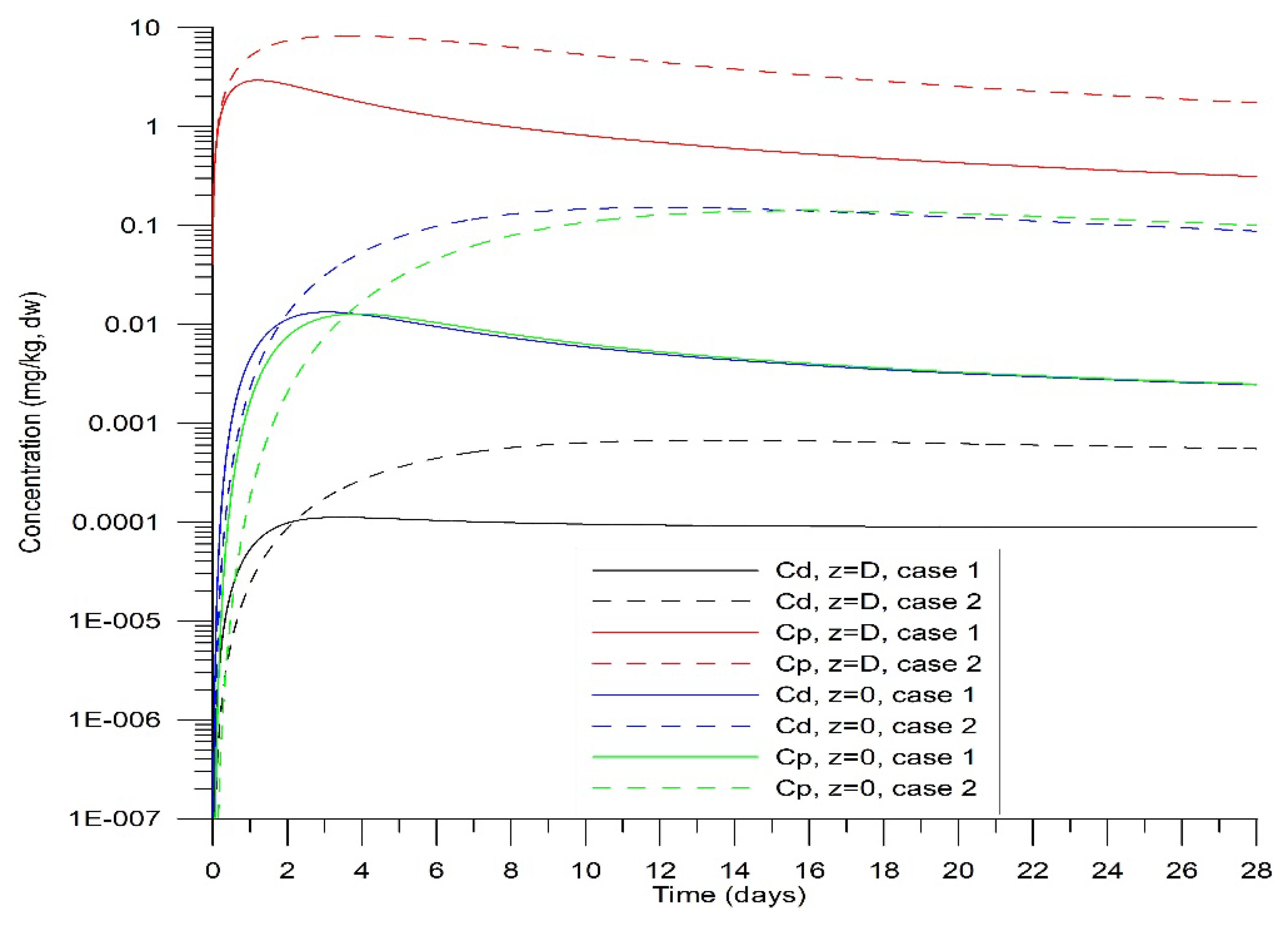
The sediment density (${\rho }_s)$ was set at 2 650 kg m⁻³, with porosity (n) fixed at 0.4. A drag coefficient ($C_D$) of 2 × 10^–3 [33], and an initial dynamic velocity of 0.01 m s⁻¹ were applied. Numerical experiments were conducted over 28 years, using a daily time step (1 d). Figure 2 illustrates the temporal evolution of $C_d$ and $C_p$ from the beginning of precipitation on both the surface and base when the desorption coefficient $\gamma$ is varied. Sedimentation was assumed to continue uniformly over the 28-year simulation at constant rates, with fixed HHM concentrations in the precipitated sediments. 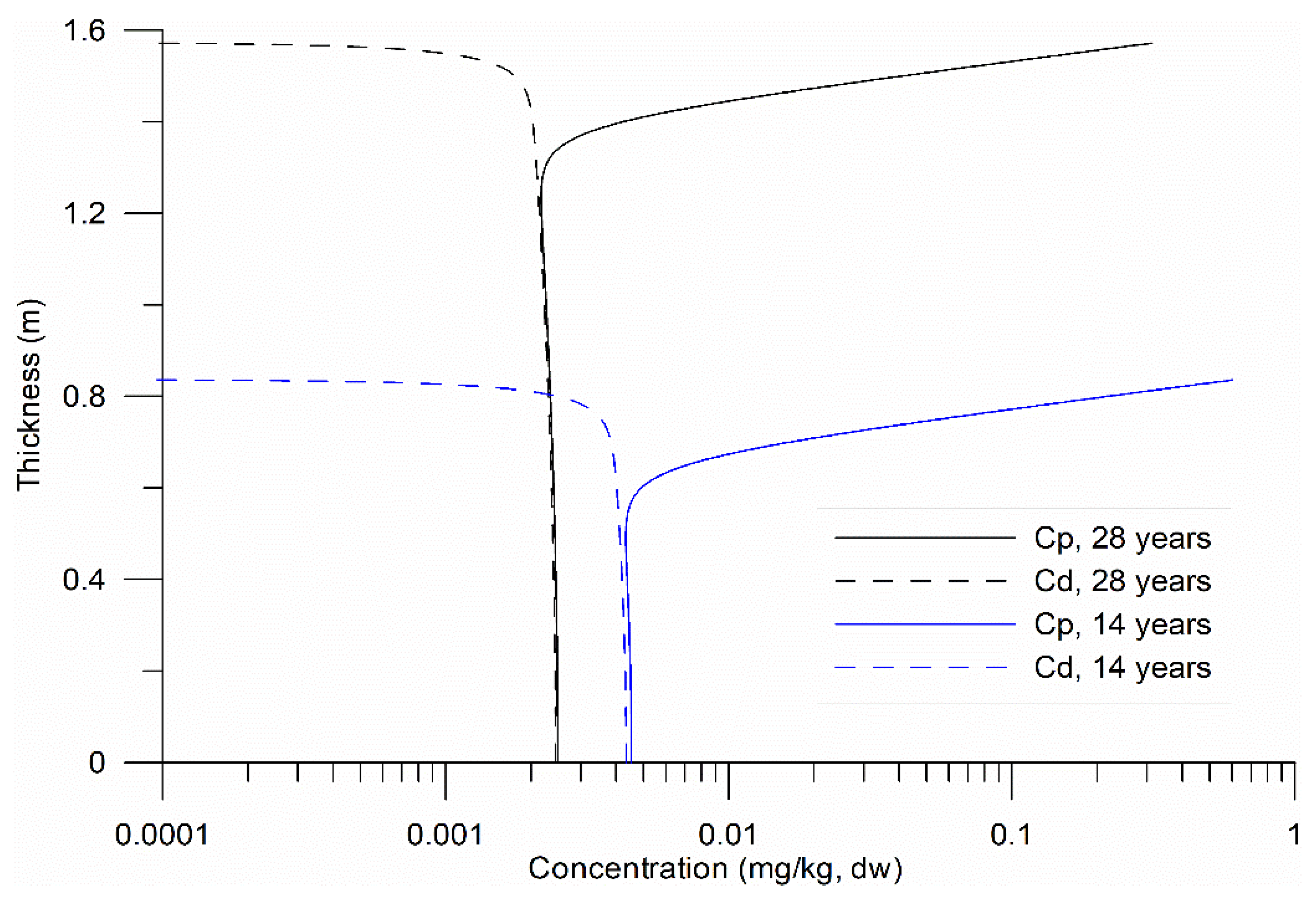In Figure 3, profiles of HHM concentrations in sediments are presented at both the midpoint and the end of the numerical experiments.

Over 28 years, the sediment layer grew to 1.6 m, which aligned well with data from CB and served as a reference for this study. Following an initial transient period (Figure 2), the $C_d$ and $C_p$ stabilized. The desorption rate was slower, corresponding to 6.3 years on the timescale of this process, compared to the reference value of 3.15 years.

The vertical profiles exhibited an exponential variation in the upper layer of the substrate (Figure 3), over 30–40 cm, followed by a uniform distribution. The variation was attributed to the vertical molecular diffusion of HHM and their loss, particularly in $C_d$, due to turbulent exchange with the water column at the bottom. The uniform distribution in the lower sublayer indicates equilibrium between the two phases; however, this equilibrium was not constant (Figure 3). Equilibrium stability between $C_d$ and $C_p$ is crucial for ecological risk assessments, as it governs HHM bioavailability and potential toxicity in benthic ecosystems.

5. Discussion

5.1. Temporal Evolution of Background Concentrations Estimated by the Model

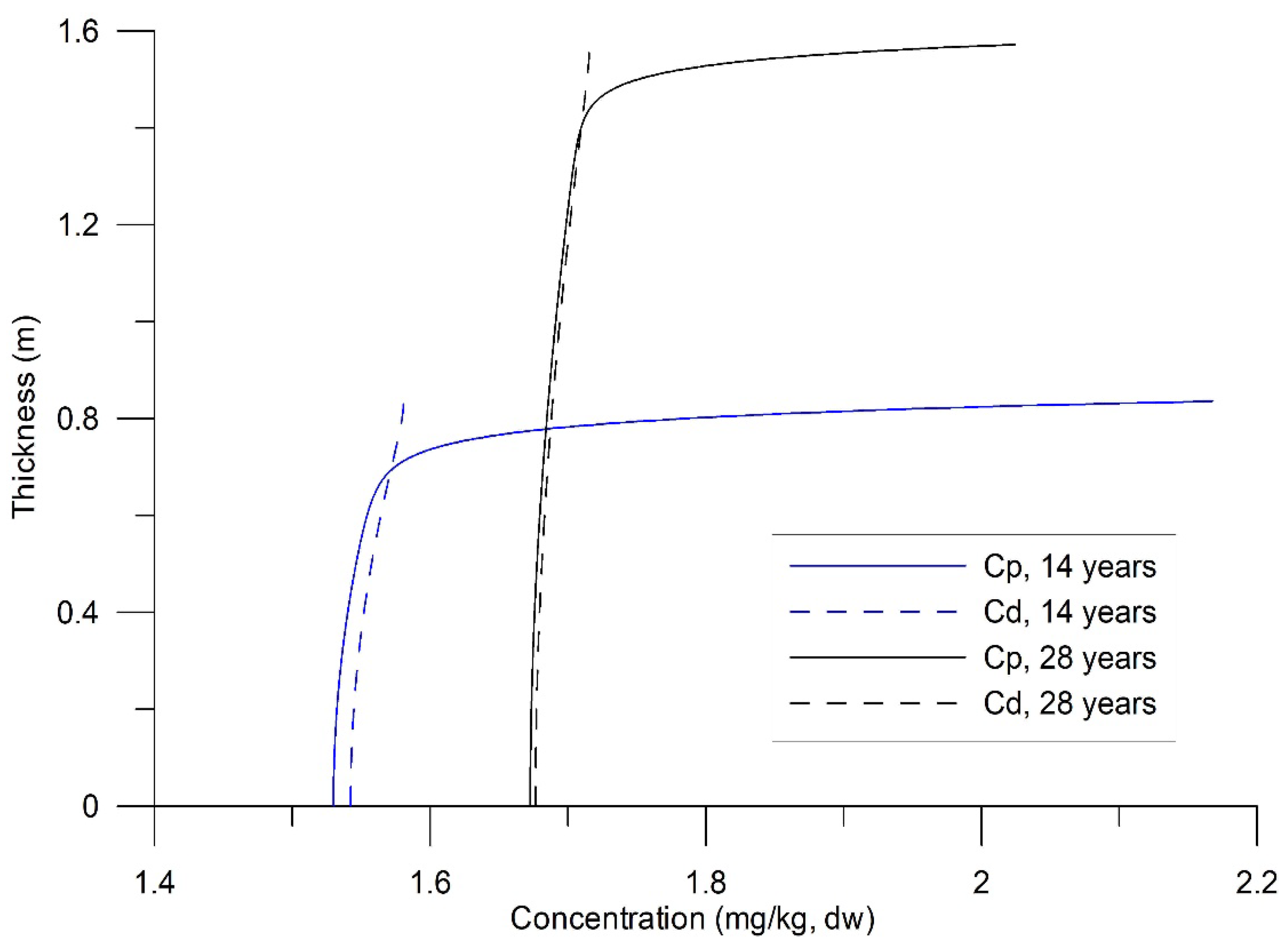
A drift value, tentatively called the background $C_{bg}$, was observed, characterized by a gradual decrease over time. This decrease is attributable to continuous slow molecular diffusion within the non-zero sediment porosity, transporting HHM towards the sediment-water interface. Subsequent experiments were conducted by minimizing the turbulent exchange of the dissolved phase with the water column above the bed. This occurs when $u_{\mathrm{*}}\to 0$ (Figure 4). A nearly uniform distribution of $C_d$ in the vertical direction was observed, along with the input of $C_p$ at the bottom surface. The total concentrations of HHM in the sediments were the sum of $C_p$ and $C_d$/$K_d$, and in the laboratory, a single value is defined: "HHM concentrations in sediments."

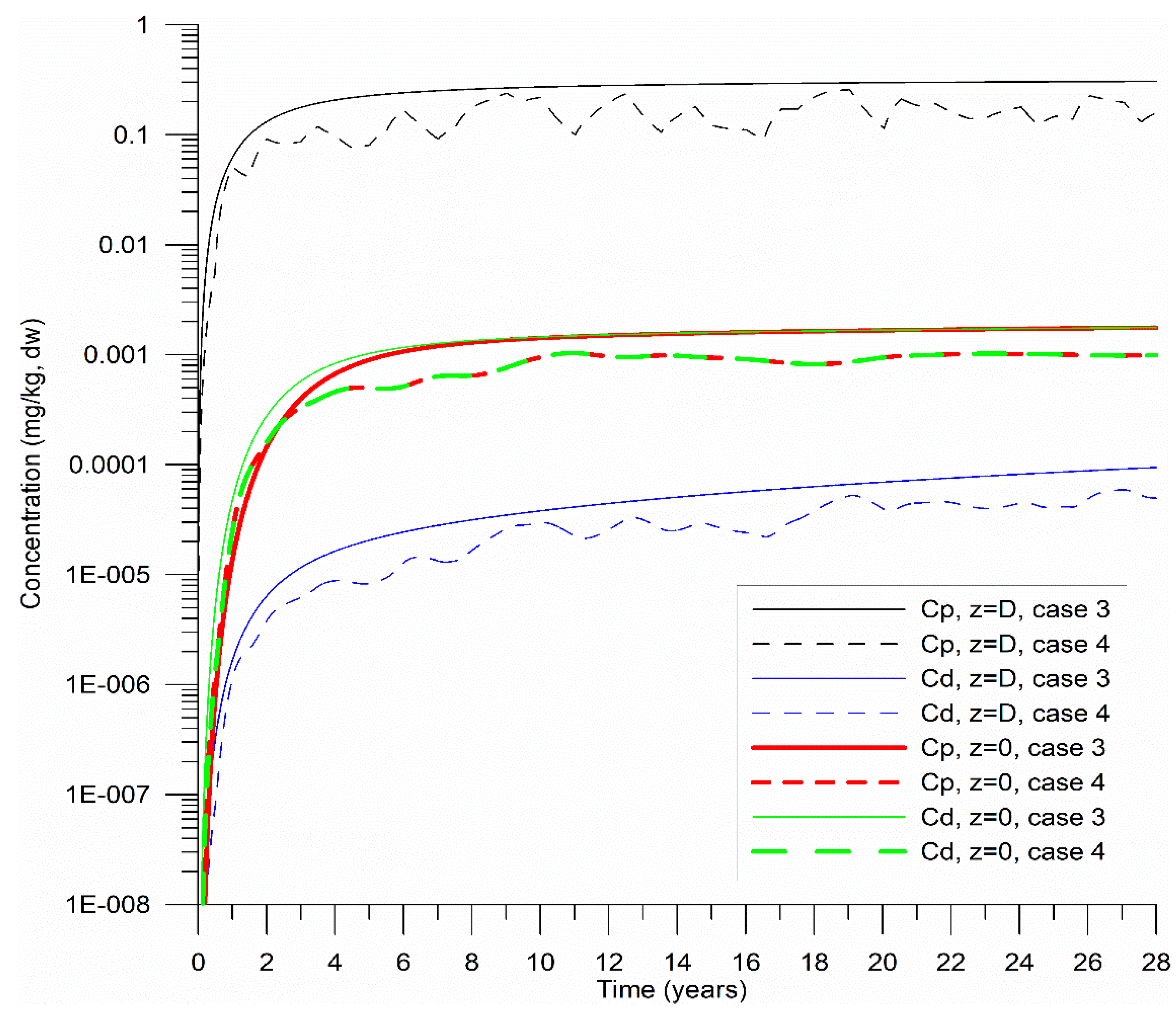
For Case 1, $\gamma$ was set to 5 × 10⁻⁸ s⁻¹, which suggested a relatively faster desorption rate compared to Case 2 ($\gamma =$ 10⁻⁸ s⁻¹). Two additional cases (Cases 3 and 4) were simulated (Figure 5). In Case 3, the initial particulate concentration $C_{p0},$increased linearly from 0 to 2.4 mg kg⁻¹ over 28 years, reflecting observed trends in CB associated with increased HHM loading from a distant source, the Magdalena River. Case 4 was similar to Case 3, but with a variable sediment input varied between 55 and 250 m³ s⁻¹ to replicate the Dique Channel’s seasonal flow, using annually periodic white-noise perturbations (stochastic values 0–1).

The cases in Figure 5 were compared to Case 1 in Figure 2, where HHM in sediments accumulated more slowly. Notably, when HHM loading gradually increased (Case 3), the concentrations at the sediment base (z = 0) consistently reached equilibrium ($C_d$ = $C_p$ = $C_{bg}$). Conversely, seasonal variations in sediment load from the Dique Channel (Case 4) did not significantly alter the equilibrium $C_{bg}$value. These findings imply that $C_{bg}$ remain stable despite short-term fluctuations, highlighting their value as robust indicators for long-term ecological risk assessment.

Table 2. Model-derived Hg background concentrations ($C_{bg}$) at boundary (z = 0) under different simulation cases.

Case	Description	$\mathbf{Estimated}{\mathit{C}}_{\mathit{b}\mathit{g}}$mg kg⁻¹ (dw)	Observation
1	γ = 5 × 10⁻⁸ 1/s	1.4 – 1.7	Long-term equilibrium at z = 0
2	γ = 10⁻⁸ 1/s	1.0 – 1.2	Slower equilibrium from low γ
3	$C_{p0}$ increasing over 28 yr	2.0 – 2.4	Closest to observed CB field data
4	Variable sediment input*	2.0 – 2.2	Dynamic but consistent $C_{bg}$at z = 0
-	Average Hg $C_{bg}$(model)	0.2 ± 1.7	Variability across all cases

^* seasonal sediment variation using white noise flow 55–250 m³ s⁻¹.

Table 2. Model-derived Hg background concentrations ($C_{bg}$) at boundary (z = 0) under different simulation cases.

Case	Description	$\mathbf{Estimated}{\mathit{C}}_{\mathit{b}\mathit{g}}$mg kg⁻¹ (dw)	Observation
1	γ = 5 × 10⁻⁸ 1/s	1.4 – 1.7	Long-term equilibrium at z = 0
2	γ = 10⁻⁸ 1/s	1.0 – 1.2	Slower equilibrium from low γ
3	$C_{p0}$ increasing over 28 yr	2.0 – 2.4	Closest to observed CB field data
4	Variable sediment input*	2.0 – 2.2	Dynamic but consistent $C_{bg}$at z = 0
-	Average Hg $C_{bg}$(model)	0.2 ± 1.7	Variability across all cases

^* seasonal sediment variation using white noise flow 55–250 m³ s⁻¹.

5.1. Dimensionless Analysis and HHM Dynamics

To perform an analysis of the systems in Equations (1) and (6)–(9), dimensionless variables were introduced, as follows:

${\tilde{C}}_d={\displaystyle \frac{C_d}{C_{bg}}}$; ${\tilde{C}}_p={\displaystyle \frac{C_p}{C_{bg}}}$; ${{\tilde{t}}_1={\displaystyle \frac{t}{T}}}_1$; ${{\tilde{t}}_2={\displaystyle \frac{t}{T}}}_2$; ${{\tilde{t}}_3={\displaystyle \frac{t}{T}}}_3$; $\tilde{z}={\displaystyle \frac{z}{D}}$; ${\displaystyle \frac{{\tilde{t}}_2}{{\tilde{t}}_1}}={\displaystyle \frac{2\gamma D^2}{{\alpha }_S\nu }}=a$; ${\tilde{C}}_{p0}={\displaystyle \frac{C_{p0}}{C_{bg}}}$;

${\displaystyle \frac{{\tilde{t}}_1}{{\tilde{t}}_3}}={\displaystyle \frac{w_{g}D}{{\alpha }_S\nu }}=\beta$; $\tilde{D}={\displaystyle \frac{D}{D_0}}$ ;$\zeta ={\displaystyle \frac{{\alpha }_S\nu }{u_{*}D}}$ ; ${\tilde{C}}_{p0}={\displaystyle \frac{C_{p0}}{C_{bg}}}.$The “~” symbol implies a dimensionless variable.

The systems (6 and 7) and their respective conditions (8 and 9) are described in a dimensionless form as follows:

$${\displaystyle \frac{\partial {\tilde{C}}_p}{\partial {\tilde{t}}_1}}=-a\left({\tilde{C}}_p-{\tilde{C}}_d\right)-\beta {\tilde{C}}_{p0}\delta \left(\tilde{z}-\tilde{D}\right)$$

(6’)

$${\displaystyle \frac{\partial {\tilde{C}}_d}{\partial {\tilde{t}}_1}}=a\left({\tilde{C}}_p-{\tilde{C}}_d\right)+{\displaystyle \frac{\partial }{\partial \tilde{z}}}\left({\tilde{\alpha }}_S{\displaystyle \frac{\partial {\tilde{C}}_d}{\partial \tilde{z}}}\right),$$

(7’)

$${C_D^{{\displaystyle \frac{1}{2}}}\tilde{C}}_d+\zeta {\displaystyle \frac{\partial {\tilde{C}}_d}{\partial \tilde{z}}}=0,\mathrm{at}\tilde{z}=\tilde{D}$$

(8’)

$${\displaystyle \frac{\partial {\tilde{C}}_d}{\partial \tilde{z}}}=0,\mathrm{at}\tilde{z}=0$$

(9’)

Adding Systems (6’) and (7’,) and using conditions (8’) and (9’), the results are:

$${\int }_0^{\tilde{D}}{\displaystyle \frac{\partial {(\tilde{C}}_p+{\tilde{C}}_d)}{\partial {\tilde{t}}_1}}d\tilde{z}=\left|\beta \right|{\tilde{C}}_{p0}-{\displaystyle \frac{{C_D^{\frac{1}{2}}\tilde{C}}_d\left(\tilde{z}=\tilde{D}\right)}{\zeta }}$$

(12)

Applying Leibniz's rule and reformulating Equation (1) in terms of “fast” time ${\tilde{t}}_1$, we obtain:

$${\displaystyle \frac{\partial \tilde{D}}{\partial {\tilde{t}}_1}}={\displaystyle \frac{C_v}{\left\{\left|\beta \right|\left(1-n\right)\right\}}},$$

(1’)

The temporal variation in the total HHM concentration of sediments over the entire extent of its layers can be defined by the following equation:

$${\displaystyle \frac{\partial }{\partial {\tilde{t}}_1}}{\int }_0^{\tilde{D}}{(\tilde{C}}_p+{\tilde{C}}_d)d\tilde{z}=\left|\beta \right|{\tilde{C}}_{p0}-{\displaystyle \frac{{C_D^{\frac{1}{2}}\tilde{C}}_d\left(\tilde{z}=\tilde{D}\right)}{\zeta }}+{\displaystyle \frac{C_v}{\left\{\left|\beta \right|\left(1-n\right)\right\}{\left.{(\tilde{C}}_p+{\tilde{C}}_d)\right|}_{\tilde{D}}}}$$

(13)

The first term on the right-hand side of Equation (13) represents the input of HHM in particulate form into the sediment column, while the second term accounts for their loss through exchange with the overlying water in the dissolved phase. The final term corresponds to the increase in the total HHM concentration due to changes in substrate thickness and its redistribution in the column. This term was considered less relevant when the T₃ scale represented a slow time relative to T₁ and T₂. Within the same body of water, as exemplified by CB, the T₃ scale is spatially variable.

If ${\displaystyle \frac{\partial \tilde{D}}{\partial {\tilde{t}}_1}}\approx 0$ for the “fast” time in System (1’), then systems (6’)–(9’) are represented as parabolic equations whose asymptotes in time are ${\tilde{C}}_p={\tilde{C}}_d$. Steady-state conditions are possible only if the particle sedimentation process stops.

For $t\to \mathrm{\infty },$ ${\displaystyle \frac{\partial }{\partial \tilde{z}}}\left({\tilde{\alpha }}_S{\displaystyle \frac{\partial {\tilde{C}}_d}{\partial \tilde{z}}}\right)=0$, considering condition (9') at a given level, the molecular flow is equal to zero throughout the substrate.

In this case, ${\tilde{C}}_p={\tilde{C}}_d=1\forall t$ (background concentration). The only reason this did not occur throughout the entire sediment column is the permanent entry of HHM, owing to their precipitation on particles at the bottom and the exchange of the diluted phase with the water column at the same vertical level.

The simulated sedimentation rates ranged from 0.5 m per 25 years (low deposition) to 10 m per 25 years (at the river mouth). Therefore, the 1D model should be applied at each calculation node of a 3D hydrodynamic mesh, with local scales adjusted accordingly. Considering the timescale variation in the main processes, the desorption rate, the average speed of sediment settling by gravity, and the molecular viscosity of water were fixed. The thickness of the sediment layer and its porosity (through the Schmidt number) varied within reasonable limits, characterizing CB as an example of an estuary. The resulting values of the dimensionless parameters for systems (6’) to (9’) were: a = 10^–3 to 10³; $\beta$ = 10² to 10⁴; $\zeta$/$C_D^{{\displaystyle \frac{1}{2}}}$= 0.25 (10^–1–10^–5) and ${\tilde{\alpha }}_S$ = 10^–2 to 10².

Under these conditions, Equations (6’) and (7’) can present multiple scenarios of HHM dynamics because the ratios of scale ${\displaystyle \frac{{\tilde{t}}_2}{{\tilde{t}}_1}}$ and ${\displaystyle \frac{{\tilde{t}}_1}{{\tilde{t}}_3}}$ change four to six orders of magnitude. In the case where the parameter a = ${\displaystyle \frac{{\tilde{t}}_2}{{\tilde{t}}_1}}$, the scales become inverted. Regarding condition (8’), the relationship $\zeta$/$C_D^{{\displaystyle \frac{1}{2}}}$<< 1 implied an abrupt gradient ${\displaystyle \frac{\partial {\tilde{C}}_d}{\partial \tilde{z}}}$, which was observed in Figure 3 at the interface between sediments and water. This detail was not observed in the measurements of HHM in sediments because the laboratories analyze the total concentrations, where $C_d$/$K_d$+ $C_p$, and the $C_p$concentration predominates in the samples.

5.1. Model Assumptions, Limitations, and Ecological Implications

The proposed 1D model was developed under the assumptions of continuous sedimentation without bottom erosion events. Technically, erosion could be easily included in the model; however, it may be difficult to control over extended periods of sediment dynamics. Changes in the porosity and tortuosity were also considered, which influence HHM transport and accumulation. These mechanisms may require a rheological model. Since the model operated under the assumption that the muddy substrate was not in motion, no assumption of the fluid type or the Newtonian fluid approximation is required.

This modeling approach adressess a critical gap in the representation of sediment processes, particularly the understanding of $C_{bg}$of HHM in estuarine sediments by integrating transport and reaction processes with site-specific hydro-sedimentary influences which are often simplified or omitted in traditional frameworks. The relevance of $C_{bg}$ lies in its strong association with toxicological thresholds, bioavailability, and long-term ecological risks related to HHM pollution. Although a 1D framework offers notable advantages in computational efficiency and vertical resolution, it limits horizontal transport and spatial interactions across estuarine gradients. Future initiatives could benefit from integrating diagenetic and hydrodynamic models to support evidence-based environmental management for preserving estuarine and coastal ecosystems.

6. Conclusions

Under physically valid assumptions, a novel one-dimensional mathematical model was developed to simulate HHHM dynamics in estuarine sediments, with broad applicability to water bodies influenced by HHM-contamination. This numerical framework advances prior approaches by integrating coupled transport-reaction processes while dynamically accounting for porosity and tortuosity. Unlike conventional models, this approach includes molecular diffusion (T₁), desorption (T₂), sedimentation (T₃), and water-turbulence exchange (T₄) as a distinct method to estimate HHM $C_{bg}$. A notable innovation is the separation of $C_d$ and $C_p$, reaching an asymptotic equilibrium ($C_d$ = $C_p$= $C_{bg}$) at the sediment base (z = 0). This mathematical formulation has not been previously reported in existing sediment models.

The $C_{bg}$ for Hg in CB ranged from 1.0 to 2.4 mg kg⁻¹ dw, providing a valuable reference for future ecological risk assessments, pollution indexing, and numerical model calibration in estuarine sediments. $C_{bg}$ of Hg

were characterized by very slow desorption. Particularly, $C_{bg}$ values did not remain constant but exhibited a drift, influenced by limited exchange with upper layers and overlying water. These findings may improve ecological risk assessment, environmental monitoring, and policy formulation to mitigate HHM impacts in CB and similar contaminated ecosystems.

Spatial and temporal variability in $C_{bg}$ arise from local sediment dynamics, precisely variations in precipitation rates, highlighting the need for zone-specific assessments within the same water body. Consequently, the 1D model can be applied to each node of the general hydrodynamic model of the basin.

The observed drift in $C_{bg}$ values demonstrate that profiling sediment layers dated with the 14C do not necessary reflect historical in-situ concentrations, as reported by Fukue et al. [38]. This issue draws attention and stimulates future research using inverse models to restore HHM ancient profiles from in-situ measurements.

Future works will focus on integrating the 1D model into a three-dimensional hydrodynamic framework to continuously simulate the long-term fate of sediments and HHM, to compare the model’s stratification predictions to in-situ measurements of the vertical substrate. Such advancements could significantly aid in developing more effective management strategies to mitigate HHM pollution in coastal marine environments.