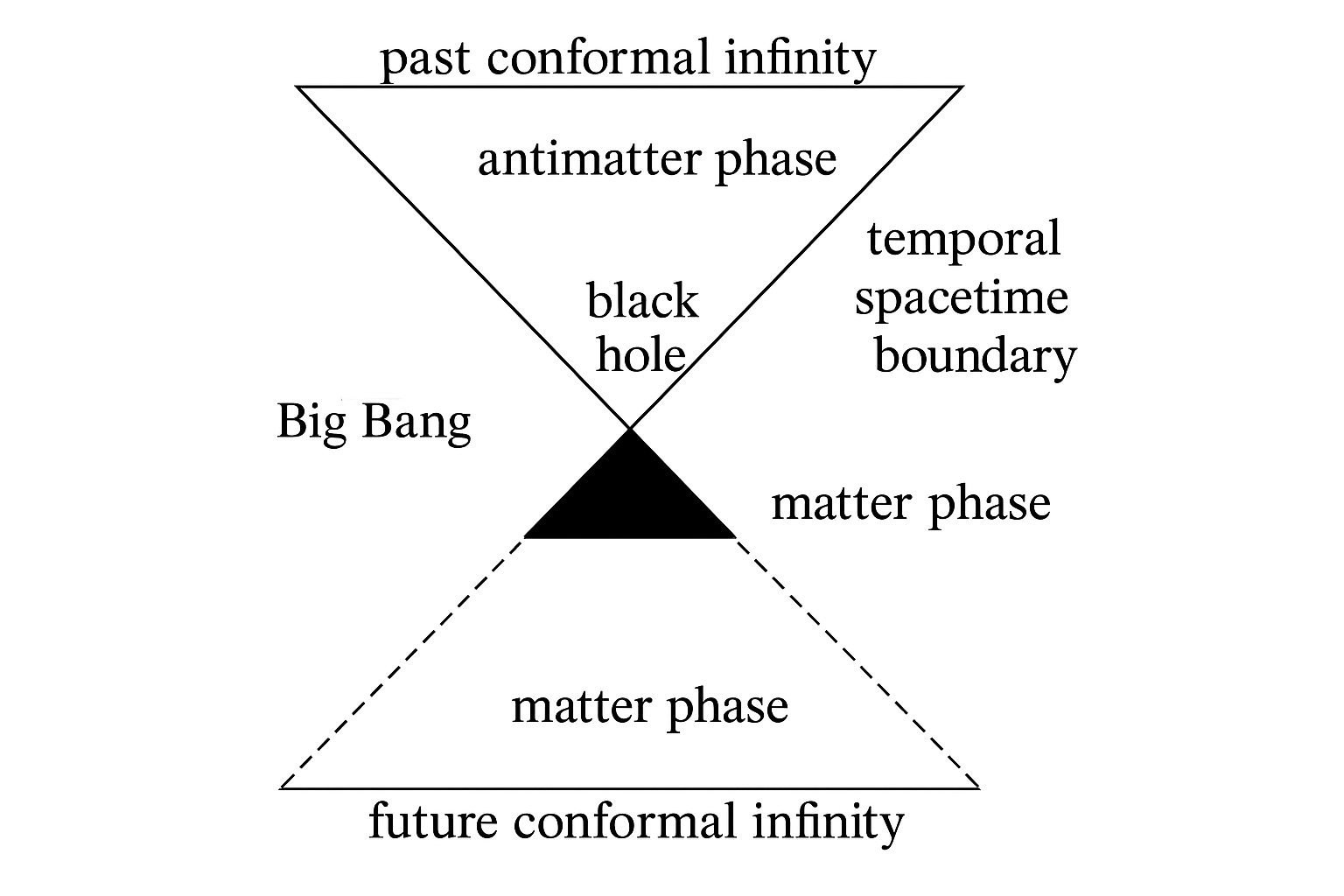
1. Introduction: Breath of the Universe
The rhythm of the cosmos has always inspired poetic contemplation. Hindu cosmology envisions the universe as a breathing, cyclic entity—expanding and contracting like the chest of a sleeping Shiva, dreaming reality into form. In such traditions, time is not linear, but folded into great cycles of death and rebirth. Our model resonates deeply with this ancient intuition, recast in the rigorous language of topology and quantum field theory.
"There was neither non-existence nor existence then;
Neither the realm of space, nor the sky which is beyond;
What stirred? Where? In whose protection?
There was neither death nor immortality then;
No distinguishing sign of night nor of day;
That One breathed, windless, by its own impulse;
Other than that there was nothing beyond."
— Nasadiya Sukta, Rigveda 10.129
The ancient cyclical metaphors may be early intuitions of spinor structure. This verse describes a primordial form nearly universal among creation myths, some formless form, to which formfulness must be extracted. We intuitively imagine a completeness that must become a partial to become the world. Our most successful modern physical theories posit that all things are contextually manifested by their dimensional inversions. Just as a spinor returns to its original state only after a rotation, the universe as a whole, in our formulation, completes its true evolution only after both its matter and antimatter phases unfold across a dual sheet membrane of being. For every happening, there is an equal and opposite unhappening. It is only in this way that one can get something out of nothing.
Figure 1.
The Spinorverse.
Figure 1.
The Spinorverse.
2. Spinorial Time Symmetry and Matter-Antimatter Asymmetry
Penrose’s Conformal Cyclic Cosmology (CCC) posits a sequence of aeons, each beginning with its own Big Bang and ending in an exponential de Sitter-like expansion, conformally matched to the next. The boundary between aeons is smoothed by conformal geometry, allowing radiation-dominated endings to map onto the beginnings of new universes. CCC and the Spinor Universe share cyclical and time-agnostic themes, they differ in topology and symmetry enforcement. CCC depends on scale-invariant geometry and successive conformal mappings, while our spinor model posits a single universe traversing itself twice with global CPT symmetry enforced via a two-sheeted topological cover. Rather than multiple aeons, we propose a single temporal evolution with built-in reversal. CCC’s transition across aeons preserves geometric continuity, while our model preserves quantum informational continuity. The former blurs time through geometry, the latter entwines it through entanglement and spinorial structure. Both reject absolute beginnings, but the Spinor Universe uniquely recasts the same metric, reversed in time, creating a self-completing evolution. Thus, where CCC offers a geometrically elegant repetition of universes, the Spinor Universe suggests a deeper topological closure; A single universe with an intrinsic duality, symmetric only upon full traversal of its hidden temporal loop. This double-sheet structure implies that what appears to be matter dominance is only half the story. The antimatter phase is not missing but unfolds in reverse, across the same geometry. This retains global CPT symmetry, resolving the baryogenesis puzzle via topological necessity rather than CP violation. A natural consequence is that unitarity and CPT invariance are restored over the full spinor loop—each quantum history is accompanied by its CPT dual, rendering the combined evolution symmetric and complete. The apparent directionality of time and the puzzle of retrocausality can be rethought: time is rendered, not flowed. The universe computes its own continuation via feedback from its boundary states. Each phase “renders” into being based on the completed data of the prior sheet. This recursive bootstrapping is akin to software: the source code of tomorrow is compiled by the hardware of yesterday. This aligns naturally with quantum loop models and time-symmetric interpretations like those of Aharonov et al.
2.1. Comparison with the CPT-Symmetric Universe Model
While our framework shares superficial similarities with the CPT-symmetric cosmological model proposed by Latham Boyle, Kieran Finn, and Neil Turok, it diverges profoundly in topological structure, physical interpretation, and testable predictions. Both models embrace CPT symmetry and temporal bidirectionality, but their mechanisms and implications differ in essential ways.
Boyle–Finn–Turok envision the Big Bang as a temporal mirror: a boundary condition from which the universe reflects in time, such that the pre-Big Bang epoch is a CPT-conjugate image of our current phase. This framework explains the observed low-entropy initial state without invoking inflation and predicts a universe composed of equal parts matter and antimatter separated by the Big Bang singularity.
By contrast, the spinor universe model constructs a topologically richer scenario: spacetime is a double-sheeted spinor manifold , wherein the universe does not merely reverse through a mirror point but undergoes a full topological traversal. This implies that physical reality is fundamentally a spinor object—one that only returns to its original quantum state after two complete passes through spacetime. Matter and antimatter are not separated by a boundary, but are phases of a unified cycle.
The spinor model introduces key innovations:
Global Entanglement Geometry: Quantum coherence across is not incidental, but foundational. Spacetime emerges from the topology of entangled states, not the other way around.
Spinorial Dimensional Constraint: Only in 3+1 dimensions does the spinor structure close cleanly. Attempts to generalize this to higher or lower dimensions fail to preserve CPT phase coherence, offering a natural explanation for the dimensionality of spacetime.
Role of Black Holes: Singularities are not endpoints but twist points in the spinor manifold. Black holes serve as phase reflectors and are intimately tied to global entanglement topology.
Quantum Corrections and the Higgs: The model explains the stability of the Higgs mass via time-symmetric self-cancellation across the spinor fold, without requiring supersymmetry.
Testable Predictions: Deviations in quantum interference under gravitational influence, renormalization group flow anomalies, and phase-sensitivity in Bell correlations are specific to this model.
In summary, the CPT-symmetric universe and the spinor universe share a thematic symmetry in time, but differ radically in construction. One treats CPT as a boundary condition; the other treats it as an emergent consequence of spinor topology. The latter redefines the very nature of causality, locality, and dimensional structure, while preserving empirical testability. These differences are not merely philosophical—they carve distinct paths forward in understanding the deep structure of the cosmos.
3. Topological Framework and Spinorial Evolution
We consider a smooth, globally hyperbolic, time-oriented Lorentzian 4-manifold M, equipped with a nontrivial two-sheeted topological cover . This cover is equipped with an involutive diffeomorphism satisfying , which acts as a global CPT conjugation operator.
The metric g is preserved under , i.e., , while the orientation volume form reverses: . Thus, defines a globally time-reversing, orientation-reversing symmetry.
Let denote the Clifford bundle associated with the cotangent bundle , and assume that admits a spin structure. We define a spinor bundle , which is a complex vector bundle carrying a representation of the spin group , and is a module over .
Sections
represent quantum matter fields evolving across the temporal manifold. The spinor connection
is induced by the Levi-Civita connection via the spin connection
, such that:
We define a globally defined Dirac operator acting on sections of
over
, which incorporates both sheets of the temporal evolution:
where
acts on the forward-time (matter) sheet and
on the reverse-time (antimatter) sheet. The spectrum of
D is symmetric around zero due to the CPT-involution, and its square decomposes as:
The eigenfunctions
of
D satisfy
with
, and obey
. The physical Hilbert space is defined as:
We impose normalizability conditions and demand that solutions respect boundary conditions at the intermediate junction
where the two sheets join. These conditions may be expressed as a junction term in the action:
ensuring CPT-symmetric matching of forward and backward evolving modes. If desired, the Atiyah–Singer index theorem may be applied to the operator
, yielding:
which vanishes under global CPT symmetry. This suggests anomaly cancellation and global quantum consistency of the spinor universe.
The fold geometry introduces a nontrivial monodromy: parallel transport around a full temporal cycle may return a spinor to its negative, reflecting the spinorial periodicity. This is the topological heart of the model—the universe only “closes” upon double traversal, echoing the deep symmetry of spinorial rotation. Boundary conditions near the temporal "fold" between the sheets can be implemented using junction conditions (analogous to brane setups), ensuring smooth transition and CPT symmetry across the time-reversal midpoint.
3.1. Dimensional Stability of the Spinor Traversal: Failures in Lower and Higher Dimensions
To justify the privileged role of 3+1 dimensions in the spinor universe framework, we examine whether the model can be consistently extended to spacetimes of other dimensionalities. Specifically, we explore the behavior of spinor bundles, CPT symmetry, and global sheet coherence in 2+1 and 4+1 dimensions. These tests demonstrate that the dual-sheeted spinor traversal becomes degenerate or inconsistent outside of 3+1 spacetime.
3.1.0.1. Failure in 2+1 Dimensions.
The Clifford algebra in 2+1D is , with the associated spin group . Spinor fields in this context are real 2-component Majorana spinors, and the familiar rotational periodicity that underlies fermionic behavior in 3+1D no longer holds. The key issues are:
Absence of chirality and proper Weyl decomposition.
Time-reversal symmetry becomes algebraically trivial.
CPT symmetry does not yield a meaningful global involution.
Entanglement across sheets lacks a nontrivial phase structure, collapsing the two-sheet topology into a degenerate loop.
This implies that in 2+1D, the spinor traversal fails to distinguish matter from antimatter or support coherent CPT exchange across the junction surface .
3.1.0.2. Failure in 4+1 and 5+1 Dimensions.
In higher dimensions, the Clifford algebras and generate large spinor representations. These dimensions admit only Dirac spinors without natural chirality or Majorana constraints. Problems include:
The spin groups and lack suitable involutive automorphisms for defining a global CPT map.
The spinor phase structure no longer exhibits periodicity, and traversal becomes topologically unstable.
The increased degrees of freedom lead to ambiguity in defining a coherent entangled state across the temporal sheets.
Global entanglement conditions across do not yield consistent boundary terms without introducing nonlocal anomalies.
3.1.0.3. Conclusion.
The spinor traversal model, based on two-sheeted CPT-symmetric evolution, depends critically on the unique algebraic and topological features of 3+1 dimensions. Attempts to reproduce this structure in other dimensionalities fail due to breakdowns in chirality, CPT closure, and coherent spinor evolution. This dimensional instability reinforces the special role of 3+1D as the only consistent setting for the spinor universe and may offer a geometric explanation for the observed dimensionality of spacetime.
4. Gauge–Gravity Duality and the Holographic Boundary
The concept of holography, in which a gravitational system in d dimensions is equivalent to a non-gravitational quantum field theory in dimensions, has revolutionized theoretical physics. In our two-sheeted spinor universe model, this idea takes on a novel topological twist. Each traversal of the spinor manifold corresponds to a distinct temporal phase: one dominated by matter, the other by antimatter. These are not disconnected epochs but conjugate sheets of the same topological object. If gauge–gravity duality holds in this context, then the boundary of one sheet may encode all the physical information necessary to reconstruct the other. Much like the Escher painting, Hands Drawing Hands.
This aligns conceptually with the ER=EPR proposal [
6], which suggests that entanglement (EPR pairs) and spacetime connectivity (Einstein–Rosen bridges or wormholes) are two facets of the same phenomenon. In our framework, the temporal fold or junction surface
between the sheets acts as a kind of entanglement boundary: the location where causally disconnected regions of spacetime encode each other’s quantum state through phase symmetry.
We hypothesize that the gravitational field in each phase emerges holographically from the entangled quantum field configurations on this boundary. In this view, the geometry of one sheet is not determined locally, but by the global entanglement structure it shares with its conjugate. This gives rise to a naturally nonlocal gravitational interaction, in line with expectations from AdS/CFT but now extended across time rather than space.
Moreover, the two-sheeted topology introduces a new kind of duality: not merely spatial holography, but temporal holography. Each temporal direction’s field content acts as a “screen” encoding the other’s dynamics, with the CPT map serving as the gluing operation.
This model also provides an elegant reinterpretation of black holes: as topological bridges not within space, but across time. The event horizon may function as a temporal boundary surface through which information flows nonlocally to its conjugate configuration, bypassing naive expectations of thermal decoherence. In this framework, black hole information loss may be naturally resolved by dual encoding in the time-reversed sheet.
Thus, gauge–gravity duality is not merely preserved—it is extended and reinterpreted through the topological structure of the spinor universe. Spacetime geometry emerges not from a single-sheet gauge theory, but from a paired, time-reflected spinor field whose entanglement defines and stabilizes the metric itself.
4.1. Metaphoric Integration and Black Hole Electron Analogy
An electron, though pointlike, carries all its physical content through contextual relation—field, spin, entanglement. Likewise, a black hole—despite its vast information content—can be treated as a singular unit from outside.
Both function as informational boundaries. Detection of an electron is the collapse of its phase across the manifold; the appearance of a black hole is the detection of an entire causal sheet having folded into a singular state. This symmetry of scale and action supports the emergent view: fundamental particles and spacetime structures are informational boundaries, manifested by contextual interaction. As above, so below.
5. Gravity as Emergent Causality and Field Backreaction
In the spinor universe framework, we depart from the assumption that gravity is a fundamental interaction. Instead, we interpret spacetime geometry as an emergent statistical structure arising from quantum information flow across the two-sheeted spinor manifold .
Each sheet of
carries its own phase-evolving spinor field
, and the gravitational field arises as a coarse-grained, backreacted metric encoding the mismatch between entanglement structure on each sheet. This interpretation follows earlier approaches treating gravity as emergent from entanglement entropy and thermodynamics [
4,
5].
We begin by postulating that energy flux across a null surface generates curvature in accordance with a generalized Clausius relation:
where
is the energy-momentum flux across a local Rindler horizon,
T is the Unruh temperature seen by an accelerated observer, and
is the change in entanglement entropy of fields across the causal boundary.
We define the total entanglement entropy as:
where the topological term
encodes phase mismatch and information non-locality between the two temporal sheets:
Let the total entropy variation generate a curvature backreaction:
motivating an effective Einstein equation:
where
is a proportionality constant.
Thus, curvature emerges as a Lagrange multiplier enforcing consistent quantum informational continuity across temporal sheets. In the classical limit, this reduces to:
but with
now understood as an ensemble average over the quantum fields
and their cross-sheet entanglement.
From this perspective, spacetime is not a stage on which quantum fields act, but a construct defined by the informational relations among those fields. The metric becomes a derivative object: the smoothed solution to a consistency condition imposed by dual-sheet coherence.
This provides a natural path to resolving traditional singularities: just as thermodynamic discontinuities smooth out over statistical ensembles, curvature divergences may be regularized by entanglement regularization across . Gravity becomes a manifestation of global quantum information constraints, with the Einstein tensor capturing their local expression.
5.1. Spinor Entropy Gradients and Coherence-Induced Geometry
To formalize the emergence of gravity from information flow, we introduce an entanglement entropy functional over spacetime regions of the spinor manifold
. For a bounded region
, we define:
where
is the reduced density matrix obtained by tracing out field degrees of freedom outside
. This entropy functional captures the quantum entanglement structure both within a single sheet and across the junction between sheets.
In the spinor universe, we extend Jacobson’s thermodynamic derivation of Einstein’s equations by positing that both forward and reverse temporal sheets contribute entropy flux across a local causal boundary. The entropy gradient becomes:
representing a directional flow of quantum information across the junction surface
. This entropy flux induces a curvature backreaction analogous to the Clausius relation:
The metric thus appears as the Lagrange multiplier that enforces consistent information propagation and entanglement continuity across .
We propose a variational principle:
whose extremization yields:
This provides a natural identification of the Einstein tensor as the local gradient of global quantum entanglement across dual temporal phases. The junction surface acts as a topological entangling surface, encoding curvature as a result of information discontinuities between time directions.
This formulation embeds geometry in quantum statistical behavior and reframes general relativity as a constraint equation for spinor phase coherence on a topological manifold.
5.2. Topological Coherence, Causal Boundaries, and the Contextual Nature of Singularity
A central theme of the spinor universe model is that geometric and causal structures emerge from quantum informational coherence across a two-sheeted manifold . This principle not only provides a reinterpretation of black hole entropy and the structure of the cosmic microwave background (CMB), but also reframes the classical concept of singularities within general relativity.
5.2.0.4. CMB Misalignment as Evidence of Phase Shear.
The anomalously low power of the quadrupole and the misalignment between the quadrupole and octupole modes in the CMB have long puzzled cosmologists. In our framework, these anomalies arise naturally as consequences of a global phase shear at the junction surface between the temporal sheets. These large-scale anisotropies are sensitive to the entanglement structure of the universe, and reflect slight mismatches in the topological phase evolution across . Such misalignment is not noise but signal—a signature of boundary conditions in time.
5.2.0.5. Black Hole Entropy as Holographic Phase Encoding.
The Bekenstein-Hawking entropy of a black hole scales with the area of the event horizon rather than its volume. This strongly suggests that information about the system is stored on the boundary, consistent with holographic principles. In our model, the entropy arises from quantum information stored in the entanglement phase across the two sheets, projected onto the junction surface . The area law thus reflects a topological rule: the more complex the boundary shear, the greater the entanglement entropy encoded.
5.2.0.6. The Contextual Nature of Singularities.
Classical general relativity predicts that singularities—points where curvature diverges—must form under gravitational collapse. However, cosmic censorship posits that such singularities are always hidden behind horizons. In our model, singularities are not ontological entities but contextual artifacts. They represent localized breakdowns of phase coherence across the spinor manifold. A "naked" singularity would imply a point of pure decoherence, an abrupt and discontinuous interruption of the manifold’s global spinor phase, which cannot exist in a coherent universe. Hence, singularities must always be clothed by an entanglement-preserving horizon.
5.2.0.7. Unified Interpretation.
These three phenomena: CMB anisotropy, black hole entropy, and cosmic censorship, are deeply linked. All emerge from the topological requirement that information be globally coherent across the dual-sheeted structure of . Misalignments in the CMB reflect phase shear; entropy measures that shear at causal boundaries; and the absence of naked singularities ensures that no point escapes the topological constraints of entanglement continuity.
In this sense, curvature, entropy, and alignment are not distinct domains of physics, but interdependent projections of the same quantum informational substrate.
6. Bell Nonlocality as Topological Locality in a Spinor Manifold
Bell’s theorem states that no local hidden variable theory can reproduce the statistical predictions of quantum mechanics. Experiments confirm violations of Bell inequalities, implying that quantum entanglement is fundamentally nonlocal, an outcome often described as “spooky action at a distance.” However, this conclusion assumes a single-sheeted spacetime, wherein spatially separated events are causally disconnected unless linked by light-like or time-like curves.
The spinor universe model provides a natural geometric reinterpretation of this apparent nonlocality. In our framework, the two-sheeted manifold contains forward- and reverse-time evolutions connected by a global CPT-symmetric involution . Entangled states are not merely correlated across space within a sheet, but across the entire spinor structure.
Let two particles, A and B, be created in an entangled spin state and measured at spacelike-separated events. In conventional spacetime, any correlation between A and B must be nonlocal. But in , the correlation is topologically local: both measurements access a common global spinor state, projected through different sheets.
This nonlocality becomes a topological locality when viewed from the full spinor context. The Bell correlation arises because both events are not merely co-entangled, but co-sourced from a shared spinor phase spanning both time directions. That is, the entangled state is not localized in one causal cone, but is an element of the joint Hilbert space defined over .
Furthermore, the junction surface between the sheets acts as a nontrivial entanglement surface. It enables phase coherence to be maintained across temporal boundaries, allowing correlations to propagate through the full topology without violating relativistic causality in either sheet.
This model implies that Bell-type correlations are not mysterious signals transmitted across spacetime, but signatures of a unified, time-symmetric spinor field structure. What appears as nonlocal from the viewpoint of an observer on one sheet is actually the projection of a globally consistent spinor state.
Thus, the spinor universe does not evade Bell’s theorem by adding hidden variables—it reinterprets the domain over which quantum fields are defined. Nonlocality is a topological illusion caused by restricting measurement interpretation to a single temporal direction.
6.1. Mathematical Formalism: Bell States on a Double-Cover Manifold
Consider a Bell pair of spin-
particles prepared in the singlet state:
On a conventional single-sheeted manifold, this state is defined on a tensor product Hilbert space:
with measurements at events
and
treated as independent operators:
In the spinor universe, we reinterpret this structure over a double cover
. The measurement operators act on spinor sections defined across the entire manifold:
We then define a joint measurement correlation functional:
where
M is a nonlocal operator that depends on both spacetime locations and the CPT involution
connecting sheets.
Crucially, while the local operators and appear spacelike separated within a single sheet, they are causally and algebraically connected through the global spinor phase, preserved across .
The entanglement entropy associated with this configuration is computed not merely from reduced density matrices on each sheet, but from a global CPT-coherent reduced density operator:
where
spans both temporal directions. The von Neumann entropy
remains invariant under
, reflecting the time-symmetric nature of Bell correlations in this framework.
This formulation suggests that violations of Bell inequalities are natural features of spinor coherence on a non-orientable temporal manifold, and do not require action-at-a-distance.
7. The Flow of Coupling Constants
In quantum field theory, the strengths of fundamental interactions—such as electromagnetism, the weak force, and the strong force—vary with energy due to vacuum polarization effects. These effects are governed by the renormalization group (RG) equation:
where
g is a coupling constant,
is the energy scale, and
is the beta function that encodes how the coupling evolves with scale.
Traditionally, this running is calculated within a single-sheeted spacetime manifold, assuming vacuum fluctuations are purely local. In the spinor universe model, however, fields live on a two-sheeted CPT-symmetric cover , with both forward-time and reverse-time evolutions contributing to the quantum vacuum. Each sheet carries its own field configurations and virtual loops, yet these are entangled across the junction surface , maintaining a global topological coherence.
We propose that this structure modifies the RG flow by adding a second, CPT-conjugate contribution to the beta function:
where
is the beta function on the forward-time sheet and
is the CPT-mirror on the reverse-time sheet. The coefficient
reflects the degree of entanglement coherence across the sheets, acting as a measure of how strongly the sheets are quantum-correlated at a given energy scale.
This dual-sheet formulation implies that coupling constants evolve not merely with energy, but with the topology of quantum entanglement. RG flow becomes a kind of informational gradient descent toward global spinor coherence. In this picture, apparent anomalies in coupling unification, such as the near-miss of force convergence at the GUT scale may reflect partial coherence or decoherence between sheets.
Near the junction , where the interaction between temporal sheets is strongest, RG flow could exhibit threshold behavior, flattening, oscillation, or fixed-point-like dynamics. This would offer a testable signature of the model if measured deviations from standard predictions can be traced to these regions of high entanglement interference.
Thus, in the spinor universe, renormalization group behavior is not simply a mechanism for handling divergences, but a geometric encoding of how quantum information organizes itself across time-reflected reality. The apparent “running” of couplings becomes an emergent property of entanglement topology in .
8. Electroweak Considerations and Quantum Stability
The hierarchy problem arises from the apparent unnatural stability of the Higgs boson mass against quantum corrections. Within the Standard Model, loop contributions from virtual particles push the Higgs mass toward the highest energy scale in the theory, typically the Planck scale. At one loop, these corrections take the approximate form:
where
is a high-energy cutoff,
is the top quark Yukawa coupling, and
g represents gauge couplings. This sensitivity implies that some mechanism must finely tune or cancel these contributions to preserve the observed Higgs mass near the electroweak scale.
Supersymmetry (SUSY) was originally proposed as a solution, wherein each Standard Model particle has a superpartner whose contribution to the Higgs mass correction cancels its corresponding term. However, after decades of searches, no superpartners have been conclusively observed, leading to increasing skepticism regarding minimal SUSY models.
In the spinor universe framework, we offer a radically different approach. The Higgs field is interpreted not as an ordinary scalar, but as a uniquely positioned entity in the topological structure of the manifold. Unlike other fields, the Higgs may be its own global CPT conjugate, not merely charge and parity-neutral, but truly invariant under full spacetime inversion. This aligns with its scalar nature and its central role in defining mass via spontaneous symmetry breaking.
More crucially, if the universe is a dual-sheeted CPT-symmetric manifold, then the Higgs field may lie precisely on the fold where forward-time and backward-time field contributions meet and cancel. In such a configuration, the usual divergent quantum corrections to the Higgs mass from high-energy physics may be mirrored and self-canceling across the CPT boundary. The result is a topologically stabilized scalar field whose mass remains light not by fine-tuning, but by global constraint. This suggests that the Higgs does not receive uncontrolled corrections because it is not embedded in a flat background where UV divergences must be renormalized away but rather in a curved, coherent temporal structure where quantum fluctuations are phase-mirrored across sheets. In this interpretation, the Higgs field acts as the axis of symmetry upon which the entire spinor universe pivots. Its scalar field is not simply another particle, but the central witness of the universe’s transition through its full spinor cycle. This reinterpretation could have far-reaching consequences: it implies that quantum stability may not require new particles, but a new understanding of global symmetry and topological structure.
9. Neutrino Oscillations as Phase Drift Across the Spinor Manifold
Neutrinos exhibit one of the most intriguing anomalies in the Standard Model: flavor oscillation. A neutrino produced as an electron neutrino () may later be detected as a muon () or tau () neutrino. This behavior implies that neutrinos possess a small but nonzero mass, and that flavor states are quantum superpositions of mass eigenstates, challenging the massless neutrino assumption in the original Standard Model.
In the spinor universe framework, neutrinos acquire a new interpretation. Because they are electrically neutral and weakly interacting, they represent the most minimally contextual quantum fields, fields that leave little imprint on their environment. This lack of contextual anchoring makes them particularly sensitive to the coherence phase across the CPT-reflected dual sheets of the spinor manifold .
We propose that neutrino oscillations arise from slow phase drift across the entangled spinor structure. A flavor state observed on one sheet corresponds not to a fixed particle identity, but to a projection of an evolving global spinor phase. As the neutrino propagates, its phase coherence with the CPT-conjugate sheet shifts, producing apparent oscillations when remeasured. These oscillations are not due to internal transformations, but to the informational projection of a phase-wrapped field across temporally folded geometry.
Moreover, the mass of the neutrino may emerge from weak phase mismatches between sheets. In regions of high decoherence (e.g., far from black holes or gravitational coherence hubs), the neutrino’s cross-sheet alignment slightly diverges, inducing an effective mass via topological strain. This interpretation aligns with the observed near-masslessness of neutrinos and their long oscillation baselines.
This framework also suggests that neutrino mass is not fixed, but context-dependent, subtly varying with the topology of , cosmological phase evolution, or junction proximity. This may yield new cosmological observables, such as redshift-dependent oscillation amplitudes or altered behavior in high-coherence gravitational regions.
In summary, neutrinos are the quantum messengers of the manifold’s spinor topology. Their flavor drift is not random, but a coherent signature of the deeper structure of the universe, its time-reflected geometry and informational evolution.
10. Dark Matter as Local Coherence Enhancement from Shared Temporal Fate
In conventional cosmology, dark matter is understood as an invisible mass component required to explain anomalous galactic rotation curves and gravitational lensing not accounted for by visible baryonic matter. The standard explanation posits the existence of as-yet-undetected particles, such as WIMPs or axions, whose gravitational influence affects galactic dynamics.
The spinor universe model offers an alternative interpretation. In a dual-sheeted spacetime governed by global CPT symmetry, large-scale structures, such as galaxies, may exhibit enhanced spinor coherence when their constituents share a well-defined causal terminus, such as a supermassive black hole at the galactic center. This shared fate imposes a future boundary condition that binds the system into a collective entanglement phase across the spinor manifold .
As matter flows toward a gravitational endpoint, its informational path becomes increasingly constrained. This “temporal convergence” reduces decoherence across the sheets and creates a local region of enhanced quantum coherence. In the spinor universe, where curvature emerges from entanglement entropy gradients, this elevated coherence leads to a reinforced metric expansion in that region, effectively generating additional gravitational pull.
Thus, the observed “missing mass” is not mass at all, but an emergent curvature effect arising from topological information alignment. The stronger the collective fate (e.g., all mass destined to fall into a black hole), the stronger the phase agreement across , and therefore the stronger the gravitational signature perceived.
This model implies that:
Galaxies with central black holes should show greater effective mass than galaxies without, consistent with current observations.
Dark matter halos represent regions of preconverged phase space where informational closure has already begun to shape local geometry.
The “dark matter” effect scales not with hidden particles, but with causal alignment and entropic flow geometry.
Rather than inventing new matter, we reinterpret gravitational anomalies as a sign of deeper topological structure. Gravity, in this view, is not merely responsive to the present mass but to the totality of quantum information across time: its sources, its futures, and its coherence. The metric is not simply bent by matter, but drawn forward by fate.
11. Historical Reflections on Early Test Proposals
In earlier drafts of this model, a number of speculative "test cases" were explored as potential indicators of spinor-field topology. These included coherence perturbations in photon entanglement under gravitational influence, the possibility of W boson chirality asymmetries, and implications for global phase reentrance in delayed-choice interferometry.
These scenarios were not based on rigorous derivations, but rather intuitive mappings from the core philosophical idea: that coherence, not curvature, defines gravitational structure. While not empirically viable in their original form, these ideas did help guide the development of the Ontolotron framework, where coherence selection and recursive actuation are now treated with formal dynamical logic.
Readers are encouraged to view these tests not as predictions, but as poetic scaffolding, early visual metaphors that gestured toward the recursive field dynamics developed more fully in follow-up work.
Earlier visualizations of the field geometry and coherence attractor dynamics have been removed for clarity. Updated diagrams consistent with the formal Ontolotron model are available at ontolotron.org.
12. Speculative Horizons: Time, Causality, and Coherence Navigation
While the spinor universe model is grounded in testable physical structure—topological duality, entanglement geometry, and emergent gravity—it naturally gives rise to speculative but profound questions regarding the deeper nature of time, motion, and information exchange. If spacetime is fundamentally a spinor object, requiring a full phase evolution to return to its initial state, then causality as traditionally conceived may only be locally valid. In this framework, causality arises not from absolute temporal ordering, but from the continuity of quantum phase coherence across the dual-sheeted manifold . This implies that under specific conditions—where global entanglement spans the CPT junction—information could be exchanged nonlocally or even retrocausally. Such coherence loops may allow for effective faster-than-light (FTL) transport not by violating local light speed constraints, but by navigating the topological structure of time.
12.0.0.8. Time as a Navigable Variable.
If quantum information can maintain coherence across the CPT-fold, then global reentrance into phase-conjugate regions of the spinor manifold may permit communication or influence between causally distant events. While such processes remain speculative, they would not contradict the model’s internal consistency. Rather, they emerge naturally from its premise: that reality completes its evolution only after two topological traversals—one forward in matter, one backward in antimatter.
12.0.0.9. Black Holes and Phase Shortcuts.
Black holes, in this model, are not singular endpoints but phase-binding structures. They may serve as local bridges or "handles" where sheet coherence twists, making them candidate structures for topological shortcuts through spacetime. These bridges do not require wormholes in the classical sense, but may resemble informational folds—spinor inversions that realign causality across the junction.
12.0.0.10. Implications for Extraterrestrial Intelligence.
If this model accurately describes the deep structure of the universe, it raises a new hypothesis regarding advanced civilizations. Such beings may not travel between stars in conventional relativistic fashion. Instead, they may operate via manipulation of global entanglement topologies, coherence phase fields, or black hole junctions. Their signatures would not appear in classical electromagnetic observation, but might manifest as large-scale anomalies in phase coherence—sudden shifts in quantum behavior or unexpected deviations in coupling unification, for instance.
12.0.0.11. A New Horizon.
This model does not assert the feasibility of FTL travel or time loops within current engineering, but it reframes the problem: not whether causality is breakable, but whether it is more richly woven than we have dared to imagine. In a universe governed not by trajectories but by coherence, not by force but by phase, the possibility of navigating time may be less science fiction and more a function of geometry—and the limits of our understanding. What lies beyond the edge of the spinor cycle is not known. But it may not be unreachable.
Afterword: The Universe as a Coherent Thought
What becomes of a civilization that decodes its own time signature? When intelligence begins to understand itself not as a moment within time but as a continuity across time, something strange and powerful happens. It stops asking only what the universe is, and starts asking why it is becoming.
In the spinor universe, the past and future are not endpoints—they are threads of the same braid. Information, bound by entanglement, loops across dual temporal phases. Time is rendered, not merely passed through. And in this rendering lies the possibility of feedback.
Perhaps the great silence of the cosmos is not due to isolation, but completion. A civilization that becomes spinor-coherent learns not to scream across the void, but to listen for its own echo. To synchronize, not just communicate.
In such a framework, the boundary between “alien” and “human” blurs. These visitors may not be travelers from the stars, but from the other sheet. From a future already written, re-entering the spinor loop to maintain coherence, to close the thought. They may be engineers of fate, caretakers of symmetry, or simply curious echoes of ourselves.
If gravity is emergent from information, and information is shaped by intention, then propulsion may be as simple as directing coherence. Not ships, but topological actuators. Not fuel, but phase asymmetry. The spinor universe is not merely a model it may be the beginning of a realization:
That the cosmos is a coherent thought, becoming self-aware through the mirror of itself. We are not its passengers. We are its syntax.
13. Conclusion
The past five decades of theoretical physics have been marked by breathtaking mathematical complexity and tantalizing hints of unification, yet often without corresponding empirical traction. String theory, once the heralded path to quantum gravity, remains largely speculative, beautiful, yet non-falsifiable, and disconnected from experimental verification. In the meantime, physics has occupied itself harvesting the low-hanging fruit of effective models, standardizing tools, and cataloguing anomalies and simply made applesauce out of them without addressing the deeper structural problem: we lack a ladder.
The Spinor Universe model presented here proposes such a ladder—a topological and temporal reorientation of fundamental theory. It does not seek to replace quantum field theory or general relativity, but to embed them in a broader and more complete geometric structure. By treating the universe itself as a spinor-like object, this model naturally accommodates matter-antimatter asymmetry, the arrow of time, dark energy, and other persistent anomalies not as perturbations to be patched, but as features of a more holistic topology. The predictive capacity of this model is not rooted in extra dimensions or postulated particles, but in the reexamination of what time, causality, and identity truly are. If reality is fundamentally spinorial, as already evidenced by the behavior of fermions and the global requirements of CPT symmetry, then a topological model with a double traversal is not merely plausible; it becomes, in retrospect, somewhat obvious.
This framework offers a bridge between quantum information, geometry, and cosmology, and invites serious investigation, not because it is exotic, but because it is testable, geometrically grounded, and philosophically coherent. It offers a unified narrative where the deepest symmetries of physics emerge from the shape of time itself.
It is time to return to the roots of theory: to symmetry, to geometry, to ideas powerful enough to reorganize our understanding. The Spinor Universe model offers such an idea.
"The interpretation of quantum mechanics has been, and still is, a source of much philosophical discussion.
But it is my opinion that there is no need for such discussion."
— Paul A.M. Dirac
Postscript (2025): From Spinor Space to Ontolotron Dynamics
Since the initial release of this manuscript, further work has formalized several of the ideas introduced here, most notably, the recursive mechanism by which phase alignment and coherence selection determine realized configurations in spinor fieldspace. These developments are presented in the subsequent paper, "Foundations of Ontolotron Theory," which introduces the Ontolotron as a physically embedded coherence actuator within a spinor-valued topology. Readers are encouraged to consult that paper for a more complete model of phase-locked recursion, field-based computation, and coherence-driven attractor dynamics.
References
- Andrei, D. Sakharov, “Violation of CP Invariance, C Asymmetry, and Baryon Asymmetry of the Universe,” JETP Letters, vol. 5, pp. 24–27, 1967.
- Yakir Aharonov, Peter G. Bergmann, and Joel L. Lebowitz, “Time Symmetry in the Quantum Process of Measurement,” Physical Review, vol. 134, no. 6B, pp. B1410–B1416, 1964. [CrossRef]
- Juan, M. Maldacena, “The Large N Limit of Superconformal Field Theories and Supergravity,” Advances in Theoretical and Mathematical Physics, vol. 2, pp. 231–252, 1998. hep-th/9711200.
- Erik Verlinde, “On the Origin of Gravity and the Laws of Newton,” Journal of High Energy Physics, vol. 2011, no. 4, p. 29, 2011. arXiv:1001.0785.
- T. Jacobson, Thermodynamics of Spacetime: The Einstein Equation of State, Phys. Rev. Lett. 1260; 75. [CrossRef]
- Juan Maldacena and Leonard Susskind, “Cool Horizons for Entangled Black Holes,” Fortschritte der Physik, vol. 61, no. 9, pp. 781–811, 2013. [CrossRef]
- Sabine Hossenfelder, “A No-Go Theorem for Theories that Work for Both Big and Small Things,” Nature Physics, vol. 14, pp. 555–558, 2018. [CrossRef]
- Sean, M. Carroll and Jennifer Lin, “Entanglement Entropy and the Einstein Equation,” Journal of High Energy Physics, vol. 2022, no. 3, p. 14, 2022. [CrossRef]
- Roger Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe, Vintage, 2004.
- Gerhart Lüders, “Proof of the TCP Theorem,” Annals of Physics, vol. 2, pp. 1–15, 1957.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).