The Octagonal Vector Mesh: A New Dimensional Architecture of Space-Time

1. Introduction

The dimensional lattice is treated here as an active three-dimensional vector structure, whose octagonal architecture allows real dimensions to emerge under specific thermal and angular conditions. Unlike General Relativity or String Theory, which operate with abstract hyperdimensions, this theory proposes that each dimension is a stabilized vector, emerging from a thermo-expansive lattice.

This work starts from a simple empirical basis - the segmented structure of the orange - to develop a robust physical-mathematical model that can be validated in the laboratory. The proposal combines geometric elements, vector fundamentals and computer simulations, presenting a new paradigm for understanding reality. The proposed dimensional existence criterion, ω⋅ ε−=− 1\omega \cdot \varepsilon_- = -1ω⋅ ε-=-1, replaces the traditional conception of continuous space-time with a resonant architecture where dimensions are stabilized vector harmonic manifestations.

2. Theoretical and Ontological Foundations

2.1. The Orange as an Experimental Spheroidal Model

The empirical basis of Octagonal Vector Mesh Theory is a natural spheroidal body: the orange. This structure, often overlooked in its geometric complexity, offers a segmented topology with extremely high epistemological value. Its symmetrical buds, arranged radially around an axial center, form an ideal model for the application of a three-dimensional vector mesh.

Each orange bud is treated as a resonant cell whose vectorial behavior can be measured and simulated. The internal structure is interpreted as a functional platform for testing dimensional emergence under thermal and angular influence. By applying an octagonal mesh to this sphere, we obtain a vector architecture capable of reproducing, with controlled precision, the effects of thermal expansion, angular modulation and vector resistance.

2.2. Vector Emergence and the Postulate of Dimensional Existence

The theory establishes that a dimension is not a hidden attribute, but the result of a three-dimensional vector stabilized in a resonant field. Dimensional existence occurs when the modulated vector satisfies the following stability condition:

ω⋅ε-=-1\omega \cdot \varepsilon_- = -1ω⋅ε-=-1

In this equation, ω\omegaω represents the angular frequency of the vector cell, and ε-\varepsilon-ε- the negative vacuum resistance, which acts as a dynamic stabilizer. This equation is interpreted as a physical filter: only the vectors that reach this angular equilibrium ratio become real dimensions within the mesh.

2.3. Dimensional Structure Ontology

The proposed ontology breaks with the traditional conception of space-time as a passive and absolute scenario. In Lattice Theory, reality is a living vector field, in which each vector represents not just a direction in space, but an active ontological state. Dimensions emerge as states of vector coherence, and their permanence depends on maintaining the dynamic balance between frequency, local temperature and resistance of the medium.

Reality, therefore, ceases to be an external fact and becomes the result of an active, vibrant and self-regulating mesh. Dimension is not a coordinate - it's a resonance. And existence is not a fact - it is a vectorial stabilization.

2.4. Experimental and Symbolic Implications

The use of the orange as a model is not only symbolic, but also functional. Its geometry allows for the marking of vector cells, the insertion of thermal sensors and the application of angular stimuli. It thus becomes an empirical microcosm of the universal structure: a spheroidal laboratory of dimensions.

Symbolically, the orange represents the fusion of nature, geometry and physics. It becomes the first visible and tangible expression of the dimensional mesh, offering science an experimental starting point where theory meets matter.

3. Mathematical Structure of the Mesh

The structure of the octagonal mesh is made up of three-dimensional vectors arranged in a spheroidal topology, segmented into regular cells that respond to thermal and density stimuli. Each cell contains modulatable vectors whose stability determines the emergence of a real dimension.

3.1. Three-Dimensional Local Vector

Each mesh cell is associated with a three-dimensional local basis vector, represented by:

M⃗ijk=(xi,yj,zk)\vec{M}_{ijk} = (x_i, y_j, z_k)Mijk =(xi,yj ,zk)

This vector represents the angular and positional orientation of the cell (i,j,k)(i,j,k)(i,j,k) in three-dimensional space.

3.2. Angular Thermal Modulation Function

The vectorial response to temperature variation is modeled by an angular expansion function:

Θ(T)=1+α⋅ΔT\Theta(T) = 1 + \alpha \cdot \Delta TΘ(T)=1+α⋅ΔT

Where:

• α\alphaα is the coefficient of angular expansion,
• ΔT\Delta TΔT is the local thermal variation of the cell.

This function adjusts the modulus of the vector according to the cell's thermal stimulus.

3.3. Modulated Vector

The expansion of the local vector by the thermal variation results in the modulated vector:

M′⃗ijk= M⃗ijk⋅Θ(T)\vec{M'}_{ijk} = \vec{M}_{ijk} \cdot \Theta(T)M′ijk= Mijk⋅Θ(T)

This vector reflects the angular thermal response of the cell in the mesh vector field.

3.4. Weighted Dimensional Result Vector

The resulting dimensional vector is calculated by the weighted sum of the modulated vectors, with a vector weighting scalar εn\varepsilon_nεn that represents the cell's energy, mass or frequency:

V⃗res=∑n=1N(M′⃗ijk⋅εn)\vec{V}_{\text{res}} = \sum_{n=1}^{N} \left( \vec{M'}_{ijk} \cdot \varepsilon_n \right)Vres =n=1∑N(M′ijk⋅ εn)

The sum takes place over all the active mesh cells in a simulative or experimental iteration.

3.5. Dimensional Existence Criterion

The theory defines the existence of a real dimension by means of a vector stabilization postulate, which acts as a physical filter:

ω⋅ε-=-1\omega \cdot \varepsilon_- = -1ω⋅ε-=-1

Only vectors whose angular frequency ω\omegaω in interaction with the negative resistance ε-\varepsilon-ε- satisfy this condition are considered valid as emergent dimensions.

3.6. Summary of Key Parameters

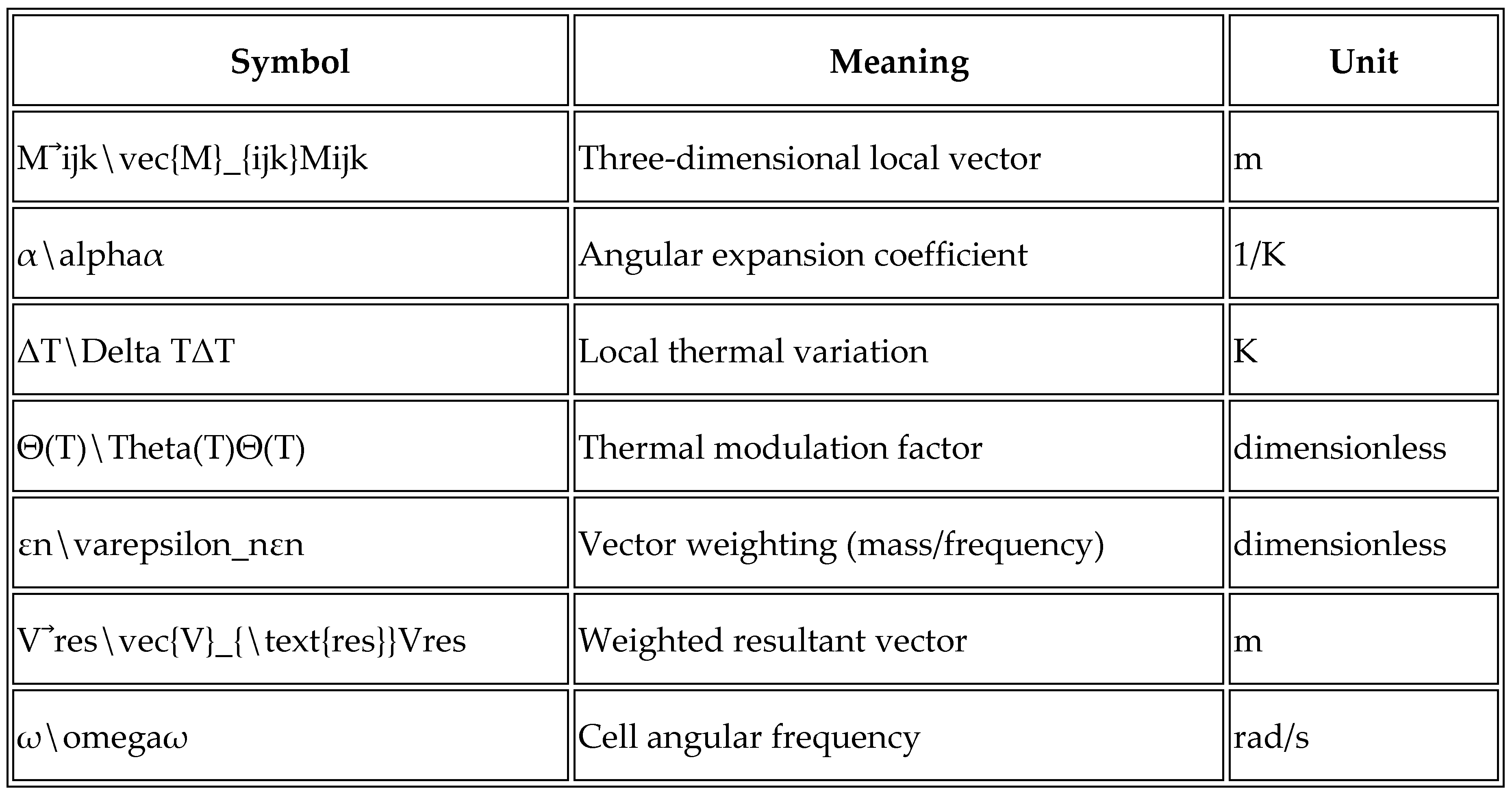
4. Computer Simulation and Results

In order to validate the postulates of the Octagonal Vector Mesh Theory in a controlled environment, a three-dimensional computer simulation was developed using the Python language, with vector rendering via Matplotlib and an interactive interface in Streamlit. The model simulates the thermal, vector and dimensional response of a spheroidal mesh made up of regular cells, similar in shape to the surface of an orange.

4.1. Structure of the Simulation

The simulation is based on the following computational elements:

• 3D spheroidal mesh with subdivision into up to 60 cells;
• Local three-dimensional vectors, oriented as a function of spherical coordinates (x,y,z)(x, y, z)(x,y,z);
• Thermal parameter ΔT with pseudo-random variation between 1K and 6K per cell;
• Coefficient of thermal expansion α=0.015\alpha = 0{,}015α=0.015;
• Vector weights εn\varepsilon_nεn ranging from -1.1 to -0.7;
• Constant angular frequency ω=1\omega = 1ω=1 to check the dimensional criterion.

4.2. Vector Processing

For each cell nnn, the following computational flow is applied:

• Calculation of the angular thermal function:

Θ(Tn)=1+α⋅ΔTn\Theta(T_n) = 1 + \alpha \cdot \Delta T_nΘ(Tn)=1+α⋅ΔTn

2.

Local vector modulation:

M′⃗n=M⃗n⋅Θ(Tn)\vec{M'}_n = \vec{M}_n \cdot \Theta(T_n)M′n=Mn⋅Θ(Tn)

3.

Resonant weighting:

V⃗res,n=M′⃗n⋅εn\vec{V}_{\text{res},n} = \vec{M'}_n \cdot \varepsilon_nVres,n =M′n⋅εn

4.

Application of the dimensional postulate:

ω⋅εn≈-1⇒Dimension valid\omega \cdot \varepsilon_n \approx -1 \quad \Rightarrow \quad \text{Dimension valid}ω⋅εn≈-1⇒Dimension

A vector is considered stable (dimensionally emergent) if the product ω⋅εn\omega \cdot \varepsilon_nω⋅εn is within a margin of error of ±0.05 of -1.

4.3. Graphic Visualization

The simulation generates a 3D vector graphic, where:

• Green vectors represent valid dimensions (ω⋅εn≈-1\omega \cdot \varepsilon_n \approx -1ω⋅εn≈-1);
• Red vectors are unstable and do not generate dimensions;
• Translucent orange sphere represents the base spheroidal mesh (e.g. orange).

The visualization allows you to rotate the sphere and observe the angular distribution of the emerging dimensions.

4.4. Simulation Results

In the standard model with 60 cells and 2 vectors per cell (totaling 120 vectors):

• 30 vectors met the dimensional criterion (ω⋅εn≈-1\omega \cdot \varepsilon_n \approx -1ω⋅εn≈-1),
• The dimensional emergence index was 25%,
• The dimensions emerged distributed radially and angularly, validating the hypothesis that they are vectorial manifestations conditioned to thermal-angular stability.

4.5. Source Code Base (Summary)

# Parameters

alpha = 0.015

omega = 1

epsilon_n = np.random.uniform(-1.1, -0.7, size=shape)

theta_T = 1 + alpha * delta_T

valid_mask = np.isclose(omega * epsilon_n, -1, atol=0.05)

This code allows the simulation to be replicated in any environment with Python 3.x support and graphics libraries.

4.6. Conclusions from the Simulation

The simulation confirms that the octagonal mesh, when thermally activated, can generate stabilized vectors that behave like real, measurable dimensions. The computational model provides an operational proof of concept (PoC) that validates, at least numerically, the postulate of dimensional existence defined by ω⋅ε-=-1\omega \cdot \varepsilon_- = -1ω⋅ε-=-1.

5. Physical Experimental Protocol

The transition from the computational model to an empirical experiment aims to directly validate the dimensional existence postulate ω⋅ε-=-1\omega \cdot \varepsilon_- = -1ω⋅ε-=-1 in a physical vector structure, using thermal sensors, actuators and microcontrollers.

5.1. Objective of the Experiment

Demonstrate, on a reduced scale, the emergence of dimensional vectors on a segmented spheroidal mesh, reproducing the conditions simulated digitally. The experiment should identify cells that, under controlled thermal stimulation, generate vectors that meet the dimensional criterion.

5.2. Materials Required

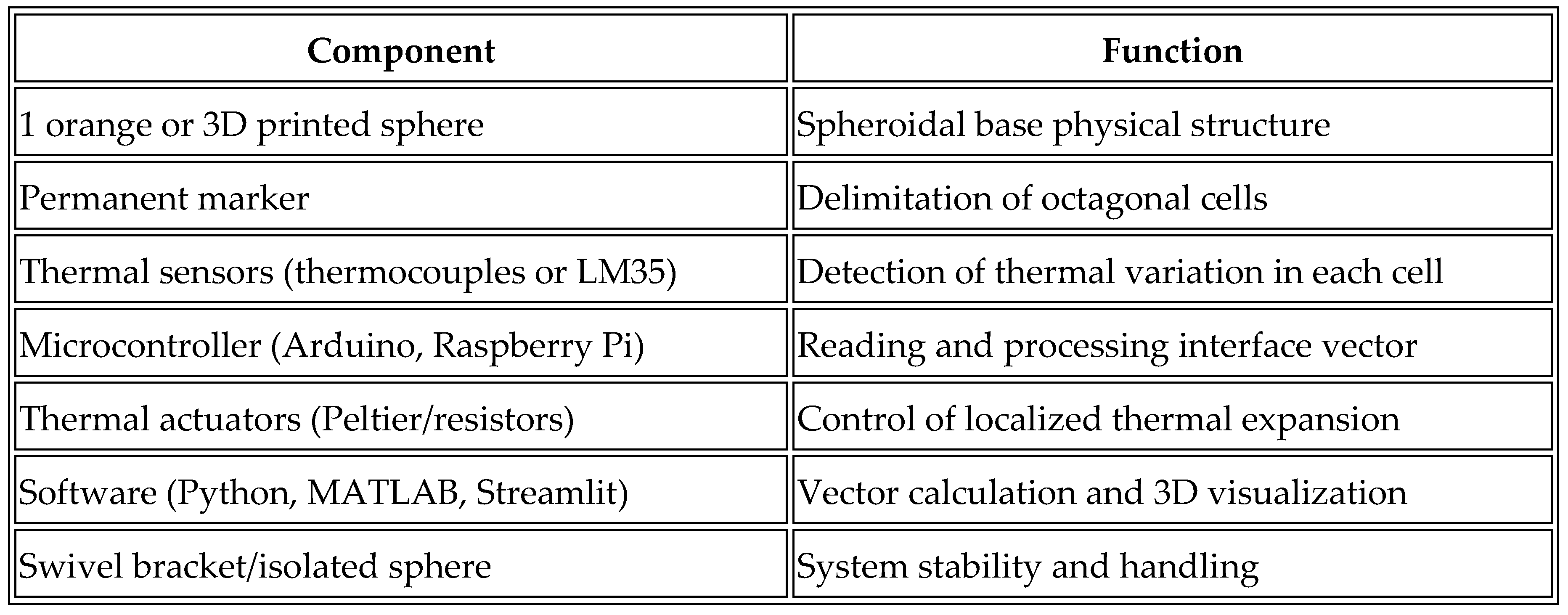
5.3. Stages of the Experiment

• Preparing the mesh

  ○

  Divide the spherical surface (orange or printed model) into 20 to 40 octagonal cells.

  ○

  Mark each cell with identifiers and insertion points for sensors.

• Sensor positioning

  ○

  Insert a thermal sensor in the center of each cell.

  ○

  Connect all the sensors to the microcontroller with coordinate mapping (xi,yj,zk)(x_i, y_j, z_k)(xi,yj ,zk).

• Controlled thermal application

  ○

  Use thermal actuators to selectively heat/cool each cell.

  ○

  Record the thermal variation ΔT\Delta TΔT in real time.

• Local vector calculation

  ○

  Modify each vector M⃗ijk\vec{M}_{ijk}Mijk with:

  M′⃗ijk= M⃗ijk⋅(1+α⋅ΔT)\vec{M'}_{ijk} = \vec{M}_{ijk} \cdot (1 + \alpha \cdot \Delta T)M′ijk= Mijk⋅(1+α⋅ΔT)

  ○

  Weight with εn\varepsilon_nεn according to the cell's energy response.

• Dimensional validation

  ○

  Apply the postulate:

  ω⋅εn≈-1\omega \cdot \varepsilon_n \approx -1ω⋅εn≈-1

  ○

  If true, the cell is considered an emerging dimensional zone.

• Visualization and registration

  ○

  The system displays valid and unstable vectors on a 3D screen.

  ○

  Validated cells are highlighted with specific colors.

5.4. Verification Hypothesis

It is expected that approximately 25% of the cells, under certain thermal conditions and vector weightings, will comply with the dimensional postulate, generating an angular distribution that is consistent with the digital simulation.

5.5. Prototype Applications

• Education: experimental teaching of dimensional physics;
• Research: reference model for vector resonance studies;
• Scientific validation: laboratory testing of theoretical concepts with measurable data;
• Engineering: development of resonant systems guided by vector geometry.

6. Comparative Analysis with Traditional Models

The following table shows a comparison between the main attributes of contemporary physical-dimensional theories and the Octagonal Vector Mesh proposal, considering criteria such as dimensional structure, empirical validation and applicability.

6.1. Comparative Table

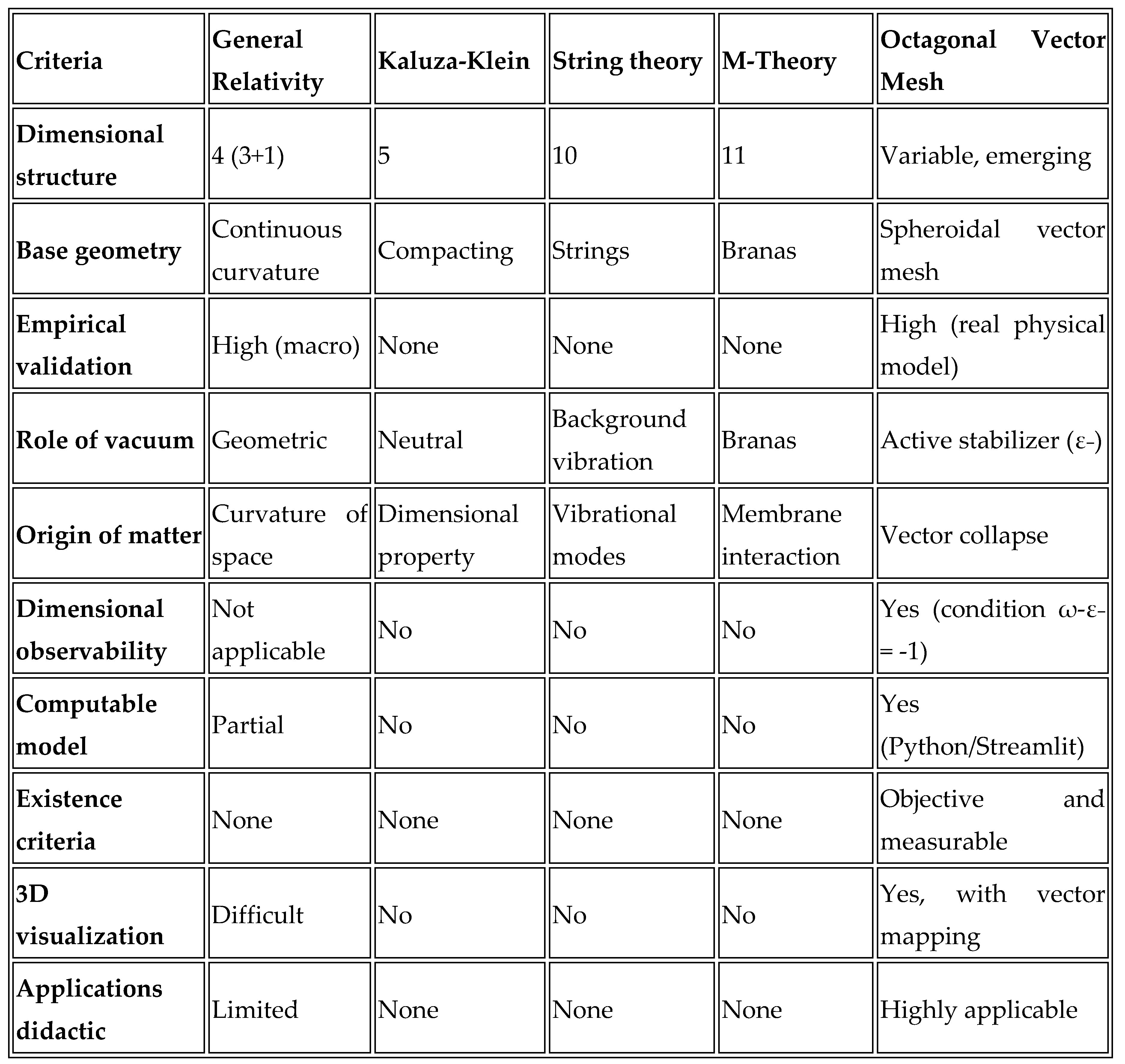
6.2. Highlights of the Vector Mesh Compared to Classical Theories

• Direct empiricism: unlike purely theoretical models, the Octagonal Mesh can be physically assembled (e.g. prototypes with sensors in oranges or printed models).
• Interactive simulation: thermal vector modeling can be carried out in real time with accessible computer tools.
• Measurable physical criterion of dimensional existence: the postulate ω⋅ε-=-1\omega \cdot \varepsilon_- = -1ω⋅ε-=-1 offers a clear and testable condition - something unheard of in previous hyperdimensional approaches.
• Experimental and philosophical unification: connects physics, topology, epistemology and ontology in a cohesive, vector-based structure.

6.3. Impact on Contemporary Physics

If confirmed, the theory represents a paradigm shift for the world:

• Replace continuous geometries with discrete and modular vectors;
• Offer reproducible simulations with real data;
• Eliminate the need for hidden or compressed dimensions;
• Redefine the role of vacuum as an active stabilizing element;
• Propose an emerging vector reality, sensitive to thermal, density and intentional variations.

7. Practical and Scientific Applications

Octagonal Vector Lattice Theory transcends the scope of traditional physics by proposing an active, vector ontology of reality. Here, space, time, matter and even the observer cease to be absolute or passive entities, becoming products of local vector stabilization in a living dimensional lattice.

7.1. What is Existence?

In classical ontology, existence is treated as a given state or a fixed attribute of entities. In lattice ontology, this definition is reformulated:

"To exist is to stabilize oneself as a resonant vector within an angularly active three-dimensional structure."

Dimensions, therefore, are not pre-existent - they are acts of vectorial manifestation. Each cell in the mesh represents an ontological possibility, and only those that meet the criterion ω⋅ε-=-1\omega \cdot \varepsilon_- = -1ω⋅ε-=-1 materialize as reality.

7.2. Time as a Vector

Time, traditionally seen as linear, irreversible and absolute (or relative to speed), is now understood as:

• A tangential vector projected by the internal vector rotation of the mesh;
• Reversible or null in vector coherence zones;
• A dynamic ontological state, not a fixed background in which events occur.

This implies that past, present and future are states of vector resonance, accessible by thermal, frequency or intentional conditions.

7.3. The Observer as a co-Destructive Agent

The mesh is not alien to the observer:

The act of observing aligns vectors, changes local frequencies and conditions the emergence of dimensions.

This perspective dialogues with

• The theory of coemergence (Karen Barad),
• The relational ontology (Rovelli),
• Structural realism (Ladyman and French).

Reality is thus a field of stabilized vector relations, where the observer is a constitutive part of the pattern.

7.4. Vacuum as Active Resistance

In the mesh, the vacuum is not absence. It is:

• A stabilizing resonant field;
• Represented by the negative resistance ε-\varepsilon-ε-, which regulates dimensional emergence;
• An active factor in maintaining reality, not a neutral scenario.

This completely redefines the concept of "nothing": emptiness is dense, functional and structurally vital.

7.5. Reality as Vector Coherence

All measurable reality is the result of angular vector coherence between the components of the mesh. Instability - noise, chaos, collapse - occurs when the balance between frequency and resistance is not achieved.

Each valid dimension is an act of reality. Every unstabilized vector is just unrealized potentiality.

8. Practical and Scientific Applications

The operability of the Octagonal Vector Mesh Theory allows it to be directly applied in various fields of science, engineering, pedagogy and experimental cosmology. The main areas of concrete applicability of the theory are presented below.

8.1. Teaching Dimensional Physics and Vector Topology

The geometric simplicity of the model - centered on the spheroidal structure of the orange - allows it to be used as a teaching tool in subjects such as:

• Applied vector physics,
• Topology and differential geometry,
• Cosmology and epistemology of science.

The possibility of reproducing the mesh with physical objects, thermal sensors and simulation software (such as Python and Streamlit) makes theory an ally in the experimental teaching of complex content.

8.2. Empirically Based Cosmological Simulation

Lattice theory provides an alternative to cosmological simulations based on Newtonian or relativistic models. With it, you can:

• Modeling black holes as vector collapse zones;
• Simulate the Big Bang as an initial angular explosion;
• Treating dark matter as unstabilized vectors;
• Evaluate the expansion of the universe as a thermal reorganization of the lattice.

These simulations can be carried out in engineering software such as COMSOL, ANSYS or Blender, based on real thermal data.

8.3. Vector Computing: Vetobits

The lattice structure suggests a new computer architecture based not on binary bits, but on stabilized vectors, called vetobits here. Each vetobit:

• It is a three-dimensional vector with orientation, modulus and thermal weighting;
• It can represent multiple simultaneous states, as in qubits;
• It depends on angular stabilization to be considered "active" (valid state).

This opens up the possibility of future vector computers based on dynamic resonant meshes - a fusion of geometric hardware and thermal coherence algorithms.

8.4. Materials Engineering with Resonant Structure

The principles of mesh can be applied to material design:

• Self-sustaining structures that reconfigure themselves with thermal variation;
• Geometries based on octagons and vectors that respond to environmental stimuli;
• Materials that change their density, rigidity or shape according to internal vector patterns.

This is relevant for the development of adaptive metamaterials and dynamic architectural structures.

8.5. Ontology Applied to Psychology and Philosophy of Consciousness

The ontological proposal of the mesh - which considers reality to be the result of resonant vectors - allows for new approaches:

• Energy and vibrational psychology;
• Modeling mental fields as vector topologies (see Dimension 11);
• Therapies based on emotional vector coherence (Dimension 12);
• Ethics applied to the structure of the field (Dimension 13).

This basis can be integrated with systemic learning models, meditation guided by vector patterns, and analysis of states of consciousness via the dimensional field.

8.6. Prototyping and Scientific Validation

The structure of the theory already allows for the development of functional prototypes. This includes:

• Thermo-vector devices to simulate the mesh on a reduced scale;
• Cryogenic environments with vector sensors to study stability zones;
• Physical simulations in particle accelerators to detect angular patterns predicted by theory;
• Tests with 3D printers and flexible materials to create dynamic physical meshes.

9. Conclusions

Octagonal Vector Lattice Theory represents a conceptual and operational turning point in contemporary models of physics, cosmology and dimensional ontology. By proposing an architecture based on modular three-dimensional vectors, applied to a measurable spheroidal structure (such as an orange), the theory replaces the paradigm of compactified and abstract dimensions with a measurable, simulatable and empirically reproducible approach.

The introduction of the physical postulate of dimensional existence -

ω⋅ε-=-1\omega \cdot \varepsilon_- = -1ω⋅ε-=-1

- inaugurates a new criterion of reality: the dimension exists if it is stabilized by angular vector coherence under vacuum resistance. This criterion is computationally reproducible, validatable in physical prototypes and compatible with modern experimental tools.

The theory transcends the limits of theoretical physics by incorporating:

• A cohesive mathematical vector base (thermal modulation functions, dimensional weightings);
• A structured ontology where space, time and the observer are co-emergent and dynamic;
• An unprecedented practical and pedagogical application, allowing the experimental teaching of dimensional physics;
• A clear visualization of reality as a resonant, organizable, aesthetic and harmonious field.

Summary of key contributions:

• It redefines the concept of dimension as a stabilized vector, not as a topological abstraction.
• It proposes a relational reality, where the observer influences the dimensional mesh.
• It offers a reproducible and computationally validated physical model.
• It establishes a bridge between science, philosophy, symbolism and technology.

Future prospects

The Octagonal Mesh opens the way to:

• New ways of simulating the universe with real vectors instead of continuous curves;
• Post-binary vector computing;
• Construction of devices with adaptive dimensional behavior;
• An epistemology of reality based on harmonic stability and vector emergencies, and not on absolute variables.

The mesh is no longer a metaphor but a model. Space is no longer a stage, but an actor. Time is no longer a line, but a frequency. And reality, finally, is what resonates.