Profit Optimization Modeling for Amazonian Tour Operators using Linear Programming: A Geographically Specific Approach

1. Introduction

Tourism constitutes a fundamental axis for economic and social development [1], particularly in regions with high tourism potential such as Puerto Francisco de Orellana, Ecuador. However, despite its relevance, local tourism operators face serious difficulties in maximizing their profitability, a situation that mainly derives from inefficient resource management, the seasonality of demand, and the lack of technical optimization tools [2].

In this context, the study is based on three conceptual pillars: firstly, linear programming, as a mathematical methodology to optimize objective functions under specific constraints [3]; secondly, sustainable tourism management, which integrates economic, environmental, and social dimensions [4]; and finally, the strategic role of Information and Communication Technologies (ICT) as facilitators of competitiveness in the sector.

It is worth noting that the research has a triple relevance: economic, by providing practical solutions to improve the profitability of tourism SMEs; academic, by enriching the literature on optimization applied to emerging contexts; and social, by promoting employment and local development through sustainable tourism [5]. To this end, the general objective is to evaluate the potential of linear programming in optimizing the profitability of tourism operators in Puerto Francisco de Orellana, broken down into three specific objectives: to analyze the factors that influence their profitability, to develop a model adapted to the sector, and to measure the impact of optimization on decision-making.

The justification for the study lies in the fact that, although optimization through linear programming has proven effective in other productive sectors, its application to tourism in this region remains unexplored. Furthermore, operators lack quantitative tools for decision-making, which limits their competitiveness. On the other hand, although there are previous studies that use techniques such as Revenue Management or Data Envelopment Analysis (DEA), none has approached the problem from the perspective of linear programming, as evidenced by the work of [6] in catering or [7] in manufacturing.

From a theoretical framework, the research is based on optimization theory, which provides the mathematical foundations for modeling [8]; the theory of sustainable tourism development, which links profitability with sustainability [5]; and the theory of tourism competitiveness, which highlights the role of ICT and strategic management [9].

The scope of the study is limited to Puerto Francisco de Orellana, a city known as "The Gateway to the Amazon," where tourism represents a key economic activity [10], despite the profitability limitations faced by the sector’s SMEs. Thus, the central question guiding the research is: How can the linear programming method be applied to optimize the profits of tourism operators in Puerto Francisco de Orellana, Ecuador?

2. Background

The study introduces a theoretical framework on linear programming (LP) and its role in decision-making, particularly in the tourism sector of the Ecuadorian Amazon, with a focus on Francisco de Orellana canton. LP is presented as a mathematical tool for optimizing resources under linear constraints, applicable in logistics, transportation, and tourism planning. Additionally, the tourism offer is defined as a combination of basic (accommodation, transportation) and complementary (recreational activities) services as pointed out by [11,12], while tourist destinations are described as comprising natural/cultural attractions and integrated services [13], the **tour operators** act as intermediaries between tourists and service providers ([14,15]). While the theoretical foundation is solid, the discussion remains abstract, lacking practical examples of LP applied to tourism in Orellana. The cited sources (e.g., [16,17]) support the general concept but do not bridge the gap between theory and real-world application. Moreover, the definition of tourism services, though clear, does not address how LP can specifically enhance them. To strengthen this section, the authors should include case studies where LP has optimized tourism logistics (e.g., route planning for tour operators). Additionally, integrating local data on tourist services in Orellana would make the framework more relevant.

The Ecuadorian Amazon is highlighted for its biodiversity and tourism potential, though it faces challenges such as deficient infrastructure and seasonality [18]. Specifically, Orellana’s tourism diagnosis reveals issues like poor road conditions and ineffective promotion, despite having attractions like Yasuní National Park [19]. The analysis relies on outdated statistics (2015–2019), reducing its current validity. Furthermore, while problems like road conditions are identified, no optimization-based solutions (e.g., LP models for infrastructure investment) are proposed. The discussion on seasonality also lacks quantitative analysis, such as demand fluctuations affecting resource allocation. Updating data with post-pandemic tourism trends would improve accuracy. Additionally, applying LP models to prioritize road repairs or distribute promotional budgets seasonally could turn challenges into actionable strategies.

The study acknowledges LP’s potential in tourism but does not demonstrate its real-world implementation in Orellana. Similarly, while sustainable tourism is mentioned, there is no detailed analysis of ecological or community-based strategies. The lack of applied LP models (e.g., optimizing visitor flows in Yasuní) weakens the argument. Additionally, sustainability is treated superficially—no LP applications balancing economic benefits with environmental protection are discussed. Proposing an LP-based ecotourism model (e.g., maximizing visitor numbers without exceeding ecological carrying capacity) would align economic and environmental goals. Partnerships with local communities for equitable benefit distribution could also be explored using optimization techniques.

The study suggests using LP for: tourist route optimization (variables: tourist numbers, lodging capacity), infrastructure investment prioritization, dynamic promotion budgeting based on seasonality, community tourism profit-sharing models. While the solutions are well-structured, they remain hypothetical without pilot testing or real data integration. For instance, how would budget constraints be quantified in practice? A pilot project in Orellana, applying LP to one tourist circuit, would validate feasibility. Collaboration with local governments to gather real-time data on tourist flows and infrastructure costs would also enhance practicality.

In conclusion, **linear programming** can be a key tool for optimizing tourism in Orellana. However, its effective application requires **updated data**, a **practical approach**, and **comprehensive solutions** that combine economic efficiency, environmental sustainability, and social inclusion. Only then can the tourism potential of the Ecuadorian Amazon be fully realized.

Table 1. Abstract Summary of Reviewed Articles

Abstract
This article assesses the application of Linear Programming to aid decision-making in Small and Medium Enterprises (PYMES)...
The article presents a log management model for supporting information audits...
This study proposes a Sustainable Tourism Management Model...
This study explores consumer loyalty towards sun and beach destinations...
This study aimed to improve the dissemination of tourist information in Tarapoto...
The Territorial Development and Planning Plan (PDOT)...
The updated Development and Territorial Planning Plan...

Table 1. Abstract Summary of Reviewed Articles

Abstract
This article assesses the application of Linear Programming to aid decision-making in Small and Medium Enterprises (PYMES)...
The article presents a log management model for supporting information audits...
This study proposes a Sustainable Tourism Management Model...
This study explores consumer loyalty towards sun and beach destinations...
This study aimed to improve the dissemination of tourist information in Tarapoto...
The Territorial Development and Planning Plan (PDOT)...
The updated Development and Territorial Planning Plan...

Table 2. Main Findings of Reviewed Articles

Results
The model, applied to a Costa Rican farm, used Linear Programming to maximize income...
The model was applied in several systems, notably the ERP Cedrux in Cuba...
The model includes strategic programs such as administrative improvements...
The empirical results validate a theoretical model that links country image...
The results showed a significant improvement in the dissemination...
Key findings include critical insights into climate change impacts, deforestation...
Key findings include assessments of biophysical, sociocultural, economic...

Table 2. Main Findings of Reviewed Articles

Results
The model, applied to a Costa Rican farm, used Linear Programming to maximize income...
The model was applied in several systems, notably the ERP Cedrux in Cuba...
The model includes strategic programs such as administrative improvements...
The empirical results validate a theoretical model that links country image...
The results showed a significant improvement in the dissemination...
Key findings include critical insights into climate change impacts, deforestation...
Key findings include assessments of biophysical, sociocultural, economic...

Table 3. References from Reviewed Articles

References
Alvarado, J. Introducción LA PROGRAMACIÓN LINEAL...
Gómez, O.; Estrada, V.; Bauta, R.; García, I. Modelos de gestión...
CEDEÑO, F. MODELO DE GESTIÓN DE TURISMO SOSTENIBLE...
Amaya, C. El proceso de lealtad del consumidor turístico...
Aranda, C. Implementación de una aplicación móvil para la promoción turística...
GADPO-ORELLANA. PLAN DE DESARROLLO Y ORDENAMIENTO TERRITORIAL...
GAD de la Municipalidad de Francisco de Orellana. PDOT 2020–2023...

Table 3. References from Reviewed Articles

References
Alvarado, J. Introducción LA PROGRAMACIÓN LINEAL...
Gómez, O.; Estrada, V.; Bauta, R.; García, I. Modelos de gestión...
CEDEÑO, F. MODELO DE GESTIÓN DE TURISMO SOSTENIBLE...
Amaya, C. El proceso de lealtad del consumidor turístico...
Aranda, C. Implementación de una aplicación móvil para la promoción turística...
GADPO-ORELLANA. PLAN DE DESARROLLO Y ORDENAMIENTO TERRITORIAL...
GAD de la Municipalidad de Francisco de Orellana. PDOT 2020–2023...

3. Materials and Methods

The main objective of this research is to create a tool that allows tourism operators to obtain greater profit from their activity. To this end, Puerto Francisco de Orellana is first taken as a reference, where there are 8 tourism operators registered as companies; therefore, the model must be adjusted to the characteristics and singularities of these entities. Next, a detailed study will be carried out on the services they offer, the rates they charge for them, and the associated costs. Subsequently, with the information collected, a generic mathematical model will be developed that can be adapted to each specific case.

The optimization will seek to improve prices and the minimum number of reservations for each service, considering limitations such as the number of workers, available business hours, lodging capacity in the area, among other factors. For the development of the tool, Python will be used together with the necessary libraries for data processing, optimization, and results presentation.

It is worth noting that this work is novel, as there are no similar studies focused on companies in the tourism sector in Ecuador, unlike what occurs in the industrial sector. In this way, it is hoped that the research will establish a favorable precedent for the advancement of applied mathematics in this field and in the region.

To achieve the stated objectives, a structured process is followed. First, the scope of the research is determined, delimiting the geographical area to Puerto Francisco de Orellana and taking the city’s tourism operators as the study population. Then, information related to the tourism activities carried out by these companies is collected.

Once the data has been obtained, the linear programming model is defined, establishing the study variables, the constraints, and the parameters necessary for its adjustment. Subsequently, an application is developed that allows configuring and executing the optimization process based on the designed model. Finally, simulations based on real cases of tourism operators are executed, and the results obtained are analyzed.

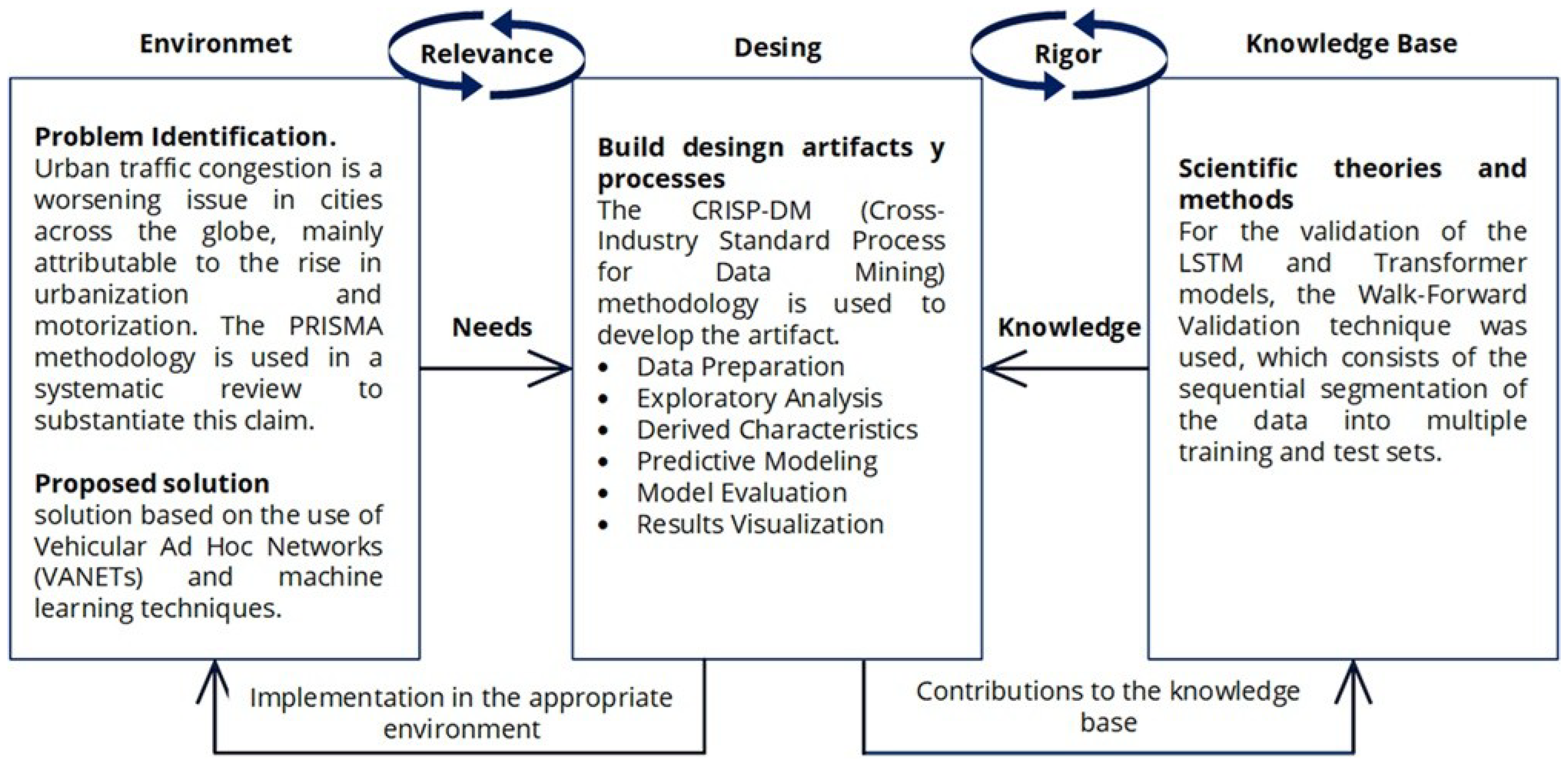
Furthermore, this study is based on the Design Science Research (DSR) methodology, a framework composed of three main phases: relevance, design, and rigor. Firstly, the relevance phase involves identifying the problem to be addressed and defining the application context of the solution, focusing on ensuring a significant impact [20]. Subsequently, the design phase focuses on creating innovative solutions by developing prototypes or models that directly meet the identified needs. Finally, the rigor phase focuses on validating the proposed solutions, ensuring their theoretical and practical robustness through scientific methods and exhaustive evaluations. This methodology facilitates a systematic process for developing useful and applicable artifacts in real-world environments.

Figure 1. Design Science Research (DSR) Methodology

Figure 1. Design Science Research (DSR) Methodology

3.1. Relevance Cycle

There is a need to develop an application that optimizes the profits of a travel agency in Puerto Francisco de Orellana, Ecuador, through a mathematical model that allows determining the optimal combination of tour packages and individual activities. The problem lies in the fact that local tour operators do not have a tool that allows them to efficiently calculate the number of services they must offer to cover their operating costs and guarantee an adequate profit margin, considering key factors such as seasonality, price variability, and the diversity of services offered.

Among the main challenges are the management of high and low seasons, price fluctuations due to external factors, and the complexity of offering both complete packages and individual services. Operators provide a wide range of services, including lodging, food, guided tours, transportation, interpretation, and souvenirs, which makes the manual determination of the most profitable combination difficult.

To solve this problem, it is proposed to design a mathematical optimization model that considers all relevant variables, such as fixed and variable costs, selling prices, seasonal demand, and available resources. This model will allow agencies to identify the optimal quantity of packages and individual activities that maximize their profits, while ensuring the coverage of their operating expenses.

In addition, the application will include a graphical representation of the results, facilitating strategic decision-making. By implementing this solution, operators will be able to improve their profitability, adapt to market fluctuations, and offer competitive prices without compromising their profit margins. In this way, it will contribute to the sustainable growth of the tourism sector in the region.

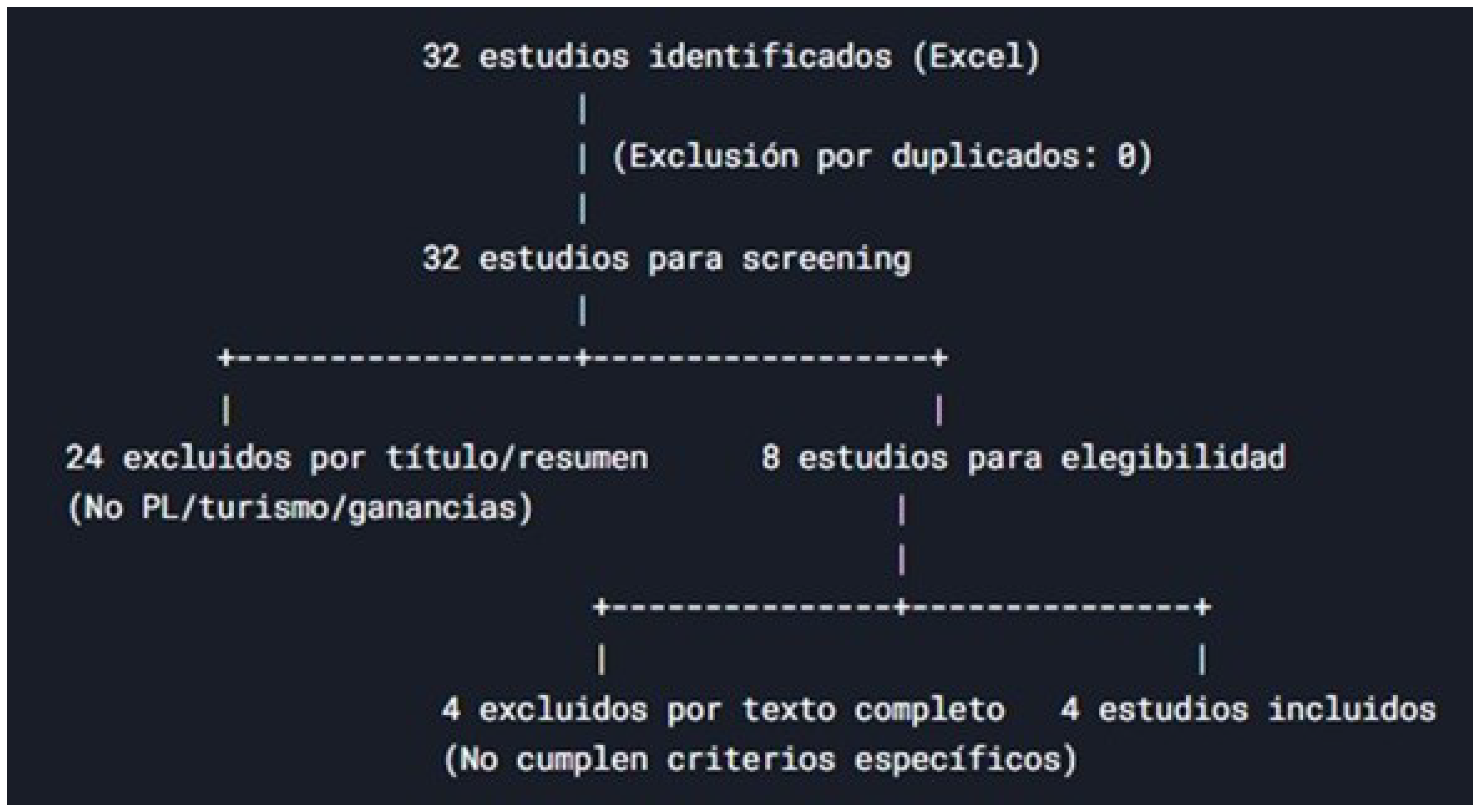
The PRISMA methodology was applied to systematize the literature, with the objective of identifying relevant studies on profit optimization for tour operators in the Amazon region using linear programming. Initially, 32 studies were identified in the database, of which no duplicates were detected, so all were considered for the title and abstract screening phase.

Subsequently, inclusion criteria based on thematic relevance were applied, focusing on studies that used linear programming and were related to profit optimization or tourism in the Amazon region. As a result, 24 studies were excluded for not meeting these requirements, leaving a total of 8 studies for a more detailed full-text evaluation.

In the eligibility phase, the remaining 8 studies were analyzed to determine their alignment with the research question. Of these, only 4 met the established criteria: one addressed cost optimization in companies using linear programming, another identified profitable agricultural activities using linear models, a third applied this methodology to nature-based tourism, and the last one employed fuzzy linear programming to design sustainable tourism itineraries. The remaining 4 studies were discarded for not specifically focusing on profit optimization for tour operators.

Finally, the 4 selected studies were considered suitable for review, highlighting their key contributions, such as the identification of more profitable integrated systems, the consideration of constraints in human resources, and the combination of economic and environmental objectives. However, a gap in the literature was evident, as few studies directly address the application of linear programming to maximize profits in the context of Amazonian tourism. Therefore, it is suggested to delve deeper into research that integrates optimization models with socioeconomic and environmental variables specific to this region, in order to fill this gap in knowledge.

Figure 2. PRISMA Diagram Adapted

Figure 2. PRISMA Diagram Adapted

Table 4. Research Papers on Linear Programming Applications

No.	Paper Title	Key Findings
2	POPULAR AND SOLIDARITY ECONOMY ENTERPRISES...	LP model to optimize costs...
3	Identifying profitable activities...	LP identifies integrated systems...
4	Managing change in nature-based tourism...	LP applied to nature tourism...
12	Multi-Objective Fuzzy Tourist Trip...	Fuzzy LP to maximize profits...

Table 4. Research Papers on Linear Programming Applications

No.	Paper Title	Key Findings
2	POPULAR AND SOLIDARITY ECONOMY ENTERPRISES...	LP model to optimize costs...
3	Identifying profitable activities...	LP identifies integrated systems...
4	Managing change in nature-based tourism...	LP applied to nature tourism...
12	Multi-Objective Fuzzy Tourist Trip...	Fuzzy LP to maximize profits...

3.2. Design Cycle

3.2.1. Formulating a Mathematical Program

To formulate the mathematical program, one starts with the methods available in linear programming, among which the Simplex method, the ellipsoid method, and the interior point method stand out, each with its own particularities in terms of efficiency and applicability.

In this context, decision variables play a fundamental role, as they represent the choices that must be optimized. These variables, which must be of real type to encompass any value within a defined range, allow for the structuring of both the objective function and the constraints of the model. The objective function, which can be of maximization or minimization, is constructed as a linear combination of these variables, multiplied by their respective coefficients, in order to reach the desired optimal value.

On the other hand, the constraints establish the conditions that guarantee the feasibility of the solutions. These are expressed through linear inequalities that limit the space of possible values for the decision variables. In maximization problems, the constraints prevent the objective function from exceeding certain limits, while in minimization problems, they ensure that it does not fall below a determined threshold. These constraints can reflect physical limitations, such as the availability of resources, or financial limitations, such as budgetary restrictions.

In this way, the linear programming model is completely defined by integrating the decision variables, the objective function, and the constraints, providing a structured framework for finding the optimal solution to the problem at hand.

3.2.2. Mathematical Model Approach

• Decision Variables:

  -

  P Tourist packages from the tour operator (unit)

  -

  S Tourist services from the tour operator (unit)

  -

  O Other products offered by the tour operator in its activities (unit)

• Objective Equation:

  $$\mathrm{Max}:G=I-G_s$$

  Where:

  -

  G Profit earned by the agency (USD)

  -

  I Revenue obtained from sales (USD)

  -

  $G_s$ Expenses incurred by the tour operator for its activity (USD)

• Revenues:

  $$I=\sum _{i=1}^{n}m{p}_i{P}_i+\sum _{i=1}^{m}m{s}_i{S}_i+\sum _{i=1}^{q}m{o}_i{O}_i$$

  Where:

  -

  $m{p}_i$ Selling price of tourist package i (USD)

  -

  $P_i$ Tourist package i (unit)

  -

  $m{s}_i$ Selling price of tourist service i (USD)

  -

  $S_i$ Tourist service i, different from packages (unit)

  -

  $m{o}_i$ Selling price of other products (gifts, souvenirs, etc.) i (USD)

  -

  $O_i$ Other product i for sale (unit)

• Expenses:

  $$G_s=\sum _{i=1}^{n}c{p}_i{P}_i+\sum _{i=1}^{m}c{s}_i{S}_i+\sum _{i=1}^{m}c{o}_i{O}_i+\sum _{i=1}^{n}t{p}_{i}m{p}_i{P}_i+\sum _{i=1}^{n}t{s}_{i}m{s}_i{S}_i+\sum _{i=1}^{n}t{o}_{i}m{o}_i{O}_i+\sum _{i=1}^f{g}_i$$

  Where:

  -

  $c{p}_i$ Cost of tourist package i (USD)

  -

  $c{s}_i$ Cost of tourist service i (USD)

  -

  $c{o}_i$ Cost of other products (gifts, souvenirs, etc.) i (USD)

  -

  $t{p}_i$ Tax rate on the selling price of tourist package i (USD)

  -

  $t{s}_i$ Tax rate on the selling price of tourist service i (USD)

  -

  $t{o}_i$ Tax rate on the selling price of other product i (USD)

  -

  $g_i$ Annual expenses for tourism activity development (USD)

• Constraints:
  Mathematical Constraints:
  The number of units of each product that generates income for the agency must be positive integers.

  $$P_i\ge 0;P_i\in \mathbb{Z}$$

  $$S_i\ge 0;S_i\in \mathbb{Z}$$

  $$O_i\ge 0;O_i\in \mathbb{Z}$$
  Economic Constraints:

  $$G_s\le {\beta }_{1}I$$

  $$\sum _{i=1}^f{g}_i\le {\beta }_{2}I$$

  $$\sum _{i=1}^{q}m{o}_i{O}_i\ge {\beta }_{3}I$$

  Where:

  -

  ${\beta }_1$ Fraction corresponding to total costs in relation to income.

  -

  ${\beta }_2$ Fraction corresponding to permanent costs in relation to income.

  -

  ${\beta }_3$ Fraction corresponding to sales of other products in relation to income.

  Working Hours of Guides and Workers:

  $$\sum _{i=1}^{n}h{p}_i{P}_i+\sum _{i=1}^{m}h{s}_i{S}_i\le n_t{A}_{10}{A}_{11}$$

  Where:

  -

  $n_t$ Number of workers or tourist guides.

  -

  $A_{10}$ Average working hours per day per worker (h/day).

  -

  $A_{11}$ Working days per year (days/year).

  -

  $h{p}_i$ Labor hours required for tourist package i (h/unit).

  -

  $h{s}_i$ Labor hours required for tourist service i (h/unit).

  Vehicle Usage Hours:

  $$\sum _{i=1}^{n}hv{p}_i{P}_i+\sum _{i=1}^{m}hv{s}_i{S}_i\le n_v{A}_{20}{A}_{11}$$

  Where:

  -

  $n_v$ Number of vehicles owned by the operator.

  -

  $A_{20}$ Average daily usage time of the vehicles (h/day).

  -

  $hv{p}_i$ Vehicle usage hours for tourist package i (h/unit).

  -

  $hv{s}_i$ Vehicle usage hours for tourist service i (h/unit).

  Projected Packages to Sell:

  $$\sum _{i=1}^n{P}_i+\sum _{i=1}^m{S}_i\le n_{PST}$$

  Where:

  -

  $n_{PST}$ Projected total number of package or service sales (units)

3.2.3. Application Design

The design of a simple application for Linear Programming (LP) is a structured process consisting of several stages. First, the problem to be solved is defined by identifying the decision variables, objective function, and constraints. Next, the user interface is designed, establishing the application’s structure, graphical elements, and their interaction. Subsequently, the app is developed, implementing both the logic and visual components. Then, testing is conducted to ensure proper functionality using different datasets and scenarios. Finally, the application is deployed.

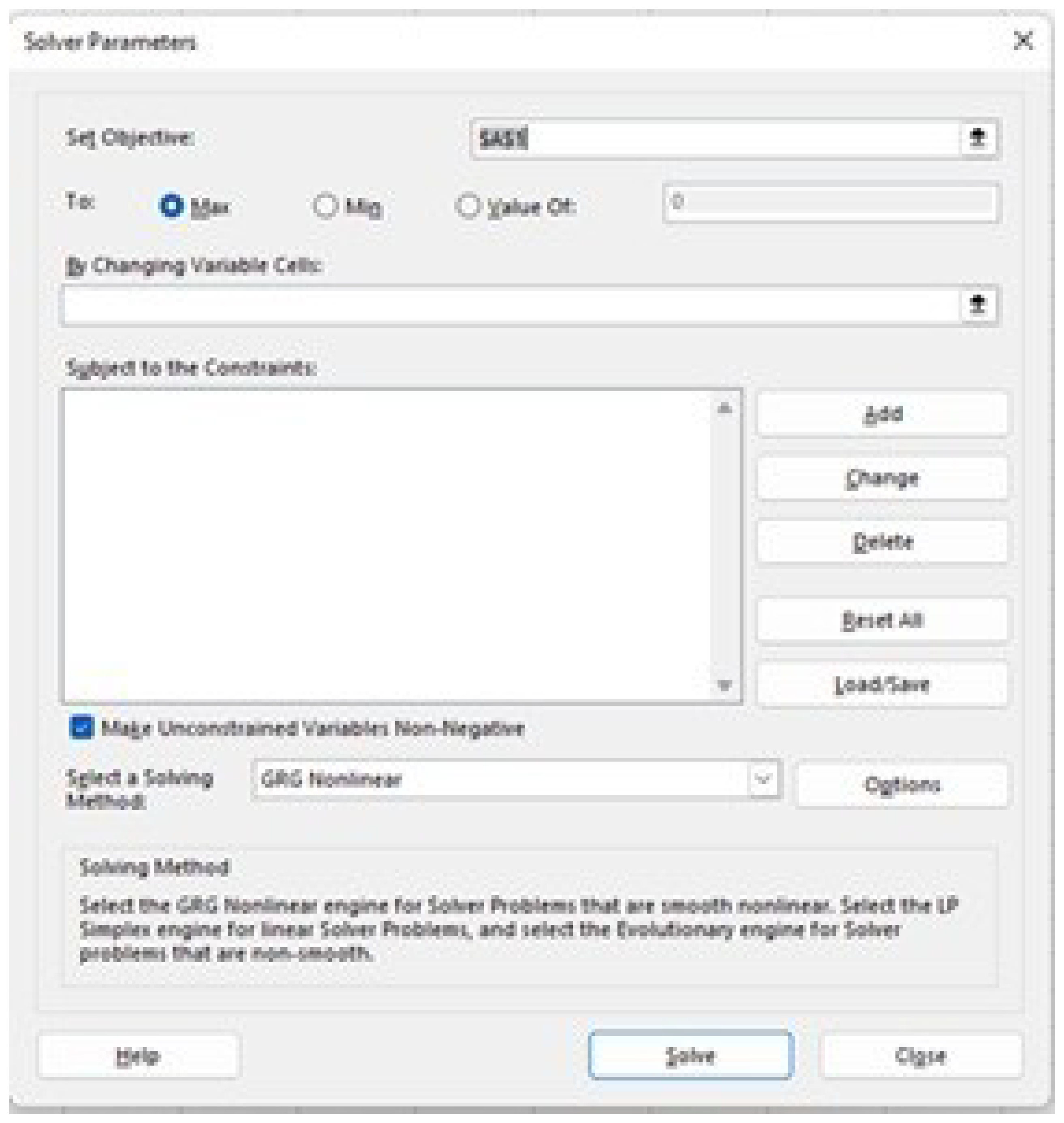
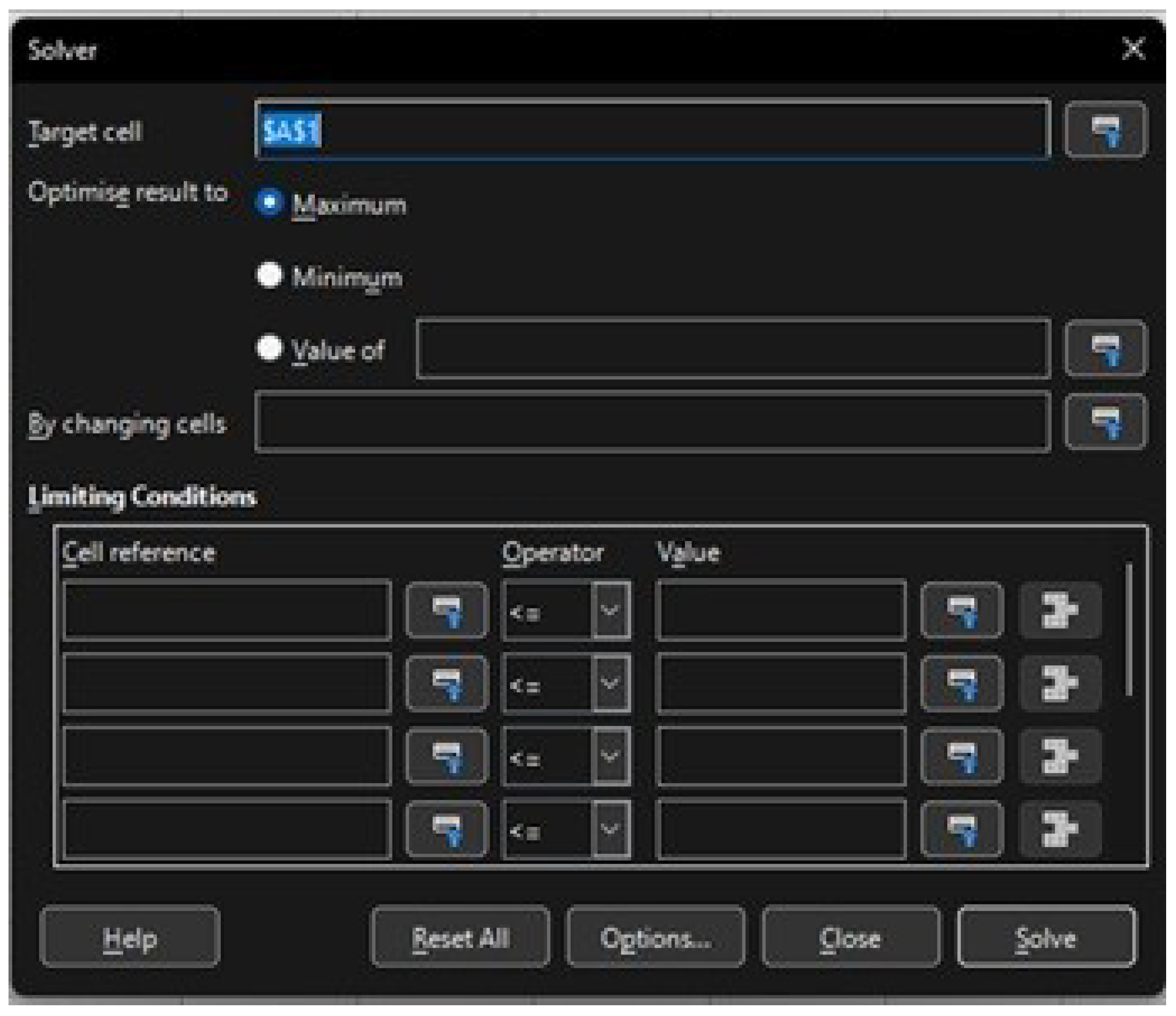
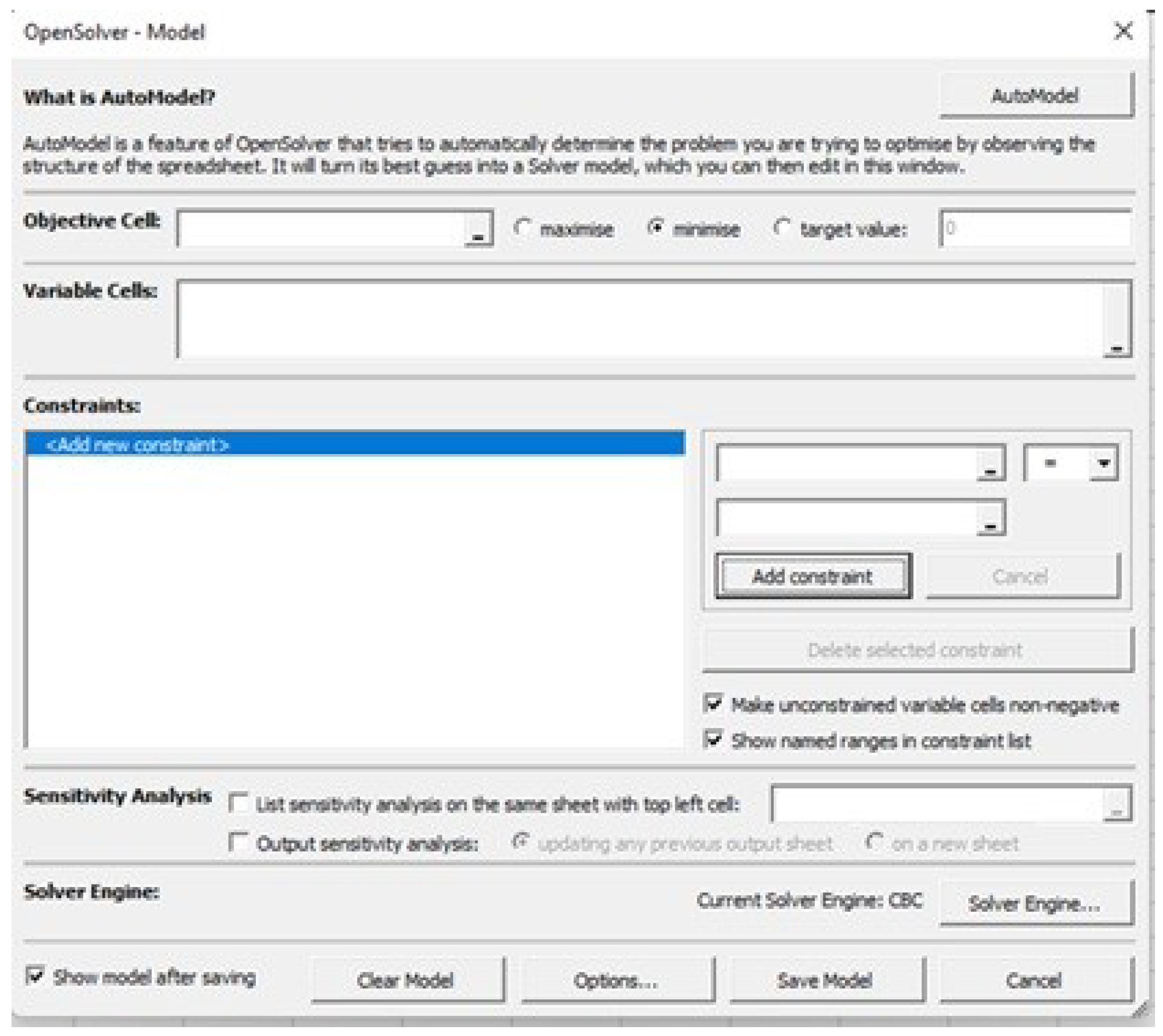
Prior to development, optimization applications were analyzed to understand the layout of controls and windows. Among these, the Solver in Microsoft Excel (see Figure 3) stands out, allowing users to define cell ranges for the objective function, decision variables, and constraints, leveraging the spreadsheet structure. Similarly, the Solver in LibreOffice (see Figure 4) follows an analogous approach, based on cell references. Another alternative is OpenSolver (see Figure 5), an Excel add-in that incorporates additional methods for solving LP problems.

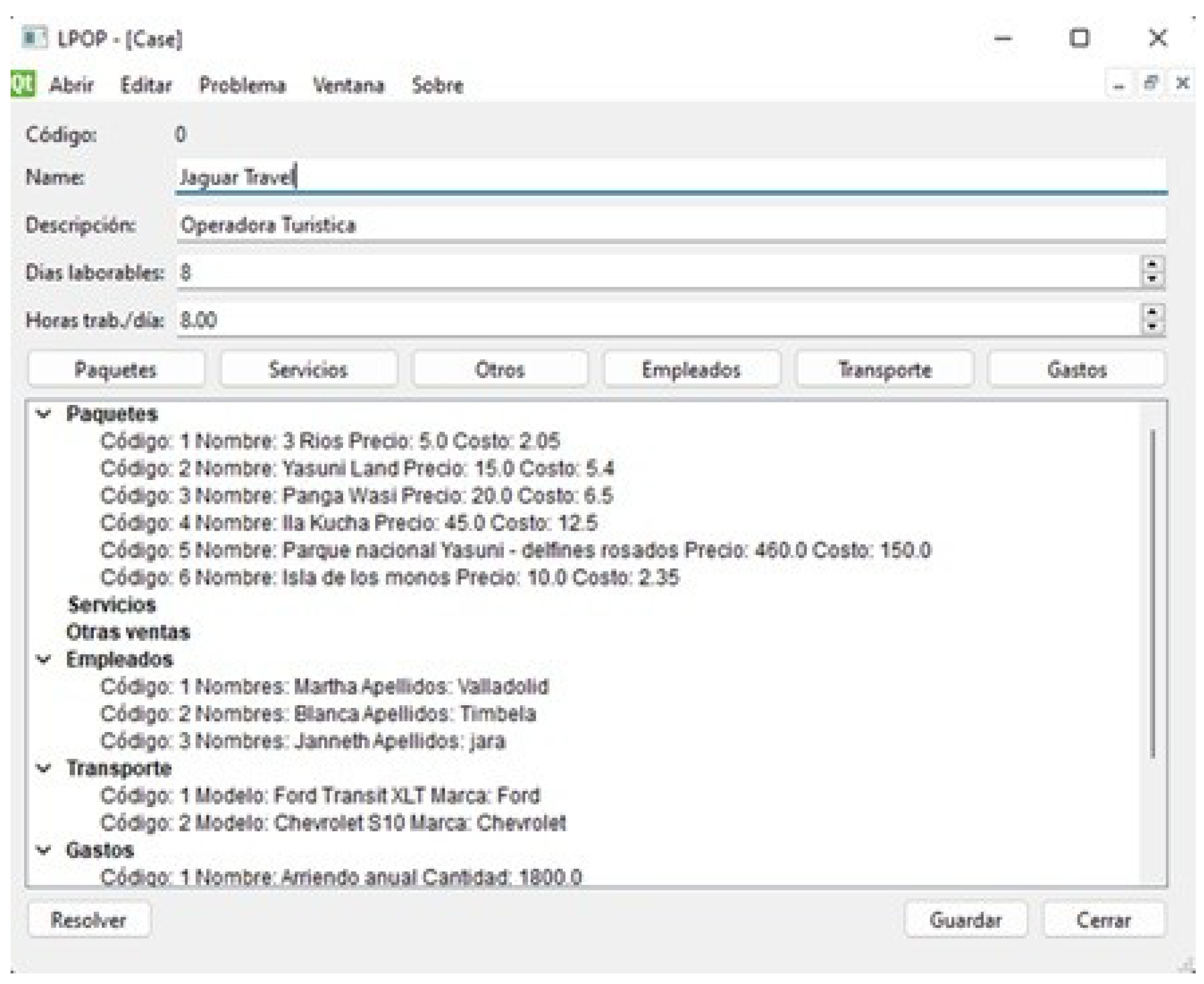
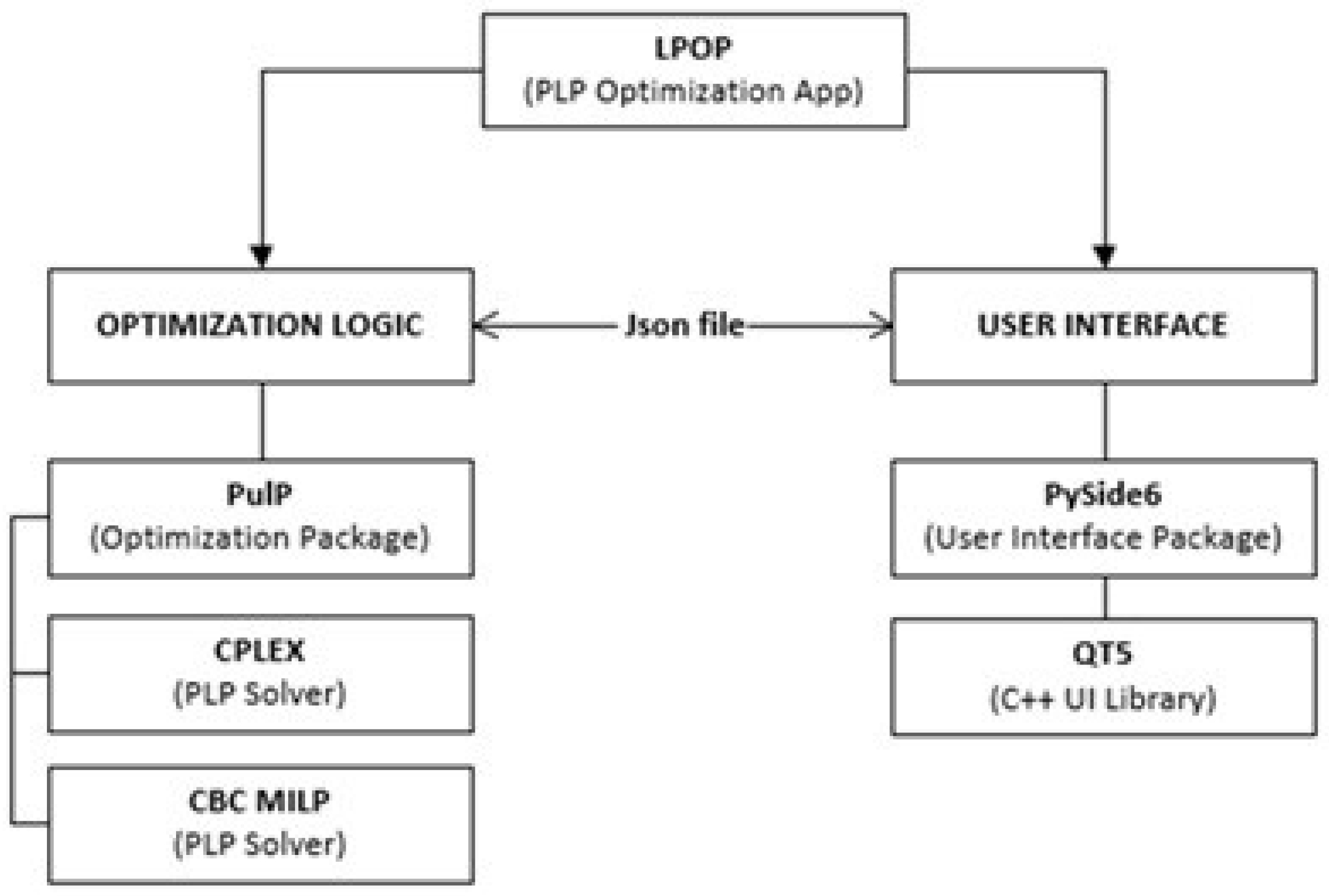
Considering these references, but lacking the convenience of a spreadsheet for data organization, an application called LPOP (Linear Programming and Optimization Program) (see Figure 6) was developed. This tool stores information in files using a specific format, enabling the saving and retrieval of case studies. Its structure (see Figure 7) is divided into two main components: the user interface, built with Python and the PySide6 library (based on QT5/QT6), and the program logic, which uses the PuLP library for optimization. It is worth noting that communication between both modules is done through .json files.

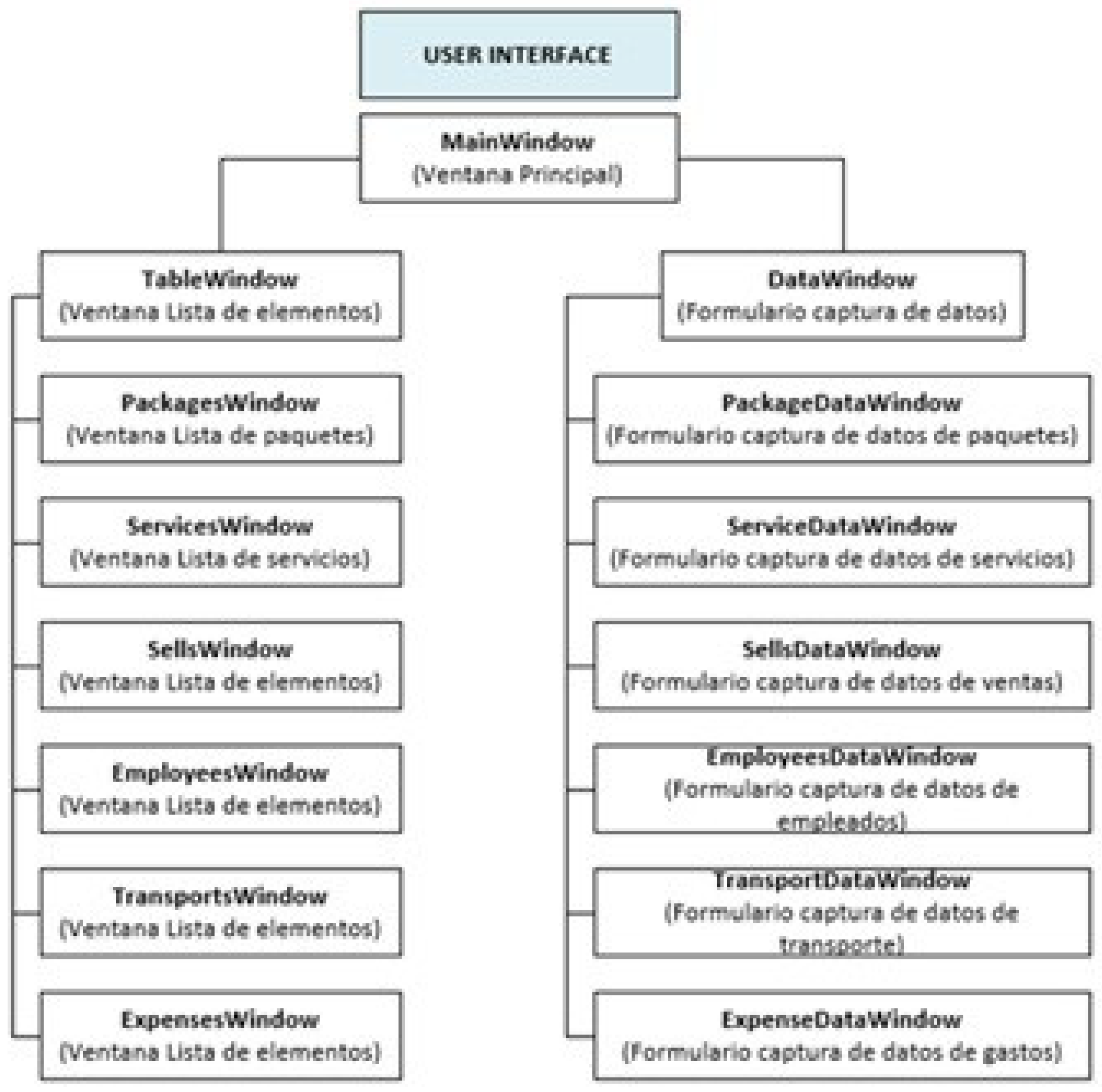
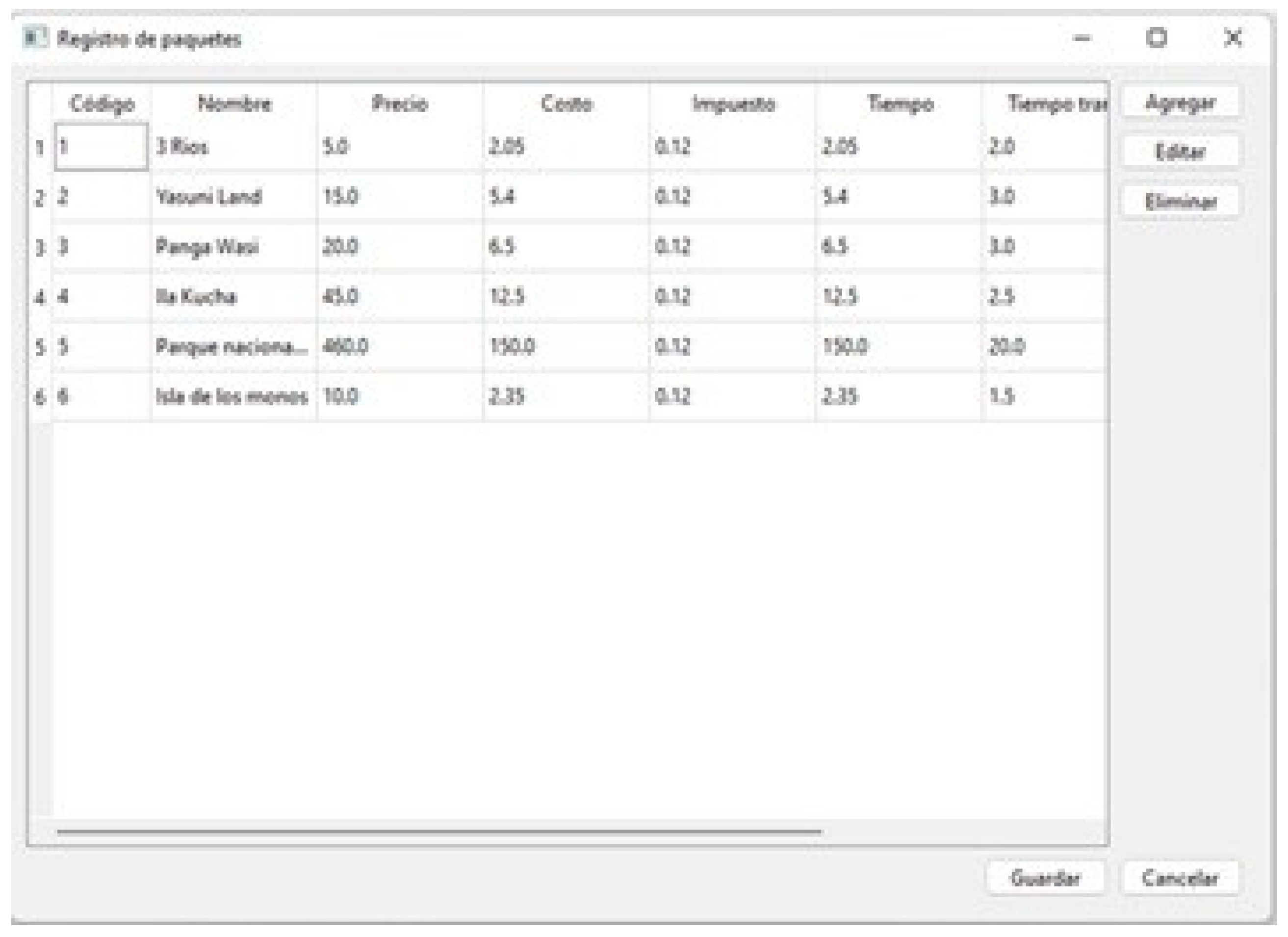
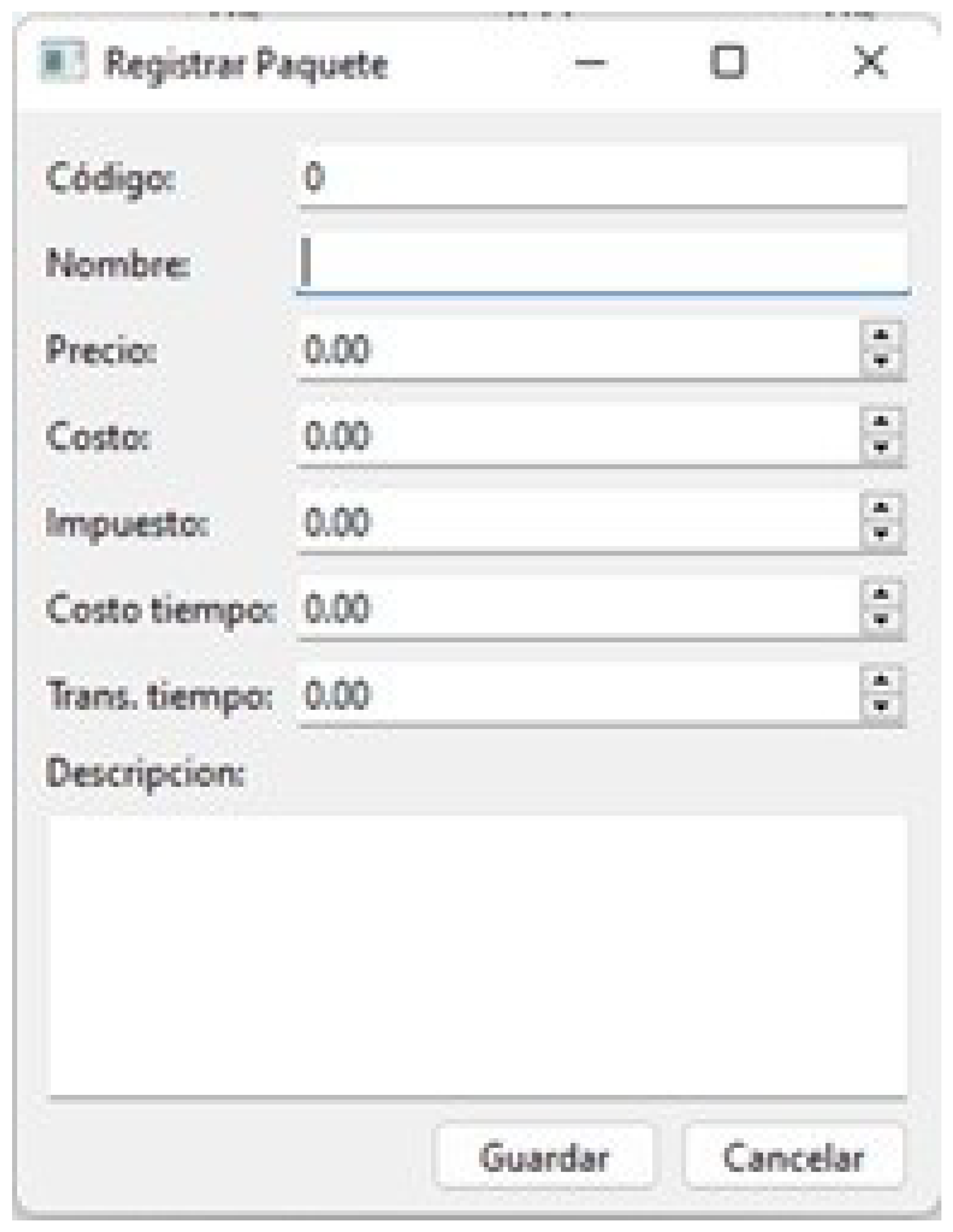
Regarding the graphical interface, it consists of a main window and two types of secondary windows: TableWindow and DataWindow. On one hand, TableWindow (see Figure 8) displays a list of model elements (tour packages, services, employees, etc.). On the other hand, DataWindow (see Figure 9, see Figure 10) is a form that allows data entry, such as codes, prices, costs, and requirements. Each field varies depending on the selected element.

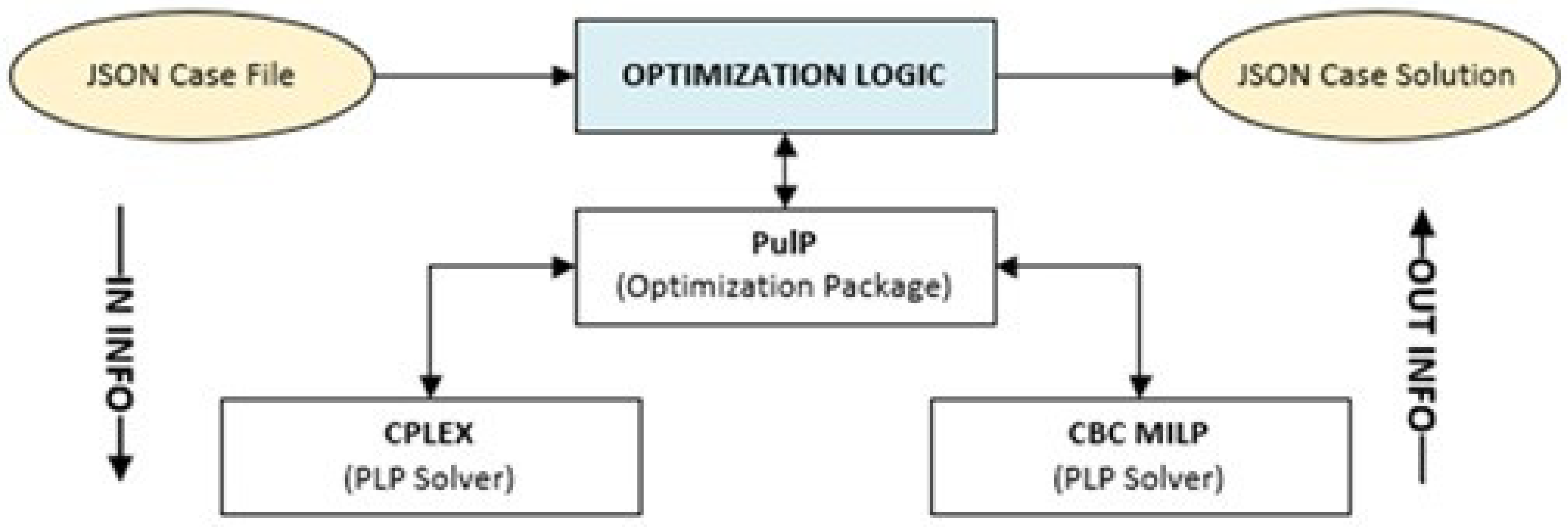
As for the logic component, it processes .json files to convert them into an optimization problem, solving it using PuLP with the configured solvers (CPLEX or CBC MILP). The data flow (see Figure 11) illustrates how information is transferred between the interface and the optimization module, generating results also in .json format. In this way, the application efficiently integrates an intuitive design with robust mathematical processing.

3.3. Rigor Cycle

The methodological rigor cycle in this research aligns with the principles of the DRS (Design Research in Science) method, which integrates an iterative process of design, development, and validation to ensure the scientific robustness and applicability of the results. Firstly, the study begins with a rigorous diagnosis of the problem, supported by statistical data and official sources, such as the Ministry of Tourism of Ecuador and local development plans, which allows for contextualizing the profitability difficulties in tour operators of Puerto Francisco de Orellana. This initial phase not only identifies gaps in the existing literature but also establishes a clear connection between theory and practice, ensuring that the proposed model responds to the real needs of the sector.

Subsequently, the design of the mathematical model is based on consolidated theories of linear programming, supported by authors such as [16,21], who highlight its utility in resource optimization. The selection of decision variables (tourist packages, services, and other sales) and constraints (working hours, vehicle use, and operational capacity) is justified by a comprehensive analysis of the specific characteristics of the tourism sector, which reinforces the internal validity of the study. Furthermore, the use of computational tools such as Python and the PulP library ensures that the model is reproducible and scalable, thus meeting the criteria of methodological reliability.

The development phase included the creation of an interactive application (LPOP) that facilitates data collection and model execution, demonstrating a commitment to the transferability of results. Validation was carried out through real case studies with the operators Jaguar Travels and Amazon Travel, whose data were incorporated into the system to test the effectiveness of the model. This empirical approach not only allowed for adjusting variables and constraints but also highlighted practical limitations, such as the dependence on accurate data from the companies.

Finally, the cycle concludes with a critical analysis of the results, where the projected profits are contrasted with the operational realities of the companies, providing transparency to the process. The suggestions for future research, such as the inclusion of stochastic variables or the use of artificial intelligence, reflect a commitment to the continuous improvement of the model, ensuring that methodological rigor is maintained in future applications. In this way, the study not only meets the standards of the DRS method but also sets a precedent for similar research in emerging tourism contexts.

4. Results

4.1. Optimization Cases

In this section of the research, two practical cases are presented to evaluate the proposed model, using real data from tour operators that include both revenue-generating products and the costs associated with their activity.

In the first case, corresponding to the operator Jaguar Travels, an operational structure that exclusively offers six tourist packages is analyzed, each with its respective taxes and operating costs. The company has four workers whose workday is eight hours daily, as well as three operational vehicles with a working capacity of twelve hours per day. It is worth noting that the operator carries out its activities for 248 days per year, which establishes a clear framework for calculating the availability of human and logistical resources. These elements allow the linear programming model to be applied considering the operator’s actual constraints, which facilitates a precise evaluation of its capacity to maximize profits under specific conditions.

Table 5. Jaguar Travel package tour operator data

n	${\mathit{P}}_{\mathit{i}}$	Nombre	$\mathit{m}{\mathit{p}}_{\mathit{i}}$ (USD)	$\mathit{h}{\mathit{p}}_{\mathit{i}}$ (h)	$\mathit{h}\mathit{v}{\mathit{p}}_{\mathit{i}}$ (h)	$\mathit{c}{\mathit{p}}_{\mathit{i}}$	$\mathit{t}{\mathit{p}}_{\mathit{i}}$
1	P1	3 Ríos	5	0.75	2	2.05	0.12
2	P2	Yasuní land	15	3.5	3	5.4	0.12
3	P3	Panga Wasi	20	4	3	6.5	0.12
4	P4	Ila Kucha	45	5	2.5	12.5	0.12
5	P5	Parque nacional Yasuní	460	80	20	150	0.12
6	P6	Isla de los monos	10	2	1.5	2.35	0.12

Table 5. Jaguar Travel package tour operator data

n	${\mathit{P}}_{\mathit{i}}$	Nombre	$\mathit{m}{\mathit{p}}_{\mathit{i}}$ (USD)	$\mathit{h}{\mathit{p}}_{\mathit{i}}$ (h)	$\mathit{h}\mathit{v}{\mathit{p}}_{\mathit{i}}$ (h)	$\mathit{c}{\mathit{p}}_{\mathit{i}}$	$\mathit{t}{\mathit{p}}_{\mathit{i}}$
1	P1	3 Ríos	5	0.75	2	2.05	0.12
2	P2	Yasuní land	15	3.5	3	5.4	0.12
3	P3	Panga Wasi	20	4	3	6.5	0.12
4	P4	Ila Kucha	45	5	2.5	12.5	0.12
5	P5	Parque nacional Yasuní	460	80	20	150	0.12
6	P6	Isla de los monos	10	2	1.5	2.35	0.12

Table 6. Tour packages sold by Jaguar Travels

${\mathit{P}}_{\mathit{i}}$	Temporada baja					Temporada alta
	Diario	Semanal	Mensual	Anual		Diario	Semanal	Mensual	Anual
P1	2	14	47	564		5	48	78	936
P2	1	5	20	240		6	20	80	960
P3	1	4	17	204		5	20	80	960
P4	0	0	2	24		3	3	3	36
P5	0	0	0	0		1	2	3	36
P6	2	6	12	144		4	10	50	600
Total				1176					3528

Table 6. Tour packages sold by Jaguar Travels

${\mathit{P}}_{\mathit{i}}$	Temporada baja					Temporada alta
	Diario	Semanal	Mensual	Anual		Diario	Semanal	Mensual	Anual
P1	2	14	47	564		5	48	78	936
P2	1	5	20	240		6	20	80	960
P3	1	4	17	204		5	20	80	960
P4	0	0	2	24		3	3	3	36
P5	0	0	0	0		1	2	3	36
P6	2	6	12	144		4	10	50	600
Total				1176					3528

Table 7. Permanent expenses of the operator Jaguar Travels

n	Nombres	${\mathit{g}}_{\mathit{i}}$	${\mathit{g}}_{\mathit{i}}$ (USD)
1	Arriendo local	$g^1$	1800
2	Facturas de Luz eléctrica	$g^2$	300
3	Sueldos	$g^3$	28800
4	Factura internet	$g^4$	360
5	Impuesto municipal	$g^5$	180
6	Viajes canoeros	$g^6$	120
Total			31560

Table 7. Permanent expenses of the operator Jaguar Travels

n	Nombres	${\mathit{g}}_{\mathit{i}}$	${\mathit{g}}_{\mathit{i}}$ (USD)
1	Arriendo local	$g^1$	1800
2	Facturas de Luz eléctrica	$g^2$	300
3	Sueldos	$g^3$	28800
4	Factura internet	$g^4$	360
5	Impuesto municipal	$g^5$	180
6	Viajes canoeros	$g^6$	120
Total			31560

Upon applying the optimization model using the methods available in the PulP library, the results presented in Table 8 are obtained, which show a remarkable consistency between both solution approaches. Subsequently, upon verifying the fulfillment of the established constraints, the results reflected in Table 9 demonstrate that all imposed conditions – relating to quantity limits, available working hours, and vehicle usage capacity – were adequately satisfied. This analysis confirms the validity of the proposed model, as the solutions obtained scrupulously respect the operational parameters defined for each case, which reinforces the reliability of the recommendations generated for strategic decision-making in the analyzed tour operators.

Table 8. Comparison of results between CPLEX and CBC MILP

P	CPLX	CBC MILP
$P_1$	1000	984
$P_2$	1000	1000
$P_3$	0	0
$P_4$	1000	1000
$P_5$	5	6
$P_6$	34	0

Table 8. Comparison of results between CPLEX and CBC MILP

P	CPLX	CBC MILP
$P_1$	1000	984
$P_2$	1000	1000
$P_3$	0	0
$P_4$	1000	1000
$P_5$	5	6
$P_6$	34	0

Table 9. Comparison of results under different constraints

$\mathit{P},\mathit{S}$ y O	$\mathit{P},\mathit{S},\mathit{O}\le 3552$			${\mathit{h}}_{\mathit{t}}\le 7968$			${\mathit{h}}_{\mathit{v}}<7151.5$
	CPLX	CBC MILP		CPLX	CBC MILP		CPLX	CBC MILP
$P_1$	1000	984		750	738		1000	984
$P_2$	1000	1000		1750	1750		2000	2000
$P_3$	0	0		0	0		0	0
$P_4$	1000	1000		5000	5000		4000	4000
$P_5$	5	6		400	480		100	120
$P_6$	34	0		68	0		51	0
Total	3039	2990		7968	7968		7151	7104

Table 9. Comparison of results under different constraints

$\mathit{P},\mathit{S}$ y O	$\mathit{P},\mathit{S},\mathit{O}\le 3552$			${\mathit{h}}_{\mathit{t}}\le 7968$			${\mathit{h}}_{\mathit{v}}<7151.5$
	CPLX	CBC MILP		CPLX	CBC MILP		CPLX	CBC MILP
$P_1$	1000	984		750	738		1000	984
$P_2$	1000	1000		1750	1750		2000	2000
$P_3$	0	0		0	0		0	0
$P_4$	1000	1000		5000	5000		4000	4000
$P_5$	5	6		400	480		100	120
$P_6$	34	0		68	0		51	0
Total	3039	2990		7968	7968		7151	7104

In the second case study, corresponding to the operator Amazon Travel, a more diversified operational structure is analyzed, which includes six tourist packages complemented by two additional services, each with its respective associated costs and taxes. The company has five tour guides who work eight-hour days, as well as four operational vehicles with a capacity of twelve hours of continuous use, maintaining an annual schedule of 248 working days that establishes the baseline parameters for resource optimization.

Table 10. Amazon Travel package tour operator data

n	${\mathit{P}}_{\mathit{i}}$	$\mathit{m}{\mathit{p}}_{\mathit{i}}$ (USD)	$\mathit{h}{\mathit{p}}_{\mathit{i}}$ (h)	$\mathit{h}\mathit{v}{\mathit{p}}_{\mathit{i}}$ (h)	$\mathit{c}{\mathit{p}}_{\mathit{i}}$	$\mathit{t}{\mathit{p}}_{\mathit{i}}$
1	River tour	6.25	1	1.25	1.25	0.12
2	Yasuní Rainforest	18.5	2	2.5	5.5	0.12
3	Panga Wasi Tour	22.5	3	3	7.2	0.12
4	Ila Kucha Visit	50	6	4	16.5	0.12
5	Yasuní National Park Trip	450	72	25	165	0.12
6	Monkey Island Walk	12.5	2	3	3	0.12

Table 10. Amazon Travel package tour operator data

n	${\mathit{P}}_{\mathit{i}}$	$\mathit{m}{\mathit{p}}_{\mathit{i}}$ (USD)	$\mathit{h}{\mathit{p}}_{\mathit{i}}$ (h)	$\mathit{h}\mathit{v}{\mathit{p}}_{\mathit{i}}$ (h)	$\mathit{c}{\mathit{p}}_{\mathit{i}}$	$\mathit{t}{\mathit{p}}_{\mathit{i}}$
1	River tour	6.25	1	1.25	1.25	0.12
2	Yasuní Rainforest	18.5	2	2.5	5.5	0.12
3	Panga Wasi Tour	22.5	3	3	7.2	0.12
4	Ila Kucha Visit	50	6	4	16.5	0.12
5	Yasuní National Park Trip	450	72	25	165	0.12
6	Monkey Island Walk	12.5	2	3	3	0.12

Table 11. Tour packages sold by Amazon Travel

${\mathit{P}}_{\mathit{i}}$	Temporada baja					Temporada alta
	Diario	Semanal	Mensual	Anual		Diario	Semanal	Mensual	Anual
P1	2	12	42	504		6	48	67	804
P2	2	6	16	192		4	20	74	888
P3	1	5	12	144		6	20	76	912
P4	0	0	2	24		2	1	1	12
P5	0	0	0	0		1	2	2	24
P6	1	5	8	96		3	10	43	516
S1	1	2	2	24		1	2	1	24
S2	0	1	1	12		0	2	3	36
Total				996					3216

Table 11. Tour packages sold by Amazon Travel

${\mathit{P}}_{\mathit{i}}$	Temporada baja					Temporada alta
	Diario	Semanal	Mensual	Anual		Diario	Semanal	Mensual	Anual
P1	2	12	42	504		6	48	67	804
P2	2	6	16	192		4	20	74	888
P3	1	5	12	144		6	20	76	912
P4	0	0	2	24		2	1	1	12
P5	0	0	0	0		1	2	2	24
P6	1	5	8	96		3	10	43	516
S1	1	2	2	24		1	2	1	24
S2	0	1	1	12		0	2	3	36
Total				996					3216

Table 12. Permanent expenses of the Amazon Travel operator

n	Nombres	${\mathit{g}}_{\mathit{i}}$	${\mathit{g}}_{\mathit{i}}$ (USD)
1	Arriendo local	$g^1$	3600
2	Facturas de Luz eléctrica	$g^2$	300
3	Sueldos	$g^3$	36000
4	Factura internet	$g^4$	360
5	Impuesto municipal	$g^5$	180
6	Viajes canoeros	$g^6$	120
Total			40560

Table 12. Permanent expenses of the Amazon Travel operator

n	Nombres	${\mathit{g}}_{\mathit{i}}$	${\mathit{g}}_{\mathit{i}}$ (USD)
1	Arriendo local	$g^1$	3600
2	Facturas de Luz eléctrica	$g^2$	300
3	Sueldos	$g^3$	36000
4	Factura internet	$g^4$	360
5	Impuesto municipal	$g^5$	180
6	Viajes canoeros	$g^6$	120
Total			40560

Through the application of the optimization model using the methods available in the PulP library, the results presented in Table 13 were obtained, which show a notable coherence between the different methodological approaches employed. Upon conducting a thorough verification of the fulfillment of the operational constraints, the results recorded in Table 14 demonstrate that all established conditions – relating to production limits, availability of working hours, and vehicle fleet capacity – were fully satisfied. This analysis confirms the robustness of the implemented model, demonstrating its capacity to generate viable solutions that scrupulously respect the defined operational parameters, which validates its applicability in business contexts with more complex service structures.

Table 13. Results obtained for Amazon Travel

P	CPLX	CBC MILP
$P_1$	0	0
$P_2$	197	194
$P_3$	0	0
$P_4$	997	998
$P_5$	22	22
$P_6$	0	0
$S_1$	1000	1000
$S_2$	1000	1000

Table 13. Results obtained for Amazon Travel

P	CPLX	CBC MILP
$P_1$	0	0
$P_2$	197	194
$P_3$	0	0
$P_4$	997	998
$P_5$	22	22
$P_6$	0	0
$S_1$	1000	1000
$S_2$	1000	1000

Table 14. Results restrictions for Amazon Travel

$\mathit{P},\mathit{S}$ y O	$\mathit{P},\mathit{S},\mathit{O}\le 3216$			${\mathit{h}}_{\mathit{t}}\le 9960$			${\mathit{h}}_{\mathit{v}}<5027$
	CPLX	CBC MILP		CPLX	CBC MILP		CPLX	CBC MILP
$P_1$	6.25	1		1.25	0		0	0
$P_2$	18.5	2		2.5	197		194	394
$P_3$	22.5	3		3	0		0	0
$P_4$	50	6		4	997		998	5982
$P_5$	450	72		25	22		22	1584
$P_6$	12.5	3		2	0		0	0
$S_1$	15	1		0	1000		1000	1000
$S_2$	20	1		0	1000		1000	1000
Total	3216	3214		9960	9960		5031	5027

Table 14. Results restrictions for Amazon Travel

$\mathit{P},\mathit{S}$ y O	$\mathit{P},\mathit{S},\mathit{O}\le 3216$			${\mathit{h}}_{\mathit{t}}\le 9960$			${\mathit{h}}_{\mathit{v}}<5027$
	CPLX	CBC MILP		CPLX	CBC MILP		CPLX	CBC MILP
$P_1$	6.25	1		1.25	0		0	0
$P_2$	18.5	2		2.5	197		194	394
$P_3$	22.5	3		3	0		0	0
$P_4$	50	6		4	997		998	5982
$P_5$	450	72		25	22		22	1584
$P_6$	12.5	3		2	0		0	0
$S_1$	15	1		0	1000		1000	1000
$S_2$	20	1		0	1000		1000	1000
Total	3216	3214		9960	9960		5031	5027

4.2. Analysis of Results

In the case of the operator Jaguar Travel, the results show that the tourist packages that meet all the restrictions are P1 (3 Ríos) with 1000 units, P2 (Yasuní Land) with 1000 units, P4 (Ila Kucha) with 1000 units and, to a lesser extent, P5 (Yasuní National Park) and P6 (Monkey Island), all corresponding to an annual quantity. Furthermore, the model indicates that the greatest focus should be directed towards the promotion and sale of packages P1, P2, and P4, as they guarantee compliance with the conditions related to working hours, vehicle use, and the operator’s execution capacity for the packages. On the other hand, the objective function yields an annual profit of 4880.40 USD, which represents a minimum profit margin. It should be noted that this result could be due to the inaccurate information provided by the agency regarding the costs of each package and the annual sales projections.

In contrast, when analyzing the results of the Amazon Travel agency, it is observed that, due to the profit margin obtained, it is advisable to focus on services S1 (translation) and S2 (transportation). Additionally, the model reveals that, due to its profitability and low consumption of human and transportation resources, package P4 (Ila Kucha Visit), with 998 units, should be promoted more intensely. Similarly, package P2 (Yasuní Rainforest), with 194 units, should also be promoted, although to a lesser extent, while package P5 (Yasuní National Park Trip), with only 22 units, should be promoted in a limited way due to its high demand for resources. In this case, the profit obtained amounts to USD 13,358.32 annually, which represents a significantly better performance compared to the previous one.

Finally, it is important to highlight that these results are based on a simplified model. Therefore, to achieve a more precise approximation, it would be necessary to incorporate more decision variables, as well as additional restrictions linked to the resources required for the development of the tourism operations of both agencies.

5. Discussion

The research presents significant theoretical implications by demonstrating the applicability of linear programming in a little-explored context: the tourism sector of Puerto Francisco de Orellana. This theoretical contribution enriches the existing literature, which has traditionally focused on industrial or mass service sectors, by adapting mathematical models to the specific characteristics of tour operators, such as seasonality and variability in demand. Furthermore, the study reinforces the idea that resource optimization through mathematical techniques can be a valuable tool for improving profitability in complex and dynamic economic environments, which opens new lines of research in the field of sustainable tourism management.

Regarding practical implications, the study offers an accessible and replicable model for tour operators, allowing them to maximize their profits through the efficient allocation of resources. The implementation of a graphical interface developed in Python and PySide6 facilitates the adoption of this tool by operators, even those with technical limitations. The results obtained in the cases of Jaguar Travels and Amazon Travel show that, despite the differences in their cost structures and resources, the proposed model can generate viable recommendations to improve their profitability. This not only benefits individual companies but can also contribute to local economic development by fostering more efficient and sustainable tourism.

However, the study is not without limitations. Firstly, the simplified model only considers three decision variables (tourist packages, services, and other sales), which could omit critical factors such as the quality perceived by tourists or market fluctuations. Furthermore, the results depend heavily on the accuracy of the data provided by the operators, as observed in the case of Jaguar Travels, where potential errors in reported costs affected the calculated profit margin. Another limitation is the lack of integration of external variables, such as changes in public policies or environmental impacts, which could influence the model’s operability in the long term.

For future research, it is suggested to expand the model by incorporating additional variables that reflect the dynamics of the tourism sector more accurately. For example, seasonal factors, customer satisfaction indicators, or restrictions related to the tourist carrying capacity of destinations could be included. Likewise, it would be valuable to explore the use of stochastic programming techniques to handle uncertainty in demand and costs. Another promising line of research would be the integration of artificial intelligence tools to analyze tourist behavior patterns and adjust optimization strategies in real time. Finally, it is recommended to validate the model in diverse geographical and cultural contexts, which would allow for the evaluation of its scalability and adaptability to different tourism realities.

6. Conclusions

This research evaluated the potential of linear programming to optimize the profitability of tour operators in Puerto Francisco de Orellana. To this end, a simplified model was developed that considered income and expenses, establishing restrictions related to human resources, transportation, and the execution capacity of tourist packages, services, and other sales. As a result, the key decision variables were identified—number of tourist packages (P), services (S), and other sales (O)—which directly impact the economic profitability of these companies.

The proposed model was based on maximizing profit through the difference between income and expenses, breaking down each component according to its category. The restrictions incorporated limitations on working hours, vehicle use, and operational capacity, while the data was stored in JSON files to adapt to the specific characteristics of each operator. By applying the model to two specific cases—Jaguar Travels and Amazon Travel—positive profit margins were obtained, although in the first case these were reduced, possibly due to inconsistencies in the cost data provided.

The relevance of this study lies in its practical approach, demonstrating how linear programming can be an effective tool for decision-making in the tourism sector, especially in contexts with limited resources. Furthermore, the use of JSON files facilitates the customization of the model, which expands its applicability to different operators with diverse structures and needs.

Regarding future perspectives, it is suggested to delve deeper into the incorporation of dynamic variables, such as demand seasonality or special events, to improve the accuracy of the model. Likewise, it would be valuable to explore the integration of additional restrictions, such as inventory management or route optimization, in order to increase its robustness and adaptability. These improvements would allow for a more realistic approach to the operational challenges of the sector, offering even more efficient solutions for profit maximization.