Submitted:
12 April 2025
Posted:
15 April 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Literature Review
1.2. Scope and Objectives
2. Mathematical Modeling
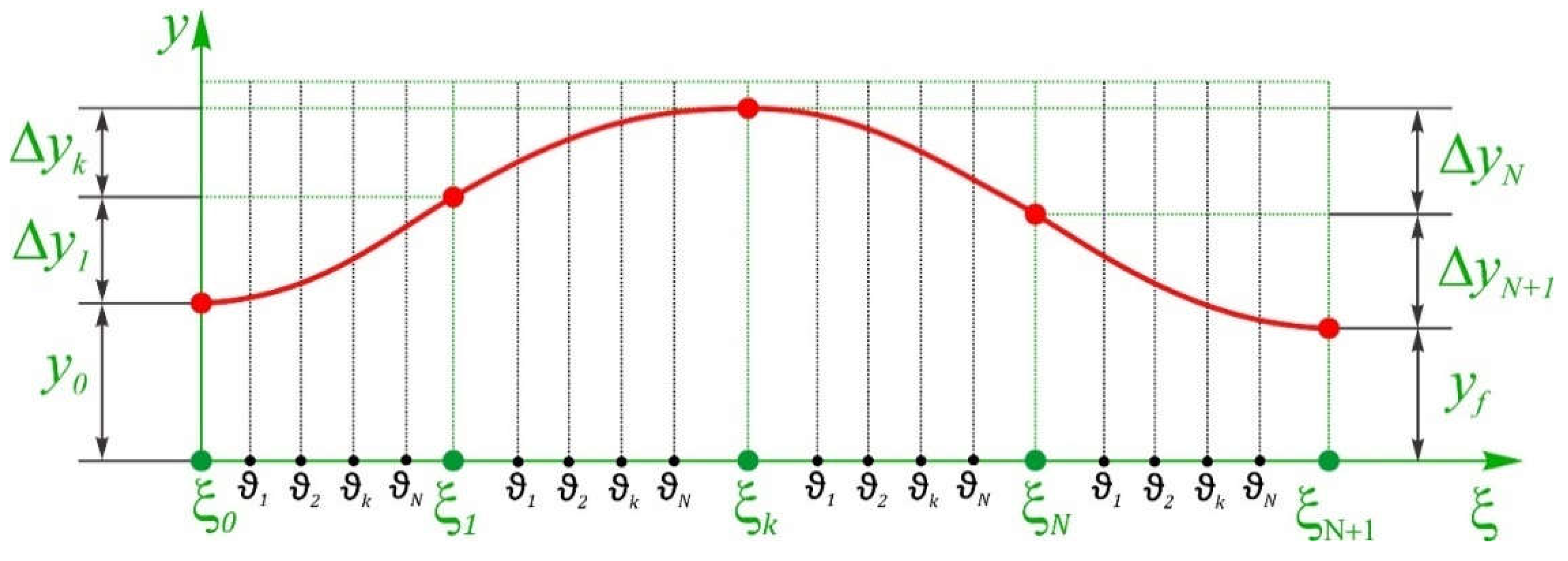
2.1. Representing Sought-for Functions with Piecewise Polynomials
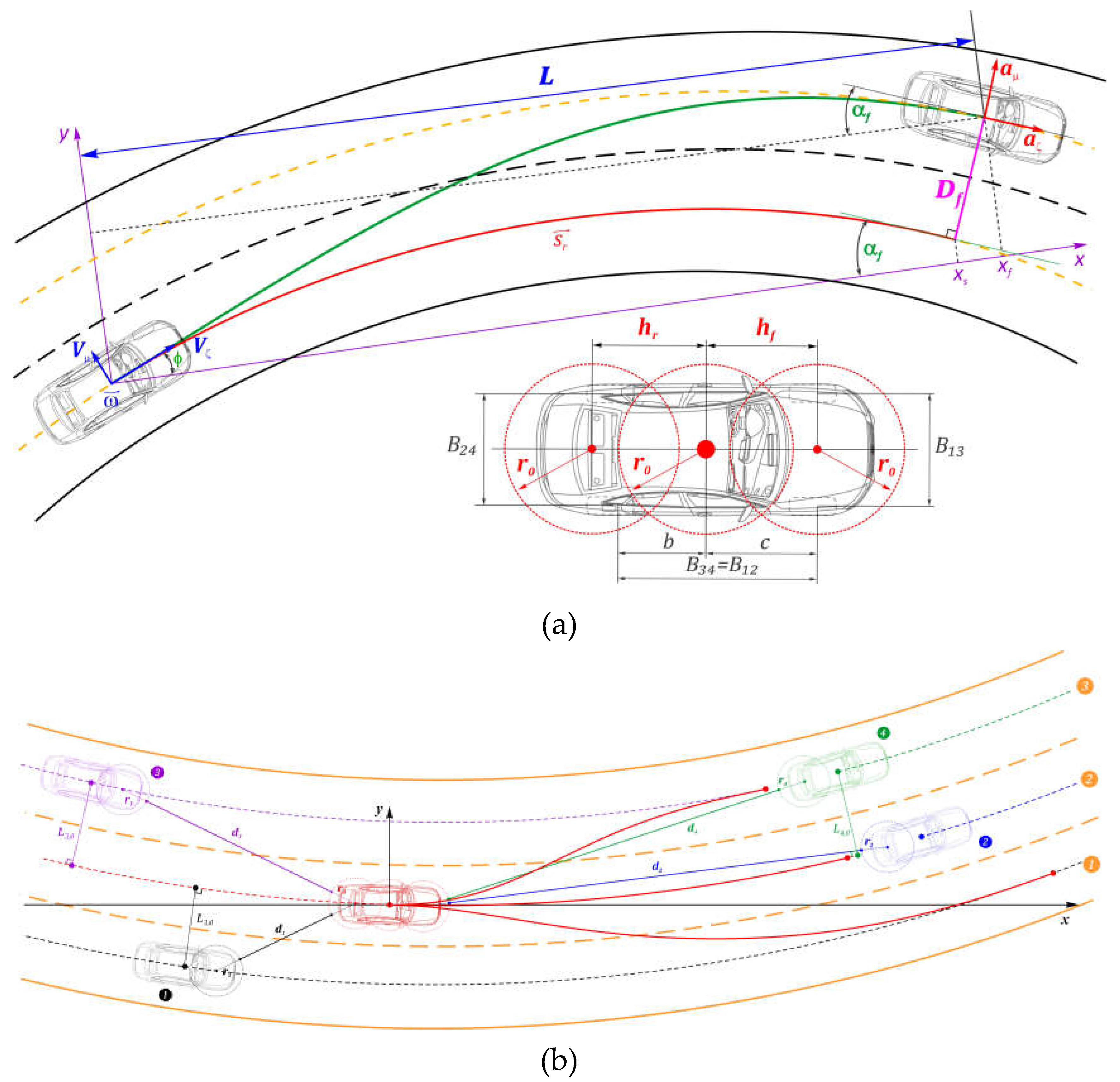
2.2. Vehicle Kinematics
3. Motion Planning Models
3.1. Planning Concept
3.1. Trajectory Numerical Modeling
3.2. Speed Distribution Modeling
3.3. Full set of parameters
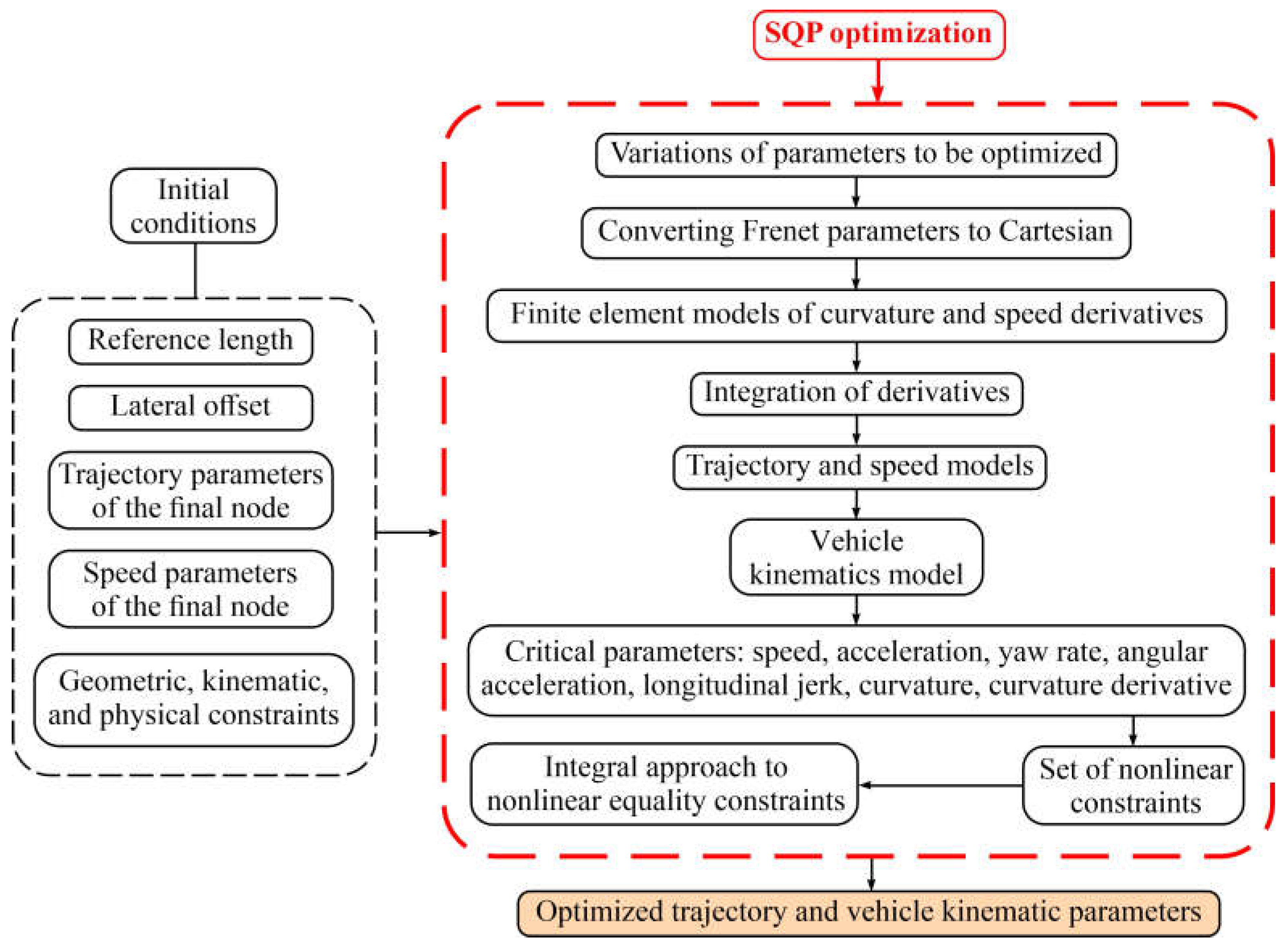
4. Optimization Model
4.1. Nonlinear Optimization and Numerical Integration
4.2. Optimization Criteria
4.3. Constraints
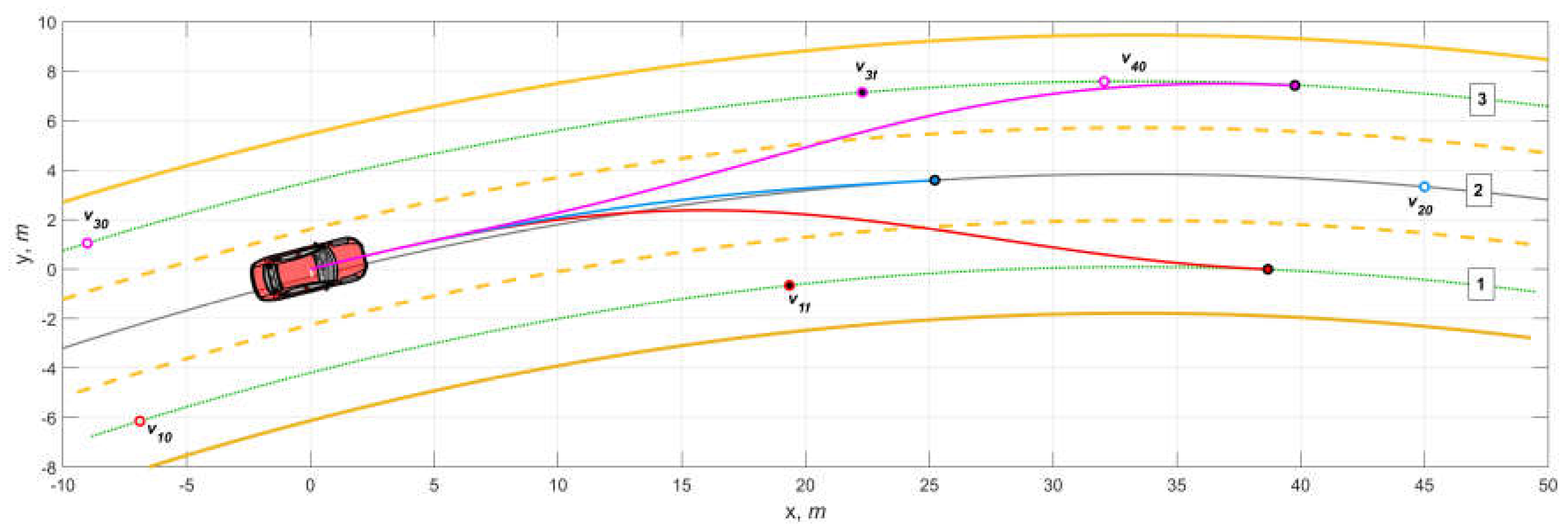
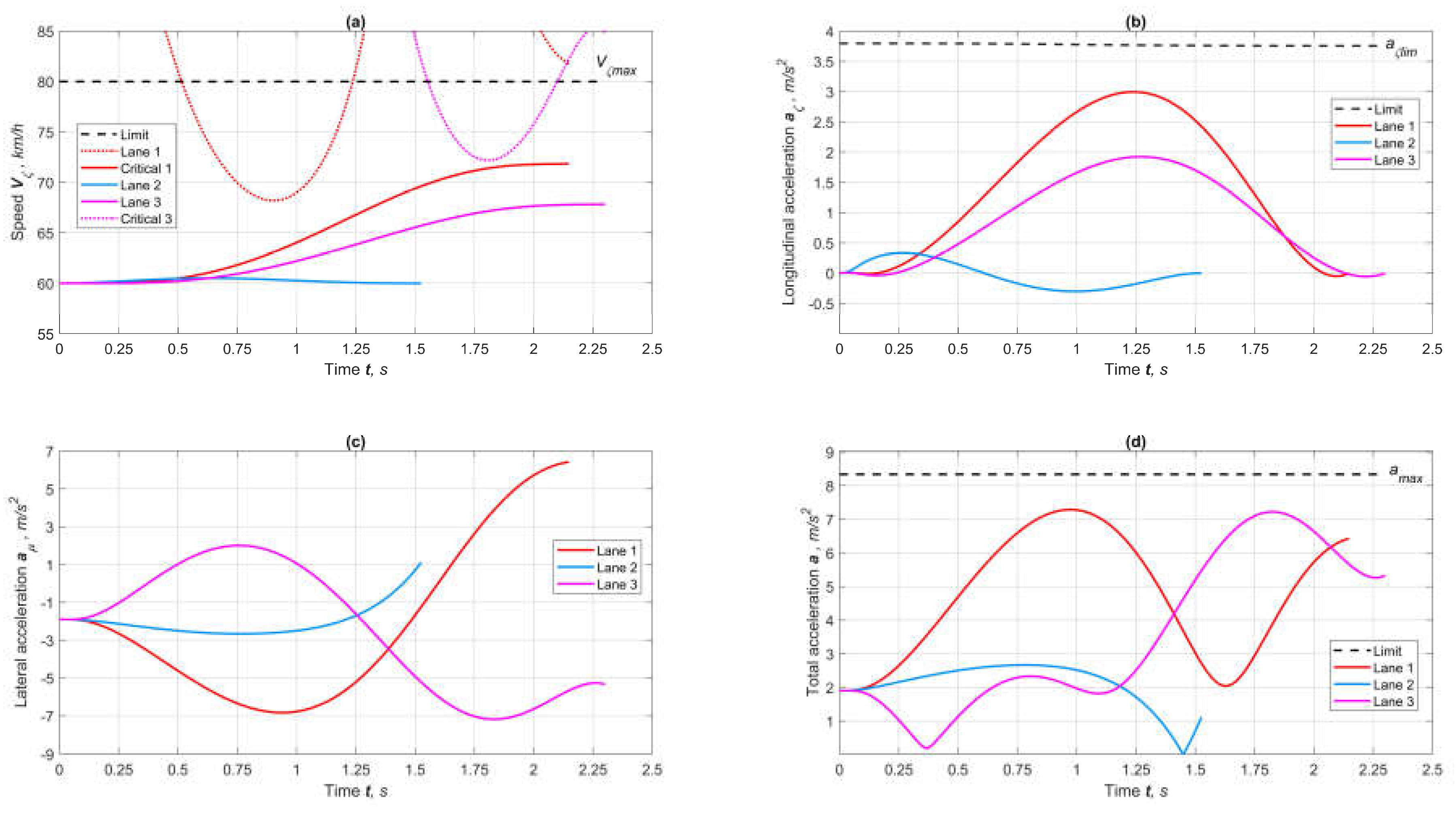
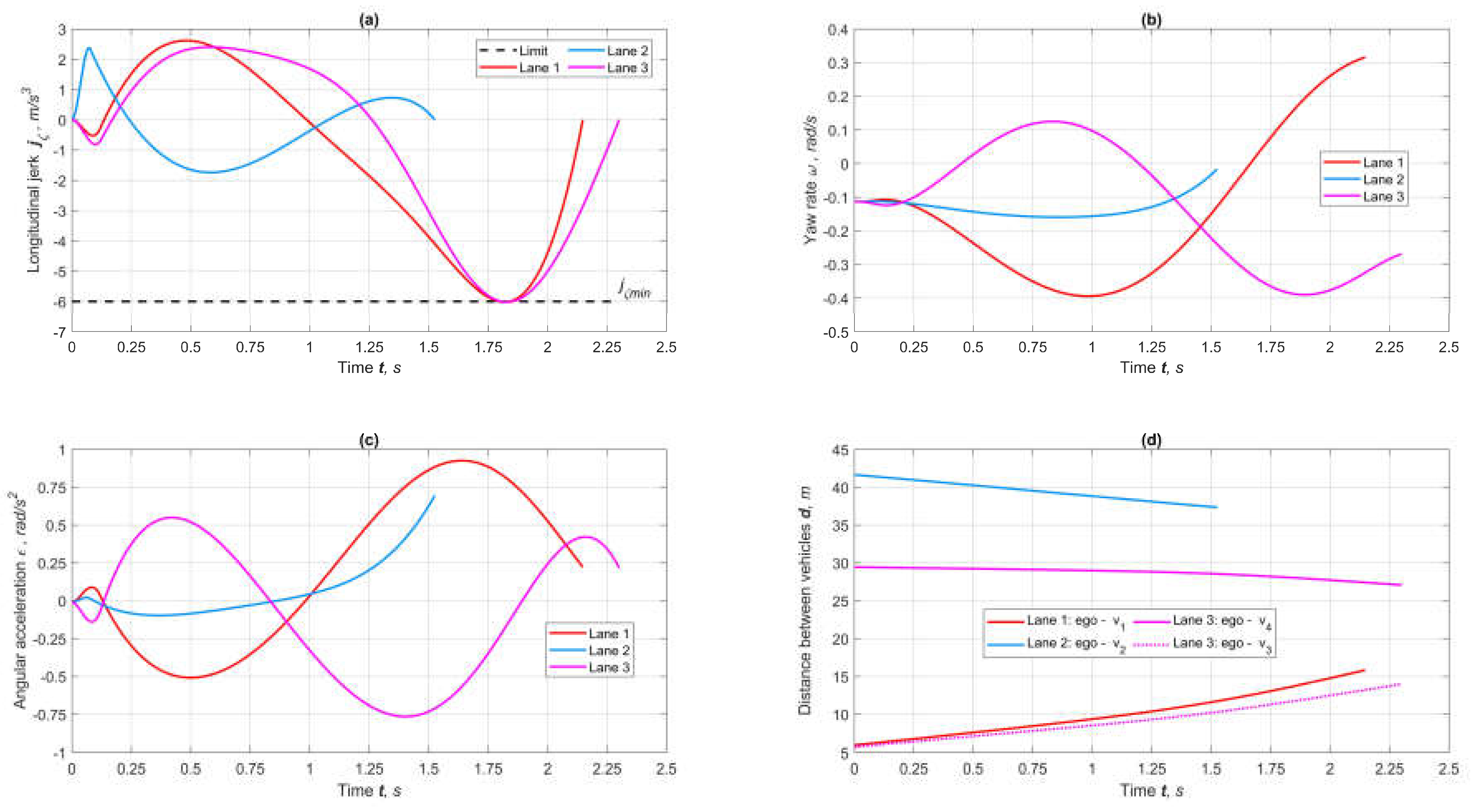
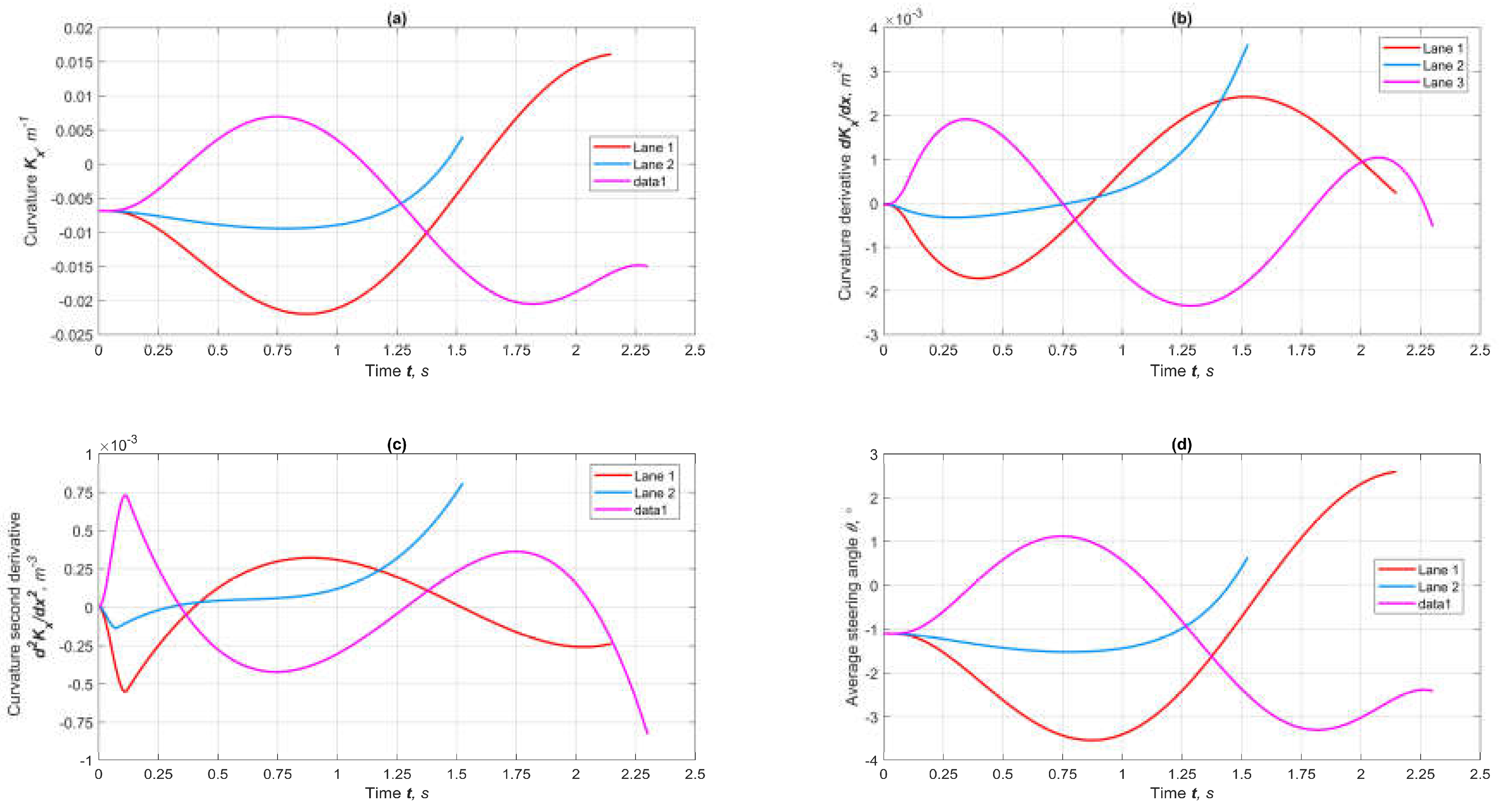
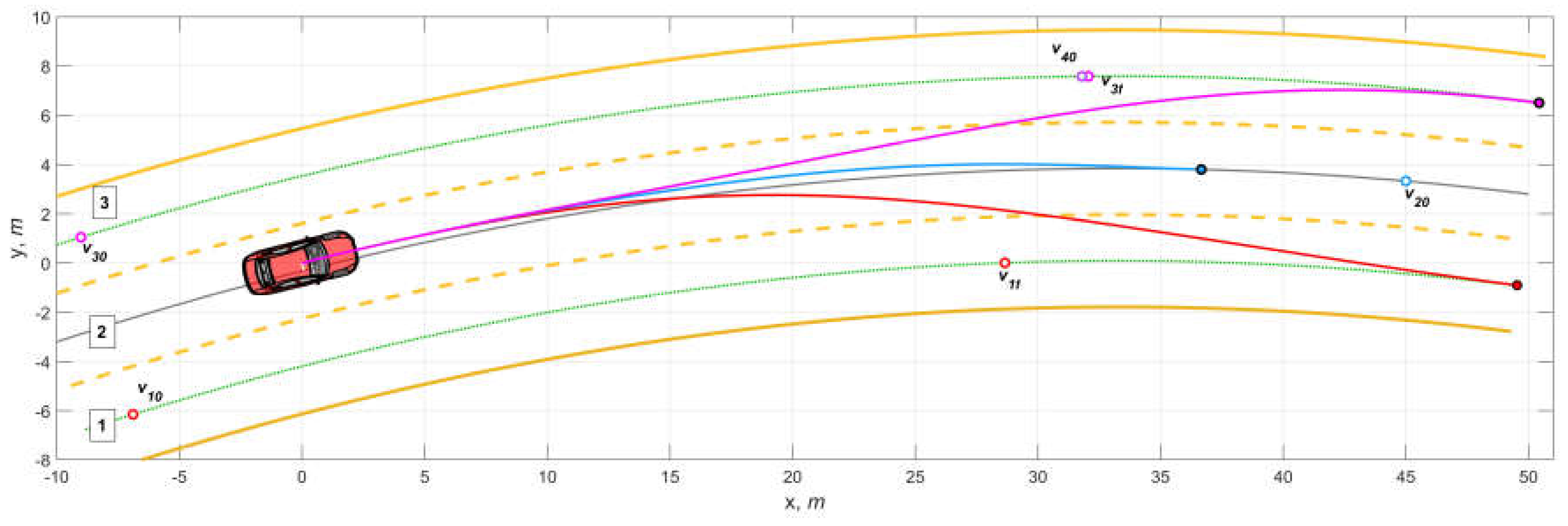
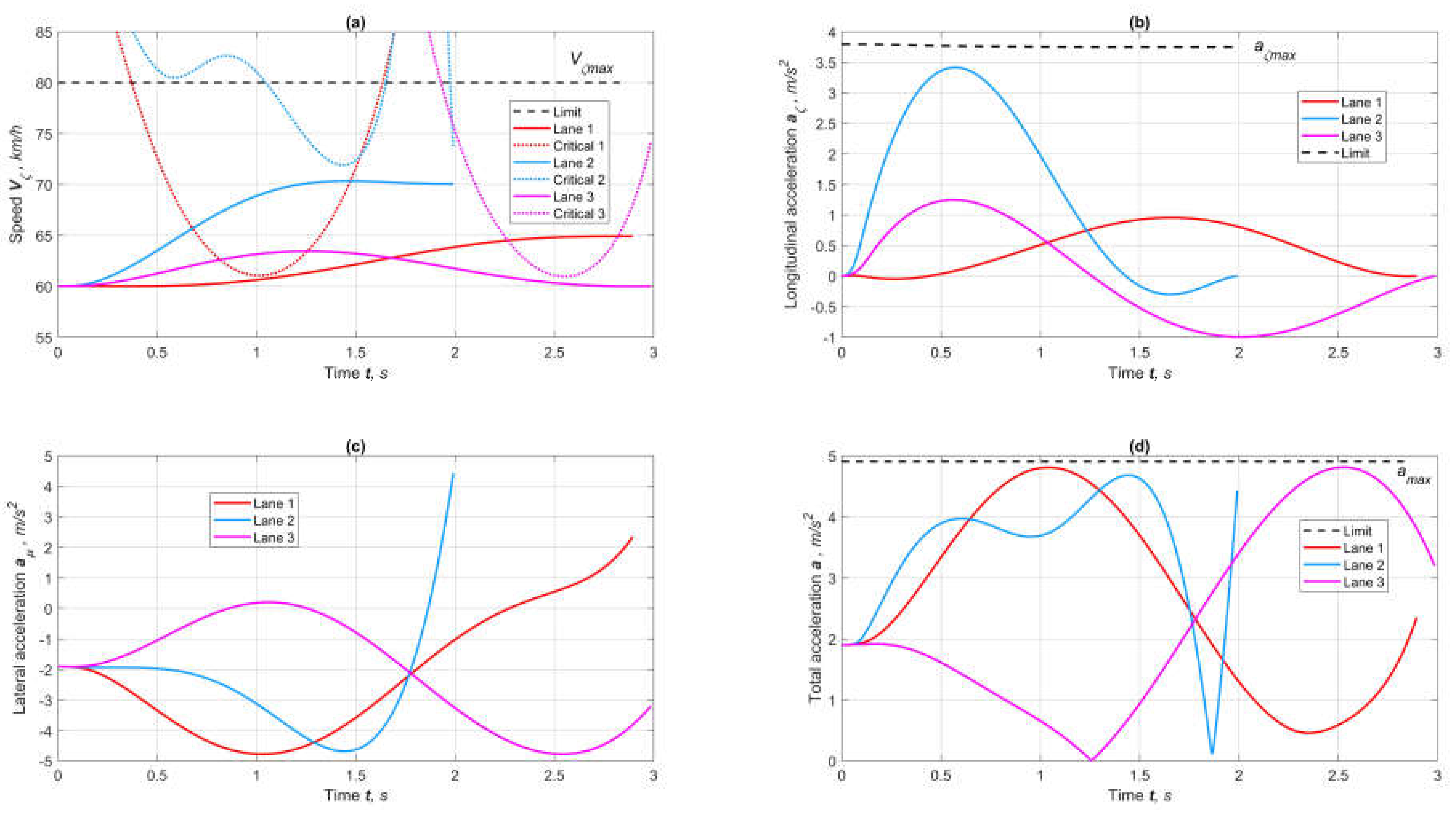
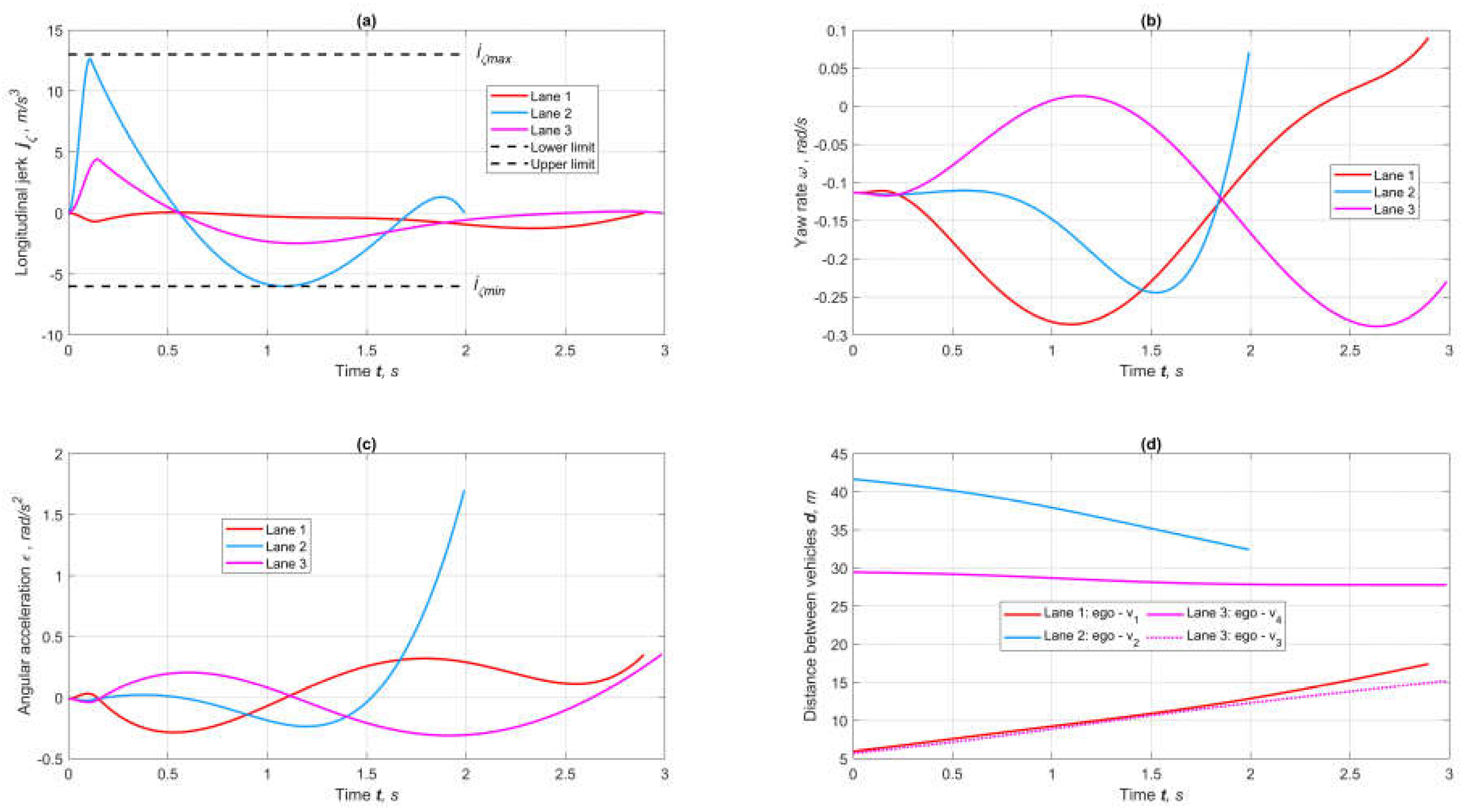
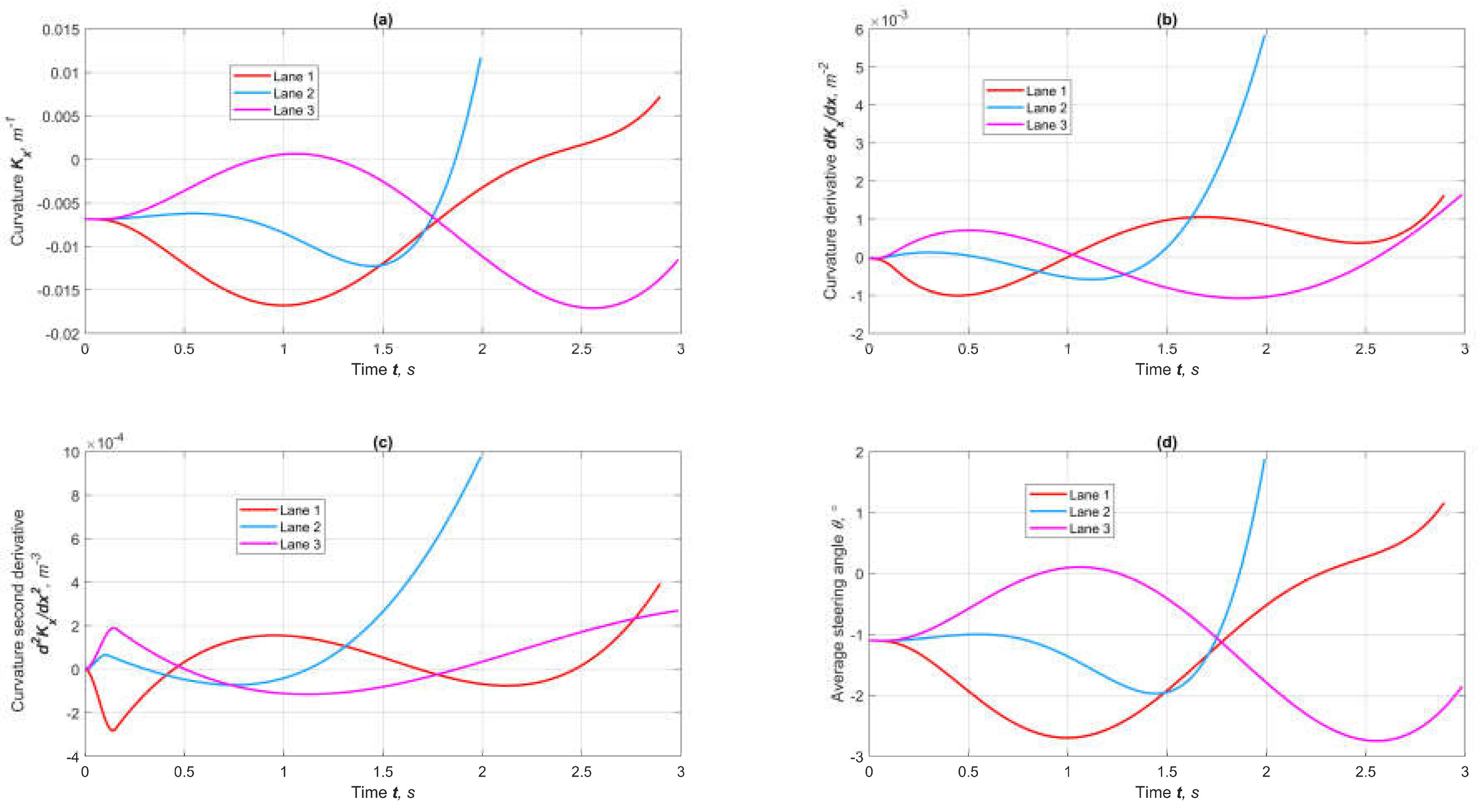
5. Simulation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xia, T.; Chen, H. A Survey of Autonomous Vehicle Behaviors: Trajectory Planning Algorithms, Sensed Collision Risks, and User Expectations. Sensors 2024, 24, 4808. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, H.; Waslander, S.L.; Gong, J.; Xiong, G.; Yang, T.; Liu, K. Hybrid Trajectory Planning for Autonomous Driving in Highly Constrained Environments. IEEE Access 2018, 6, 32800–32819. [Google Scholar] [CrossRef]
- Jiang, Y.; Jin, X.; Xiong, Y.; Liu, Z. A Dynamic Motion Planning Framework for Autonomous Driving in Urban Environments. 5429-5435. 10.23919/CCC50068.2020.9188504.
- Dang, D.; Gao, F.; Hu, Q. Motion Planning for Autonomous Vehicles Considering Longitudinal and Lateral Dynamics Coupling. Appl. Sci. 2020, 10, 3180. [Google Scholar] [CrossRef]
- Li, G.; Zhang, X.; Guo, H.; Lenzo, B.; Guo, N. Real-Time Optimal Trajectory Planning for Autonomous Driving with Collision Avoidance Using Convex Optimization. Automot. Innov. 2023, 6, 481–491. [Google Scholar] [CrossRef]
- Tang, X.; Li, B.; Du, H. A Study on Dynamic Motion Planning for Autonomous Vehicles Based on Nonlinear Vehicle Model. Sensors 2023, 23, 443. [Google Scholar] [CrossRef]
- Liniger, A.; Van Gool, L. Safe Motion Planning for Autonomous Driving using an Adversarial Road Model. Robotics: Science and Systems 2020.
- Yang, W.; Li, C.; Zhou, Y. A Path Planning Method for Autonomous Vehicles Based on Risk Assessment. World Electr. Veh. J. 2022, 13, 234. [Google Scholar] [CrossRef]
- Hu, Z.; Yang, Z.; Liu, X.; Zhang, W. Radar-based path planning of autonomous surface vehicle with static and dynamic obstacles in a Frenet Frame. J. Navig. 2023, 76, 487–505. [Google Scholar] [CrossRef]
- Jin, X.; Li, Z.; Ikiela, N.V.O.; He, X.; Wang, Z.; Tao, Y.; Lv, H. An Efficient Trajectory Planning Approach for Autonomous Ground Vehicles Using Improved Artificial Potential Field. Symmetry 2024, 16, 106. [Google Scholar] [CrossRef]
- Dong, D.; Ye, H.; Luo, W.; Wen, J.; Huang, D. Collision Avoidance Path Planning and Tracking Control for Autonomous Vehicles Based on Model Predictive Control. Sensors 2024, 24, 5211. [Google Scholar] [CrossRef]
- Jeng, S-L. & Chieng, W-H. & Wang, Y-Ch. (2021). Real-Time Heuristic Motion Planning for Autonomous Vehicle Driving. Journal of the Society of Mechanical Engineers. 42. 187-196. 10.29979/JCSME.200908.0002.
- Lu, Y.; He, S.; Li, Y.; Wu, Y.; Zhong, W. A real-time decoupling trajectory planning method for on-road autonomous driving. IET Control. Theory Appl. 2022, 17, 1800–1812. [Google Scholar] [CrossRef]
- Cheng, J.; Chen, Y.; Zhang, Q.; Gan, L.; Liu, C.; Liu, M. Real-Time Trajectory Planning for Autonomous Driving with Gaussian Process and Incremental Refinement. 2022 IEEE International Conference on Robotics and Automation (ICRA); pp. 8999–9005.
- Jiang, Y.; Liu, Z.; Qian, D.; Zuo, H.; He, W.; Wang, J. Robust Online Path Planning for Autonomous Vehicle Using Sequential Quadratic Programming. 2022 IEEE Intelligent Vehicles Symposium (IV); pp. 175–182.
- Li, B.; Ouyang, Y.; Li, L.; Zhang, Y. Autonomous Driving on Curvy Roads Without Reliance on Frenet Frame: A Cartesian-Based Trajectory Planning Method. IEEE Trans. Intell. Transp. Syst. 2022, 23, 15729–15741. [Google Scholar] [CrossRef]
- Scheffe, P.; Henneken, T.M.; Kloock, M.; Alrifaee, B. Sequential Convex Programming Methods for Real-Time Optimal Trajectory Planning in Autonomous Vehicle Racing. IEEE Trans. Intell. Veh. 2023, 8, 661–672. [Google Scholar] [CrossRef]
- Diachuk, M.; Easa, S.M.; Bannis, J. Path and Control Planning for Autonomous Vehicles in Restricted Space and Low Speed. Infrastructures 2020, 5, 42. [Google Scholar] [CrossRef]
- Pérez-Dattari, R.; Brito, B.; de Groot, O.; Kober, J.; Alonso-Mora, J. Visually-guided motion planning for autonomous driving from interactive demonstrations. Eng. Appl. Artif. Intell. 2022, 116, 105277. [Google Scholar] [CrossRef]
- Diachuk, M.; Easa, S.M. Improved Technique for Autonomous Vehicle Motion Planning Based on Integral Constraints and Sequential Optimization. Vehicles 2022, 4, 1122–1157. [Google Scholar] [CrossRef]
- Pöllänen, M.; Liimatainen, H.; Kallionpää, E.; Utriainen, R.; Tiikkaja, H.; Liljamo, T.; Viri, R.; O'Hern, S. Perceptions of Transport Automation amongst Small- and Medium-Sized Road Haulage Companies in Finland. Vehicles 2022, 4, 433–444. [Google Scholar] [CrossRef]
- Diachuk, M. & Easa, S. M. ( 17(3), 210–230. [CrossRef]
- Deufel, F.; Jhaveri, P.; Harter, M.; Gießler, M.; Gauterin, F. Velocity Prediction Based on Map Data for Optimal Control of Electrified Vehicles Using Recurrent Neural Networks (LSTM). Vehicles 2022, 4, 808–824. [Google Scholar] [CrossRef]
- Diachuk, M.; Easa, S.M. Using Inverse Dynamics Technique in Planning Autonomous Vehicle Speed Mode Considering Physical Constraints. Highlights Veh. 2023, 5. [Google Scholar] [CrossRef]
- Dorpmüller, P.; Schmitz, T.; Bejagam, N.; Bertram, T. Time-Optimal Trajectory Planning in Highway Scenarios Using Basis-Spline Parameterization. 2023 IEEE 26th International Conference on Intelligent Transportation Systems (ITSC), Bilbao, Spain, 2023; pp. 596–601.
- Wang, Y.; Lin, Z. Research on path planning for autonomous vehicle based on Frenet system. J. Eng. Res. 2023, 11, 100080. [Google Scholar] [CrossRef]
- Trauth, R.; Moller, K.; Würsching, G.; Betz, J. FRENETIX: A High-Performance and Modular Motion Planning Framework for Autonomous Driving. IEEE Access 2024, 12, 127426–127439. [Google Scholar] [CrossRef]
- Huang, H.; Liu, Y.; Liu, J.; Yang, Q.; Wang, J.; Abbink, D.; Zgonnikov, A. General Optimal Trajectory Planning: Enabling Autonomous Vehicles with the Principle of Least Action. Engineering 2024, 33, 63–76. [Google Scholar] [CrossRef]
- Diachuk, M.; Easa, S.M. Planning Speed Mode of All-Wheel Drive Autonomous Vehicles Considering Complete Constraint Set. Vehicles 2024, 6, 191–230. [Google Scholar] [CrossRef]
- Piotrowski, A.; Zaborski, A.; Tyliszczak, A. Computer-Aided Analysis of the Formation of the Deformation Zone in the Burnishing Process. Appl. Sci. 2024, 14, 1062. [Google Scholar] [CrossRef]
- Yang, X.-S. , 2021. Cuckoo search (cs) algorithm. https://www.mathworks.com/ matlabcentral/fileexchange/29809-cuckoo-search-cs-algorithm, mATLAB Central File Exchange.
- Audi A4 Quatro Characteristics. (2023). Available online: http://www.automobile-catalog.com/car/2011/1187660/audi_a4_3_2_fsi_quattro_attraction_tiptronic.html (accessed on 19 January 2023).

| Category | Reference (Date) | Study Focus | Methodology | Context | Strengths | Limitations |
|---|---|---|---|---|---|---|
| Dynamic Motion Planning | Jiang et al. [3] (2020) | Urban motion planning framework | Dynamic optimization | Intersections, urban | Effective in complex environments | Limited to low-speed scenarios |
| Dang et al. [4] (2020) | Motion planning with coupled dynamics | Nonlinear MPC with coupled lateral-longitudinal model | High-speed highways | Better normal driving performance | High computational complexity. Simplified obstacle avoidance | |
| Li et al. [5] (2022) | Cartesian-based planning (non-Frenet) | CC, dynamic constraints | Rural winding roads | Avoids Frenet frame distortions | Less efficient in structured roads | |
| Tang et al. [6] (2023) | Nonlinear vehicle dynamics for motion planning | Nonlinear MPC, dynamic constraints, T-S fuzzy model | Urban highways | High-fidelity vehicle dynamics modeling | Computationally intensive | |
| Obstacle Avoidance | Liniger & Gool [7] (2020) | Adversarial road model for safety | Game theory and H-J = reachability | Highways, multi-vehicles | Enables cooperative planning | Requires V2V infrastructure |
| Yang et al. [8] (2022) | Risk-based path planning | Risk model, graph search, APF | Mixed traffic (urban) | Explicit risk quantification | Conservative dynamic scenarios | |
| Hu et al. [9] (2023) | Radar-based path planning | Frenet frame optimization | Maritime (harbours) | Effective marine navigation | Limited to aquatic environments | |
| Jin et al. [10] (2024) | Improved artificial potential field | APF with local minima avoidance | Off-road, restricted space | Smooth collision avoidance | Prone to local minima | |
| Dong et al. [11] (2024) | MPC-based collision avoidance | Nonlinear MPC, safety constraints | Intersections, urban | Robust collision avoidance | High computational load | |
| Real-Time Planning | Jeng et al. [12] (2021) | Heuristic motion planning | Rule-based heuristic approach | Campuses | Fast computation | Less optimal |
| Lu et al. [13] (2022) | Real-time decoupled trajectory planning | Decoupling method, MPC | Highways (trucks) | Fast computation, handles uncertainty | Simplified dynamics | |
| Cheng et al. [14] (2022) | Real-time planning | GP, incremental refinement | Pedestrian zones | Balances accuracy and efficiency | Sensitive to sensor noise | |
| Jiang et al. [15] (2022) | Robust online path planning | SQO | Construction sites | Handles uncertainties | High computational load | |
| Li et al. [16] (2023) | Real-time optimal planning | CO, collision avoidance | Tight spaces, urban | Guarantees safety | Requires convex constraints | |
| Scheffe et al. [17] (2023) | Real-time trajectory planning for racing | Sequential CO | Race trucks | Handles aggressive maneuvers | Specialized for racing contexts | |
| Modeling and Control | Diachuk & Easa [18] (2020) | Low-speed path planning | Constrained optimization | Parking/warehouses | Effective tight spaces | Limited to low-speed scenarios |
| Pérez-Dattari et al. [19] (2022) | Visually guided planning | Interactive learning | Parking lots | Incorporates human-like planning | Requires extensive training data | |
| Diachuk & Easa [20] (2022) | Powertrain modeling for improved vehicle dynamics | Inverse dynamics, powertrain modeling | Off-road (4x4 vehicles) | Integrates vehicle mechanics | Requires detailed powertrain data | |
| Diachuk & Easa [24] (2023) | Speed planning considering physical constraints | Inverse dynamics technique | Autonomous vehicles | Realistic speed profiles | Requires precise vehicle dynamics model | |
| Trajectory Optimization | Dorpmüller et al. [25] (2023) | Time-optimal trajectory planning | B-spline parameterization | Highway (lane change) | Time-efficient smooth trajectories | Assumes ideal vehicle dynamics |
| Wang & Lin [26] (2023) | Frenet-based path planning | Frenet coordinate system | Highway, merging | Simplifies path representation | Over-reliance on reference line | |
| Trauth et al. [27] (2024) | Modular motion planning framework | Frenet-based planning | Highways, urban | High flexibility, real-time performance | Complex implementation | |
| Huang et al. [28] (2024) | Least-action principle for optimal trajectories | Variational optimization, physics-inspired | General roads | Generalizable framework | High computational complexity | |
| Diachuk & Easa [29] (2024) | Simultaneous trajectory-speed planning | Inverse dynamics, GQ, SO | Highways (AWD) | Comprehensive constraint handling | Increased computational load | |
| Present Study (2025) | Simultaneous trajectory-speed planning, optimizing kinematic parameters for smoothness/continuity. | Inverse numerical integration with GQ, SQO with nonlinear constraints. | Highway, urban environments | Ensures jerk continuity, handles kinematic/dynamic constraints. Considers LC and moving obstacles. | Computationally heavy (0.5-2.4 sec/maneuver) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




