Measuring Entropy with Tactile Geometry: A Physical Surface Framework for Complex Systems

1. Introduction

Entropy remains one of the most foundational yet abstract quantities in physics, information theory, and systems science. While its mathematical formalism is well established—appearing in forms such as Shannon entropy, Gibbs entropy, and von Neumann entropy—its physical representation often remains elusive, especially in systems that do not lend themselves to conventional thermodynamic modeling. This paper proposes an unconventional yet biologically grounded solution: tactile surface geometry as a measurable analog for entropy distribution.

Building on prior work [1], this paper explores how skin surface structures can be extended into a framework for modeling topological entropy fields. Specifically, it proposes that conformal mapping of tactile geometries offers a real-world surface for understanding how entropy resolves, concentrates, or distributes across complex systems—particularly those governed by probabilistic collapse and localized input.

Rather than treating entropy purely as a statistical abstraction, this approach treats it as a field-bound phenomenon—one that obeys constraints, distributes according to surface boundaries, and interacts with geometrically structured collapse.

2. Background

Entropy, in its many forms, serves as a foundational quantity for describing uncertainty, disorder, and energy distribution across systems. In classical thermodynamics, Gibbs entropy characterizes macro-level energy distributions, while Shannon entropy provides a probabilistic framework for uncertainty in information systems. In quantum mechanics, von Neumann entropy describes the collapse or purity of quantum states, further extending entropy’s role into probabilistic field resolution.

Despite these rigorous formalisms, entropy is rarely treated as a structured, surface-bound phenomenon—especially in systems governed by localized tension, collapse geometry, or sensory feedback. Topological and conformal entropy frameworks attempt to bridge this gap by describing how spatial or network-based configurations may give rise to measurable entropy fields, but these models still lack a biologically grounded substrate.

Recent work in General Probabilistic Theories (GPTs) [2] has introduced the concept of self-dual cones and perfect state spaces, where entropy emerges from the structure of the system’s probabilistic resolution. This paper proposes that biological tactile systems, particularly the line-pore geometries of human skin, offer a uniquely qualified candidate for physical entropy modeling.

3. Theoretical Framework

In prior work [1], it was proposed that skin surfaces exhibit structured microgeometries that may play active roles in sensory interpretation. These include tension-guiding lines and pore matrices that together form a living interface capable of resolving external input via geometrically structured feedback.

The current paper extends this model into the domain of entropy by proposing that tactile surfaces can be treated as conformal substrates for entropy distribution and resolution. In this framework:

• Skin lines function as local entropy vectors, guiding collapse toward lower-tension zones.
• Pores act as slow-release entropy points, regulating diffusion over time.
• The surface as a whole forms a topological entropy field.

By interpreting entropy behavior through physical geometry, this framework opens the possibility of measurable collapse signatures tied directly to surface-based entropy resolution zones.

4. Visual Models & Conical Interpretation

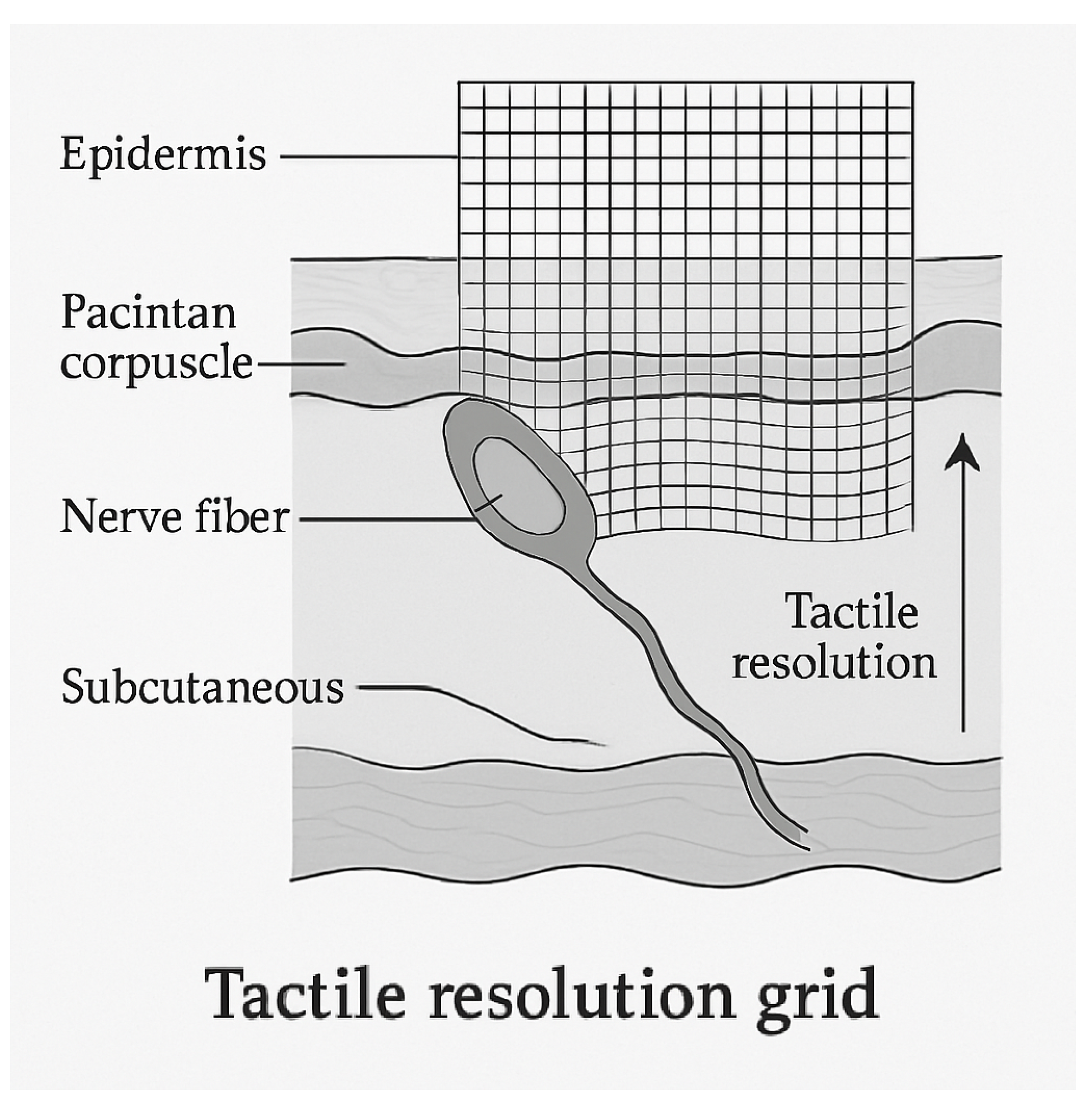
Figure 1. Tactile Resolution Grid showing tension lines and pore zones

Figure 1. Tactile Resolution Grid showing tension lines and pore zones

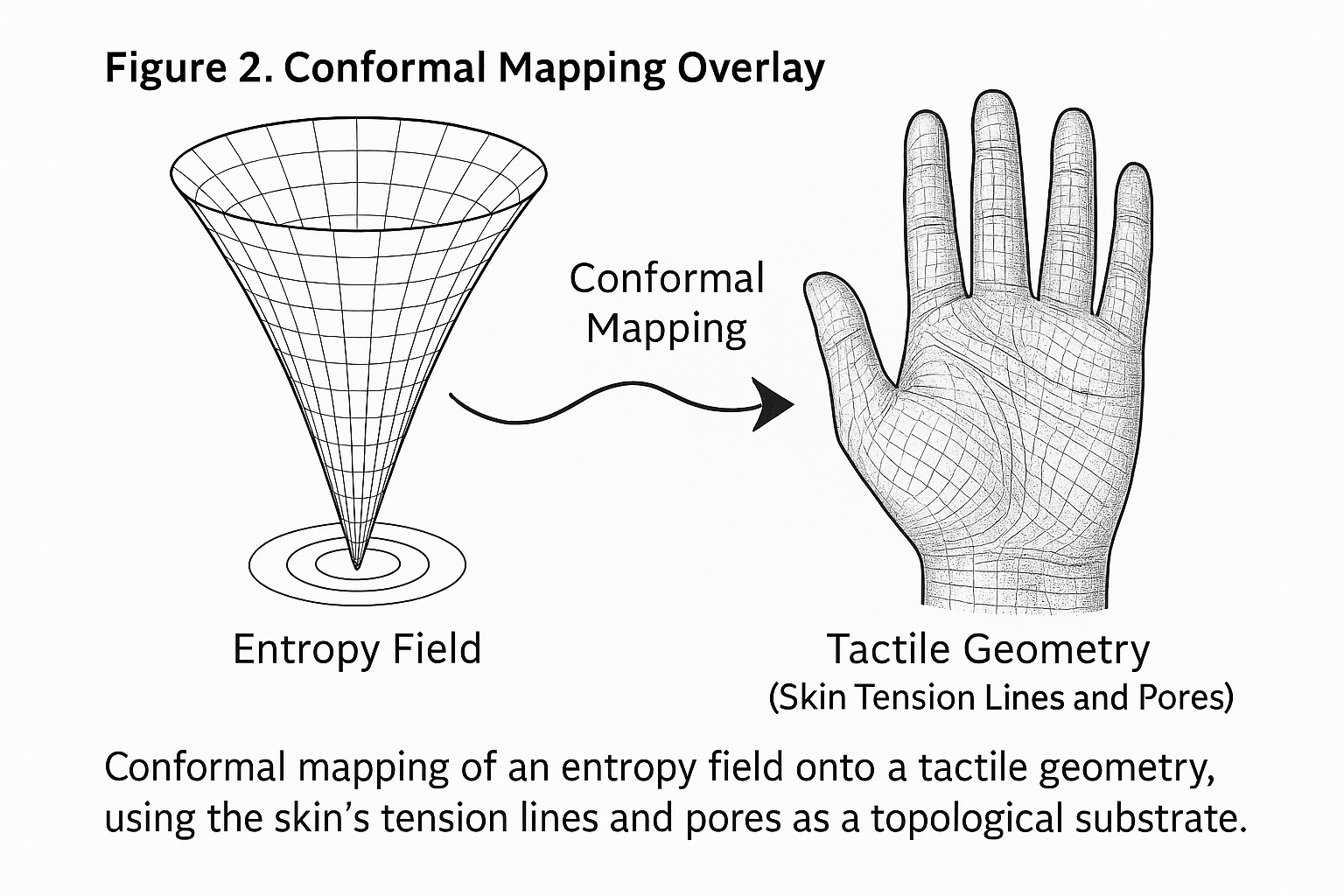
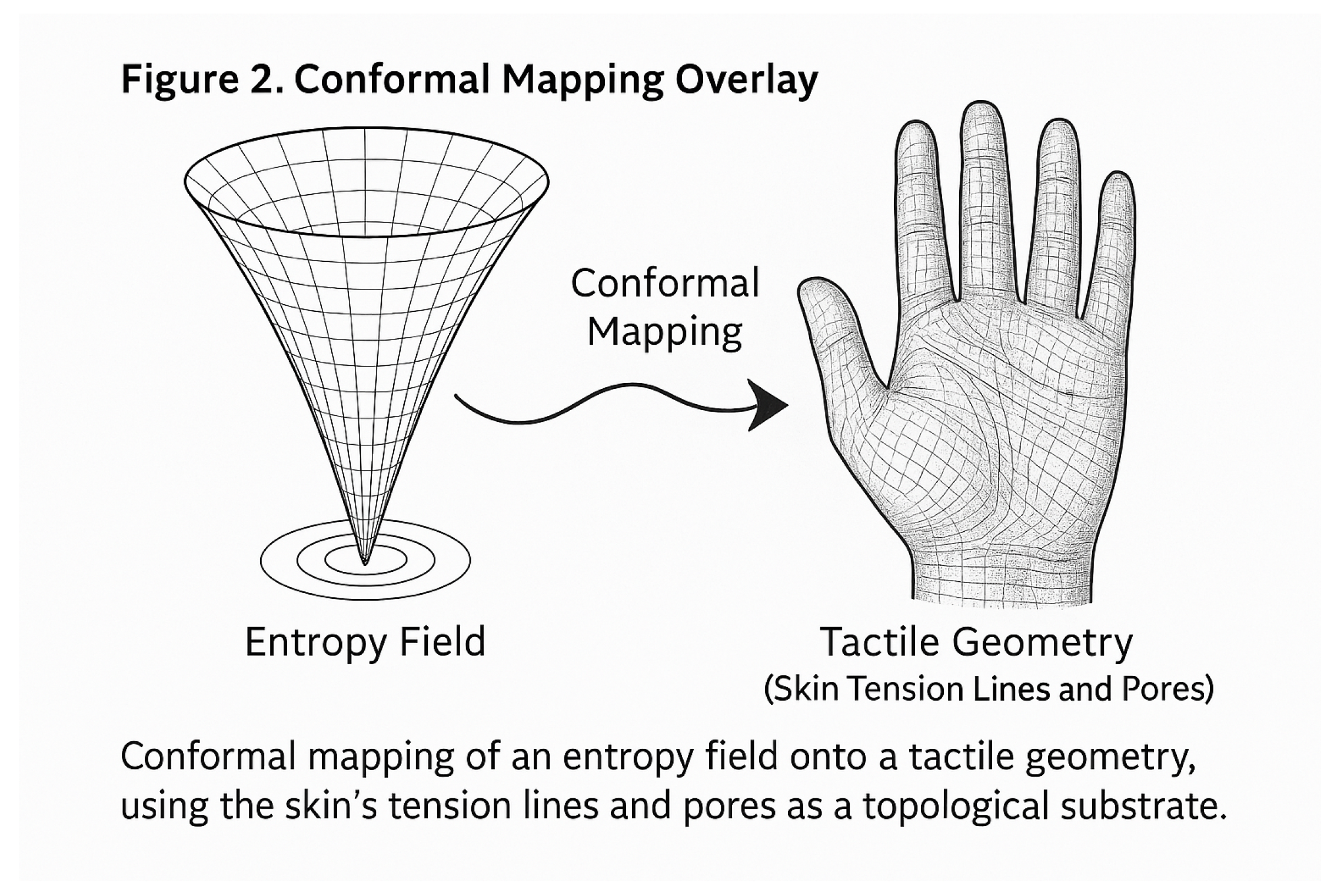
Figure 2. Conformal Mapping Overlay applied to tactile surface

Figure 2. Conformal Mapping Overlay applied to tactile surface

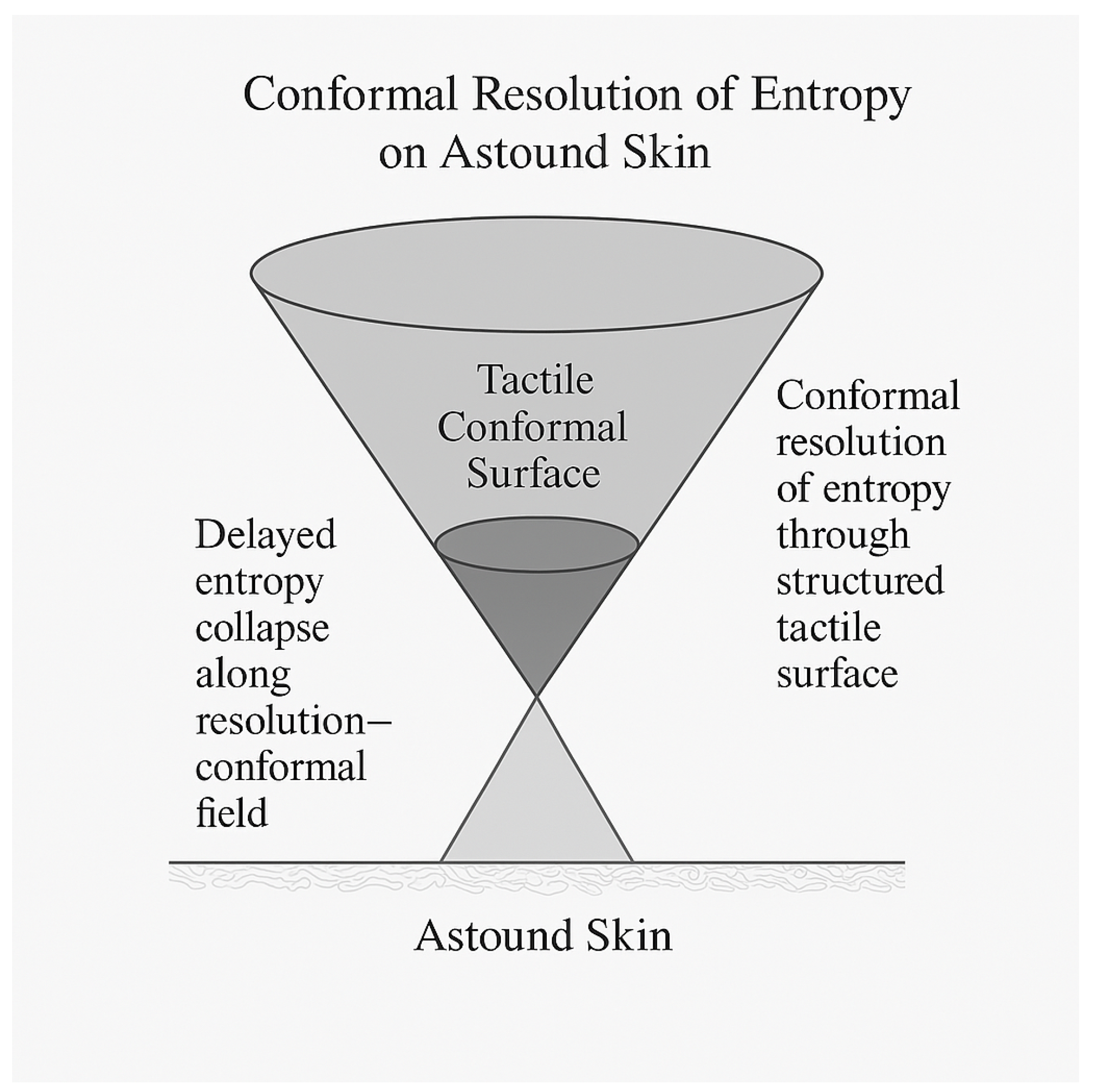
Figure 3. Cross-sectional Conical Entropy Model beneath the skin

Figure 3. Cross-sectional Conical Entropy Model beneath the skin

5. Implications for Entropy Measurement

If entropy fields conform to tactile geometries, then biological surfaces may offer dynamic measurement substrates for entropy itself. Specific regions of the skin may act as entropy concentrators. These zones could be mapped and analyzed for collapse density over time.

This opens the door for:

• Measurable entropy gradients through sensory feedback
• Simulation of entropy flow in neural or AI systems using tactile analogs
• Conformal entropy maps using physical or synthetic surfaces
• Physical models of state collapse akin to GPT cones

6. Conclusion and Future Work

This paper introduces a new framework for understanding entropy through structured tactile geometry. By extending anatomical microstructures into thermodynamic and probabilistic field theory, we offer a unified surface-based model for entropy collapse. Future work will explore computational simulation, sensor validation, and entropy modeling in conformal AI systems.