Description of the Condensed Phases of Water in Terms of Quantum Condensates

1. Introduction

Water, the matrix of life, covers two-thirds of our planet and is one of the most abundant substances in the universe. It is of paramount importance in physics and chemistry, earth and life sciences, cosmology and technology. No other molecule exists as a solid, liquid, or gas at normal pressure. At the microscopic level, the most popular descriptions deal with the classical statistics of distinguishable ${\mathrm{H}}_2$O molecules subject to local forces and nuclear quantum effects [1,2,3,4,5,6,7,8,9,10]. Schematically, ice Ih is a frustrated hexagonal lattice of O atoms containing an exponential number of proton configurations according to the “ice rules” [11,12,13], liquid water is a tetra-coordinated network of cooperative H-bonds in a jumble of molecular clusters constantly breaking and forming, and vapor is composed of dimers linked by transient H-bonds.

However, these descriptions do not explain why water is in a class by itself with extraordinary anomalous properties quite different from those found in other materials. Divergent models abound [1,14,15,16], but the physical reality underlying the properties of water is still a mystery, hindering progress in many disciplines.

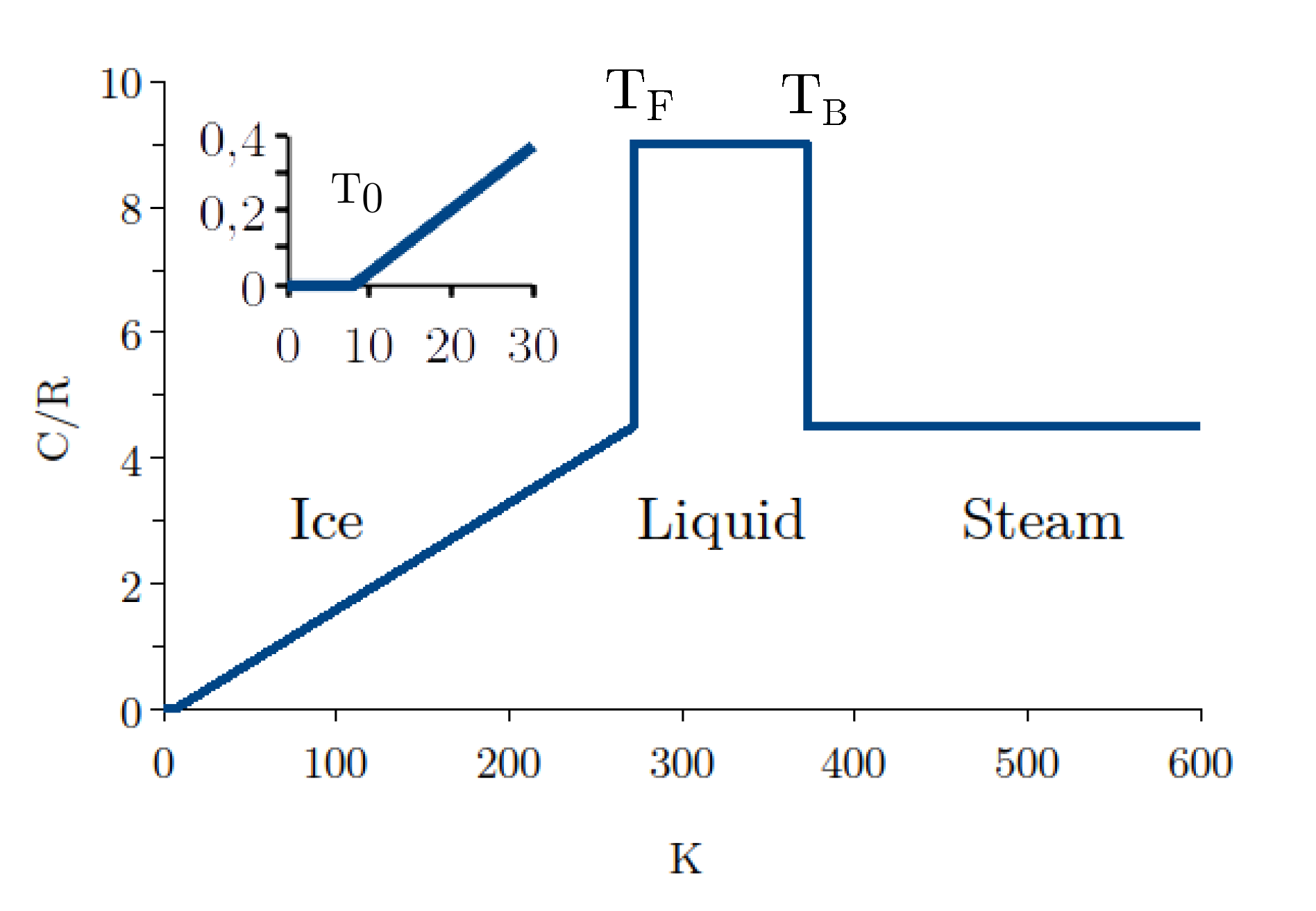
The aim of this work is to propose a new line of reasoning from microscopic to macroscopic physics, which is convincing in every respect and based solely on objective facts without arbitrary hypotheses. One of the goals is to explain the anomalous evolution of the heat capacity throughout the phase diagram (Figure 1 and Table 1). According to Debye’s model and the energy equipartition theorem, the heat capacity should be proportional to $9\mathcal{R}$ and increase continuously from zero as $T\to 0$ to $9\mathcal{R}$ as $T\to \infty$. Instead, we see that $C_W\approx 9\mathcal{R}$ is a constant for the liquid in a temperature range far from the infinite limit. It results that the heat capacity is not determined by the thermal density of phonon states. Similarly, $C_I=0$ for ice below $T_0\approx 8$ K violates Debye’s $T^3$law [21]. Furthermore, the heat capacity of the liquid is halved at $T_F$ (fusion) and $T_B$ (boiling), violating the equipartition theorem. Another anomaly (not shown) is the dramatic increase in heat capacity by supercooling the liquid to the temperature of homogeneous crystallization at $T_H\approx 226$ K [3,22].

The starting point of the new argument under consideration is the boson character of ${\mathrm{H}}_2\mathrm{O}$. In condensed matter physics, a Bose-Einstein condensate (BEC) is typically formed when a gas of monoatomic bosons at very low density is close to absolute zero. A macroscopic fraction of the atoms described by the same one-particle wavefunction occupy the lowest state, and microscopic quantum phenomena, in particular wavefunction interference, become macroscopically apparent. Quantum condensate also refers to the macroscopic occupation of multiple thermally accessible states, but proving the existence of BECs with complex interactions and internal degrees of freedom (DOF) is a major open problem in mathematical physics. Such a proof is beyond the scope of this present paper. Here, the existence of condensates is inferred from two properties of the H-bonds (the dissociation energy and the electric dipole) and this inference is subsequently validated by its ability to explain the extraordinary properties in question.

This work is structured as follows. The existence of condensates of water molecules is justified in Section 2. The dipole eigenstates are introduced in Section 3, where it is shown that quantum entanglement of opposite dipole orientations cancels the equipartition. In Section 4 the thermal properties are related to microscopic observables, and the degeneracy entropy is introduced. The gas phase and the aerosol of droplets are treated in Section 5.

2. Quantum Condensates

The model consists of a macroscopic number, N, of molecules at normal pressure in a sealed container in diathermal equilibrium with a black body at T. The density is phase dependent. Boundary effects are negligible. The spin states are degenerate.

At the microscopic level, the existence of stationary states of the H-bonded molecules is precluded by the internal decoherence due to the low dissociation energy of dimers ${\left({\mathrm{H}}_2\mathrm{O}\right)}_2$ that is typically $D_0=(1105\pm 10){\mathrm{cm}}^{-1}$ in molecular jets [23]. The calculated potential energy surface shows that $D_0$ essentially corresponds to doubly H-bonded dimers [24], so that the dissociation energy of a single H-bond is likely to be about $D_0/2$. Since the H-bond dynamics induced by spectroscopy are composed of proton modes above $1600$, librations in the range 400-$700$, and $\mathrm{O}\cdots \mathrm{O}$ translations below $200$, $D_0/2$ means that these modes are not stationary, as shown by their extremely broad infrared absorption bands [3]. In the absence of quantum measurement, internal decoherence unavoidably leads to classical modes.

At the macroscopic level the condensed phases are condensates of O atoms dressed with classical oscillators, and an electric field due to the strong H-bond dipole ($\left|\mu \right|\approx 3$ D in the liquid). The many-body wavefunction of the dressed O, $\Phi ({\mathbf{r}}_1{\mathbf{r}}_2\cdots {\mathbf{r}}_N,t)$, is symmetric with respect to the exchange ${\mathbf{r}}_i\rightleftarrows {\mathbf{r}}_j$ of any two coordinates. This leads to the hexagonal structure, consisting of honeycomb sheets whose unit cell is a hexagon with an atom in the center. The isomorphic electric field is described by the single dipole wavefunction.

3. The Dipole States

The classical model of a H-bonded dimer ${\mathrm{HO}}_{\mathrm{d}}-\mathrm{H}\cdots {\mathrm{O}}_{\mathrm{a}}{\mathrm{H}}_2$ composed of a donor ${\mathrm{H}}_2{\mathrm{O}}_{\mathrm{d}}$ and an acceptor ${\mathrm{H}}_2{\mathrm{O}}_{\mathrm{a}}$, consists of a dimensionless proton in an asymmetric double well along the O⋯O coordinate. The O⋯O length is $\approx 2.6$ Å. The asymmetry is the energy difference between the ${\mathrm{HO}}_{\mathrm{d}}-\mathrm{H}\cdots {\mathrm{O}}_{\mathrm{a}}{\mathrm{H}}_2$ (L) and ${\mathrm{HO}}_{\mathrm{d}}\cdots \mathrm{H}-{\mathrm{O}}_{\mathrm{a}}{\mathrm{H}}_2$ (R) configurations with opposite orientations of the dipole moments, so that the inter well proton transfer and the dipole flip occur simultaneously. The inter well separation is $\approx 0.6$ Å. With this model, Bove et al. [7] have fitted the inelastic neutron scattering (INS) spectra of ice at different temperatures with quasi-elastic profiles and they estimated the relaxation rates of thermally activated over-barrier proton jumps. However, they found that the absence of a temperature effect was inconsistent with the model and ultimately concluded that quantum effects are likely, but they did not pursue this lead.

In the quantum description of the water dimer in the absence of quantum measurement, the internal decoherence decouples the quantum flip of the dipole moment from the classical coordinates of the dressed O, including the H transfer coordinate. The dipole eigenstates of the L configuration are [25,26]:

$$\begin{array}{ccc}\hfill |{\psi }_{L0}\rangle & =& cos\varphi |{\psi }_L\rangle +sin\varphi |{\psi }_R\rangle ;E_0;\hfill \\ \hfill |{\psi }_{L1}\rangle & =& sin\varphi |{\psi }_L\rangle -cos\varphi |{\psi }_R\rangle ;E_0+\hslash {\omega }_1.\hfill \end{array}$$

(1)

$|{\psi }_L\rangle$ and $|{\psi }_R\rangle$ are the zero order localized states for opposite dipole orientations. $\hslash {\omega }_1$ is the flipping energy. $|{\psi }_{L0}+{\psi }_{L1}{|}^2$ describes the quantum beat at ${\omega }_1$. The tiny amplitude proportional to $2\left|\mu \right|{sin}^2\varphi$ is far too small to perturb the normal modes by interacting with the residual charges carried by these modes. Thus, classical oscillators in thermal equilibrium are subject to equipartition. A drawback of this approximation is that it does not account for the shift of the maximum probability density to longer distances in the upper state due to a slight stretching of the H-bond.

The eigenstates for the R configuration are obtained by swapping ${\psi }_L$ and ${\psi }_R$, and superposition occurs when the L and R configurations are indistinguishable (e.g., in the gas):

$$\begin{array}{ccc}\hfill |{\psi }_{0\pm }\rangle & =& {\displaystyle \frac{1}{\sqrt{2}}}\left[\right|{\psi }_{L0}\rangle \pm |{\psi }_{R0}\rangle ];\hfill \\ \hfill E_{0\pm }& =& E_0+{\displaystyle \frac{1}{2}}\hslash (-{\omega }_{\mu }\pm {\omega }_t);\hfill \\ \hfill |{\psi }_{1\pm }\rangle & =& {\displaystyle \frac{1}{\sqrt{2}}}\left[\right|{\psi }_{L1}\rangle \pm |{\psi }_{R1}\rangle ];\hfill \\ \hfill E_{1\pm }& =& E_0+\hslash [{\omega }_1+{\displaystyle \frac{1}{2}}({\omega }_{\mu }\pm {\omega }_t)].\hfill \end{array}$$

(2)

$\hslash {\omega }_{\mu }$ is the energy difference between parallel and antiparallel dipoles. ${\omega }_t\approx 2\varphi {\omega }_1\ll {\omega }_{\mu }$ is the tunneling frequency. The O⋯O bond length is stretched by the larger asymmetry. $|{\psi }_{0+}+{\psi }_{0-}{|}^2$ and $|{\psi }_{1+}+{\psi }_{1-}{|}^2$ describe the quantum beat at ${\omega }_t$, out of resonance with the normal modes. The huge amplitude proportional to $2\left|\mu \right|$ enslaves the classical oscillators to the massless dipole with zero kinetic energy. There is no equipartition.

According to (1) and (2), Figure 1 shows entangled dipoles in ice and vapor versus untangled dipoles in liquid. These equations are also consistent with neutron scattering data for the condensed phases.

First, neutron Compton scattering (NCS) probes the mean kinetic energy of the protons. The temperature law expected for equipartition is $\overline{E}\left(T\right)={\overline{E}}_0+{\displaystyle \frac{3}{2}}{k}_{B}T$, where the zero point energy ${\overline{E}}_0$ is practically T independent, $k_B$ is the Boltzmann constant, and ${\displaystyle \frac{3}{2}}{k}_B\approx 0.12$ meV.${\mathrm{mol}}^{-1}$.${\mathrm{K}}^{-1}$. The observed temperature law is quite different [9]. For $T\le T_F$, $\overline{E}=(153\pm 2)$ meV.${\mathrm{mol}}^{-1}$ is practically a constant. The kinetic energy is zero, in agreement with (2). For $T_F\le T\le T_B$, $\overline{E}\left(T\right)\approx {\overline{E}}_0+{\displaystyle \frac{3}{2}}{k}_B(T-T_F)$ means equipartition in the liquid, in agreement with (1), and vanishing of the kinetic energy at the crystallization point $T_F$.

Second, for INS, the question is whether the spectra consist of the broad quasi-elastic profile in favor of the classical model preferred by Bove et al. [7] or, alternatively, whether they consist of tunneling transitions partially resolved from the elastic peak. The spectra are prima facie ambiguous. However, the absence of a temperature effect [7], the split probability density of the protons [27], the NCS data [9], and the heat capacity are against the classical option. As a result, the observed intensity humps at $\pm (0.10\pm 0.01)$ meV can be attributed to the INS-induced proton tunneling splitting $\hslash {\omega }_t/k_B=(1.2\pm 0.2)\mathrm{K}$, with semi-subjective error bars.

4. The Condensed Phases of Water

4.1. Ice Ih

The empirical relation $k_B{T}_0\approx 7\hslash {\omega }_t$ (Table 1 and Table 2) gives the tunneling gap of the honeycomb unit cell of the field. Unlike INS, this gap is independent of the measurement. It does not involve protons. The eigenenergies are 7 times those given in (2), and $\hslash ({\omega }_1+{\omega }_{\mu })/k_B$ is proportional to $T_F$ (Table 2). The field degeneracy of ${\displaystyle \frac{3}{2}}$ due to the geometrical frustration calculated by Pauling for an empty hexagon [12] is squared by the atom in the center, which is part of another ring. The ice is a mixture of ${\Omega }_I={\left({\displaystyle \frac{3}{2}}\right)}^2$ degenerate fields. The entropy $S_I=\mathcal{R}ln{\Omega }_I$ is deterministic and independent of temperature.

Since the tunneling gap is forbidden, $C_I\equiv 0$ for $T\le T_0$. The ice is a “superinsulator” and $\mathcal{R}{T}_0$ is the lowest state accessible by cooling.

For $T_0\le T\le T_F$, the field wavefunction deduced from (2) is:

$$\begin{array}{ccc}\hfill {\Psi }_I\left(t\right)& =& \sqrt{N_{0-}}{\psi }_{0-}{e}^{i{\omega }_{tI}t}\hfill \\ \hfill & +& \sqrt{N_1}({\psi }_{1+}{e}^{i{\omega }_{1+I}t}+{\psi }_{1-}{e}^{i{\omega }_{1-I}t});\hfill \\ \hfill {\displaystyle \frac{N_{0-}}{N_7}}& =& {\displaystyle 1-{\Theta }_I;}\hfill \\ \hfill {\displaystyle \frac{2N_1}{N_7}}& =& {\displaystyle {\Theta }_I;}\hfill \end{array}$$

(3)

where $N_7=N/7$; $N_{0-}$ and $N_1$ are the occupation numbers; ${\omega }_{tI}=7{\omega }_t$; ${\omega }_{1+I}=7({\omega }_1+{\omega }_{\mu })$; ${\omega }_{1-I}=7({\omega }_1+{\omega }_{\mu }+{\omega }_t)$. ${\Theta }_I$ is the partition coefficient (Table 3). Apart from its normalization, ${\Psi }_I\left(t\right)$ is the Schrödinger wavefunction, which can be considered a classical quantity without thermal and quantum fluctuations [28]. The probability density $|{\Psi }_I{\left(t\right)|}^2$ describes quantum beats corresponding to coherent oscillations of the field at ${\omega }_{BI1}={\omega }_{1-I}-{\omega }_{1+I}$ and ${\omega }_{BI2}={\omega }_{1+I}-{\omega }_{tI}$. The coherent heat transfer by photons $\hslash {\omega }_{BI1}$ to the enslaved oscillators with zero kinetic energy gives the heat capacity $C_I={\displaystyle \frac{9}{2}}\mathcal{R}{\Theta }_I$ (Table 1 and Table 3). According to Plank’s law, the relative power radiated at ${\omega }_{BI2}$ is ${({\omega }_{BI2}/{\omega }_{BI1})}^3\sim {10}^{-9}$, so the contribution of $\hslash {\omega }_{BI2}$ to the heat capacity is insignificant.

4.2. Liquid Water

The fusion to the high density liquid (HDL) at $T_F$ separates each of the ${\Omega }_I$ fields composed of 7 entangled dipoles (2) into 14 degenerate fields of untangled dipoles (1) consisting of two by two complementary clockwise and counterclockwise honeycomb units composed of XL and (7−X)R, or XR and (7−X)L (X = 1⋯7) configurations. The HDL degeneracy ${\Omega }_{HD}=14{\Omega }_I$ gives the heat of fusion,

$$\Delta F\left(T_F\right)=\mathcal{R}{T}_{F}ln{\displaystyle \frac{{\Omega }_{HD}}{{\Omega }_I}}\approx 5993\mathrm{J}.{\mathrm{mol}}^{-1},$$

(4)

in reasonable agreement with the measured value of $\approx 6005\mathrm{J}.{\mathrm{mol}}^{-1}$[3,20]. Since $\mathcal{R}{T}_F$ is the field ground state, the transition is purely quantum. No H-bond dissociation and no disorder. Preservation of ${\Omega }_I$ means preservation of the honeycomb structure [29,30]. The HDL is a liquid crystal whose superfluidity is prevented by the electric field. Since there is no change in the internal energy, the kinetic energy of the liquid (${\displaystyle \frac{9}{2}}\mathcal{R}{T}_F$) is frozen in the ice crystallized at $T_F$.

The eigenstates at $\mathcal{R}{T}_F$ and $\mathcal{R}{T}_B$ have identical structures with slightly different O⋯O distances. $\hslash {\omega }_1/k_B$ is proportional to $T_F-T_B$ (Table 2). The coherent heat transfer to the classical modes is temperature independent and $C_{HDL}=9\mathcal{R}$ (Table 3). By heating, each L→R flip is accompanied by a R→L flip in the complementary unit cell, so the density decreases quadratically. The kinetic energy at the macroscopic level ${\displaystyle \frac{9}{2}}\mathcal{R}(T-T_F)$ is in agreement with NCS at the microscopic level.

The density of liquid water has two puzzling properties: (i) it is maximal at $T_{MD}\approx 4$ K above $T_F$; (ii) it decreases with supercooling. These properties make sense for the condensate.

$T_{MD}$ is consistent with the existence of a constant fraction $X_{HD}={[12{\left({\displaystyle \frac{3}{2}}\right)}^2-1]}^{-1}\approx 0.038$ of non-interacting complementary hexagons with antiparallel dipole configurations. These are shielded against thermal waves. By cooling from $T_B$, the density reaches a maximum value for ${\Theta }_{HD}=X_{HD}$, at $T_{MD}=T_F[1+X_{HD}(T_B-T_F)]\approx 277$ K, when the occupancy of $\mathcal{R}{T}_B$ is completely shielded. $\mathcal{R}{T}_{MD}$ is the lowest HDL field state accessible by cooling, and $T_{MD}$ is the critical temperature for the onset of the supercooled liquid.

Below $T_{MD}$, the untangled association of the antiparallel dipoles of the complementary units form non-degenerate units with zero dipole moment (${\Omega }_{LD}=1$), which cluster into the ground state of the low density liquid (LDL) field at $\mathcal{R}{T}_H=\mathcal{R}(T_F-\hslash {\omega }_{\mu }/k_B)$ (Table 2). $T_H\approx 226$ K is the temperature of homogeneous crystallization reported in various papers in the range of $226-232$ K [3,22]. The supercooled liquid is a mixture of ${\Theta }_{SC}$HDL and $(1-{\Theta }_{SC})$LDL (Table 3). Supercooling is a continuous quantum transition between the ground states of the HDL and LDL fields whose energy gain cannot be radiated away (Table 3). (This puts the metastable LDL at a disadvantage to the HDL above $T_{MD}$.) The heat capacity $C_{SC}=\mathcal{R}(9+{\Theta }_{SC}^{2}ln{\Omega }_{HD})$ increases from $9\mathcal{R}\approx 75$ J.mol.⁻¹$T^{-1}$ at $T_{MD}$ to about $12.5\mathcal{R}\approx 103$ J.mol.⁻¹$T^{-1}$ at $T_H$, in agreement with the measurements [22]. The density decreases quadratically. Homogeneous crystallization at $T_H$ is a quantum transition from the ground state of the LDL field, whose latent heat is removed from the liquid. The frozen kinetic energy of ice crystallized at $T_H$ is ${\displaystyle \frac{9}{2}}\mathcal{R}{T}_H$.

As a result, the isomorphic condensed phases differ in that the kinetic energy in the liquid allows collective excitations that are forbidden in the solid. In contrast, the degeneracy is not critical for the physical state.

5. Other Phases of Water

5.1. Gaseous Water

Ebullition at $T_B$ and evaporation below $T_B$ can be treated on the same foot. The molar volume expansion of $\approx 1700$ at normal pressure dissociates 6 of the 7 H-bonds per unit cell and destroys the condensate. This leads to a gas of distant entangled dimers (2) whose tunneling splitting is $\hslash {\omega }_t/k_B\approx 0.94$ K [31]. The heat capacity ${\displaystyle \frac{9}{2}}\mathcal{R}$ (Table 1) means that $\hslash {\omega }_t$ is independent of the act of measurement and there is no decoherence.

The energy of the transition is

$$\begin{array}{ccc}\hfill \Delta F_G\left(T\right)& =& {\displaystyle 6D_0-\mathcal{R}T\left(9+ln{\Omega }_{HD}\right).}\hfill \end{array}$$

(5)

The heat of ebullition $\Delta F_G\left(T_B\right)=(40575\pm 700)\mathrm{J}.{\mathrm{mol}}^{-1}$ agrees with the measured value of $(40660\pm 80)\mathrm{J}.{\mathrm{mol}}^{-1}$[32], and the measured heat of sublimation of ice at $T_F$, namely $\approx 51059$ J.${\mathrm{mol}}^{-1}$[19], matches $\Delta F_F+\Delta F_G\left(T_F\right)\approx 51058$ J.${\mathrm{mol}}^{-1}$ for a two-step process through the liquid state.

Two points are worth noting. First, the ${\Omega }_I$ value derived from the honeycomb structure is confirmed against Pauling’s estimate for the empty hexagonal structure. Second, the dissociation energy of the untangled H-bonds in the liquid is exactly $D_0/2$. Thus the entanglement (2) is energy free. The H-bond is essentially electrostatic in nature, with no directional valence bond energy [24], and there is no significant cooperative effect in the condensed phases.

5.2. Water Droplets

Condensation of the vapor over the locally heated water surface can produce long-lived, self-organizing, honeycomb-patterned aggregates composed of equidistant monodisperse droplets ($r\approx 5\mu$m) as a single layer floating above the surface, and the spatial order is maintained even as the layer moves horizontally [33,34,35,36,37]. The self-assembly mechanism is thought to be a balance of hydrodynamic forces. However, while the upward flow of steam can explain the repulsive force, there is no convincing explanation for the attractive forces between droplets.

In fact, the self-organized honeycomb pattern makes sense in itself since the droplets are bosons with negligible local interactions due to classical forces. When they emerge from the vapor with zero center of mass kinetic energy, they are subject to two vertical forces, one due to gravity proportional to $r^3$ and the other due to the upward vapor flow proportional to $r^2$. For a critical value, $r_c\left(T\right)$, they drift downward and cluster over the surface in a condensate of monodisperse microparticles whose stability is ensured by the symmetry of the many body wavefunction. This 2-D supersolid can flow as a superfluid with zero viscosity. In the reported experiments, the layer hinders upward vapor flow and prevents multilayer formation. In the open air, however, large-scale condensates in 3-D can explain the existence of long-lived clouds drifting in the troposphere.

6. Conclusion

The physical reality underlying the H-bonded dimer in the absence of quantum measurement is the coexistence of the classical degrees of freedom of the water molecules and the quantum states of the electric dipole. The condensed phases are condensates of O atoms dressed with classical oscillators and a degenerate electric field. The classical oscillators are either the normal modes subject to equipartition in the liquid or enslaved to the massless electric field in the ice.

This description is based on objective facts, without arbitrary hypotheses, and it is much more parsimonious than the other models. It captures properties that lie outside the bounds of classical statistics and thermodynamics by a set of four microscopic observables and degeneracy entropy. It explains why water is in a class by itself with extraordinary properties. It shows that the hexagonal structure is not due to local forces and that the difference between the liquid and solid is only a matter of kinetic energy, not of disorder. It also shows how both quantum and classical physics interact at the microscopic and macroscopic levels of the same material.

Compared to monoatomic systems, the condensed phases of water and the aerosol extend the size, temperature, and density ranges of condensates by orders of magnitude to the scale of our everyday environment under standard conditions. This is likely to change our understanding of the chemistry in water and how life works.