Characteristics of the Damping Ratio of Undisturbed Offshore Silty Clay in Eastern Guangdong, China

1. Introduction

Guided by the “Dual Carbon” goals of peaking emissions by 2030 and achieving carbon neutrality by 2060, China has vigorously developed offshore wind power. By the end of 2023, the total installed capacity had reached 37.6 GW. Looking ahead, China’s offshore wind power industry will maintain robust growth. According to the “2022 Global Offshore Wind Power Conference Initiative,” by the end of the 14th Five-Year Plan, China’s cumulative offshore wind capacity should exceed 100 GW, surpass 200 GW by 2030, and not fall below 1,000 GW by 2050. However, in 2021, the Ministry of Finance canceled central government subsidies for offshore wind power. This policy shift aims to promote industry development through market-driven mechanisms and achieve grid parity for offshore wind power. Against this backdrop, there is an urgent need for technological innovation and refined design to optimize offshore wind turbine structures and reduce construction and installation costs. The damping effect from soil-pile interaction plays a positive role in lowering turbine loads and mitigating monopole foundation fatigue, especially under shutdown conditions and misaligned wind-wave scenarios. However, compared to soil-pile stiffness, studies on soil-pile damping in offshore wind turbines remain limited, and no consensus has been reached in the industry.

Hysteretic damping in soil-pile interaction refers to the energy dissipated by the soil in the mobilized zone of the pile when subjected to cyclic shear loading. At the microscopic level, the energy dissipation in each soil element is influenced by the soil’s intrinsic damping properties and the amplitude of cyclic shear strain. For a given soil type, larger amplitudes of cyclic shear strain lead to higher damping. However, different soils-due to factors such as overconsolidation ratio and plasticity index-demonstrate varying damping behaviors. Within the mobilized zone of the pile, the magnitude of shear strain varies across different regions and distances. Based on extensive finite element parametric analyses, Zhang et al. [1] studied the hysteretic foundation damping for a 1-metre-height horizontal pile slice, which was constrained to mobilise a flow-around mechanism, which is thought to represent a p-y segment of a slender pile. Through a comprehensive set of parametric analyses, a scaling relationship between the cyclic horizontal displacement-damping ratio curve of soil-pile interaction at the p-y spring level and the cyclic shear strain-damping ratio curve at the soil element level was established, as illustrated by Figure 1. This soil-pile interaction damping model captures the nonlinear response of soil-pile interaction damping and incorporates the effects of foundation soil properties. Clearly, the damping properties at soil element level are a prerequisite for studying soil-pile interaction damping.

Extensive research on the damping ratio of clay has been conducted by scholars worldwide [2,3,4,5,6,7,8,9,10,11,12,13,14], leading to a relatively mature understanding of its damping behavior. A classic study by Darendeli [15] identified plasticity index as a critical factor affecting soil damping ratio and classified all relevant factors into soil physical parameters and static-dynamic loading conditions. Building on this, a damping ratio prediction model was developed using the plasticity index, overconsolidation ratio, effective mean consolidation pressure, number of loading cycles, and vibration frequency as parameters. Zhang et al. [16] studied the damping ratios of Quaternary, Tertiary, and older strata, as well as organic soils in the United States, noting significant effects of stratum age and consolidation stress on damping. They proposed a polynomial damping ratio prediction model based on normalized dynamic shear modulus. Senetakis et al. [17] investigated the damping of sandy and silty soils, concluding that particle shape, grain-size distribution, and silt content significantly influence the damping of non-plastic soils. Lee et al. [18] conducted experimental studies on silty clay and found that the Ramberg–Osgood function accurately predicts the damping ratio at small to medium strains but overestimates it at large strains.

Focusing on soils in China’s offshore regions, Chen et al. [19] indicated that the damping characteristics of silty clay are broadly similar between continental and marine deposits, whereas silt and fine sand show significant differences between the two depositional environments. Lan et al. [20] compiled 372 sets of dynamic nonlinear soil parameters from the dynamic triaxial tests in seismic safety reports for nearly 40 offshore oil platforms in the Bohai Sea. The soils tested included silty clay, silty fine sand, silt, sandy silt, and silty fine sand, and they provided only recommended damping ratio values. Using cyclic triaxial tests, Li et al. [21] investigated the damping ratios of offshore silty clay, silt, silty sand, and sand in the Yellow Sea off Jiangsu Province. Compared to Bohai Sea soils, their results revealed marked differences in damping ratio characteristics across different marine regions. Using dynamic triaxial tests, Song et al. [22] conducted a preliminary study on silty clay from the Eastern Henan Plain under medium-to-high strain levels and observed that the damping ratio increases with higher confining pressure. By performing resonant column tests, Song et al. [23] studied the small-strain damping of soils from Liaodong Bay and found that, at the same strain levels, marine soils have a lower damping ratio than terrestrial soils. He et al. [24] reviewed and analyzed China’s recent studies on soil damping ratios and noted several issues, including insufficiently detailed soil classifications, inconsistencies in testing instruments and data-processing methods, and weak correlations between results and fundamental soil properties. In summary, most existing research on soil damping has focused on clay and sand, with relatively few studies addressing silty clay. Silty soils, which lie between clay and sand in terms of particle composition, exhibit complex mechanical behavior. Therefore, the damping characteristics of clay or sand cannot be directly applied to silty soils. Given the widespread occurrence of silty soils along China’s coasts, targeted studies on the damping ratios of typical silty soils are crucial.

This This paper presents an experimental study on the damping ratio characteristics of representative silty clay from an offshore wind farm in eastern Guangdong. Resonant column and cyclic direct simple shear tests were conducted to measure the damping ratio across the full strain range, and the results were compared with predictions from widely used empirical models. The findings not only expand the database of damping ratios for typical silty clays in China’s offshore regions but also provide valuable insights for seismic engineering and structural optimization in offshore wind power projects.

2. Experimental Method

2.1. Soil Sample Overview

The silty clay samples used in this experimental study were collected from an offshore wind farm in eastern Guangdong at depths ranging from 16 to 18 meters. This type of soil is widely distributed in the offshore regions of Guangdong Province, making it highly representative. All soil samples were collected on-site using a static pressure method with a wave-compensating, ship-mounted drill rig. The sampler used had an outer diameter of 76 mm and an inner diameter of 72 mm. A variety of basic physical property tests were conducted on the samples, providing data on parameters such as moisture content, saturated unit weight, plasticity index, and particle gradation. One-dimensional consolidation tests indicated an overconsolidation ratio (OCR) of 2 for the soil samples. The detailed test results are shown in Table 1

2.2. Experimental Plan

Figure 1 illustrates the approximate strain level ranges for dynamic property testing of soils. From the figure, it is evident that obtaining the damping ratio of soil across low, medium, and high strain levels using a single test method is not currently feasible. This study combines resonant column tests (for strain levels ≤ 0.01%) and cyclic direct simple shear tests (for strain levels ≥ 0.1%) to obtain a complete damping ratio-cyclic shear strain curve, as shown in Figure 3. To investigate the damping ratio characteristics of both overconsolidated and normally consolidated silty clay, two series of tests were conducted. In the first series, the soil was consolidated to its in-situ stress level, maintaining its original overconsolidation ratio (OCR = 2). This series involved performing both cyclic direct simple shear and resonant column tests on the overconsolidated silty clay to assess its damping characteristics. In the second series, the SHANSEP method was applied to consolidate the soil samples to four times their original vertical in-situ stress, effectively eliminating the soil’s stress history. This was followed by conducting cyclic direct simple shear and resonant column tests on the normally consolidated silty clay to evaluate its damping characteristics.

Figure 2. Approximate Strain Level Ranges for the Dynamic Property Testing of Soils.

Figure 2. Approximate Strain Level Ranges for the Dynamic Property Testing of Soils.

Figure 3. Resonant column apparatus and direct simple shear test.

Figure 3. Resonant column apparatus and direct simple shear test.

To determine the damping ratio of silty clay at medium and high strains, a series of symmetric and asymmetric cyclic direct simple shear tests (DSScy) were conducted to simulate wave loading. The cyclic loading period was set to 10 seconds per cycle. Initial undrained static direct simple shear tests (DSS) were performed to provide undrained shear strength parameters for the corresponding cyclic direct simple shear tests. Both the static direct simple shear tests and the corresponding cyclic direct simple shear tests used the same consolidation stress and consolidation procedure to ensure consistent consolidation conditions. The cyclic direct simple shear tests were terminated once the cyclic shear strain (γ_cy) or average shear strain (γ_a) reached 15%, whichever occurred first. If the test reached 1,500 cycles without meeting the termination criteria, the test was stopped, refer to Figure 4 for the schematic representation of the stress and strain components.

Table 2 summarizes the applied loads and soil properties for the different tests conducted in this study. The overconsolidated silty clay sample, taken from a depth of 16-17 meters, was found to have an average in-situ effective vertical stress of σ_a’ =119kPa. A consolidation undrained static shear test was performed on the natural sample of this overconsolidated silty clay, with the effective consolidation stress set to match the in-situ effective vertical stress. The resulting stress-strain curve is shown in Figure 5, from which the undrained shear strength (s_u^DSS) of the soil at this consolidation stress was determined to be 52.4 kPa. Based on the undrained shear strength obtained from the static shear test, consolidation undrained cyclic shear tests were designed and conducted. The vertical effective consolidation stress was maintained at 119 kPa throughout the tests. The cyclic stress conditions for these tests were as follows: when the normalized average shear stress (τ_a/σ_a’) was 0 (representing symmetric cyclic loading, as shown in Figure 8), the normalized cyclic shear stress (τ_cy/σ_a’) was varied at values of 0.15, 0.22, 0.26, 0.30, and 0.36. In the case of asymmetric cyclic loading (with a normalized average shear stress τ_a/σ_a’ of 0.18 , as shown in Figure 9), the normalized cyclic shear stress τ_cy/σ_a’ was set to 0.15, 0.21, and 0.22 for the cyclic shear tests.

For the normally consolidated silty clay tests (soil depth 17-18m), the average in-situ effective vertical stress was calculated to be σ_a’ = 126.5kPa. Since the soil sample had an overconsolidation ratio (OCR ≈ 2), the SHANSEP method was applied, consolidating the soil sample to four times its original effective vertical stress, i.e., 506 kPa, to ensure that the sample reached a normally consolidated state (OCR = 1). An undrained static direct simple shear test was performed, and the stress-strain curve is shown in Figure 2. The undrained shear strength (s_u^DSS) of the soil layer under the consolidation stress was found to be 140 kPa. Based on the results of the static direct simple shear test, undrained cyclic direct simple shear tests were designed and conducted. The vertical effective consolidation stress was maintained at 506 kPa. The tests were conducted under symmetric cyclic conditions (with normalized average shear stress τ_a/σ_a’=0), as shown in Figure 10. Normalized cyclic shear stresses (τ_cy/σ_a’) of 0.14, 0.17, 0.19, 0.22, and 0.25 were used.

To determine the damping ratio of silty clay at low strains, GDS resonant column tests were conducted. The resonant column tests employed isotropic consolidation, with the consolidation stress set to the effective consolidation mean stress, which corresponds to the cyclic direct simple shear tests. The coefficient of earth pressure at rest (K0) for the silty clay layer was estimated to be 0.6, resulting in a consolidation confining pressure of 87.3 kPa for the 16–17 meter deep silty clay layer and 371.1 kPa for the 17-18 meter deep layer in the resonant column tests.

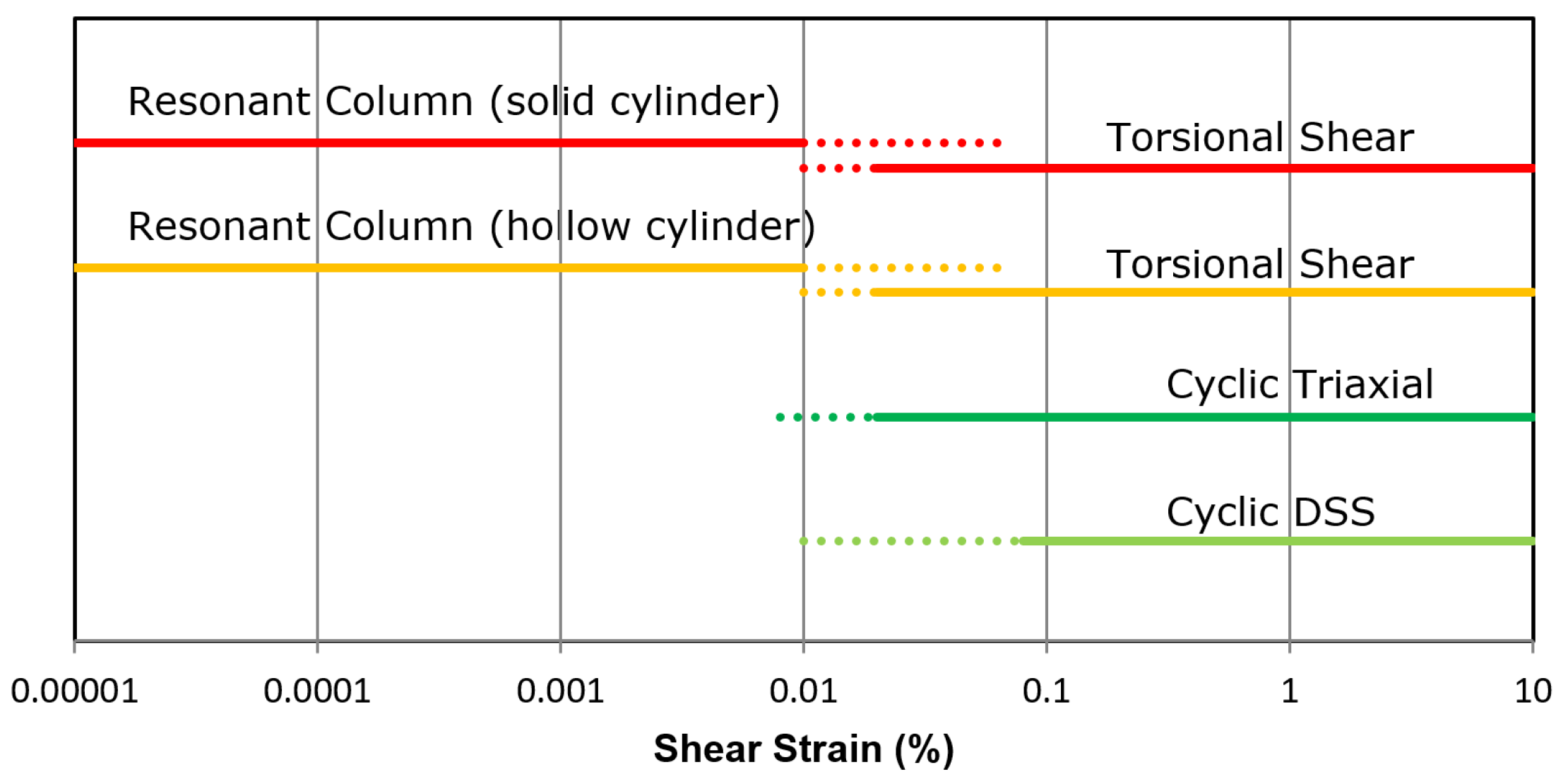
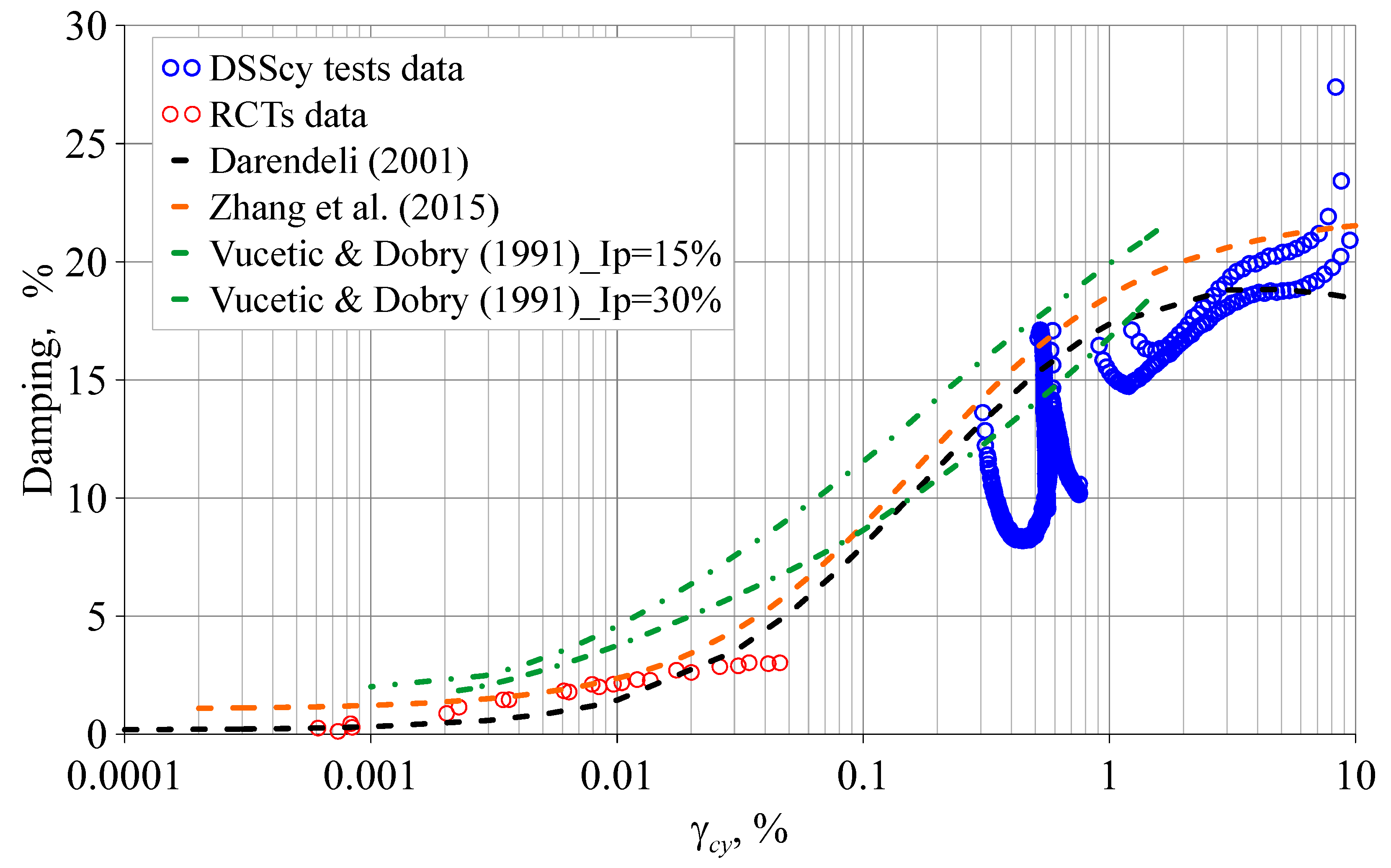
3. Results and Analysis

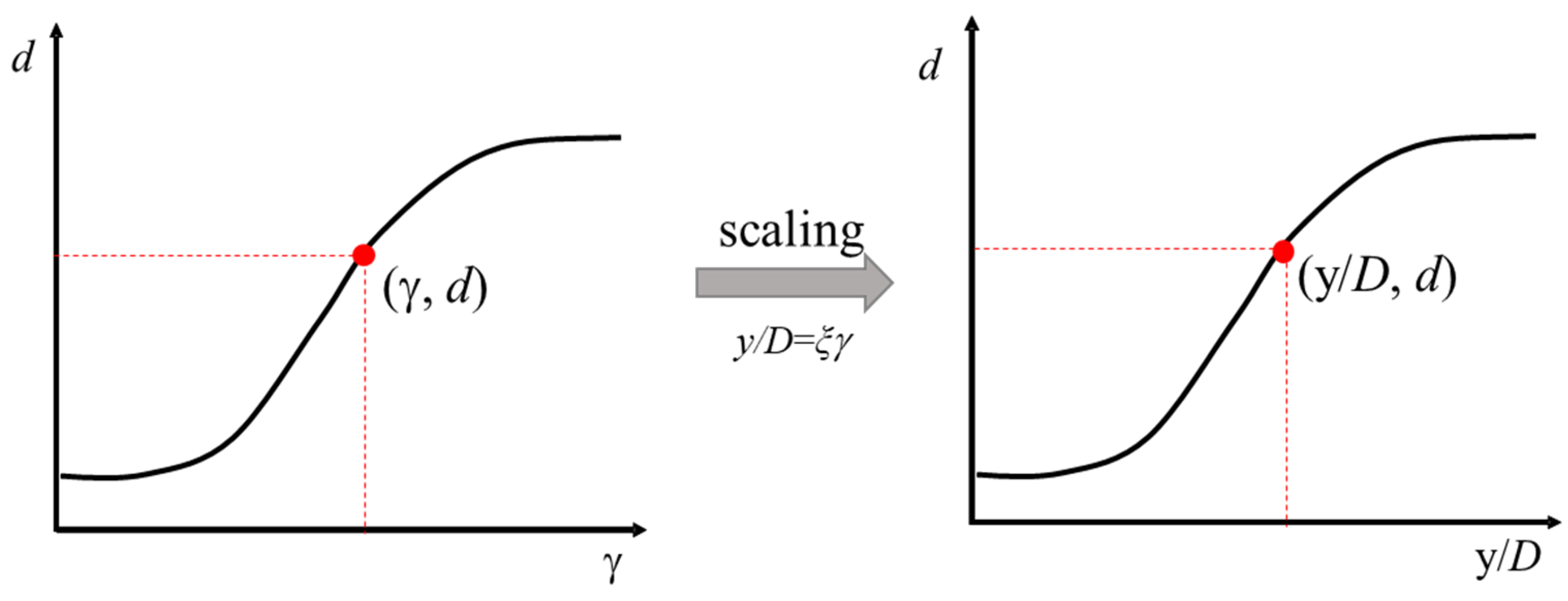
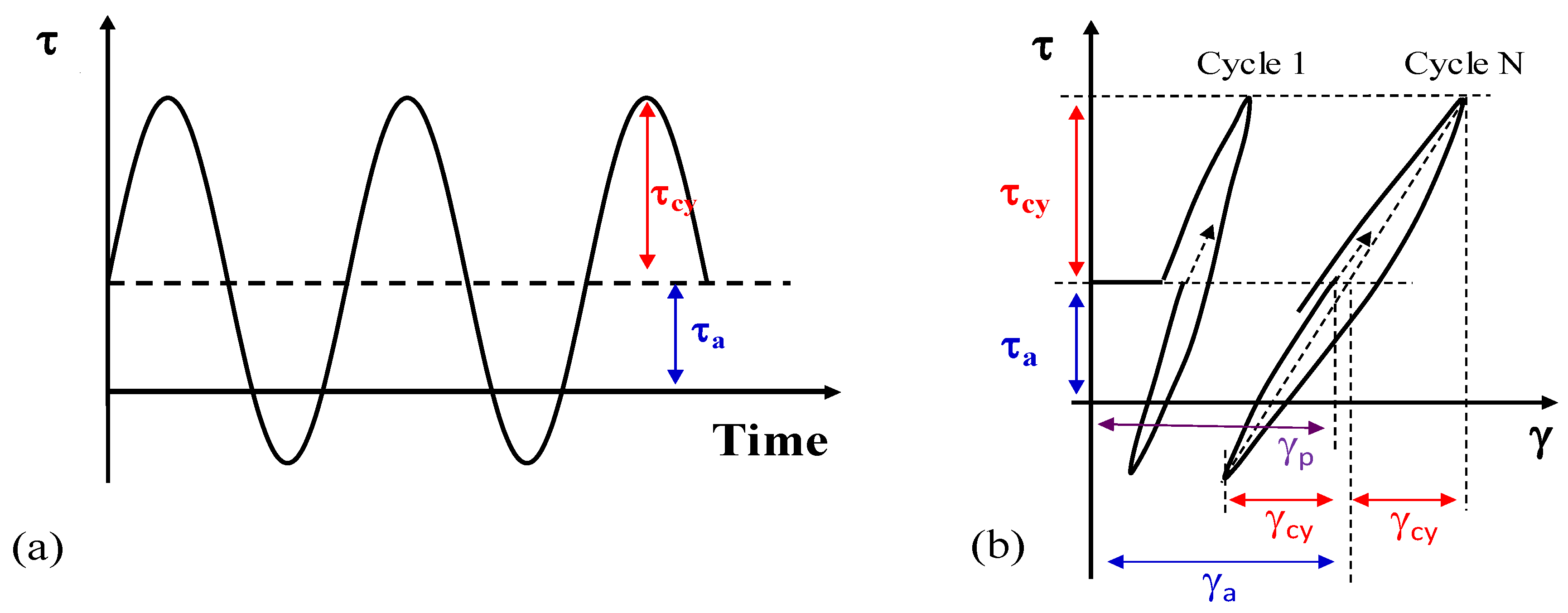
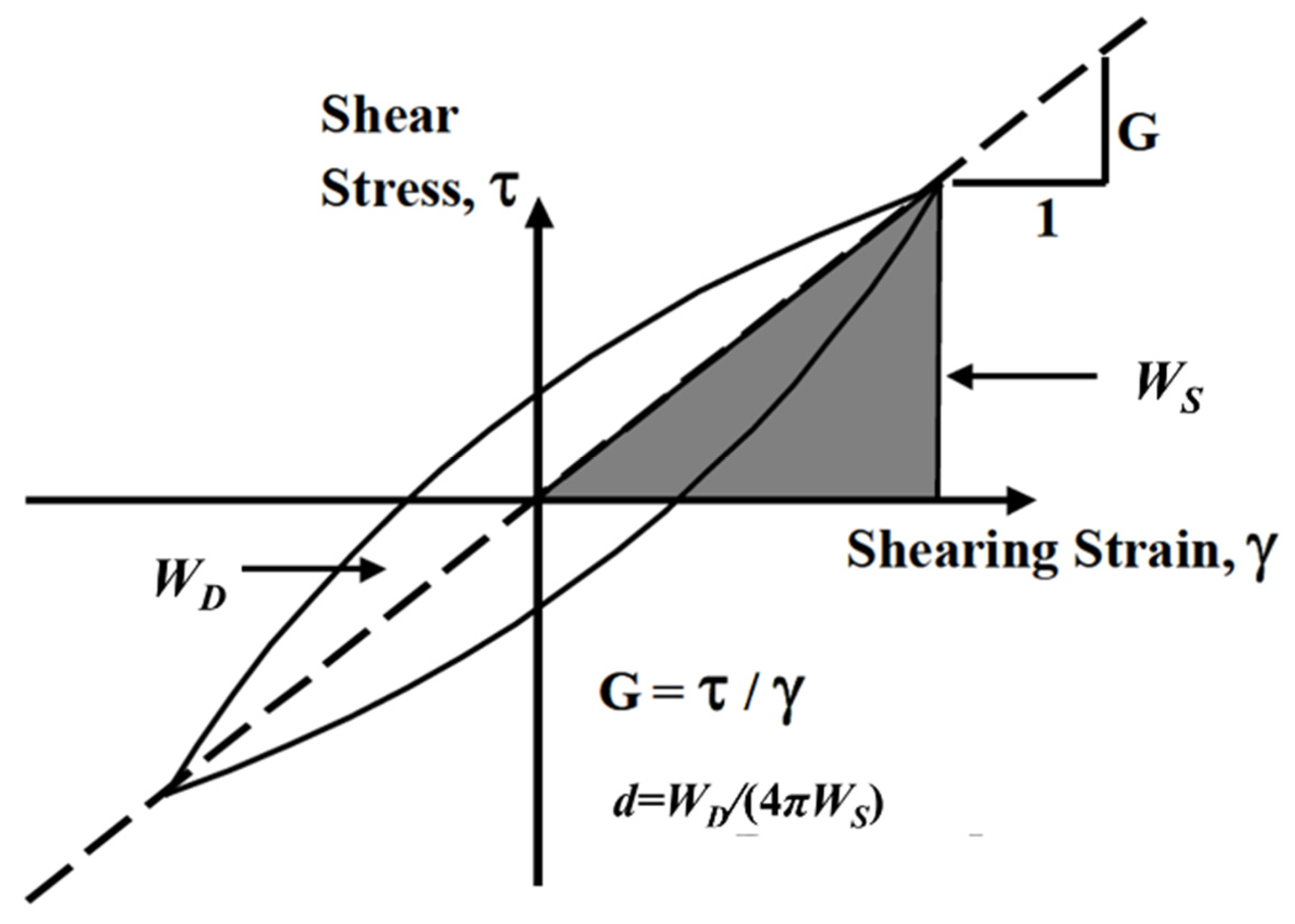
3.1. Damping Ratio Calculation Method

The viscous damping ratio D (%) obtained from the resonant column test is derived from the free vibration decay curve. This curve is measured by an accelerometer mounted on the drive plate of the resonant column. A sinusoidal wave is applied to the soil, after which the excitation is stopped, and the results of the free vibration are measured.

As shown in Figure 8, the damping ratio D (%) from cyclic direct simple shear tests is calculated based on the dissipated energy W_D and total input energy W_s over one cycle. The relevant equations are as follows:

$$D={\displaystyle \frac{1}{4\pi }}{\displaystyle \frac{W_D}{W_S}}$$

(1)

$$W_D={\displaystyle \oint ({\tau }_{cy})({\gamma }_{cy})}d\gamma$$

(2)

$$W_S={\displaystyle \frac{1}{2}}{\tau }_{cy}{\gamma }_{cy}$$

(3)

For cyclic direct simple shear tests under symmetric loading, the damping ratio is directly calculated using Equation (1). In cases with asymmetric loading (i.e., with a nonzero average shear stress), cumulative strain develops during cycling, causing the stress-strain hysteresis loops to remain open. In this study, we processed the test data using Equation (4) [25], and Figure 7 shows the resulting curves. Once the stress-strain hysteresis loops are obtained via this method, Equation (1) is used to calculate the damping ratio.

$${\gamma }_{i,c}={\gamma }_{i,o}-{\displaystyle \frac{i}{n}}\Delta {\gamma }_p$$

(4)

In the equation, γ_i,c is the strain data after processing, γ_i,o is the raw (original) strain data, n is the number of data points in the current cycle, and Δγ_p is the accumulated shear strain generated during that cycle.

Figure 7. Illustration of Hysteresis Loop Processing under Asymmetric Cyclic Loading.

Figure 7. Illustration of Hysteresis Loop Processing under Asymmetric Cyclic Loading.

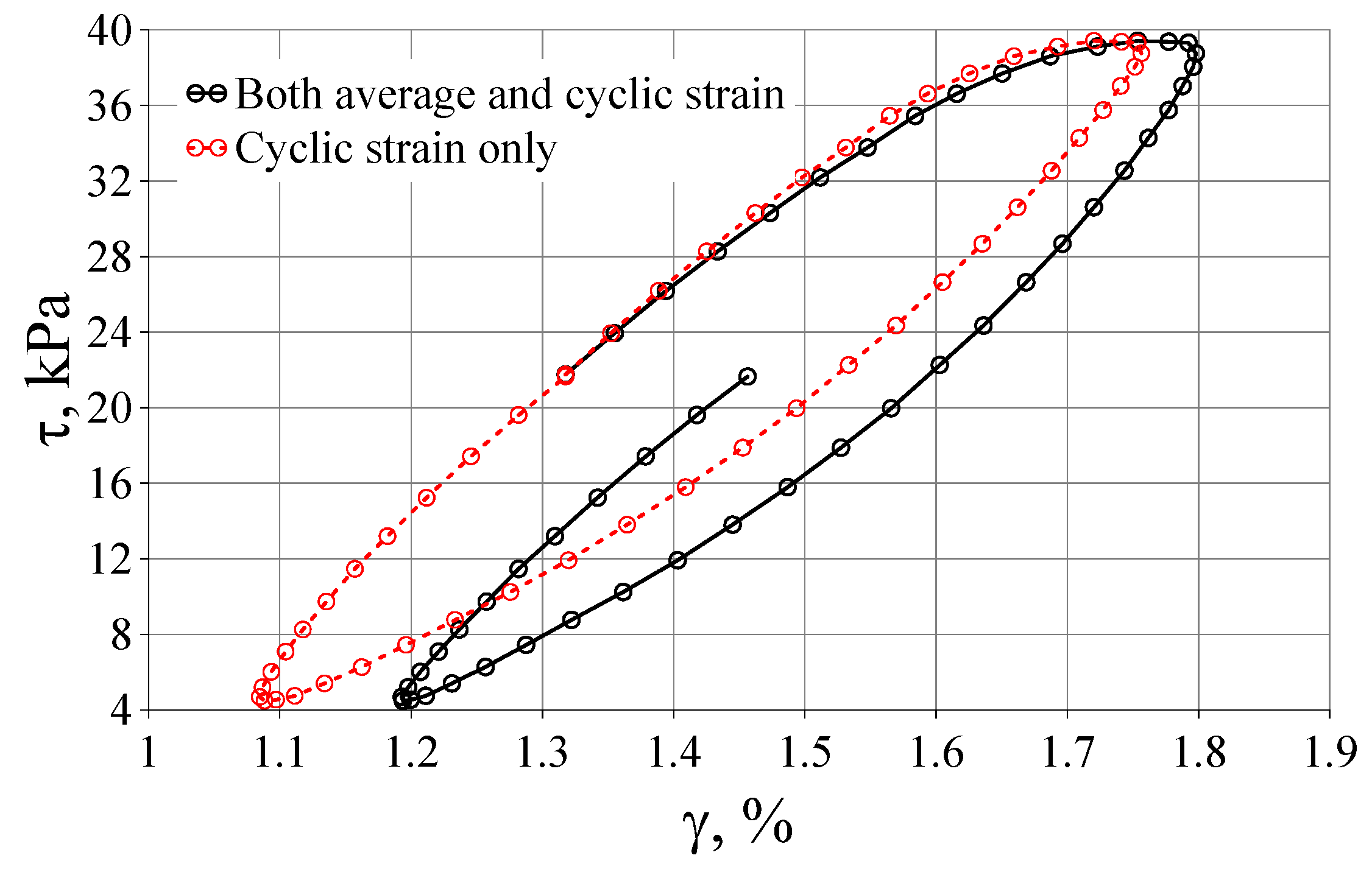
3.2. The Influence of Initial Deviatoric Stress and Cyclic Stress History

Figure 8 and Figure 9 present the stress-strain curves and damping ratio-cyclic shear strain curves for over-consolidated silt clay under symmetrical and asymmetrical loading, respectively. The influence of cyclic stress history on the damping ratio is significant; when the initial deviatoric stress is zero, the development of the damping ratio generally exhibits three stages: an initial decrease, followed by an increase, and subsequently another decrease. In comparing Figure 8 and Figure 9, it is evident that the presence of initial deviatoric stress significantly influences the damping ratio. This initial stress leads to a larger damping ratio at the same cyclic shear strain.

Figure 8. Stress-strain and damping curve under symmetric cyclic loading for overconsolidated silty clay.

Figure 8. Stress-strain and damping curve under symmetric cyclic loading for overconsolidated silty clay.

Figure 9. Stress-strain and damping curve under asymmetric cyclic loading for overconsolidated silty clay.

Figure 9. Stress-strain and damping curve under asymmetric cyclic loading for overconsolidated silty clay.

Figure 10 shows the stress-strain curves and damping ratio-cyclic shear strain curves for normally consolidated silt clay under symmetrical loading. Unlike the behavior observed in over-consolidated clay, the development of the damping ratio for normally consolidated silt clay generally exhibits two stages: an initial decrease followed by an increase. It is important to note that, due to the limited number of undisturbed samples, the impact of cyclic stress history on the damping ratio of silt clay can only be qualitatively described in this study.

Figure 10. Stress-strain and damping curve under asymmetric cyclic loading for normally consolidated silty clay.

Figure 10. Stress-strain and damping curve under asymmetric cyclic loading for normally consolidated silty clay.

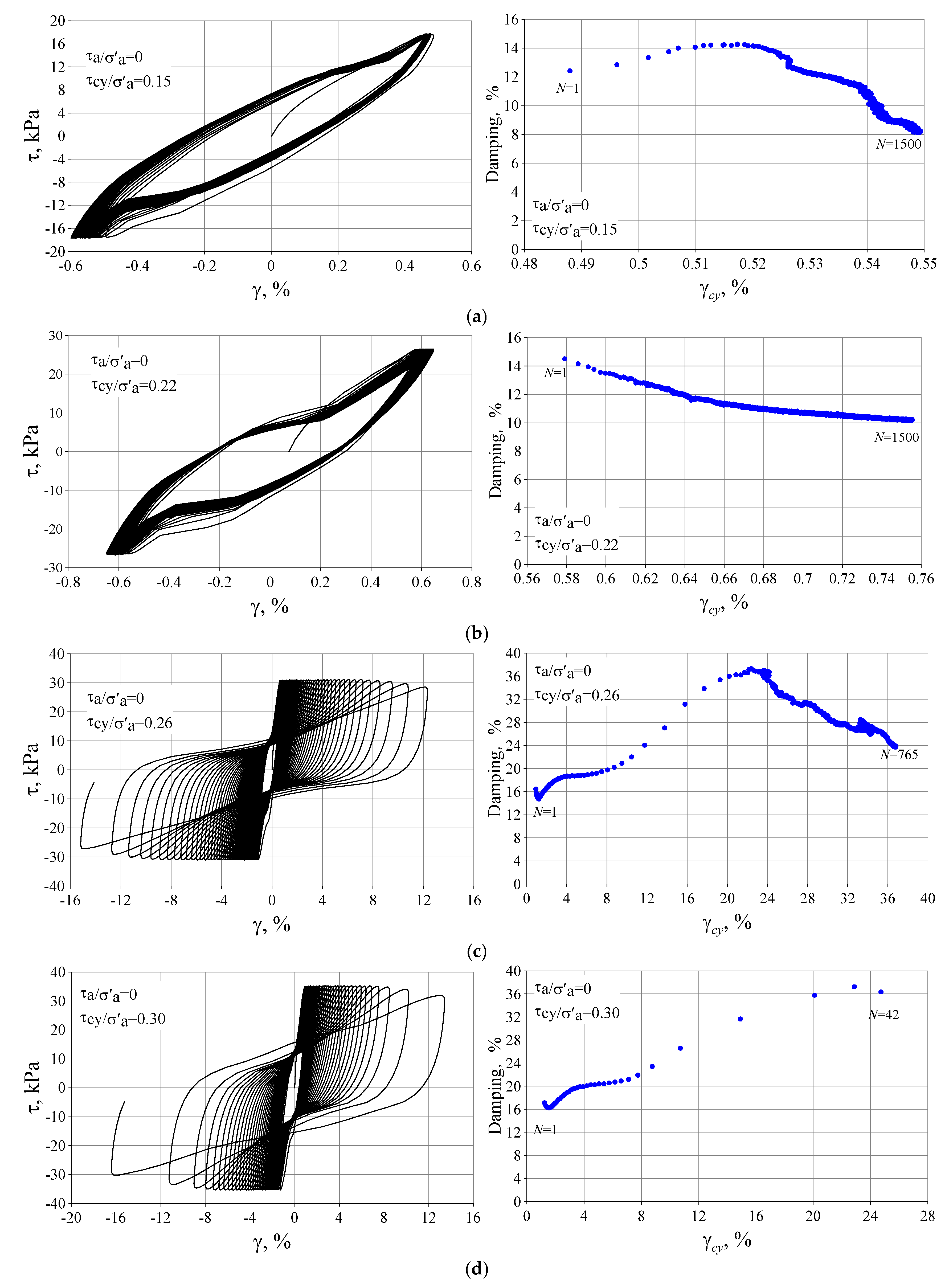
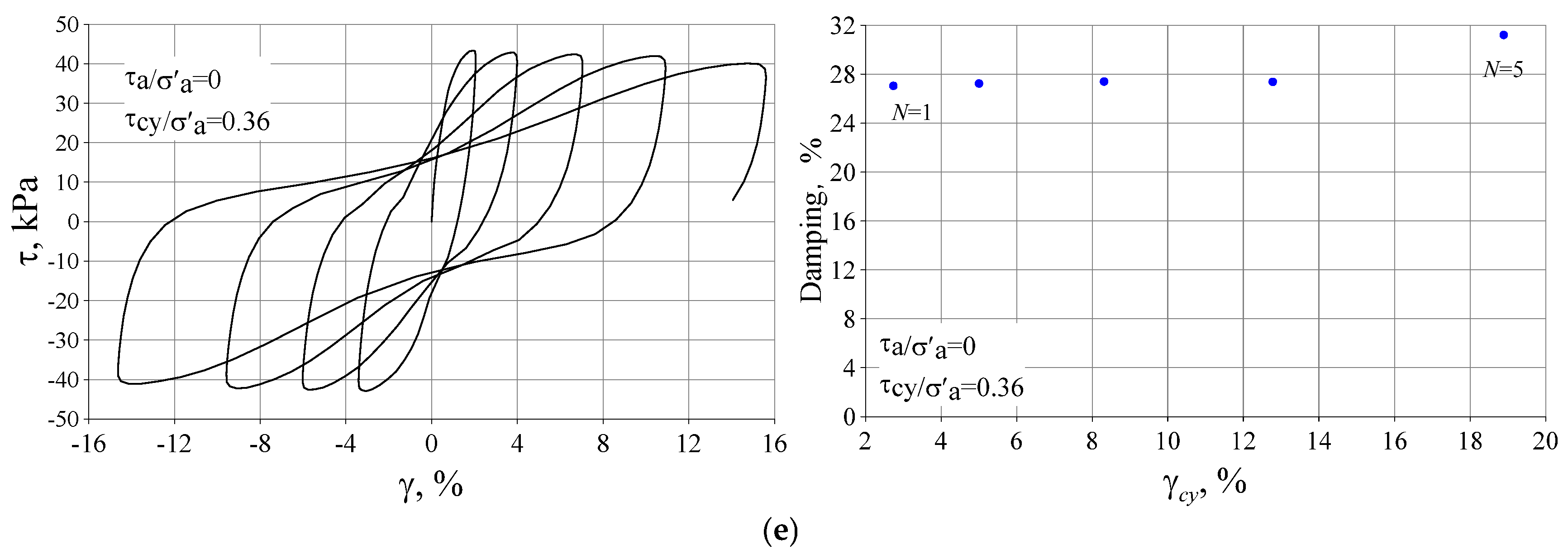
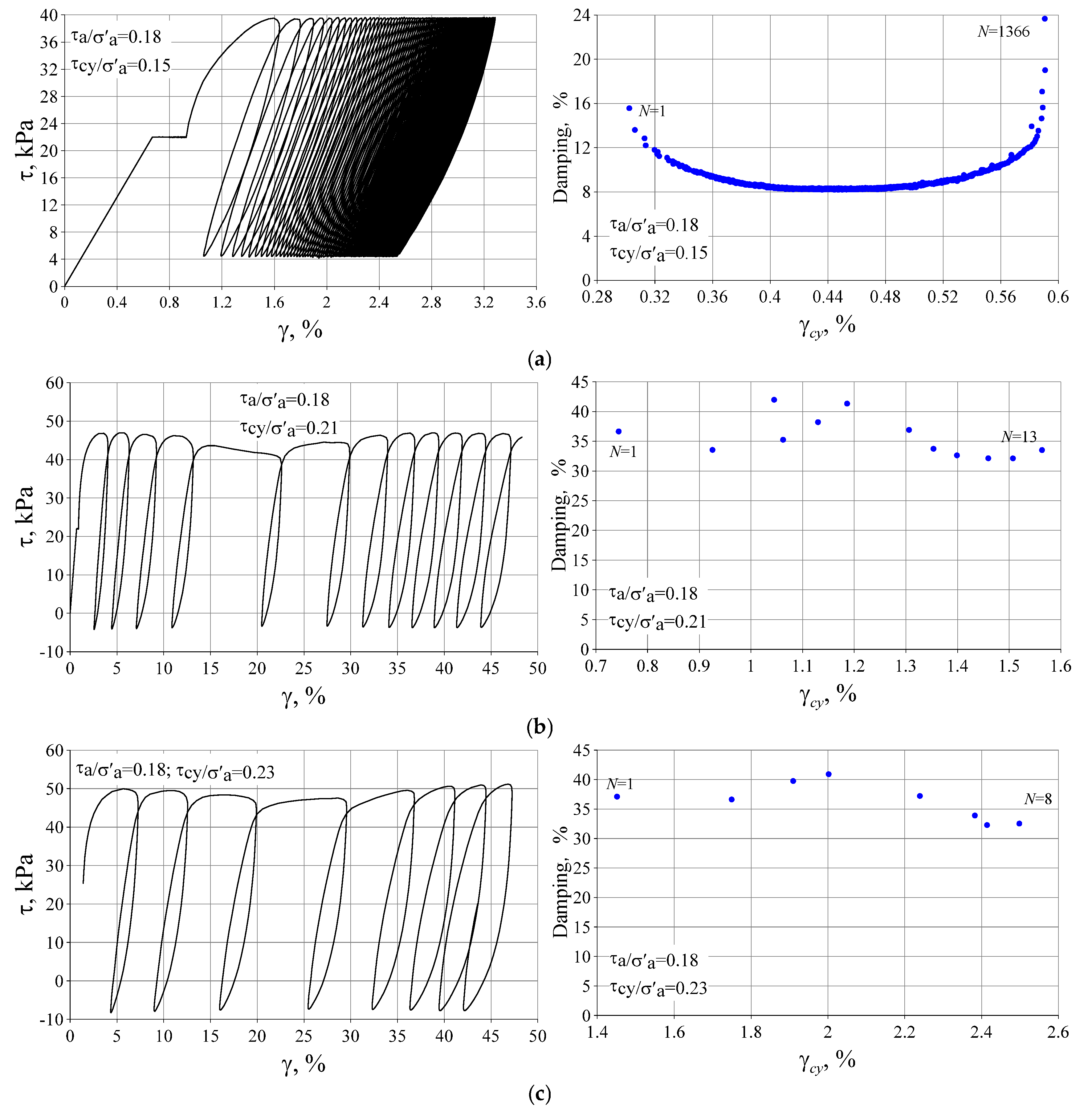
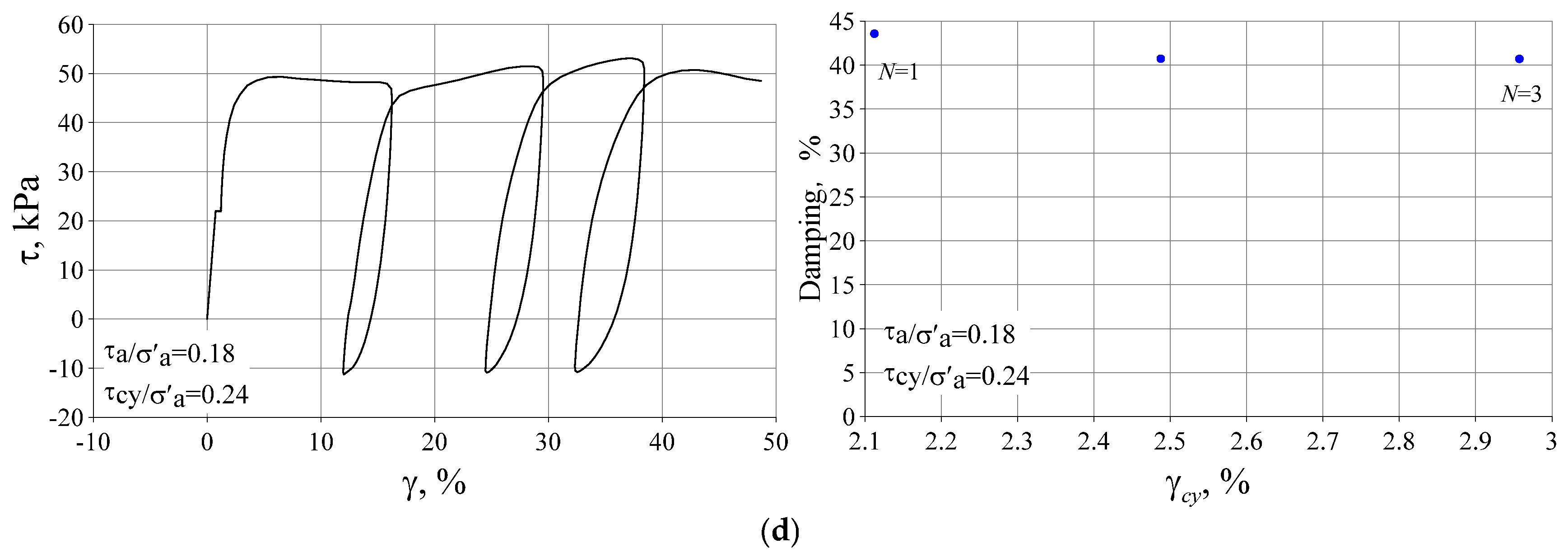
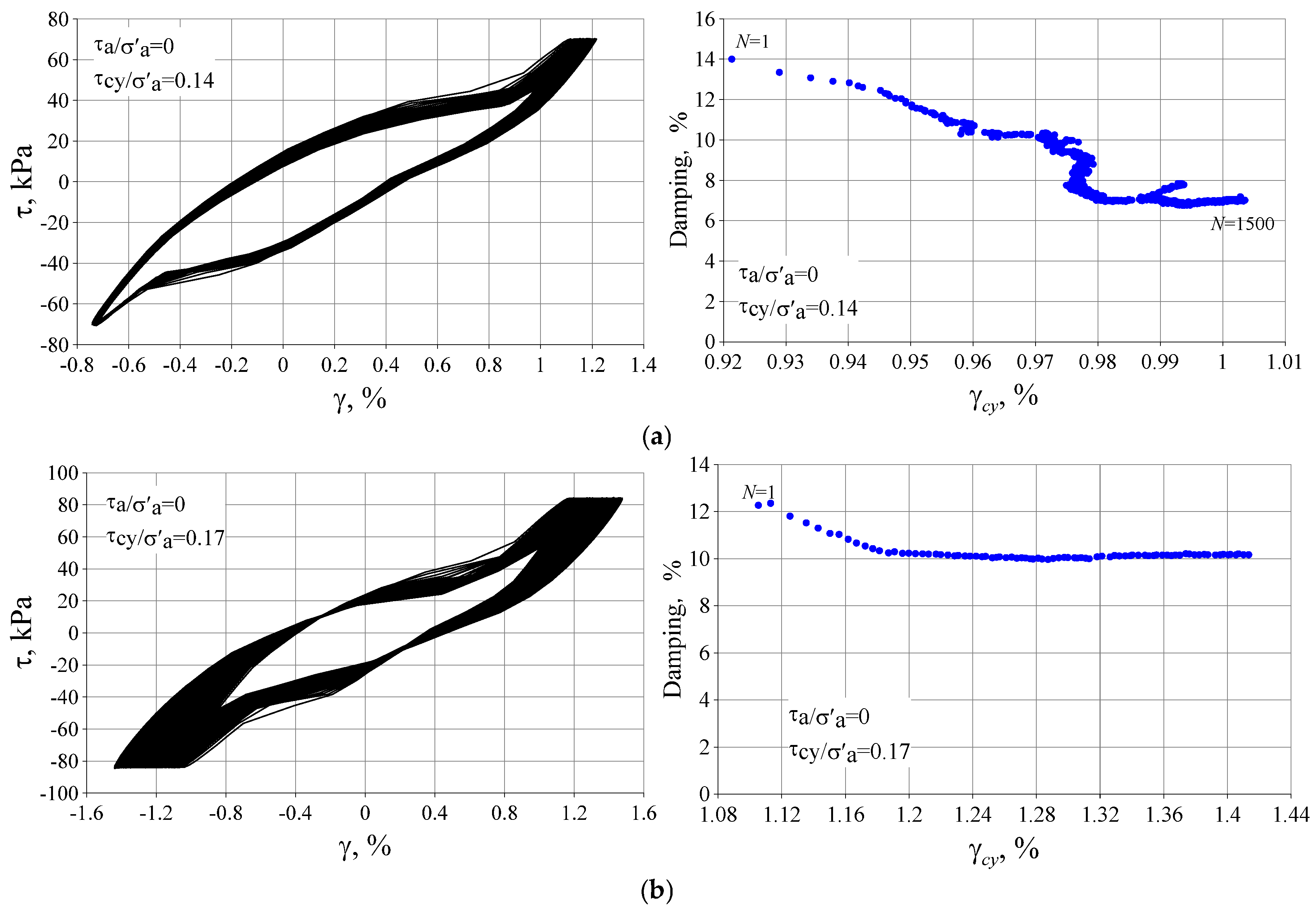
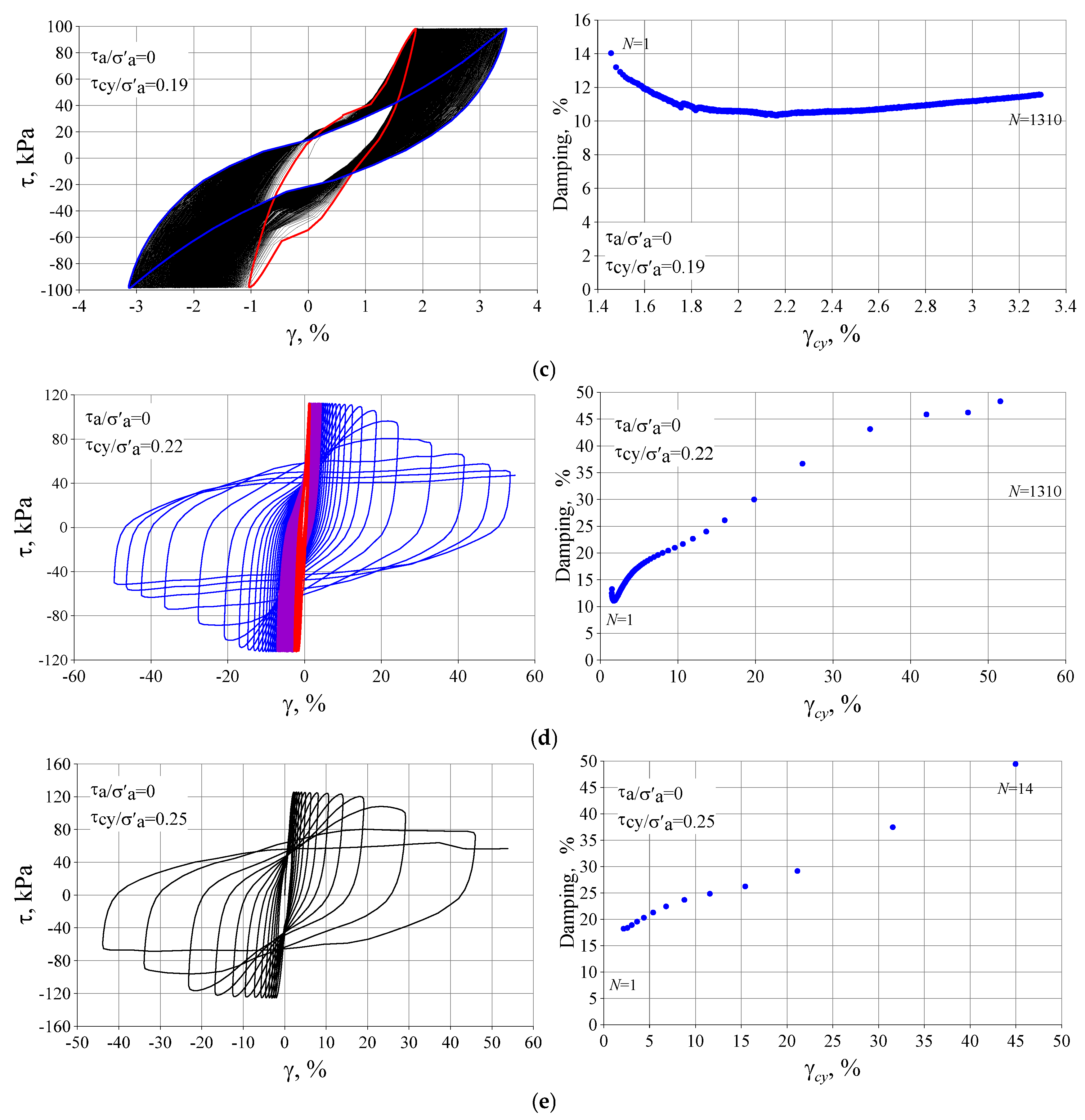
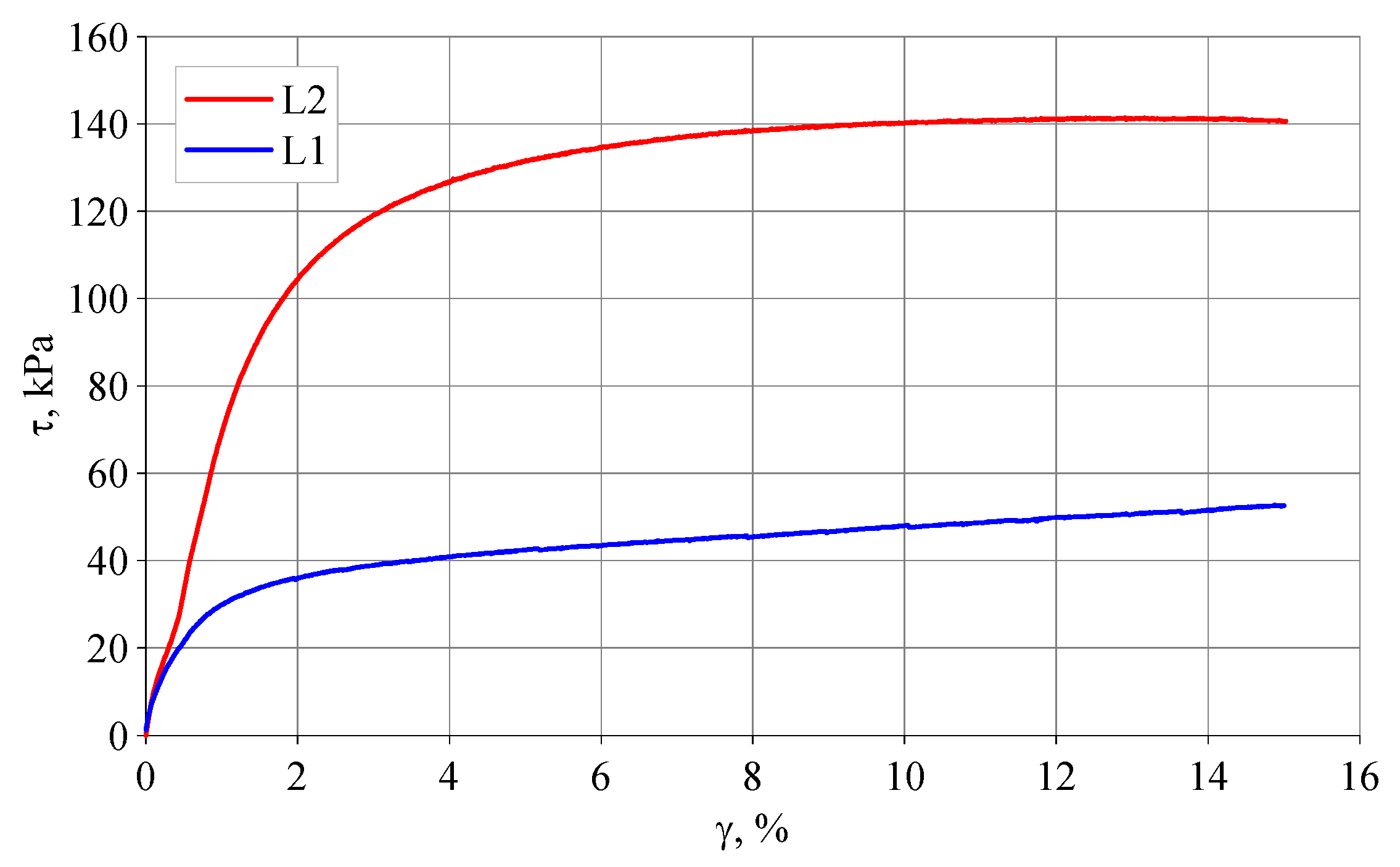
3.3. Damping Ratios of Silty Clay

To investigate the damping characteristics of cohesive soils, we compared our experimental results with the empirical models proposed by Vucetic and Dobry [26], Derendeli [15], and Zhang et al. [16]. Vucetic and Dobry [26], based on extensive testing, observed that the overconsolidation ratio (OCR) of clays has a limited impact on damping ratios under certain conditions. The primary controlling factors are cyclic shear strain (γ_cy) and plasticity index (Ip). They proposed damping ratio curves for clays with different plasticity indices, which are recommended by the DNV (2021) guidelines [27]. Derendeli [15] developed a four-parameter damping ratio model-reference strain, curvature coefficient, small-strain damping ratio, and scaling factor-for various soil types based on extensive geotechnical testing, which is widely utilized in seismic engineering analyses. Similarly, Zhang et al. [16], in agreement with Vucetic and Dobry [26], suggested that OCR has only a minor influence on the damping ratio within a certain range. They proposed an empirical damping model for cohesive soils, accounting for plasticity index and consolidation stress, while omitting the effect of OCR on the damping curve.

Figure 11 and Figure 12 compare the experimental damping ratios for overconsolidated and normally consolidated silty clay with predictions from these empirical models. The overconsolidated silty clay at 16-17 m depth has a plasticity index (I_p) of 26.6%, and the normally consolidated silty clay at 17-18 m has an I_p of 20.9%. As shown in Figure 10 and Figure 11, for the Vucetic and Dobry [21] model, the damping ratios obtained from both the resonant column and cyclic direct simple shear tests are lower than those predicted by the empirical model. Similarly, applying the average effective confining pressure, plasticity index, overconsolidation ratio, equivalent number of cycles, and cyclic loading frequency from this study to Darendeli’s empirical model [14] yields predicted damping ratio curves. Comparing these with the test data shows that for both silty clay layers (16-17 m and 17-18 m), the resonant column results (i.e., at low cyclic strain levels) generally align well with the predictions of Darendeli’s empirical model, while the cyclic direct simple shear test results (at medium-to-high strain levels) yield lower damping ratios than the model predicts. Using the empirical clay model proposed by Zhang et al. [16] to predict damping in both silty clay layers (16-17 m and 17-18 m) and comparing with the test data reveals that the Zhang et al. [16] predictions are broadly similar to Darendeli’s empirical model [14]. While the model accurately predicts damping ratios at low strain levels, it overestimates damping at medium-to-high strains. Overall, all three empirical damping models tend to overestimate the damping of silty clay at medium-to-high strain levels.

4. Conclusion

(1) Soil-pile interaction damping plays a significant role in reducing loads on offshore wind turbine structures, and the soil-element damping ratio is fundamental for studying this interaction. Silty clay, which is widely distributed along China’s coastline, is an important soil type. However, current research on soil damping has primarily focused on clay and sand, with relatively little attention given to silty soils. Therefore, targeted studies on the damping ratio of typical silty clay are essential for optimizing offshore wind power designs in China.

(2) The damping ratio–cyclic shear strain curve for silty clay exhibits an “S” shape, and the damping behaviors of both overconsolidated and normally consolidated silty clay are nearly identical. The influence of cyclic stress history on the damping ratio is significant.

(3) Currently, no empirical model accurately predicts the damping ratio of silty clay across the entire range of low to high strains. While the Darendeli and Zhang et al. models provide relatively accurate predictions at low strain levels, they tend to overestimate the damping of silty clay at medium to high strains. This limitation should be considered when empirical models are used in practical engineering applications in place of test data.

(4) Given the significant challenges and high costs associated with obtaining undisturbed silty clay samples, this study is not exhaustive and does not encompass parametric or mechanistic analyses. Future research should aim to further investigate the damping characteristics of silty clay and silty sand, with the objective of developing a universal empirical damping ratio model for typical silty soils in China. Such a model would have substantial implications for offshore seismic engineering and the optimization of offshore wind power designs.