Submitted:
28 March 2025
Posted:
29 March 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Definitions and Theorem
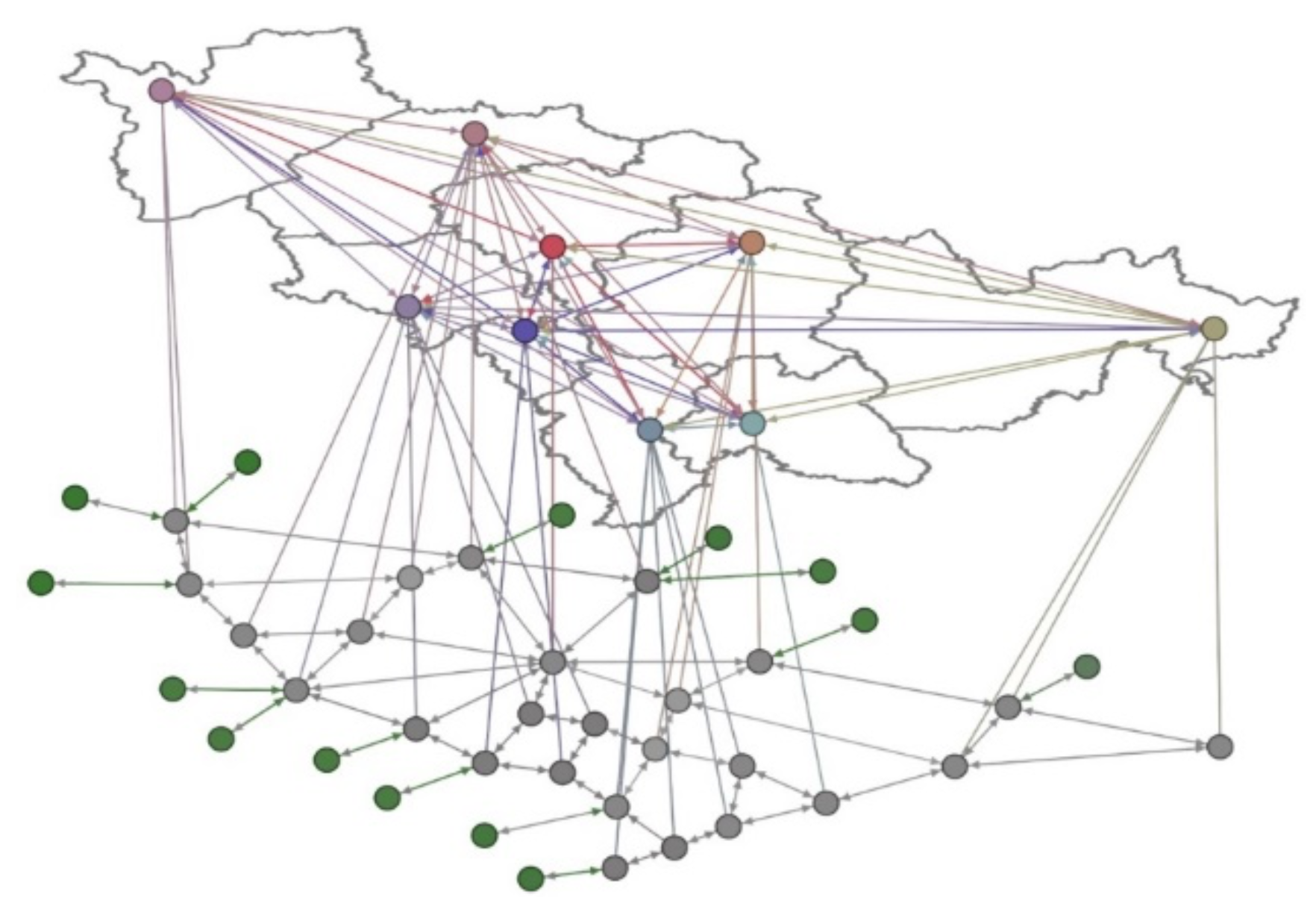
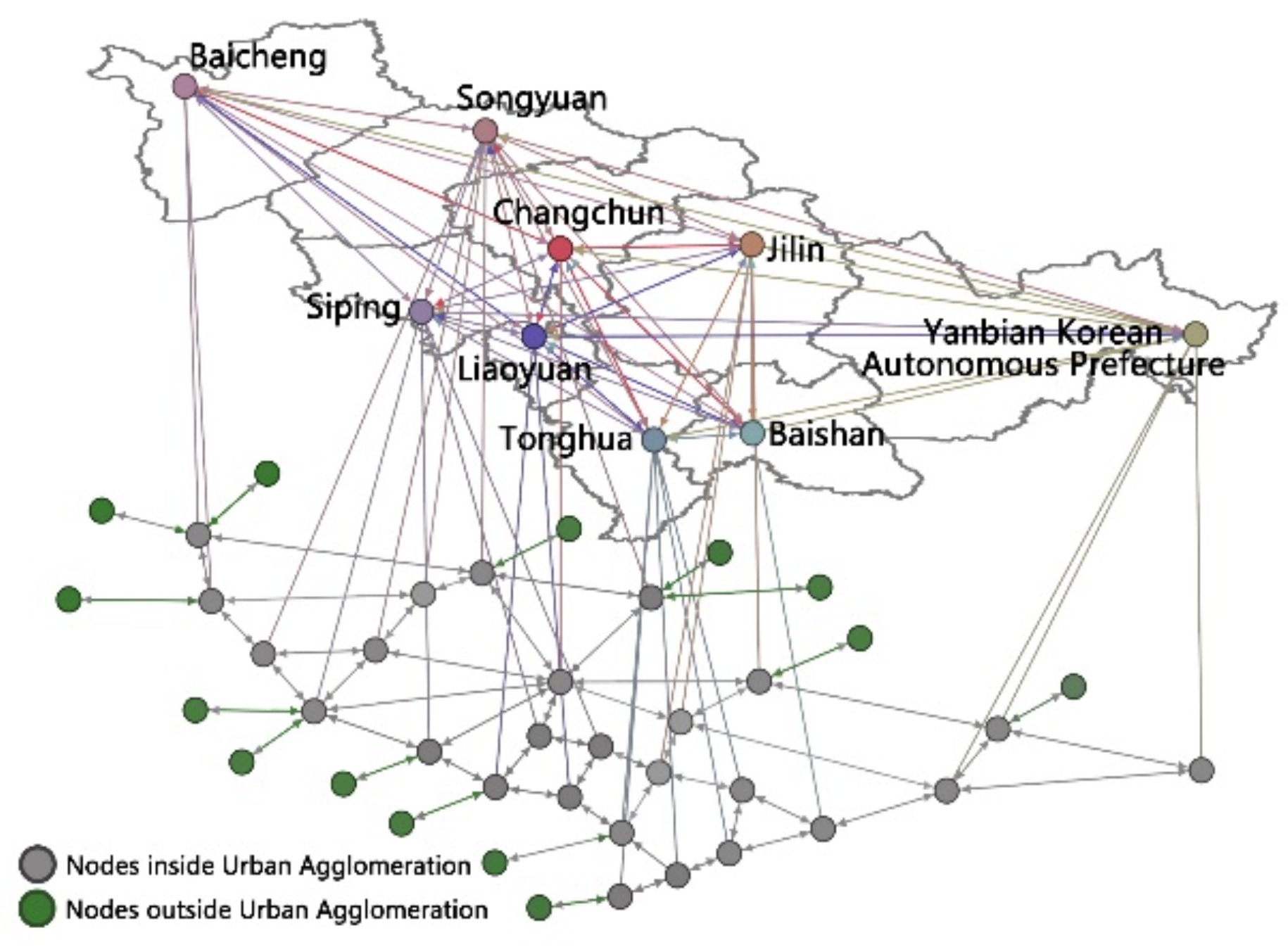
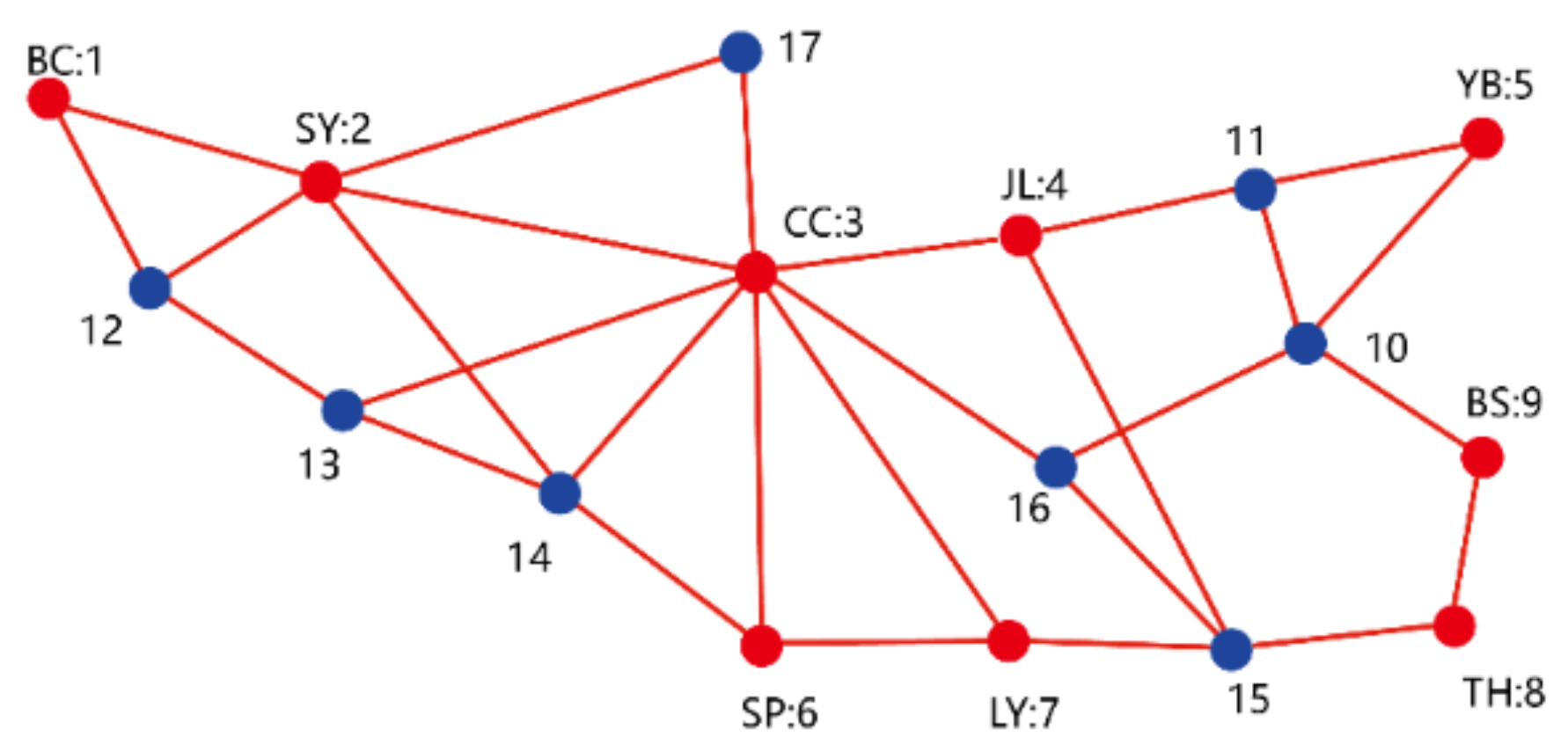
3. Double-Layer Complex Network Model
3.1. Single-Layer Transportation Network Model
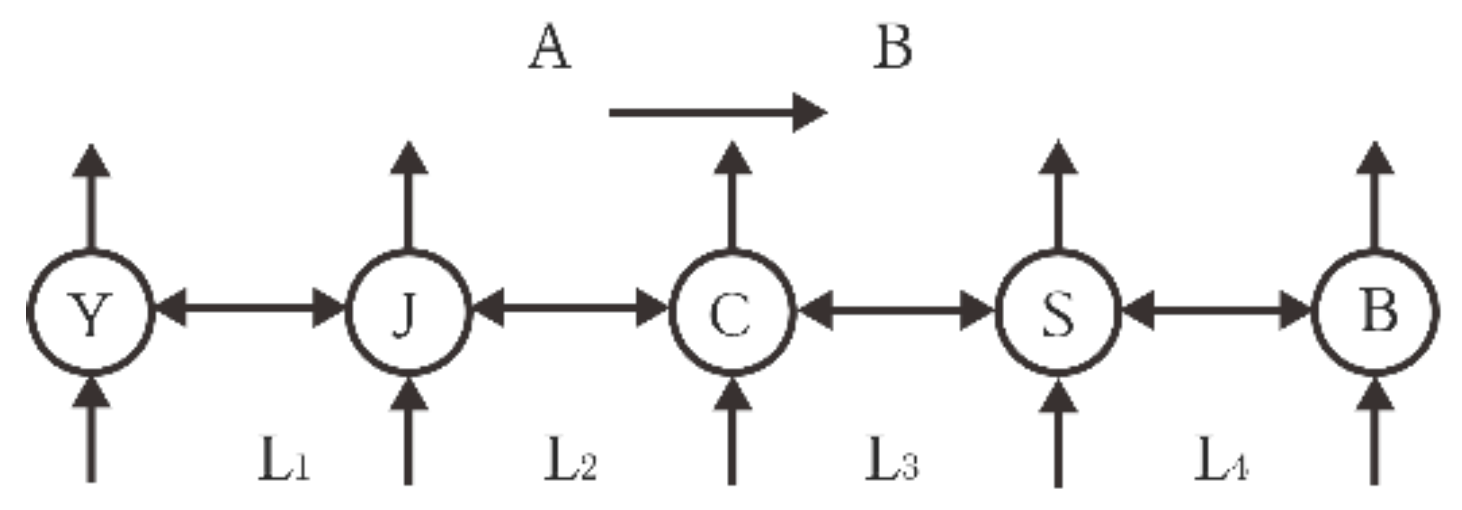
3.1.1. Urban Agglomeration Transportation Network Model (GU)
3.1.2. Expressway Transportation Network Model (GU)
3.2. Double-Layer Complex Network
4. Transportation Volume Regulation Model
4.1. Objective Function and Constraint Conditions
4.1.1. Constraint Conditions of the Upper Layer Network
4.1.2. Constraint Conditions of the Lower Layer Network
4.2. Solving Method for the Objective Function
- Step2.
- Calculate initial weights (), the max weights (), and weight change ();
- Step3.
- Calculate the updated weight () and value of the objective function (;
- Step4.
-
Determine whether the iteration end conditions ((40) and (41)) are satisfied.Yes, go to next step;No, go to Step3;
- Step5.
- End the iteration and output the result.
4.3. Regulation and Correction of Transportation Volume Based on Lower Layer Constraints
5. Case Analysis and Simulation
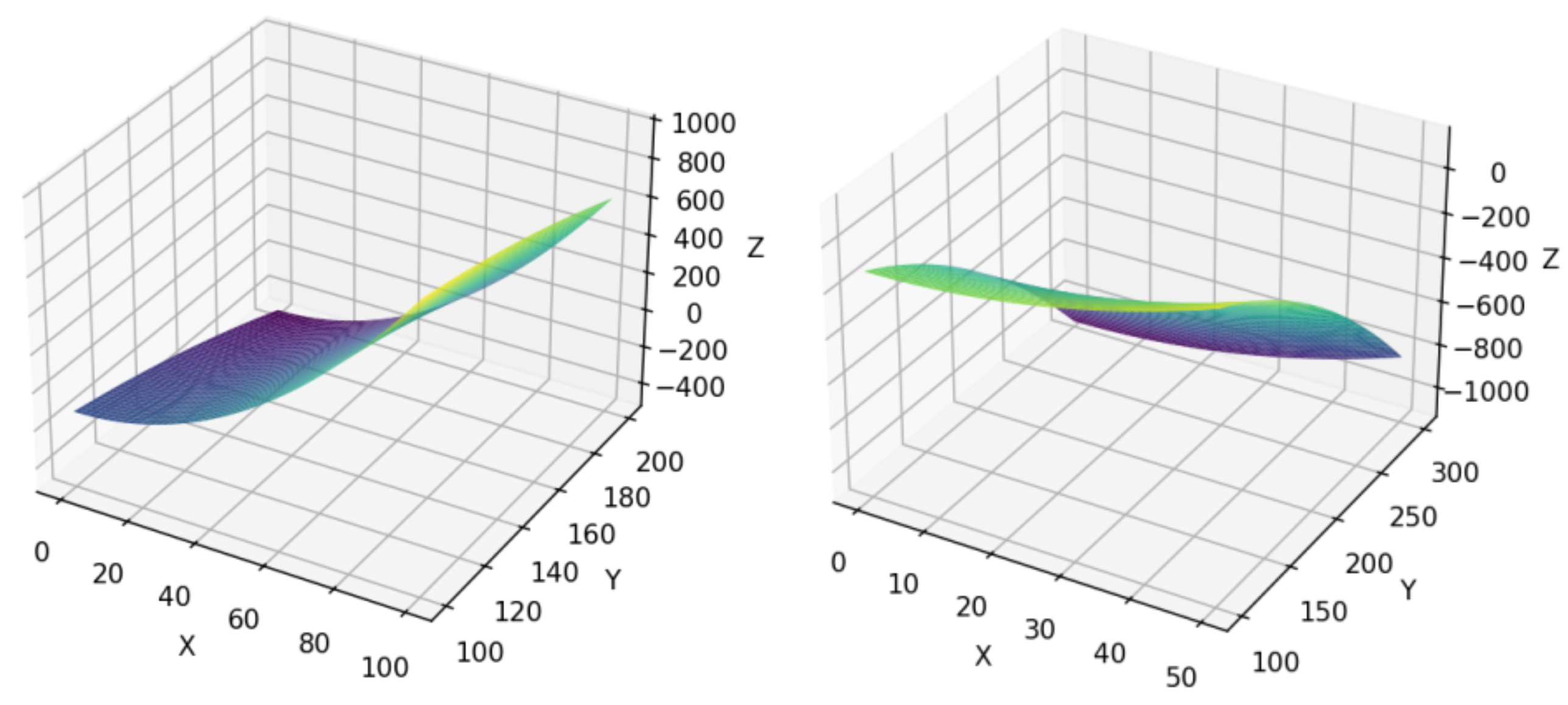
5.1. Transportation Volume Allocation Between Cities


5.2. Regulation of Transportation Volume Based on Lower Layer Constraints
| Forward road segment(A-B) | Reverse road segment(B-A) | |||||||
|---|---|---|---|---|---|---|---|---|
| Name | ||||||||
| 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | |
| Current speed | 90 Km/h |
66 Km/h |
90 Km/h |
90 Km/h |
90 Km/h |
90 Km/h |
80 Km/h |
90 Km/h |
| Estimated cars | 38 | 130 | 86 | 45 | 73 | 68 | 110 | 61 |
| New cars | 90 | 225 | 267 | 32 | 171 | 112 | 287 | 64 |
| Estimated | 0.32 | 0.82 | 0.82 | 0 | 0.69 | 0.54 | 0.86 | 0.29 |
| regulation | No | Yes | Yes | No | No | No | Yes | No |
| Regulated volume | 0 | -105 | -103 | 0 | 0 | 0 | -147 | 0 |
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wang, S, Q. Regulation Strategy of Coordinated Development and Collaborative Transportation for Urban Agglomeration Based on Highway Transportation. Jilin University in China, 2024.
- Wang, S, Q, Wang, Z. Z. Collaborative Development and Transportation Volume Regulation Strategy for an Urban Agglomeration. Sustainability, 2023(20): 14742.
- Song, J.T., Fang, C. L, Song, D. J. Stability analysis of the spatial structure of Chinese urban agglomeration. Acta Geographica Sinica, 2006, 61(12): 1311–1325.
- Fang, C. L., Qi, W. F., Song, J. T. Comprehensive measurement analysis of the compactness of Chinese urban agglomeration. Acta Geographica Sinica, 2008, 63(10): 1011–1021.
- Fang, C. L, Song,J. T, Lin, X. Q. Theory and practice of China’s sustainable urbanization. Beijing: Science Press, 2010, 56–89.
- Xiong, G.; Chen, X.; Shuo, N.; Lv, Y.; Zhu, F.; Qu, T.; Ye, P. Collaborative Optimization of Cyber Physical Social Systems for Urban Transportation Based on Knowledge Automation. IFAC-PapersOnLine 2020, 53, 572–577. [Google Scholar] [CrossRef]
- Li, F.; Guo, X.; Zhou, L.; Wu, J.; Li, T. A capacity matching model in a collaborative urban public transport system: integrating passenger and freight transportation. Int. J. Prod. Res. 2022, 60, 6303–6328. [Google Scholar] [CrossRef]
- Melo, P.C.; Graham, D.J. Transport-induced agglomeration effects: Evidence for US metropolitan areas. Reg. Sci. Policy Pr. 2018, 10, 37–48. [Google Scholar] [CrossRef]
- Wei, G.; Li, X.; Yu, M.; Lu, G.; Chen, Z. The Impact of Land Transportation Integration on Service Agglomeration in Yangtze River Delta Urban Agglomeration. Sustainability 2022, 14, 12580. [Google Scholar] [CrossRef]
- Rong, C. H. From Transport Development to Sustainable Transport. China Railway Science, 2001, 22 (3): 1-8.
- Luo, R. J. Development Ideas of Modern Integrated Transport System in China. China Transportation Review, 2004, 1: 22-25.
- Badada, B.; Delina, G.; Baiqing, S.; Krishnaraj, R. Economic Impact of Transport Infrastructure in Ethiopia: The Role of Foreign Direct Investment. SAGE Open 2023, 13. [Google Scholar] [CrossRef]
- Banerjee, A.V.; Duflo, E.; Qian, N. On the road: Access to transportation infrastructure and economic growth in China. J. Dev. Econ. 2020, 145, 102442. [Google Scholar] [CrossRef]
- Zhao, P. Sustainable urban expansion and transportation in a growing megacity: Consequences of urban sprawl for mobility on the urban fringe of Beijing. Habitat Int. 2010, 34, 236–243. [Google Scholar] [CrossRef]
- Zhao, J.; Li, X.; Lu, H.; Yang, X.; Shen, K. Research on Carrying Capacity of Integrated Transportation in Guanzhong Plain Urban Agglomeration. 19th COTA International Conference of Transportation Professionals. LOCATION OF CONFERENCE, ChinaDATE OF CONFERENCE; pp. 4829–4840.
- Liu, Z.Y, Gao, Y.Y, Wang, J. J. Study on adaptability of urban agglomeration freight transport supply and demand structure based on entropy theory. Proceedings of the 2017 3rd International Forum on Energy, Environment Science and Materials (IFEESM 2017), 2017, 120:1814-1822.
- Liu, Z.Y.; Li, C.B.; Jian, M.Y. Study on the Equilibrium Discriminant Model of Urban Agglomeration Transport Supply and Demand Structure. J. Adv. Transp. 2018, 2018, 1–10. [Google Scholar] [CrossRef]
- Bie, Y. M, Ji Y.T, Ma D.F. Multi-Agent Deep Reinforcement Learning Collaborative Traffic Signal Control Method Considering Intersection Heterogeneity[J]. Transportation Research Part C: Emerging Technologies, 2024, 164: 104663.
- Fang, S.; Yang, L.; Zhao, X.; Wang, W.; Xu, Z.; Wu, G.; Liu, Y.; Qu, X. A Dynamic Transformation Car-Following Model for the Prediction of the Traffic Flow Oscillation. IEEE Intell. Transp. Syst. Mag. 2023, 16, 174–198. [Google Scholar] [CrossRef]
- Zhang, M.; Li, Z.; Wang, X.; Li, J.; Liu, H.; Zhang, Y. The Mechanisms of the Transportation Land Transfer Impact on Economic Growth: Evidence from China. Land 2021, 11, 30. [Google Scholar] [CrossRef]
- Mamede, F.P, da Silva RF, de Brito I Jr, et al. Deep Learning and Statistical Models for Forecasting Transportation Demand: A Case Study of Multiple Distribution Centers]. Logistics-Basel, 2023,7(4):58-69.
- Ghafouri-Azar, M.; Diamond, S.; Bowes, J.; Gholamalizadeh, E. The sustainable transport planning index: A tool for the sustainable implementation of public transportation. Sustain. Dev. 2023, 31, 2656–2677. [Google Scholar] [CrossRef]
- Wang, Z.; Chu, R.; Zhang, M.; Wang, X.; Luan, S. An Improved Selective Ensemble Learning Method for Highway Traffic Flow State Identification. IEEE Access 2020, 8, 212623–212634. [Google Scholar] [CrossRef]
- Shi, Q.; Yan, X.; Jia, B.; Gao, Z. Freight Data-Driven Research on Evaluation Indexes for Urban Agglomeration Development Degree. Sustainability 2020, 12, 4589. [Google Scholar] [CrossRef]
- An, J. Y., Fu ,L., Hu, M,. et al. A novel fuzzy-based convolutional neural network method to traffic flow prediction with uncertain traffic accident information. IEEE Access, 2019, 7:20708-20722.
- Viljoen, N.M.; Joubert, J.W. Multilayered complex network datasets for three supply chain network archetypes on an urban road grid. Data Brief 2018, 16, 1069–1077. [Google Scholar] [CrossRef]
- Viljoen, N.M.; Joubert, J.W. The Road most Travelled: The Impact of Urban Road Infrastructure on Supply Chain Network Vulnerability. Networks Spat. Econ. 2017, 18, 85–113. [Google Scholar] [CrossRef]
- Choe, T.; Kim, J.; Shin, M.; Kim, K.; Kim, M. Complex disaster response framework to reduce urban disaster vulnerability. Sci. Prog. 2023, 106. [Google Scholar] [CrossRef]
- Gomes, E.; Abrantes, P.; Banos, A.; Rocha, J.; Buxton, M. Farming under urban pressure: Farmers' land use and land cover change intentions. Appl. Geogr. 2019, 102, 58–70. [Google Scholar] [CrossRef]
- Dai, L.; Derudder, B.; Liu, X. The evolving structure of the Southeast Asian air transport network through the lens of complex networks, 1979–2012. J. Transp. Geogr. 2018, 68, 67–77. [Google Scholar] [CrossRef]
- Pu, H.; Li, Y.; Ma, C. Topology analysis of Lanzhou public transport network based on double-layer complex network theory. Phys. A: Stat. Mech. its Appl. 2022, 592. [Google Scholar] [CrossRef]
- Cai, B.; Zeng, L.; Wang, Y.; Li, H.; Hu, Y. Community Detection Method Based on Node Density, Degree Centrality, and K-Means Clustering in Complex Network. Entropy 2019, 21, 1145. [Google Scholar] [CrossRef]
- Wang, X.; Tejedor, A.; Wang, Y.; Moreno, Y. Unique superdiffusion induced by directionality in multiplex networks. New J. Phys. 2021, 23, 013016. [Google Scholar] [CrossRef]
- Kumar, S.; Mallik, A.; Sengar, S.S. Community detection in complex networks using stacked autoencoders and crow search algorithm. J. Supercomput. 2022, 79, 3329–3356. [Google Scholar] [CrossRef]
- Yu, A.; Wang, N.; Wu, N. Scale-Free Networks: Characteristics of the Time-Variant Robustness and Vulnerability. IEEE Syst. J. 2020, 15, 4082–4092. [Google Scholar] [CrossRef]
- Milano, M.; Guzzi, P.H.; Cannataro, M. Design and Implementation of a New Local Alignment Algorithm for Multilayer Networks. Entropy 2022, 24, 1272. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, H.; He, K.; Jiang, S. Multi-objective particle swarm optimization algorithm based on objective space division for the unequal-area facility layout problem. Expert Syst. Appl. 2018, 102, 179–192. [Google Scholar] [CrossRef]
- Abdullah, K., David, W. C., Alice, E. S. Multi-objective optimization using genetic algorithms: A tutorial, Reliability Engineering & System Safety, vol.91, no.9, pp.992-1007, 2006.
- Ruhul, S., Liang, K.H., Newton, C. A new multi-objective evolutionary algorithm, European Journal of Operational Research, vol.140, no.1, pp.12-23, 2002.


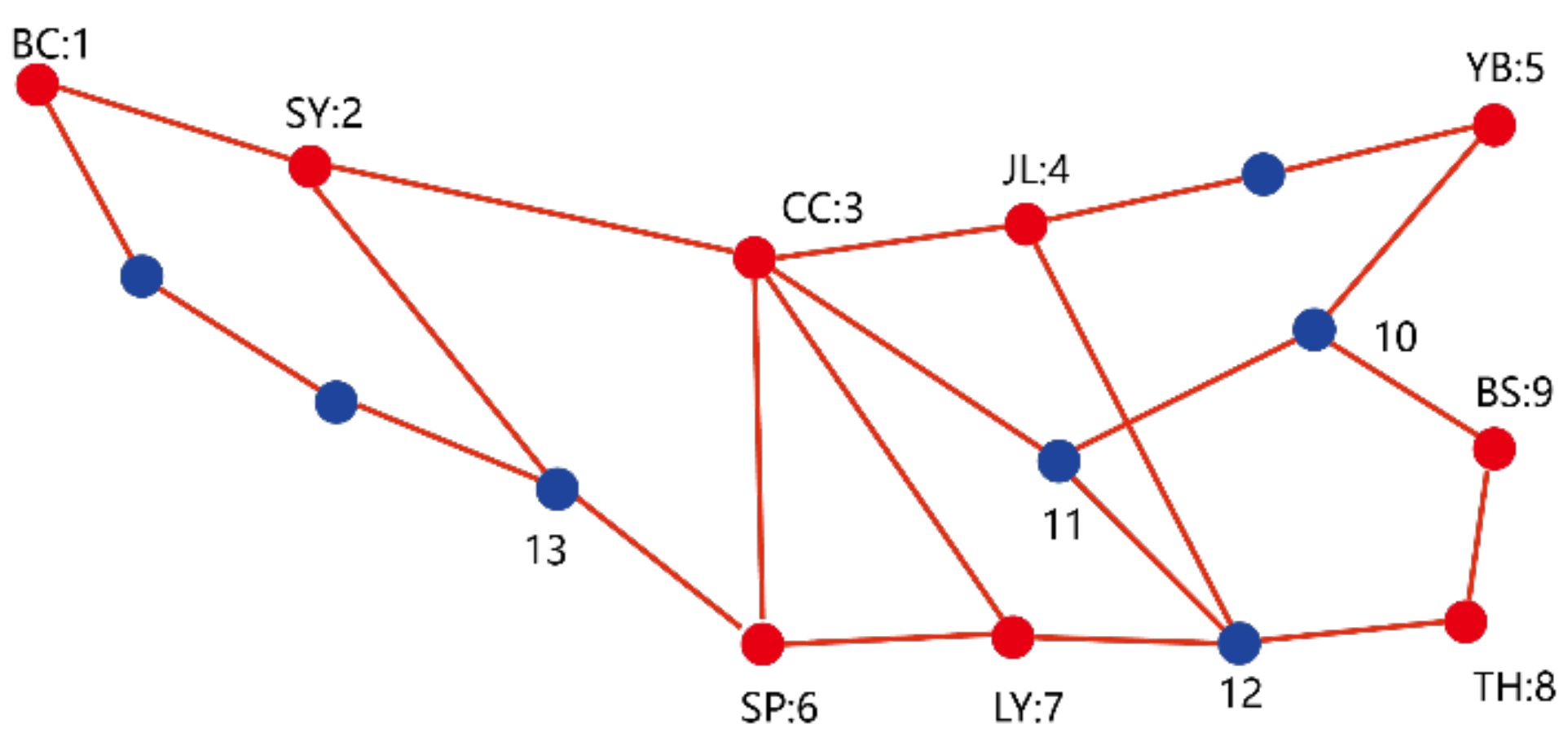
| City | YB | JL | CC | SY | BC |
|---|---|---|---|---|---|
| YB | 0 | 21 | 38 | 12 | 19 |
| JL | 38 | 0 | 121 | 69 | 35 |
| CC | 48 | 239 | 0 | 146 | 121 |
| SY | 16 | 48 | 21 | 0 | 32 |
| BC | 19 | 32 | 38 | 71 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





