Modeling of Compound Curves on Railway Lines

1. Introduction

Since for many years the development of design documentation in the field of railways has been carried out using commercial computer software [1,2], it has become established that conducting research work on the methodology of designing track geometrical systems is now less important. Of course, such work is carried out [3,4,5], but its scope is often limited to detailed issues, such as transition curves [6] or railway turnouts [7,8].

Due to the competitive conditions with other transport systems, new railway lines are usually adapted to the increased speed of trains; in fact, a significant part of them are high-speed railways. On the other hand, traditional lines (existing, most often built in the 19th century) are disappearing from the field of research interest, as they would have to be modified to adapt to contemporary requirements. This applies especially to railway lines running in difficult terrain conditions (e.g. in mountainous terrain), where there are small radii of horizontal curves, and additionally controversial geometric arrangements, such as compound curves and reverse curves. Improving the quality of these lines, leading to an increase in travel speed, requires appropriate modernization activities. In the case of compound curves and reverse curves, this would consist in introducing transition curves between the occurring horizontal curves.

This article addresses the issue of designing compound curves, i.e. a geometric system consisting of two circular arcs of different radii, pointing in the same direction and directly connected to each other. Compound curves are currently used on tram lines; they also occur on railways, but new ones are not built there any more. Therefore, in relation to railway lines, the aim is to obtain the possibility of reproducing (i.e. modeling) the existing geometric layout with compound curves, so that it is then possible to correct the horizontal ordinates in the area where the circular arches connect. For this purpose, it was necessary to develop an effective method for designing such a system, which, however, by assumption, will not be used to determine the coordinates of a new compound curve, but to model the existing system (with a view to its later modification).

At this point it should be noted that the analytical method of designing compound curves had already been developed and presented in [9]. It concerned a model solution, i.e. creating a geometric system from scratch, in which circular arcs of different radii are connected with each other by means of an appropriate transition curve. A classic compound curve, in which the transition curve does not occur, was a special case in this method. The issue of modifying the existing geometric system was not considered. Meanwhile, as it seems, the real problem lies somewhere else. After all, it is not about creating new model systems of compound curves (with appropriate transition curves), but modernizing the existing systems. In this situation, the classic compound curve becomes the subject of interest.

In this paper, the solution to the problem is obtained analytically. The standard procedure of the analytical design method in its previous versions [10,11,12] requires operating in the local coordinate system and is characterized – in its initial phase – by the lack of knowledge of the location of the origin of this system in relation to the appropriate global system (in Poland – in relation to flat coordinates – it is the national spatial reference system PL-2000 [13]). Full integration of both of these systems requires carrying out the design procedure in the local system until the very end. The location of the origin of this system in relation to the appropriate main point of the route and its resulting coordinates in the global system are determined only in the final phase of the procedure. This may constitute the basic methodological reservation to the discussed design method. For this reason, certain interpretation problems may also arise.

As it turns out, these difficulties can be avoided by locating the origin of the local coordinate system at the point of intersection of both main directions of the route, whose Cartesian coordinates in the global system are known. Such a version of the analytical design method was presented in [14]; it is universal in nature and covers the areas of connection of adjacent main directions of the railway route (both symmetrical and asymmetrical). In this paper, an analogous approach was used in the design of classic compound curves.

2. Local Coordinate System

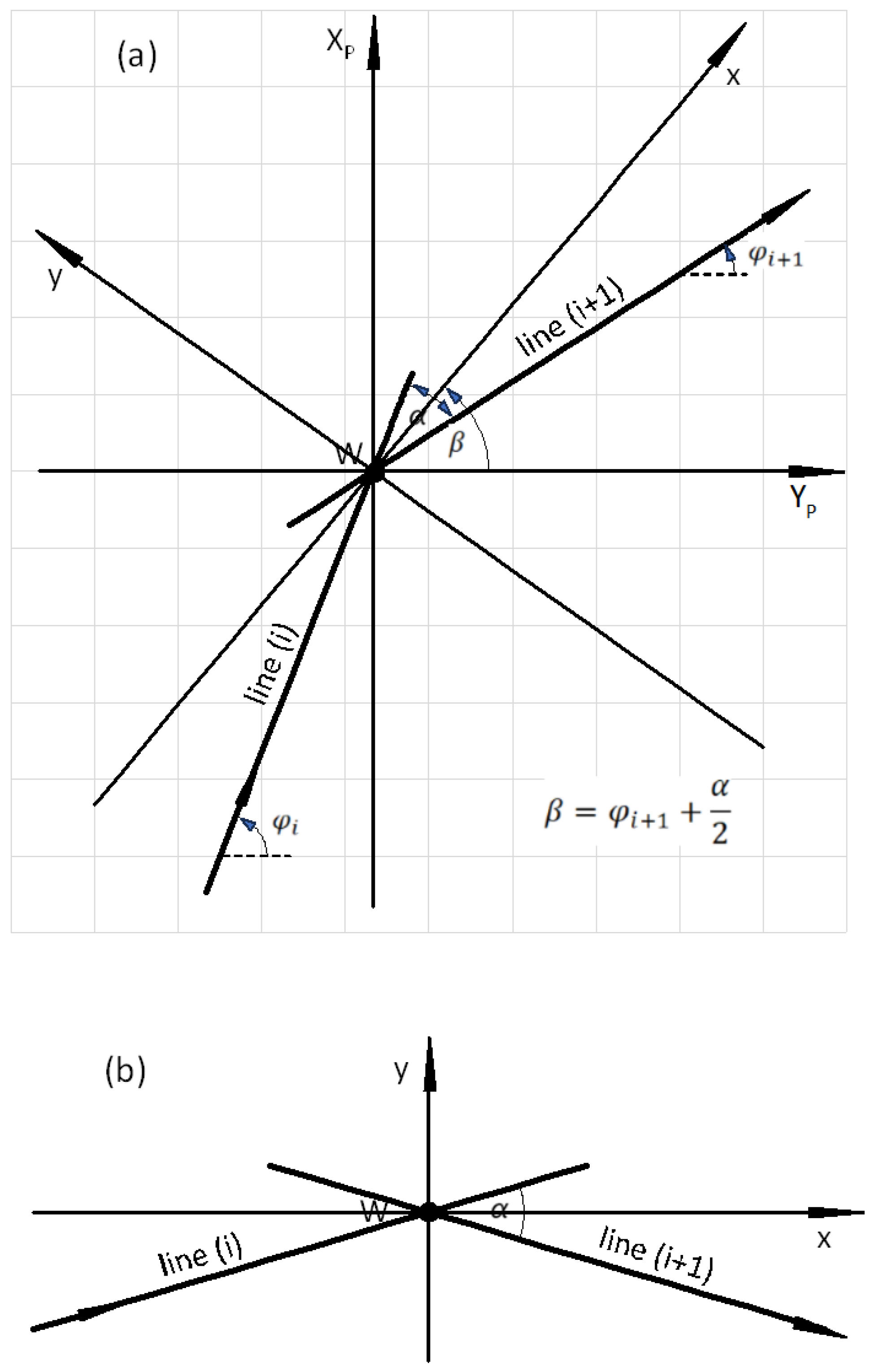
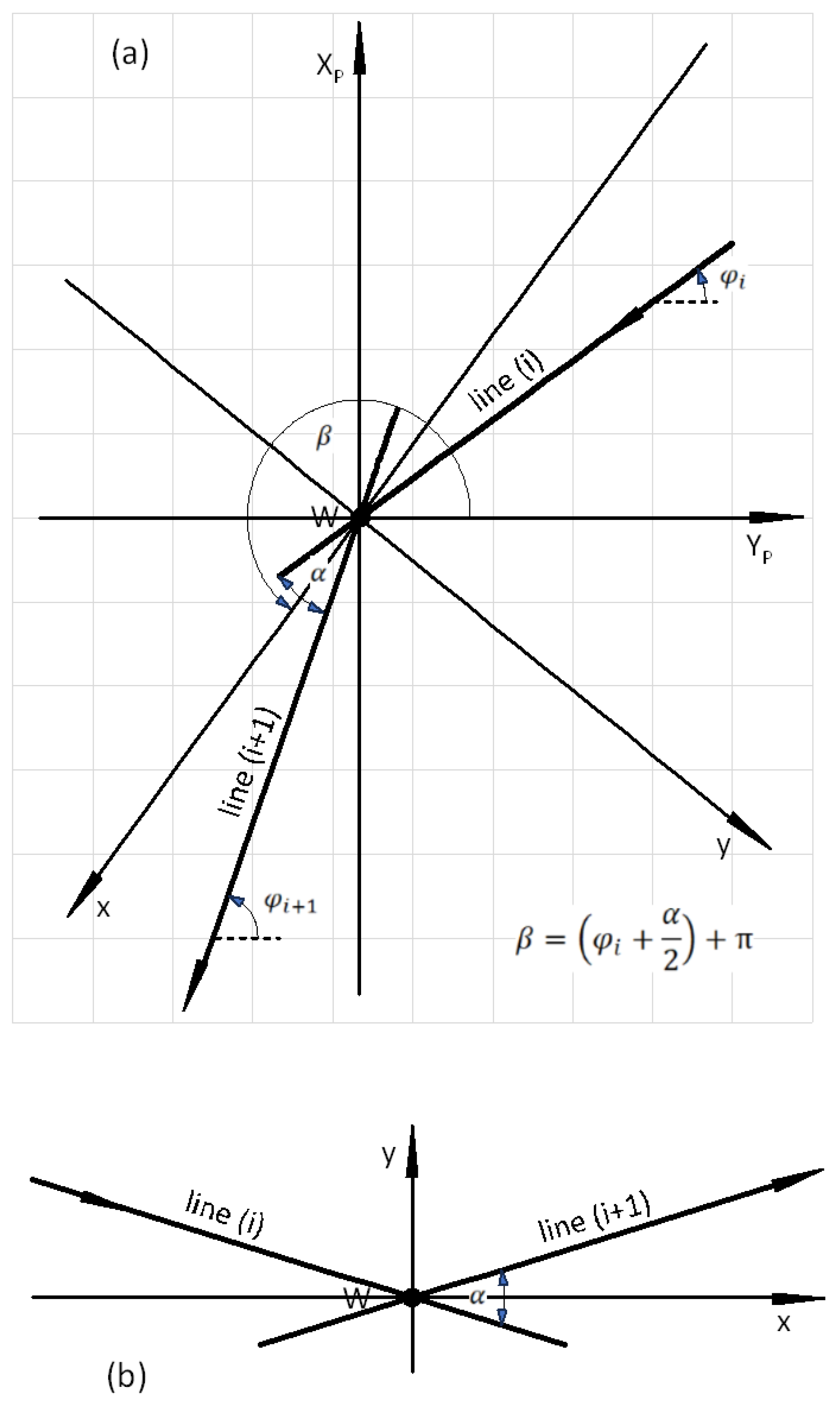
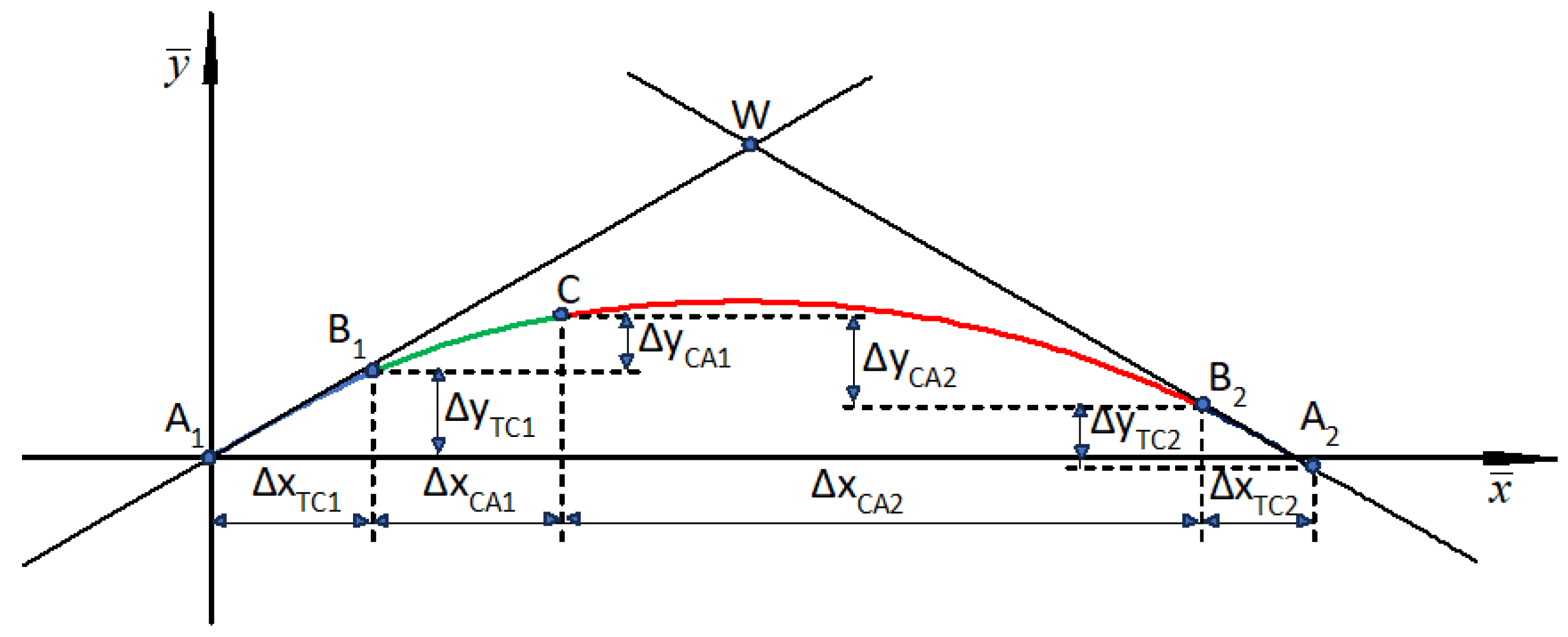
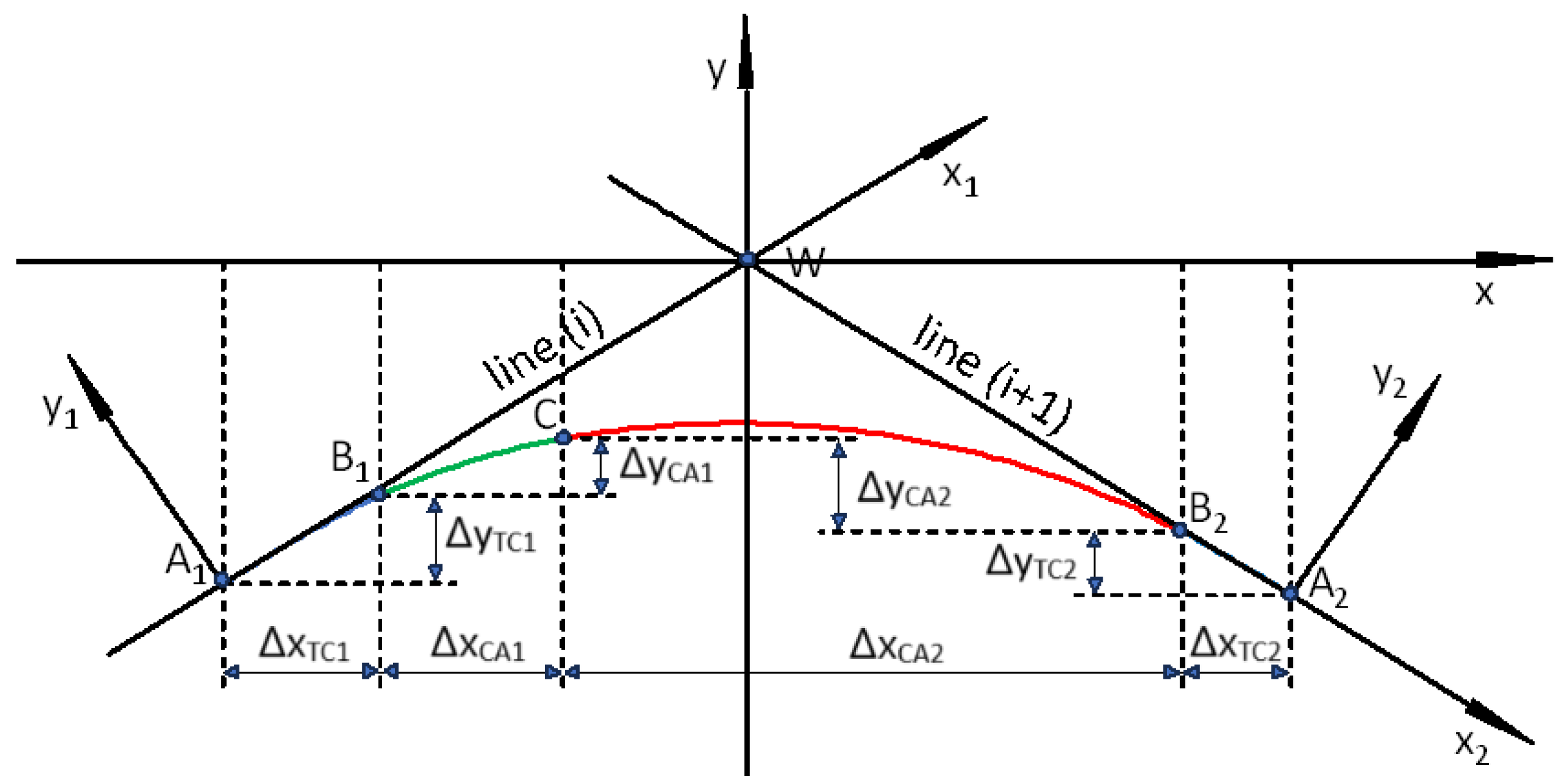
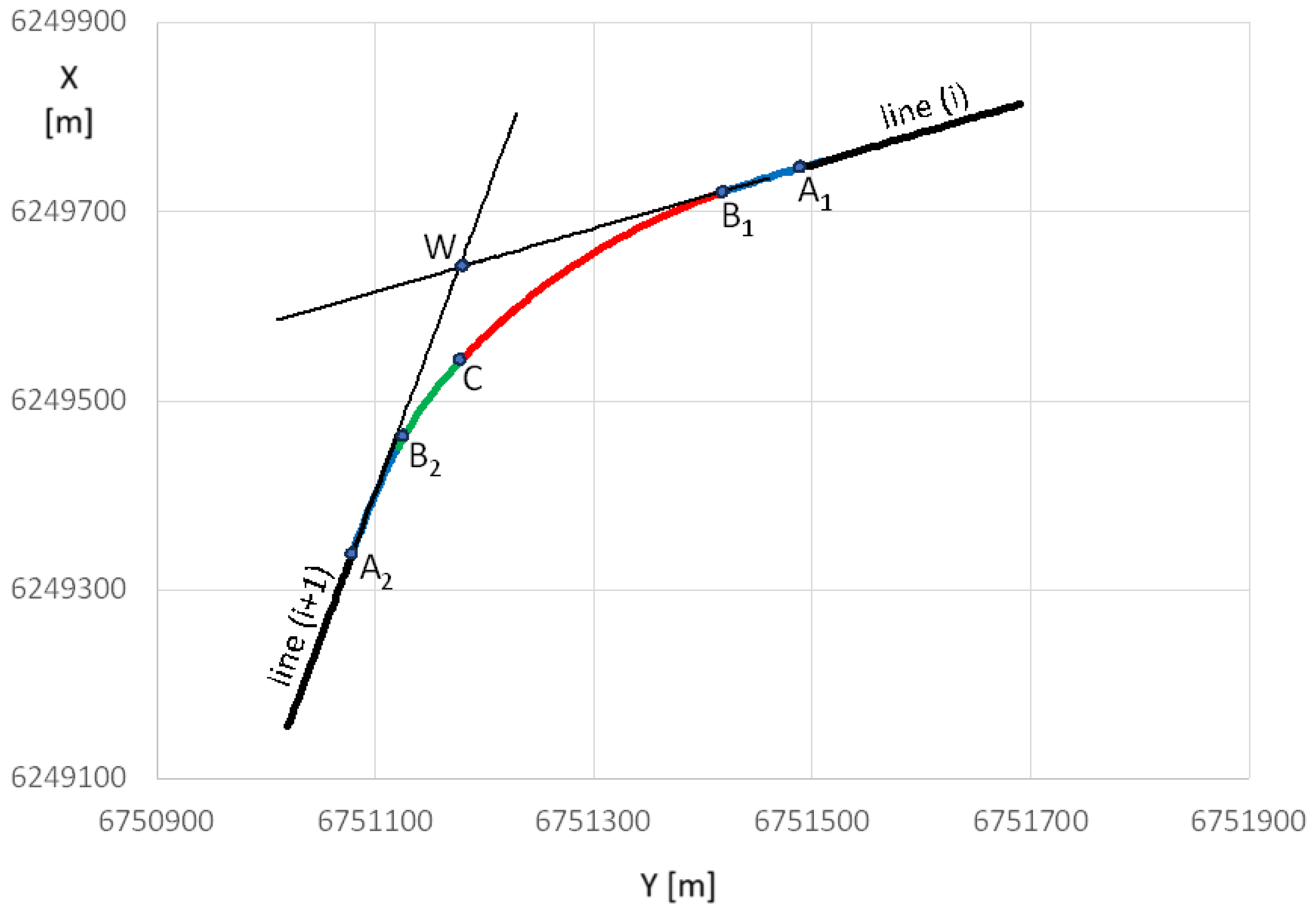
Similarly to other variants of the analytical design method, when designing classic compound curves (in which horizontal arcs of different radii are directly connected to each other), it was assumed that the design of a given area of ​​route direction change will be carried out in the appropriate local Cartesian coordinate system x, y (marked as LCS). The basis of this system is the symmetrically set adjacent main directions. In order to obtain such a setting of the main directions, an appropriate transformation (i.e. shift and rotation) of the global system must be performed.

Design activities carried out in the global rectangular coordinate system, i.e. creating a polygon of the main directions of the route and determining the mathematical equations of these directions, the coordinates of their intersection points (i.e. main points) and the angles of return, were presented in [14]. This work also explains the method of creating a local coordinate system for a given area of ​​changing the route direction, consisting in shifting the origin of the global system to the point of intersection of two adjacent main directions (i.e. to point W), and then rotating the shifted system Y_P, X_P by such an angle β as to obtain a symmetrical setting of the main directions in the local coordinate system x, y. Examples of this operation are shown in Figure 1 and Figure 2.

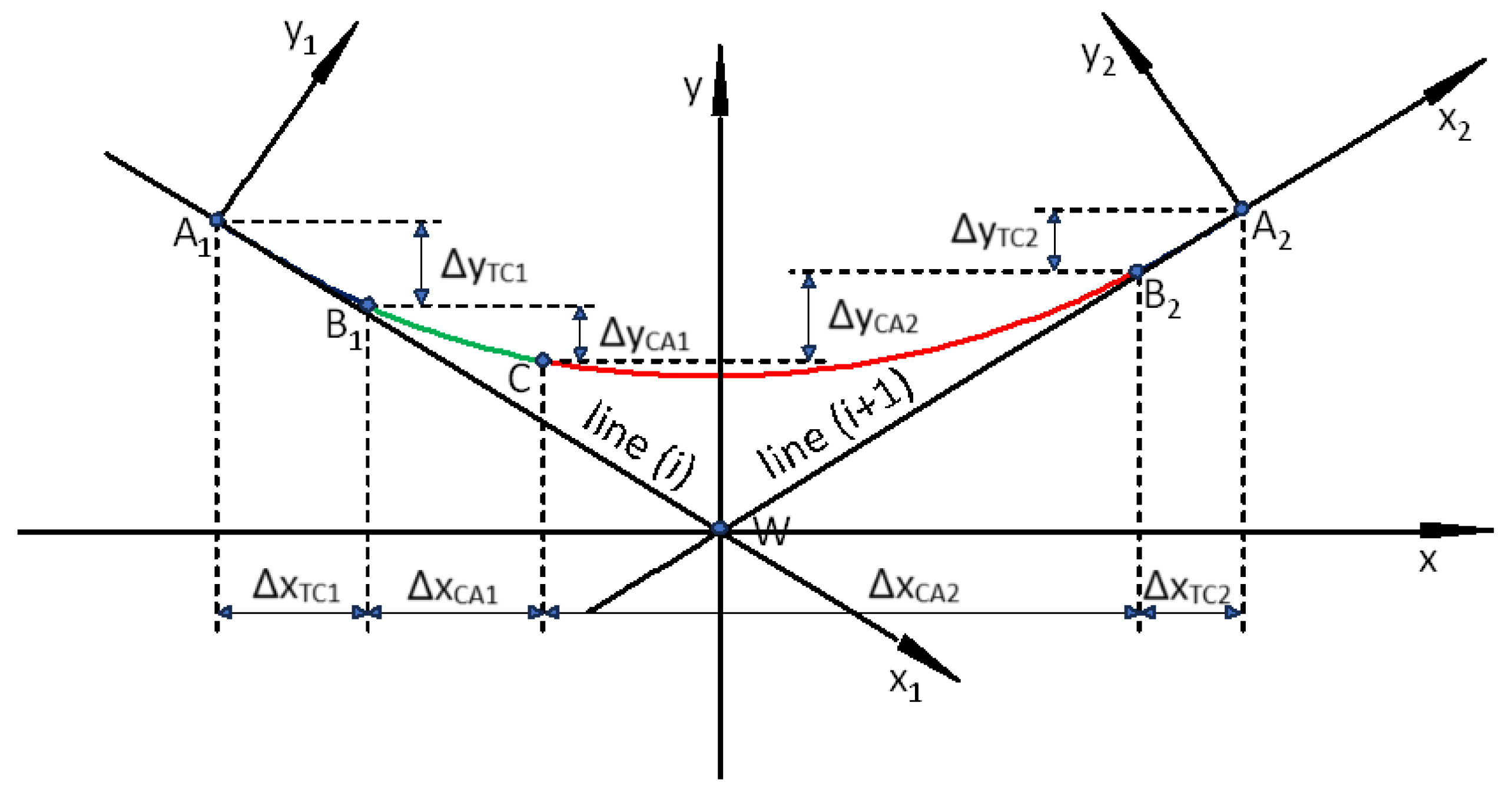
It should be noted that the setting of the main directions of the route in the PL-2000 system can be very diverse; Figure 1a and Figure 2a show only two selected cases. However, after the transformation to the local coordinate system (as shown in Figure 1b and Figure 2b), there are only two possibilities for locating the designed geometric system: under the x axis, with negative ordinates and the convexity of the curvilinear elements directed upwards, and above the x axis, with positive ordinates and the convexity of the curvilinear elements directed downwards. Therefore, when considering the procedure in detail, it is necessary to present the computational algorithms related to these two situations. This means that when determining the formulas for the coordinates of characteristic points in the local coordinate system, two possible cases should be taken into account:

• Case I – for a geometric system located below the W vertex and resulting negative ordinates (as in Figure 1b), and
• Case II – for a geometric system located above the W vertex and resulting positive ordinates (as in Figure 2b).

The paper presents the procedure for creating a geometric system covering Case I. The design of the geometric system is carried out in several stages, which are presented later in the article.

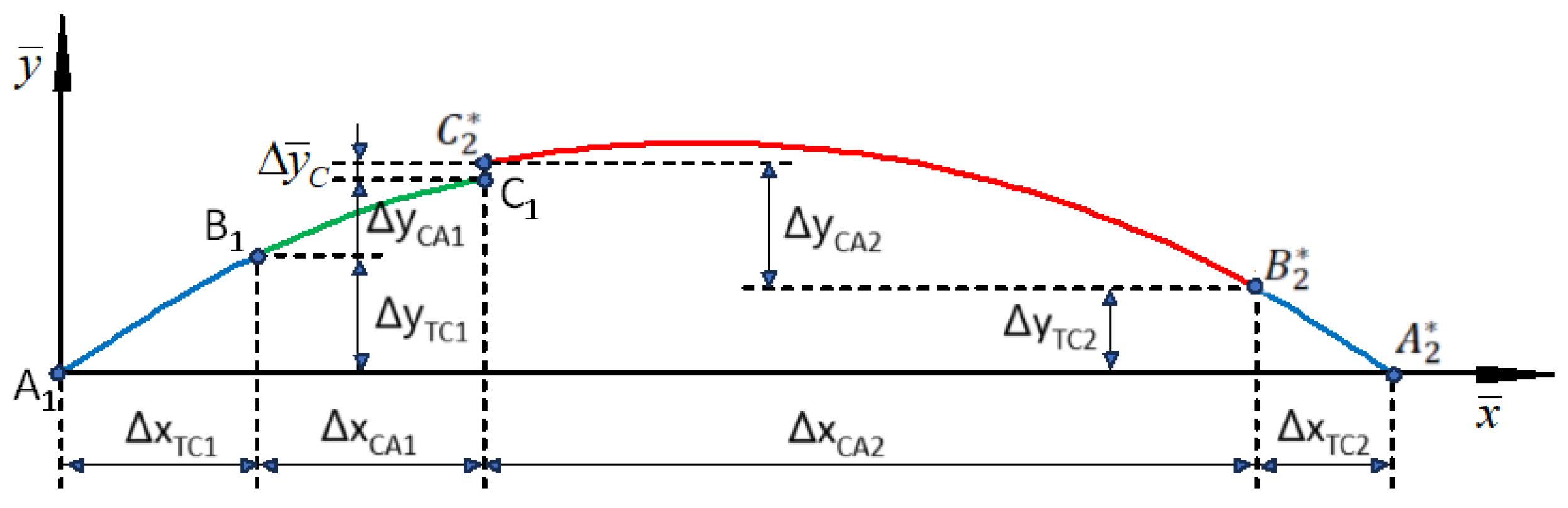
3. Determination of Basic Calculation Quantities

In order to be able to operate in the local coordinate system, it is necessary to first perform an auxiliary procedure, which aims to determine the basic calculation quantities. These quantities refer to the regions of the geometric system connecting the ends of the extreme straight segments (i.e. the beginnings of the transition curves) with the connection point of both circular arcs. This refers to the lengths of the projections of the transition curve ($\Delta x_{TC}$) and the circular arc ($\Delta x_{CA}$) on the horizontal axis, as well as the lengths of the projections of the transition curve ($\Delta y_{TC}$) and the circular arc ($\Delta y_{CA}$) on the vertical axis. The calculations of the searched parameters, separately for both occurring horizontal arcs, are carried out in the system shown in Figure 3.

We start by drawing a straight line simulating the main direction i through point A(0, 0) in the coordinate system $\tilde{x},\tilde{y}$; it is described by the equation

$$\tilde{y}=\tan {\displaystyle \frac{\alpha }{2}}\cdot \tilde{x}.$$

(1)

This straight line is the abscissa axis of the coordinate system x_c, y_c , associated with the transition curve of length l_c, which is connected to a circular arc of radius R. We are interested in the coordinates of the end point of the curve in this system, which result from the corresponding parametric equations x_c(l) and y_c(l) for l = l_c . In the case of using the transition curve in the form of a clothoid, these coordinates are as follows:

$$x_c(l_c)=l_c-{\displaystyle \frac{l_c^3}{40\cdot R^2}}+{\displaystyle \frac{l_c^5}{3456\cdot R^4}},$$

(2)

$$y_c(l_c)=-{\displaystyle \frac{l_c^2}{6\cdot R}}+{\displaystyle \frac{l_c^4}{336\cdot R^3}}-{\displaystyle \frac{l_c^6}{42240\cdot R^5}},$$

(3)

while the angle Θ_c(l_c) of inclination at the end of the curve is determined from the dependence

$${\mathrm{\Theta }}_c(l_c)=-{\displaystyle \frac{l_c}{2\cdot R}}.$$

(4)

The transformation of the transition curve to the $\tilde{x},\tilde{y}$ coordinate system is performed by rotating the reference system by an angle of α/2. The appropriate formulas depend on the direction of rotation. As a result of this operation, the required value of the projection of the transition curve onto the horizontal and vertical axes is obtained. In the case of a right rotation of the x_c, y_c system (as in Figure 3), the following values ​​are obtained:

$$\begin{array}{l}\Delta y_{TC}=\tilde{y}(l_c)=x_c(l_c)\cdot \sin {\displaystyle \frac{\alpha }{2}}+y_c(l_c)\cdot \cos {\displaystyle \frac{\alpha }{2}}\end{array},$$

(5)

$$\begin{array}{l}\Delta y_{TC}=\tilde{y}(l_c)=x_c(l_c)\cdot \sin {\displaystyle \frac{\alpha }{2}}+y_c(l_c)\cdot \cos {\displaystyle \frac{\alpha }{2}}\end{array}.$$

(6)

The value of the tangent at the end is described by the formula

$$s_{TC}=\tan \left[{\mathrm{\Theta }}_c(l_c)+{\displaystyle \frac{\alpha }{2}}\right].$$

(7)

Knowing the position of the transition curve, we can inscribe a circular arc of radius R in the geometric system. The center of this arc (point S) lies on the line perpendicular to the tangent at the end of the transition curve (i.e. at point B), at a distance R from this point. The coordinates of point S are as follows:

$${\tilde{x}}_S=\Delta x_{TC}+{\displaystyle \frac{s_{KP}}{\sqrt{1+s_{TC}^2}}}R,$$

(8)

$${\tilde{y}}_S=\Delta y_{TC}-{\displaystyle \frac{1}{\sqrt{1+s_{TC}^2}}}R.$$

(9)

A circular arc is described by the equation

$$\tilde{y}={\tilde{y}}_S+\sqrt{R^2-{\left({\tilde{x}}_S-\tilde{x}\right)}^2},$$

(10)

and the value of the tangent to the geometric system is

$$\tilde{y}\text{'}={\displaystyle \frac{{\tilde{x}}_S-\tilde{x}}{\sqrt{R^2-{\left({\tilde{x}}_S-\tilde{x}\right)}^2}}}.$$

(11)

The important characteristic point is point H, where the slope of the tangent to the geometric system is zero (i.e. $\tilde{y}\text{'}$= 0). Its coordinates are as follows: ${\tilde{x}}_H={\tilde{x}}_S$, ${\tilde{y}}_H={\tilde{y}}_S+R$. The connection of both circular arcs (i.e. point C) should be located to the left or right of point H. The condition ${\tilde{x}}_C\in \left(\Delta x_{TC},2{\tilde{x}}_H-\Delta x_{TC}\right)$ must be met.

The value of the abscissa of point C results from the arbitrarily assumed difference $\Delta x_{CA1}$, relating to a circular arc of radius R₁; it is

$${\tilde{x}}_C=\Delta x_{TC1}+\Delta x_{CA1}.$$

(12)

The ordinate of this point is determined based on equation (10).

$${\tilde{y}}_C={\tilde{y}}_S+\sqrt{R_1^2-{\left({\tilde{x}}_S-{\tilde{x}}_C\right)}^2}.$$

(13)

The difference $\Delta y_{CA1}$ for the circular arc CA1, associated with the first transition curve (TC1), is determined from the formula

$$\Delta y_{CA1}={\tilde{y}}_C-\Delta y_{TC1}.$$

(14)

The key quantity for further actions is the slope of the tangent at point C, which is the same for both connected arcs. It is

$${\tilde{y}}_C^{\text{'}}=s_C={\displaystyle \frac{{\tilde{x}}_S-{\tilde{x}}_C}{\sqrt{R_1^2-{\left({\tilde{x}}_S-{\tilde{x}}_C\right)}^2}}}.$$

(15)

When constructing the entire circular arc, the differences $\Delta x_{TC1}$ and $\Delta y_{TC1}$ for the transition curve TC1 (determined using formulas (5) and (6)) should be used, as well as the arbitrarily assumed difference $\Delta x_{CA1}$ and difference $\Delta y_{CA1}$ (determined by formula (14)) for the circular arc CA1. After entering the radius R₂, the differences $\Delta x_{TC2}$ and $\Delta y_{TC2}$ for the transition curve TC2 are obtained. Determining the values $\Delta x_{CA2}$ ​​and $\Delta y_{CA2}$ for the circular arc CA2 requires an additional calculation procedure.

Knowing the position of the transition curve TC2 in the $\tilde{x},\tilde{y}$ system shown in Figure 3, we can inscribe a circular arc of radius R₂ in the geometric system. The coordinates of the center of this arc (i.e. point S₂) result from equations (8) and (9). In the $\tilde{x},\tilde{y}$ coordinate system, the second circular arc is also described by equation (10), and the value of the tangent at its end by equation (11).

In the target geometric system (i.e. in a compound curve), this arc will be mirrored relative to the abscissa ${\tilde{x}}_C$, so the tangent at its end point must satisfy the condition

$${\tilde{y}}_C^{\text{'}}=s_C={\displaystyle \frac{{\tilde{x}}_{S2}-{\tilde{x}}_C}{\sqrt{R_2^2-{\left({\tilde{x}}_{S2}-{\tilde{x}}_C\right)}^2}}}=-{\displaystyle \frac{{\tilde{x}}_{S1}-{\tilde{x}}_C}{\sqrt{R_1^2-{\left({\tilde{x}}_{S1}-{\tilde{x}}_C\right)}^2}}}.$$

After taking into account formula (12) we get

$${\displaystyle \frac{{\tilde{x}}_{S2}-\left(\Delta x_{TC2}+\Delta x_{CA2}\right)}{\sqrt{R_2^2-{\left[{\tilde{x}}_{S2}-\left(\Delta x_{TC2}+\Delta x_{CA2}\right)\right]}^2}}}=-{\displaystyle \frac{{\tilde{x}}_{S1}-\left(\Delta x_{TC1}+\Delta x_{CA1}\right)}{\sqrt{R_1^2-{\left[{\tilde{x}}_{S1}-\left(\Delta x_{TC1}+\Delta x_{CA1}\right)\right]}^2}}}.$$

The right hand side of the above expression is already known at this stage, as it results from equation (15). Therefore, we need to solve the following equation with the unknown $\Delta x_{CA2}$:

$${\displaystyle \frac{{\tilde{x}}_{S2}-\left(\Delta x_{TC2}+\Delta x_{CA2}\right)}{\sqrt{R_2^2-{\left[{\tilde{x}}_{S2}-\left(\Delta x_{TC2}+\Delta x_{CA2}\right)\right]}^2}}}=-s_C.$$

As a result of this operation we get

$$\Delta x_{CA2}={\tilde{x}}_{S2}-\Delta x_{TC2}+{\displaystyle \frac{s_C}{\sqrt{1+s_C^2}}}{R}_2.$$

(16)

The coordinates of the end of the second circular arc are as follows:

$${\tilde{x}}_{C2}=\Delta x_{TC2}+\Delta x_{CA2},$$

(17)

$${\tilde{y}}_{C2}={\tilde{y}}_{S2}+\sqrt{R_2^2-{\left({\tilde{x}}_{S2}-{\tilde{x}}_{C2}\right)}^2}.$$

(18)

The difference $\Delta y_{CA2}$ is determined by the formula

$$\Delta y_{CA2}={\tilde{y}}_{C2}-\Delta y_{TC2}.$$

(19)

The position of a circular arc of radius R₂ in the $\tilde{x},\tilde{y}$ system, with marked the differences $\Delta x_{CA2}$ and $\Delta y_{CA2}$, is shown in Figure 3.

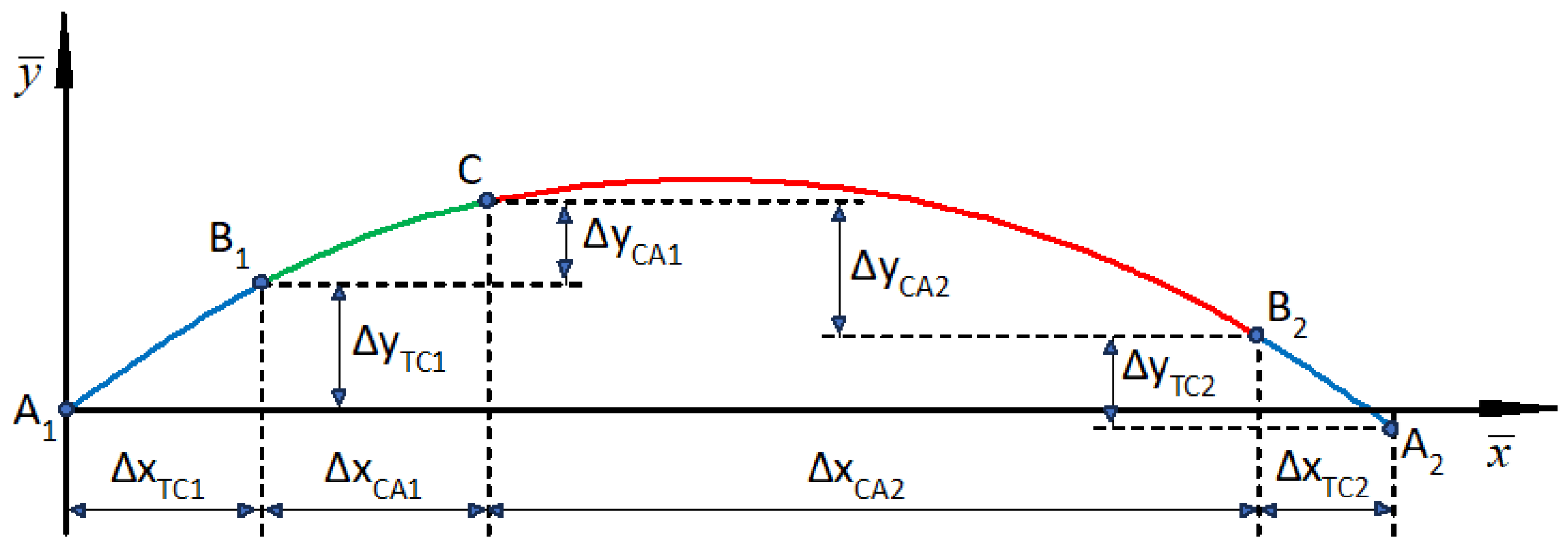
4. Connection of Both Horizontal Arcs

The construction of a compound curve, i.e. connecting the existing horizontal arcs with radii R₁ and R₂ , will be performed in the auxiliary $\overline{x},\overline{y}$ coordinate system shown in Figure 4. The case of a geometric system located below the vertex W (i.e. shown in Figure 1) was considered.

For the transition curve TC1 and the circular arc CA1, this system is identical to the system $\tilde{x},\tilde{y}$; this means that $\overline{x}=\tilde{x}$ and $\overline{y}=\tilde{y}$. Therefore, the coordinates of the characteristic points are:

For the TC2 curve and the CA2 arc it will be necessary to perform an appropriate transformation, consisting in performing a mirror reflection with respect to the abscissa ${\overline{x}}_C$. The characteristic points $A_2^{*}$, $B_2^{*}$ and $C_2^{*}$, obtained as a result of this operation do not yet occupy their final position and will require correction. Their coordinates are as follows:

$$\begin{array}{lll}{\overline{x}}_{A2*}=\Delta x_{TC1}+\Delta x_{CA1}+\Delta x_{CA2}+\Delta x_{TC2},& \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& {\overline{y}}_{A2*}=0,\\ {\overline{x}}_{B2*}=\Delta x_{TC1}+\Delta x_{CA1}+\Delta x_{CA2},& \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& {\overline{y}}_{B2*}=\Delta y_{TC2},\\ {\overline{x}}_{C2*}=\Delta x_{TC2}+\Delta x_{CA2},& \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& {\overline{y}}_{C2*}=\Delta y_{TC2}+\Delta y_{CA2}.\end{array}$$

As can be seen in Figure 4, at the assumed connection point of both arcs there is a difference in ordinates $\Delta {\overline{y}}_C$, which is

$$\Delta {\overline{y}}_C={\overline{y}}_{C2}-{\overline{y}}_C=\left(\Delta y_{TC2}+\Delta y_{CA2}\right)-\left(\Delta y_{TC1}+\Delta y_{CA1}\right).$$

(20)

In order to obtain a smooth connection of both parts of the geometric system, the ordinates of this system related to the arc of radius R₂ should be corrected (while maintaining the abscissa $\overline{x}$ values​​). For Case I, we obtain

$${\overline{y}}_{A2}={\overline{y}}_{A2*}-\Delta {\overline{y}}_C,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\overline{y}}_{B2}={\overline{y}}_{B2*}-\Delta {\overline{y}}_C,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\overline{y}}_{C2}={\overline{y}}_C={\overline{y}}_{C2*}-\Delta {\overline{y}}_C.$$

Figure 5 shows the geometric system of the corresponding compound curve in the $\overline{x},\overline{y}$ coordinate system.

For the geometric system located above the vertex W (Case II in Figure 2b), the same formulas for the abscissa values ​​apply, but the ordinates take negative values. This means that

$$\begin{array}{lll}{\overline{y}}_{A1}=0,& \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& {\overline{y}}_{A2}=\Delta {\overline{y}}_C,\\ {\overline{y}}_{B1}=-\Delta y_{TC1},& \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& {\overline{y}}_{B2}=-(\Delta y_{TC2}-\Delta {\overline{y}}_C),\\ {\overline{y}}_{C1}={\overline{y}}_C=-(\Delta y_{TC1}+\Delta y_{CA1}),& \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& {\overline{y}}_{C2}={\overline{y}}_C=-(\Delta y_{TC2}+\Delta y_{CA2}-\Delta {\overline{y}}_C).\end{array}$$

5. Transferring the Solution to the Local Coordinate System

Knowing the coordinates of the extreme points of the geometric system A₁(0,0) and $A_2\left({\overline{x}}_{A2},{\overline{y}}_{A2}\right)$, we can transfer the obtained solution to the local coordinate system x, y (shown in the given case in Figure 1b). To do this, we need to derive from these points two tangent lines inclined at an angle α/2 – positive from point A₁ and negative from point A₂ (Figure 6). The equations of these lines are as follows:

$$\overline{y}=\tan {\displaystyle \frac{\alpha }{2}}\cdot \overline{x},$$

(21)

$$\overline{y}={\overline{y}}_{A2}-\tan {\displaystyle \frac{\alpha }{2}}\cdot \left(\overline{x}-{\overline{x}}_{A2}\right).$$

(22)

The intersection point of lines (21) and (22) is the origin of the local coordinate system. Its coordinates in the $\overline{x},\overline{y}$ system are as follows:

$${\overline{x}}_W={\displaystyle \frac{{\overline{y}}_{A2}+\tan \frac{\alpha }{2}\cdot {\overline{x}}_{A2}}{2\cdot \tan \frac{\alpha }{2}}},$$

(23)

$${\overline{y}}_W={\displaystyle \frac{1}{2}}\cdot \left({\overline{y}}_{A2}+\tan {\displaystyle \frac{\alpha }{2}}\cdot {\overline{x}}_{A2}\right).$$

(24)

In Case II, the coordinates of point W are described by the formulas:

$${\overline{x}}_W={\displaystyle \frac{-{\overline{y}}_{A2}+\tan \frac{\alpha }{2}\cdot {\overline{x}}_{A2}}{2\cdot \tan \frac{\alpha }{2}}},$$

(25)

$${\overline{y}}_W={\displaystyle \frac{1}{2}}\cdot \left({\overline{y}}_{A2}-\tan {\displaystyle \frac{\alpha }{2}}\cdot {\overline{x}}_{A2}\right).$$

(26)

Thanks to their knowledge, it is possible to transform the points of the geometric system into the local coordinate system using the formulas:

$$x=\overline{x}-{\overline{x}}_W,$$

(27)

$$y=\overline{y}-{\overline{y}}_W.$$

(28)

Figure 7 shows the geometric system of the compound curve from Figure 6 transferred to the local coordinate system.

Knowing the assumed values ​​of the radii R₁ and R₂ of the compound curve and the lengths l₁ and l₂ of the transition curves, one must first determine – using the appropriate formulas – the values $\Delta x_{TC1}$ and $\Delta x_{TC2}$, $\Delta y_{TC1}$ and $\Delta y_{TC2}$, $s_{TC1}$ and $s_{TC2}$, $\Delta x_{CA1}$ and $\Delta x_{CA2}$, and $\Delta y_{CA1}$ and $\Delta y_{CA2}$. In the local coordinate system x, y, the beginning of the transition curve TC1 (point A₁) is located in the main direction (i), and the beginning of the curve TC2 (point A₂) is located in the main direction (i+1). The list of formulas for the coordinates of all characteristic points is provided in Table 1.

The values ${\overline{x}}_W$ and ${\overline{y}}_W$ appearing in Table 1 result from formulas (23-26), and $\Delta {\overline{y}}_C$ from formula (20).

6. Computational Algorithms

After determining the coordinates of the characteristic points, the design process should be finalized by determining the course of the route sections located between these points. The differentiation of calculation algorithms related to the directions of rotation of the coordinate systems related to the transition curves must be taken into account. In practice, this involves separate determination of coordinates in the x, y system for the geometric system located below the W vertex (i.e. for Case I) and above the W vertex (i.e. for Case II). In Case I, the situation is shown in Figure 8, while in Case II – the situation is shown in Figure 9.

To determine the computational algorithms, we must first determine the coordinates of the centers of both connected arcs in the local coordinate system. This is done using the knowledge of the computational parameters of point C – the abscissa x_C, the ordinate y_C and the slope of the tangent s_C. The centers of both arcs (points S₁ and S₂) lie on the line perpendicular to the tangent at point C, at distances R₁ and R₂ from this point. The corresponding formulas are presented in Table 2. In the formulas for the abscissa values, the sign of the slope of the tangent s_C plays an important role.

Table 3 presents a list of formulas necessary to determine the coordinates of individual elements of the designed geometric system. It includes:

• parametric equations of the transition curve TC1 in the auxiliary x₁, y₁ coordinate system (for $l\in 〈0,l_1〉$),
• equation of the angle of inclination of the tangent in the x₁, y₁ auxiliary coordinate system (for $l\in 〈0,l_1〉$),
• parametric equations of the transition curve TC1 in the local coordinate system x, y (for $l\in 〈0,l_1〉$),
• formula for the tangent value at the end of the transition curve TC1,
• equation of a circular arc CA1 with radius R₁,
• equation of a circular arc CA2 with radius R₂,
• parametric equations of the transition curve TC2 in the auxiliary x₂, y₂ coordinate system (for $l\in 〈-l_2,0〉$),
• equation of the angle of inclination of the tangent in the auxiliary x₂, y₂ coordinate system (for $l\in 〈-l_2,0〉$),
• parametric equations of the transition curve TC2 in the local coordinate system x, y (for $l\in 〈-l_2,0〉$),
• formula of the tangent value at the end of the transition curve TC2.

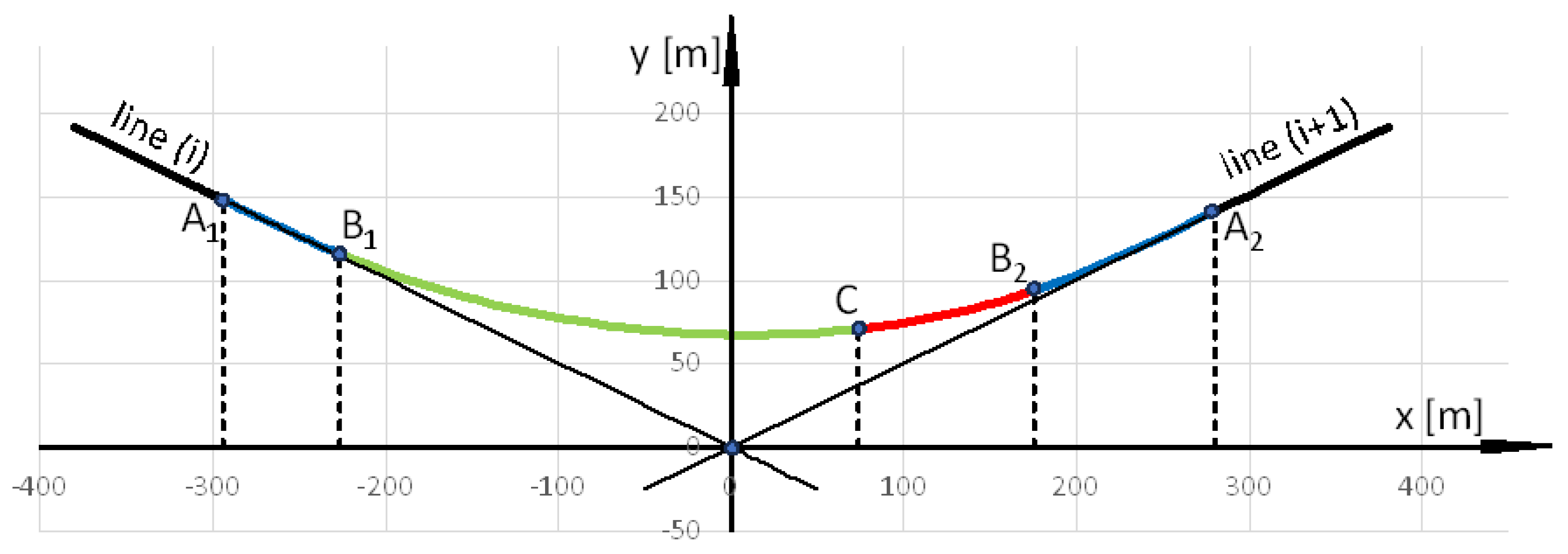
7. Calculation Example

In the presented calculation example, a system of main directions of the route was assumed, intersecting at point W, whose coordinates in the PL-2000 system are: Y_W = 6,751,176.928 m, X_W = 6,249,641.342 m. We are dealing with a turn of the route to the left, with increasing mileage from right to left (which corresponds to the situation in Figure 2).

The assumed train speed on the designed compound curve is V = 90 km/h. It results from the smaller radius of the circular arc R₂ = 450 m and the cant h₂ = 125 mm, where the unbalanced acceleration is a_m = 0.571 m/s². The length of the corresponding transition curve in the form of a clothoid is l₂ = 115 m (the wheel lifting speed on the gradient due to cant is f = 27.174 mm/s). The circular arc radius R₁ = 600 m and cant h₁ = 75 mm were assumed, which determines the unbalanced acceleration a_m = 0.551 m/s². The length of the transition curve in the form of a clothoid is l₁ = 75 m (the wheel lifting speed on the gradient due to cant is f = 25.000 mm/s). In the PL-2000 system, the straight line representing the main direction (i) is described by the formula

$$X=3,982,362.559+0.33583460\cdot Y,$$

and the line describing the direction (i +1) by equation

$$X=-14,625,109.428+3.09201655\cdot Y.$$

From the given equations of the main directions it follows that the angles of inclination of the lines are: φ_i = 0.324 rad and φ_i+1 = 1.258 rad. On this basis, the angle of return of the route α = φ_i+1 – φ_i = 0.934 rad.

Obtaining the local coordinate system x, y, with symmetrically set adjacent main directions, requires shifting the origin of the PL-2000 system to point W and rotating it with respect to this point to the left by an angle β = (φ_i + α/2) + π = 3.284 rad. In the coordinate system x, y, the angles of inclination of the straight lines will be: ${\overline{\phi }}_i$= – α/2 = – 0.467 rad, ${\overline{\phi }}_{i+1}$= α/2 = 0.467 rad.

The actual design begins with an auxiliary operation to determine the coordinates of characteristic points using the formulas given in Chapter 3. The following values ​​were obtained: $\Delta x_{TC1}$= 67.646 m, $\Delta y_{TC1}$= 32.358 m, $s_{TC1}$= 0.428108, $\Delta x_{CA1}$= 300 m (assumed value), $\Delta y_{CA1}$= 45.012 m, $\Delta x_{TC2}$ = 104.721 m, $\Delta y_{TC2}$= 47.321 m, $s_{TC2}$= 0.352862, $\Delta x_{CA2}$= 101.841 m and $\Delta y_{CA2}$= 23.087 m. The formulas given in Table 1 allowed us to determine the coordinates of points A₁, B₁, C, B₂ and A₂ (Figure 8). The values of these coordinates (and the tangents) are given in Table 4.

Further design operations are performed in the local coordinate system x, y, using the formulas given in Table 3. First, an auxiliary coordinate system x₁, y₁ is assumed, related to the transition curve TC1. The beginning of this curve (i.e. point A₁) is also the beginning of the designed geometric system. The clothoid coordinates x₁(l) and y₁(l) were determined for $l\in 〈0;75〉$ m. The value of the angle of inclination of the tangent at the end of the curve was Θ₁(l₁) = – 0.0625 rad. The next stage of the operations is to rotate the system x₁, y₁ to the right by an angle α/2. For the parametric equations x(l) and y(l) of the curve TC1, the condition $x\in 〈-294.007;-226.361〉$ m applies. The coordinates of the circular arc related to the curve TC1 were determined for $x\in 〈-226.361;73.639〉$ m.

Then, the auxiliary coordinate system x₂, y₂, related to the transition curve TC2, was used. The beginning of this curve (i.e. point A₂) is the end of the designed geometric system. The clothoid coordinates x₂(l) and y₂(l) were determined for $l\in 〈-115;0〉$ m. The value of the angle of inclination of the tangent at the end of the curve was Θ₂(l₂) = – 0.12778 rad. As a result of rotating the system x₂, y₂ to the left by an angle α/2, the parametric equations x(l) and y(l) of the curve TC2 were obtained, and the condition $x\in 〈175.480;280.201〉$ m is valid. The coordinates of the circular arc related to the curve TC2 were determined for $x\in 〈73.639;175.480〉$ m.

The length of the projection of the entire system on the abscissa axis was 574.208 m. Figure 10 shows the modeled geometric system in the local coordinate system. The green color indicates the circular arc CA1, the red color indicates the arc CA2, the blue color indicates the transition curves, and the purple color indicates the straight sections.

Finally, the obtained solution was transformed to the PL-2000 system, performing the reverse operation than was done when creating the LCS. Therefore, in the formulas used [15]

$$Y=Y_W+x\cdot \cos \left(-\beta \right)+y\cdot \sin \left(-\beta \right),$$

(29)

$$X=X_W-x\cdot \sin \left(-\beta \right)+y\cdot \cos \left(-\beta \right)$$

(30)

there is a negative value of the angle β. The final form of the geometric system is presented in Figure 11 (the colors of the markings are as in Figure 10).

8. Conclusions

This article addresses the issue of designing classic compound curves, i.e. a geometric system consisting of two circular arcs of different radii, pointing in the same direction and connected directly to each other. Compound curves are currently used on tram lines; they also occur on railways, but new ones are not built there any more. Therefore, in relation to railway lines, the aim is to obtain the possibility of reproducing (i.e. modeling) the existing geometric layout with compound curves, so that it is then possible to correct the horizontal ordinates in the area where the circular arches connect. For this purpose, it was necessary to develop an effective method for designing such a system, which, however, by assumption, will not be used to determine the coordinates of a new compound curves, but to model the existing system (with a view to its later modification).

To solve the problem, an analytical design method was used, in which individual elements of these geometric systems are described by mathematical equations. The design itself is carried out in the appropriate local Cartesian coordinate system, the basis of which are the symmetrically set adjacent main directions of the route. The origin of the local coordinate system is located at the intersection point of the adjacent main directions, the coordinates of which in the global system are known.

In order to be able to operate in the local coordinate system, one must first perform an auxiliary procedure aimed at determining the basic computational quantities. These quantities refer to the regions of the geometric system connecting the ends of the extreme straight segments (i.e. the beginnings of transition curves) with the connection point of both circular arcs. This refers to the lengths of the projections of transition curves and circular arcs on the horizontal and vertical axes.

The construction of a compound curve, i.e. the connection of the existing horizontal arcs with radii R₁ and R₂, is carried out in the auxiliary coordinate system and then transferred to the local coordinate system. The formulas for the coordinates of characteristic points are presented, in order to then finalize the design process by determining the course of the route sections located between these points. The obtained possibilities of modeling the compound curve are illustrated by the included calculation example.