1. Introduction
The automation of manipulator arm has gained tremendous attention in recent decades due to their wide range of engineering applications, such as agricultural mobile robotics [
1], mining mobile robotics [
1], space exploration mobile robotics [
2], lower limb rehabilitation robotics [
3], biped walking robotics [4[, unmanned ground vehicle [
5] and underwater robotics [
6]. There are two types of manipulator arm: underactuated one [
7,
8,
9], which is a kind of a nonlinear system with fewer control inputs than degrees of freedom, and fully actuated one [
5,
6,
10,
11], which is not. In general, underactuated manipulator arms are grouped into vertical types which are controlled by gravity and planar types which are not.
For the vertical underactuated manipulator, the linear Jacobian approximated model of the inverted equilibrium position is completely controllable because the controllability matrix of the linear Jacobian approximated model is full rank. For most traditional approaches of solving the complexity of vertical underactuated manipulator, the operation space is mainly separated into a swing-up space and a balance space. In the swing-up space, the control methods include posture-energy approach [
12], energy-based approach [
13], direct fuzzy control approach [
11], fuzzy model reference learning control approach [
11], adaptive fuzzy control approach [
11], and then the linear quadratic regulator (LQR) optimal method [
14] is applied in the balance space. However, to be quickly captured in the swing-up space for the manipulator arm, the control needs to be built an exact combination of energy and posture, and this property is difficult to be accomplished due to the complexity of the system dynamics [
9]. Moreover, some torque chattering change occurs in the swing-up space and then the energy is quickly pumped into the system [
9]. In general, in order to control the nonlinear dynamics well, the disturbance decoupling and the global stability should be simultaneously required [
15]. To achieve these requirements, some significant approaches, such as model predictive control [
16], deep rcement learning [
17], multi-objective control [
18], backstepping control [
19] and preview control [
20], have been adopted for complex nonlinear systems. However, in the aforementioned approaches, a serious common drawback is that the considered nonlinear systems should be approximated to be linear dynamics by the Taylor expansion for small effect operating range. This serious drawback may be impractical for the FLMA. To solve nonlinear serious drawback of the FLMA, nonlinear function approximators, such as neural network optimal approach [
21] and famous fuzzy method [
22], have been adopted to reduce the caused errors [
23]. The main drawback of famous fuzzy method is that constructing fuzzy rule base needs to rely on many past accumulated knowledges, and then the system performance is almost determined by the constructed experience rule base [
24]. The neural network optimal approach is an intelligent supervised learning approach that requires the operating network to offer many sample points [
25]. The performance of controller design for the neural network method is completely limited by only applying the current state value. Moreover, complicated interconnecting structure and digital computing loads let the physical realization of nonlinear function approximators be impractical. LQR is a common method that calculates the weighting matrices Q and R for a Jacobian linearized system via trial and error operation. Some improved approaches of calculating the weighting matrices, such as genetic algorithm approach and Kalman’s pole-assignment approach, have been proposed in recent decades. However, their main serious drawbacks including high computing effort and slowly convergent rate of globally optimal solution limit their performances [
26].
On the other hand, planar underactuated manipulator is not constrained by gravity, so any position of the manipulator arm is the equilibrium point and the linear Jacobian approximated model at any equilibrium point is uncontrollable [
27]. The control approaches for the vertical underactuated manipulator cannot be applied for planar underactuated manipulator. The researches of controlling planar underactuated manipulator are extensive and some important methods, such as the nilpotent approximated method [
28], the converting-chained form method [
29] and the order-reduction method [
30], have been proposed to perform the position control for planar underactuated manipulator. However, the aforementioned approaches of controlling the planar underactuated manipulator are only valid for the nominal plant model. In real systems, nonlinear acting factors need to be considered [
31] and then aforementioned approaches cannot be applied for the practical planar underactuated manipulator.
So far, it is obvious to see that the robust and tracking controller design for manipulator arm still is a challenging subject due to the strict global stability requirement and disturbances reduction involving on the nonlinear system dynamics. Stimulated by these points, we apply feedback linearized approach to construct the robust and tracking controller of manipulator arm with the almost disturbance decoupling, adjustable convergence rate and “globally” exponentially stable performances and take the place of “locally” Jacobian linearized method. Feedback linearized approach have contributed many significant researches [
32,
33,
34,
35,
36] in industrial applications, such as the dual parallel-PMSM system [
32], the grid-tied packed e-cell inverter [
33], PHEVs charging station [
34], artificial pancreas [
35] and the weak AC grid integration [
36].
References [
37,
38] had exploited the fact that the stricter tracking error condition of almost disturbance decoupling performance including absolute error, integral error and input-to-state-stable error is involved to reduce the disturbance effect. However, they can only achieve the almost disturbance decoupling performance of nonlinear system without the nonlinearity multiplied with disturbance requirement and the non-Lipschitz nonlinearity requirement. Therefore, the almost disturbance decoupling performance cannot be achieved for the following nonlinear system:
,
,
, where
and
are the output and control input, respectively. On the contrary, the almost disturbance decoupling performance can be well achieved by the proposed method. The main novelty of this study is to design robust and tracking controller for nonlinear complex FLMA. Major contributions of this study are summarized as follows:
(i) This study has “first” presented the convergence rate formula of the nonlinear FLMA.
(ii) The FLMA is first designed by applying the feedback linearized approach with the almost disturbance decoupling performance that takes the place of the traditional posture-energy approach and avoids some torque chattering change behaviour in the swing-up space. Moreover, the proposed approach takes the place of LQR approach without the necessary trial and error operations.
(iii)A robust and tracking controller is presented to possess the global exponential stability without solving the Hamilton-Jacobi equation that requires to be solved for the famous H-infinity approach.
(iv)The study has proposed a new approach to improve the shortcoming of traditional fuzzy function approximators without many design experiences and knowledges.
(v)The implications of this proposed method are “globally” valid, whereas the Jacobian linearized approach is “locally” valid.
2. Complete Mathematical Model for Four-link Manipulator Arm
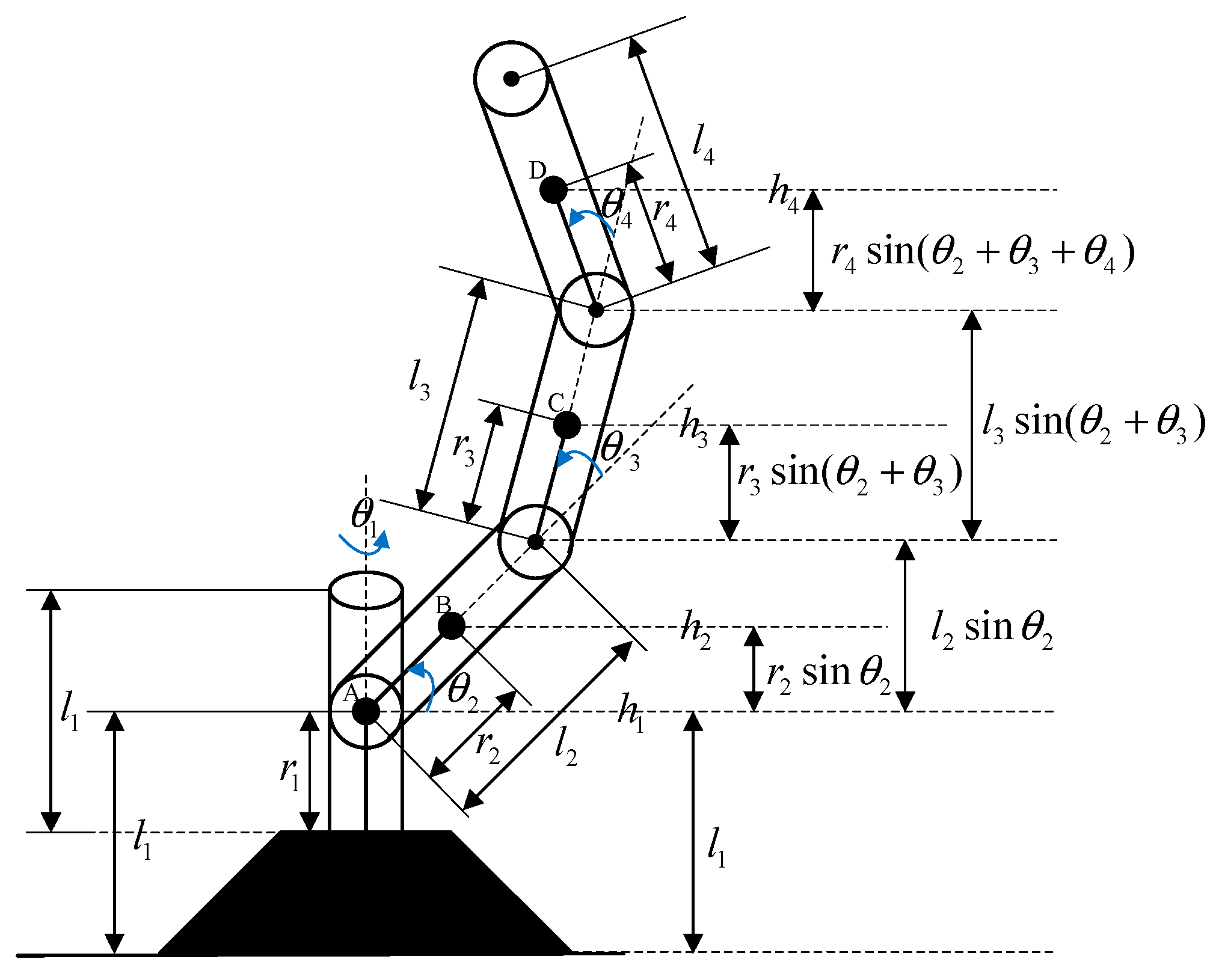
The FLMA is a great platform for industrial mechanics as it is highly nonlinear control system with disturbances. In this section, we will apply Euler-Lagrange equation to derive the dynamic equations of the FLMA shown in
Figure 1.
Four-link manipulator arm is made up of aluminum. The dynamic model parameters are selected as follows: the length of link
, the distance for the center of mass
, the mass of link
and the inertia moment of link
. Defining the potential energy
, the kinetic energy
, the joint torque
, the Lagrangian term
as the difference between the kinetic energy and potential energy, and applying the Euler–Lagrange equation yield the dynamic equation of the FLMA to be
Let the centroid translational position vector and velocity vector of link
be
and
, and centroid rotational position vector and velocity vector of link
be
and
. From the fundamental definitions of position vector and velocity vector, we get
and
Then the kinetic energy
of the manipulator arm will be given by
Substituting (10)~(12) to (9) obtains
From (1)(2) and (13), we get
Since the matrix
possesses positive definite property and
, we get
i.e.
From (17)~(19), it is more practical to rewrite the Euler–Lagrange equation of the manipulator arm in more compact form for control purpose as follows:
where
is the vector of gravity force,
denotes the Coriolis matrix of the manipulator arm. Observing the structure of (19) obtains
where
Then (12) can be rewritten to be
Observing
Figure 1 yields the centroid translational position vector to be
,
,
and
where
and
.
,
,
,
. Applying (6) to the centroid translational position vector gets
Observing
Figure 1 yields the centroid rotational position vector to be
,
,
and
. Using (8) to the centroid rotational position vector obtains
Substituting (24)~(25) and (27)~(34) to (25) yields the matrix
as
where
Let us combine (21) and (22) and get the matrix
as
where
From
Figure 1, we get the potential energy of manipulator arm as
where
. Applying (19) gets
Using (35) yields the inverse of the matrix
to be
where
From (43) and (63), we get
where
Multiplying (63) with (19) yields
where
Substituting (63), (72) and (87) to (92) gets
Define the state, input and noise variables of the FLMA to be the following physical quantities: ,,,,,,,,,,, , and .
Therefore, the state-space dynamic model of the FLMA with real physical values can be represented as
Then the nominal system will be
and it is assumed to have the vector relative frequency
[
39]:
<i> The following condition holds:
for all
,
, where the symbol
is the Lie operator.
<ii>The square matrix
has nonsingular property. The norms of pre-specified tracking signals
and its first
derivatives are bounded by positive constants
as
and the spanning distribution
is involutive.
3. Robust and Tracking Controller Design of the FLMA System
Since the FLMA system has the well-defined relative degree property and involutive distribution performance, then the mapping
defined as
and
is an one-to-one and onto, infinitely continuous and differentiable function according to reference [
39,
40], i.e,
Assume that the nonlinear FLMA system possesses the well-defined involutive property. Then the mapping
defined by (124)~(127) is a one-to-one and onto, infinitely continuous and differentiable function and it will transform original nonlinear system into partially linear subsystem and partially nonlinear subsystem as follows [
39,
40] as follows:
Since
the transformed dynamics of nonlinear FLMA system (139)~(145) can be rewritten to be
To build the robust feedback linearization controller
we use the vector
and the virtual input [
39]
Then we can transform (152) into the following model
Next we will demonstrate in detail how to design the robust and tracking controlle
with the pre-specified tracking signals
. The initial values of the states are set to be
The desired robust and tracking controller is built by
where
is the desired tracking signal and
are elements of the Hurwitz matrix shown by
Based on feedback linearization approach, then we propose the robust controller with the pre-specified tracking signals
as follows:
For the convenience of the following discussions, let’s define some related parameters as
where the Lyapunov system matrix
is a Hurwitz matrix whose eigenvalues lies in the left half coordinate plane and one can use Matlab to obtain the adjointing Lyapunov system matrix
of the following Lyapunov equation:
and
To demonstrate further the complete feedback linearization control design of nonlinear FLMA system, let’s define one assumption and two definitions as
Assumption 1. The following inequality holds:
where
and
.
Definition 1. Consider a nonlinear system
with an Lipschitz input
, where
is Lipschitz state variable,
is differentiable and infinitely continuous. This system is defined to be input-to-state stable if
where
is a
-class function and
denotes a
-class function.
Definition 2. A nonlinear system with noise inputis defined to possess the almost disturbance decoupling performance, if the following properties hold:
<i>The nonlinear system has input-to-state stable property for noise input.
<ii>Output tracking errors meet the following two inequalities for initial time
and the initial state
:
and
where
belongs to
-class function,
and
are positive constants, and
,
belong to
-class functions. From (159), we get
From (171),(173) and (188), we obtain
Substituting (161) and (162) into (189) obtains
Then, from (145), (153), (162), (174) and (190), we obtain
where
It is worth noting that the one-to-one and onto, infinitely continuous and differentiable function converts the original nonlinear FLMA into a partially nonlinear subsystem and partially linear subsystem whose state variables are denoted by
and
, respectively. In order to meet the requirements (184) and
we construct
and
to be the Lyapunov functions of nonlinear subsystem (192) and linear subsystem (191), respectively and then combine these Lyapunov functions to be a composite Lyapunov function
as follows:
where the function
satisfies
and
Then, the differentiation of the composite Lyapunov function
is described as
where the matrix
is positive definite, and
i.e.
where
denotes the minimum eigenvalue of the matrix
.
Applying (217) into (216) yields
Next, we will prove the fact that the proposed feedback linearization control achieves the almost disturbance decoupling performance, and the globally exponential stability of the FLMA system in
Appendix A. Therefore, the proposed robust tracking control (163) will indeed drive the tracking errors of the FLMA system into the global ultimate attractor.
Noting that we can extend above complete design process to obtain one more general significant theorem for general uncertain nonlinear control systems with disturbances as follows:
i.e.,
where
,
denote the input and output, respectively,
is the state variable,
is the noise vector,
denotes the noise_adjoint vector. Assume
,
and
to be continuous functions, and
to be the matched uncertainty vector term
, where
is defined to be the uncertainty vector.
Assumption 2. The following inequality holds:
where
and
.
Then the nominal system will be
and it is assumed to have the vector relative frequency
[
39]:
<i>The following condition holds:
for all
,
, where the symbol
is the Lie operator.
<ii>The square matrix
has nonsingular property. The norms of pre-specified tracking signals
and its first
derivatives are bounded by positive constants
as:
and the spanning distribution
is involutive. Then the mapping
defined as
and
is an one-to-one and onto, infinitely continuous and differentiable function according to reference [
39].
Let
and
be the Lyapunov functions of nonlinear subsystem and linear subsystem, respectively and then combine these Lyapunov functions to be a composite Lyapunov function
as follows:
Theorem 1. A differentiable and infinitely continuous function
for transformed nonlinear subsystem can be found to make the following three inequalities hold:
Design the robust and tracking controller to be
Then the nonlinear system possesses the almost disturbance decoupling performance with the globally exponential stability:
where the matrix
is positive definite, and the continuous function
satisfies
and
Moreover, the desired tracking errors can be exponentially reduced by adjusting the parameter
with the convergence rate formula
and the desired tracking errors of control system are exponentially attracted into a global final attractor
with the convergence radius formula
To effectively build robust and tracking controller, a significant algorithm of FLMA is summarized as follows, and then a powerful Python software system of controller design is constructed in the next section according to this proposed algorithm.
(Step 1)Obtain the vector relative frequencyaccording to the given outputs.
(Step 2)Appropriately construct the one-to-one and onto, infinitely continuous and differentiable functionbased on (123)~(127).
(Step 3)From (162) and (178), appropriately choose parameterssuch thatare Hurwitz matrices with stable eigenvalues and obtain the positive definiteof the Lyapunov equation with the aid of Matlab toolbox.
(Step 4)Choose the Lyapunov functionto meet the requirements (184) and (198)~(200). If the vector relative frequency is equal to the system dimension, i.e. , then this step will be omitted and directly go to (Step 5).
(Step 5)From (212)~(215), (217)~(220), appropriately design parameters to meet. It is worth noting that if the value ofis larger, the convergence rate is faster.
(Step 6)Finally, the robust and tracking controller can be built by (163).
5. Comparisons to Traditional Approaches
In this section, we will compare the performance of proposed approach with traditional fuzzy approach [
41] and the singular perturbation method with high-gain feedback [
38].
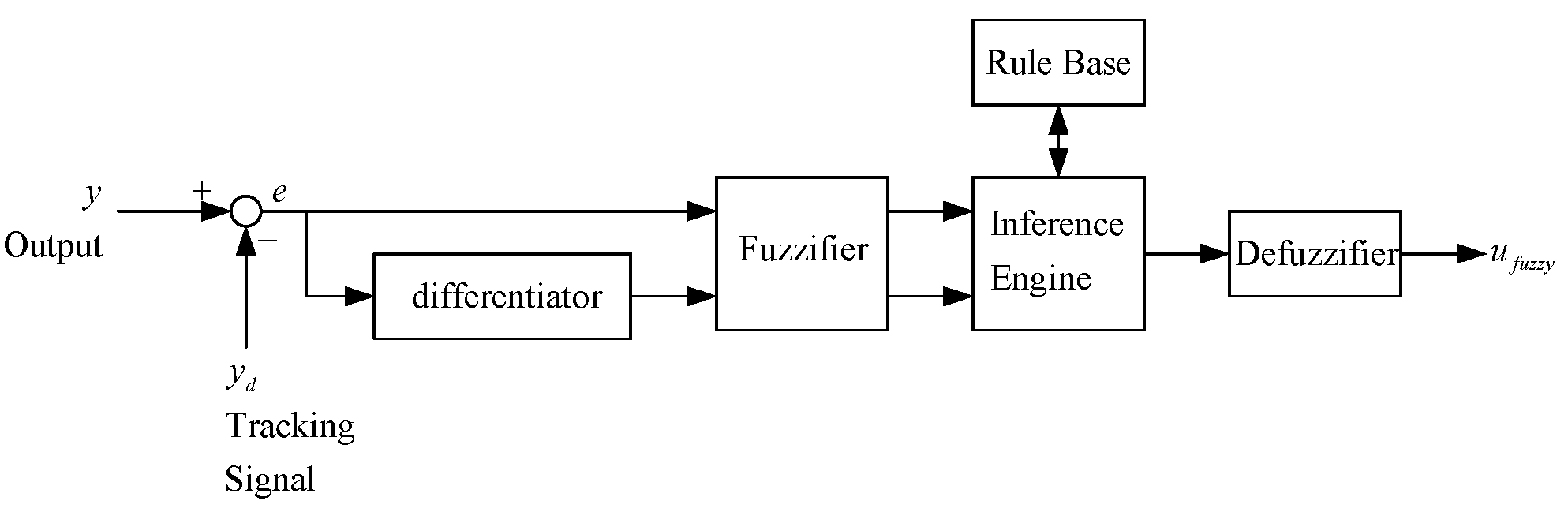
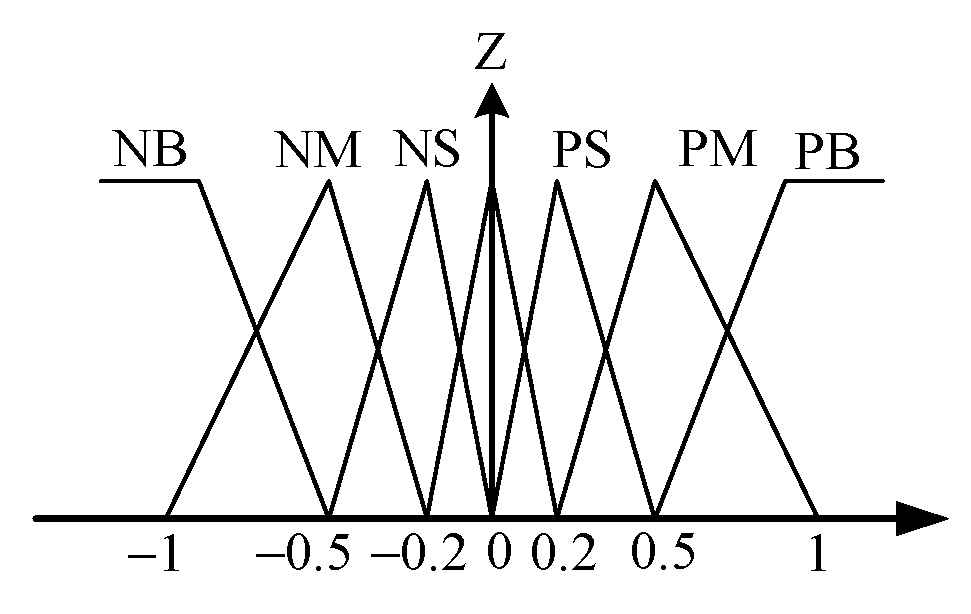
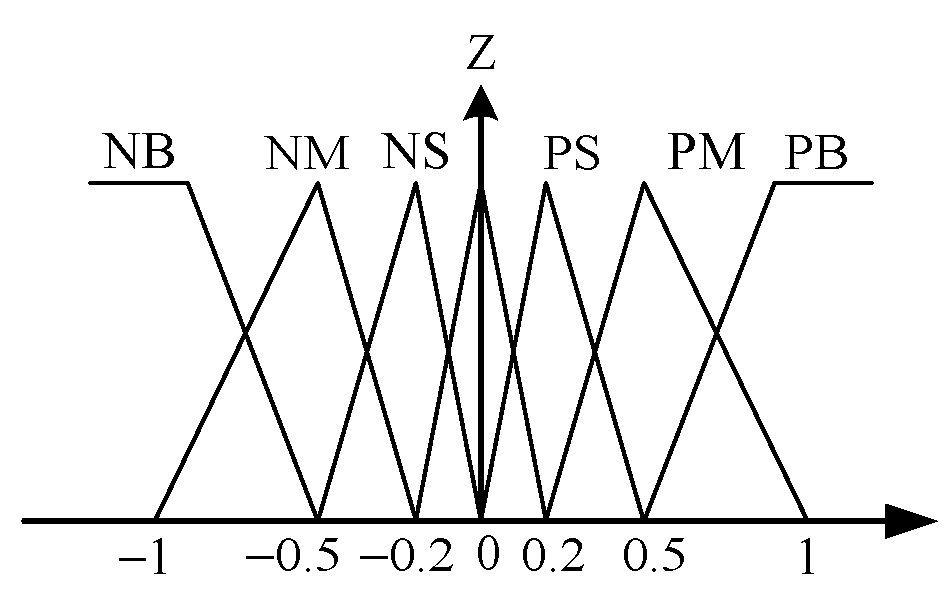
Figure 7 is the general structure of traditional fuzzy approach whose input variables of the IF-THEN rules are assigned to be the tracking error
and its time derivative
. The output variable is the fuzzy control
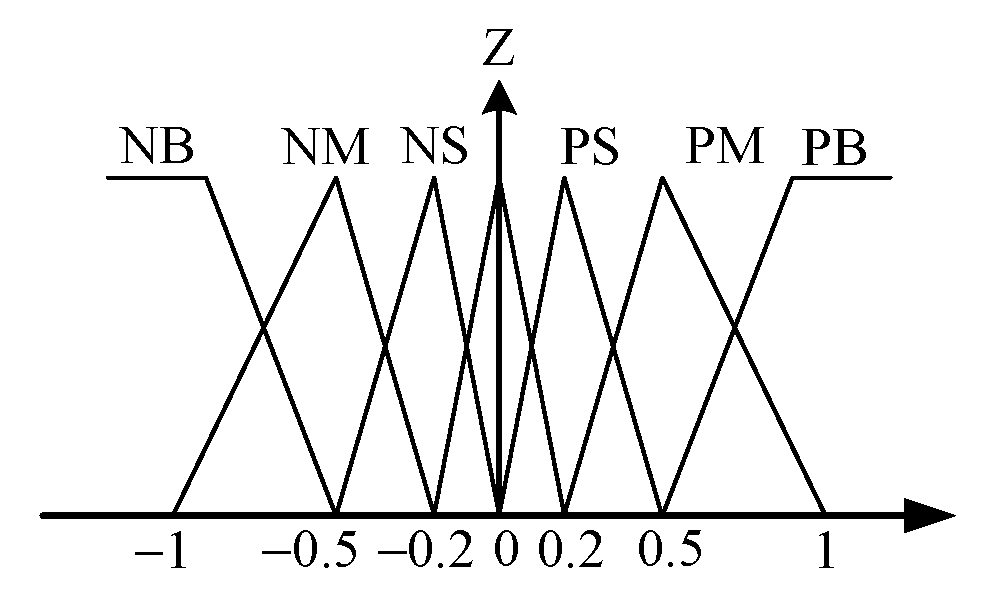
. For easy calculation, the desired membership functions of
,
and
are assigned to be the triangular shape functions as shown in
Figure 8,
Figure 9 and
Figure 10. The desired fuzzy control rule base for
is constructed in
Table 1. The rule base, fuzzy inference engine and defuzzifier adopt the standard Macvicar-Whelan rule base, the Mamdani method and the centroid method, respectively.
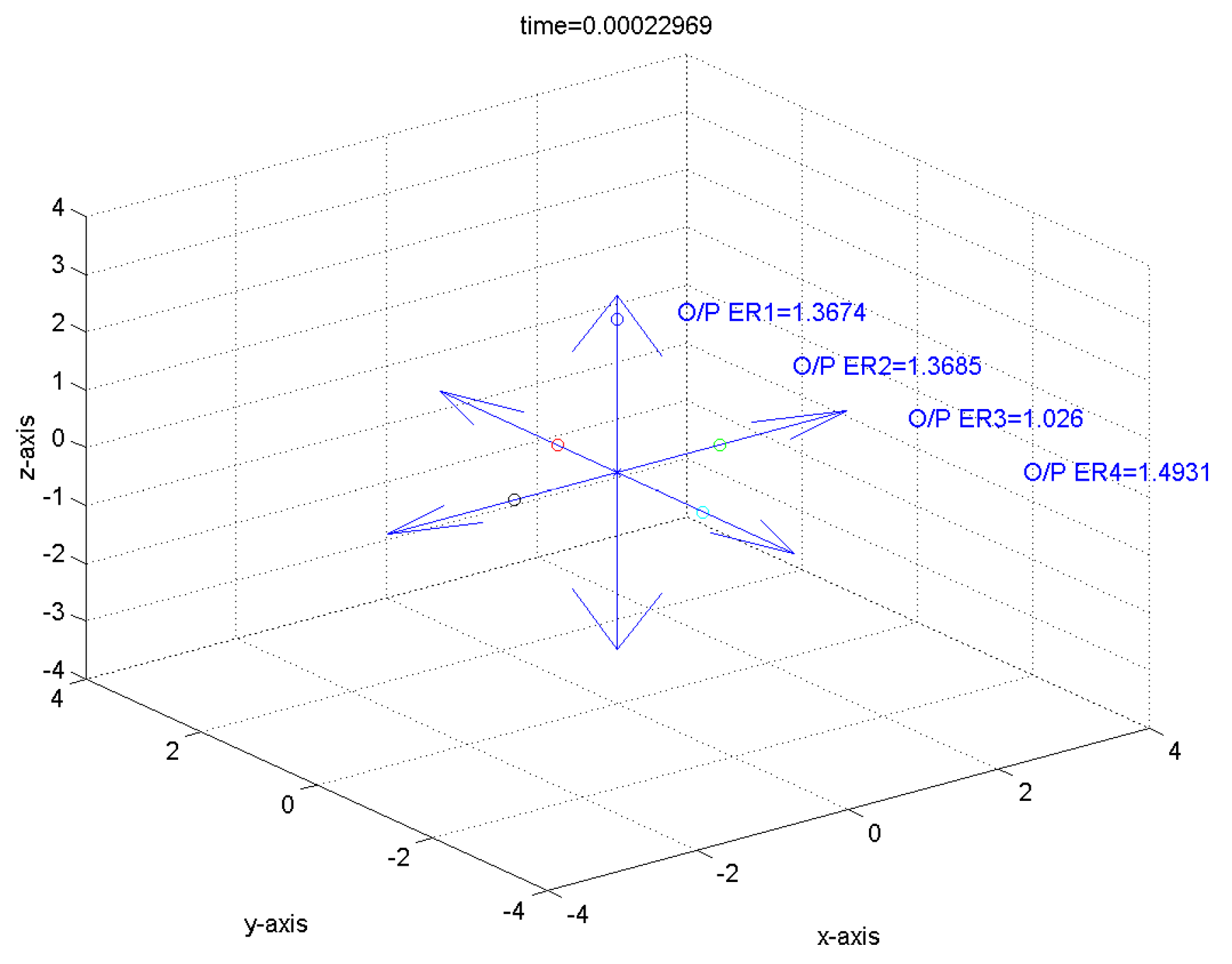
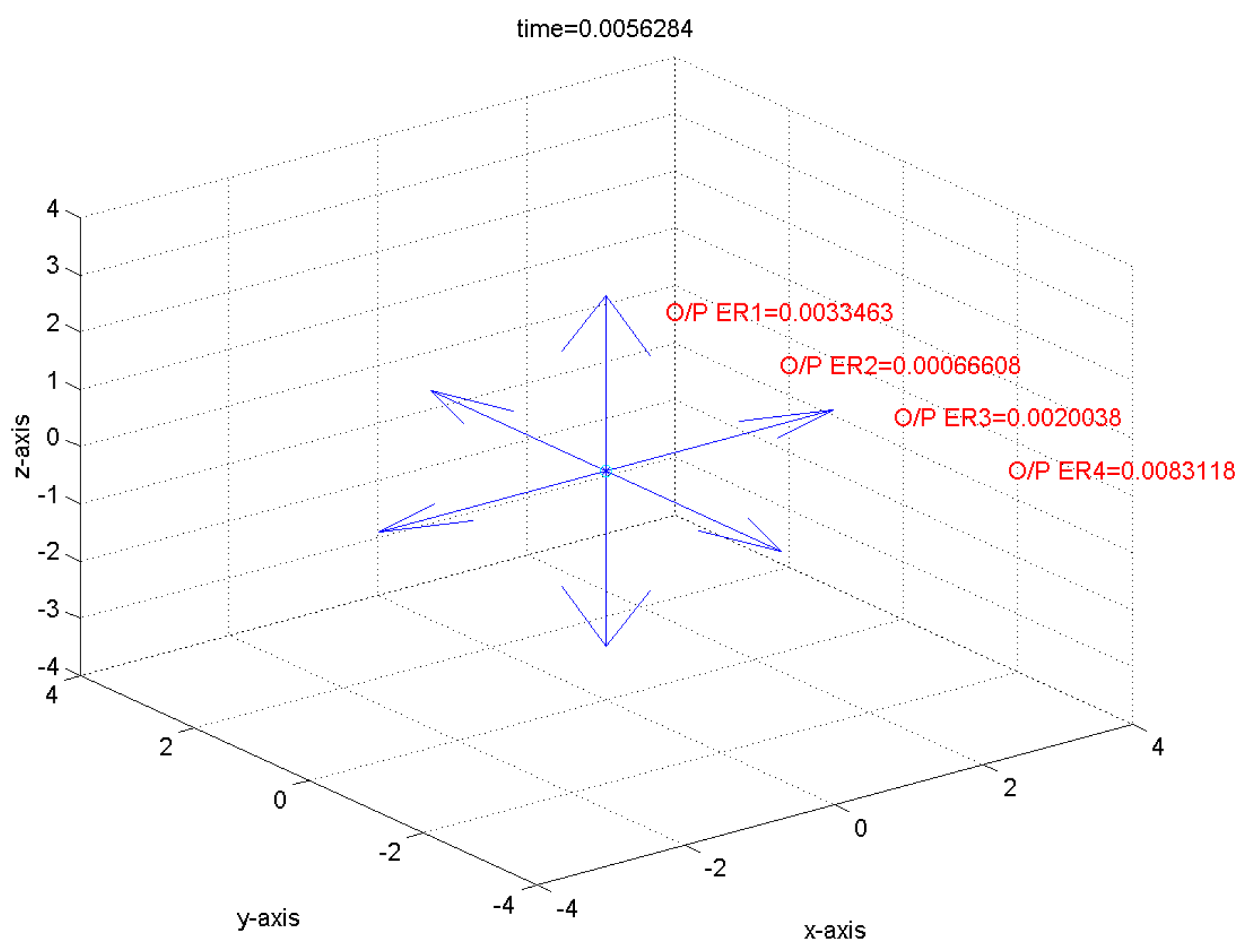
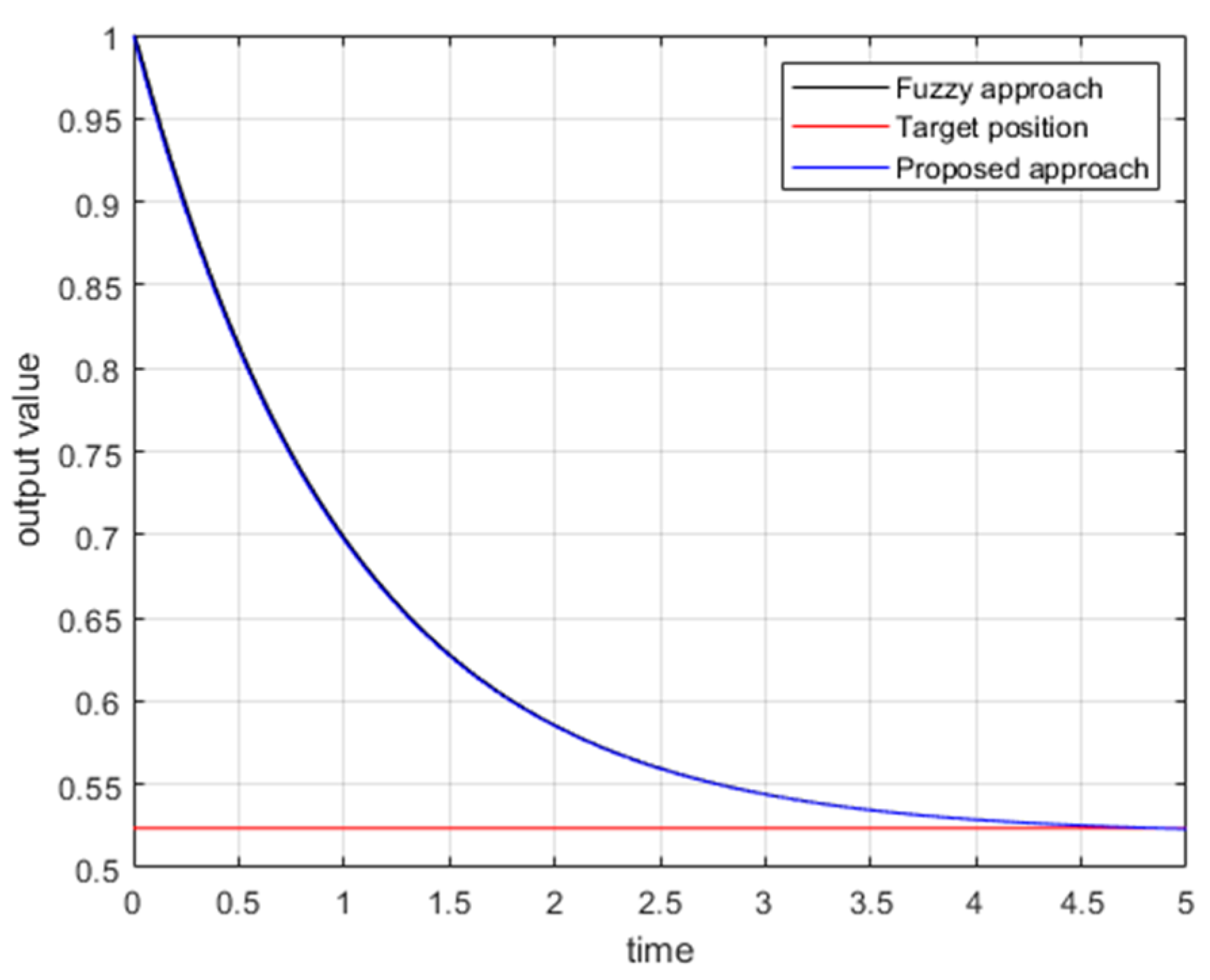
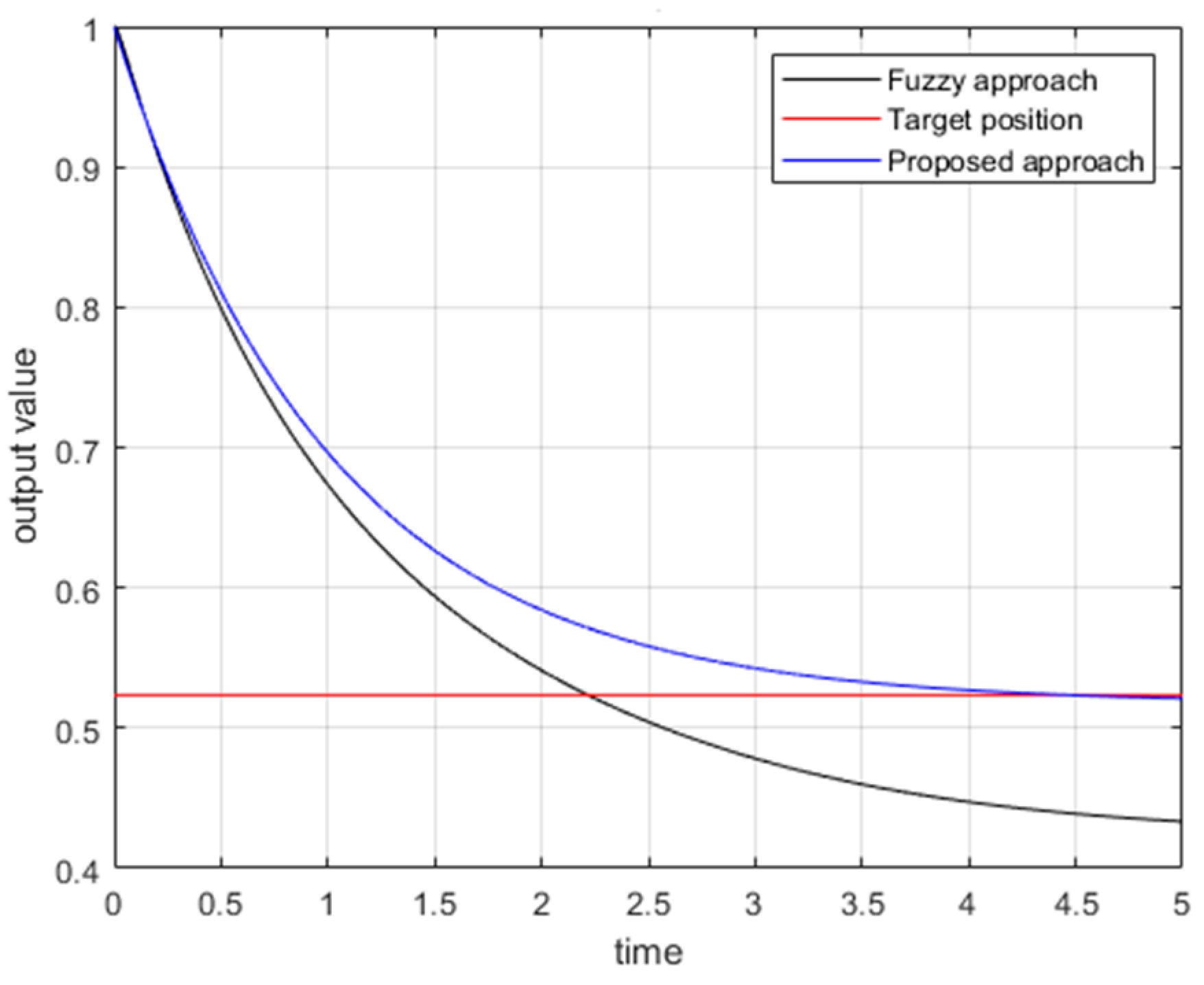
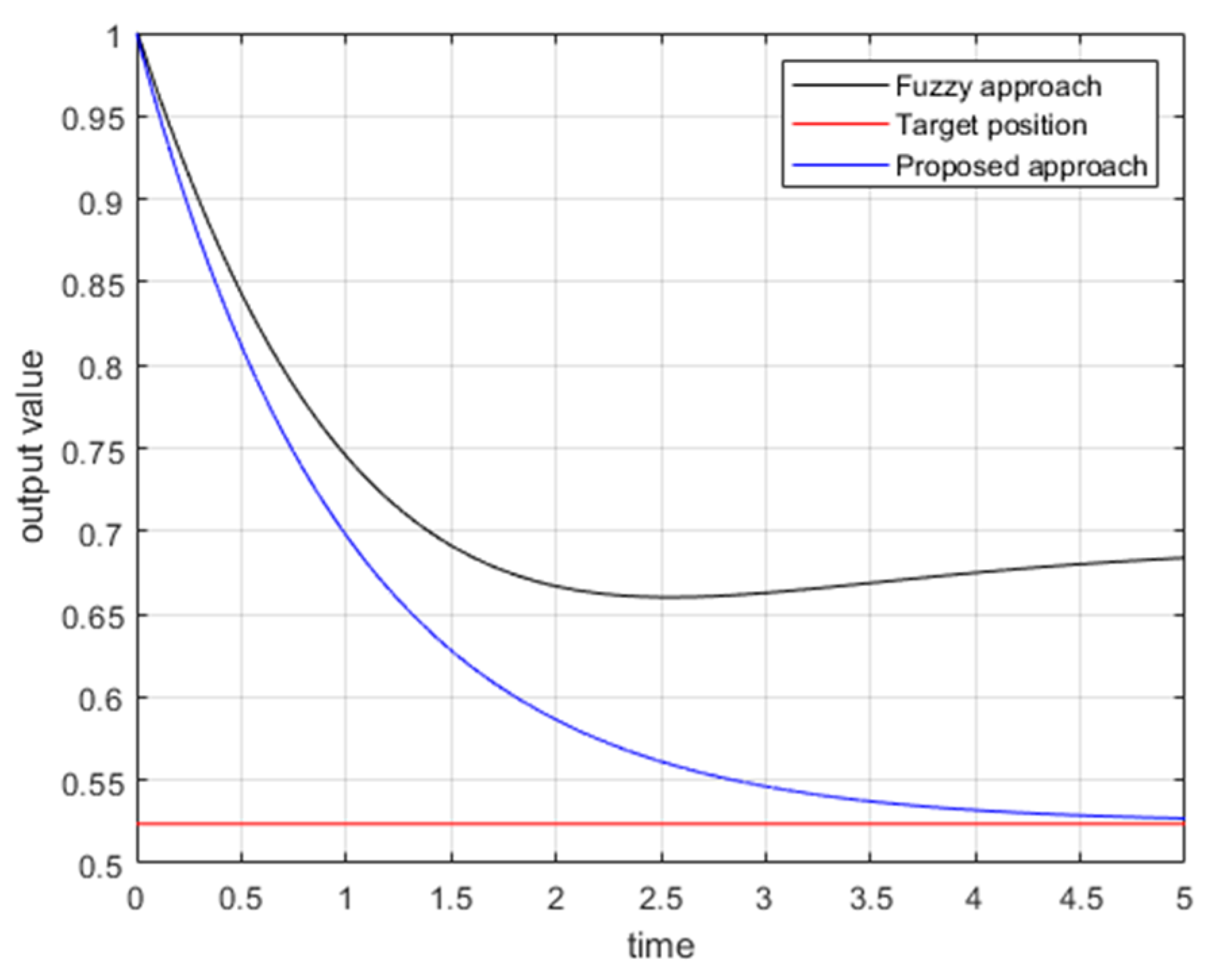
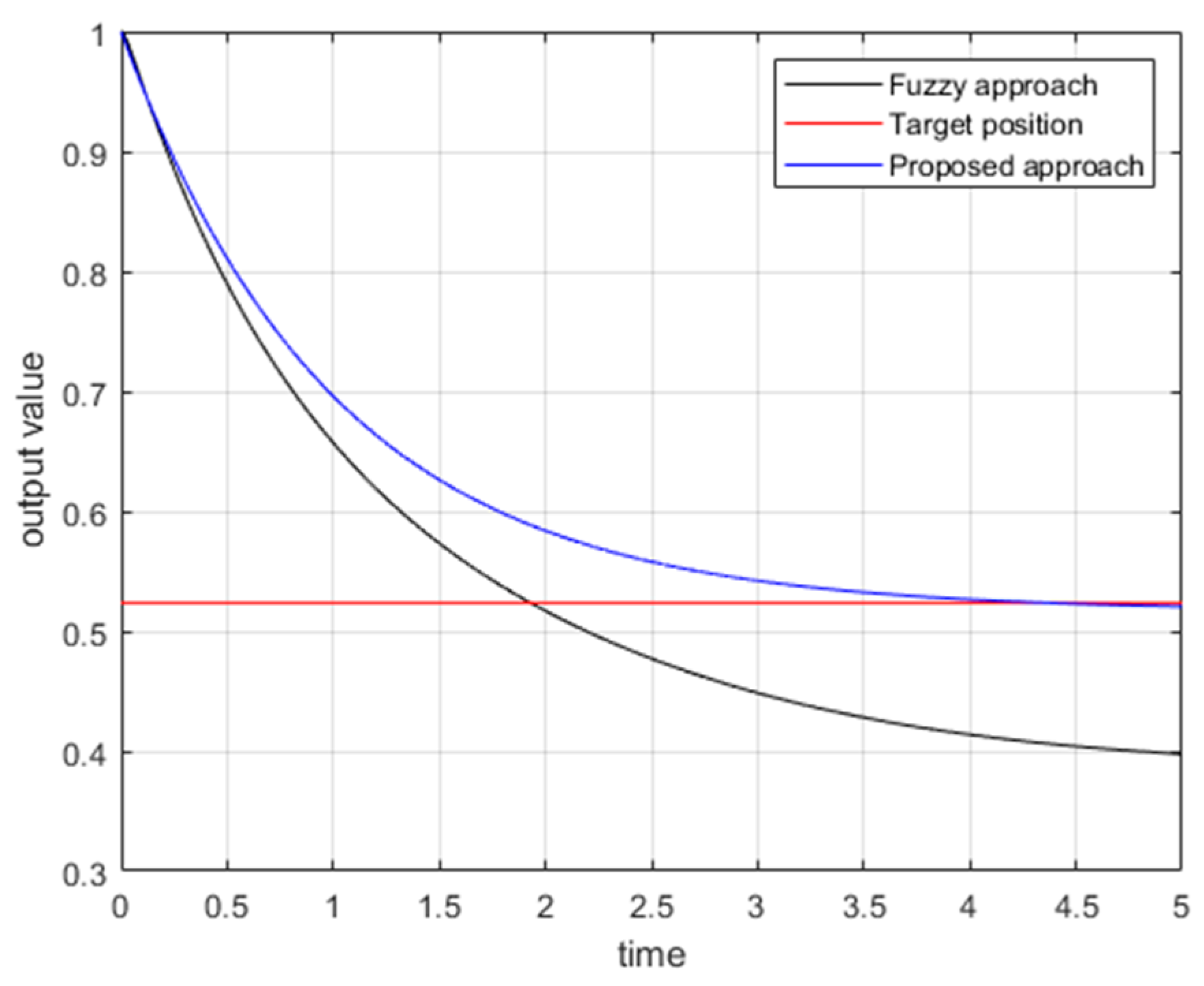
With the aid of Matlab fuzzy toolbox, comparative tracking error responses of the proposed approach and traditional fuzzy controller design for the FLMA are shown in
Figure 11,
Figure 12,
Figure 13 and
Figure 14. From
Figure 11,
Figure 12,
Figure 13 and
Figure 14, it is obvious to see that the convergence rate of the proposed approach is faster than the traditional fuzzy approach.
Following the second comparative example, we will make some comparison between the proposed approach and the famous singular perturbation method [
37,
38]. The sufficient condition in [
37,
38] needs that the nonlinearity multiplied by the disturbance meets the structural triangle criterion.
References [
37,
38] had exploited the fact that the following system cannot achieve the almost disturbance decoupling performance:
It is easy to derive the following items:
,
,
,
and
Hence the sufficient condition of [
37,
38] is not satisfied since
is not complete, and then the almost disturbance decoupling problem cannot be not solved. On the contrary, this almost disturbance decoupling problem can be solved via the proposed approach by the controller
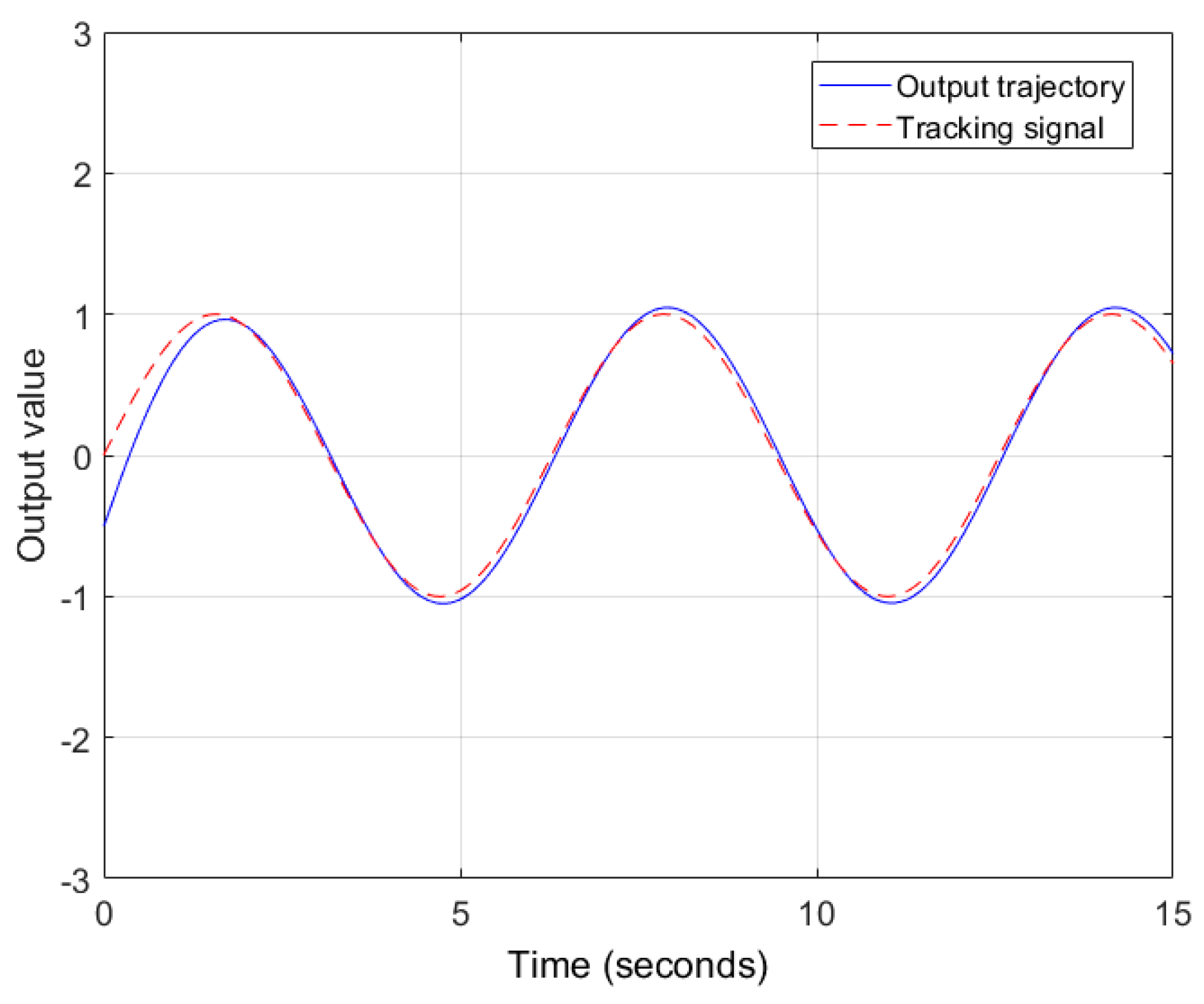
The output response of the nonlinear system for (263) is shown in
Figure 15. Therefore, the designed controller can indeed make the output track the pre-specified signals
and achieve the almost disturbance decoupling performance.