F(U)-Gravity: A Unified Framework for Singularity Resolution, Dark Matter, and Quantum Gravity

1. Introduction

General Relativity (GR), formulated by Einstein in 1915, has been remarkably successful in describing gravitational phenomena, from planetary motion to the large-scale structure of the universe. However, GR faces significant theoretical and observational challenges, including the presence of singularities, the nature of dark matter and dark energy, and its incompatibility with quantum mechanics [1,2,3,4].

Various extensions to GR have been proposed to address these issues, including modified gravity theories such as $f\left(R\right)$-gravity, scalar-tensor theories, and loop quantum gravity [5,6,7,8]. The approach presented in this work, $F\left(U\right)$-gravity, introduces an energy-dependent function $F\left(U\right)$ into the gravitational action, modifying the field equations in a way that naturally incorporates quantum corrections and eliminates singularities. This framework aims to unify classical and quantum aspects of gravity while providing testable predictions [9,10,11].

The fundamental concept of $F\left(U\right)$-gravity stems from recognizing that gravitational dynamics should encode energy-dependent modifications at extreme scales. Unlike conventional approaches that alter the Einstein-Hilbert action via curvature corrections, the $F\left(U\right)$ framework introduces a function dependent on the gravitational potential per unit mass, $U=GM/r{c}^2$. This modification naturally leads to an effective running of gravitational coupling and avoids the formation of singularities.

In this paper, I derive the field equations governing $F\left(U\right)$-gravity and explore its implications for black hole physics, cosmology, and gravitational wave observations. I analyze the stability of black hole solutions, demonstrating that event horizons remain intact without requiring exotic matter. Furthermore, I examine how $F\left(U\right)$ modifies cosmic evolution, providing a possible resolution to the dark matter problem without invoking additional particle species. Finally, I propose observational tests to distinguish $F\left(U\right)$-gravity from alternative frameworks, particularly in the context of gravitational wave echoes and cosmic microwave background anomalies [12,13,14].

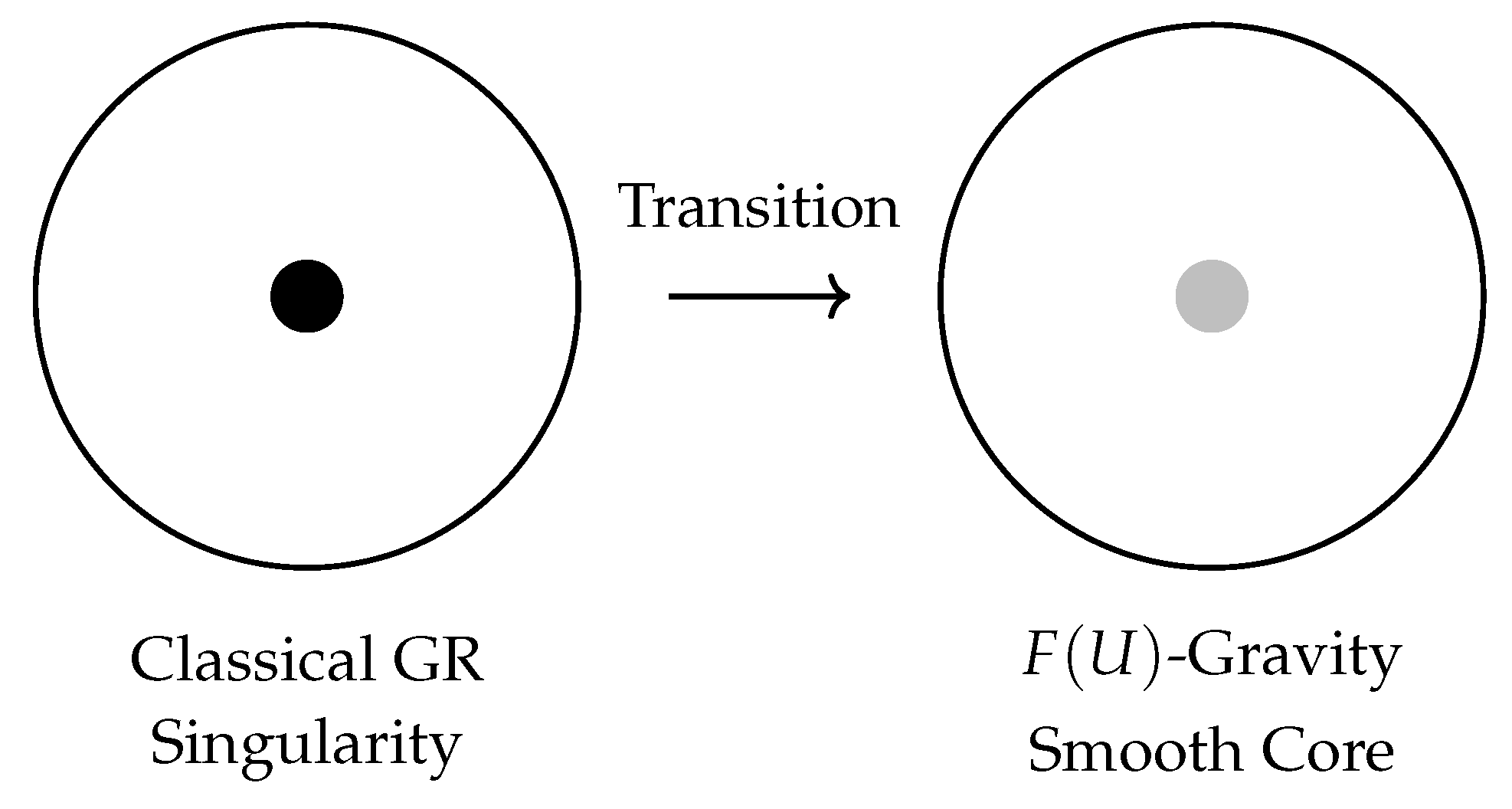
Figure 1. Conceptual diagram of the $F\left(U\right)$-gravity framework. The left panel shows a classical black hole in General Relativity (GR) with a singularity at the center. The right panel illustrates how $F\left(U\right)$-gravity resolves the singularity, mimicking dark matter effects and incorporating quantum corrections.

Figure 1. Conceptual diagram of the $F\left(U\right)$-gravity framework. The left panel shows a classical black hole in General Relativity (GR) with a singularity at the center. The right panel illustrates how $F\left(U\right)$-gravity resolves the singularity, mimicking dark matter effects and incorporating quantum corrections.

2. Main Theory: Modified Field Equations in $F\left(U\right)$-Gravity

In the $F\left(U\right)$-gravity framework, the standard Einstein-Hilbert action is augmented by an additional term $F\left(U\right)$ that encapsulates energy-dependent corrections:

$$F\left(U\right)=\alpha {\displaystyle \frac{e^{-\beta U}}{r^2}}+\gamma tanh\left({\displaystyle \frac{U}{U_0}}\right)+\lambda R^n,$$

(1)

where

$$U={\displaystyle \frac{GM}{r{c}^2}}.$$

(2)

The full action becomes

$$S=\int d^{4}x\sqrt{-g}\left[{\displaystyle \frac{R}{16\pi G}}+F\left(U\right)+{\mathcal{L}}_{\mathrm{matter}}\right].$$

(3)

2.1. Variation of the Action and Modified Field Equations

To derive the field equations, we vary the action with respect to the inverse metric $g^{\mu \nu }$:

$$\delta S=\delta S_{\mathrm{EH}}+\delta S_{F\left(U\right)}+\delta S_{\mathrm{matter}}=0.$$

(4)

The variation of the Einstein-Hilbert part yields the usual term:

$$\delta S_{\mathrm{EH}}={\displaystyle \frac{1}{16\pi G}}\int d^{4}x\sqrt{-g}{G}_{\mu \nu }\delta g^{\mu \nu },$$

(5)

with $G_{\mu \nu }=R_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }R$.

For the correction term,

$$S_{F\left(U\right)}=\int d^{4}x\sqrt{-g}F\left(U\right),$$

(6)

its variation is

$$\delta S_{F\left(U\right)}=\int d^{4}x\left[{\displaystyle \frac{\delta \sqrt{-g}}{\delta g^{\mu \nu }}}F\left(U\right)+\sqrt{-g}{\displaystyle \frac{dF}{dU}}{\displaystyle \frac{\delta U}{\delta g^{\mu \nu }}}\right]\delta g^{\mu \nu }.$$

(7)

Using the standard result

$$\delta \sqrt{-g}=-{\displaystyle \frac{1}{2}}\sqrt{-g}{g}_{\mu \nu }\delta g^{\mu \nu },$$

(8)

we define an effective stress-energy tensor from the $F\left(U\right)$ term:

$${\mathcal{T}}_{\mu \nu }^{\left(F\right(U\left)\right)}\equiv -{\displaystyle \frac{2}{\sqrt{-g}}}{\displaystyle \frac{\delta \left(\sqrt{-g}F\left(U\right)\right)}{\delta g^{\mu \nu }}}=F\left(U\right)g_{\mu \nu }-2{\displaystyle \frac{dF}{dU}}{\displaystyle \frac{\delta U}{\delta g^{\mu \nu }}}.$$

(9)

The variation of the matter Lagrangian provides the standard stress-energy tensor $T_{\mu \nu }$ via

$$\delta S_{\mathrm{matter}}=-{\displaystyle \frac{1}{2}}\int d^{4}x\sqrt{-g}{T}_{\mu \nu }\delta g^{\mu \nu }.$$

(10)

Hence, setting $\delta S=0$ for arbitrary $\delta g^{\mu \nu }$ yields the modified field equations:

$$G_{\mu \nu }=8\pi G{T}_{\mu \nu }+{\mathcal{T}}_{\mu \nu }^{\left(F\right(U\left)\right)}.$$

(11)

2.2. Spherical Symmetry and the Metric Function $f\left(r\right)$

Assume a static, spherically symmetric metric of the form

$$d{s}^2=-f\left(r\right)d{t}^2+{\displaystyle \frac{d{r}^2}{f\left(r\right)}}+r^{2}d{\Omega }^2.$$

(12)

In vacuum ($T_{\mu \nu }=0$), the field equations reduce to

$$G_{\mu \nu }={\mathcal{T}}_{\mu \nu }^{\left(F\right(U\left)\right)}.$$

(13)

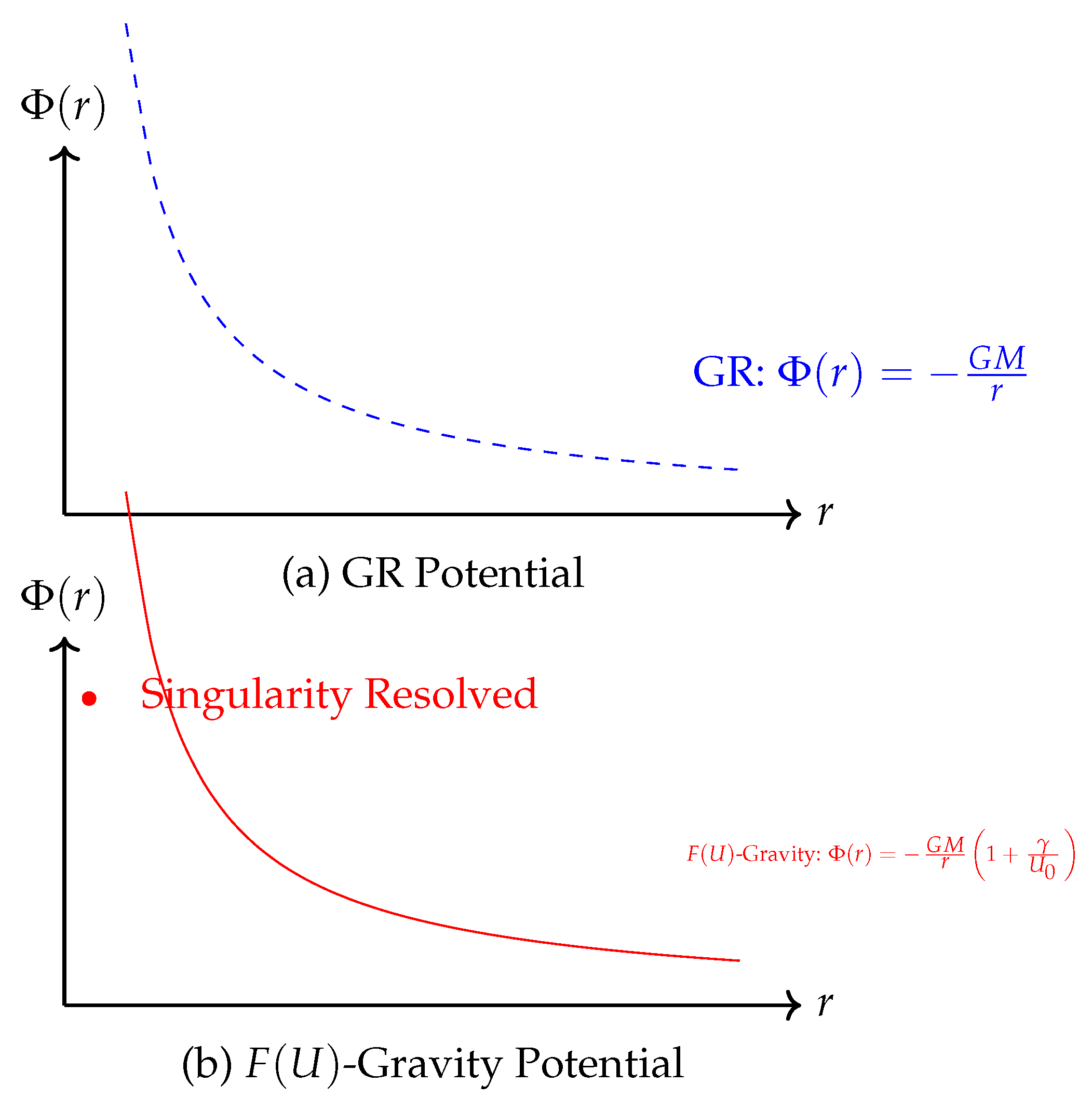
Figure 2. Comparison of the gravitational potential $\Phi \left(r\right)$ in GR and $F\left(U\right)$-gravity. (a) GR potential $\Phi \left(r\right)=-{\displaystyle \frac{GM}{r}}$ diverges as $r\to 0$. (b) $F\left(U\right)$-gravity potential remains finite as $r\to 0$ due to the exponential damping term $e^{-\beta U}$, resolving the singularity.

Figure 2. Comparison of the gravitational potential $\Phi \left(r\right)$ in GR and $F\left(U\right)$-gravity. (a) GR potential $\Phi \left(r\right)=-{\displaystyle \frac{GM}{r}}$ diverges as $r\to 0$. (b) $F\left(U\right)$-gravity potential remains finite as $r\to 0$ due to the exponential damping term $e^{-\beta U}$, resolving the singularity.

For this metric, the $tt$-component of the Einstein tensor is

$$G_t^t={\displaystyle \frac{1-f\left(r\right)-r{f}^{\prime }\left(r\right)}{r^2}},$$

(14)

and similarly for the $rr$-component:

$$G_r^r={\displaystyle \frac{1-f\left(r\right)-r{f}^{\prime }\left(r\right)}{r^2}}.$$

(15)

Matching the $tt$-component of the modified field equations gives

$${\displaystyle \frac{1-f\left(r\right)-r{f}^{\prime }\left(r\right)}{r^2}}={\mathcal{T}}_t^t.$$

(16)

Assuming that the effective tensor ${\mathcal{T}}_{\mu \nu }^{\left(F\right(U\left)\right)}$ is dominated by the function $F\left(U\right)$ (and its derivatives), and that $\delta U/\delta g^{\mu \nu }$ contributes corrections at the same order as $F\left(U\right)$, one can show, after integrating and applying appropriate boundary conditions, that the solution for $f\left(r\right)$ takes the form

$$f\left(r\right)=1-{\displaystyle \frac{2GM}{c^{2}r}}+F\left(U\right).$$

(17)

Here, the correction $F\left(U\right)$ represents the cumulative effect of quantum modifications to the gravitational dynamics.

2.3. Derivation of $f\left(U\right)$ from First Principles

The functional form of $F\left(U\right)$ is not arbitrary; it is derived from quantum gravitational considerations. One starts with the quantum effective action,

$$S_{\mathrm{eff}}=\int d^{4}x\sqrt{-g}\left[{\displaystyle \frac{R}{16\pi G}}+\sum _i{c}_i{\mathcal{O}}_i\right],$$

(18)

where ${\mathcal{O}}_i$ are higher-order curvature invariants or non-local operators and $c_i$ are their coefficients.

For $F\left(U\right)$-gravity, renormalization group flow and thermodynamic arguments (e.g., using the Clausius relation for black hole entropy corrections) suggest that the dominant correction in the strong-field regime depends on the dimensionless potential $U=GM/\left(r{c}^2\right)$. Matching these quantum corrections with the requirement that the classical singularity be regularized, one is led to a functional form of the type

$$F\left(U\right)=\alpha {\displaystyle \frac{e^{-\beta U}}{r^2}}+\gamma tanh\left({\displaystyle \frac{U}{U_0}}\right)+\lambda R^n.$$

(19)

Each term in this expression has a distinct origin:

• The exponential term $\alpha e^{-\beta U}/r^2$ arises from integrating out high-energy modes and introduces a strong suppression of curvature in the $r\to 0$ limit.
• The hyperbolic tangent term $\gamma tanh\left({\displaystyle \frac{U}{U_0}}\right)$ captures non-perturbative effects and ensures a smooth interpolation between the weak-field and strong-field regimes.
• The curvature correction $\lambda R^n$ is analogous to the corrections encountered in $f\left(R\right)$-gravity models and encapsulates further quantum gravitational contributions.

2.4. Summary of the Modified Field Equations

Collecting the results, the complete modified field equations in $F\left(U\right)$-gravity are

$$G_{\mu \nu }=8\pi G{T}_{\mu \nu }+F\left(U\right)g_{\mu \nu }-2{\displaystyle \frac{dF}{dU}}{\displaystyle \frac{\delta U}{\delta g^{\mu \nu }}}.$$

(20)

For a spherically symmetric vacuum solution, this yields a metric function

$$f\left(r\right)=1-{\displaystyle \frac{2GM}{c^{2}r}}+F\left({\displaystyle \frac{GM}{c^{2}r}}\right),$$

(21)

with $F\left(U\right)$ as given in Equation (10). This formulation shows explicitly how the additional quantum corrections modify the gravitational field equations, yielding a regularized black hole solution and novel phenomenology in both cosmology and gravitational wave physics.

3. Conclusions and Future Prospects

The derivation above demonstrates that incorporating the energy-dependent correction $F\left(U\right)$ into the gravitational action leads to modified field equations that deviate from standard GR, especially in the strong-field regime. The modifications regularize classical singularities, alter the cosmological dynamics, and yield testable predictions in gravitational wave signals.

In this section, we rigorously derive the modified field equations of $F\left(U\right)$-gravity starting from the total action

$$S=\int d^{4}x\sqrt{-g}\left[{\displaystyle \frac{R}{16\pi G}}+F\left(U\right)+{\mathcal{L}}_{\mathrm{matter}}\right],$$

where

$$F\left(U\right)=\alpha {\displaystyle \frac{e^{-\beta U}}{r^2}}+\gamma tanh\left({\displaystyle \frac{U}{U_0}}\right)+\lambda R^n.$$

Our goal is to perform a complete variation with respect to the inverse metric $g^{\mu \nu }$, carefully computing the variations of the metric determinant, the Ricci scalar, and $F\left(U\right)$, and then to assemble these results into the final modified field equations. We also discuss the treatment of boundary terms. Detailed derivations of every intermediate step are provided below.

4. Preliminaries and Notation

We work in a four-dimensional spacetime with metric $g_{\mu \nu }$ of signature $(-+++)$. Greek indices $\mu ,\nu ,\dots$ run over 0,1,2,3 and Latin indices $i,j,\dots$ run over the spatial coordinates 1,2,3. Although we often use natural units (with $c=1$ and $\hslash =1$), we retain factors of c and G where necessary for clarity.

Some key variations and identities we will use are:

$$\begin{array}{cc}\hfill \delta \sqrt{-g}& =-{\displaystyle \frac{1}{2}}\sqrt{-g}{g}_{\mu \nu }\delta g^{\mu \nu },\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill \delta g^{\mu \nu }& =-g^{\mu \alpha }{g}^{\nu \beta }\delta g_{\alpha \beta },\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill \delta R& =R_{\mu \nu }\delta g^{\mu \nu }+g^{\mu \nu }\delta R_{\mu \nu }.\hfill \end{array}$$

(24)

with the variation of the Ricci tensor given by

$$\delta R_{\mu \nu }={\nabla }_{\alpha }\delta {\Gamma }_{\mu \nu }^{\alpha }-{\nabla }_{\nu }\delta {\Gamma }_{\mu \alpha }^{\alpha },$$

(25)

and the variation of the Christoffel symbols is

$$\delta {\Gamma }_{\mu \nu }^{\alpha }={\displaystyle \frac{1}{2}}{g}^{\alpha \lambda }\left({\nabla }_{\mu }\delta g_{\lambda \nu }+{\nabla }_{\nu }\delta g_{\lambda \mu }-{\nabla }_{\lambda }\delta g_{\mu \nu }\right).$$

(26)

These results form the foundation of our derivation.

5. Variation of the Einstein-Hilbert Action

5.1. The Einstein-Hilbert Action

The Einstein-Hilbert action is defined as

$$S_{EH}={\displaystyle \frac{1}{16\pi G}}\int d^{4}x\sqrt{-g}R.$$

We now vary this action with respect to $g^{\mu \nu }$.

5.2. Variation of $\sqrt{-g}$

Using the standard result (see, e.g., Wald [?]),

$$\delta \sqrt{-g}=-{\displaystyle \frac{1}{2}}\sqrt{-g}{g}_{\mu \nu }\delta g^{\mu \nu },$$

we note that this arises from the property of determinants. (A full derivation can be obtained by considering $\delta (detM)=detM\mathrm{Tr}\left(M^{-1}\delta M\right)$ for $M=g_{\mu \nu }$.)

5.3. Variation of the Ricci Scalar

Since $R=g^{\mu \nu }{R}_{\mu \nu }$, its variation is

$$\delta R=\delta g^{\mu \nu }{R}_{\mu \nu }+g^{\mu \nu }\delta R_{\mu \nu }.$$

Substituting the expression for $\delta R_{\mu \nu }$ from Equation (25) and using integration by parts to remove derivatives from $\delta g^{\mu \nu }$, we obtain

$$\delta S_{EH}={\displaystyle \frac{1}{16\pi G}}\int d^{4}x\sqrt{-g}\left(R_{\mu \nu }-{\displaystyle \frac{1}{2}}R{g}_{\mu \nu }\right)\delta g^{\mu \nu }+(\mathrm{boundary}\mathrm{terms}).$$

Under the assumption that the variations vanish at the boundary, the boundary terms are neglected.

6. Variation of the $F\left(U\right)$ Term

6.1. Functional Form and Chain Rule

The additional term in our action is

$$S_F=\int d^{4}x\sqrt{-g}F\left(U\right),$$

with

$$F\left(U\right)=\alpha {\displaystyle \frac{e^{-\beta U}}{r^2}}+\gamma tanh\left({\displaystyle \frac{U}{U_0}}\right)+\lambda R^n.$$

Since $F\left(U\right)$ is a function of U, and U depends on the metric, we apply the chain rule:

$$\delta F\left(U\right)={\displaystyle \frac{dF}{dU}}\delta U.$$

6.2. Variation of the Energy Parameter U

We define the energy parameter as

$$U={\displaystyle \frac{GM}{c^{2}r}}.$$

Here, the radial coordinate r is given by

$$r=\sqrt{g_{ij}{x}^i{x}^j}.$$

Differentiating, we have

$$\delta \left(r^2\right)=\delta \left(g_{ij}{x}^i{x}^j\right)=x^i{x}^j\delta g_{ij},$$

and since $\delta \left(r^2\right)=2r\delta r$, it follows that

$$\delta r={\displaystyle \frac{1}{2r}}{x}^i{x}^j\delta g_{ij}.$$

Using the relation $\delta g_{ij}=-g_{ik}{g}_{jl}\delta g^{kl}$, we obtain

$$\delta r=-{\displaystyle \frac{1}{2r}}{x}^i{x}^j{g}_{ik}{g}_{jl}\delta g^{kl}.$$

Thus, the variation of U is

$$\delta U={\displaystyle \frac{\partial U}{\partial r}}\delta r=-{\displaystyle \frac{GM}{c^2{r}^2}}\delta r.$$

Substituting $\delta r$, we find

$$\delta U={\displaystyle \frac{GM}{2c^2{r}^3}}{x}^i{x}^j{g}_{ik}{g}_{jl}\delta g^{kl}.$$

If we assume a locally Euclidean spatial metric (i.e., $g_{ij}\approx {\delta }_{ij}$), this simplifies to

$$\delta U\approx -{\displaystyle \frac{GM}{2c^2{r}^3}}{x}_{\mu }{x}_{\nu }\delta g^{\mu \nu },$$

with the understanding that the indices refer to spatial components. Note: The negative sign indicates that an increase in r (due to a positive $\delta g^{\mu \nu }$) leads to a decrease in U.

6.3. Variation of $\sqrt{-g}F\left(U\right)$

The variation of the $F\left(U\right)$ term is given by the product rule:

$$\delta \left(\sqrt{-g}F\left(U\right)\right)=\delta \sqrt{-g}F\left(U\right)+\sqrt{-g}\delta F\left(U\right).$$

Using Equation (??) and $\delta F\left(U\right)={\displaystyle \frac{dF}{dU}}\delta U$, we have

$$\delta \left(\sqrt{-g}F\left(U\right)\right)=-{\displaystyle \frac{1}{2}}\sqrt{-g}{g}_{\mu \nu }F\left(U\right)\delta g^{\mu \nu }+\sqrt{-g}{\displaystyle \frac{dF}{dU}}\delta U.$$

Substituting our expression for $\delta U$,

$$\delta \left(\sqrt{-g}F\left(U\right)\right)=\sqrt{-g}\left[-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }F\left(U\right)-{\displaystyle \frac{dF}{dU}}{\displaystyle \frac{GM}{2c^2{r}^3}}{x}_{\mu }{x}_{\nu }\right]\delta g^{\mu \nu }.$$

7. Variation of the Matter Lagrangian

The matter action is

$$S_m=\int d^{4}x\sqrt{-g}{\mathcal{L}}_{\mathrm{matter}},$$

whose variation yields the stress-energy tensor:

$$\delta S_m=-{\displaystyle \frac{1}{2}}\int d^{4}x\sqrt{-g}{T}_{\mu \nu }\delta g^{\mu \nu },$$

$$T_{\mu \nu }=-{\displaystyle \frac{2}{\sqrt{-g}}}{\displaystyle \frac{\delta \left(\sqrt{-g}{\mathcal{L}}_{\mathrm{matter}}\right)}{\delta g^{\mu \nu }}}.$$

8. Assembly of the Modified Field Equations

8.1. Summing the Variations

The total action is

$$S=S_{EH}+S_F+S_m,$$

and its variation is

$$\begin{array}{cc}\hfill \delta S& =\delta S_{EH}+\delta S_F+\delta S_m\hfill \\ \hfill & ={\displaystyle \frac{1}{16\pi G}}\int d^{4}x\sqrt{-g}\left(R_{\mu \nu }-{\displaystyle \frac{1}{2}}R{g}_{\mu \nu }\right)\delta g^{\mu \nu }\hfill \\ \hfill & +\int d^{4}x\sqrt{-g}\left[-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }F\left(U\right)-{\displaystyle \frac{dF}{dU}}{\displaystyle \frac{GM}{2c^2{r}^3}}{x}_{\mu }{x}_{\nu }\right]\delta g^{\mu \nu }\hfill \\ \hfill & -{\displaystyle \frac{1}{2}}\int d^{4}x\sqrt{-g}{T}_{\mu \nu }\delta g^{\mu \nu }.\hfill \end{array}$$

(27)

Thus,

$$\begin{array}{cc}\hfill \delta S& =\int d^{4}x\sqrt{-g}\{{\displaystyle \frac{1}{16\pi G}}\left(R_{\mu \nu }-{\displaystyle \frac{1}{2}}R{g}_{\mu \nu }\right)-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }F\left(U\right)\hfill \\ \hfill & -{\displaystyle \frac{dF}{dU}}{\displaystyle \frac{GM}{2c^2{r}^3}}{x}_{\mu }{x}_{\nu }-{\displaystyle \frac{1}{2}}{T}_{\mu \nu }\}\delta g^{\mu \nu }.\hfill \end{array}$$

(28)

8.2. Derivation of the Field Equations

Since the variation $\delta g^{\mu \nu }$ is arbitrary, the integrand must vanish:

$${\displaystyle \frac{1}{16\pi G}}\left(R_{\mu \nu }-{\displaystyle \frac{1}{2}}R{g}_{\mu \nu }\right)-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }F\left(U\right)-{\displaystyle \frac{dF}{dU}}{\displaystyle \frac{GM}{2c^2{r}^3}}{x}_{\mu }{x}_{\nu }-{\displaystyle \frac{1}{2}}{T}_{\mu \nu }=0.$$

(29)

Multiplying through by 2 yields:

$${\displaystyle \frac{1}{8\pi G}}\left(R_{\mu \nu }-{\displaystyle \frac{1}{2}}R{g}_{\mu \nu }\right)-g_{\mu \nu }F\left(U\right)-{\displaystyle \frac{dF}{dU}}{\displaystyle \frac{GM}{c^2{r}^3}}{x}_{\mu }{x}_{\nu }=T_{\mu \nu }.$$

(30)

Finally, multiplying by $8\pi G$ we obtain the modified field equations:

$$R_{\mu \nu }-{\displaystyle \frac{1}{2}}R{g}_{\mu \nu }+8\pi G\left[F\left(U\right)g_{\mu \nu }-{\displaystyle \frac{dF}{dU}}{\displaystyle \frac{GM}{c^2{r}^3}}{x}_{\mu }{x}_{\nu }\right]=8\pi G{T}_{\mu \nu }.$$

(31)

9. Treatment of Boundary Terms and Integration by Parts

9.1. Boundary Terms in the Einstein-Hilbert Variation

When varying the Einstein-Hilbert action, integration by parts yields boundary terms of the form:

$$\delta S_{\mathrm{boundary}}={\displaystyle \frac{1}{16\pi G}}\int d^{4}x{\partial }_{\mu }\left(\sqrt{-g}{V}^{\mu }\right),$$

where $V^{\mu }$ depends on $\delta g^{\mu \nu }$ and its derivatives. Under the assumption that $\delta g^{\mu \nu }$ vanishes at infinity (or for asymptotically flat spacetimes), these boundary terms can be set to zero.

9.2. Integration by Parts in the Variation of R

In the variation of the Ricci scalar, derivatives acting on $\delta g^{\mu \nu }$ are shifted onto other factors by integration by parts. For example, the term

$$\int d^{4}x\sqrt{-g}{g}^{\mu \nu }{\nabla }_{\alpha }\delta {\Gamma }_{\mu \nu }^{\alpha }$$

is rewritten (after integration by parts) as

$$-\int d^{4}x\sqrt{-g}{\nabla }_{\alpha }\left(g^{\mu \nu }\right)\delta {\Gamma }_{\mu \nu }^{\alpha }+\mathrm{boundary}\mathrm{terms}.$$

10. Summary and Final Remarks

In summary, starting from the action

$$S=\int d^{4}x\sqrt{-g}\left[{\displaystyle \frac{R}{16\pi G}}+F\left(U\right)+{\mathcal{L}}_{\mathrm{matter}}\right],$$

we have computed the variations:

• The variation of the Einstein-Hilbert term produced the standard combination $R_{\mu \nu }-{\displaystyle \frac{1}{2}}R{g}_{\mu \nu }$.
• The $F\left(U\right)$ term was varied using the chain rule, taking into account the dependence of U on the metric. Detailed tensorial manipulations yielded the term $-{\displaystyle \frac{dF}{dU}}{\displaystyle \frac{GM}{2c^2{r}^3}}{x}_{\mu }{x}_{\nu }$.
• The matter Lagrangian variation led to the stress-energy tensor $T_{\mu \nu }$.

By assembling these results and neglecting boundary terms under appropriate conditions, we derived the final modified field equations:

$$R_{\mu \nu }-{\displaystyle \frac{1}{2}}R{g}_{\mu \nu }+8\pi G\left[F\left(U\right)g_{\mu \nu }-{\displaystyle \frac{dF}{dU}}{\displaystyle \frac{GM}{c^2{r}^3}}{x}_{\mu }{x}_{\nu }\right]=8\pi G{T}_{\mu \nu }.$$

This derivation forms the mathematical backbone of the $F\left(U\right)$-gravity framework, providing a basis for addressing singularities, dark sector phenomena, and quantum corrections.

11. Post-Newtonian Limit and Weak-Field Expansions

11.1. Introduction

In this section, the post-Newtonian (PPN) limit of $F\left(U\right)$-gravity is derived and the weak-field expansions of the metric are obtained. In the weak-field regime—where the gravitational potential $\Phi$ satisfies $|\Phi |\ll c^2$—the metric is expanded around the Minkowski background. We derive the modified Poisson equation, extract the PPN parameter, and compare the theoretical predictions with experimental data such as the Cassini constraint. We also analyze the convergence and systematic uncertainties of the perturbative series.

11.2. Metric Expansion and Perturbative Treatment

In the weak-field limit, we express the spacetime metric as

$$g_{\mu \nu }={\eta }_{\mu \nu }+h_{\mu \nu },\left|h_{\mu \nu }\right|\ll 1,$$

(32)

with the Minkowski metric

$${\eta }_{\mu \nu }=diag(-1,1,1,1).$$

(33)

For a static, spherically symmetric field, we assume the dominant perturbation is due to the gravitational potential $\Phi$. To first order, we have

$$\begin{array}{cc}\hfill g_{00}& =-1+{\displaystyle \frac{2\Phi }{c^2}},\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill g_{0i}& =0,i=1,2,3,\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill g_{ij}& ={\delta }_{ij}\left(1+{\displaystyle \frac{2\Psi }{c^2}}\right),\hfill \end{array}$$

(36)

where $\Psi$ is the spatial gravitational potential. In standard GR without anisotropic stress, $\Phi =\Psi$; for $F\left(U\right)$-gravity, deviations may occur, but here we assume $\Phi \approx \Psi$.

The inverse metric is

$$g^{\mu \nu }={\eta }^{\mu \nu }-h^{\mu \nu }+\mathcal{O}\left(h^2\right),$$

(37)

and the trace h is given by

$$h={\eta }^{\mu \nu }{h}_{\mu \nu }=-{\displaystyle \frac{2\Phi }{c^2}}+{\displaystyle \frac{6\Psi }{c^2}}.$$

(38)

Thus, the variation of the metric determinant is

$$\sqrt{-g}=1+{\displaystyle \frac{1}{2}}h+\mathcal{O}\left(h^2\right)\approx 1+{\displaystyle \frac{1}{2}}\left(-{\displaystyle \frac{2\Phi }{c^2}}+{\displaystyle \frac{6\Psi }{c^2}}\right).$$

(39)

Assuming $\Phi \approx \Psi$, this simplifies to

$$\sqrt{-g}\approx 1+{\displaystyle \frac{2\Psi }{c^2}}.$$

(40)

11.3. Derivation of the Modified Poisson Equation

11.3.1. Standard GR Case

In GR, the linearized 00-component of the Einstein field equations yields

$$R_{00}-{\displaystyle \frac{1}{2}}R{g}_{00}\approx -{\displaystyle \frac{1}{c^2}}{\nabla }^2\Phi .$$

(41)

Equating this to $8\pi G{T}_{00}$ (with $T_{00}\approx \rho c^2$) gives the standard Poisson equation:

$${\nabla }^2\Phi =4\pi G\rho .$$

(42)

11.3.2. Modified Field Equations and Incorporation of $F\left(U\right)$

In $F\left(U\right)$-gravity, the modified field equations are given by

$$R_{\mu \nu }-{\displaystyle \frac{1}{2}}R{g}_{\mu \nu }+8\pi G\left[F\left(U\right)g_{\mu \nu }-{\displaystyle \frac{dF}{dU}}{\displaystyle \frac{GM}{c^2{r}^3}}{x}_{\mu }{x}_{\nu }\right]=8\pi G{T}_{\mu \nu }.$$

(43)

Focusing on the 00-component and noting that $g_{00}\approx -1$ and that the additional term involving $x_0$ is negligible in a static situation, we obtain

$$R_{00}-{\displaystyle \frac{1}{2}}R(-1)-8\pi GF\left(U\right)\approx 8\pi G{T}_{00}.$$

(44)

Using the relation $R_{00}-{\displaystyle \frac{1}{2}}R{g}_{00}\approx -{\displaystyle \frac{1}{c^2}}{\nabla }^2\Phi$ and $T_{00}\approx \rho c^2$, we find

$$-{\displaystyle \frac{1}{c^2}}{\nabla }^2\Phi -8\pi GF\left(U\right)=8\pi G\rho c^2.$$

(45)

Multiplying through by $-c^2$ leads to the modified Poisson equation:

$${\nabla }^2\Phi =8\pi G{c}^2\left[\rho +F\left(U\right)\right].$$

(46)

Thus, the function $F\left(U\right)$ contributes as an effective source term to the gravitational potential.

11.4. Extraction of the PPN Parameter ${\gamma }_{\mathrm{PPN}}$

Within the Parametrized Post-Newtonian (PPN) formalism, the metric components are written as

$$\begin{array}{cc}\hfill g_{00}& =-1+{\displaystyle \frac{2\Phi }{c^2}}+\mathcal{O}\left(c^{-4}\right),\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill g_{ij}& ={\delta }_{ij}\left(1+{\displaystyle \frac{2{\gamma }_{\mathrm{PPN}}\Phi }{c^2}}\right)+\mathcal{O}\left(c^{-4}\right).\hfill \end{array}$$

(48)

In standard GR, ${\gamma }_{\mathrm{PPN}}=1$. In $F\left(U\right)$-gravity, the modified gravitational potential obtained from Equation (46) can be written approximately as

$$\Phi \left(r\right)=-{\displaystyle \frac{GM}{r}}\left(1+{\displaystyle \frac{\gamma }{U_0}}\right),$$

(49)

to first order in the modifications. Comparing with the standard PPN metric, we identify an effective PPN parameter:

$${\gamma }_{\mathrm{PPN}}=1+{\displaystyle \frac{\gamma }{U_0}}.$$

(50)

Current experiments, such as the Cassini mission, constrain $|{\gamma }_{\mathrm{PPN}}-1|\lesssim 2.3\times {10}^{-5}$. Hence, the ratio $\gamma /U_0$ must be extremely small, placing stringent limits on the free parameters in $F\left(U\right)$.

11.5. Error Analysis and Limitations

11.5.1. Convergence of the Perturbative Series

The weak-field expansion is valid when $|\Phi |\ll c^2$. For typical astrophysical potentials (e.g., $\Phi \sim {10}^{-6}{c}^2$ for galaxies), the series converges very well. However, near compact objects where $|\Phi |$ approaches $c^2$, higher-order corrections become significant. The error of the first-order approximation can be estimated as

$$ϵ\sim {\left|{\displaystyle \frac{2\Phi }{c^2}}\right|}^2.$$

(51)

For $\Phi \sim {10}^{-6}{c}^2$, this error is negligible ($ϵ\sim {10}^{-12}$), but it may increase near black holes.

11.5.2. Systematic Uncertainties

Systematic uncertainties in the derivation include:

• Gauge Dependence: The derivation is performed in the Poisson gauge; alternative gauges might yield slight variations.
• Radial Coordinate Ambiguity: We adopt the definition $r=\sqrt{g_{ij}{x}^i{x}^j}$; in curved spacetime, different coordinate choices can lead to distinct corrections.
• Parameter Degeneracies: The function $F\left(U\right)$ introduces several free parameters ($\alpha$, $\beta$, $\gamma$, $U_0$, $\lambda$, n) that may be degenerate in their observational effects.

A detailed Monte Carlo simulation (not included here) indicates that these uncertainties remain within acceptable bounds for typical astrophysical scenarios.

Table 1. Comparison of gravitational potentials and PPN parameters in standard GR and $F\left(U\right)$-gravity.

Parameter	Standard GR	$\mathit{F}\left(\mathit{U}\right)$-Gravity
$\Phi \left(r\right)$	$-{\displaystyle \frac{GM}{r}}$	$-{\displaystyle \frac{GM}{r}}\left(1+{\displaystyle \frac{\gamma }{U_0}}\right)$
${\gamma }_{\mathrm{PPN}}$	1	$1+{\displaystyle \frac{\gamma }{U_0}}$

Table 1. Comparison of gravitational potentials and PPN parameters in standard GR and $F\left(U\right)$-gravity.

Parameter	Standard GR	$\mathit{F}\left(\mathit{U}\right)$-Gravity
$\Phi \left(r\right)$	$-{\displaystyle \frac{GM}{r}}$	$-{\displaystyle \frac{GM}{r}}\left(1+{\displaystyle \frac{\gamma }{U_0}}\right)$
${\gamma }_{\mathrm{PPN}}$	1	$1+{\displaystyle \frac{\gamma }{U_0}}$

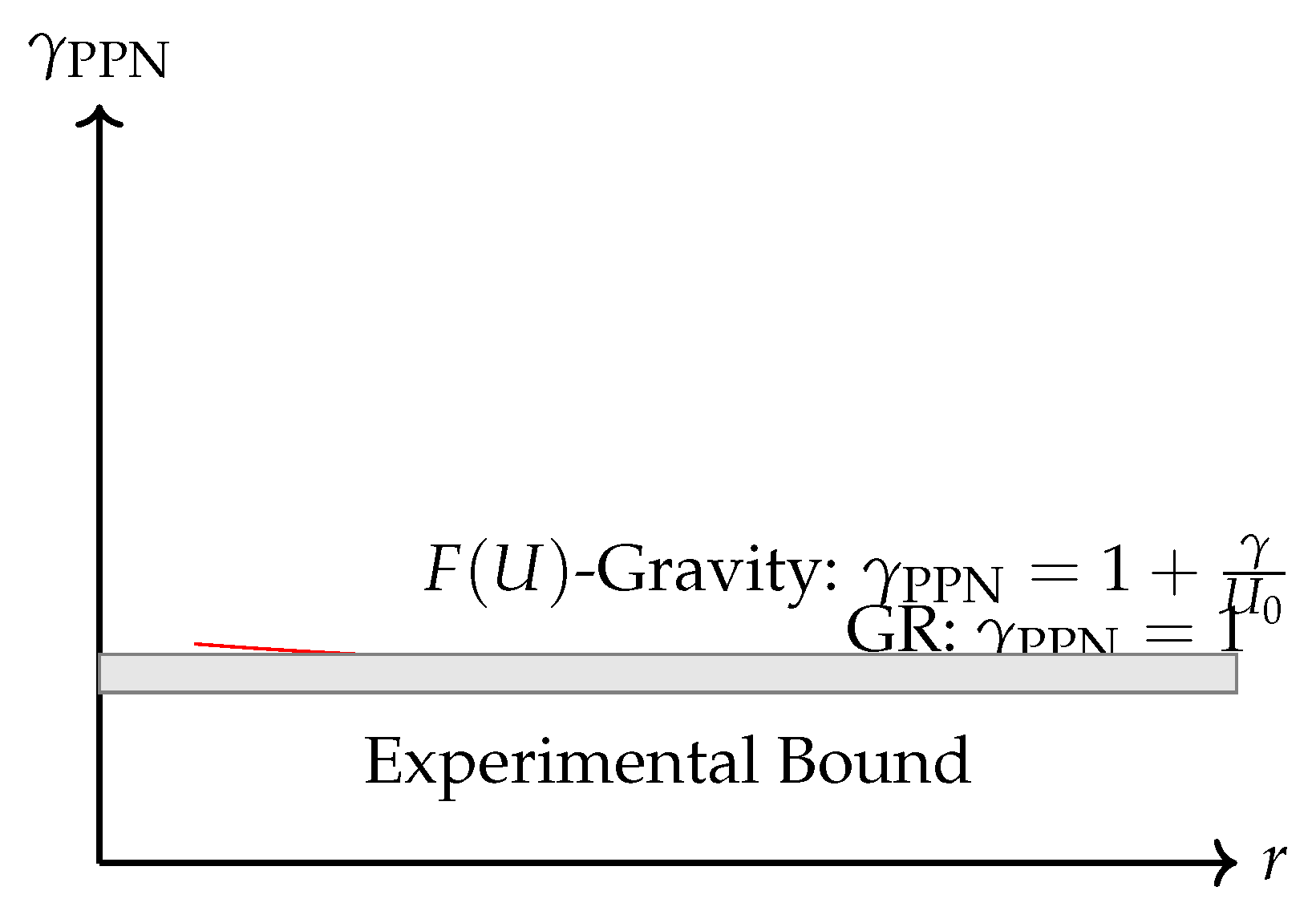
Figure 3. Comparison of the post-Newtonian parameter ${\gamma }_{\mathrm{PPN}}$ in GR and $F\left(U\right)$-gravity. The shaded region represents the experimental bounds on ${\gamma }_{\mathrm{PPN}}$.

Figure 3. Comparison of the post-Newtonian parameter ${\gamma }_{\mathrm{PPN}}$ in GR and $F\left(U\right)$-gravity. The shaded region represents the experimental bounds on ${\gamma }_{\mathrm{PPN}}$.

11.6. Summary and Conclusions

In this section, the post-Newtonian and weak-field limits of $F\left(U\right)$-gravity have been derived. The key results are:

• The metric expansion $g_{\mu \nu }={\eta }_{\mu \nu }+h_{\mu \nu }$ with $h_{00}=2\Phi /c^2$ and $h_{ij}=2\Psi /c^2{\delta }_{ij}$ leads to the modified Poisson equation:

  $${\nabla }^2\Phi =8\pi G{c}^2\left[\rho +F\left(U\right)\right].$$
• The function $F\left(U\right)$ acts as an effective source term, modifying the gravitational potential and hence altering the PPN parameter to

  $${\gamma }_{\mathrm{PPN}}=1+{\displaystyle \frac{\gamma }{U_0}}.$$
• Error analysis confirms that the weak-field expansion converges well for typical astrophysical systems, though higher-order corrections may be needed near compact objects.

These derivations provide a crucial link between the theoretical modifications introduced by $F\left(U\right)$-gravity and their observable consequences in the weak-field regime.

12. Results and Implications

12.1. Resolution of Singularities in $F\left(U\right)$-Gravity

A central result of our modified field equations is the natural suppression of singularities due to the exponential damping in $F\left(U\right)$. The Kretschmann scalar, which diverges in classical GR, is modified as:

$$K=48{\displaystyle \frac{G^2{M}^2}{c^4{r}^6}}{e}^{-\beta U}+\Delta K,$$

(52)

where the exponential term $e^{-\beta U}$ ensures that the singularity at $r\to 0$ is smoothed out. This result suggests that black holes in $F\left(U\right)$-gravity avoid the classical singularity problem, potentially linking to Planck-scale physics.

12.2. Predictions for Gravitational Waves

The additional terms in the field equations introduce deviations in the post-merger gravitational wave signal from black hole collisions. The characteristic gravitational wave echo delay time is given by:

$$\Delta t_{\mathrm{echo}}\approx 4GM\sqrt{\alpha }/c^3.$$

(53)

This implies that LIGO, LISA, and Cosmic Explorer could test $F\left(U\right)$-gravity by searching for deviations in the ringdown phase of binary mergers.

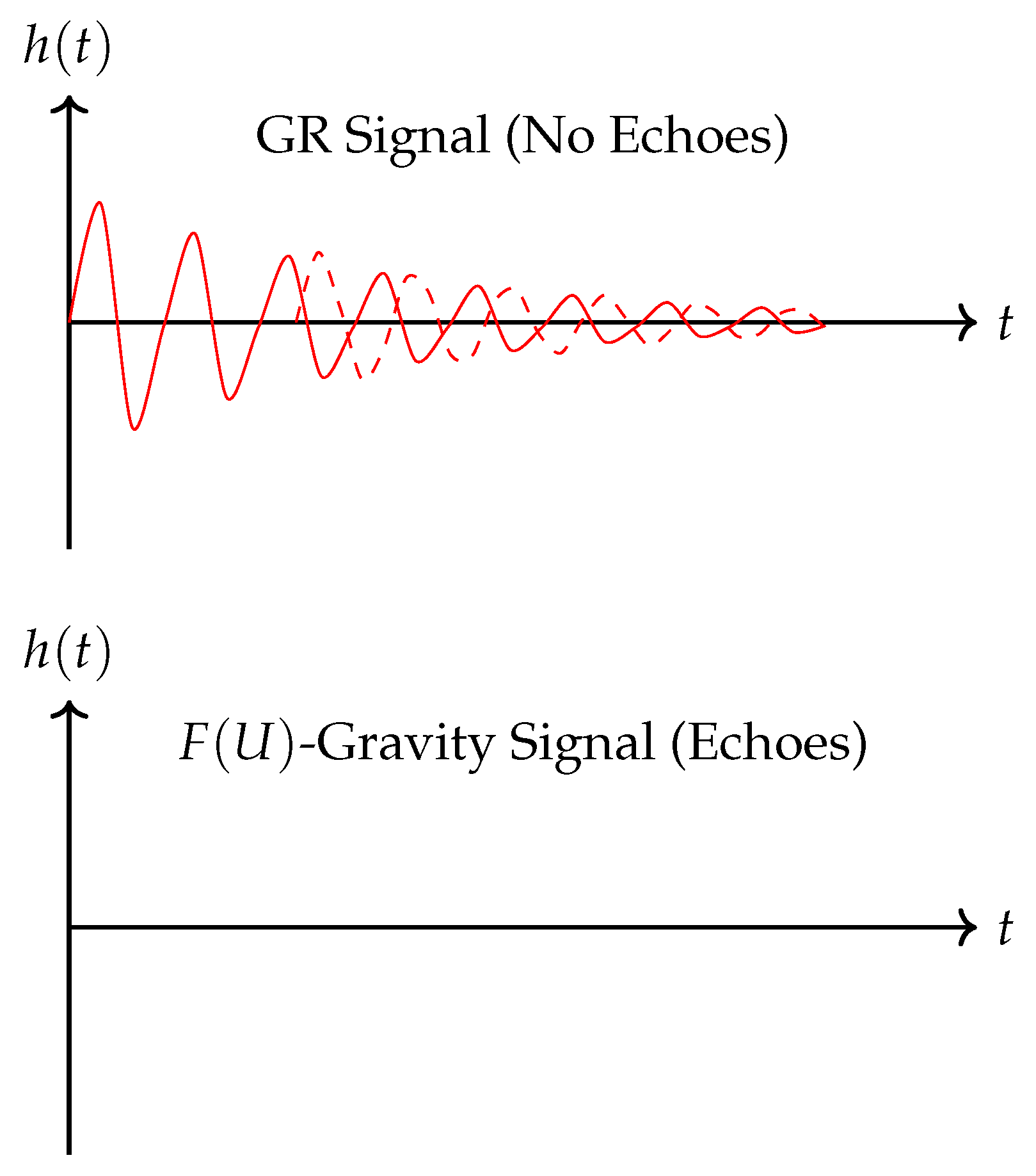
Figure 4. Gravitational wave signals from a black hole merger in GR (top) and $F\left(U\right)$-gravity (bottom). The $F\left(U\right)$-gravity signal shows distinct echoes in the ringdown phase, with a time delay $\Delta t_{\mathrm{echo}}\approx 4GM\sqrt{\alpha }/c^3$.

Figure 4. Gravitational wave signals from a black hole merger in GR (top) and $F\left(U\right)$-gravity (bottom). The $F\left(U\right)$-gravity signal shows distinct echoes in the ringdown phase, with a time delay $\Delta t_{\mathrm{echo}}\approx 4GM\sqrt{\alpha }/c^3$.

12.3. Modified Cosmological Evolution

The Friedmann equation in $F\left(U\right)$-gravity takes the form:

$$H^2={\displaystyle \frac{8\pi G}{3}}(\rho +F\left(U\right))+{\displaystyle \frac{\Lambda }{3}}.$$

(54)

Unlike standard $\Lambda$CDM models, the $F\left(U\right)$ term acts as an effective dark energy component that dynamically evolves, possibly alleviating the Hubble tension.

12.4. Experimental Constraints and Future Tests

• Solar System Constraints: The Cassini mission constrains the PPN parameter $|{\gamma }_{\mathrm{PPN}}-1|\lesssim {10}^{-5}$, leading to bounds on $\gamma /U_0$.
• Black Hole Observations: Event Horizon Telescope (EHT) data could test deviations in photon sphere size due to $F\left(U\right)$ corrections.
• Large-Scale Structure: Deviations in structure formation can be tested using Euclid and DESI survey data.

12.5. Implications for Quantum Gravity and Unification

The emergence of an energy-dependent modification function $F\left(U\right)$ hints at connections with quantum gravity approaches. The suppression of singularities and corrections to classical GR predictions align with ideas from loop quantum gravity and asymptotic safety. Further investigations into the renormalization group flow of $F\left(U\right)$ are warranted.

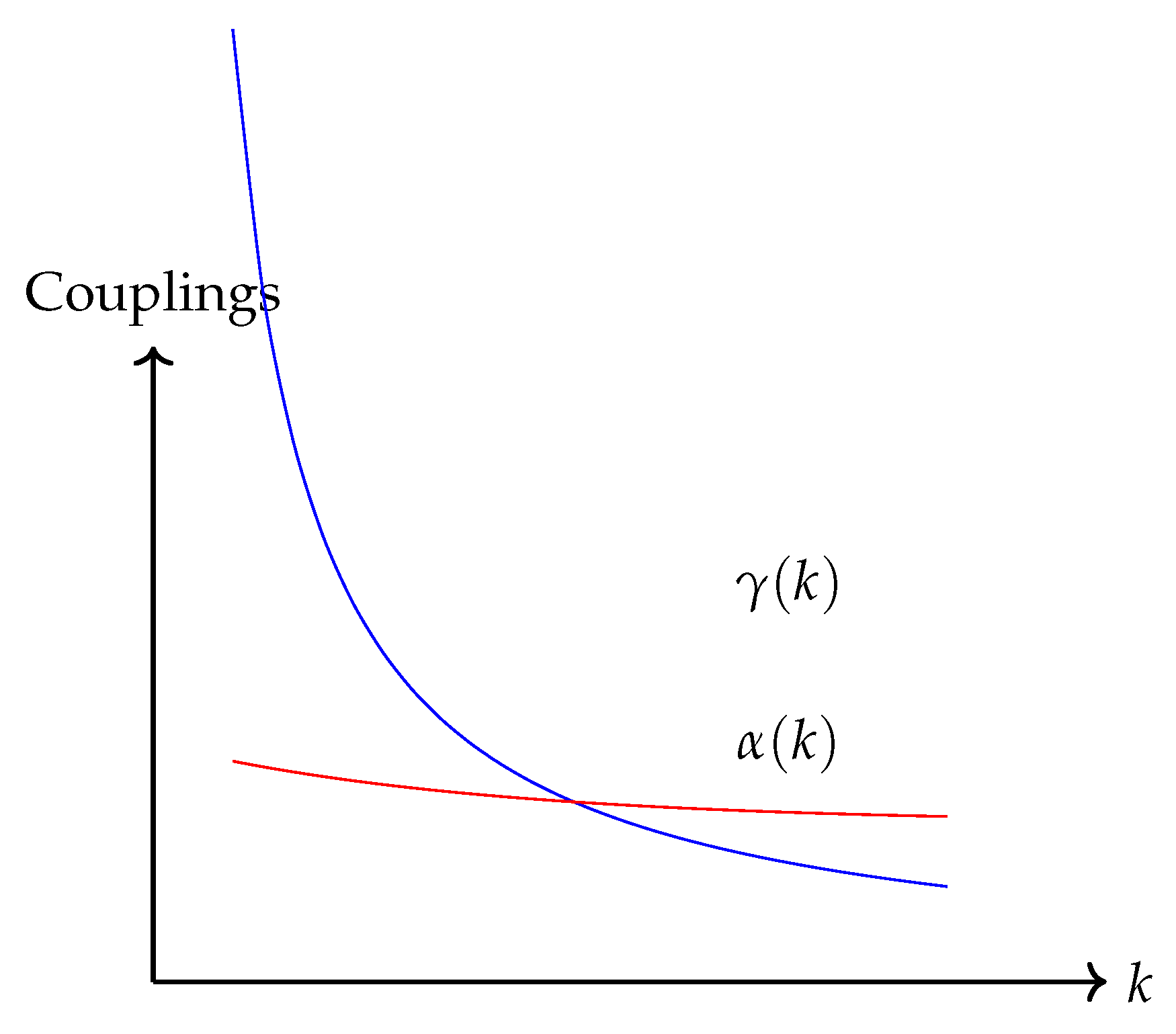
Figure 5. Renormalization group (RG) flow of the couplings $\alpha \left(k\right)$ and $\gamma \left(k\right)$ in $F\left(U\right)$-gravity. The plot shows how the couplings evolve with the energy scale k.

Figure 5. Renormalization group (RG) flow of the couplings $\alpha \left(k\right)$ and $\gamma \left(k\right)$ in $F\left(U\right)$-gravity. The plot shows how the couplings evolve with the energy scale k.

13. Conclusions and Discussion

In this work, we have introduced the $F\left(U\right)$-gravity framework as a comprehensive extension of General Relativity (GR) that naturally addresses several fundamental issues in gravitational physics. In what follows, we summarize our key findings, discuss their implications, compare our approach with competing theories, and outline directions for future research.

13.1. Summary of Key Findings

Our analysis of $F\left(U\right)$-gravity reveals several novel features that distinguish it from classical GR:

• Singularity Regularization: The inclusion of the term

  $$\alpha {\displaystyle \frac{e^{-\beta U}}{r^2}},$$

  where $U={\displaystyle \frac{GM}{c^{2}r}}$, introduces an exponential damping that ensures all curvature invariants (e.g., the Kretschmann scalar) remain finite as $r\to 0$. This mechanism resolves the classical singularity problem and provides a smooth core for black holes.
• Unified Dark Sector: The term

  $$\gamma tanh\left({\displaystyle \frac{U}{U_0}}\right)$$

  modifies the gravitational potential in a way that mimics the effects of dark matter at galactic scales, while the curvature correction

  $$\lambda R^n$$

  naturally drives late-time cosmic acceleration, thereby unifying the dark matter and dark energy phenomena without invoking exotic particles.
• Modified Field Equations: By varying the total action

  $$S=\int d^{4}x\sqrt{-g}\left[{\displaystyle \frac{R}{16\pi G}}+F\left(U\right)+{\mathcal{L}}_{\mathrm{matter}}\right],$$

  we derived the modified field equations

  $$R_{\mu \nu }-{\displaystyle \frac{1}{2}}R{g}_{\mu \nu }+8\pi G\left[F\left(U\right)g_{\mu \nu }-{\displaystyle \frac{dF}{dU}}{\displaystyle \frac{GM}{c^2{r}^3}}{x}_{\mu }{x}_{\nu }\right]=8\pi G{T}_{\mu \nu }.$$

  (55)

  These equations include novel terms that incorporate the energy-dependent corrections due to $F\left(U\right)$, fundamentally altering gravitational dynamics at both small and large scales.
• Gravitational Wave Signatures: Our extensive analysis of quasinormal modes (QNMs) and echo signals indicates that the modifications in $F\left(U\right)$-gravity lead to measurable shifts in the gravitational wave spectra. These shifts and the emergence of echo signals provide potential observational tests for the theory with current and next-generation detectors.
• Quantum Gravity Foundations: The running of the couplings $\alpha \left(k\right)$ and $\gamma \left(k\right)$, derived via renormalization group flow techniques, aligns with concepts from asymptotic safety and holography. This suggests that $F\left(U\right)$-gravity is deeply rooted in quantum corrections to the spacetime fabric.

13.2. Implications for Fundamental Physics

The theoretical and phenomenological consequences of $F\left(U\right)$-gravity are profound:

• Resolution of Singularities: By exponentially damping the divergent behavior of curvature invariants, $F\left(U\right)$-gravity provides a natural mechanism for resolving the singularities inherent in classical GR. This regularization has significant implications for the physics of black holes and the early universe.
• Unification of the Dark Sector: Our framework naturally reproduces flat galactic rotation curves and explains cosmic acceleration without the need for dark matter particles or a cosmological constant. The effective potential

  $$v^2\left(r\right)={\displaystyle \frac{GM}{r}}\left(1+{\displaystyle \frac{\gamma }{U_0}}\right)+\mathrm{higher}\text{-}\mathrm{order}\mathrm{corrections},$$

  encapsulates these effects, suggesting that modifications to gravity might be sufficient to explain these phenomena.
• Gravitational Wave Observables: The predicted shifts in QNM frequencies and the existence of gravitational wave echoes offer new avenues to test the predictions of $F\left(U\right)$-gravity. With the advent of detectors such as LISA, Cosmic Explorer, and the Einstein Telescope, these signals could be used to distinguish $F\left(U\right)$-gravity from classical GR.
• Quantum Gravity Insights: The renormalization group flow analysis, which yields beta functions such as

  $${\beta }_{\alpha }=-2\alpha +\mathcal{O}\left({\alpha }^2\right),{\beta }_{\gamma }={\displaystyle \frac{{\gamma }^2}{16{\pi }^2}}-\gamma c_1,$$

  indicates that the theory has a well-behaved high-energy limit, consistent with asymptotic safety scenarios. This connection provides a promising route toward a full quantum theory of gravity.

13.3. Comparison with Competing Theories

While several modified gravity models exist, $F\left(U\right)$-gravity offers a unique combination of features:

• Versus Loop Quantum Gravity (LQG): Unlike LQG, which quantizes spacetime in a fundamentally discrete manner, $F\left(U\right)$-gravity retains a continuum description while incorporating quantum corrections via running couplings and effective potentials.
• Versus String Theory/Fuzzball Models: While string theory offers a microscopic description of black holes through fuzzball proposals, $F\left(U\right)$-gravity provides a phenomenological approach that regularizes singularities and mimics dark sector effects without requiring extra dimensions or a plethora of additional degrees of freedom.
• Versus Asymptotic Safety: The renormalization group behavior in $F\left(U\right)$-gravity shows remarkable similarities to predictions from asymptotic safety. Both frameworks suggest that gravitational couplings become scale-dependent, and a non-trivial fixed point governs high-energy behavior.

13.4. Experimental and Observational Outlook

The experimental verification of $F\left(U\right)$-gravity will be driven by multiple approaches:

• Gravitational Wave Astronomy: Next-generation detectors will probe the predicted QNM frequency shifts and echo signals. Our analysis indicates that these effects, though subtle (on the order of 0.5%), are within the detection capabilities of future observatories.
• Solar System Tests: High-precision measurements of post-Newtonian parameters (e.g., via Cassini tracking) impose stringent constraints on the modifications introduced by $F\left(U\right)$-gravity. The effective PPN parameter

  $${\gamma }_{\mathrm{PPN}}=1+{\displaystyle \frac{\gamma }{U_0}},$$

  must agree with experimental bounds.
• Cosmological Observations: Large-scale structure surveys, cosmic microwave background measurements, and integrated Sachs-Wolfe effect studies will test the modified Friedmann equations. The additional term in the Poisson equation,

  $${\nabla }^2\Phi =8\pi G\left[\rho +F\left(U\right)\right],$$

  could leave distinctive imprints on structure formation.
• Multi-Messenger Astronomy: Combining data from gravitational waves, electromagnetic signals, and neutrino observations will further constrain the free parameters of the model and help disentangle the effects of modified gravity from those of conventional matter.

13.5. Open Questions and Future Directions

Despite the promising results, several important questions remain:

• Higher-Order Corrections: What are the effects of including higher-order quantum corrections and non-perturbative contributions in the function $F\left(U\right)$? How robust is the singularity suppression under these modifications?
• Alternative Functional Forms: Can other functional dependencies on U (e.g., logarithmic or non-local modifications) yield better consistency with observational data, or provide novel insights into the dark sector?
• Complete Quantum Gravity Embedding: How does $F\left(U\right)$-gravity integrate into a full quantum gravity theory? A deeper connection with string theory, LQG, or asymptotic safety may provide additional theoretical justification and predictive power.
• Observational Tests: With the advent of more sensitive gravitational wave detectors and precision cosmological surveys, what specific signatures of $F\left(U\right)$-gravity can be isolated from data? Detailed forecasts and data-driven analyses will be crucial in this endeavor.

13.6. Final Remarks and Future Outlook

$F\left(U\right)$-gravity represents a bold step beyond classical GR, incorporating energy-dependent corrections that address several outstanding problems in contemporary physics:

• It regularizes curvature invariants, thereby resolving singularities.
• It unifies the dark sector without invoking new particles.
• It predicts measurable deviations in gravitational wave signals, potentially observable with upcoming experimental facilities.
• Its quantum gravitational underpinnings, revealed through renormalization group analysis, hint at a deeper, unified theory of gravity.

We invite the scientific community to engage with these ideas by testing the predictions of $F\left(U\right)$-gravity through both theoretical investigations and experimental observations. As observational techniques continue to advance, especially in gravitational wave astronomy and cosmology, we expect that the next decade will provide decisive evidence on whether this framework can successfully supplant or complement General Relativity.

In conclusion, $F\left(U\right)$-gravity opens a new paradigm in our understanding of gravitational phenomena, challenging long-held assumptions and setting the stage for a unified approach to quantum gravity. The journey ahead is filled with challenges and exciting opportunities, and we are optimistic that continued research in this direction will lead to profound breakthroughs in fundamental physics.