Quantumistor: A Novel Semiconductor Device

1. Introduction

Recent advancements in nanofabrication and quantum engineering have necessitated the exploration of devices that overcome the intrinsic limitations of conventional transistor designs. In response to these challenges, a novel multi-terminal quantum transistor is introduced. The device is designed using a tight-binding model on a two-dimensional square lattice where disorder is introduced via random perturbations to the on-site potentials. Quantum transport is then analyzed through scattering matrix formalism, an approach that intrinsically accounts for all possible electron trajectories as postulated by Feynman’s path integral formulation. This theoretical framework enables electrons to traverse an infinite number of paths, thereby generating interference effects that can be harnessed to encode information in a manner that exceeds the binary on/off functionality of classical transistors.

The device design is inspired by the critical need for increased computational density and enhanced performance in VLSI systems. By integrating millions of such quantum devices on a single chip, it is envisaged that each unit, capable of conveying multiple bits of information simultaneously, can effectively replace hundreds of traditional transistors. This paradigm shift is expected to yield an exponential increase in computing power while simultaneously reducing energy consumption and physical dimensions of the circuitry.

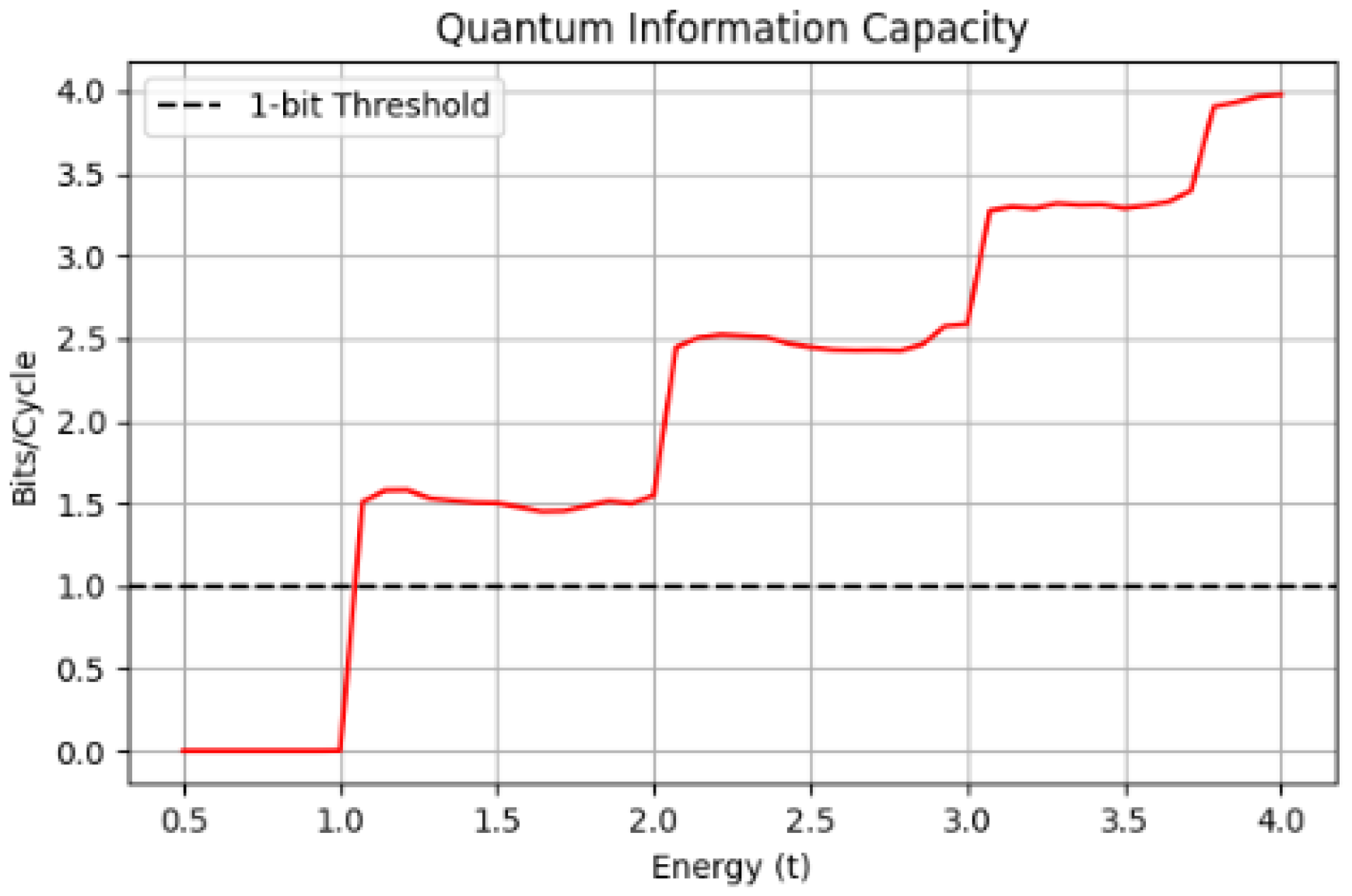
Figure 1. The computed Shannon entropy $S\left(E\right)$ quantifies the information processing capability of the device. For specific energy ranges, $S\left(E\right)$ exceeds 1 bit per cycle, suggesting that a single quantum transistor could replace multiple classical transistors in logic circuits.

Figure 1. The computed Shannon entropy $S\left(E\right)$ quantifies the information processing capability of the device. For specific energy ranges, $S\left(E\right)$ exceeds 1 bit per cycle, suggesting that a single quantum transistor could replace multiple classical transistors in logic circuits.

Numerical simulations were implemented using Python and several specialized libraries. The kwant package was employed to construct the quantum device and to simulate quantum transport under varying disorder configurations. Progress tracking was facilitated via tqdm, and parallel computations were performed using joblib. The simulation protocol involved generating multiple disorder realizations, calculating the energy-dependent transmission matrices, and subsequently averaging these matrices over the ensemble. The Shannon entropy of the averaged transmission matrix was then computed as a metric for the device’s information capacity. Four distinct analyses were carried out:

• An energy-dependent plot of the average total transmission, highlighting the interplay between disorder and channel connectivity.
• A quantification of information capacity, expressed as bits per cycle, which exceeded the conventional single-bit threshold over a range of energies.
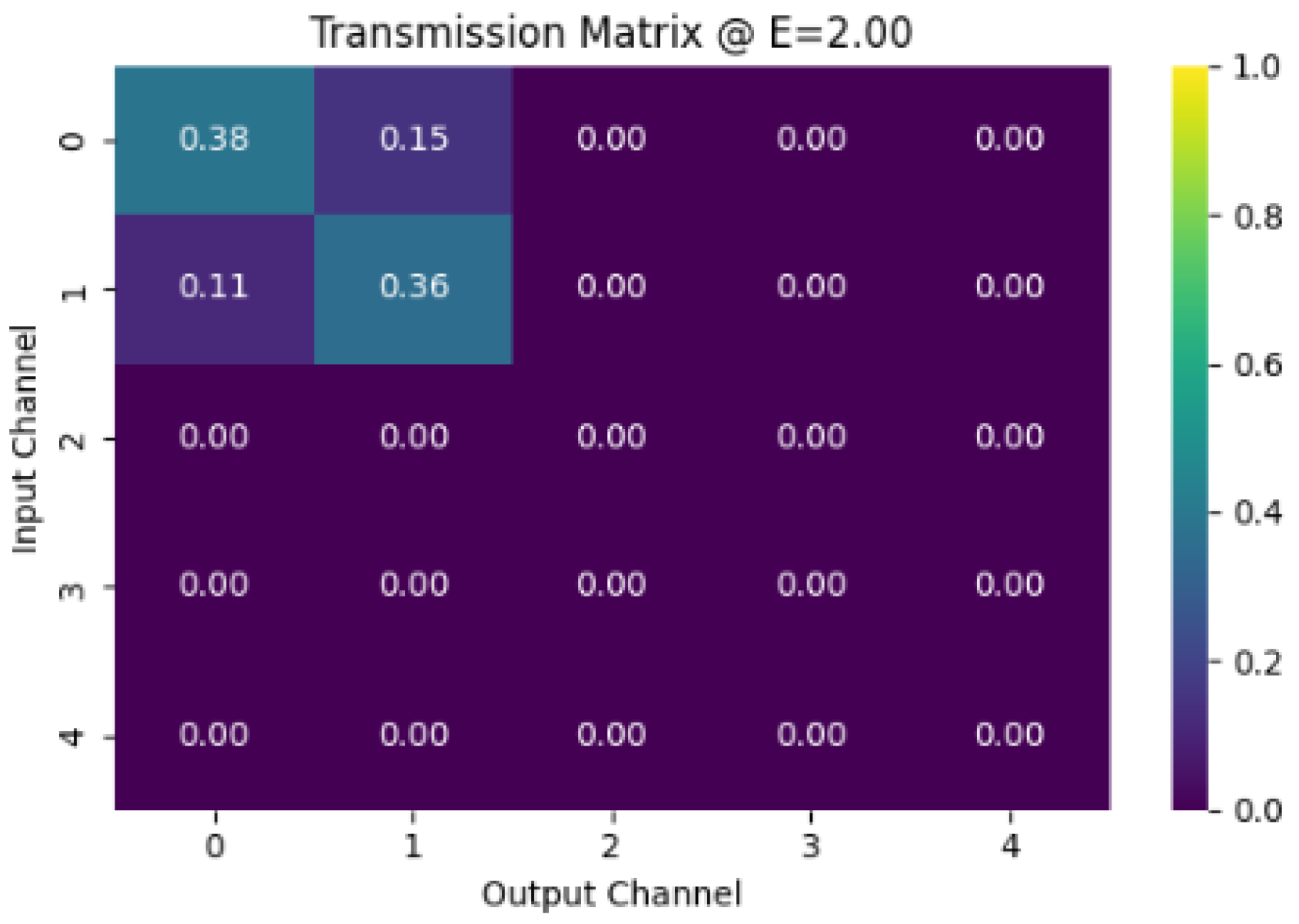
• A heatmap visualization of the channel-resolved transmission matrix at a representative energy (e.g., $E=2.0$), illustrating the multi-channel coupling.
• A histogram depicting the distribution of Shannon entropy values across the energy spectrum.

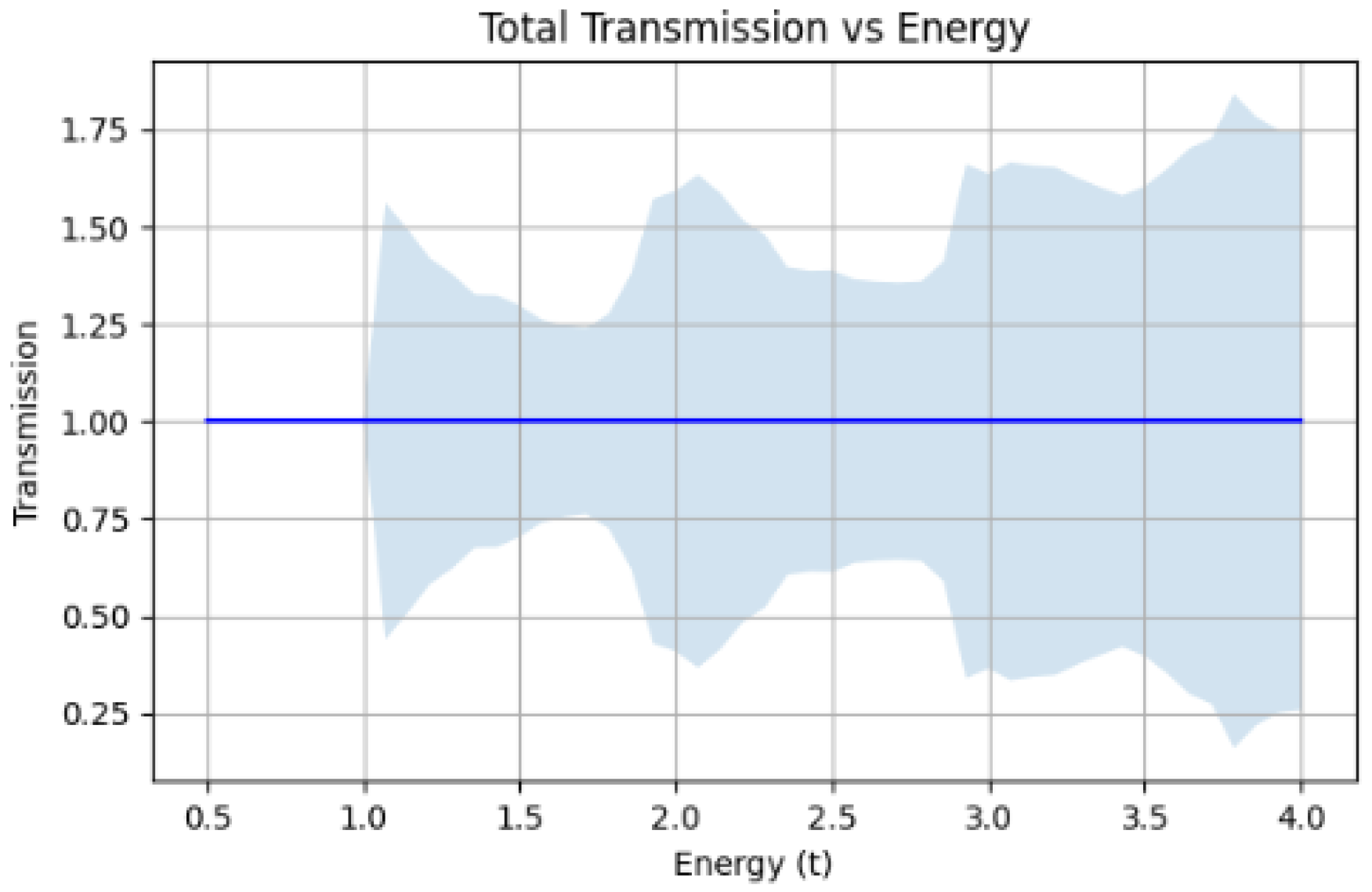
Figure 2. The average total transmission $\langle T\left(E\right)\rangle$ is plotted as a function of energy. The results indicate that disorder plays a significant role in modulating channel connectivity. At lower energies, transmission is suppressed due to localized states, while at higher energies, the device supports multiple propagating modes.

Figure 2. The average total transmission $\langle T\left(E\right)\rangle$ is plotted as a function of energy. The results indicate that disorder plays a significant role in modulating channel connectivity. At lower energies, transmission is suppressed due to localized states, while at higher energies, the device supports multiple propagating modes.

Figure 3. The variation of total transmission $\langle T\left(E\right)\rangle$ with energy for different disorder configurations. The fluctuations in transmission highlight the sensitivity of transport properties to disorder, with transmission peaks corresponding to energy windows where extended states dominate.

Figure 3. The variation of total transmission $\langle T\left(E\right)\rangle$ with energy for different disorder configurations. The fluctuations in transmission highlight the sensitivity of transport properties to disorder, with transmission peaks corresponding to energy windows where extended states dominate.

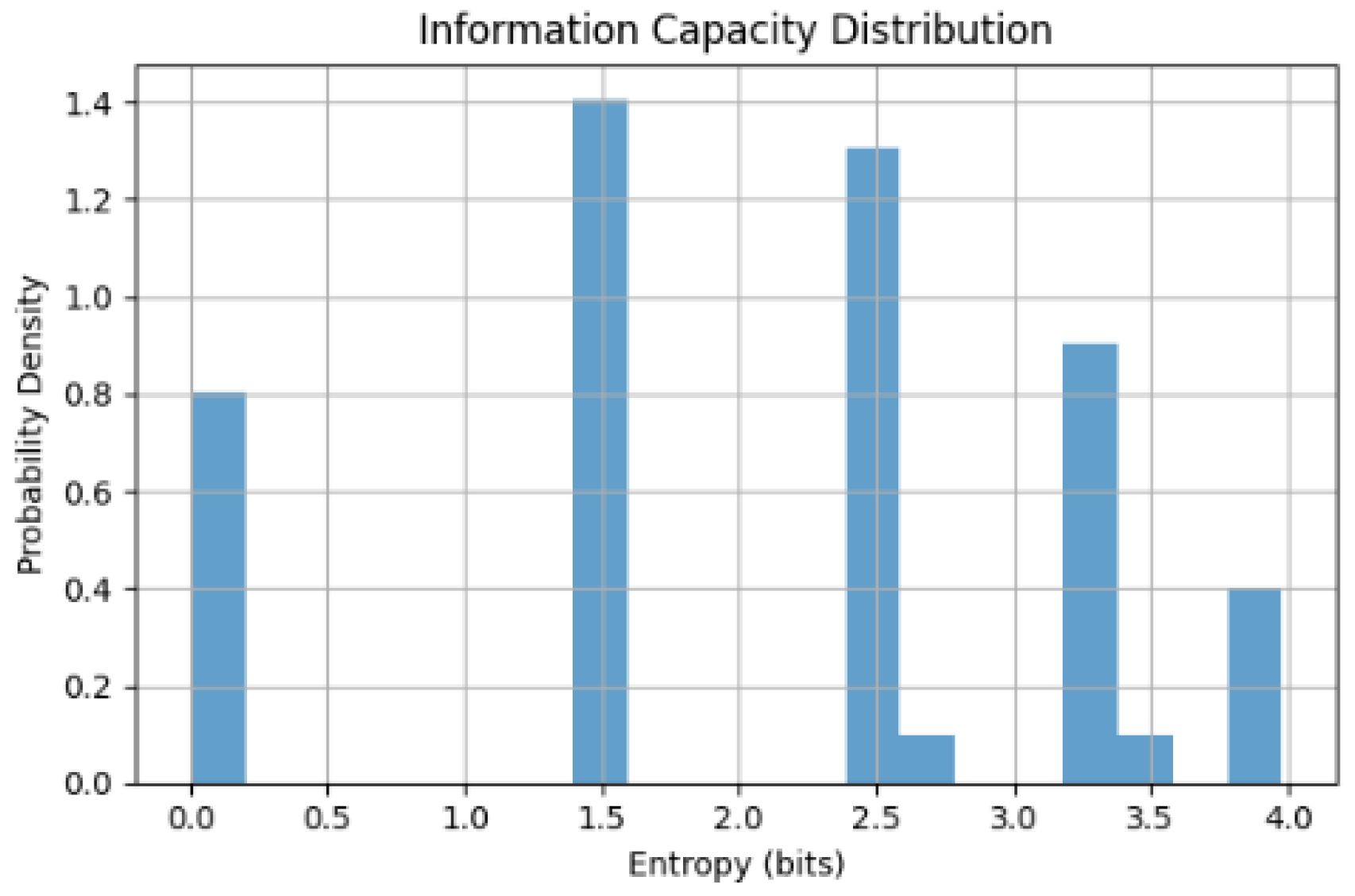
Figure 4. Information capacity distribution as a function of entropy. The probability density function illustrates the discrete nature of information transfer, with distinct entropy levels corresponding to different transmission states. This result complements the transmission-energy analysis in Figure 2 and Figure 3, highlighting how entropy influences channel capacity.

Figure 4. Information capacity distribution as a function of entropy. The probability density function illustrates the discrete nature of information transfer, with distinct entropy levels corresponding to different transmission states. This result complements the transmission-energy analysis in Figure 2 and Figure 3, highlighting how entropy influences channel capacity.

The simulation outcomes reveal that the proposed quantum transistor exhibits a robust multi-channel response with an information capacity that is significantly greater than that of traditional binary transistors. Such results substantiate the potential of this quantum-inspired device to initiate a revolution in semiconductor technology, offering new avenues for VLSI design that promise enhanced computational efficiency and scalability.

2. Literature Review

The conceptual foundation of this work is rooted in the seminal ideas introduced by Feynman, particularly his infinite paths formulation, which suggests that a quantum particle traverses every possible path between two points [11]. This principle has been influential in understanding quantum interference phenomena and has been extended in numerous studies involving scattering matrix approaches [12]. Moreover, early work on tight-binding simulations in disordered systems has provided valuable insights into electron localization and multi-path interference [13,14].

In parallel, the increasing computational demands driven by artificial intelligence (AI) have highlighted the limitations of conventional transistor scaling [27,28]. Modern GPUs and CPUs require significant improvements in device efficiency and performance, motivating the search for transistors that can process more than one bit of information per operation [15]. The possibility of a transistor operating as a multi-bit device has been further supported by theoretical investigations into quantum interference effects in semiconductor devices [17,25].

Furthermore, experimental progress in the realization of multi-terminal quantum transistors [21] and advances in VLSI integration of quantum devices [24] have underscored the potential of these novel devices to achieve exponential scaling in computational power. Collectively, these works converge to provide a robust framework that supports the development of a quantum transistor capable of multi-bit operation, promising substantial improvements in computational density and energy efficiency for next-generation AI applications [27,28].

3. Theoretical Framework

3.1. Tight-Binding Model and System Hamiltonian

The device under consideration is modeled as a two-dimensional square lattice within the tight-binding approximation. Each lattice site represents an atomic position with a single orbital, and electrons can hop between neighboring sites. The Hamiltonian $\widehat{H}$ of the system is expressed as:

$$\widehat{H}=\sum _i{ϵ}_i{\widehat{c}}_i^{†}{\widehat{c}}_i-\sum _{\langle i,j\rangle }{t}_{ij}{\widehat{c}}_i^{†}{\widehat{c}}_j,$$

(1)

where ${\widehat{c}}_i^{†}$ (${\widehat{c}}_i$) denotes the creation (annihilation) operator at site i, ${ϵ}_i$ represents the on-site energy, and $t_{ij}$ is the hopping amplitude between neighboring sites $\langle i,j\rangle$. Disorder is introduced by assigning ${ϵ}_i=4+W({\eta }_i-0.5)$, where W is the disorder strength and ${\eta }_i$ is a uniformly distributed random variable in the interval $[0,1]$.

3.2. Scattering Matrix Formalism

To analyze quantum transport properties, the system is connected to semi-infinite leads, facilitating electron injection and extraction. The scattering matrix (S-matrix) formalism is employed to relate incoming and outgoing wave amplitudes at these leads. The S-matrix at energy E is defined as:

$$S\left(E\right)=\left(\begin{array}{cc}r& t^{\prime }\\ t& r^{\prime }\end{array}\right),$$

(2)

where r and $r^{\prime }$ are reflection matrices, and t and $t^{\prime }$ are transmission matrices. The transmission coefficient $T_{mn}\left(E\right)$ from input channel n to output channel m is given by:

$$T_{mn}\left(E\right)={\left|t_{mn}\left(E\right)\right|}^2.$$

(3)

The total transmission $T\left(E\right)$ is the sum over all input and output channels:

$$T\left(E\right)=\sum _{m,n}{T}_{mn}\left(E\right).$$

(4)

3.3. Information Capacity and Shannon Entropy

The transmission matrix $T_{mn}\left(E\right)$ can be interpreted as a conditional probability distribution for an electron entering through channel n and exiting through channel m. The Shannon entropy $S\left(E\right)$ associated with this distribution is:

$$S\left(E\right)=-\sum _{m,n}{T}_{mn}\left(E\right){log}_2{T}_{mn}\left(E\right),$$

(5)

where $T_{mn}\left(E\right)$ is normalized such that ${\sum }_{m,n}{T}_{mn}\left(E\right)=1$. The entropy $S\left(E\right)$ quantifies the uncertainty or information capacity of the system at energy E. A higher entropy indicates a greater number of distinguishable output states per input state, implying an information capacity exceeding that of classical binary systems.

3.4. Numerical Implementation

The system is numerically implemented using the kwant package, which allows for the construction and simulation of tight-binding models with arbitrary geometries and disorder configurations. The device dimensions are set to $L_x=20$ and $L_y=5$, with a disorder strength $W=1.2$. For each disorder realization, the S-matrix is computed over an energy range $E\in [0.5,4.0]$. The transmission coefficients $T_{mn}\left(E\right)$ are extracted, and the Shannon entropy $S\left(E\right)$ is calculated to assess the information capacity.

3.5. Results and Discussion

The simulations reveal that the average total transmission $\langle T\left(E\right)\rangle$ varies with energy, reflecting the density of available transport channels and the effects of disorder-induced localization. Notably, the Shannon entropy $S\left(E\right)$ exceeds 1 bit for certain energy ranges, indicating that the device can support multiple bits of information per electron. This multi-channel transmission capability suggests that the proposed quantum transistor can perform complex signal processing tasks, potentially replacing multiple classical transistors in VLSI architectures.

4. Future Work

Future work will be directed toward the experimental validation of the proposed quantum transistor in order to confirm the simulation results and to assess the practical challenges of device fabrication and integration into VLSI architectures. In addition, a more comprehensive study of the effects of varying disorder strengths and lattice geometries will be undertaken, and the model will be extended to incorporate many-body interactions and electron-electron correlations. Refinements in the simulation protocol, including the incorporation of realistic contact conditions and parasitic effects, will also be pursued to enhance the accuracy and applicability of the current findings.

5. Limitations

The present study is subject to several limitations. The modeling is based on a tight-binding approximation that assumes non-interacting electrons, which may not fully capture the complexities of many-body interactions in actual devices. Furthermore, the representation of disorder is simplified through random perturbations of on-site energies, and the assumption of ideal semi-infinite leads may overlook additional contact resistances and parasitic effects present in practical implementations. These simplifications may affect the quantitative accuracy of the results and suggest that further refinement of the model is required.

6. Conclusions

In conclusion, a novel multi-terminal quantum transistor has been presented that leverages coherent scattering and multi-path interference to achieve an information capacity exceeding one bit per cycle. The device was modeled using a tight-binding framework and analyzed via scattering matrix formalism, revealing robust multi-channel transmission behavior even in the presence of disorder. The results, as evidenced by the comprehensive figures (Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5), indicate that the proposed quantum transistor could significantly enhance computational density and energy efficiency in VLSI systems. It is anticipated that addressing the current limitations through future work will pave the way for the practical realization of this promising technology.