This study introduces a variation of the Roman domination problem in graphs. In previous works, we explored the [k]-Roman domination model, which involves defending against single attacks requiring at least k units, focusing on the case. In this work, we extend the model by guaranteeing that stronger vertices are not isolated.
The concept of total domination can be incorporated into the triple Roman domination model to prevent isolated vertices among labeled ones, strengthening the network at the potential cost of higher expense.
A total triple Roman dominating function (t3RDF) satisfies both triple Roman domination and secures no isolated vertices in the induced subgraph by vertices with positive labels. The total triple Roman domination number, is the minimum weight of a t3RDF.
This paper introduces the total triple Roman domination model. We examine the algorithmic complexity of the decision problem, provide bounds, describe extremal graphs, and find exact values for several graph families.
2. Complexity
The goal of this section is to prove that the total triple Roman domination decision problem (t3RDP) is NP-complete even for bipartite graphs.
We prove it by showing the equivalence of any instance of the t3RDP with an instance of one of the Exact 3-Cover (X3C) problem. Formally, we consider the following decision problems:
PROBLEM
Instance: Graph and a positive integer K.
Question: Does G have a t3RD function f with ?
PROBLEM
Instance: A finite set and a collection C of 3-element subsets of X.
Question: Does there exist a subset such that every element of X appears in exactly one element of ?
Proposition 1. is -complete for bipartite.
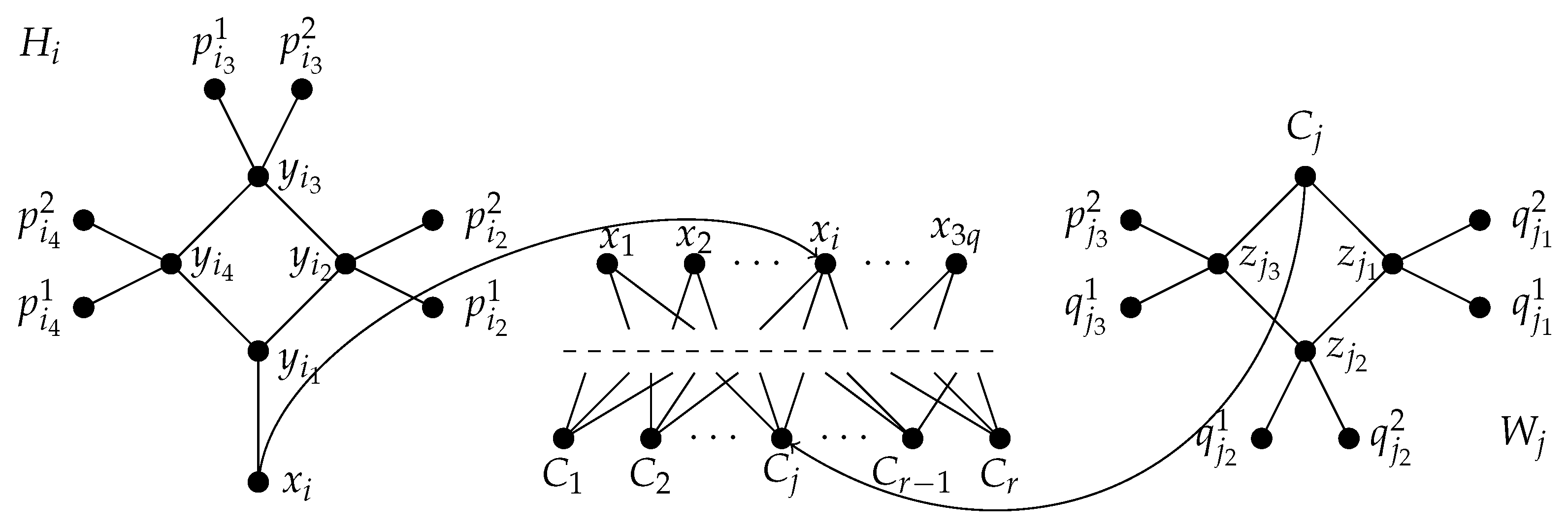
Proof. We can readily prove that t3RDP is in the NP-class because any potential solution can be verified in polynomial time. We now show that converting any instance of to an instance of t3RDP results in equivalent solutions for both problems. Consider and , an instance of . For each , we include a gadget by adding two pendant vertices to each vertex for of the cycle . Additionally, for each , we construct the gadget by adding two pendant vertices to each vertex of the path .
We construct the graph as follows: we start with a bipartite graph with set of vertices such that is adjacent to if and only if We add the gadgets by joining the vertices with a new edge, for and, analogously, we add the gadgets to the graph by the edges for .
Clearly, the constructed graph is bipartite with vertex classes
and
Now, assume that there exists
which is an exact cover for the set
Let
f be a function over the vertices of
defined as follows:
if
and
otherwise. Since
is a solution of the
for the instance
we may deduce that
. On the other hand,
for all
and the induced subgraph by the set of vertices with a positive label has no isolated vertices. Hence,
f is a t3RD function with
To complete the proof, suppose that f is a t3RDF with Since are support vertices and f is a t3RDF, we may assume that for all Analogously, without loss of generality, we may assume that for
If for some then we may define a new function as follows: , , where is a clause containing . As the vertex is total triple dominated by any of the vertices with we have that is a t3RDF with weight at most . So, we may assume that for all
Analogously, if for some , the function , , where is a clause containing . Since the vertices are adjacent to both with then we have that is a t3RDF having weight at most . Then, we may assume that for all
In such a case, we have that which implies that
Let be
and suppose that
Then the number of vertex
with some neighbour in
is at most
As a result,
and also
for each vertex
without neighbours in
And, given that the cardinality of
is three, it must be
which is a contradiction.
Therefore with if and if Besides, as and for all then there exist with . And taking into account that and the cardinality of is three, then the elements of are disjoint from each other.
Hence, solves the instance of the problem. □
Figure 1.
Gadgets and bipartite graph .
Figure 1.
Gadgets and bipartite graph .
3. Bounds
Once we have shown that calculating the exact value of the total triple Roman domination number (t3RDN) is an NP-hard problem, it is a natural step forward to bound this parameter in terms of well-known structural features of a graph.
Clearly, the t3RDN of a non-connected graph is the sum of the t3RDN of its components. Besides, as we have mentioned above, the total version of this domination problem only makes sense for isolated vertex-free graphs. Therefore, since we need any undefended vertex to be able to receive at least 3 units from its active neighbors, it is straightforward to derive a first upper bound by assigning a label 2 to each vertex in the graph.
Proposition 2. Let G be a connected graph of order n. Then . Equality holds if and only G is the corona product of a connected graph H with a .
Proof. Let f be the function defined as for all Clearly, f is a t3RDF and therefore
If and f is a -function then is an even integer and for each leaf where v is the corresponding support vertex. Hence, and the equality holds.
On the other hand, suppose that . If then and the result holds. So, we may assume that If then which is impossible because So, assume that
Let v be a vertex with maximum degree in G and denote by its neighborhood. First, suppose that . If there exists a vertex w such that then consider such a vertex having minimum degree and denote by its neighbors. Now, we may define a function f as follows ; ; and otherwise. By our choice of w, every vertex labeled with a 2 is adjacent to a vertex with a positive label. The vertices having a label 0 are adjacent to both v and w, therefore f is a t3RDF in G and a contradiction. If for all then we may define a function f as follows ; ; and otherwise. We can readily check that f is a t3RDF in G and hence again a contradiction.
So, we can deduce that it must be . If there exists a strong support vertex v such that are its leaves, then we can define a function f as follows: ; and otherwise. It is straightforward to check that f is a t3RDF and then Hence, there are only weak support vertices in G. If there exists a vertex which is neither a leaf nor a support vertex then we may define a function f as follows and otherwise. Since then f is a t3RDF and which is not possible.
Then, every vertex in G is either a leaf or a weak support vertex, which finishes the proof. □
Our next results give us an upper bound for the t3RDN in terms of the maximum degree of the graph.
Proposition 3. Let G be an ntc-graph maximum degree . Then .
Proof. Consider a vertex with maximum degree and let be the neighborhood of v. Let us define the function as follows for and for the remaining vertices. Then f is t3RDF and □
Some graphs, including the path and the cycle attain this bound. Furthermore, we can readily verify that the upper bound given in Proposition 3 improves upon the one presented in Proposition 2 whenever .
Proposition 4.
Let G be an ntc-graph of order n, , girth and maximun degree Then
Proof. Consider a vertex
with maximum degree
and let
be the neighborhood of
v. Let us define the function
as follows
for
and
for the remaining vertices. Let
z be any vertex belonging to
. Since
and
then
. Therefore, there exists
such that
and
Since
has not isolated vertices, then
f is a t3RDF and
□
As shown in
Table 1, these bounds are not comparable. There are graphs for which each bound is better (boxed) than the others.
The upper bound can be significantly improved in the case of dealing with a regular graph, as demonstrated by the result we prove next.
Proposition 5. Let G be an r-regular connected graph of order n and girth . Then
Proof. Let
v be any vertex of the graph
G and let us denote by
and
. Clearly,
and
because the girth is at least
Consider the function
defined as follows:
for all
for all
and
otherwise. Since
and the girth is greater than or equal to 7, we may readily verify that
f is a t3RDF. Hence
□
Although the upper bound matches the exact value, for example, of , it is worth pointing out that the girth condition is essential. It is not difficult to check that whereas the upper bound given by Proposition 5 would imply that
In what follows, it is important to keep in mind certain conditions that, without loss of generality, we may assume a -function satisfies.
Remark 1. Let f be a -function of an ntc-graph G. Let v be a support vertex whose leaves are the vertices , with . Then,
If v is a weak support vertex then and
If v is a strong support vertex such that for all then we may suppose that ; and , for all
If v is a strong support vertex such that there is a vertex with then we may assume that and for all the leaves .
To close this section, we prove several results in which we bound the total triple Roman domination number of a graph in terms of other domination parameters such as the (total) domination number or the total double Roman domination number.
Proposition 6. Let G be an ntc-graph, then .
Proof. Let
D be a
-set and
the isolated vertices in the induced subgraph
. For each
we consider a vertex
and let us denote by
. Consider the function
defined as follows:
, for all
for all
and
for the remaining vertices. Then
□
This bound is met by infinitely many graphs, such as those that contain a universal vertex.
Corollary 1. Let G be an ntc-graph. Then, if and only if every γ-set is a 3-independent set.
Proof. If
then the inequalities in (
1) become equalities. Therefore,
and all the dominating vertices are isolated in
. Since
then there is no common neighbor
for any pair
of distinct vertices. Consequently, every
-set is a 3-independent set. □
Proposition 7. Let G be an ntc-graph with at least 3 vertices. Then .
Proof. Let S be a -set of G and let . We can readily prove the upper bound by considering a function g such that for all . This function g is a t3RDF and hence
Next, we prove the lower bound. Assume that
is a
-function. Since
is a total dominating set, we have that
If then and we are done. So, assume that If then either or or , and therefore So, the only case that remains to consider is But in this situation, which concludes the proof. □
Proposition 8.
Let G be an ntc-graph. Then
Proof. First, to prove the lower bound, consider a -function. If then is a tdRDF with weight and hence
Assume now that , which implies that . Let be a vertex and consider the function defined as follows: and otherwise. First, observe that the set still total-dominates the graph G. On the other hand, the set of active neighbors of all vertices of V does not change regardless of which function f or g we consider. Therefore, if and then If and then Hence g is a tdRD function having weight and
To prove the upper bound, we consider
a
-function and let us define the following function
if
if
and
otherwise. Then,
f is a t3RDF of
G and we may readily deduce that
This fact, and the bound given by the Proposition 6, leads us to the desired result. □
We conclude by providing two lower bounds in terms of the order, maximum degree and domination number of the graph, some of which follow from well-known bounds for the triple Roman domination number.
Proposition 9. Let G be an ntc-graph with . Then
Proof. Let
f be a
-function of
G. Then
because
(resp.
) is a total dominating (resp. dominating) set of
□
Proposition 10.
Let G be an ntc-graph of order n. Then
Proof. This bound is an immediate consequence of
and the following lower bound, proved in [
2],
□
Besides, by applying the upper bound proved in [
15] we may derive that
Remark 2.
For any ntc-graph G of order and maximum degree we have that
4. Exact Values of the Total Triple Roman Domination Number
Our aim in this section is to characterize those graphs that have the first few smallest values of the parameter
. Also, prove several results regarding the exact values of the t3RD-number for certain graph families. In what follows, we make use of the following notation. Given a positive integer
, let
and
Proposition 11. Let G be an ntc-graph with order . Then if and only if
Proof. Let u be a vertex with maximum degree and . Consider a function defined as follows and , for al . We can readily check that f is a t3RDF of G. Hence, On the other side, assume that G is an ntc-graph with at least 3 vertices and let be a -function. If then for any vertex we have that and therefore If then either , which implies that or and or In any case, we deduce that
Assume now that and . Let be a -function. If , then either or . In any case, since f is a t3RDF, the vertex labeled 3 or 4 is universal. Hence, .
Otherwise, suppose that , which implies that because f has minimum weight. Since we have that either and or and . In these cases, and we are done. □
Proposition 12. There is no ntc-graph G such that
Proof. Let G be an ntc-graph with and let be a -function of G. If either or or or then the vertex having the greatest label is a universal vertex because f is a t3RD function, which is a contradiction with Proposition 11.
If and , then , and once again, we deduce that the vertex in is universal. Hence, . If , then at least one of the vertices in must be adjacent to the other two vertices in . Furthermore, since every vertex in must be adjacent to each vertex in , we conclude that , once again leading us to a contradiction.
Lastly, suppose that and , which implies that . The vertices in must all be adjacent, and each vertex in must be adjacent to both vertices in . Therefore, both vertices in are universal, which completes the proof. □
Next, we provide some technical results that will allow us to establish the main results of this section concerning the exact value of the t3RD number for paths and cycles.
Lemma 1. Let G be an ntc-graph of order n and Let f be a -function such that the number of vertices assigned 0 under f is minimized and let be an ordered set of vertices that induces a path in G. Then the following conditions hold,
- L1
for all .
- L2
If and , then there exists a -function g such that and .
- L3
If and , then there exists a -function g such that and .
- L4
If and , then there exists a -function g such that and .
Proof. Since G is an ntc-graph with , it follows that G is either a path or a cycle. Let be the vertices of G.
L1. Suppose a vertex exists, say , such that . If and , then we can define g as follows: and for . So, g is a t3RDF of G with weight , which is a contradiction. Without loss of generality, assume that and . Then the function g defined by , and for , is a t3RDF of G with weight . Thus, g is also a -function, with against our assumptions. Therefore, the result holds.
L2. Since f is a t3RD function, and then it must be . On the other hand, as and then we have that So, we can define a function g as follows and otherwise. Hence, g would be a t3RDF of G with weight and The proof of items L3 and L4 are quite similar to this one and we leave the details to the reader. □
Lemma 2. Let G be an ntc-graph with If is an ordered set of vertices that induces a path in G, then there exists a -function g such that
Proof. Let f be a -function such that the number of vertices labeled with a 0 under f is minimized and let be the set of vertices of G. Suppose on the contrary, that , for all . We have to consider several cases,
Case 1. If and , for all and then we can define a function g in the following way: , and otherwise. Therefore g is a t3RDF of G with weight and .
Case 2. If and , for all then we can define g as , , and otherwise. Therefore g is a t3RDF of G with weight and .
Case 3. If and, without loss of generality , then we consider , and otherwise. Therefore, g is a t3RD function with weight and .
Case 4. If , , , and then . We can define a new function g such that , and otherwise. Hence, g is a t3RDF of G with weight and . □
Proposition 13. Let G be an ntc-graph with maximum degree , order and let be a -function such that is minimized. Then .
Proof. First of all, note that since we only have to prove the result for cycles. For we may readily check that that satisfies the inequality.
Let us suppose that , f be a -function and be consecutive vertices of . Without loss of generality, by applying Lemmas 1 and 2, we only have to consider the following situation
If
then
. Therefore, the function
g defined as
and
otherwise, is a total double Roman dominating function in the cycle
with weight
By applying Proposition 8, since
we can conclude that
□
Proposition 14. Let G be an ntc-graph with , and let be a t3RDF on G, such that the number of vertices assigned 0 under f is minimum. Then .
Proof. Since
, we can restrict ourselves to proving the result for paths. To do that we proceed by induction on the order
of the path. The labellings shown in
Table 2 permit us to state that the bound is correct for all
So, let us assume that
and that
for all
Denote by
, where
y
and consider
a
-function. Then, the function
g defined as
and
for all
is a t3RDF in
with weight,
that finishes the proof. □
Let us point out that, by Propositions 13 and 14, we know that for any path or cycle G of order .
Lemma 3. Let T be a tree and v be a leaf vertex of T. Let M be the tree obtained from T and the star , with by adding an edge between v and a leaf of the star . Then
If then
If and there exists a -function f such that then
If and for all -function f then .
Otherwise, we have that
Proof. To begin with, let us assume that
. Let
be a
-function on
T and let
and
be the vertices of
such that
is adjacent to
v in
M. Let
g be a function defined as
and
for all
So,
g is a t3RDF on
M and
On the other hand, let f be a -function and let be the neighbor of v in T. By applying Observation 1 we have that and, therefore,
If then the function g defined as follows for every and otherwise is a t3RDF in T having weight, at most, and we are done.
Now, if , then the function g defined as follows for every and is a t3RDF in T having weight, at most, , as desired.
On the contrary, if then we have that and hence because v must be total-triple-Roman dominated by Hence, the function g defined as follows for every and is a t3RDF in T having weight, at most, .
Let us now assume that
and that there is a
-function
f such that
Since
f is a
-function such that
then we can define a function
g in the following way
for all
,
which is a t3RDF on
M and hence
Moreover, if g is a -function then by Observation 1 we have that . Let us define the function on T as follows and otherwise. The function is a t3RDF on T and therefore which lead us to as desired.
Next, let us suppose that and for all -function If f is any -function then the function for all , and is a t3RDF on M, leading us to
Now, to prove the other inequality, let us consider g a -function. Then, by Observation 1, we have that . If then is a -function and, by our assumptions, must be less than or equal to 1, which implies and a contradiction because So, it must be
Reasoning by contradiction, let us suppose that and hence As we may deduce that is not a t3RDF. This may be due to either or either We can define a function on T as follows, and otherwise. Then, and because g is a t3RDF and is an active neighbor of v. Hence, is a t3RD function on T. Moreover, if then and if then because whereas . In any case, against our assumption.
The proof of the case is analogous to the earlier case. □
Theorem 1. Let be a positive integer. Then .
Proof. We can readily check that whenever . By applying Propositions 13 and 14 we know that and .
Let be a -function on such that the number of vertices assigned 0 under f is minimum. For simplicity, we occasionally represent a domination function defined on a path with n vertices denoted by , as an ordered n-tuple , where for each .
Let us note that and the following labelings correspond to -functions for , respectively. Therefore, by applying Lemma 3, we derive that
Analogously, since and the labeling is a -function, it follows from Lemma 3 that . It is straightforward to see that and are the only minimum possible labelings of and , respectively. Thus, by applying Lemma 3 again, we deduce that and .
Let and q be positive integers such that with . Let us denote by , whenever and , otherwise.
We define the following function
whenever
. Besides, if
then
. Finally, if
then
and for the remainder vertices we establish the values of
in the
Table 3.
Observe that,
If then
If then
If then
If then
If then
If then
If then
If then
Therefore, we have that for all and that for all
To prove that for all we reason by induction. Let be an integer and assume that for all Let us denote by such that the edges of the path are whenever So, we know that and, by applying Lemma 3, we may derive that . Analogously, it is deduced that .
Let g be a -function such that the number of vertices with a label 0 is minimum. By Observation 1, we have that and, without loss of generality, we may suppose that If we are done because
Hence, assume that which implies that is not a t3RDF in because This may be due to several reasons, and we must study different situations.
Case 1: . In this case, by Lemma 1, we have that If then we have to study two different possibilities: either and or and . In both cases, we may define the following function and otherwise. The function is a t3RDF having the same weight of g. We can proceed similarly if or Therefore, we may assume that Since then
Case 1.1: . Then, and . Thus, is a t3RDF in and consequently implying that
Case 1.2: . Then, we may define the following function and otherwise. The function is a t3RDF under the conditions of Case 1.1.
Case 2: In this case, we may define the function and otherwise, which is a t3RDF under the conditions of Case 1.
Case 3: Clearly, because is not a t3RDF in Besides, and we have that is a t3RDF in and so .
Case 4: We can define the function and otherwise, which is a t3RDF under the conditions of Case 3.
Summarizing, we have shown that which concludes the proof. □
Theorem 2.
Let be a positive integer. Then
Proof.
Note that whenever and for
First, as shown in
Figure 2, we have that
for
. On the other side, since
then we also have that
for all
To prove the other inequality, we proceed by induction on the order of the cycle. By Proposition 13, we have that
Let be an integer, and assume that for all Denote by the set of consecutive vertices of the cycle. Let f be a -function such that the number of vertices labeled with 0 is minimum which by applying Lemma 1 implies that . Since , we may consider five consecutive vertices, say . By Proposition 2, we can assume that and, again by Lemma 1, we may suppose, without loss of generality, that and We have to discuss some different possibilities.
Case 1: In this case, it must be and
Case 1.1: We can readily check that for . Let and consider the cycle or order obtained by joining and Thus, is a t3RDF and
Case 1.2: Then it must be and the cycle or order obtained by joining and satisfies that is a t3RDF with
Case 1.3: which implies and If then and Thus, assume that If is adjacent to then and Thus, assume that and consider the cycle or order obtained by joining and . Again, is a t3RDF with
Case 2: Then, it must be Let be the cycle or order obtained by joining and We have that
Case 3: If so, we may consider the cycle or order obtained by joining and We can readily check that is a t3RDF and
That concludes the proof. □