On Domination and Total Domination Numbers on Strong Product of Two Path Graphs

1. Introduction

Researchers are very much inclined to investigate graph invariants with respect to graph products, in particular on the Cartesian product, the lexicographic product, the direct product or tensor product and the strong product [2]. A primary reason is the fact that a lot of challenging questions, concerning products of graphs, provide interesting insights and new growths in probes of these graph invariants such as the domination number and its modifications. It all came into lime light with Vizing’s conjecture on the domination number of the Cartesian product of graphs, raised in [3], and led to the birth of various related concepts and techniques [4]. The domination number of the Cartesian product of paths was fully found only in 2011 [5], after several endavors resulted in distinct methods to graph domination problems.

An n × m grid graph G has the vertex set V = {$u_{i,j}$: 1 ≤ i ≤ n, 1 ≤ j ≤ m} with two vertices$u_{i,j}$ and $u_{i^{\text{'}},j^{\text{'}}}$being adjacent if$u_i$ = $u_{i^{\text{'}}}$and $u_j$and $u_{j^{\text{'}}}$are adjacent or if $u_j$ = $u_{j^{\text{'}}}$ and $u_i$ and $u_{i^{\text{'}}}$are adjacent. The n × m grid graph can also be thought as a Cartesian product of two path graphs P_n and P_m, denoted by P_n × P_m of respective lengths n − 1 and m– 1.

The strong product of two graphs G and H denoted by G ⊠H has the vertex set V(G ⊠H) = V(G) × V(H). We say that a vertex ($u_1,v_1$) ∈ V(G × H) is adjacent to a vertex $u_2,v_2$∈ V(G × H) if and only if either $u_1$= $u_2$and ($v_1,v_2$) ∈ E(H) or ($u_1,u_2$) ∈ E(G) and $v_1$ = $v_2$or $u_1,u_2$∈ E(G) and ($v_1,v_2$)∈ E(H). Rarely some authors also refer to a strong product of two graphs as strong direct product or a symmetric composition [6].

A set D⊆V(G) is called a dominating set if any v ∈ V(G) – D is adjacent to at least one element in D and the size of a minimum dominating set of G is called the domination number of G denoted by γ(G).D is called a total dominating set if any v∈V(G) is adjacent to at least one element in D and the size of a minimum total dominating set of G is called the total domination number of G denoted by ${\mathsf{\gamma }}_{\mathrm{t}}$(G).D is called a captive dominating set, if it is a total dominating set and each element in D is adjacent to at least one element in V – D and the size of a minimal captive dominating set is called the captive domination number of G denoted by${\mathsf{\gamma }}_{\mathrm{c}\mathrm{a}}$(G).

The γ of grid graphs has been probed for the past fifty years. A lot attempts have been made to get lower and upper bounds on ${\mathsf{\gamma }}_{\mathrm{n},\mathrm{m}}$. For detailed investigations of general bounds on ${\mathsf{\gamma }}_{\mathrm{n},\mathrm{m}}$, one can see [7,8,9,10,11]. Also probes have been made on specific bounds for small values of either n or m or both. The authors in [12] showed ${\mathsf{\gamma }}_{\mathrm{n},\mathrm{m}}$for 1 ≤ n ≤ 4 and all m. It was then carried to the cases of n = 5, 6 and all m by the authors in [13]. In [14] the authors adopted a computational method to find ${\mathsf{\gamma }}_{\mathrm{n},\mathrm{m}}$for n = 7, 8, m ≤ 500; n = 9, m ≤ 233; and n = 10, m ≤ 125. Some of the previous findings were subsequently verified to be true in [15]. Fisher in 1990’s introduced a new technique for finding γ for grid graphs. His work was not published but is explained in [16], where the values of ${\mathsf{\gamma }}_{\mathrm{n},\mathrm{m}}$for n≤ 19 and all m are listed. By appealing to a dynamic programming algorithm, the values of ${\mathsf{\gamma }}_{\mathrm{n},\mathrm{m}}$ for n, m ≤ 29 were obtained in [17]. The authors in [17] also depicted the minimum dominating sets for square grid graphs up to a size of 29 × 29. The domination number concept finds a lot of applications in protection mechanisms and business networking [18]. For more one can refer to [19,20] and the references therein.

There are a variety of alterations on domination concept in graph. Some of them are total domination number, captive domination number, locating dominating number [21,22,23,24], independent dominating number [25,26], Roman dominating number [27,28] etc, The authors in [29] used the link among the existence of tiling’s in Manhattan metric with {1}-bowls and ${\mathsf{\gamma }}_{\mathrm{t}}$ of Cartesian products of paths and cycles to derive the asymptotical values of the ${\mathsf{\gamma }}_{\mathrm{t}}$ of these graphs and they further derived ${\mathsf{\gamma }}_{\mathrm{t}}$ of certain cartesian products of cycles. Also, they studied the problem of ${\mathsf{\gamma }}_{\mathrm{t}}$ for certain Cartesian products of two paths.

In this paper, motivated by the above works, we probe domination number, total domination number and captive domination number of strong product of graphs. In particular, the strong product of P_n and P_m .Another motivation for considering the strong product of graphs also stems from the work of the authors in [30] wherein they studied the relationship among the total k-domination number of the strong product of two graphs with the domination, k-domination and total k-domination numbers of the factors in the product. The idea of the exact value of the domination number can also applied to the multistep power consumption forecasting problem through smart grid electricity management. [31].

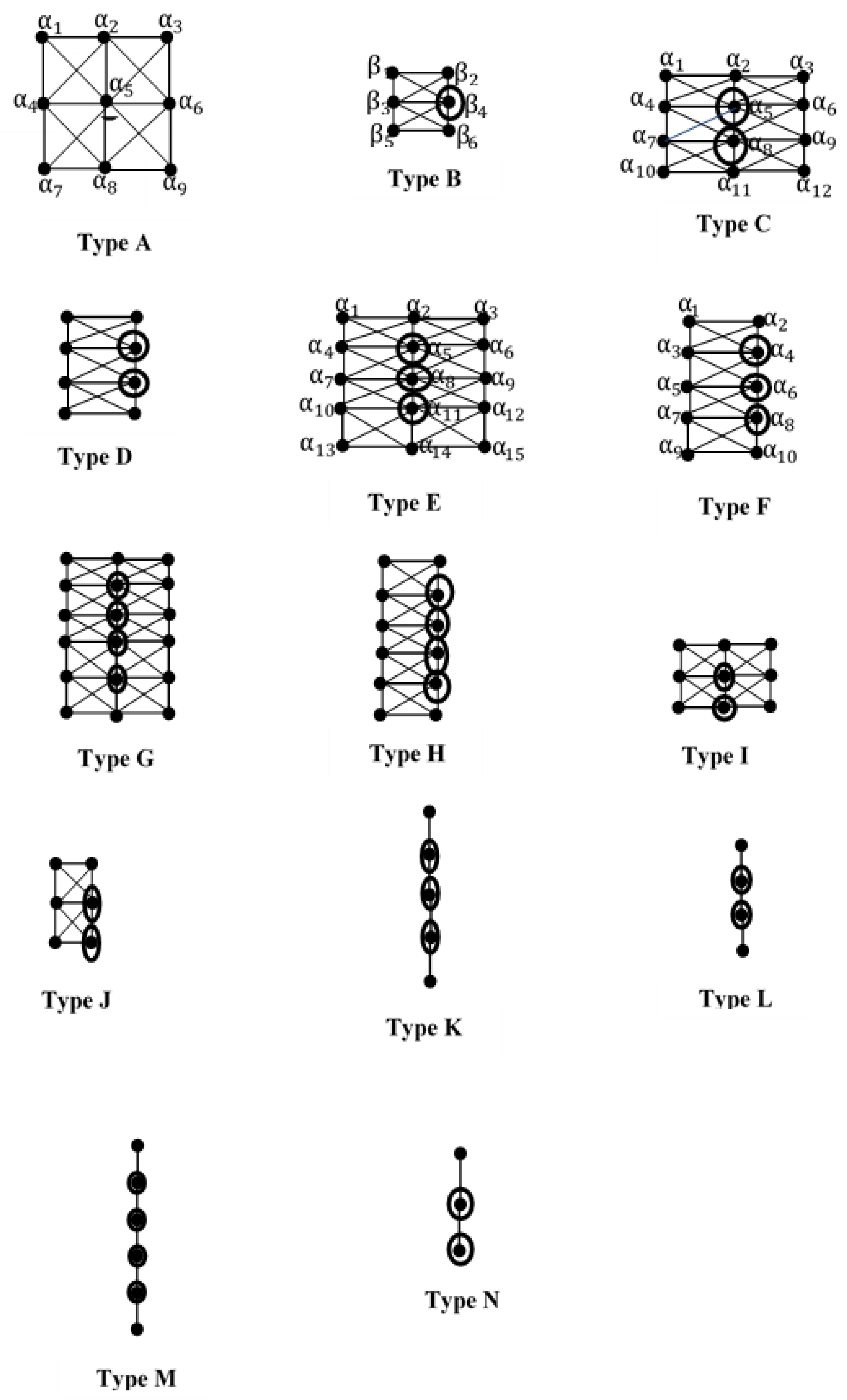
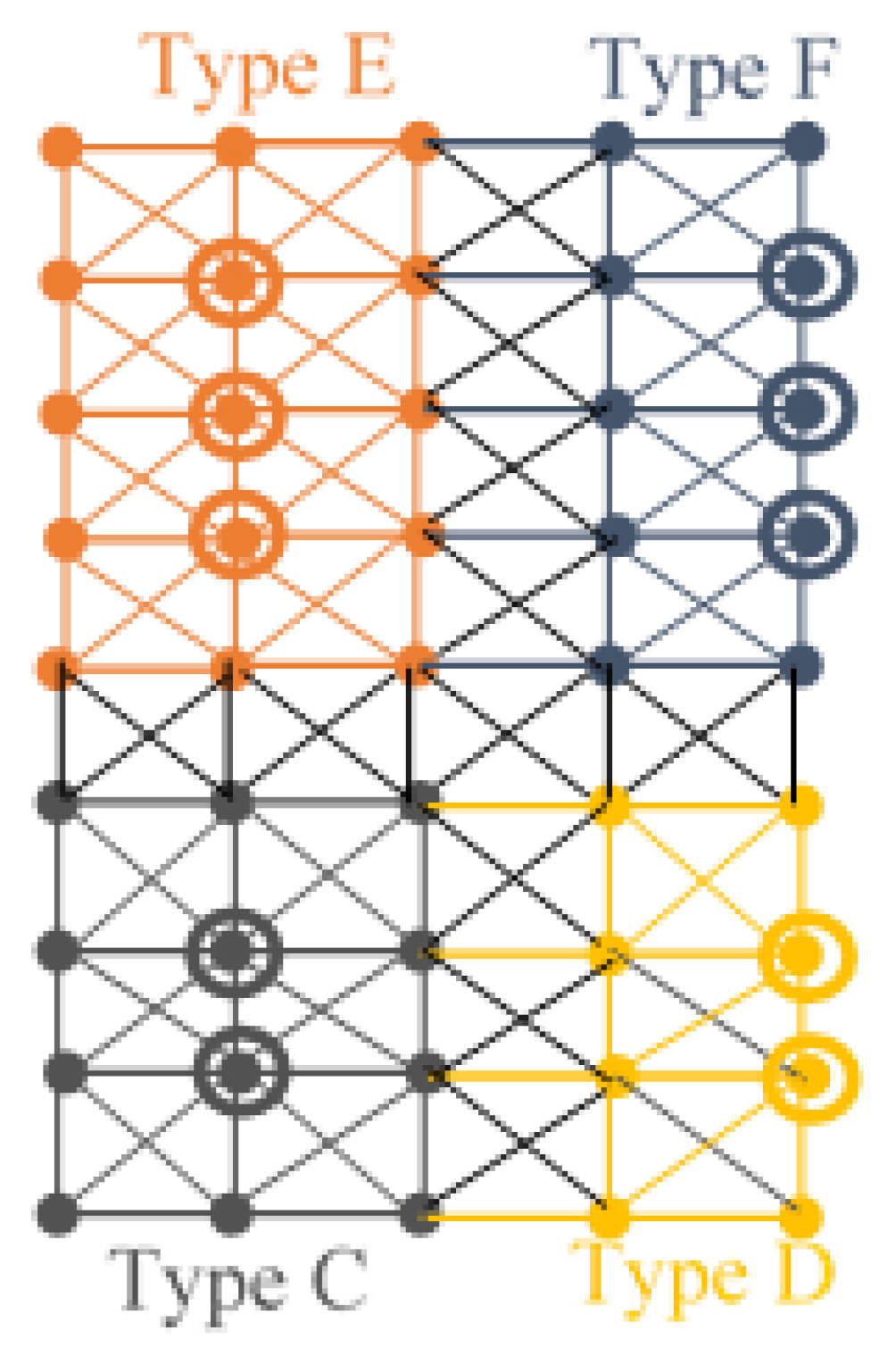
First we identify specific patterns lying in the graph P_n⊠P_m for various values of n and m and call them as Configurations. The minimum number of vertices required to dominate or totally dominate the rest of the vertices in such configurations are marked with a circle around them and are used in the proof of our results.

2. Domination number of strong product of path graphs

Theorem 2.1:

γ (P_n⊠P_m ) = r²if (n, m) = (3r, 3r-1) or (3r, 3r) or (3r-1, 3r) ;

r² + r if (n, m) = (3r, 3r+1) or (3r-1, 3r+1) or (3r+1, 3r) or (3r+1, 3r-1).

Proof: We split the proof into various cases.

Case1: (n, m) = (3r, 3r)

We call a 3 × 3 mesh for r = 1 in ${\mathrm{P}}_{3\mathrm{r}}⊠{\mathrm{P}}_{3\mathrm{r}}$a Type-A configuration. It is shown in Figure 1.

Note that each ${\alpha }_i$ is an ordered pair of vertices ${(u}_i,v_j)$for some 1≤ i, j ≤ 3r. It is easy to observe that D = {${\alpha }_5$} is a minimum dominating set for the Type–A configuration. Here we also observe that a 3 × 3 mesh can be thought as an induced subgraph of${\mathrm{P}}_{\mathrm{n}}⊠{\mathrm{P}}_{\mathrm{m}}$. There are r² Type A configurations in${\mathrm{P}}_{\mathrm{n}}⊠{\mathrm{P}}_{\mathrm{m}}$. Each such Type-A configuration yields one dominating element of that 3 × 3 mesh. Hence it is easy to see that a minimum dominating set of ${\mathrm{P}}_{\mathrm{n}}⊠{\mathrm{P}}_{\mathrm{m}}$ contains r² elements. So γ(${\mathrm{P}}_{3\mathrm{r}}⊠{\mathrm{P}}_{3\mathrm{r}}$) = r².

Case 2: (n, m) =(3r, 3r-1).

For r =1, (n, m) =(3, 2), we see that${\mathrm{P}}_3⊠{\mathrm{P}}_2$is a Type B configuration and it is shown in Figure 1.

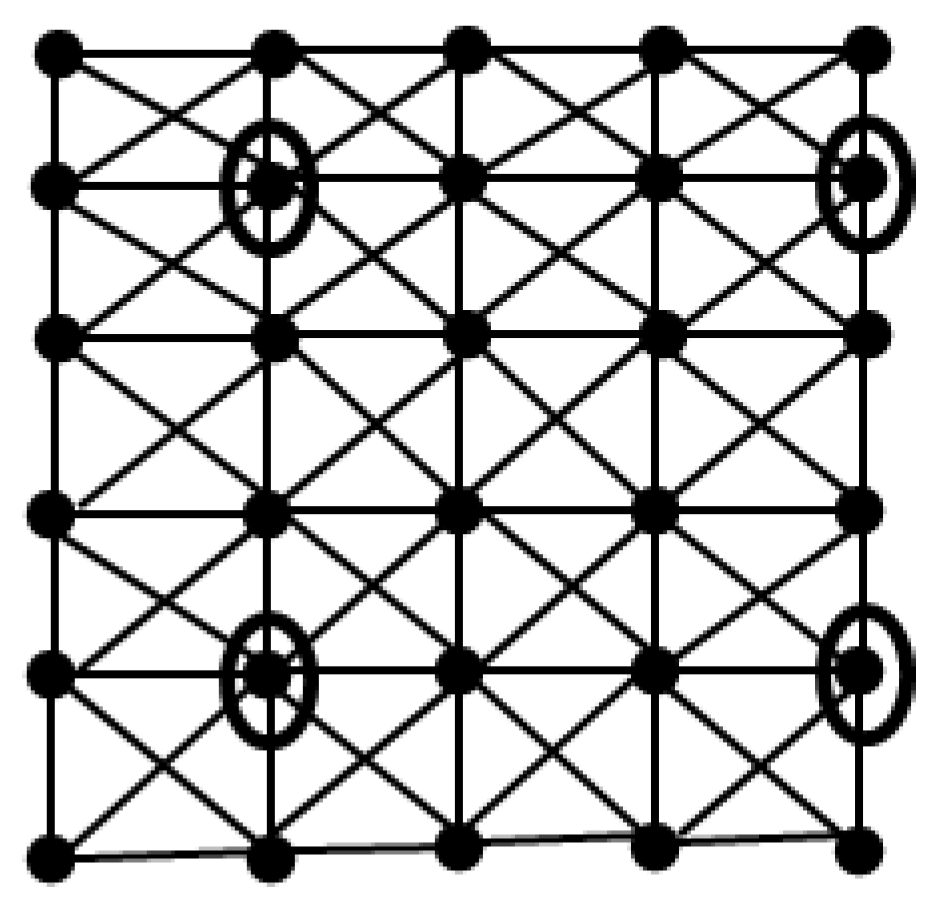
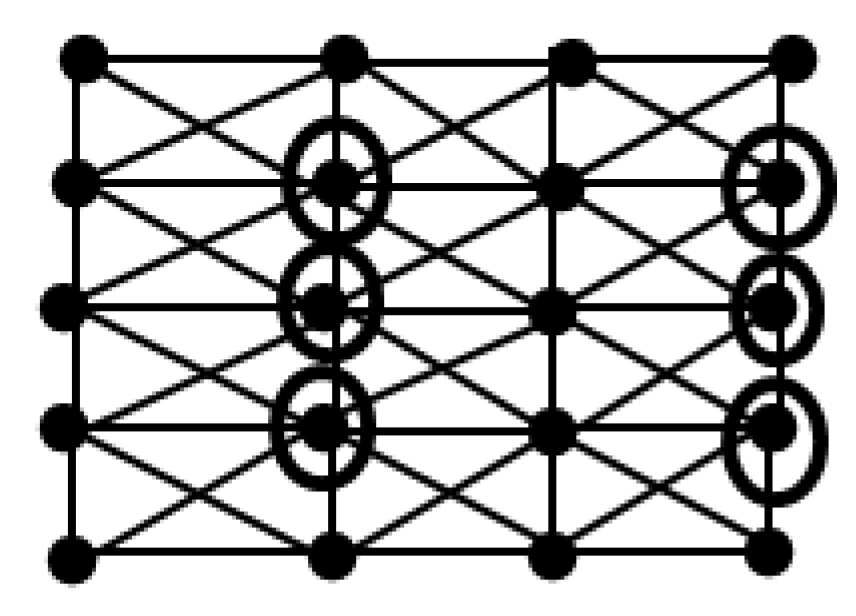
So γ(${\mathrm{P}}_3⊠{\mathrm{P}}_2$) = 1 = 1² = r². For r =2, (n, m) =(6, 5). The graph ${\mathrm{P}}_6⊠{\mathrm{P}}_5$ is shows Figure 2

${\mathrm{P}}_6⊠{\mathrm{P}}_5$consists of two disjoint Type-A configurations one below the other and also on the left-hand side two disjoint Type B configurations one below the other. The minimum dominating set D for ${\mathrm{P}}_6⊠{\mathrm{P}}_5$can be formed by adding the four elements indicated in Figure 2. So γ(${\mathrm{P}}_6⊠{\mathrm{P}}_5$) = 4 = 2²= r². In general, there are r(r-1) disjoint Type-A configurations one below the other and one after the other to the left. Also there are r disjoint Type-B configurations one below the other to the left most Type A configurations${\mathrm{P}}_{3r}⊠{\mathrm{P}}_{3r-1}$. The minimum dominating set D of ${\mathrm{P}}_{3r}⊠{\mathrm{P}}_{3r-1}$can be formed by adding all r(r-1) +r the marked elements. These marked elements in ${\mathrm{P}}_{3r}⊠{\mathrm{P}}_{3r-1}$are chosen by following the pattern of selection indicated in Figure 2. So |D| = r² -r + r = r² and γ(${\mathrm{P}}_{3r}⊠{\mathrm{P}}_{3r-1}$) = r².

Case 3: (n, m) = (3r-1, 3r+1).

For r = 1, (n, m) = (2,4). The graph ${\mathrm{P}}_2⊠{\mathrm{P}}_4$ is shown in Figure 3.

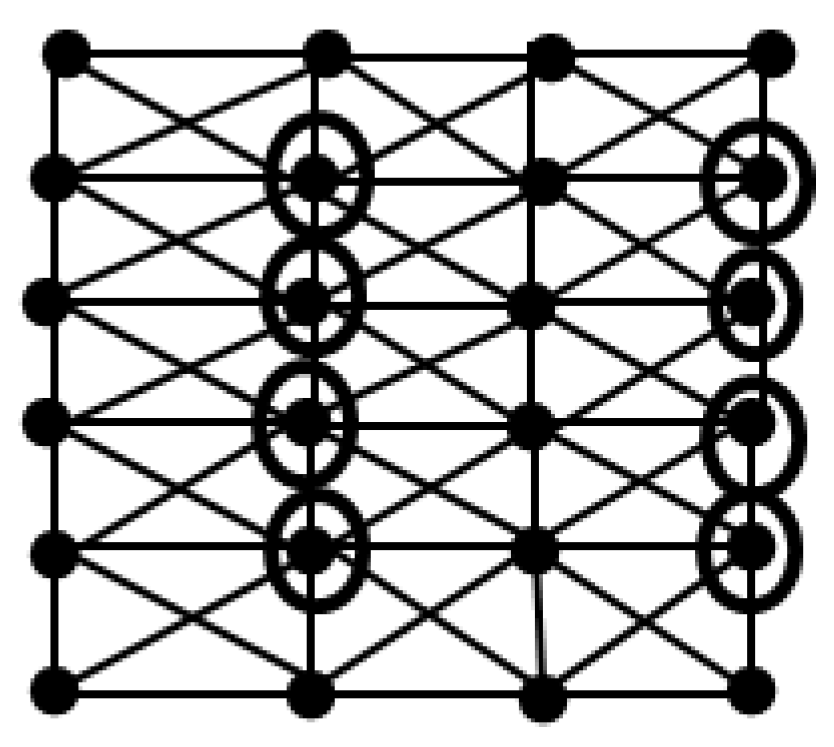
Clearly it consists of a one Type B configuration and one 2 × 2 mesh fused with it. So γ(${\mathrm{P}}_2⊠{\mathrm{P}}_4$) = 1+1 = 2 = 1² + 1 = r² + r. For r =2, (n, m) = (5, 7). The graph ${\mathrm{P}}_5⊠{\mathrm{P}}_7$ is shown Figure 4.

It consists of 2²fused Type A configuration and 2 fused Type B configurations. So the minimum dominating set D for ${\mathrm{P}}_5⊠{\mathrm{P}}_7$can be formed by including all the marked elements shown in Figure 5. Therefore |D| = 2² + 2 = r² + r = 6 andγ(${\mathrm{P}}_5⊠{\mathrm{P}}_7$) = 2² + 2= 4 + 2 = 6 = r² +r. In general,${\mathrm{P}}_{3r-1}⊠{\mathrm{P}}_{3r+1}$ consists of r²fused Type A configurations and r fused type B configurations. So if D is the minimum dominating set then it will include all the marked elements of the respective configurations chosen by following the same pattern as indicated in Figure 1. So |D| = r² + r and γ(${\mathrm{P}}_{3r-1}⊠{\mathrm{P}}_{3r+1}$) = r ²+r.

The other cases can be handled in a similar manner.

3. Total Domination Number of Strong Product of Path Graphs

Theorem 3.1:

${\mathsf{\gamma }}_{\mathrm{t}}\left({\mathrm{P}}_{\mathrm{n}}⊠{\mathrm{P}}_{\mathrm{m}}\right)$ =2r²if (n, m) = (4r, 3r) or (4r, 3r-1);

= 2r²+r if (n, m) = (4r+1, 3r) or (4r+1, 3r-1);

= 2r² +2r if (n, m) = (4r, 3r+1) or (4r+2, 3r) or (4r+2, 3r-1) or (4r+3, 3r) or

(4r+3, 3r-1);

= 2r²+3r+1 if (n, m) = (4r+1, 3r+1);

=2(r+1)² if (n, m) = (4r+2, 3r+1) or (4r+3, 3r+1).

Proof: We split the proof into various cases.

Case 1: (n, m) = (4r,3r).

We call a 4 ×3 mesh in ${\mathrm{P}}_{\mathrm{n}}⊠{\mathrm{P}}_{\mathrm{m}}$a Type C- Configuration and it is shown in Figure 1. Note that each ${\alpha }_i$is an ordered pair of vertices ($u_i,v_j$) for some 1 ≤ i ≤ 4r, 1 ≤ j ≤ 3r.

It is easy to observe that D = {${\alpha }_5,{\alpha }_8$} is a minimum total dominating set for Type C configuration. Here we also observe that a Type C configuration can be thought of as an induced subgraph of ${\mathrm{P}}_{\mathrm{n}}⊠{\mathrm{P}}_{\mathrm{m}}$. There are r² Type C configuration in${\mathrm{P}}_{\mathrm{n}}⊠{\mathrm{P}}_{\mathrm{m}}$. Each Type C configuration yields two dominating elements of that 4×3 mesh. Hence it is each to see that a minimum total dominating set of${\mathrm{P}}_{\mathrm{n}}⊠{\mathrm{P}}_{\mathrm{m}}$ contains 2r²elements. So ${\mathsf{\gamma }}_{\mathrm{t}}\left({\mathrm{P}}_{4\mathrm{r}}⊠{\mathrm{P}}_{3\mathrm{r}}\right)$ = 2r².

Case 2: (n,m) = (4r+1,3r).

For r =1, (n,m) = (5, 3). Clearly ${\mathsf{\gamma }}_{\mathrm{t}}\left({\mathrm{P}}_5⊠{\mathrm{P}}_3\right)$ = 2 ×1² +1= 2r²+r as D = {${\alpha }_5,{\alpha }_8,{\alpha }_{11}$}totally dominates all other ${\alpha }_i$’s for i = 1,2,3,4, 6,7,9,10,12,13,15.For r =2, (n,m) = (9,6). Clearly ${\mathrm{P}}_9⊠{\mathrm{P}}_6$ consists of two Type C configurations arranged side by side and two Type E configurations also arranged side by side but each one below their respective Type C configurations. So a minimum total dominating set D of ${\mathrm{P}}_9⊠{\mathrm{P}}_6$will consists of 2 ×2 + 2 ×3 = 4 + 6 = 10 elements and hence${\mathsf{\gamma }}_{\mathrm{t}}\left({\mathrm{P}}_9⊠{\mathrm{P}}_6\right)$ = 10= 2 ×2²+2. In general, there are (r-1)r Type C configurations arranged horizontally side by side and one after the other vertically and r Type E configurations arranged horizontally side by side below their respective Type C configurations. So a minimum total dominating set D of ${\mathrm{P}}_{4r-1}⊠{\mathrm{P}}_{3r}$will consist of 2(r-1)r+ 3r= 2r²+r elements. So ${\mathsf{\gamma }}_{\mathrm{t}}\left({\mathrm{P}}_{4\mathrm{r}+1}⊠{\mathrm{P}}_{3\mathrm{r}}\right)$ = 2r²+r.

Case 3: (n,m) = (4r+1, 3r-1).

For r = 1, (n,m) = (5,2) ${\mathrm{P}}_5⊠{\mathrm{P}}_2$is called a Type F configuration and it is shown in Figure 1. Clearly D = {${\mathsf{\alpha }}_4,{\mathsf{\alpha }}_6,{\mathsf{\alpha }}_8$} is a minimum total dominating set. So ${\mathsf{\gamma }}_{\mathrm{t}}\left({\mathrm{P}}_5⊠{\mathrm{P}}_2\right)$= 3.

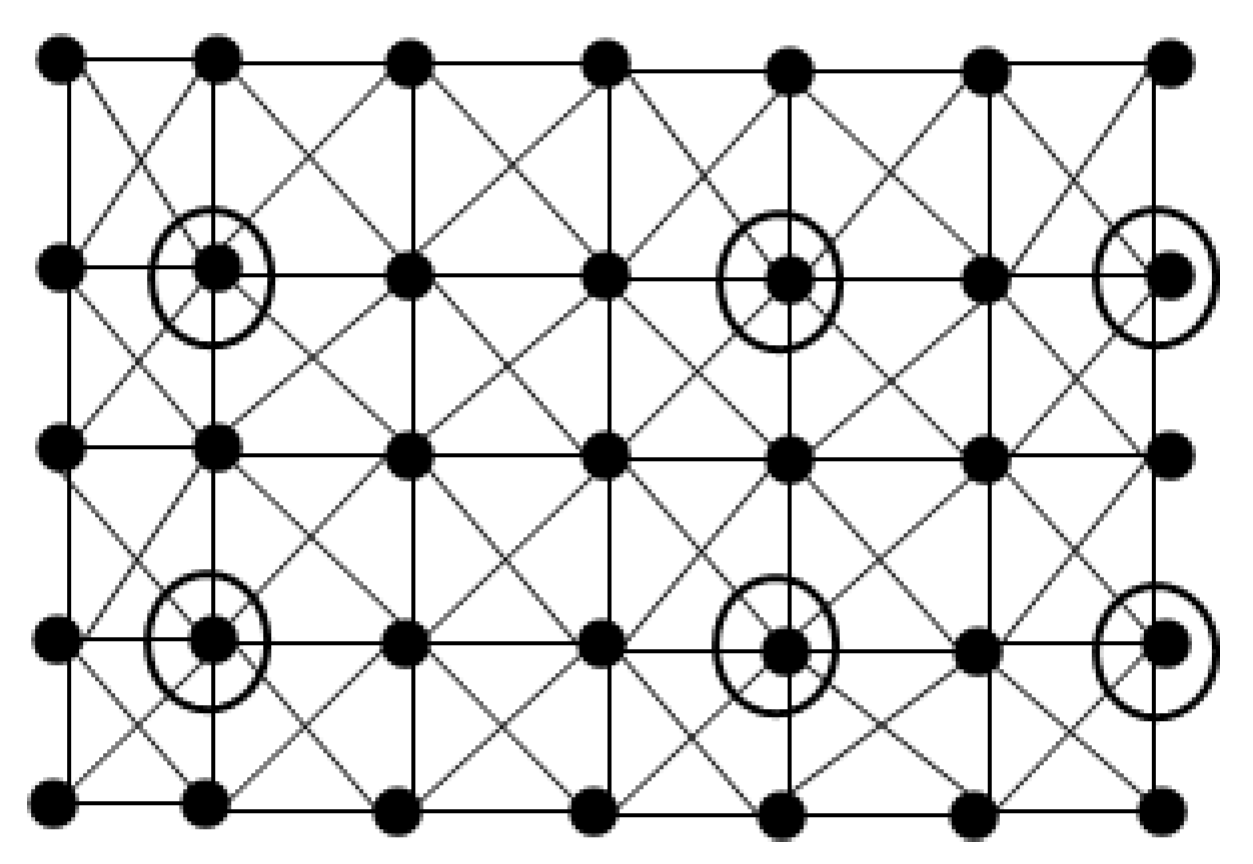
For r =2, (n,m) = (9,5). The graph ${\mathrm{P}}_9⊠{\mathrm{P}}_5$is shown in Figure 5. It consists of one Type C, one Type D, one Type E and one Type F configurations arranged as shown in Figure 1. A minimum total dominating set D of ${\mathrm{P}}_9⊠{\mathrm{P}}_5$will consist of 1 ×2 + 1 ×2 + 1 ×3 + 1 × 3 = 10 elements. So ${\mathsf{\gamma }}_{\mathrm{t}}\left({\mathrm{P}}_9⊠{\mathrm{P}}_5\right)$= 10= 2 ×2²+2 = 2r²+r. In general, ${\mathrm{P}}_{4r-1}⊠{\mathrm{P}}_{3r}$ will consist of (r-1)² Type C configurations, (r-1)

Type D configurations, (r-1) Type E configurations and 1 Type F configuration arranged by following the pattern shown in Figure 1. So a minimum total dominating set D will consist of 2(r-1)² +2(r-1)+ 3(r-1)+3.1 = 2r²+r elements. That is ${\mathsf{\gamma }}_{\mathrm{t}}\left({\mathrm{P}}_{4\mathrm{r}+1}⊠{\mathrm{P}}_{3\mathrm{r}-1}\right)$= 2r²+r.

Case 4: (n,m) = (4r+2, 3r).

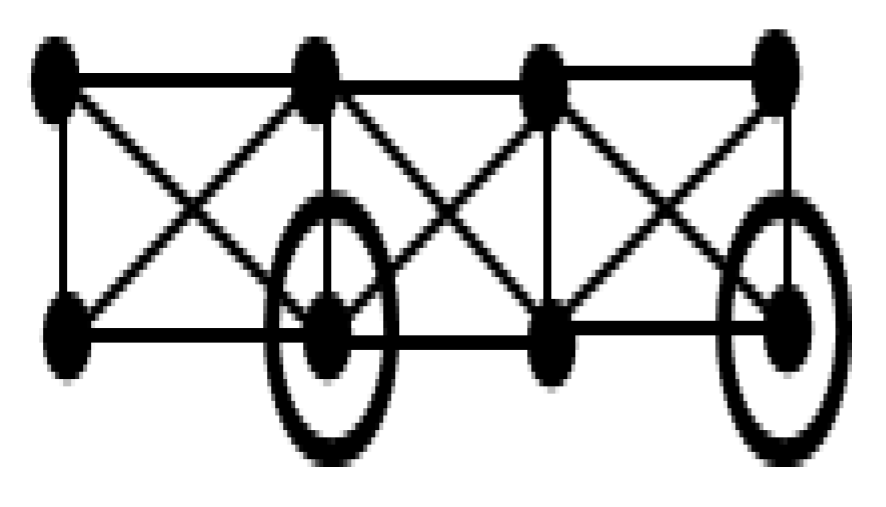
For r = 1, (n,m) = (6,3). ${\mathrm{P}}_6⊠{\mathrm{P}}_3$is shown in Figure 1.

The 4 marked elements will form a minimum total dominating set. So ${\mathsf{\gamma }}_{\mathrm{t}}\left({\mathrm{P}}_6⊠{\mathrm{P}}_3\right)$= 4. For r=2, (n,m) = (10,6). ${\mathrm{P}}_{10}⊠{\mathrm{P}}_6$comprises 2 Type G configurations and 2 Type C configurations where a Type C configuration is glued below its respective Type G configuration. So a minimum total dominating set D will consist of 2 × 4 + 2 × 2 =12 elements and ${\mathsf{\gamma }}_{\mathrm{t}}\left({\mathrm{P}}_{10}⊠{\mathrm{P}}_6\right)$= 2 ×2²+2 ×2 = 2r²+2r.In general, ${\mathrm{P}}_{4\mathrm{r}+2}⊠{\mathrm{P}}_{3\mathrm{r}}$will consist of r Type G configurations and each Type G configuration is expanded by pasting two Type C configurations one below the other. So a minimum total dominating set of ${\mathrm{P}}_{4\mathrm{r}+2}⊠{\mathrm{P}}_{3\mathrm{r}}$will consist of 4r + 2r(r-1)= 2r²+2r elements. So ${\mathsf{\gamma }}_{\mathrm{t}}\left({\mathrm{P}}_{4\mathrm{r}+2}⊠{\mathrm{P}}_{3\mathrm{r}}\right)$ = 2r²+2r. A Type H configuration ${\mathrm{P}}_6⊠{\mathrm{P}}_2$is shown in Figure 1.

Type I configuration is shown in Figure 1. Type J configuration is shown in Figure 10.

Case 5: (n,m) = (4r+1, 3r+1).

Type K configuration is shown in Figure 1. For r = 1, (n,m) = (5,4). ${\mathrm{P}}_5⊠{\mathrm{P}}_4$is shown in Figure 6. It consists of one Type E and one Type K configuration. Figure 6 shows ${\mathsf{\gamma }}_{\mathrm{t}}\left({\mathrm{P}}_5⊠{\mathrm{P}}_4\right)$= 6 = 2r²+3r+1.

Type L configuration is shown in Figure 1. In general, P4r+3⊠ P3r+1 will consist of r Type E configurations, r(r-1) Type C configurations, 1 Type K configuration and (r-1) Type L configurations. Here each Type E configurationis followed by (r-1) Type C configurations arranged one below the other and the solitary Type K configuration is followed by (r-1) Type L configurations arranged one below the other. So the minimum total dominating set will consist of 3r+2r(r-1) + 3 +2(r-1) =3r + 2r²-2r + 3+2r -2 = 2r² + 3r +1 elements. That is ${\mathsf{\gamma }}_{\mathrm{t}}\left({\mathrm{P}}_{4\mathrm{r}+3}⊠{\mathrm{P}}_{3\mathrm{r}+1}\right)$= 2r²+3r+1.

Case 6: (n,m) = (4r+2, 3r+1).

Type M configuration is shown in Figure 1.

For r = 1, (n,m) = (6,4). The graph ${\mathrm{P}}_6⊠{\mathrm{P}}_4$is shown in Figure 7.

It consists of one Type G configuration and one Type M configuration arranged side by side and glued together. Clearly${\mathsf{\gamma }}_{\mathrm{t}}\left({\mathrm{P}}_6⊠{\mathrm{P}}_4\right)$= 8 = 2(r+1)². In general, ${\mathrm{P}}_{4r+2}⊠{\mathrm{P}}_{3r+1}$ will consist of r Type G configurations, 1 Type M configuration, r(r-1) Type C configurations and (r-1) Type L configurations.Here each Type G configuration is followed by (r-1) Type C configurations arranged one after the other and the solitary Type M configuration is followed by (r-1) Type L configurations arranged one after the other. So the minimum total dominating set will consist of 4r+4+2r(r-1)+2(r-1) =4r + 4 + 2r²-2r +2r -2 = 2r² + 4r +2 =2(r+1)² elements. That is ${\mathsf{\gamma }}_{\mathrm{t}}\left({\mathrm{P}}_{4\mathrm{r}+2}⊠{\mathrm{P}}_{3\mathrm{r}+1}\right)$ = 2(r+1)². Type N configuration is shown in Figure 1.

The other cases mentioned in the statement of the Theorem 3.1 can be dealt with in a similar manner by using the appropriate types of configurations listed in Figure 1.

Note 3.2.One can check in each of the cases discussed in Theorem 3.1 that the captive domination number value is also the same as that of the value of the total domination number.

Algorithm for Computing the Captive Domination Number Cycles

$${\mathsf{\gamma }}_{\mathrm{c}\mathrm{a}}\left({\mathrm{C}}_{4\mathrm{t}}\right)=2\mathrm{t},\mathrm{t}\ge 2$$

$${\mathsf{\gamma }}_{\mathrm{c}\mathrm{a}}\left({\mathrm{C}}_{4\mathrm{t}+2}\right)=2\mathrm{t}+2,\mathrm{t}\ge 1$$

$${\mathsf{\gamma }}_{\mathrm{c}\mathrm{a}}\left({\mathrm{C}}_{4\mathrm{t}+1}\right)=2\mathrm{t}+2,\mathrm{t}\ge 2$$

$${\mathsf{\gamma }}_{\mathrm{c}\mathrm{a}}\left({\mathrm{C}}_{4\mathrm{t}+3}\right)=2\mathrm{t}+2,\mathrm{t}\ge 1$$

Input: The circle graph C_n with V(C_n) = {$u_1$, $u_2$, …, $u_n$}; E(C_n) = {($u_i,u_{i+1}$): 1≤ i ≤ n-1; ($u_1,u_n$)}

Output :${\mathsf{\gamma }}_{\mathrm{c}\mathrm{a}}\left({\mathrm{C}}_{\mathrm{n}}\right)=\left\{\begin{array}{c}2tifn\equiv 0\left(\mathrm{m}\mathrm{o}\mathrm{d}4\right),t\ge 2\\ 2t+2ifn\equiv 2\left(\mathrm{m}\mathrm{o}\mathrm{d}4\right),t\ge 1,\\ orn\equiv 1\left(\mathrm{m}\mathrm{o}\mathrm{d}4\right),t\ge 2,\\ orn\equiv 3\left(\mathrm{m}\mathrm{o}\mathrm{d}4\right),t\ge 2\end{array}\right.$

Step 1 : For n = 4t, set D₁ = {$u_2,u_3;u_6,u_7;u_{10},u_{11};\dots \dots ;u_{4t-2,}{u}_{4t-1}$} with |D₁|=2t.

Step 2 : For n = 4t+2, set D₂ = {$u_2,u_6,u_{10},\dots \dots u_{4t-2};u_3,u_7,u_{11},\dots u_{4t-1}$}⋃

{$u_{4t+1},u_{4t+2}$} with |D₂|=2t+2.

Step 3 : For n = 4t+1, set D₃ = {$u_2,u_6,u_{10},\dots \dots u_{4t-2};u_3,u_7,u_{11},\dots u_{4t-3}$}⋃

{$u_{4t+1},u_{4t+2}$}with|D₃|=2t+2.

Step 4 : For n = 4t+3, set D₄ = {$u_2,u_6,u_{10},\dots \dots u_{4t-2};u_3,u_7,u_{11},\dots u_{4t-1}$}⋃

{$u_{4t+1},u_{4t+2}$} with|D₄|=2t+2.

Step 5 : Check, whether ∀u ∈V(C_n)-D₁, ∃ v ∈ D₁, such that (u, v) ∈ E(C_n). If so,

then go to Step 6. Else go to Step 7.

Step 6 : Declare D₁ as a dominating set of C_n and go to step 14.

Step 7 : Revise the elements of D₁ and go to Step 5.

Step 8 : Check, whether ∀u ∈ D₁, ∃ v ∈ D₁, such that (u, v) ∈E(C_n). If so, then go

to Step 9. Else go to Step 10.

Step 9 : Declare D₁ as a total dominating set of C_n and go to Step 14.

Step 10 : Revise the elements of D₁ and go to Step 8.

Step 11 : Check, whether ∀ u ∈ D1, ∃ v ∈ V(Cn)-D1, such that (u, v) ∈ E(Cn). If so,

then go to Step 12. Else go to Step 13.

Step 12 : Declare D₁ as a captive dominating set of C_n and go to Step 14.

Step 13 : Revise the elements of D₁ and go to Step 11.

Step 14 : Check, whether ∃ any ${\mathrm{D}}_1^{\mathrm{*}}\subset {\mathrm{D}}_1$satisfying step5, step8, step11. If so, then

go to Step 15. Else go to Step 16.

Step 15 : Declare D₁ is not a minimum captive dominating set, revise D1 and repeat

             Step5, Step 8, Step11 and Step14.

Step 16 : Declare D₁ as a minimum captive dominating set, if ∃ no ${\mathrm{D}}_1^0$, which is a

minimum captive dominating set. Else, declare D₁ as a minimal captive dominating set and go to Step 17.

Step 17 : Repeat step 5 to step 16 for D₂, D₃ and D₄ and go to Step 18.

Step 18 : Declare${\mathsf{\gamma }}_{\mathrm{c}\mathrm{a}}\left({\mathrm{C}}_{\mathrm{n}}\right)=2\mathrm{t}\mathrm{i}\mathrm{f}\mathrm{n}\equiv 0\left(\mathrm{m}\mathrm{o}\mathrm{d}4\right),2\mathrm{t}+2\mathrm{i}\mathrm{f}\mathrm{n}\equiv 2\left(\mathrm{m}\mathrm{o}\mathrm{d}4\right),$ or 1(mod

4) or 3 (mod 4) and go to Step 19.

Step 19 : Stop.

Note 3.2.One can adopt a similar procedure for computing the captive domination number of any graph.

4. Conclusions

In this work besides settling a conjecture concerning the domination number on strong product of path graphs, we also obtained a few other interesting results. We hope that our results could lead to a better characterization for an interconnection parallel architecture concerning cellular neural networks.