A Simple Circuit Model for the Collapse Effect

1. Introduction

Loss of which-way information has recently been shown to trigger the collapse effect in a unitary universe [1]. Meanwhile a technique has been developed for modeling observation processes using quantum circuits [2]. The purpose of this note is to demonstrate the collapse effect using the circuit technique.

2. The Experiment

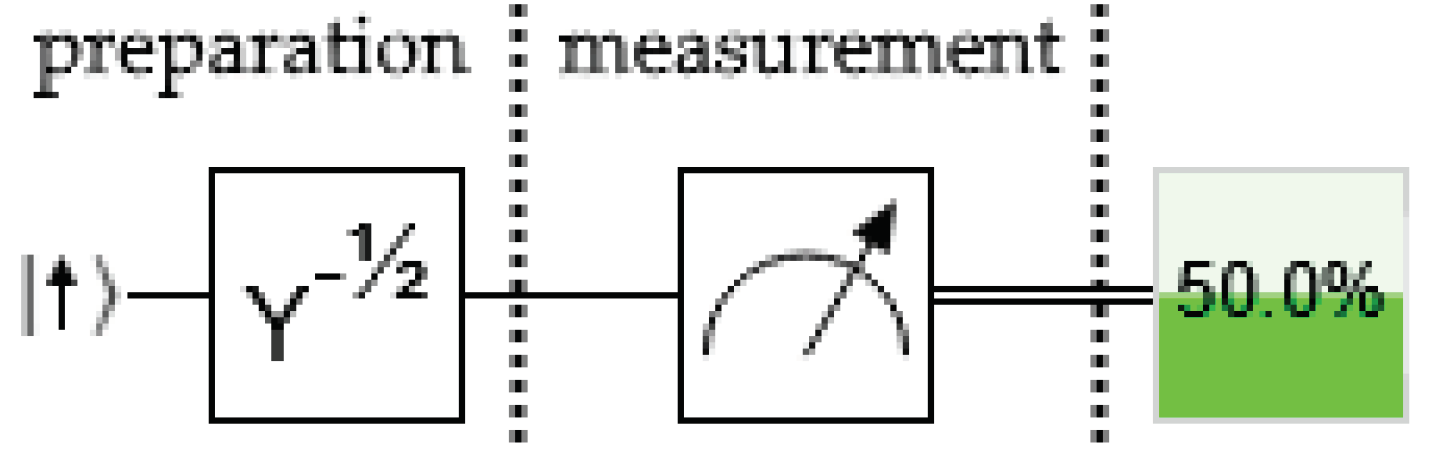
Imagine a spin is prepared aligned along the x axis, either $+x$ or $-x$. It is then measured along the z-axis. The result is written to a classical bit which the experimenter does not examine. Regardless of which result occurs, it will be impossible for the experimenter to determine which state ($\pm x$) was originally prepared.

We can perform this experiment today using a quantum computer. Physical qbits may be trapped ions or Josephson junctions, but the principle is the same. The circuit is shown in Figure 11. We ask the reader to imagine the measurement apparatus places the classical result on the same physical qbit implementation which was identified as the system, a quintessentially projective measurement. If the experimenter does not look at the bit, it will be in a mixed state

$$\rho =(|\uparrow \rangle \langle \uparrow |+|\downarrow \rangle \langle \downarrow |)/2.$$

(1)

The usual interpretation is that it is in one of the two states with equal probability. The coherence between the alternatives has been lost and there is no experiment that can be performed on the classical bit to determine which way it was prepared.

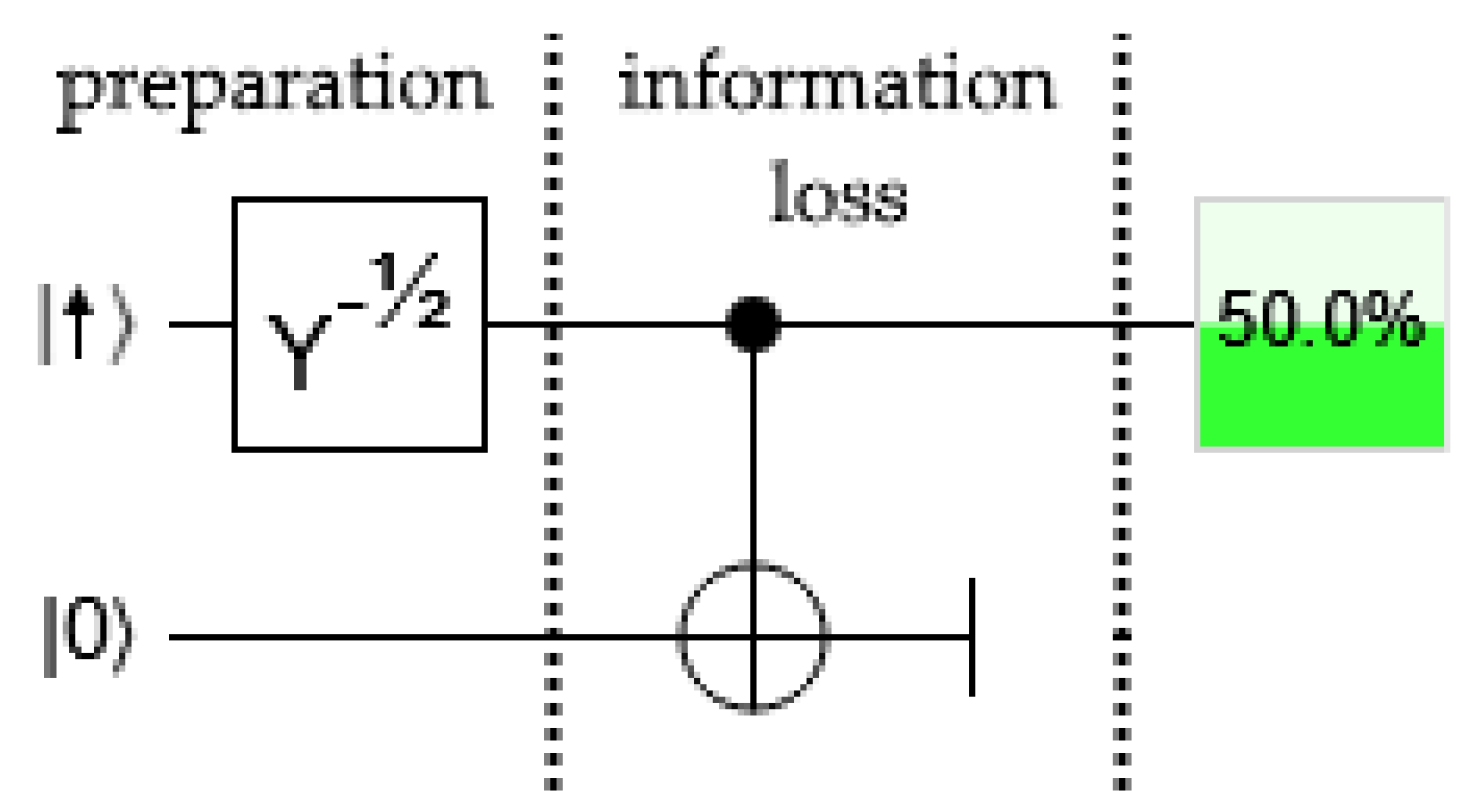
In Figure 2, the measurement gate is replaced by a CNOT gate connecting the system qbit to an ancillary qbit. This represents loss of information. We assume the loss is irreversible for some reason. We represent an irreversible loss with a vertical bar at the end of the qbit line. When part of an entangled state is lost, the state of the remaining part can be described by a partial trace over the decoupled Hilbert space2. The result is

$$\rho =(|\uparrow \rangle \langle \uparrow |+|\downarrow \rangle \langle \downarrow |)/2.$$

(2)

This is the exact same state as 1. No experiment is possible that can distinguish these states. The unitary evolution of Figure 2 is indistinguishable from the non-unitary evolution of Figure 1.

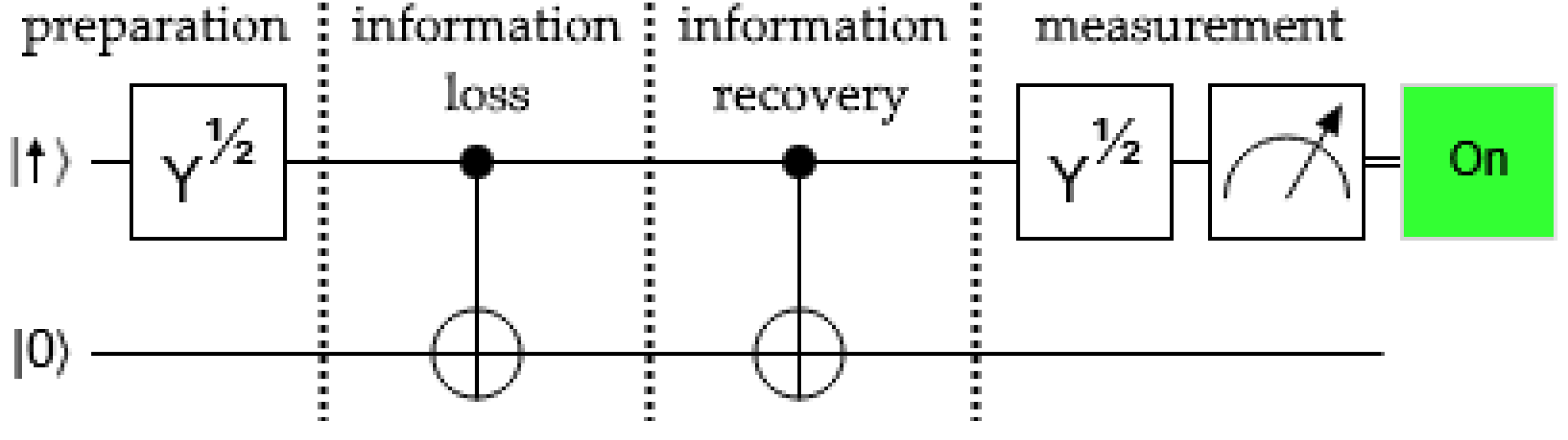
For observations in the macroscopic world, the loss of information is due to interaction with the environment [4], which is necessary in order to display a result on a macroscopic meter. In that case it is unrecoverable as a practical matter. But we can consider that an ancillary spin particle is isolated somehow by the experimenter, or is lost to outer space.

Suppose in the latter case the experimenter examines the system qbit and records the result. Later an alien captures the ancillary spin, measures it, and sends the result back to earth. The results will match, as is well known from EPR.

Suppose instead the experimenter preserves the system qbit. Later the alien captures the ancillary spin and brings it back to earth (or the experimenter retrieves it from isolation). If that occurs, it is possible to allow it to interact with the system qbit, recover coherence, and find out which spin state was originally prepared. This is shown in Figure 3.

3. Conclusions

Quantum collapse is exactly mimicked by loss of which-way information. All human measurements involve loss of which-way information because human sense organs exist in a thermal environment. Collapse is irreversible only if the lost information is irrecoverable.