On the Advancements in Agricultural Greenhouse Technologies: An Energy Management Perspective

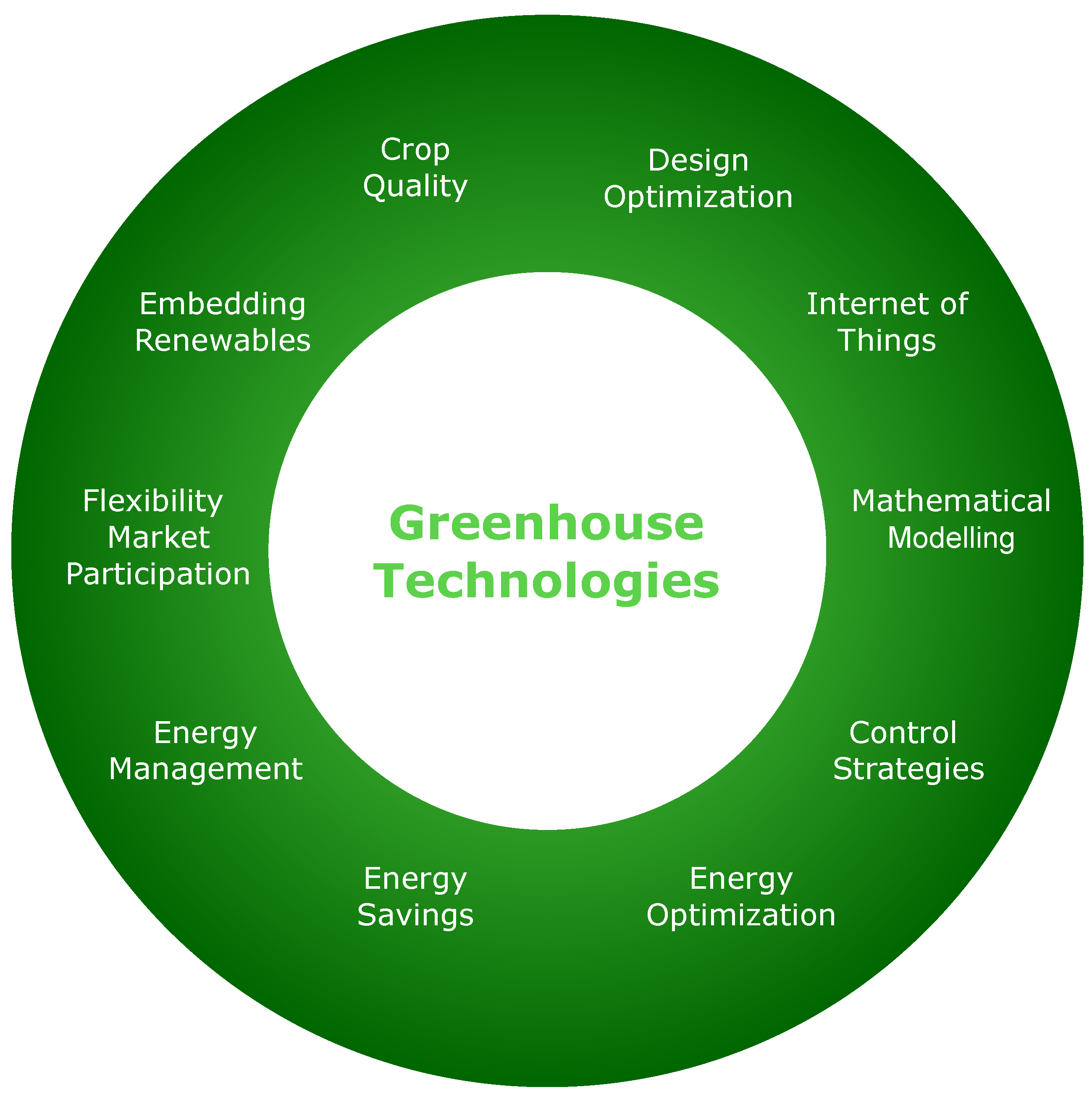
1. Introduction

The rise in the global urban population is anticipated to be substantial by 2050, reaching a staggering 9.7 billion [1]. This represents an increase of approximately 21.25%. This surge signifies a remarkable growth, equivalent to an additional 1.7 billion people within the span of three decades. This urbanization trend intensifies the demand for food by almost 70% [2], creating pressure on existing food systems as cities grow. Consequently, urban communities find themselves increasingly reliant on food sourced from rural areas or imported from distant regions [3]. Furthermore, the expanding urban footprint contributes to a growing disparity between food production and consumption. When examining the entire life cycle, it becomes evident that emissions associated with current food systems constitute a significant portion, representing one-third of the total global greenhouse gas (GHG) emissions. Besides, transportation related to the food systems alone presents one-fifth of the total emissions by the food system. This boils down to the reduction in import and development of self-sufficient sustainable food production to solve the bottleneck of anticipated uncertain climate change, transportation [4], and the never-ending demand to reduce the emissions causing global warming [5]. Importantly, self-sufficient sustainable food production is a challenging task for certain geographical realms, depending on the climate and weather conditions, limited arable land, soil quality, transportation and infrastructure, limited technological adoption and many more [6]. In Canada, import dependence varies substantially across different fruits and vegetables. Mostly, Canada relies on international imports for over 80% of its national supply [7] and provincial dependencies rely on their personal supplies. For example, in Québec, only half of the wholesale food consumed is grown/processed locally; the rest is imported. This heavy import is due to low self-sufficiency and sustainability, which stems from the vulnerabilities to climate change [7].

In addition to traditional field methods, greenhouses are vital in enhancing crop production and achieving self-sufficient fruit and vegetable growth. Their structures protect plants from unfavorable climatic conditions and allow them to grow efficiently and sustainably at any time of the year [8,9]. The greenhouses’ controlled microclimate environment ensures desired levels of indoor vitals as well as protects against external factors [9], thus providing high-quality live stocks all year-round [10]. Especially in northern climates, greenhouse production is of particular interest. Despite greenhouses evolving toward industrialization and scalability owing to the advancements in facility-based farming, one significant challenge faced is their substantial energy consumption [11]. Microclimate control activities, such as lighting, heating, ventilation, and air conditioning, contribute significantly to this energy demand. For instance, this high energy demand during winter peaks in northern climates can strain the electrical grid, leading to congestion and other potential issues [12]. Traditional rule-based control methods often fail in optimizing energy usage and ensuring constraint satisfaction [13]. That underscores the importance of the energy management perspective in greenhouse technologies. Figure 1 displays the terminologies of potential work and research in advancing greenhouse technologies towards the grids of the future.

Globally, there is a strong push towards renewable energy and smart grid technologies to create more resilient and sustainable energy systems. Specifically, in Québec, by 2035, 75% of the new electricity generation will be dedicated to decarbonizing the environment, out of which 35% will be dedicated to industrial decarbonization [14]. As a significant energy consumer, the agricultural sector has a crucial role in this transition. Improving grid performance and reducing grid stress in agricultural greenhouses involves a multifaceted approach integrating advanced mathematical modeling, sophisticated control strategies, energy optimization techniques, and demand response programs. Mathematical modeling involves creating mathematical representations of greenhouse energy systems to simulate and analyze their behavior under various conditions, including models for energy consumption, crop production, and storage [15]. That enables precise planning and dynamic response to energy demand fluctuations. Implementing automated control strategies [16], such as smart thermostats and HVAC systems, enables real-time adjustments that reduce energy consumption and shift demand away from peak grid periods. Energy optimization, through efficient lighting and insulation, coupled with adjusting energy use based on grid conditions and demand-side energy management strategy, ensures sustainable operations while maintaining crop quality [17]. Participating in flexibility markets and embedding renewable energy sources [18], like solar panels, further alleviates grid stress by providing additional flexibility and reducing reliance on fossil fuels. Design optimization of greenhouses enhances these benefits by integrating energy-efficient structures from the outset [19]. By adjusting energy use based on grid conditions, demand-side management further optimizes energy consumption patterns [20]. Collectively, these strategies contribute to significant energy savings, operational efficiency, and decarbonization, which are crucial in mitigating climate change and enhancing the sustainability of agricultural practices.

Energy management is a crucial aspect of greenhouse operations, affecting cost-effectiveness, profitability, and grid operations. In the greenhouse operations context, several reviews are available from the crop-production perspective [21,22,23]. Also, we can find several reviews describing ways to achieve energy efficiency, implementing different controls and modeling techniques, embedding renewables, and different design methods for cost-effectiveness. For instance, Qayyum et al. [24] talks about econometric models for sustainable agriculture, Zhang et al. [11] describes energy-saving design and control for sustainable greenhouses and Cuce et al. [25], Gorjian et al. [26] mention various renewable energy integration options towards sustainable energy saving. Energy efficiency in agricultural greenhouses has often been linked with control methods, modeling, and operations. Iddio et al. [27] discusses energy efficient modeling and operations, whereas Paris et al. [18] describes energy efficiency measures in greenhouses, especially for the EU region. Zhang et al. [28] has discussed various control strategies for improving energy efficiency in agricultural greenhouses. With the advent of the Internet of Things (IoT), various works have been carried out for resource management towards automated agricultural greenhouse [29,30]. The decarbonization perspective about greenhouse gas mitigation has also been explored in agricultural greenhouses [31,32]. Badji et al. [19] discusses various design trends specifically related to the construction and management of the greenhouse environment.

Although there is a plethora of existing valuable sources of information focusing on the improvements in greenhouse technologies from the agricultural and control perspective; nevertheless, with the dawning of the age of smart grids, the energy management perspective to participate in the energy markets, embedding renewables, and exploiting demand-side flexibility for the DR programs is of prime importance. To address this, the presented review article provides new perspectives and insights on developing energy management techniques and optimizing greenhouse microclimate, thereby emphasizing the importance of agricultural greenhouse participation in transactive energy platforms.

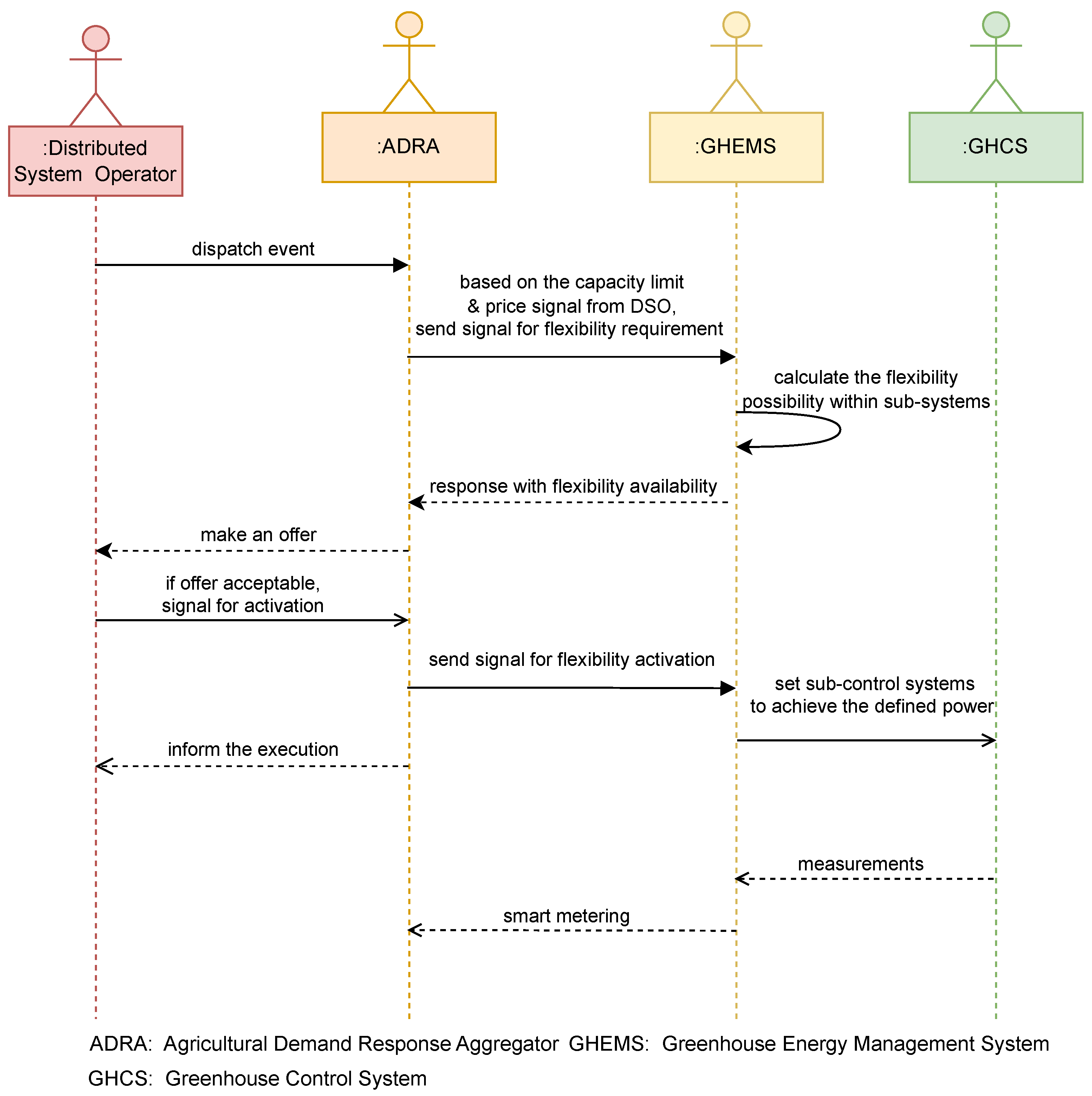
2. Greenhouse Energy Management in Smart Grid Context

Energy management within the smart grid context involves the integration of advanced technologies and strategies to optimize energy consumption and production [33]. Smart grids utilize real-time data, automation, and communication technologies to enhance the efficiency and reliability of electricity distribution. This enables the grid to adapt to fluctuations in energy demand and supply, thereby improving overall grid stability and resilience. Smart grids also facilitate the integration of renewable energy sources, distributed energy resources, and energy storage systems, which are essential for achieving sustainability goals.

One of the key components of smart grid energy management is demand response (DR) [34], which involves adjusting energy demand to match supply conditions. DR mechanisms provide grid operators with the flexibility to manage load fluctuations, particularly during peak demand periods, by incentivizing consumers to reduce or shift their energy usage. This is especially critical in managing the challenges posed by increasing energy demand during winter peaks, as it helps to alleviate pressure on distribution system operators (DSOs).

As we move towards more sophisticated energy management frameworks, the concept of Transactive Energy (TE) emerges as a promising approach. TE frameworks extend the capabilities of smart grids by integrating economic signals and market mechanisms to optimize energy use and production. This involves integrating advanced technologies and market mechanisms to optimize energy use and production within greenhouses. That includes dynamic pricing [35] and economic incentives [36,37], embedding renewable and energy storage elements [18,38], and distributed energy resources [39], among others. From a broader perspective of the TE framework, DR can be viewed as a mechanism adjusting demand to balance supply, which can be a part of a broader range of mechanisms, including automated energy trading, comprehensive grid management, and real-time pricing. Mainly, DR provides promising solutions for load management from the consumer side when the increasing load demand causes significant problems for the DSOs, especially during winter peaks [40].

Figure 2 represents a typical DR mechanism, where various sub-systems within agricultural greenhouses can interact to respond to the demand response events. That contributes to grid stability through an optimized energy consumption strategy that aligns with external grid requirements while maintaining greenhouse microclimate conditions. The process starts with a dispatch event from the distributed system operator (DSO) sending a price signal or request for flexibility to the aggregator based on capacity limits and grid distance. Then the requirement is evaluated with flexible availability, which is further activated if accepted by the DSO. The role of a greenhouse energy management system (GHEMS) is to calculate the flexibility possibility within its sub-systems. Once the offer is activated, GHEMS commands its sub-system (greenhouse control system (GHCS)) to achieve defined consumption objectives according to the received flexibility instructions based on the price policy.

Note that Figure 2 is a scenario of a grid operated by automated agents; there are mainly three bifurcations from the perspective of automation: (i) Manual DR, (ii) Semi-automated DR and (iii) Automated DR [41]. Many sources are available for energy management strategies in the TE framework. However, in the context of smart grids, agricultural greenhouses participating in the energy markets or specific DR programs are scarcely available until recently. For instance, Rezaei et al. [42] considered a network of greenhouses participating in demand response to reduce power consumption during peak hours, thereby managing power exchange with the primary grid. Table 1 shows a high-level comparison of different demand-side energy management strategies for grid-connected agricultural greenhouses to participate in DR programs. From the survey, it can be found that multi-agent DRL and MPC are the popular methodologies to employ for the specific task. Moreover, only a few research works have considered uncertainties and maximum demand limit constraints from the aggregator side. Most of the work encapsulated the PV generation for trading with the grid aggregator, whereas only a few considered the model of the crop. That is one of the important aspects of agricultural greenhouse microclimate. The importance of crop models brings the mathematical intricacies for the overall energy optimization problem, which will be further discussed in Section 3.2. To solve the demand-side and aggregator-side problems, the interaction between entities is crucial, which has become a point of interest for many researchers in recent years [43].

Substantially, game-theoretic approaches in collaboration with a multi-agent system perspective are widely used in energy optimization for greenhouses, particularly for managing energy consumption. They provide a structured way to analyze and design energy management strategies, considering participants’ interactions. These methods often involve strategic decision-making among multiple participants, such as energy prosumers, utility companies, and consumers, to achieve an optimal balance between energy supply and demand [44]. Naz et al. [45] proposed a two-stage non-cooperative Stackelberg game to capture the interconnection between the consumers and the micro-grid.

One of the principal uses of non-cooperative games has been in strategic bidding in electricity markets. Moreover, cooperative games have also found a place in energy management to improve the collective playoffs, including sharing distributed resources or coordinating energy consumption. Dynamics and static games are also often utilized for energy trading systems for demand side management [56]. Apart from individual research articles, Ji et al. [57] provides a systematic review of the game-theoretic approach for decision-making on demand-side energy management. Wang et al. [58] reviews comprehensively evolutionary game approach for sustainable energy development, encompassing energy savings, carbon emission reduction, energy vehicles, electric power market, DERs, micro-grid, smart grid, and energy storage. Similarly, He et al. [59] focused on reviewing the application of game theory in integrated energy systems.

3. Greenhouse Microclimate

GHEMS is critical to address the grid challenges and to participate in the DR programs. Figure 3 depicts the stages involved in greenhouse microclimate environment management.

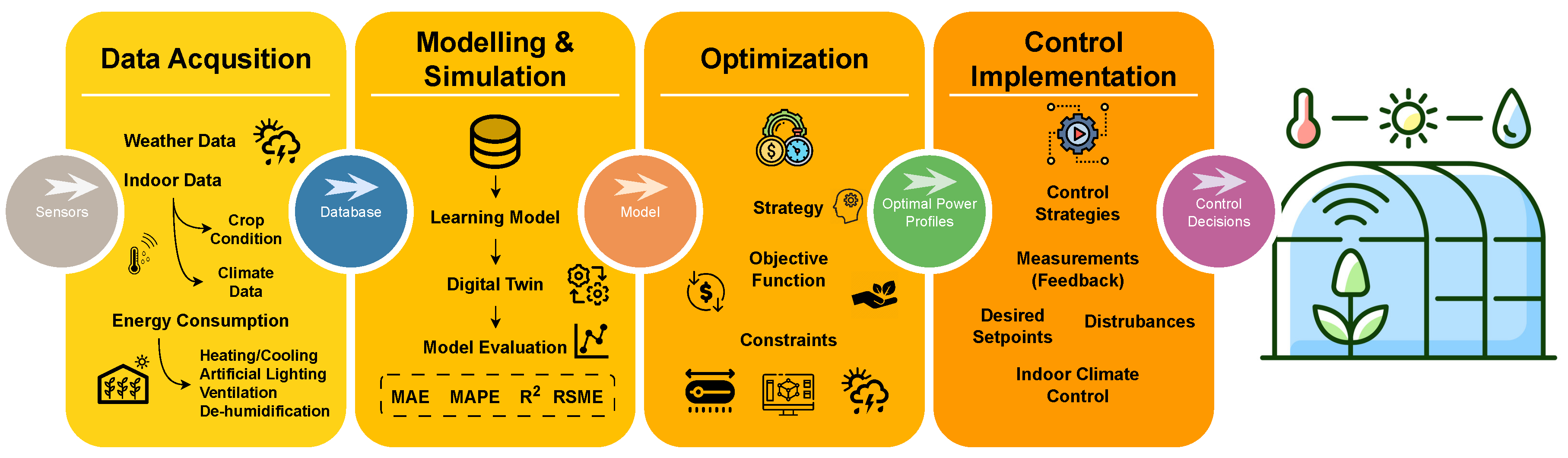
3.1. Sensors & Data Acquisition

The first stage is data acquisition and monitoring, which has caught the attention of various researchers owing to Industrial Revolution 4.0. [30]. This stage is an important practical aspect as it involves data collection from various sources, which must be robust and efficient to handle large volumes of data and ensure data quality. This stage of sensors and data acquisition has undergone numerous technological advancements over recent decades, evolving to become more industrialized and reliant on technology [60]. IoT has equipped growers with smart agricultural tools, enhancing their control over crop growth, increasing predictability, and boosting efficiency. However, the challenge comes in handling the heterogeneity and fast pace of data generation, especially with the advent of smart grids that involve numerous data points and high-frequency data [61]. At the same time, there are high capital expenditures for these newer technologies, specifically for small and medium-sized growers. Consequently, as a potential solution, a three-S strategy is also proposed by Miranda et al. [62] encapsulating sensing, smart and sustainable [63]. The question arises: what are the variables of interest specialized for the agricultural greenhouses, and what type of sensors monitor these variables?

In Table 2 of this review paper, we have summarised the measurement variables for the greenhouse microclimate that are of importance from crop growth as well as energy management perspective. Here, the measurement variables are bifurcated regarding their requirement for the most common irrigation systems acquired in greenhouses. However, their communication, environmental adaptability, characteristics, and economics are altogether different and pose exciting challenges, which are out of the scope of this paper.

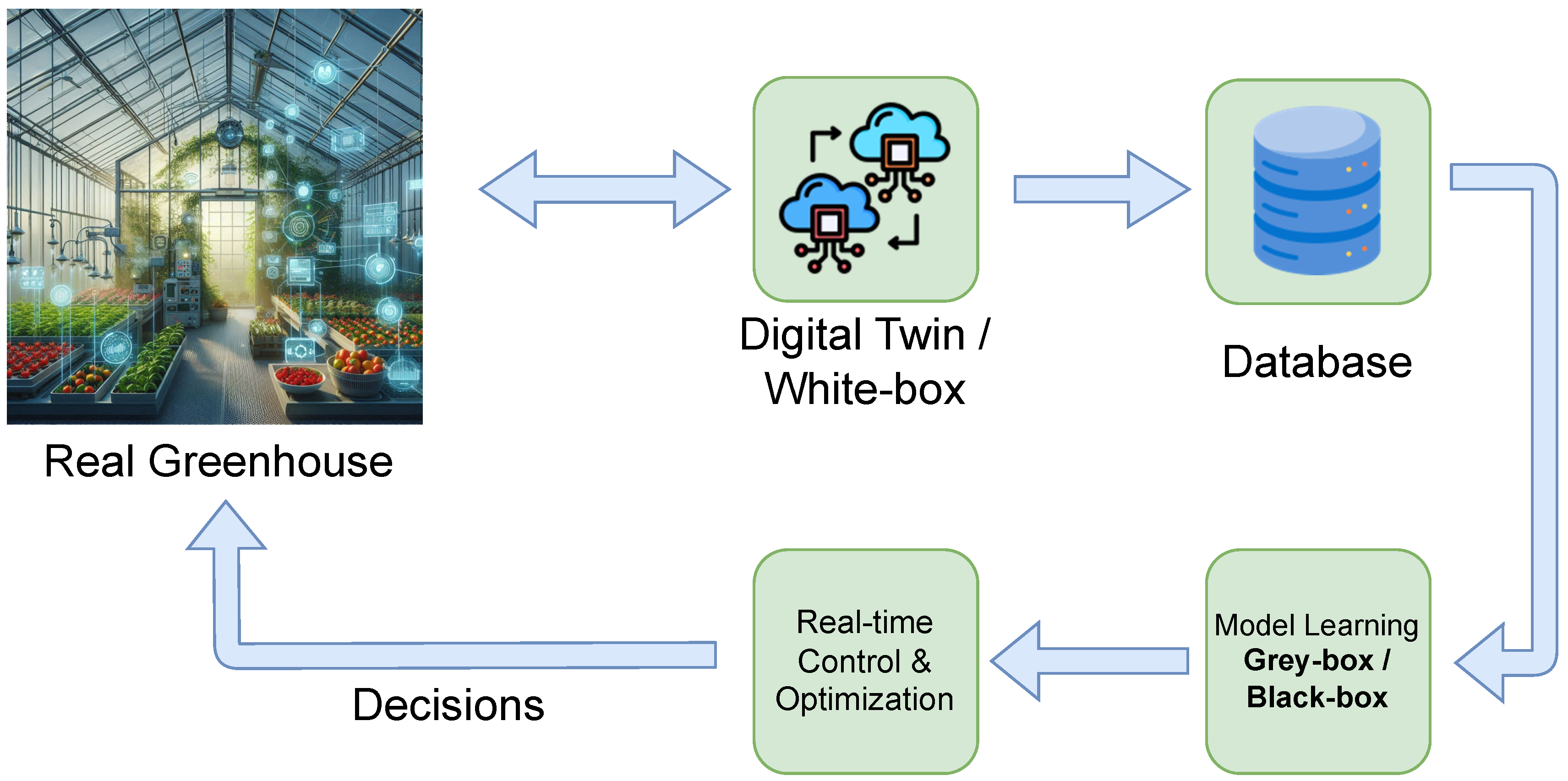
3.2. Modelling & Simulation

This stage involves creating mathematical models to simulate the system’s behavior under different conditions. The challenge is ensuring that the models accurately represent the real-world system and predict its behavior under various scenarios. As mentioned earlier, agricultural greenhouses provide a controlled environment to optimize the indoor microclimate, mitigating the variability caused by weather, diseases, and soil conditions. However, external factors, such as freezing weather, still present challenges, necessitating continuous reassessment and adjustment of cultivation strategies. For that purpose, digital twins can be considered an ideal choice to test the algorithms based on real-time data or near real-time data [64]. Digital twins are virtual representations of physical systems, processes, or assets. They mirror the real-world behavior of their counterparts and allow real-time monitoring, analysis, and prediction [65].

With smart grids, the complexity increases due to the need to model and simulate various components like renewable energy sources, storage devices, and consumer loads. It is argued that DTs can be crucial in cyber-physical system-based DR programs [66]. Van Der Veen et al. [67] talks about the importance of DTs in the interaction between the cyber and physical systems for the coordination between various stakeholders, such as prosumers, consumers, DSOs, and DRAs. With the advent of Industry 4.0, digital twins in power systems (DTiPS) have been coined with a focus on real-time or near real-time energy management systems for better decision-making [68]. DTs can have essential characteristics to be addressed, such as timeliness, fidelity, integration, intelligence, and complexity. Broadly, DTs can be based on three modeling paradigms [69]: black box, grey box, and white box.

3.2.1. White Box

These models are derived from the energy and mass balance equations and are capable of describing physics-based dynamics. These models are considered the most detailed and closest-to-reality models, which are ideal for DTs. However, their parameters carry physical meaning and hence must be obtained from technical documentation, orientation, geometry, properties, and specifications. Here are the principal benefits and drawbacks mentioned for white box models.

Benefits:

• Detailed Process Insight: Provides a comprehensive insight into the dynamics, enhancing understanding of every aspect of the system.
• Predictive Precision: Considering that all the details are rightfully mentioned and understood, it can provide extremely precise predictions of the system under study, making them ideal for DTs.
• Customizability: It can customized to the specific systems and conditions, allowing tailored solutions.
• Reliability: Complimentary to the precision, they provide reliable results under perfect details.
• Controllability: Higher controllability at a granular level.

Drawbacks:

• Complexity: As the number of variables grows, model complexity increases, demanding greater domain-specific knowledge and expertise.
• Sensitivity to Parameter Change: Model accuracy and stability can be questionable due to the model sensitivity to the parameter change.
• Time Expense: Describing the system’s aspects is tedious and time-consuming, making it computationally expensive.
• Adaptation Difficulty: Challenging to adapt quickly to new or significantly changing conditions without extensive recalibration or redevelopment.

For the brevity of the presentation, a foundational generalized greenhouse model for energy management is presented. Contributions from diverse sources [70,71,72,73] are considered to comprehensively describe the model with a particular focus on aligning with the GHEMS, including both the axes climatic as well as agronomic.

Indoor Temperature: Maintaining an appropriate indoor temperature is vital for plant health and productivity. The temperature inside the greenhouse influences several physiological processes in plants, including photosynthesis, respiration, and transpiration. From the first law of thermodynamics, we have

$$\begin{array}{cc}\hfill C_{\mathrm{air}}{\displaystyle \frac{d{T}_{\mathrm{in}}}{dt}}& =Q_{\mathrm{heat}}-Q_{\mathrm{cool}}+Q_{\mathrm{solar}}+Q_{\mathrm{vent}}-Q_{\mathrm{walls},\mathrm{cond}}\hfill \\ \hfill & -Q_{\mathrm{walls},\mathrm{conv}}-Q_{\mathrm{ex},\mathrm{air}}-Q_{\mathrm{trans},\mathrm{crop}}+Q_{\mathrm{light}},\hfill \end{array}$$

(1)

where $Q_{\mathrm{solar}}={\eta }_{\mathrm{solar}}{A}_{\mathrm{glazing}}{I}_{solar}(1-e^{-kL})$ and $Q_{\mathrm{trans},\mathrm{crop}}$ is the latent heat loss due to crop transpiration, which is proportional to ${\dot{m}}_{\mathrm{trans}}$, i.e. $Q_{\mathrm{trans},\mathrm{crop}}=\lambda {\dot{m}}_{\mathrm{trans}}$ (latent heat of vaporization $\lambda$). $Q_{\mathrm{light}}$ represents the heat generated by artificial lighting, i.e. $Q_{\mathrm{light}}=P_{\mathrm{light}}(t_{\mathrm{light}}/V_{\mathrm{air}})(T_{\mathrm{light}}-T_{\mathrm{in}})$. $Q_{\mathrm{walls},\mathrm{cond}}=(\kappa A/d)(T_{in}-T_{ext})$ and $Q_{\mathrm{walls},\mathrm{conv}}=hA(T_{in}-T_{ext})$.

Crop Canopy Temperature: The temperature of the crop canopy is a critical component of the greenhouse microclimate. The crop canopy temperature $\left(T_{crop}\right)$ affects both the indoor temperature and humidity balance. It is influenced by solar radiation, ambient air temperature, and the transpiration process. The energy balance equation for the crop canopy temperature can be written as:

$$C_{crop}{\displaystyle \frac{d{T}_{\mathrm{crop}}}{dt}}=Q_{solar,crop}-Q_{trans}+Q_{ex,air},$$

(2)

where $Q_{\mathrm{solar},\mathrm{crop}}={\eta }_{\mathrm{crop}}{A}_{\mathrm{crop}}{I}_{solar}{e}^{-k·L}$ with k as the extinction coefficient varying with the type of vegetation, leaf orientation, and solar angle. $Q_{ex,air}=h_c{A}_{crop}(T_{crop}-T_{in})$ represents the heat exchange between the crop canopy and the indoor air. Note that $Q_{trans}$ and $Q_{\mathrm{trans},\mathrm{crop}}$ refer to the same physical process of latent heat loss due to transpiration. However, their perspective is different: For (1), it is the heat loss from the air due to the latent heat of transpiration by the crop, and in (2), it is the latent heat loss from the crop canopy due to transpiration.

Leaf Area Index (LAI) Growth Model: LAI affects both the light interception and transpiration rates, influencing the greenhouse’s energy and humidity balance. LAI can be described as a function of the node development rate, which is itself influenced by temperature and other environmental conditions. The LAI dynamics can be modeled using a growth equation, such as the logistic growth model, where the rate of change in LAI depends on the node development rate and the current temperature.

$${\displaystyle \frac{dL}{dt}}=\alpha ·\mathrm{NDR}·\left(1-{\displaystyle \frac{L}{L_{\max }}}\right),$$

(3)

where $\mathrm{NDR}=f\left(T_{\mathrm{crop}}\right)$ represents the node development rate (NDR) influenced by temperature. Generally, $f\left(T_{\mathrm{crop}}\right)$ can take the form of a polynomial or an exponential function that accounts for the optimal temperature range for crop growth. Golzar et al. [15] can be referred for a more detailed model of LAI.

Indoor Humidity: Moisture balance within a greenhouse is a crucial aspect of maintaining optimal growing conditions for crops. This balance is influenced by both the ventilation system, which exchanges air with the outside environment, and the transpiration process, where plants release moisture into the air.

$${\displaystyle \frac{d{H}_{\mathrm{in}}}{dt}}={\displaystyle \frac{1}{V_{\mathrm{air}}}}({\dot{m}}_{\mathrm{w},\mathrm{in}}-{\dot{m}}_{\mathrm{w},\mathrm{out}}+{\dot{m}}_{\mathrm{evap}}-{\dot{m}}_{\mathrm{cond}}+{\dot{m}}_{\mathrm{trans}}),$$

(4)

where ${\dot{m}}_{\mathrm{trans}}$ denotes crop transpiration, which can be modeled by the Penman-Monteith method as

$${\dot{m}}_{\mathrm{trans}}={\displaystyle \frac{\Delta (R_n-G)+{\rho }_a{c}_p\frac{D_v}{r_a}}{\Delta +\gamma (1+\frac{r_s}{r_a})}}$$

(5)

or empirically as ${\dot{m}}_{\mathrm{trans}}=\beta L(1-L_{max}/L)·f(T_{crop},D_v,r_a,r_s)$. Eq. (5) uses radiative, aerodynamic, and resistive factors to estimate transpiration, whereas the simple empirical model uses a coefficient and a function of environment factors to estimate transpiration [74].

Soil temperature and humidity: Soil environment is the backbone to promote crop nutrient uptake. The temperature and humidity of the soil can be given by

$$\begin{array}{cc}\hfill C_{\mathrm{soil}}{\displaystyle \frac{d{T}_{\mathrm{soil}}}{dt}}& =k_{\mathrm{soil}}{\nabla }^2{T}_{\mathrm{soil}}+Q_{\mathrm{ex},\mathrm{air}}\hfill \\ \hfill & -Q_{\mathrm{loss}}-Q_{\mathrm{transn},\mathrm{crop}},\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{H}_{\mathrm{soil}}}{dt}}& ={\displaystyle \frac{1}{V_{\mathrm{soil}}}}({\dot{m}}_{\mathrm{w},\mathrm{in}}-{\dot{m}}_{\mathrm{w},\mathrm{uptake}}\hfill \\ \hfill & -{\dot{m}}_{\mathrm{w},\mathrm{evap}}-{\dot{m}}_{\mathrm{w},\mathrm{drain}}-{\dot{m}}_{\mathrm{trans}}).\hfill \end{array}$$

(7)

${\mathrm{CO}}_2$ Concentration:${\mathrm{CO}}_2$ in a greenhouse can enhance photosynthesis rates and improve crop yields. Importantly, ventilation and plant respiration can mainly influence ${\mathrm{CO}}_2$ concentration.

$${\displaystyle \frac{d{\mathrm{CO}}_{2,\mathrm{in}}}{dt}}={\displaystyle \frac{1}{V_{\mathrm{air}}}}({\dot{m}}_{\mathrm{CO}2,\mathrm{in}}-{\dot{m}}_{\mathrm{CO}2,\mathrm{out}}-{\dot{m}}_{\mathrm{CO}2,\mathrm{uptake}}),$$

(8)

where ${\dot{m}}_{\mathrm{CO}2,\mathrm{uptake}}=\phi ·L·f(T_{crop},{\mathrm{CO}}_{2,\mathrm{in}})$ with $\gamma$ is a coefficient that scales the ${\mathrm{CO}}_2$ uptake rate with LAI.

Ventilation System: Ventilation systems play a pivotal role in regulating temperature and humidity within the greenhouse. By exchanging air with the external environment, ventilation helps to remove excess heat and moisture, introducing fresh air and maintaining optimal growing conditions. Effective ventilation management is crucial for preventing overheating, reducing humidity to acceptable levels, and ensuring a constant supply of ${\mathrm{CO}}_2$ for photosynthesis.

$$\begin{array}{cc}\hfill Q_{\mathrm{vent}}& ={\dot{m}}_{\mathrm{air}}{c}_p(T_{\mathrm{ext}}-T_{\mathrm{in}})+{\dot{m}}_{\mathrm{air}}\left(\right(H_{\mathrm{in}}(C_{p,\mathrm{vapor}}{T}_{\mathrm{in}}+\lambda )\hfill \\ \hfill & -H_{\mathrm{ext}}(C_{p,\mathrm{vapor}}{T}_{\mathrm{ext}}+\lambda )),\hfill \end{array}$$

(9)

Eq. (9) consists of sensible and latent heat components. The first term represents the energy due to temperature difference between the inside and outside air. The second term represents the energy associated with moisture content change, including both sensible heat of water vapor and the latent heat of vaporization. This formulation ensures that both temperature and moisture dynamics are accurately captured in the ventilation system model.

$$\begin{array}{cc}\hfill {\dot{m}}_{\mathrm{w},\mathrm{vent}}& ={\dot{m}}_{\mathrm{air}}(H_{\mathrm{ext}}-H_{\mathrm{in}})+{\dot{m}}_{\mathrm{trans}},\hfill \end{array}$$

(10a)

$$\begin{array}{cc}\hfill {\dot{m}}_{\mathrm{CO}2,\mathrm{vent}}& ={\dot{m}}_{\mathrm{air}}({\mathrm{CO}}_{2,\mathrm{out}}-{\mathrm{CO}}_{2,\mathrm{in}})-{\dot{m}}_{\mathrm{CO}2,\mathrm{uptake}}.\hfill \end{array}$$

(10b)

Note that although the above mathematical model (1) to () aims to provide a comprehensive understanding of the greenhouse system dynamics, it is essential to acknowledge that specific components, such as empirical coefficients, may require more profound expertise in thermodynamics or agricultural science for precise determination. These aspects represent areas where further refinement and specialized knowledge could enhance the model’s accuracy and applicability. Additionally, the dynamics change as we add other components and distributed/renewable energy sources, such as water pumps, wind turbines, photovoltaic (PV) systems, Battery Energy Storage (BESS), and Thermal Energy Storage Systems (TESS).

3.2.2. Grey Box

Grey box models have always found a sweet spot between black and white, as they offer a more practical and flexible approach to modeling. For real-world applications, if the data from the greenhouse is accessible, then grey box models are a practical solution as they can be effectively calibrated and validated using experimental data. Grey box models balance physical principles and empirical relationships to capture the essential dynamics [75]. Below are some of the benefits and drawbacks of a typical grey box model.

Benefits:

• Development Time: Compared to white box models, grey box models take less time owing to the partial dependence on empirical data.
• Robustness: More robust to the stochasticity of the variables, such as the climate conditions, compared to black box models, enhancing crop yield predictions.
• Management: Combining simplified plant growth models and data can improve environmental management.

Drawbacks:

• Calibration Complexity: Robust parameter estimation methods are required to improve accuracy, which is one of the major challenges of grey box models.
• Computational Demand: The complexity of the model’s physical part and the objective function’s complexity can make them computationally expensive.
• Re-calibration: Periodic re-calibration is required with more recent data.
• Moderate Data and Knowledge Requirement: Though better than the black box model, it might be challenging to fit sometimes if the training period is too long. Additionally, appropriate knowledge is necessary as some of the sub-processes can have analogy or empirical

Traditionally, the RC analogy is the most widely used method to achieve a well-suited grey box model for control applications. Eqs. (11a) - () covers a simplified RC model for the greenhouse system. The RC model analogy allows us to represent the $C{O}_2$ transfers, temperature, humidity, crop, and soil dynamics in terms of capacitive and resistive elements, capturing the system’s transient response to changes in environmental conditions.

$$\begin{array}{cc}\hfill C_{\mathrm{air}}{\displaystyle \frac{d{T}_{\mathrm{in}}}{dt}}& ={\displaystyle \frac{T_{\mathrm{ext}}-T_{\mathrm{in}}}{R_{\mathrm{heating}}}}-{\displaystyle \frac{T_{\mathrm{in}}-T_{\mathrm{ext}}}{R_{\mathrm{cooling}}}}+{\displaystyle \frac{T_{\mathrm{ext}}-T_{\mathrm{in}}}{R_{\mathrm{vent}}}}-{\displaystyle \frac{T_{\mathrm{in}}-T_{\mathrm{crop}}}{R_{\mathrm{trans}}}}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +{\displaystyle \frac{T_{\mathrm{light}}-T_{\mathrm{in}}}{R_{\mathrm{light}}}}+{\eta }_{\mathrm{solar}}{A}_{\mathrm{glazing}}{I}_{\mathrm{solar}}(1-e^{-kL}),\hfill \end{array}$$

(11a)

$$\begin{array}{cc}\hfill C_{\mathrm{air}}{\displaystyle \frac{d{H}_{\mathrm{in}}}{dt}}& ={\displaystyle \frac{H_{\mathrm{ext}}-H_{\mathrm{in}}}{R_{\mathrm{humid}}}}-{\displaystyle \frac{H_{\mathrm{in}}-H_{\mathrm{ext}}}{R_{\mathrm{dehumid}}}},\hfill \end{array}$$

(11b)

$$\begin{array}{cc}\hfill C_{\mathrm{air}}{\displaystyle \frac{d{\mathrm{CO}}_{2,\mathrm{in}}}{dt}}& ={\displaystyle \frac{{\mathrm{CO}}_{2,\mathrm{ext}}-{\mathrm{CO}}_{2,\mathrm{in}}}{R_{{\mathrm{CO}}_2,\mathrm{supp}}}}-{\displaystyle \frac{{\mathrm{CO}}_{2,\mathrm{in}}-{\mathrm{CO}}_{2,\mathrm{ext}}}{R_{{\mathrm{CO}}_2,\mathrm{vent}}}}-{\displaystyle \frac{{\mathrm{CO}}_{2,\mathrm{in}}-{\mathrm{CO}}_{2,\mathrm{crop}}}{R_{{\mathrm{CO}}_2,\mathrm{uptake}}}},\hfill \end{array}$$

(11c)

$$\begin{array}{cc}\hfill C_{\mathrm{soil}}{\displaystyle \frac{d{T}_{\mathrm{soil}}}{dt}}& ={\displaystyle \frac{T_{\mathrm{ext}}-T_{\mathrm{soil}}}{R_{\mathrm{heating},\mathrm{soil}}}}-{\displaystyle \frac{T_{\mathrm{soil}}-T_{\mathrm{ext}}}{R_{\mathrm{cooling},\mathrm{soil}}}},\hfill \end{array}$$

(11d)

$$\begin{array}{cc}\hfill C_{\mathrm{crop}}{\displaystyle \frac{d{T}_{\mathrm{crop}}}{dt}}& ={\eta }_{\mathrm{crop}}{A}_{\mathrm{crop}}{I}_{\mathrm{solar}}·\mathrm{LAI}-{\dot{m}}_{\mathrm{trans}}\lambda -{\displaystyle \frac{T_{\mathrm{crop}}-T_{\mathrm{in}}}{R_{\mathrm{ex},\mathrm{air}}}},\hfill \end{array}$$

(11e)

$$\begin{array}{cc}\hfill {\dot{m}}_{\mathrm{trans}}& =\beta ·L·\left(1-{\displaystyle \frac{L}{L_{\max }}}\right)·f(T_{\mathrm{crop}},D_v,r_a,r_s).\hfill \end{array}$$

(11f)

In the indoor temperature balance (11a), thermal capacitance $C_{\mathrm{air}}$ represents the thermal inertia of the air inside the greenhouse, while the resistances (R) correspond to heat transfer rates between different components of the system, such as heating, cooling, ventilation, and crop canopy exchange. Similarly, eqs. () - () represent moisture content, $C{O}_2$ concentration, the thermal mass of the soil, and crop canopy temperature. Notice that heat gain from solar radiation is often treated separately due to its direct dependence on light interception efficiency and LAI. This term remains empirical and based on the specific characteristics of the crop and glazing, capturing the direct impact of solar radiation on the greenhouse temperature.

Various optimization techniques can be utilized to obtain the parameters of a grey box model, namely, convex optimization [75], PSO [76], genetic algorithm [71] evolutionary algorithms [77], etc. There are two stages of this parameter estimation: batch and online. Batch estimation includes minimization of the model error over a specific period of time, which can be performed offline. On the other hand, an online estimation can be argued as a filtering technique such as Kalman filtering [78], non-linear Kushner filtering [79], sequential Monte Carlo, and many others.

Figure 4 displays a potential application of integrated modeling, which can be adapted to manage the microclimate of greenhouses effectively. Notably, the DT/white box can virtually represent an actual greenhouse that creates a database by simulating various scenarios [65,80]. It could contain a detailed greenhouse simulation, including all the components in this context. Subsequently, a grey box or a black box model can be learned to capture the dynamics essential for a particular control/optimization technique, for instance, MPC. That can also take decisions and apply the changes to the real greenhouse or digital twin. Consequently, this decision-making mechanism can be of great use to interact and test various algorithms and management schemes.

Table 3 compares various simulators available based on their offerings. Altes-Buch et al. [81] provides a detailed simulator compared to others by leveraging Modelica libraries. However, the control scheme is limited to PID only. On the other hand, Szalai [82] provides a complete open-source Python-based library for greenhouse simulations. It provides predominately vertical farming simulations, where the crop models are limited to just two, and the control solution is only a proportional controller. Nevertheless, owing to its open-source nature, the framework can be further extended to improve the controller, add types of crops, and use other optimization techniques from the energy management perspective.

3.2.3. Black Box

Purely data-driven black box models rely on historical data and machine learning algorithms to predict system behavior without prior knowledge of the underlying physics-based dynamics. Broadly, black box models can be classified into parametric and non-parametric models. Parametric linear models are argued to be the simplest of all, mainly covering the offsprings of regressive and auto-regressive models [83,84]. Recently, parametric nonlinear models such as NN, ANN, LSTM, etc., are the most popular, demonstrating improved microclimate predictions [85,86]. LSTMs are flexible as they do not make strong assumptions about the form of the mapping function from inputs to outputs. Instead, they are designed to learn the patterns from the data, regardless of the underlying distribution. Gharghory [87] can be consulted for detailed time series prediction of microclimate data inside the greenhouse. On the other hand, Zhou et al. [88] claimed to improve the prediction accuracy of the process-based greenhouse with a combination of particle filtering and DNN. Also, a multi-model DL approach has recently surfaced [89], addressing the prediction imbalances in smart greenhouses arising from a single-model approach.

Benefits:

• Rapid Deployment: Quick to implement for real-time monitoring and control based on historical data.
• Cost-effective: Lower initial cost is one of the major benefits of black box models as they do not require domain-specific knowledge.
• Flexible and Scalable: Large dataset handling capacity and swiftly transformable to state space formulation for control applications.

Drawbacks:

• Generalization: Cannot be generalized as they are vulnerable to uncertain conditions previously not encountered.
• Data Dependent: As no physics-based knowledge is involved, they are highly dependent on data and can lead to inaccuracies for certain processes where knowledge is paramount, for instance, plant growth patterns or anomalies.
• Trust Issues: Lack of insights can limit understanding of predictions.

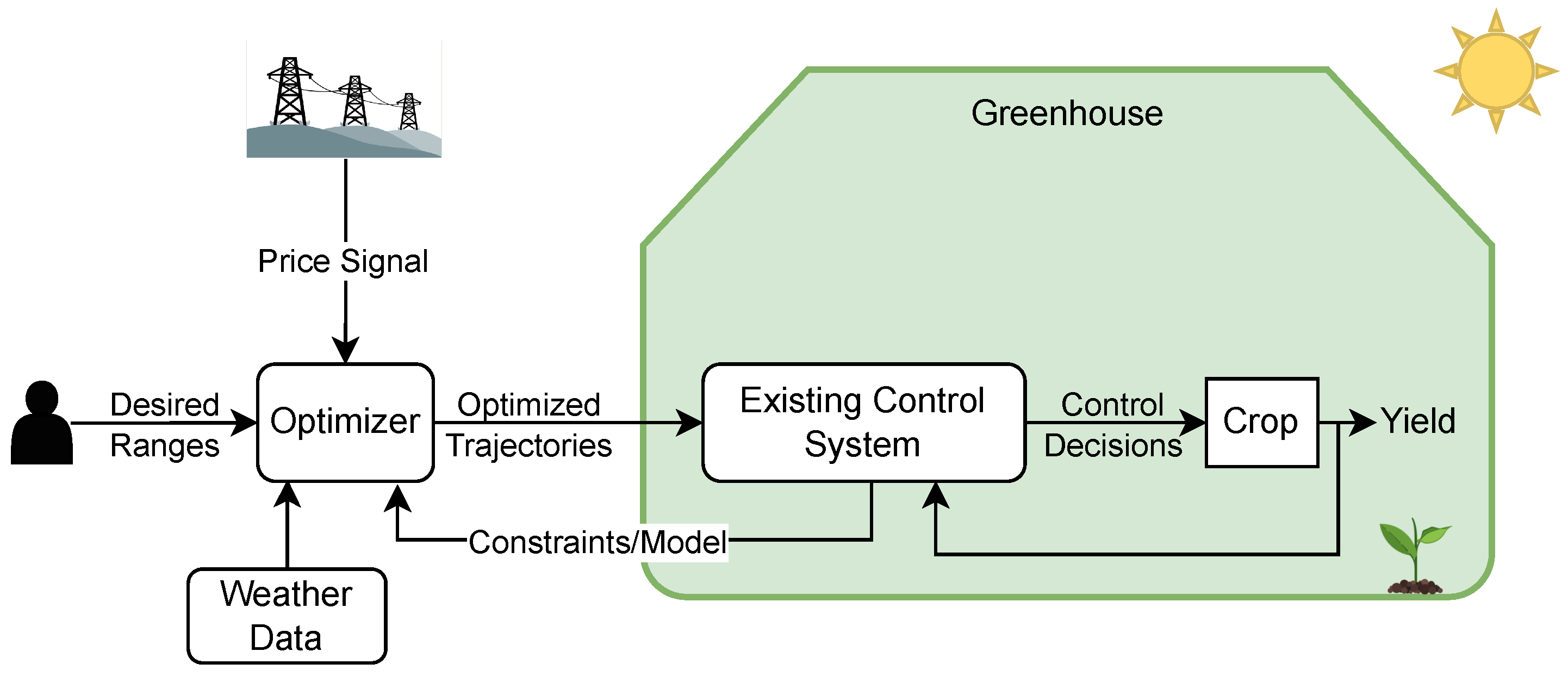
3.3. Control & Optimization

In this stage, an objective function is defined, and the system parameters are tuned to optimize this function. The challenge in this stage is to ensure that the optimization process leads to a solution that is not only optimal but also feasible in the real world. In the context of smart grids, the optimization process becomes complex due to the need to balance various factors like energy efficiency, cost, reliability, and sustainability.

Subsequently, the final stage, where the optimized strategies are put into action through control decisions. The challenge is to ensure that the control strategies are implemented correctly and can adapt to changes in the system. With smart grids, the control implementation becomes challenging due to the need to manage a large number of interconnected devices and systems, and to ensure their coordinated operation. The onset of smart grid technologies has indeed brought about numerous challenges. These include security and privacy concerns, information management issues, grid imbalance problems, inclusive participation of partners, embedding renewable and distributed resources, and the increasing complexity of the grid. However, these challenges also present opportunities for innovation and improvement in how we generate, distribute, and consume electricity. The key lies in leveraging advanced technologies and methodologies to address these challenges and make the most of the opportunities presented by smart grids.

Figure 5 depicts a schematic of an existing greenhouse system with its control system for controlling the microclimate. Here, an entity responsible for energy management is established that evaluates the greenhouse model, utility price signal, weather, and the constraints to generate optimal power profiles for optimizing energy usage with respect to the price signal as well as plant comfort. In flexibility/energy markets, this manager can respond to the ADRA in the hierarchy (Figure 2). This optimizer is essentially for demand-side problem solving; similarly, the ADRA also solves an optimization problem. As discussed in Section 2, various game-theoretic strategies can be employed for energy management encompassing case-specific optimization algorithms. Table 4 shows the comparison of control as well as optimization algorithms employed for greenhouse systems. Also, a bifurcation of the roles of various variables of the greenhouse control system is made. The objective of each methodology has to be divided into either setpoint or energy cost perspective. Moreover, comments on the results of the study, convergence/stability criteria undertaken, sensitivity, platform, and crops grown are also considered. Here, we present the most commonly used optimization problems in the literature for greenhouse control and optimization. From the energy management perspective participating in DR scenarios, the common modes of operation adopted are the grid-connected and islanded modes. The optimization problem adopted for grid-connected mode is [93],

$$\begin{array}{cc}\hfill \mathrm{minimize}& \sum _{0\le t\le T}(C_t^G+C_t^{OP}+C_t^{BP}-C_t^{SP})\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \mathrm{microclimate}\mathrm{bounds}\hfill \\ \hfill & \mathrm{power}\mathrm{generation}\mathrm{bounds}\hfill \\ \hfill & \mathrm{I}/\mathrm{O}\mathrm{bounds}\hfill \end{array}$$

(12)

In (12), $C_t^G$ denotes the cost of generation of power and startup, which can be sourced from various renewable energy resources. $C_t^{OP}$ depicts the operational cost. $C_t^{BP}-C_t^{SP}$ is for the difference in the cost of buying the power from the grid to maintain the microclimate conditions and selling the generated power to the grid. Based on the number of units for power production and type of renewables used, (12) can be modified to accommodate the changes. Importantly, the objective function in (12) is subject to certain constraints. Specifically, microclimate bounds are the indoor environmental conditions that need to be maintained within the greenhouse, such as temperature, humidity, light intensity, CO2 concentration, etc. The energy management system should ensure these conditions are kept within certain ranges for optimal plant growth. Moreover, power generation bounds could be the limits on the amount of power that can be generated or used. For instance, there might be a maximum limit on the power that can be drawn from the grid or a minimum amount of power that needs to be generated by the greenhouse’s own energy sources (like solar panels or wind turbines). On the contrary, in the islanded mode, the following objective function could be adopted:

$$\begin{array}{cc}\hfill \mathrm{minimize}& \sum _{0\le t\le T}(C_t^G+C_t^{OP}+C_t^P)\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \mathrm{microclimate}\mathrm{bounds}\hfill \\ \hfill & \mathrm{power}\mathrm{generation}\mathrm{bounds}\hfill \\ \hfill & \mathrm{I}/\mathrm{O}\mathrm{bounds}\hfill \\ \hfill & \mathrm{penalty}\mathrm{bounds}\hfill \end{array}$$

(13)

Here, in (13), a total penalty cost is added to the objective function. That covers the cost of violating the microclimate bounds, which may cover the basic penalty factor as well as an additional penalty for consecutive interval violations. This penalty term $C_t^P$ is important as the violation of not maintaining the microclimate parameters at the desired levels can adversely affect the growth of plants. Lin et al. [94] proposed an optimization to reduce the consumption of not only energy but water and $C{O}_2$ as well, i.e.

$$\begin{array}{cc}\hfill \mathrm{minimize}& \sum _{0\le t\le T}(p_t^E{\psi }_t^E+p_t^W{\psi }_t^W+p_t^{C{O}_2}{\psi }_t^{C{O}_2})\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \mathrm{ventilation}\mathrm{rate}\hfill \\ \hfill & {\mathrm{CO}}_2\mathrm{injection}\mathrm{rate}\hfill \\ \hfill & \mathrm{microclimate}\mathrm{bounds}\hfill \end{array}$$

(14)

In (14), $p_t^E$, $p_t^W$, $p_t^{C{O}_2}$ are the prices for energy $(\$/kWh)$, water $(\$/L)$ and $C{O}_2$$(\$/ton)$. ${\psi }_t^E$ is the total energy consumed by heating/cooling, ventilation, irrigation pump, and artificial lighting. ${\psi }_t^W$ is the water consumption and ${\psi }_t^{C{O}_2}$ is the $C{O}_2$ consumption. Importantly, water requirements have no constraints as they depend on the crop. [93] proposed a more growers-oriented objective function, i.e.

$$\begin{array}{cc}\hfill \mathrm{maximize}& \sum _{0\le t\le T}(C_t^G-C_t^O)\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \mathrm{input}\mathrm{bounds}\hfill \\ \hfill & \mathrm{models}\hfill \\ \hfill & \mathrm{microclimate}\mathrm{bounds}\hfill \\ \hfill & \mathrm{harvesting}\mathrm{time}\hfill \end{array}$$

(15)

where $C_t^G$ is the gross economic return of the production process by selling the harvested crops at the harvest auction and $C_t^O$ represents the overall operating cost for maintaining the microclimatic conditions. Moreover, another instance of a growers-oriented objective function can be found in [95], i.e.

$$\begin{array}{cc}\hfill \mathrm{minimize}& \sum _{0\le t\le T}(-{\gamma }_t+{\psi }_t^E)\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \mathrm{input}\mathrm{bounds}\hfill \\ \hfill & \mathrm{models}\hfill \\ \hfill & \mathrm{microclimate}\mathrm{bounds}\hfill \end{array}$$

(16)

The aim of this objective function (16) is to maximize the crop yield ${\gamma }_t$ and minimize the energy usage ${\psi }_t^E$ at the same time. [46] has utilized the most commonly used objective function comprising of the more precisely all microclimate controlled variables (from i to N) and energy consumption (17). That helps to minimize the energy consumption and maximize the plant comfort.

$$\begin{array}{cc}\hfill \mathrm{minimize}& \sum _{0\le t\le T}\sum _{0\le i\le N}{(x_t^i-{\widehat{x}}_t^i)}^2+p_t{\psi }_t^E\hfill \\ \hfill \mathrm{subject}\mathrm{to}& \mathrm{input}\mathrm{bounds}\hfill \\ \hfill & \mathrm{models}\hfill \\ \hfill & \mathrm{microclimate}\mathrm{bounds}\hfill \end{array}$$

(17)

4. Discussions and Future Research

According to the literature, the scarcity of energy management perspective for agricultural greenhouse systems is evident due to a lack of awareness, inherent intricacies attached to the multi-variable greenhouse system, and a variety of algorithms, among others. Energy management within the TE framework for agricultural greenhouses integrates advanced technologies and market mechanisms to optimize energy use and production. Key strategies include dynamic pricing, economic incentives, incorporation of renewable energy sources, and deployment of distributed energy resources. Demand response (DR) plays a crucial role in this framework, adjusting demand to match supply and offering load management solutions during peak periods, particularly in winter. DR mechanisms involve the interaction between distributed system operators (DSOs) and greenhouse energy management systems (GHEMS), which evaluate and implement flexible energy consumption strategies to maintain grid stability while meeting greenhouse microclimate requirements. The literature highlights the importance of multi-agent systems, game-theoretic approaches, and machine learning techniques such as deep reinforcement learning (DRL) and model predictive control (MPC) in optimizing these processes. Studies reveal that while many efforts focus on integrating photovoltaic generation and trading, fewer address crop modeling within greenhouses.

On the other hand, in GHEMS, as data acquisition and monitoring plays a crucial role, it also poses challenges, including handling heterogeneous and fast-paced data generation and the high costs of new technologies, especially for small and medium-sized growers. Key greenhouse monitoring variables, crucial for crop growth and energy management, require specialized sensors tailored to different irrigation systems. Moreover, though very tedious and time-consuming, white box modeling can be a great asset for making digital twins or virtual greenhouses for further testing of energy management schemes. However, according to literature mostly grey box or black box approaches are adopted for quick control implementation and energy management schemes. Also, various control and optimization algorithms have been put forth; it remains highly subjective to employ the one that best suits the needs.

4.1. Future Research Opportunities

4.1.1. Crop Model

Crop models are essential for accurately predicting the growth and yield of crops under varying environmental conditions, which directly impacts energy management in greenhouses. Integrating these models with energy models is crucial for creating a comprehensive management system that optimizes both crop production and energy usage. However, current literature often overlooks the detailed integration of crop models with energy models in the context of smart grids. Future research should focus on developing comprehensive models that incorporate both crop growth dynamics and energy consumption patterns. This integration can lead to more precise control strategies that balance the energy requirements for maintaining optimal microclimate conditions with the goal of reducing energy consumption and costs.

4.1.2. Integrated Modeling Approach

An integrated modeling approach that leverages virtual greenhouses can significantly enhance energy management strategies. Virtual greenhouses can simulate different scenarios and control strategies without impacting real-world operations, allowing for the testing and optimization of various energy management techniques. Despite the potential benefits, the inclusion of virtual greenhouses in energy management research is still limited. Future research should explore how virtual greenhouses can be used to develop and validate integrated models that combine environmental control, energy consumption, and crop production. This approach can provide a robust framework for testing new energy management technologies and strategies, ultimately leading to more efficient and sustainable greenhouse operations.

4.1.3. Smart Grid Inclined Management

Future work needs to explore the interaction between entities and the application of game theory in energy optimization to enhance energy management in greenhouse systems. The application of smart grid technologies in greenhouse energy management is an emerging field with significant potential. Multi-agent systems (MAS) can play a crucial role in this context by facilitating decentralized control and decision-making processes. These systems allow different components of the greenhouse (e.g., heating, cooling, lighting) to interact and optimize their operations collectively. However, there are few references in the current literature that address the application of MAS in greenhouse energy management. Future research should focus on developing MAS-based frameworks for smart grid-inclined management of greenhouses. By leveraging these capabilities, it is possible to enhance the efficiency, reliability, and adaptability of energy management systems in greenhouses, leading to better overall performance and sustainability.

5. Concluding Remarks

This review provides the most relevant recent advancements in greenhouse technologies, specifically inclined toward energy management for agricultural greenhouses. That supports researchers with a comprehensive overview of the present state-of-the-art and further research. The review described the main pillars of energy management in greenhouses, including a general DR program and stages of GHEMS. Various demand-side management methods have been reviewed based on their usability and fitment based on the management goals, revealing that MPC is central to the majority of the methods, with MAS equipped with DRL gaining popularity mainly due to adaptability to include renewable sources. From GHEMS’s perspective, it is recommended to include the crop growth data for model learning to achieve a more accurate impact of environmental change on crop yield and growth. However, the selection of sensor technology and measurement methods implies a trade-off between costs and data accuracy for small to medium-sized growers. For accurate representations, digital twins/virtual greenhouses are recommended to be developed through white box modeling or agricultural greenhouse simulators. Open-access simulators to generate synthetic data have emerged as an alternative; however, they lack the application to a wide range of crops. Lastly, various control and optimization techniques have been explored, where the variables are bifurcated to be selected wisely based on the optimization objective tailored to the needs of energy management.