Performance of the Reduced Polarimetric Optical Switching Demodulation Technique in different Spatio-temporal Polarization Modulation Schemes

1. Introduction

To analyze the polarization state (or full Stokes vectors) of incoming radiation, it is necessary to encode the Stokes vectors into intensity values that can be eventually registered by terminal detectors. This process is performed by an optical system, called a polarimeter, which consists of a polarization modulator and an analyzer. In other words, the polarimeter is a combination of one or more retarders (as a modulator) followed by a polarizer or a polarizing beamsplitter (as an analyzer). At least four intensity measurements are required to retrieve the full Stokes vectors. This is achieved by changing the retardance or the relative orientation between the optical components. This mainly includes the temporal and spatial modulation schemes based on different types to perform ([3], 1999). Each of them has different benefits to minimize the effects of two crucial factors on the polarimetry precision, particularly for the ground-based observations, i.e., the gain table of the detectors and the atmospheric seeing. As reviewed by [7] (2019), by far the most widespread type of polarization modulation used in solar instruments is spatio-temporal modulation in the form of a dual-beam setup. In this setting, an adequate modulator changes its properties continuously or discretely over time, and a polarizing beamsplitter is used as a linear analyzer and located after the temporal modulator to split the beam into two orthogonal polarization components (i.e., o and e components).

An alternative or supplementary technique to the spatio-temporal modulation, called $\mathit{beam}$$\mathit{exchange}$, was proposed by [4] (1990) based on the THEMIS polarimeter and successfully applied to the night astronomy (e.g., [4] (1990); [16] (1993) and solar observations ([1] 1998; [2] 2002). The beam exchange technique requires an extra measurement after exchanging the beams of two components, e.g., by using a rotating half-wave plate before the beamsplitter. The crucial step in the following demodulation involves constructing a specific formula to combine all the measurements of the two beams to retrieve the incoming $S/I$ with good approximation. [13] (2017) applied the beam exchange technique based on the FASOT-1 polarimeter for the 2013 solar total eclipse observation. They employed a liquid crystal variable retarder (LCVR), which is installed before the beam splitter, with its fast axis tilted at a 45-degree angle. One can quickly change its retardance from 0 to $\pi$ in a timescale of few milliseconds by changing the voltage to perform the beam exchange.

In short, the greatest advantage of beam exchange is to overcome the uncertainty of intensity differences between two beams, which may arise from variations in detector gain or the transparency of optical components. A specific formula is constructed based on the $ratio$ between two successive measurements (e.g., Equation (1) of [1] 1998). In this case, the flat-fielding process is theoretically unnecessary, and the accuracy is improved. However, it is a fact that this technique is inevitably time-consuming due to an extra measurement needed for each modulation step, which adversely affects the crucial assumption that the observed Stokes signal remains identical (with minimal variation) during the exchange. During one solar eclipse observation, [13] (2017) proposed an alternative method to save time. They only performed the beam exchange measurement with a polaroid installed in front of the telescope after the eclipse observations (i.e., no beam exchange was performed during the eclipse observation). It is the reason that they name it as the $reduced$ polarimetric optical switching (RPOS) technique (they rename the classical beam exchange as the polarimetric optical switching technique). It is worth noting that, in their work, only a single Stokes parameter $Q/I$ was observed. They analyzed the signal-to-noise level in the demodulated $Q/I$ profile and proposed a specific formula which is different from that of [4] (1990), while an alternative one was suggested in [14] (2022).

There are two facts that: (1) either the THEMIS or the FASOT telescope is polarization-free, i.e., no polarization cross-talk is introduced by the instrument before the polarimeter; (2) both polarimeters adopt a modulation scheme that modulates Q, U and V independently, i.e., $I\pm Q$, $I\pm U$ and $I\pm V$ are obtained successively over time. However, in the present work, we pay more attention to the performance of RPOS technique in other modulation schemes, with which the Stokes signals are $not$ modulated independently. For example, one adopts a polarimeter based on a continuously rotating wave plate as a modulator. We are also interested in the performance of the RPOS technique when there is strong cross-talk introduced by the telescope before the polarimeter.

In Section 2, we simulate three types of modulation schemes for the full Zeeman-effect-induced Stokes parameters: one involves independent modulation, while the other two involve dependent schemes. We propose an alternative approach to beam exchange in order to conveniently obtain the so-called reference measurements in the RPOS technique. Combining this approach, we re-check the validity of four formulas used by the RPOS technique and select the most appropriate one. In section 3, the performance of the RPOS demodulation technique (with the correct formula) is compared with that using the demodulation matrix. This comparison takes into account various influencing factors on the observed intensities, including atmospheric seeing, dark current, gain variation of the detectors, and photon noise. The conclusion and discussion are presented in Section 4.

2. Observation Simulation

2.1. Modulation Schemes

The observation is simulated based on a polarimeter in a dual-beam setup, and the modulation schemes are determined by three types of temporal modulators as shown below.

(1)

Scheme 1: the modulator consists of two quarter-wave plates, and both can individually rotate, e.g. the THEMIS polarimeter. Three measurements are taken by rotating two wave plates in the sequence of (0∘, 0∘), (0∘, 45∘) and (45∘, 0∘) during one modulation cycle with respect to the beam-splitter axis. In this scheme, the Stokes Q, U and V are modulated independently and temporally. The outputs of the two beams need to be merged in the demodulation process.

(2)

Scheme 2: the modulator consists of one rotating half-wave plate and one fixed quarter-wave plate. Three measurements are sequentially taken at rotation positions of the half-wave plate (-90∘, -36∘, 18∘), while the position of the quarter-wave plate is fixed at 15∘ relative to the axis of the beam splitter. This scheme is employed by the FASOT polarimeter ([12] 2011; [21] 2023) to achieve high polarization modulation efficiencies over a wide wavelength range using two commercial non-achromatic wave plates. In this way, the Stokes parameters are $not$ independently modulated, and merging the output of the two beams is also required for the demodulation.

(3)

Scheme 3: a continuously rotating wave plate with a certain retardance (e.g., 127∘) functions as a modulator. The rotation is performed at a certain frequency and synchronized observations are made by detectors. Typically eight measurements are taken during one polarimetric cycle (a half rotation) successively, i.e., the wave plate undergoes a rotation of 22.5∘ during each exposure. It is adopted by, e.g., the Advanced Stokes Polarimeter (ASP; [5]1992), the Solar Optical Telescope (SOT) polarimeter onboard $Hinode$ (SP; [8] 2008). In this way, the Stokes parameters are also dependently modulated. However, in contrast to Scheme 2, it is unnecessary to combine the output of two beams for retrieving the full Stokes parameters. In other words, the polarimeter based on a one-beam setup can utilize this scheme, e.g., the New Vacuum Solar Telescope (NVST) polarimeter ([6] 2020).

In the first step, we ignore the polarization cross-talk before the polarimeter. Then the modulated intensities in the i-th exposure for dual beams are given by,

$$\begin{array}{c}\hfill I^o\left(t_i\right)={\displaystyle \frac{1}{2}}·O^o\left({\theta }_i\right)·S_s;I^e\left(t_i\right)={\displaystyle \frac{1}{2}}·O^e\left({\theta }_i\right)·S_s\end{array}$$

(1)

Here $S_s={[I_s,Q_s,U_s,V_s]}^T$ indicates the input Stokes signals to the polarimeter from the Sun. O is the theoretical modulation matrix (i.e., $O=[1,O_q,O_u,O_v]$). Except the elements in the first column, the other elements of $O^o$ and $O^e$ have equal magnitudes but opposite signs. ${\theta }_i$ indicates the rotation angle of the wave plate in the i-th exposure. In both Scheme 1 and Scheme 2, there are three exposures in each beam (i.e., $i=0,1,2$). In Scheme 3, with the sampling scheme of eight equally spaced intervals over a modulation period, there are eight times exposure in each beam. (i.e., $i=0,1,...7$). Taking the O beam as an example, Equation (1) can be written as,

$$\begin{array}{cc}\hfill I^o\left(t_i\right)& ={\displaystyle \frac{1}{2}}[1·I_s+O_q\left({\theta }_i\right)·Q_s+O_u\left({\theta }_i\right)·U_s+O_v\left({\theta }_i\right)·V_s]\hfill \end{array}$$

(2)

supposing $X_s=[O_q,O_u,O_v]·{[Q_s,U_s,V_s]}^T$, we further have,

$$\begin{array}{c}\hfill I^o={\displaystyle \frac{1}{2}}(I_s+X_s);I^e={\displaystyle \frac{1}{2}}(I_s-X_s)\end{array}$$

(3)

Hereafter the term $X_s$, in stead of $S_s$, will be used in the following derivation.

2.2. Artificial Data $I_{obs}$

We make use of the RH code ([20] 2001) to synthesize the Zeeman effect-induced Stokes profiles $S_s\left(\lambda \right)$. The synthesis is for the typical photospheric line Fe I 630.15 nm. By modifying the predetermined magnetic field strength and orientation, Stokes profiles of I, Q, U and V are generated as shown in Figure 1. The maxima of $Q/I$, $U/I$ and $V/I$ are approximately $0.02$, $0.06$ and $0.2$, respectively. Two detectors are assumed to operate synchronously in dual beams. A single row of pixels records the modulated intensity in the spectral dimension.

Considering several factors affecting the observations, the observed intensities at time t in the dual beams can be expressed as,

$$\begin{array}{cc}\hfill I_{obs}^o(t,\lambda )& ={\displaystyle \frac{1}{2}}[I_s(t,\lambda )+X_s(t,\lambda )]·g^o\left(\lambda \right)·s\left(t\right)+D_k^o+N_p^o(t,\lambda )\hfill \\ \hfill I_{obs}^e(t,\lambda )& ={\displaystyle \frac{1}{2}}[I_s(t,\lambda )-X_s(t,\lambda )]·g^e\left(\lambda \right)·s\left(t\right)+D_k^e+N_p^e(t,\lambda )\hfill \end{array}$$

(4)

We remind that a temporal modulation is performed at the time t (e.g., 3 or 8 measurements). g describes both the detector gain with pixel variation and the intensity imbalance between the two beams caused by the beam splitter. A variable s represents the temporal impact of seeing on each instant exposure, which varies slightly and randomly around 1 with a magnitude at most few percent. $D_k$ is the dark current of the detector and is assumed to remain constant along the wavelength without pixel variation. The photon noise, $N_p$, in each pixel is signal-dependent and assumed to follow a Gaussian distribution with a standard deviation equal to the square-root of the signal.

2.3. The RPOS Technique: Formulas, Assumptions and Application

As suggested by the RPOS technique, two extra beam-exchange measurements are successively performed at out-of-observation times ($t_1$ and $t_2$), which are referred to as reference measurements. Same as Equation (3), they are expressed as,

$$\begin{array}{cc}\hfill I_{obs}^o\left(t_1\right)& ={\displaystyle \frac{1}{2}}[I\left(t_1\right)+X\left(t_1\right)]·g^o·s\left(t_1\right)+D_k^o+N_p^o\left(t_1\right)\hfill \\ \hfill I_{obs}^e\left(t_1\right)& ={\displaystyle \frac{1}{2}}[I\left(t_1\right)-X\left(t_1\right)]·g^e·s\left(t_1\right)+D_k^e+N_p^e\left(t_1\right)\hfill \\ \hfill I_{obs}^o\left(t_2\right)& ={\displaystyle \frac{1}{2}}[I\left(t_2\right)-X\left(t_2\right)]·g^o·s\left(t_2\right)+D_k^o+N_p^o\left(t_2\right)\hfill \\ \hfill I_{obs}^e\left(t_2\right)& ={\displaystyle \frac{1}{2}}[I\left(t_2\right)+X\left(t_2\right)]·g^e·s\left(t_2\right)+D_k^e+N_p^e\left(t_2\right)\hfill \end{array}$$

(4)

Next, two specific functions $f_1$ and $f_2$ are constructed to remove the influence of atmospheric seeing $s\left(t\right)$ and gain g on $I_{obs}^{o/e}\left(t\right)$. One can calculate the ratio between the two beams of each exposure neglecting the dark bias ($D_k$) and photon noise ($N_p$).

$$f_1\equiv {\displaystyle \frac{I_{obs}^o\left(t_1\right)}{I_{obs}^e\left(t_1\right)}}·{\displaystyle \frac{I_{obs}^e(t,\lambda )}{I_{obs}^o(t,\lambda )}};f_2\equiv {\displaystyle \frac{I_{obs}^o\left(t_2\right)}{I_{obs}^e\left(t_2\right)}}·{\displaystyle \frac{I_{obs}^e(t,\lambda )}{I_{obs}^o(t,\lambda )}};(D_k=N_p=0).$$

(5b)

We need to note that here functions $f_1$ and $f_2$ are calculated for each measurement throughout the temporal modulations for both the scientific observations and the reference measurements.

[13] 2017 proposed four specific formulas (${\mathcal{F}}_{1,2,3,4}$) based on $f_1$ and $f_2$ to retrieve the Stokes signal $X/I\left(t\right)$ under different assumptions, as summarized in Table 1 (it is important to note that in their work X is equivalent to S since there is no modulator in their study). Inspired by his work on the acquisition of reference measurements, we propose an alternative approach to beam exchange: one can successively use a pair of specific input lights with opposite polarization states, e.g., input $S_{in}=+Q$ at time $t_1$, and then input $S_{in}=-Q$ at $t_2$ to equally perform the beam exchange as described in Equation (4). In practice, it can be conveniently generated by using a specific optical component, known as the instrument polarization calibration unit (ICU). It consists of a linear polarizer and a retarder. Both of them can rotate independently around the optical axis to generate well-defined Stokes vectors. The benefit of this approach lies in the stability of optics components, which ensures that the polarization fraction of the input signal remains constant, only with the sign reversing during the two successive measurements. But in contrast to the previous study, we consider different modulation schemes in this work, i.e., $X=O·S_{in}$, which may lead to the assumptions of ${\mathcal{F}}_{1,2,3,4}$ regarding $S/I$ no longer being valid. In the following, we analyze the validity of each formula for three types of schemes, especially using the alternative approach to obtain reference measurements.

The main steps are: modulating the synthesized data to generate the $observed$ intensities (($D_k=N_p=0$, $g=s=1$).), then demodulating using ${\mathcal{F}}_{1,2,3,4}$ to obtain $X/I$, and finally calculating $S/I$ using $S=O^{-1}·X$. Comparison between the final result and the synthesized data is used to evaluate the validity of ${\mathcal{F}}_{1,2,3,4}$. Three types of modulation schemes are analyzed respectively in the following.

Table 1. the RPOS formulas and Assumptions.

No.	Formulas1	Assumptions
${\mathcal{F}}_1$	${\displaystyle \frac{X}{I}}\left(t\right)={\displaystyle \frac{1-\sqrt[]{f_1{f}_2}}{\sqrt[]{f_1{f}_2}+1}}$	${\displaystyle \frac{X}{I}}\left(t_1\right)=-{\displaystyle \frac{X}{I}}\left(t_2\right)$
${\mathcal{F}}_2$	${\displaystyle \frac{X}{I}}\left(t\right)={\displaystyle \frac{1}{2}}({\displaystyle \frac{1-f_1}{1+f_1}}+{\displaystyle \frac{1-f_2}{1+f_2}})$	${\displaystyle \frac{X}{I}}\left(t_{1,2}\right)·{\displaystyle \frac{X}{I}}\left(t\right)$ is negligible.
${\mathcal{F}}_3$	${\displaystyle \frac{X}{I}}\left(t\right)=(\sqrt[]{g}-1)/(1+\sqrt[]{g})$	$g\equiv (1/f_1+1)/(f_2+1)$;
		$[1-{\displaystyle \frac{X}{I}}\left(t_{1,2}\right)]·{\displaystyle \frac{X}{I}}\left(t\right)$ is negligible.
${\mathcal{F}}_4$	${\displaystyle \frac{X}{I}}\left(t\right)=(g-1)/(1+g)$	$g\equiv (1/f_3+1)/(f_4+1)$2
		$[1-{\displaystyle \frac{X}{I}}\left(t_{1,2}\right)]·{\displaystyle \frac{X}{I}}\left(t\right)$ is negligible.

¹ In [13] 2017, $X=S$ and the assumptions are regarding to S/I. ² Functions f₃ and f₄ are actually the algebraic transformations of f₁ and f₂, see the definition in the reference.

Table 1. the RPOS formulas and Assumptions.

No.	Formulas1	Assumptions
${\mathcal{F}}_1$	${\displaystyle \frac{X}{I}}\left(t\right)={\displaystyle \frac{1-\sqrt[]{f_1{f}_2}}{\sqrt[]{f_1{f}_2}+1}}$	${\displaystyle \frac{X}{I}}\left(t_1\right)=-{\displaystyle \frac{X}{I}}\left(t_2\right)$
${\mathcal{F}}_2$	${\displaystyle \frac{X}{I}}\left(t\right)={\displaystyle \frac{1}{2}}({\displaystyle \frac{1-f_1}{1+f_1}}+{\displaystyle \frac{1-f_2}{1+f_2}})$	${\displaystyle \frac{X}{I}}\left(t_{1,2}\right)·{\displaystyle \frac{X}{I}}\left(t\right)$ is negligible.
${\mathcal{F}}_3$	${\displaystyle \frac{X}{I}}\left(t\right)=(\sqrt[]{g}-1)/(1+\sqrt[]{g})$	$g\equiv (1/f_1+1)/(f_2+1)$;
		$[1-{\displaystyle \frac{X}{I}}\left(t_{1,2}\right)]·{\displaystyle \frac{X}{I}}\left(t\right)$ is negligible.
${\mathcal{F}}_4$	${\displaystyle \frac{X}{I}}\left(t\right)=(g-1)/(1+g)$	$g\equiv (1/f_3+1)/(f_4+1)$2
		$[1-{\displaystyle \frac{X}{I}}\left(t_{1,2}\right)]·{\displaystyle \frac{X}{I}}\left(t\right)$ is negligible.

¹ In [13] 2017, $X=S$ and the assumptions are regarding to S/I. ² Functions f₃ and f₄ are actually the algebraic transformations of f₁ and f₂, see the definition in the reference.

1.

For modulation Scheme 1, using specific polarized light (i.e., $\pm Q$ or $\pm U$ or $\pm V$) for reference measurements may result in the absence of intensity in one beam during temporal modulation, assuming dark current and photon noise are zero. For instance, if linearly polarized light $+Q$ with the polarization fraction equal to 1 is input at time $t_1$, the function $f_1$ becomes invalid because $I_{obs}^e\left(t_1\right)$ equals 0 during one modulation step (note the reference axis to define the Stokes parameters is aligned with the beam-splitter axis, and $+Q$ is parallel to the polarization component in the o beam). The same problem occurs even if circularly polarized light is used. As a result, formulas ${\mathcal{F}}_{1,2,3,4}$ are all meaningless. 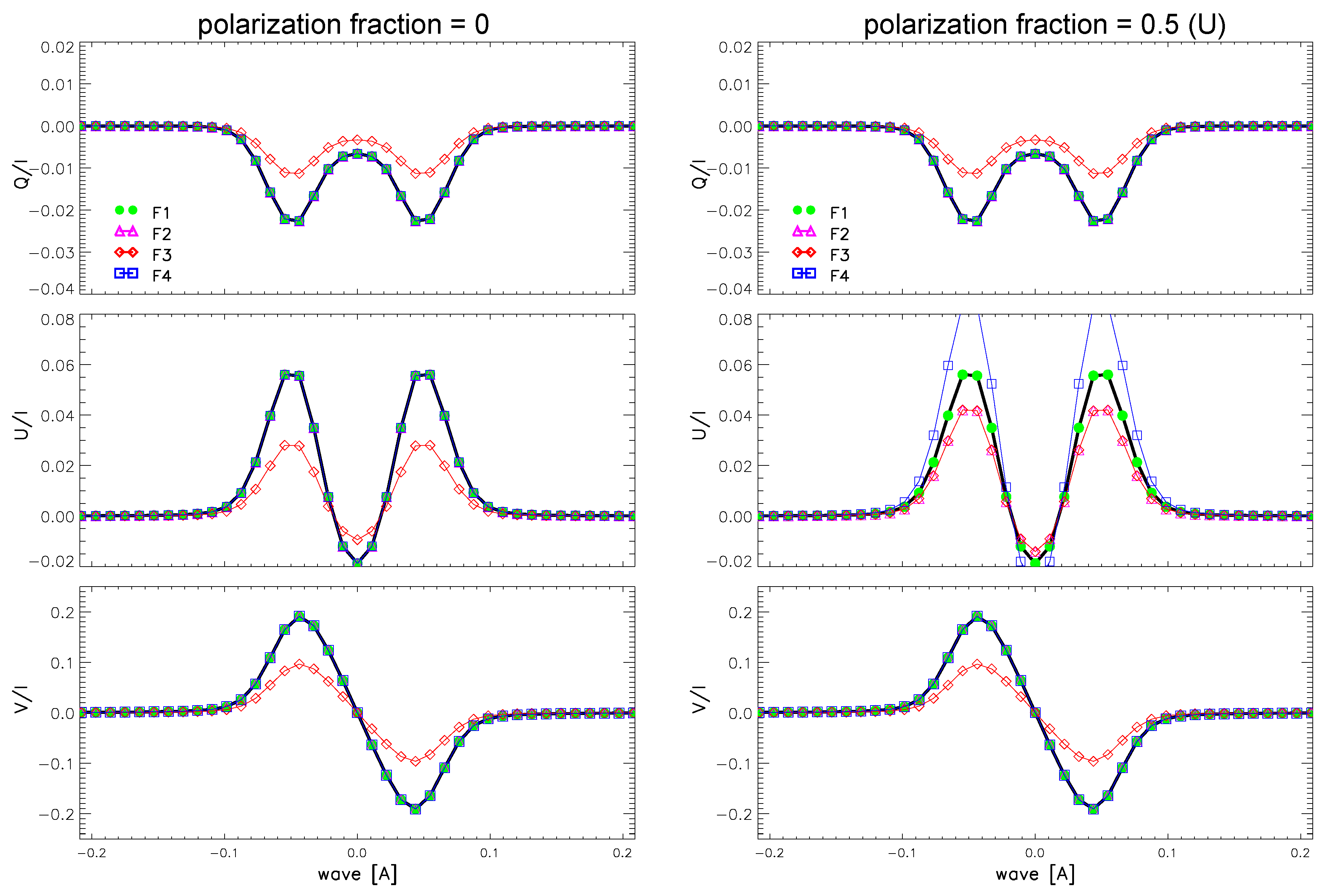To address this issue, one potential resolution is to use unpolarized light, such as light from a quiet region on the solar disk ([18] 2005), as the target for the reference measurement. In this situation, as demonstrated in the left panel of Figure 1, the functions ${\mathcal{F}}_{1,2,4}$ accurately fit the synthesized profile, but ${\mathcal{F}}_3$ underestimates the signals. However, as the polarization fraction increases, the discrepancies caused by using ${\mathcal{F}}_{2,4}$ become pronounced. For example, using $\pm U$ with a $50\%$ polarization fraction for reference measurements leads to significant discrepancies in U retrieval, as shown in the right panel.

2.

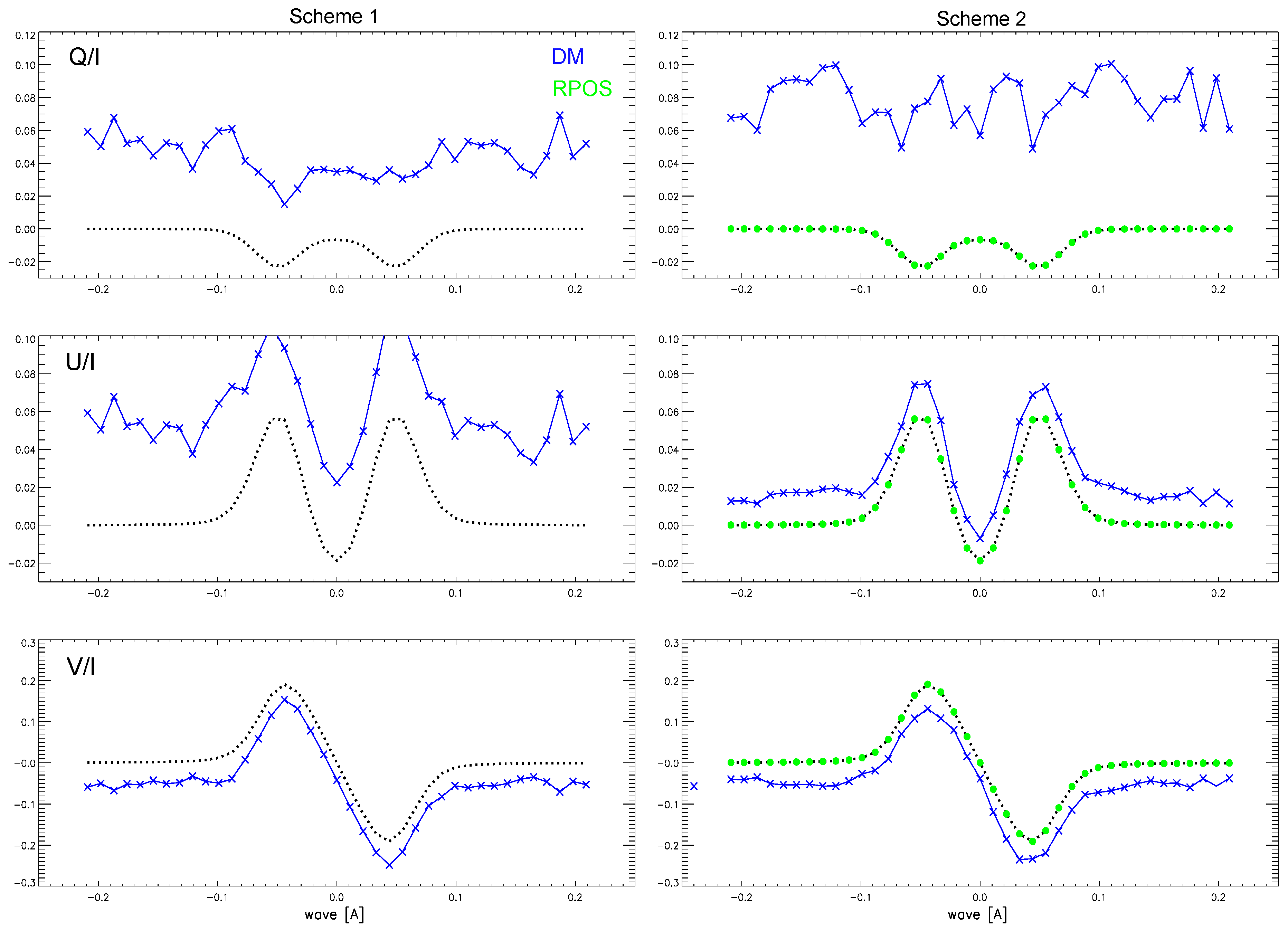
For Scheme 2, the issue in Scheme 1 is resolved by dependent modulation. However, as shown in Figure 2, using $\pm U$ with a 100% fraction for reference measurements, only the formula ${\mathcal{F}}_1$ can perfectly reproduce the synthesizedt profiles. The reason is straightforward: neither $X/I\left(t_{1,2}\right)$ nor $1-X/I\left(t_{1,2}\right)$ is negligible in this case, so the assumptions for other formulas are no longer valid. Furthermore, the validity of ${\mathcal{F}}_1$ is not influenced by the polarization fraction of the input light. For instance, as shown in the right panel, when $\pm U$ with a 10% fraction are used for reference measurements, the function ${\mathcal{F}}_1$ can still work with high accuracy compared to the functions ${\mathcal{F}}_2$ and ${\mathcal{F}}_4$, whereas the results from ${\mathcal{F}}_3$ are still seriously underestimated.

3.

For Scheme 3, from the comparisons in Figure 3, one can draw the same conclusion that formula ${\mathcal{F}}_1$ is the only one to reproduce the synthesized Stokes profiles perfectly. In addition, this validity does not depend on whether linearly polarized light (left column) or circularly polarized light (right column) is used for reference measurements.

In brief, if specific polarized light, i.e., $\pm Q$, $\pm U$ or $\pm V$, conveniently generated by an ICU, is utilized for reference measurements, and no changes of the polarization state are introduced before the modulator, the RPOS technique cannot be applied to Scheme 1. However, the RPOS technique can be applied to Schemes 2 and 3 only by performing formula ${\mathcal{F}}_1$. In addition, we admit that using unpolarized light for reference measurements is another potential method.

3. Comparison with Other Demodulation Methods

In this section, the demodulation based on formula ${\mathcal{F}}_1$ (i.e., known as the RPOS technique) is compared with that based on the demodulation matrix (DM). In this case, the artificial observations take into account the impact of dark current, atmospheric seeing, detector gain and photon noise.

Here we adopt D to represent the optimum demodulation matrix given by the pseudo inverse of O as $D={\left(O^{T}O\right)}^{-1}{O}^T$ ([19] 2000). The polarization signal is derived by $S_s=D·I_{obs}$. It is worth reminding that (1) for modulation schemes 1 and 2, it is necessary to merge the outputs of o and e beams together for the demodulation. i.e., $I_{obs}$ consists of $I_{obs}^o$ and $I_{obs}^e$, and O is composed of $O^o$ and $O^e$. (2) For the modulation scheme 3, it is more favorable to demodulate each beam separately and then merge the results, i.e., $S_s={\displaystyle \frac{1}{2}}(D^o·I_{obs}^o+D^e·I_{obs}^e)$, since each beam has its own dark current, gain table and throughput, etc. One can also use a specific operator to represent the demodulation procedure in each beam. For example, [17] (1997) defined four operators $F_j^0$ with $F_j^0=(1/\pi ){\int }_0^{\pi }{H}_j\left(\theta \right)d\theta$, where $H_0=1$, $H_1$ = sign(cos4$\theta$), $H_2$ = sign(sin4$\theta$), $H_3$ = sign(-sin2$\theta$). It is shown that these two methods are actually identical.

3.1. Effect of Dark Current $D_k$

Dark current, including the stray light, is added to the intrinsic signal, so the dark current only affects the Stokes I profile, because the demodulation actually retrieves Stokes Q, U and V by performing differences of measured intensities. As a result, the bias of Stokes I caused by the dark current will decrease the magnitude of retrieved Stokes $Q/I$, $U/I$ and $V/I$, and neither the RPOS technique nor DM has advantage in this issue.

In order to minimize the Stokes I bias, one needs to have a good knowledge about the dark current to an accuracy. Most science requirements are met if the Stokes I level is known to about 1% ([9] 2013). In practice, the magnitude of stray light, as well as the spectral resolution, can be determined by comparing the fully reduced Stokes I profiles observed at disk center with a Fourier Transform Spectrum (FTS) obtained by [11] (1994).

3.2. Effect of Detector Gain Variation $g\left(\lambda \right)$

In the case of modulation Scheme 3, either o or e beam can be regarded as a single-beam configuration, the lack of knowledge about the gain variation of the detector can be overcome since all measurements are recorded by one detector. In other words, if there is no image displacement in these measurements, the flat-fielding is theoretically unnecessary to retrieve $S_s/I$. In this section, therefore, our numerical test is only for Schemes 1 and 2, in which the gain variation treatment is essential.

We consider not only the pixel-to-pixel variations of each detector but also the different throughputs between the two beams (i.e., the imbalance between the two beam intensities): we assume that both detectors have a pixel-to-pixel variation with an amplitude of $2\%$, which is approximately equal to the magnitude of $Q/I$. Besides, we suppose there is an imbalance of $5\%$ in the throughputs between two beams. As a result, for one detector, the gain factor is $g_o=1.05\pm 0.02$, and for the other detector, it is $g_e=0.95\pm 0.02$. The demodulated results are illustrated in Figure 4. It is seen that in Scheme 1 (left column), the retrieved Stokes profiles using the DM exhibit a zero-line offset (the blue line) compared to the input synthesized profile (the black line). This offset is attributed to the $5\%$ difference between $g_e$ and $g_o$, and the pixel-to-pixel variation reduces the signal-to-noise ratio, making the $Q/I$ profile almost indistinguishable. As mentioned in Sec.2.3, the RPOS technique is not applicable in this scheme because we use specifically polarized signals for reference measurements. In Scheme 2 (right column), performance of the RPOS technique (the green lines) demonstrates a significant advantage compared to the DM method, effectively mitigating these effects.

3.3. Effect of Atmospheric Seeing $s\left(t\right)$

The independent modulation scheme based on a dual-beam setup, such as Scheme 1, is well-known for its effective reduction of atmospheric turbulence, so in this section, we only consider Schemes 2 and Scheme 3, which account for atmospheric seeing effects with random intensity fluctuations of up to $5\%$ in each exposure.

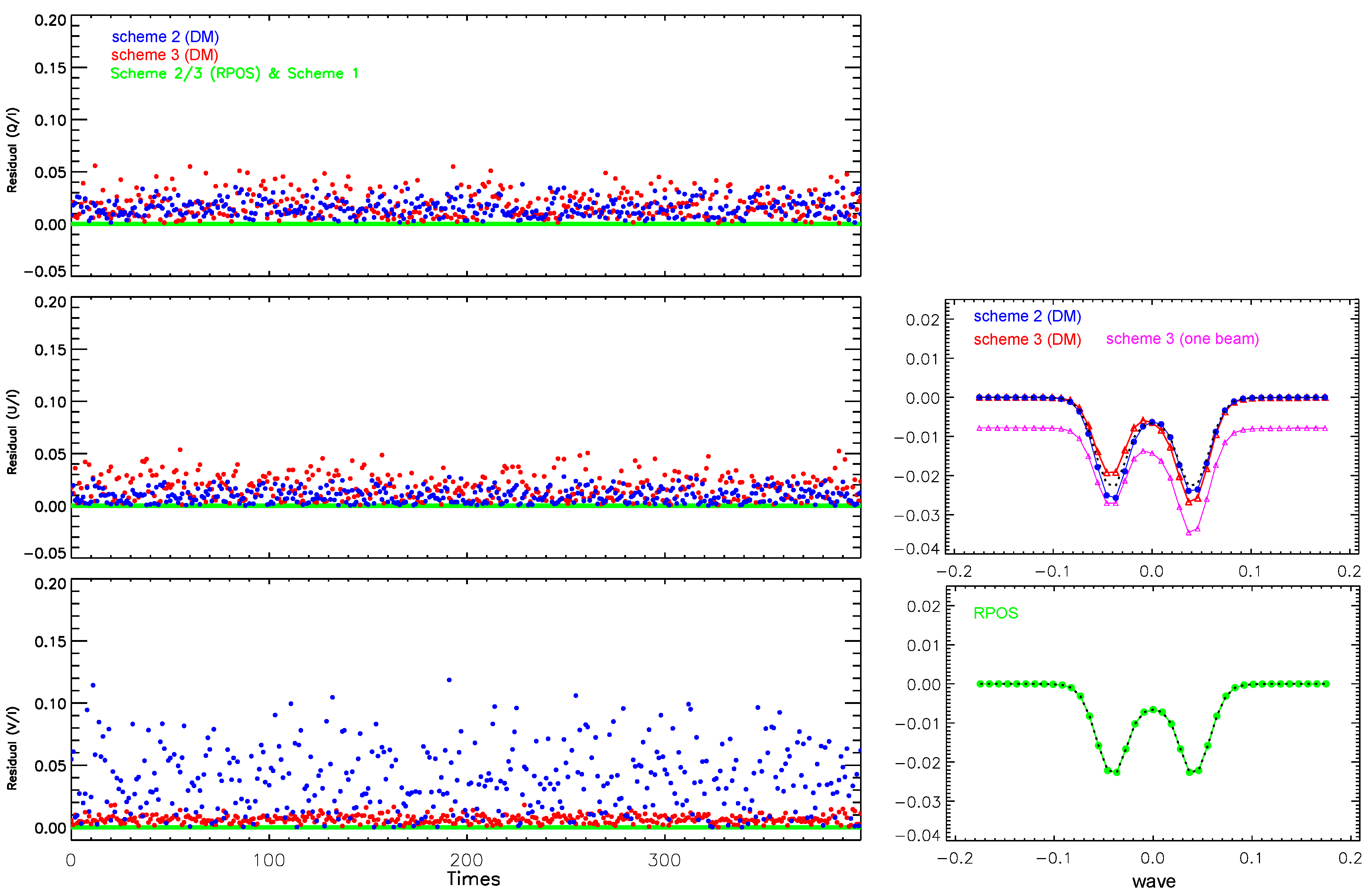
Firstly, in both Scheme 2 and Scheme 3, unlike the impact of dark current, random intensity fluctuations result in an asymmetry discrepancy in all the retrieved Stokes profiles when using the DM method. As an example, we show the retrieval of $Q/I$ in the upper-right panel of Figure 5 (see the blue and red profiles).This panel also displays the DM result of Scheme 3 using single-beam measurements (the pink profile), which also exhibits a zero-line offset proportional to the magnitude of the intensity fluctuation. This comparison further highlights the advantage of the two-beam configuration when intensity fluctuation is considered. However, when the RPOS technique is employed (in the lower-right panel), both the asymmetric discrepancy and the zero-line offset problems have been effectively addressed.

Secondly, regarding the DM method only, we further compare its performance in Schemes 2 and Scheme 3 by calculating the residuals between the input synthesized ($S_{in}$) and the final retrieved ($S_{out}$) Stokes profiles. The residual is defined as,

$$residual=\int |S_{out}-S_{in}|d\lambda ,$$

(6)

and the discrepancy is integrated across the wavelengths. We perform 400 trial attempts for both schemes,each with a random intensity fluctuations of up to $5\%$ in each exposure. The statistical results are shown in the left panel of Figure 5. It is found that, despite Scheme 3 (red dots) involving eight exposures compared to the three in Scheme 2 (blue dots), the residuals in Scheme 3 are notably smaller, especially when the circular polarization signal is taken into account.

3.4. Effect of Photons Noise $N_p(t,\lambda )$

In this section, we still focus on Scheme 2 and Scheme 3 since the RPOS technique is not applicable to Scheme 1. We assume that the photon noise in each pixel is signal-dependent and follows a Gaussian distribution with the standard deviation being the square-root of the signal,

$${\sigma }_{N_p}^{o/e}(t,\lambda )=\sqrt{{\displaystyle \frac{1}{2}}[I(t,\lambda )\pm X(t,\lambda )]}$$

(7)

additionally, we set $D_k=0$, $g^{o/e}=1$, $s\left(t\right)=1$. We perform 400 trial attempts for both schemes and make a statistical analysis for the residuals.

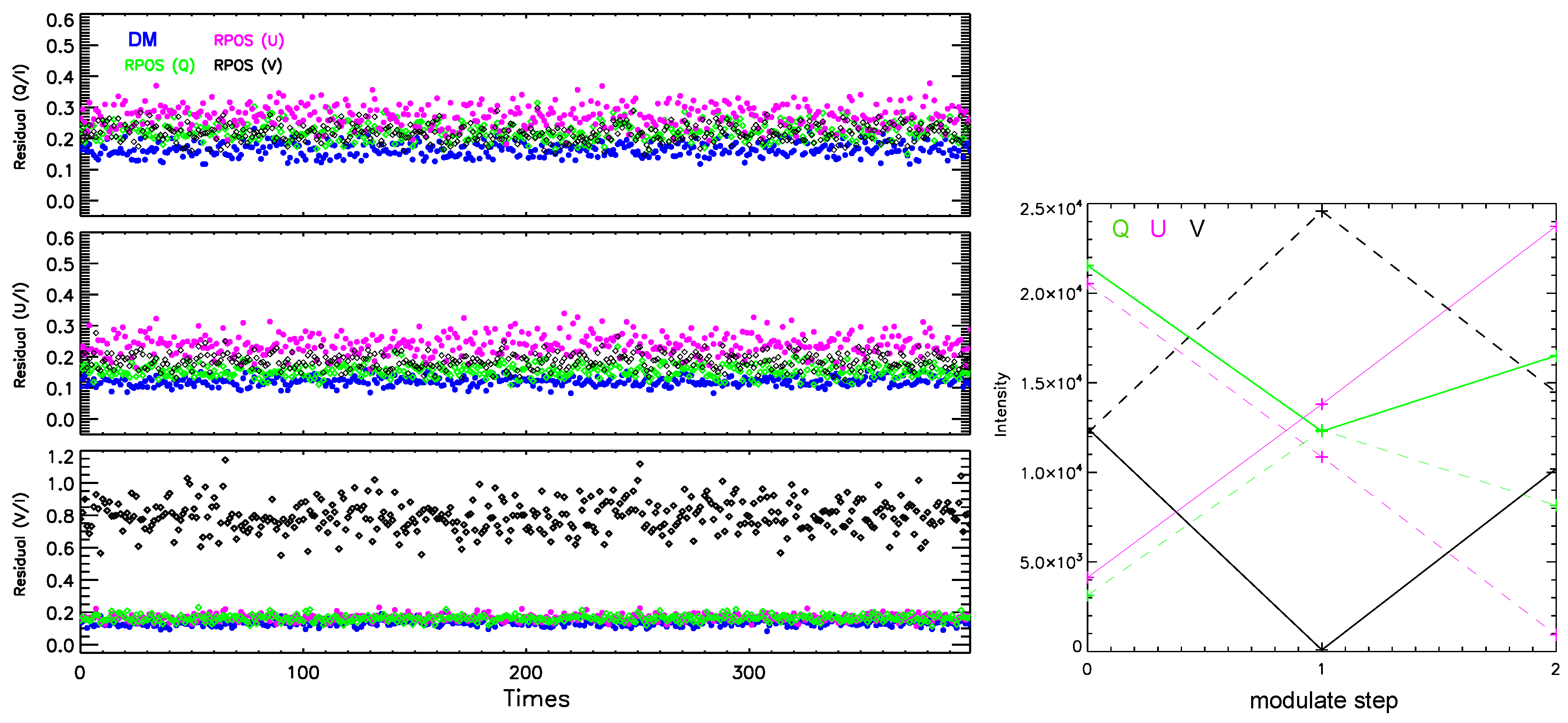
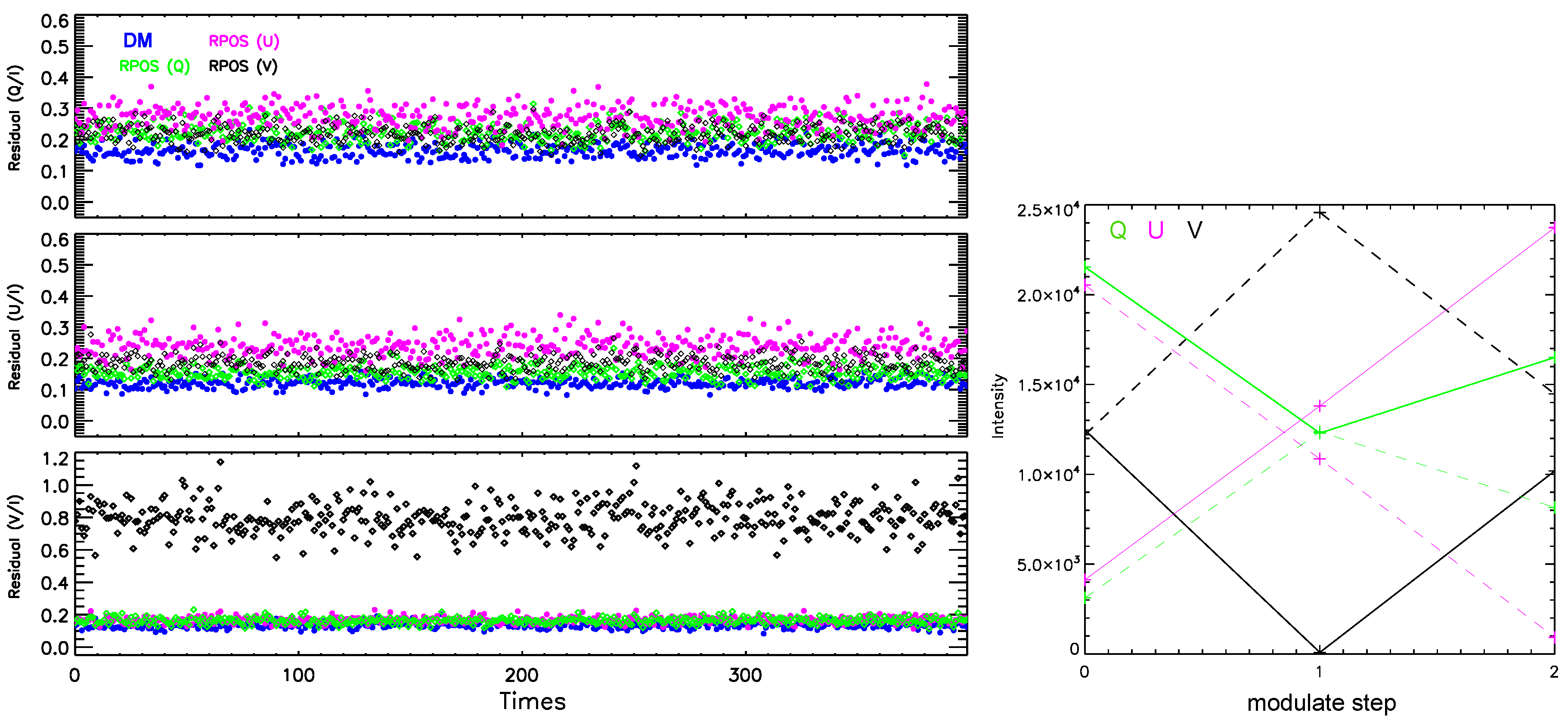
Firstly, it is found that the residuals of DM method is slightly smaller than that of the RPOS technique in both schemes. For example, in Scheme 3, the residual of the DM method is approximately 0.09±0.011, whereas that of the RPOS method is around 0.12±0.014 regardless of the specific polarized signal used for reference measurements. In Scheme 2, however, the issue becomes more complex as shown in the left panel of Figure 6: The residual of the DM method is about 0.14±0.02 (the blue dots), while the residual of the RPOS technique varies depending on the polarization single used for reference measurements. Specifically, using $\pm Q$ for reference measurements (green dots) yields the smallest average demodulation residual for the three Stokes parameters ($Q/I$, $U/I$ and $V/I$ from up to bottom), which are approximately $0.22\pm 0.03$, $0.15\pm 0.02$ and $0.16\pm 0.02$ for $Q/I$, $U/I$ and $V/I$, respectively. While, using $\pm V$ for reference measurements (black dots) results in noticeable errors, especially in $V/I$, reaching up to $0.79\pm 0.09$.

In fact the reason can be found from the modulation matrix of Scheme 2. The modulation matrix of the o beam can be written as

$$M_{Fasot}^o=\left[\begin{array}{cccc}1.000& 0.747& -0.665& 0.011\\ 1.000& -0.003& 0.119& -0.993\\ 1.000& 0.339& 0.925& -0.174\end{array}\right],$$

(8)

It is noted that the values of $M^o$[2,4] is nearly equal to -1, it meas that, when V signal is input for reference measurements, the intensity of the o beam at the second modulation step is almost 0 (see the black solid line in Figure 6). Similarly, as $M^e$ [3,3]=0.925, when $-U$ is input, the intensity at the third step becomes quite small (Note: the pink dashed line shows the case in e beam with U input, they are equal). In both cases, photon noise can seriously affect the modulated intensity. Therefore, we suggest that $\pm Q$ is the optimal choice for reference measurements in Scheme 2.

3.5. Effect of Photons Noise $N_p(t,\lambda )$

In this section, we still focus on Scheme 2 and Scheme 3 since the RPOS technique is not applicable to Scheme 1. We assume that the photon noise in each pixel is signal-dependent and follows a Gaussian distribution with the standard deviation being the square-root of the signal,

$${\sigma }_{N_p}^{o/e}(t,\lambda )=\sqrt{{\displaystyle \frac{1}{2}}[I(t,\lambda )\pm X(t,\lambda )]}$$

(9)

additionally, we set $D_k=0$, $g^{o/e}=1$, $s\left(t\right)=1$. We perform 400 trial attempts for both schemes and make a statistical analysis for the residual.

Firstly, it is found that the residuals of DM method are slightly smaller than those of the RPOS technique in both schemes. For example, in Scheme 3, the residual of the DM method is approximately 0.09±0.011, whereas that of the RPOS method is around 0.12±0.014 regardless of the specific polarized signal used for reference measurements. In Scheme 2, however, the issue becomes more complex as shown in the left panel of Figure 6: The residual of the DM method is about 0.14±0.02 (the blue dots), while the residual of the RPOS technique varies depending on the polarization signal used for reference measurements. Specifically, using $\pm Q$ for reference measurements (green dots) yields the smallest average demodulation residual for the three Stokes parameters ($Q/I$, $U/I$ and $V/I$ from top to bottom), which are approximately $0.22\pm 0.03$, $0.15\pm 0.02$ and $0.16\pm 0.02$ for $Q/I$, $U/I$ and $V/I$, respectively. While, using $\pm V$ for reference measurements (black dots) results in noticeable errors, especially in $V/I$, reaching up to $0.79\pm 0.09$.

In fact, the reason can be found from the modulation matrix of Scheme 2. The modulation matrix of the o beam can be written as

$$M_{Fasot}^o=\left[\begin{array}{cccc}1.000& 0.747& -0.665& 0.011\\ 1.000& -0.003& 0.119& -0.993\\ 1.000& 0.339& 0.925& -0.174\end{array}\right],$$

(10)

It is noted that the value of $M^o$[2,4] is nearly equal to -1, which means that, when the V signal is input for reference measurements, the intensity of the o beam at the second modulation step is almost 0 (see the black solid line in Figure 7). Similarly, as $M^e$ [3,3]=0.925, when $-U$ is input, the intensity at the third step becomes quite small (Note: the pink dashed line shows the case in the e beam with U input, they are equal). In both cases, photon noise can seriously affect the modulated intensity. Therefore, we suggest that $\pm Q$ is the optimal choice for reference measurements in Scheme 2.

4. Discussion and Conclusions

Compared to the traditional beam-exchange technique, [13] proposed the RPOS technique, which performs the beam exchange outside the observation time using a specific polarization signal for reference measurements. Inspired by this work, we firstly propose an alternative approach for reference measurements by successively inputting a pair of light with opposite polarization states into the polarimeter, instead of performing the beam exchange. This pair of input light, i.e., Q and $-Q$, or U and $-U$, or V and $-V$ signals, can be conveniently generated by a well-designed optical unit (e.g., an ICU) to ensure that only the polarization state, not the polarization degree (fraction), is changed in this process. In this context, we re-evaluate the applicability of four previously proposed formulas to other spatio-temporal modulation schemes in a two-beam setup, such as those in the THEMIS, FASOT, and Hinode polarimeter (the Schemes 1, 2 and 3). Our conclusions are as follows.

1.

If specific polarized light is utilized for reference measurements, and no changes in the polarization state are introduced before the polarimeter (modulator), the RPOS technique is not suitable for Scheme 1. In this case, we suggest using unpolarized light, e.g., light from a quiet region near the solar disk center. In contrast, the RPOS technique can be applied to Scheme 2 and Scheme 3, but only by performing the formula ${\mathcal{F}}_1$, other formulas are no longer valid. Furthermore, we find that the validity of ${\mathcal{F}}_1$ is independent of the polarization fraction of the input signal. This implies that unpolarized light is also applicable in these scenarios.

2.

If specific polarized light is utilized for reference measurements, but significant cross-talk between the polarization states may occur due to the instruments before the polarimeter (modulator). Given that the cross-talk is stable during both the scientific and reference measurements, the RPOS technique (with ${\mathcal{F}}_1$) can be appropriate for these three schemes. However, it introduces a zero-line offset in the continuum of retrieved Stokes profiles.

3.

A dual-beam setup offers the advantage of decreasing the effects of atmospheric seeing, while the RPOS technique further addresses issues related to detector gain variation and differences in throughput between two beams, particularly, compared with the DM method. However, when the effect of photon noise is considered, the performance of the RPOS technique is comparable to that of the DM method. Meanwhile, we note that for certain modulation schemes (e.g., Scheme 2), the selection of specific polarized signals used for reference measurements can influence the impact of photon noise.