Study on Optimization Method of Polarization Balance for Weak Starlight System

1. Introduction

In optical measurements, particularly for the acquisition and detection of weak targets, the stray light in the field of view and the light emanating from the target to be measured mix with each other and are difficult to separate, which has become the main bottleneck in accurately recognizing weak targets[1,2,3]. This problem is also particularly important in case of weak starlight simulation systems[4,5]. As an important device in the ground verification test of spacecraft attitude measurement, a weak starlight simulation system is a standard target source that can produce the dynamic output of a faint-star map. However, owing to the polarization effect of the optical engine in this system, the nonimaging polarized stray light inundates the entire field of view of the system. Such stray light shares the optical path with the output star map, deviating the energy center of each star point in the output star map from the theoretical value. Furthermore, it drowns some star points in the simulated star map, thereby reducing the reliability of the test. Therefore, suppressing the nonimaging stray polarized light for improving the simulation accuracy of the star point position has become critical.

To suppress the polarization effect of the optical engine, the optical engine can be reconstructed by splicing multiple polarization-splitting prisms, optimizing the structure of the polarization-splitting film in the optical engine, using 3M prisms as the polarizing element of the optical engine, and compensating polarization elements. However, these methods share a common problem[6,7,8] . When light is incident at a certain aperture angle on the optical engine, the amplitude and phase of the nonimaging polarized stray light and the simulated star map outgoing light change with the incident angle, resulting in the convergence of the polarization states of the simulated star point outgoing light and the nonimaging polarized stray light, which makes it difficult to separate these two lights[9,10] .

Considering the aforementioned factors, a method for optimizing the polarization balance of the optical engine is proposed in this study. Furthermore, a theoretical model of the incident light aperture angle and the outgoing light polarization state of an optical engine thin film is established, and a mechanism for optimizing the polarization balance of the optical engine thin film is developed. By expanding the aperture angle margin of the incident light of the optical engine, the polarization difference between the imaging polarized light and nonimaging polarized stray light can be ensured, which solves the degradation problem of the simulation accuracy of the star point position caused by the nonimaging polarized stray light. Thus, this study provides a method for the ground calibration and testing of high-end spacecraft.

2. Working Principle and Suppression Mechanism of Polarization Effect of Optical Engine

2.1. Working Principle

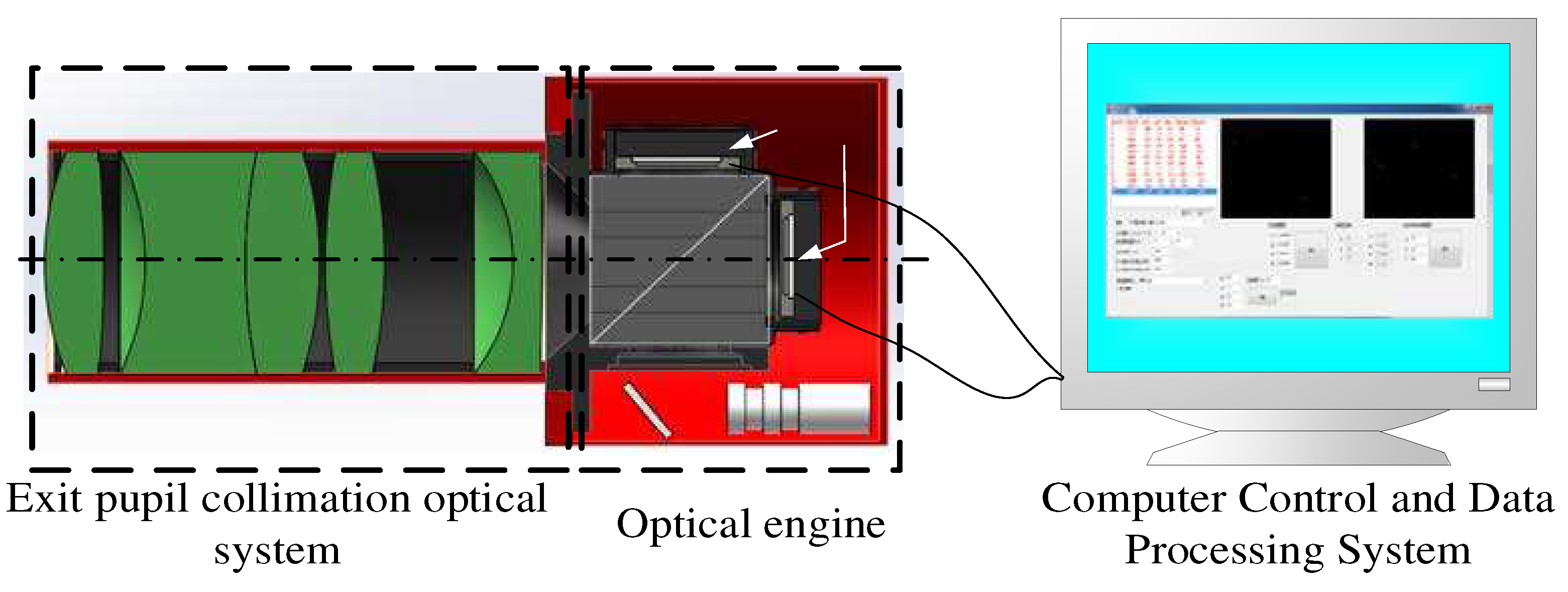
The weak starlight simulation system mainly comprises a computer control and processing system, an optical engine, and an exit pupil collimation optical system (Figure. 1). The working principle of the system is similar to that of a projector. The star map image displayed by the liquid crystal on silicon (LCOS) in the optical engine is projected through the collimating optical system to simulate the infinity characteristics of the star map[11,12]. Among them, the optical engine can be regarded as a polarizer with optical multiplexing function.

Figure 1. Composition diagram of weak starlight simulation system.

Figure 1. Composition diagram of weak starlight simulation system.

Under ideal conditions, there is no polarization effect in the system. The position of each star point in the simulated star map is determined by its gray energy center. The gray energy distribution of the star point can be expressed as follows[13,14,15]:

$$\mathrm{g}(x_i,y_i)=\frac{A}{2\pi {\sigma }^2}\exp \left[-\frac{{(x-x_i)}^2+{(y-y_i)}^2}{2{\sigma }^2}\right]$$

(1)

where A represents the gray energy coefficient, σ represents the gaussian radius, and (x_i,y_i) represents the energy center coordinates of the star point.

Under real conditions, there is polarization effect in the system. The grayscale distribution g₁(x_i,y_i) of the star point with the connotation of stray light can be expressed as follows:

$${\mathrm{g}}_1(x_i,y_i)=\frac{A}{2\pi {\sigma }^2}\exp \left[-\frac{{(x_i-\Delta x)}^2+{(y_i-\Delta y)}^2}{2{\sigma }^2}\right]-\Delta \mathrm{h}(x_i,y_i)$$

(2)

where Δh(x_i,y_i) represents the gray level corresponding to the nonimaging stray light, and ∆x and ∆y represent the offset of the simulated star point position along two axes caused by the stray light.

A comparison of Eqs. (1) and (2) shows that the position of the simulated star will deviate from the theoretical value owing to the introduction of polarization effect. Therefore, to improve the simulation accuracy of star position, it is essential to analyze the cause of the polarization effect and determine a mechanism to suppress it.

2.2. Causes of Polarization Effect of Optical Engine and Its Suppression Mechanism

The effect of the optical engine on the polarization state of the incident light can be quantitatively analyzed using the Jones matrix multiplication method. Because the film in the optical engine is the main factor affecting the polarization state of the incident light, deriving a mathematical model of the incident light aperture angle, the polarization parameters of the optical engine film, and the polarization state of the outgoing light is essential.

The Jones matrix of the optical engine film can be expressed as follows[16]:

$$J=\frac{1}{2}{e}^{i\Delta }\left[\begin{array}{cc}\sqrt{T_p}{e}^{-i\frac{D}{2}}+\sqrt{T_s}{e}^{i\frac{D}{2}}+\left[\sqrt{T_p}{e}^{-i\frac{D}{2}}-\sqrt{T_s}{e}^{i\frac{D}{2}}\right]\cos 2\phi & \left[\sqrt{T_p}{e}^{-i\frac{D}{2}}-\sqrt{T_s}{e}^{i\frac{D}{2}}\right]\sin 2\phi \\ \left[\sqrt{T_p}{e}^{-i\frac{D}{2}}-\sqrt{T_s}{e}^{i\frac{D}{2}}\right]\sin 2\phi & \sqrt{T_p}{e}^{-i\frac{D}{2}}+\sqrt{T_s}{e}^{i\frac{D}{2}}+\left[\sqrt{T_p}{e}^{-i\frac{D}{2}}-\sqrt{T_s}{e}^{i\frac{D}{2}}\right]\cos 2\phi \end{array}\right]$$

(3)

where φ represents the aperture angle of the incident light corresponding to the point on the axis of the collimating optical system. Tp and Ts represent the transmittance of P-polarized and S-polarized light in the transmitted light field. Δ = (δs + δp)/2 represents the average phase, and D = δs − δp represents the phase difference.

To determine the influence of the polarization effect of the optical engine film on the incident light, the vibration direction of the incident light is assumed to be along the x-axis. The polarization state of the outgoing light can then be expressed as follows:

$$\left[\begin{array}{c}{E}_x{e}^{i{\Delta }_x}\\ E_y{e}^{i{\Delta }_y}\end{array}\right]=T{e}^{i\Delta }\left[\begin{array}{c}\cos \frac{\mathrm{D}}{2}-i\sin \frac{\mathrm{D}}{2}\cos 2\phi \\ -i\sin \frac{\mathrm{D}}{2}\sin 2\phi \end{array}\right]$$

(4)

As can be seen from Eq. (4), for the transmitted light path of the optical engine, the polarization state of the outgoing light will deviate from the theoretical value under the joint action of φ, Ts, Tp, and D. Moreover, because φ is a system parameter and is never zero, the target values of Tp, Ts, and D should be determined to ensure that the polarization state of the outgoing light does not deviate from the theoretical value.

If only the phase difference is considered, then T = Ts = Tp; accordingly, Eq. (4) simplifies to

$$\left[\begin{array}{c}{E}_x{e}^{i{\Delta }_x}\\ E_y{e}^{i{\Delta }_y}\end{array}\right]=T{e}^{i\Delta }\left[\begin{array}{c}\cos \frac{\mathrm{D}}{2}-i\sin \frac{\mathrm{D}}{2}\cos 2\phi \\ -i\sin \frac{\mathrm{D}}{2}\sin 2\phi \end{array}\right]$$

(5)

Equation (5) shows that the transmittance T will not change the polarization state of the outgoing light. When D gradually approaches zero, the polarization state of the outgoing light approaches the polarization state of the incident light, which effectively inhibits the change in the polarization state caused by oblique incidence.

If only the influence of transmittance on the polarization state of the outgoing light is considered, then D = 0 and Eq. (4) simplifies to

$$\left[\begin{array}{c}{E}_x{e}^{i{\Delta }_x}\\ E_y{e}^{i{\Delta }_y}\end{array}\right]=(T_p+T_s)e^{i\Delta }\left[\begin{array}{c}1+\mathrm{R}\cos 2\phi \\ \mathrm{R}\sin 2\phi \end{array}\right]$$

(6)

where R = (Tp − Ts)/(Tp + Ts) represents the transmittance attenuation. The abovementioned formula indicates that when the difference Tp − Ts increases, the transmittance attenuation (Tp − Ts)/(Tp + Ts) increases and the polarization state of the outgoing light changes drastically. If Tp = Ts, the polarization state of the outgoing light approaches the polarization state of the incident light, inhibiting the changes in the polarization state caused by oblique incidence.

The aforementioned analysis shows that when the incident light has a certain aperture angle, the vibration state of the corresponding outgoing light is ellipsoidal after being deflected by the optical engine. Therefore, when the outgoing light passes through the polarizer, the vibration component parallel to the optical axis is no longer absorbed, resulting in stray light.

Therefore, to suppress the polarization effect of the optical engine and thereby inhibit the generation of stray light, the polarization parameters of the optical engine film should be D = 0 and R = 0 at the same time under ideal conditions.

3. Optimization Mechanism of Polarization Balance of Optical Engine

3.1. Derivation of Screening Conditions

To determine the relation between star position simulation accuracy and optical engine film parameters, a mathematical model of star position simulation accuracy and optical engine film polarization parameters was established by considering the extinction ratio as a link[17,18]. The relation between the extinction ratio k and the polarization parameters Rs and Ts of the optical engine film can be expressed as

$$k(\gamma ,\phi )=\frac{{\mathrm{R}}_s(\gamma ,\phi )T_s(\gamma ,\phi )+\epsilon T_s(\gamma ,\phi )}{\epsilon (T_p(\gamma ,\phi )+{\mathrm{R}}_s(\gamma ,\phi ))}$$

(7)

In Eq. (7), ε represents the extinction ratio of the polarizer in the optical engine, Ts and Rs represent the transmittance of S-polarized light and P-polarized light emitted from the optical engine, respectively. φ represents the aperture angle of the incident light, and γ represents the space angle of the incident light.

The star point simulated by the weak starlight simulation system is usually represented by the 3 × 3 pixel primitive on the LCOS. Because the energy ratio of the edge pixel exerts the greatest influence on the energy center of the simulated star point, the relation between the extinction ratio k and the stray light gray scale mi when all the stray light converges at the edge point is

$$m_i=\frac{255\mathrm{k}}{1-k}$$

(8)

Based on the centroid formula, the relation between the optical engine extinction ratio k and the target value θ of the star position simulation accuracy is

$$\theta =\arctan \left(\frac{\frac{255k}{1-k}{x}_{i+1}+255x_i-1.5\left(\frac{255k}{1-k}+255\right)}{f\text{'}\left(\frac{255k}{1-k}+255\right)}\right)$$

(9)

where xi + 1 represents the horizontal coordinate of the position of the edge point of the simulated star point, x_i represents the horizontal coordinate of the position of the simulated star point, and f' represents the focal length of the optical system. Similarly, the relationship between θ, the simulated star edge position ordinate y_{i + 1}, and the simulated star position ordinate yi can be calculated. The maximum value of k is considered as the screening condition of the optical engine film.

Under the influence of the polarization film of the optical engine, the polarization states of the incident light with different incident aperture angles and azimuth angles are different in each part of the pupil plane after exiting the optical engine. Therefore, the optimization can be accurately estimated by determining the polarization states of the sampling points (i, j) at different positions on the pupil plane.

Based on the calculation concept of the weighted evaluation function in the least squares algorithm, the polarization-balance evaluation function model of the films at different positions on the pupil plane is derived. The model is expressed as

$$MF={\left[\frac{y_d}{mn}{\displaystyle \sum _{i=1}^m{{\displaystyle \sum _{j=1}^n\left(\frac{D(i,j)-\tilde{D}(i,j)}{\Delta D(i,j)}\right)}}^2}+\frac{y_{\mathrm{r}}}{mn}{\displaystyle \sum _{i=1}^m{{\displaystyle \sum _{j=1}^n\left(\frac{R(i,j)-\tilde{R}(i,j)}{\Delta R(i,j)}\right)}}^2}\right]}^{1/2}$$

(10)

where D(i,j) and R(i,j) represent the current values of transmittance attenuation and phase delay, respectively, corresponding to the current pupil sampling point; ΔD(i,j) and ΔR(i,j) represent the tolerances for transmittance attenuation and phase delay; yd and yr, represent the weights of the transmittance attenuation and phase delay, respectively; m and n represent the number of sampling points in the x and y directions on the pupil, respectively; and $\tilde{D}(i,j)$ and $\tilde{R}(i,j)$ represent the optimization target of transmittance attenuation and phase delay, respectively.

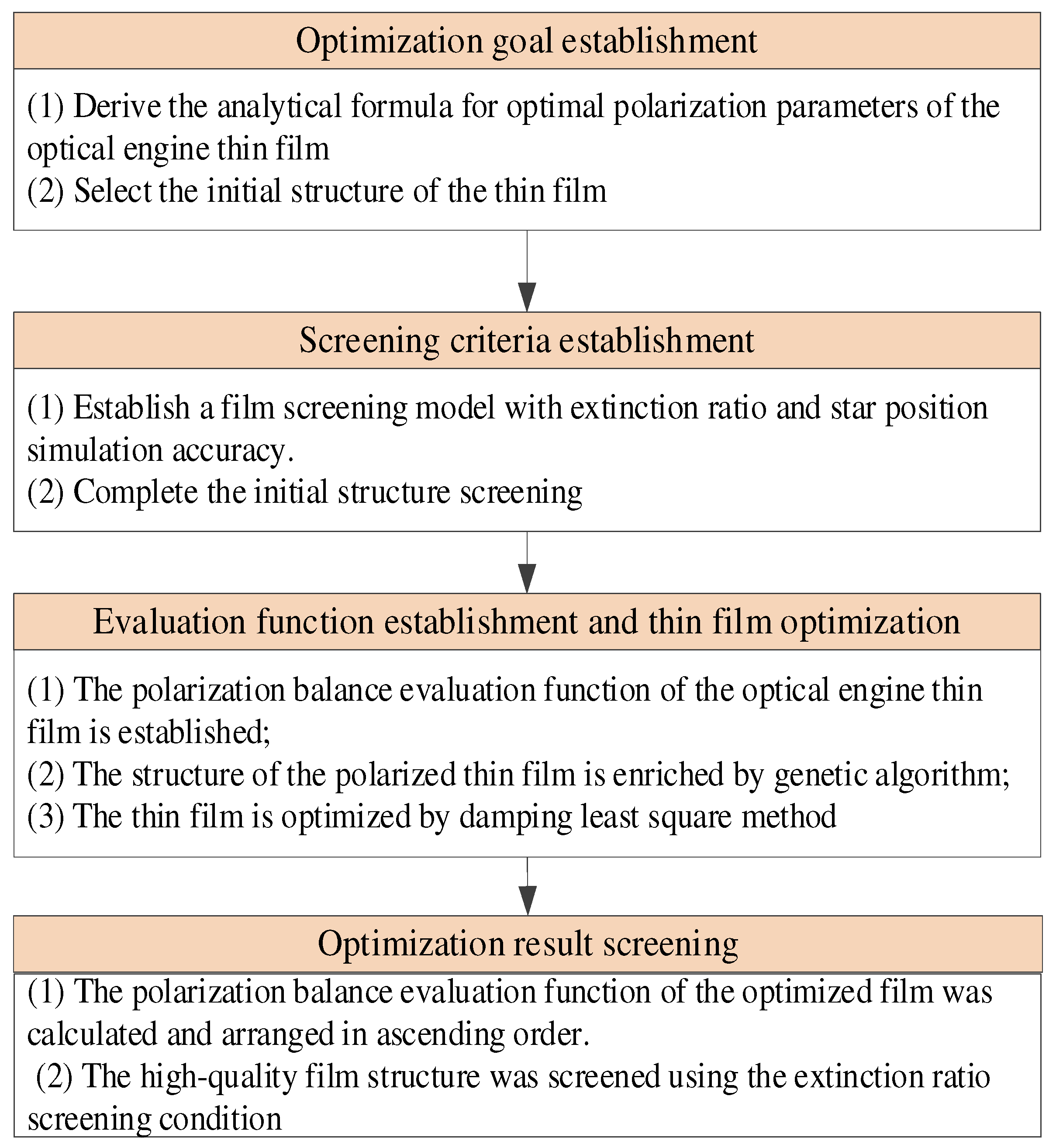
3.2. Optimization Process and Results

Figure 2 shows the polarization-balance optimization process of the optical engine thin film. Aiming at D = R = 0, the initial film expression selected is G|HLHLH|G, where G represents the substrate glass; H and L represent materials with high and low refractive indices, respectively. In particular, ZnS with a refractive index of 2.36 was selected as the material with a high refractive index (H), Ag with a refractive index of 0.055 was selected as the material with a low refractive index (L), the thickness was $\lambda /4$, and the central wavelength was set as 550 nm.

To increase the diversity of the films to be optimized, the film thickness was considered as the optimization variable in the optimization process and the number of films to be optimized was increased to 100 using crossover and mutation operations in the genetic algorithm. During the mutation operation, the film thickness assignment range was set to 3–5 times the minimum film layer thickness.

The composition of the optimized polarization-balanced film is shown in Table 1.

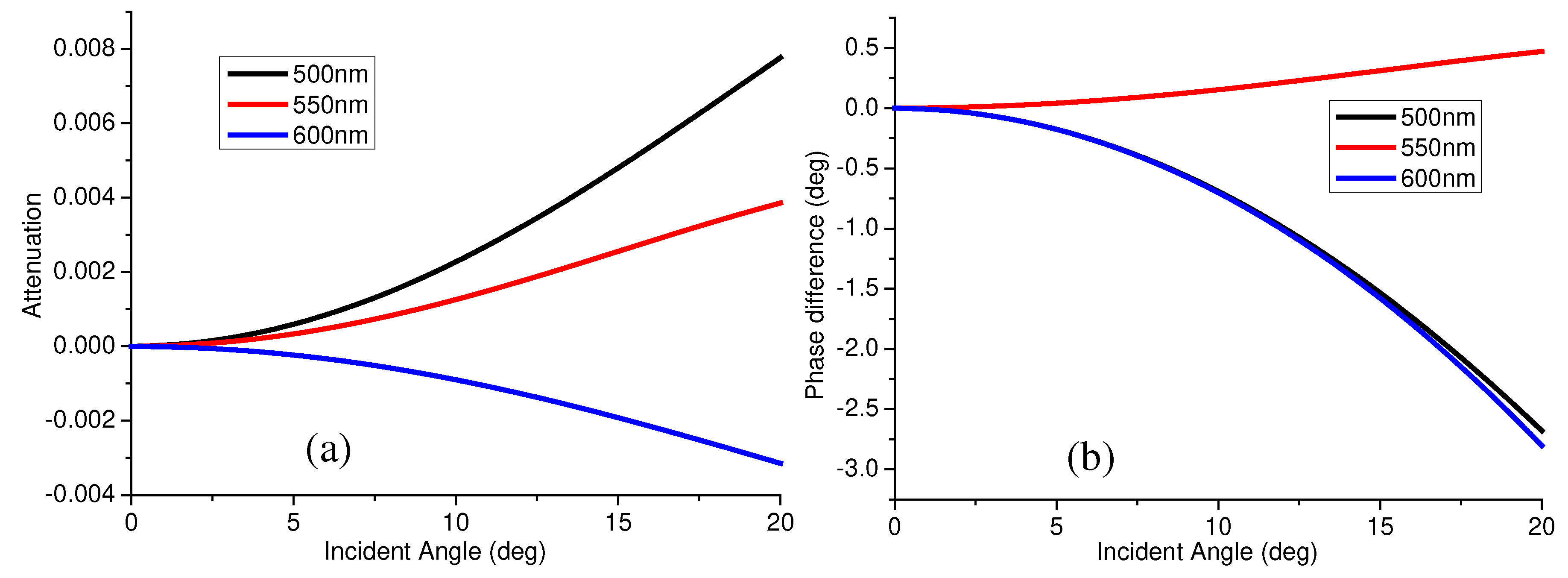
Figure 3 shows the polarization-balanced optical engine thin film binomial attenuation and phase delay curves. The figure shows that the binomial attenuation and phase delay exhibit a positive correlation with the aperture angle of the incident light. When the aperture angle of the incident light is <8°, the corresponding full-band binomial attenuation is <0.001 and the phase delay is <1°, which satisfies the optimization objective.

Because the optical engine film is plated on a 45° inclined plane, the extinction ratio corresponding to different incident light space angles is asymmetrical when considering the same incident light aperture angle. Therefore, analyzing the extinction ratio corresponding to different space angles and different aperture angles is essential.

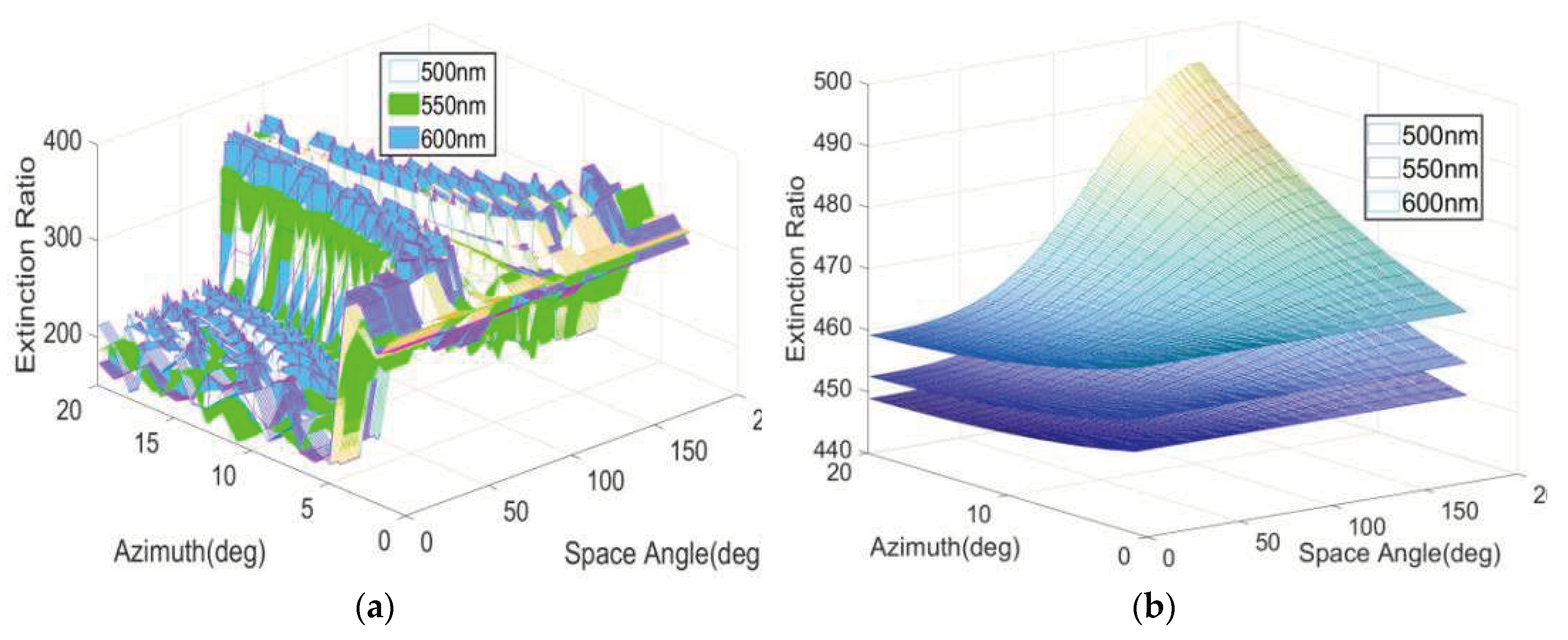
We set the aperture angle range of the incident light to be [0°–20°] and the space angle range to be [0°–180°] and subsequently calculated the optical engine extinction ratio distribution before and after the improvement. Figure 4 shows the calculation results. When considering the same incident light aperture angle, the extinction ratio is different for different space angles. When the aperture angle of the incident light is <8°, the minimum extinction ratio of the optical engine before the improvement is 149:1 and that of the polarization-balanced optical engine is 446 : 1. The stray light suppression ability of the polarization-balanced optical engine is improved nearly threefold.

4. Experiment

An experimental device was built for conducting the star position simulation accuracy test, as shown in Figure. 5(a). This device mainly comprises a weak star simulation system, theodolite, and six-dimensional adjustment table. The adopted exit pupil collimation optical system has a focal length f = 93.12 mm, an aperture D = 40 mm, and a single LCOS pixel size of 8 μm[19,20,21], as shown in Figure. 5(b).

As the star position in the center field of view is minimally affected by stray light and the corresponding extinction ratio is the optimal value, the extinction ratio corresponding to this position is selected as the critical screening condition. The boundary coordinates of the center field of view star point are (2.5, 2.5), the center position coordinates are (1.5, 1.5), and star position simulation accuracy target value θ=10". Substituting the aforementioned values into Eq. (9) shows that the screening conditions in the polarization-balance optimization mechanism of the optical engine thin film should satisfy k > 251:1.

Simultaneously, to ensure the optimization rate, m = n = 9, weight yd = yr = 1, the initial $\Delta D(i,j)$ and $\Delta R(i,j)$ are set to 2%. We then gradually reduce the tolerance until $\Delta D(i,j)<1\%$ and $\Delta R(i,j)<1°$ during the optimization process.

Because the glass material of the optical engine does not undergo changes before and after the improvement, the image quality is not affected; therefore, the same external collimating optical system of the exit pupil can be used for comparative experiments.

Figure 5. Star position simulation accuracy test experimental device and image plane real shot: (a) star position simulation accuracy test device (b) image plane real shot map.

Figure 5. Star position simulation accuracy test experimental device and image plane real shot: (a) star position simulation accuracy test device (b) image plane real shot map.

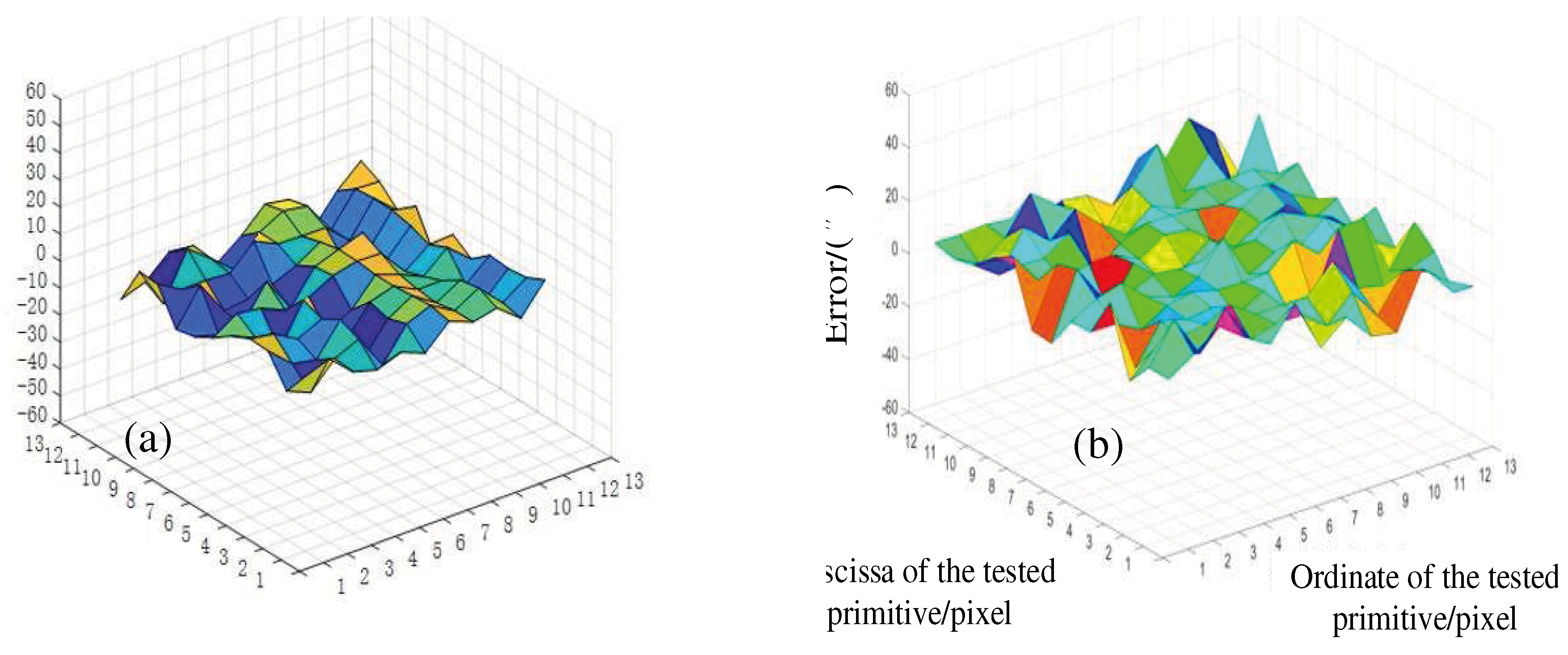
To generalize, the entire field of view is covered with a 13 × 13 grid version and the grid intersection points are used as simulation star points. The test results are shown in Figure 6(a) and (b). A comparison of the two Figures shows that when using the polarization-balanced optical engine, the simulation error of the star point position in the whole field of view is reduced by a factor of 1.64 from 15.99" to 9.76", which validates the proposed method.

5. Conclusions

To overcome the problem of the effect of nonimaging polarized stray light on the star position simulation accuracy in current weak starlight simulation systems, an optimization method involving the polarization balance of an optical engine thin film is proposed in this study. First, the results demonstrate that the polarization parameters of the optical engine thin film should satisfy D = 0 and R = 0 under ideal conditions, which is considered as the optimization objective. Next, the mathematical models of the optical engine extinction ratio, polarization parameters, and star position simulation accuracy are established. At the same time, extinction ratio k is used as the screening condition of optimization mechanism. Finally, the polarization-balance evaluation function of the optical engine is constructed using the pupil sampling point as the minimum evaluation unit. The simulation results reveal that when the aperture angle of the incident light is >8°, the corresponding full-band binomial attenuation is <0.001 and the phase delay is <1° ; and the stray light suppression is nearly threefold greater than those before the improvement of the optical engine film. The experimental results confirm that after the polarization-balance optimization of the optical engine, the simulation error of the star position in the full field of view decreases by a factor of 1.64 from 15.99" to 9.76", which validates our proposed method.