1. Introduction
Random numbers are widely used in a variety of application, including statistics, computer programming, videogames, numeric analysis, cryptography, among others [
1,
2,
3]. Random numbers can be obtained from random sequences produced by random number generators (RNGs) [
1]. The quality of an RNG is determined by its ability to produce sequences with good statistical properties, minimal predictability and uniform digit distribution [
4,
5,
6,
7].
The development of random number generation methods dates back to the 1940s, with contributions from Von Neumann, Metropolis, Ulam and Lehmer. They pioneered the Montecarlo simulation method [
8,
9,
10]; which was published by N. Metropolis and Stanislaw M. Ulam in 1949 [
9,
11]. The method estimates outcomes in unpredictable events across multiple fields, including sales forecasting, integral approximations, sampling experiments and artificial intelligence [
12,
13,
14,
15]. The Monte Carlo method is based on sequences of pseudorandom numbers, where a set of results is predicted in an estimated range of values, building a model with possible results [
12,
13,
14,
15]. However, unlike random numbers, pseudorandom numbers are deterministic, meaning their sequences eventually repeat [
6,
7]. Thus, pseudorandom numbers must meet specific statistical criteria to ensure unpredictability, e.g. the random appearance of the length and uniformly distributed bits [
6,
7]. Some applications of pseudorandom sequences include cryptography, financial models, communications, artificial intelligent, etc. [
6,
7,
16,
17].
Random Number Generators RNG and Pseudorandom Number Generator PRNG
Various types of random number and pseudorandom number generators (RNGs and PRNGs) have been designed. Examples of RNGs are the QRNG
Quantum Random Generator and the TRNG
True Random Generator [
18,
19,
20], which used physical variables, such as electronic noise from electronic circuits, biological signals and quantum processes (e.g. semiconductors) [
18,
19,
20]. The quality of the generators depends on the concordance between their output properties and those of a process of generating uniform and independent data [
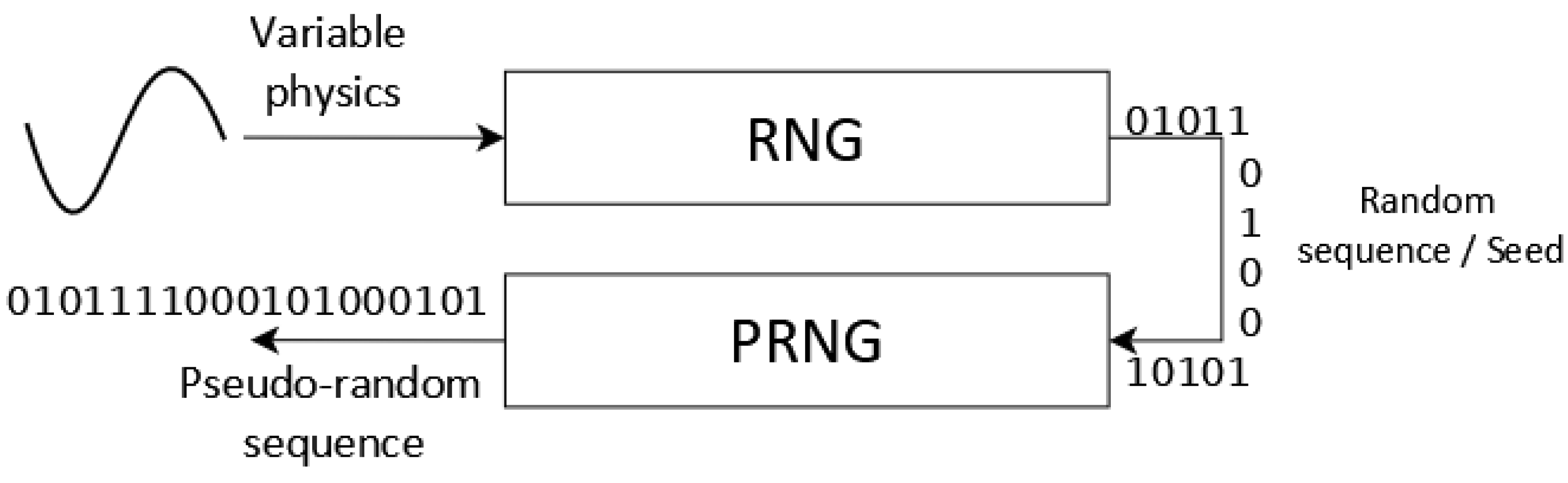
21]. The goal is to ensure that the random number sequences meet the necessary characteristics for various applications, such as generating initial data or seed data for a PRNG, as shown in
Figure 1. From the seed data, the PRNG is initialized to produce a new pseudorandom sequence [
4].
PRNGs use deterministic algorithms to generate sequences, ensuring uniformity and independence [
22]. A common method is the
Linear Congruential Generator (LCG) invented by D. H. Lehmer, defined by the recursive relation in equation (1) where each number is computed as a function of the previous number.
is defined as seed (
),
a is the constant multiplier (
),
is the active constant (
c > 0) and
m is the modulus (
). According to the recursive relation,
is the remainder when dividing
by the modulus [
22,
23,
24,
25,
26,
27].
Another widely used PRNG method is the
Linear Feedback Shift Register (LFSR), which employs storage registers that shifts bits in response to clock pulses, generating pseudorandom sequences. Each register cell stores a bit that is shifted one position to the right for each clock pulse [
28,
29,
30,
31,
32,
33]. This component is often used in generators for stream encryption, due the flexibility of hardware implementation. Additionally, the register’s statistical properties [
28,
29,
30,
31,
32,
33] allow it to be used for the design of news generators.
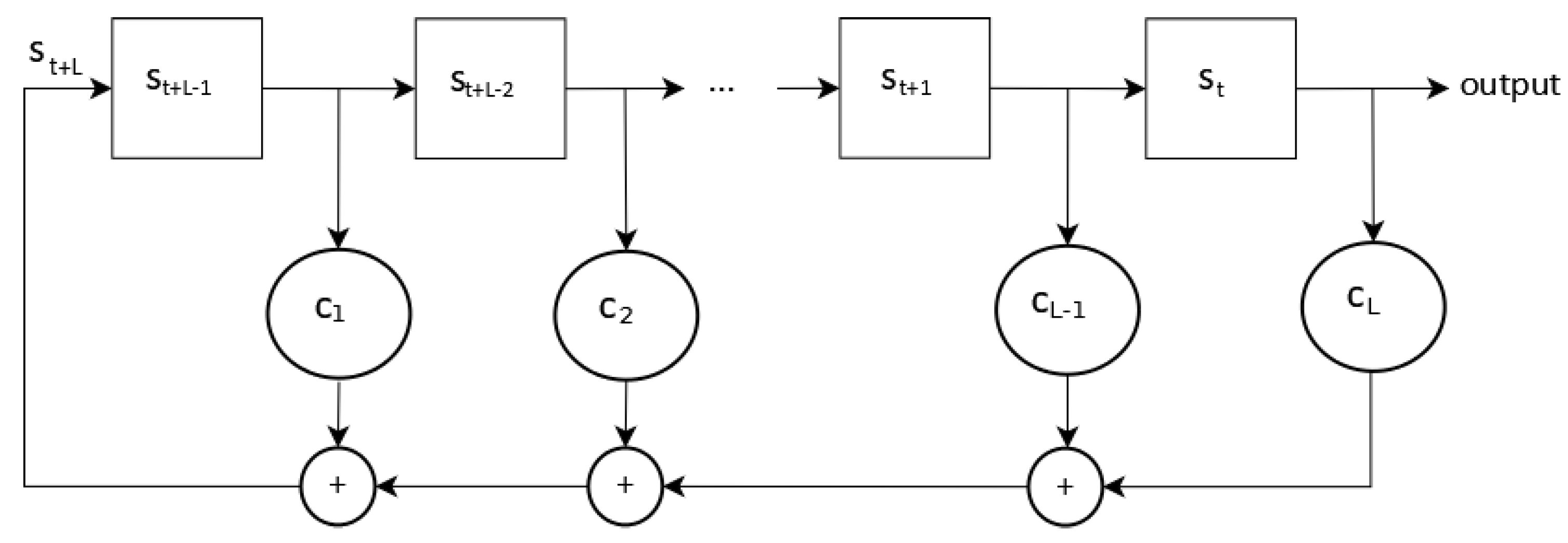
Every time a shift to the right occurs in the LFSR, a cell in the register becomes empty, allowing a new bit to be stored in the vacant position [
28,
29,
30,
31,
32,
33]. Feedback is a linear feedback function, as shown in equation (2). In an LFSR of length L over
, the system functions as a finite state automaton that generates a semi-infinte sequence of element of
, denoted
, which satisfies a linear recurrence relation of degree L over
[
28,
29,
30,
31,
32,
33]. The coefficients of L
are elements of
and are referred to as feedback coefficients of the LFSR;
Figure 2 illustrates, an LFSR representing this concept [
28].
All random and pseudorandom number generators must be validated through statistical tests to determine whether the sequences they produce exhibit randomness or pseudo-randomness. Examples include the Diehard tests and the NIST statistical tests [
34,
35,
36,
37], which consists of 15 tests proposed by the National Institute of Standard and Technology to evaluate the RNG or PRNG generator sequences. Some of the tests include: the Frequency (Monobit) test [
35,
38,
39], which ensures that the sequence contains approximately equal proportions of zeros and ones, with uniform a distribution [
35,
38]; The Frequency within a Block test, which examine the proportion of ones within M-bits bocks [
35,
38,
40]; the Runs test, which evaluates the total number of runs (uninterrupted by identical) in the entire sequence [
35,
38,
43]; the Binay Matrix Rank test, which checks the linear dependence between fixed length substrings of the original sequence [
34,
35,
38,
42]; the Maurer’s Universal Statistical test, which measures the number of bits between matching patterns to determine whether the sequence can be compressed without losing information [
35,
38,
43]; the Linear Complexity test, which assesses whether the sequence is complex enough to be consider random [
35,
38,
44,
45]; the Cumulative Sums (Cusums), which analyzes the maximum deviation from zero in a random walk defined by the cumulative sum, where sequence digits are adjusted to -1 and +1 [
35,
38,
46]; the Random Excursion test, which determine the number of K visit cycles in a cumulative random walk [
35,
38,
46] and the Random Excursion Variant test, which examines the total number of times a particular state is visited in a sequence [
35,
38,
46]. These statistical tests help validate the quality of RNG and PRNG sequences, ensuring their suitability for cryptographic, simulation, and other applications.
Each test in the suite evaluates pseudo-randomness independently. A sequence is considered satisfactory only if the
P-Value is greater than 0.01; otherwise, the sequence is deemed completely non-random or non-pseudorandom [
35,
38]. The
P-Value is derived from hypothesis testing, assessing whether the observed result is consistent with the assumption of randomness [
35,
38]. Each test follows a hypothesis testing framework: under the null hypothesis H0, the sequence is random, while under the alternative hypothesis Ha, the sequence is not random [
35,
38]. Two types of errors can occur during hypothesis tests: type I error, where H0 is rejected (concluding non-randomness) when the sequence is actually random [
35,
38], or type II error, where H0 is accepted (concluding randomness) when the sequence is actually non-random [
35,
38]. For a sequence to pass the test, it must be random enough to accept H0; if it is non-random, H0 is rejected in favor of Ha [
35,
38].
This work presents the design and implementation of a system incorporating PRNGs generators and neuro-generators on the
Virtex 7 xc7vx485t-ffg1761 reconfigurable FPGA (
Field Programmable Gate Array) device [
38,
47,
48,
49]. The system features four internal PRNG generators with good statistical properties and a uniform bit distribution, which meet the criteria to pass various NIST tests. The system allows for the generation of new pseudorandom sequences by selecting from all internal generators. In addition, a specific generator can be chosen to produce a previously validated sequence. Some of the tests confirming the pseudo-randomness of the generated sequences include the Frequency (Monobit) test, Frequency within a Block test, Linear Complexity test, Binary Matrix Rank test, among others. The results demonstrate that the generators system is suitable for various applications, such as biological systems, simulations, for testing electronic circuits, etc.
2. Design of a System of PRNG Generators and Neuro-Generators
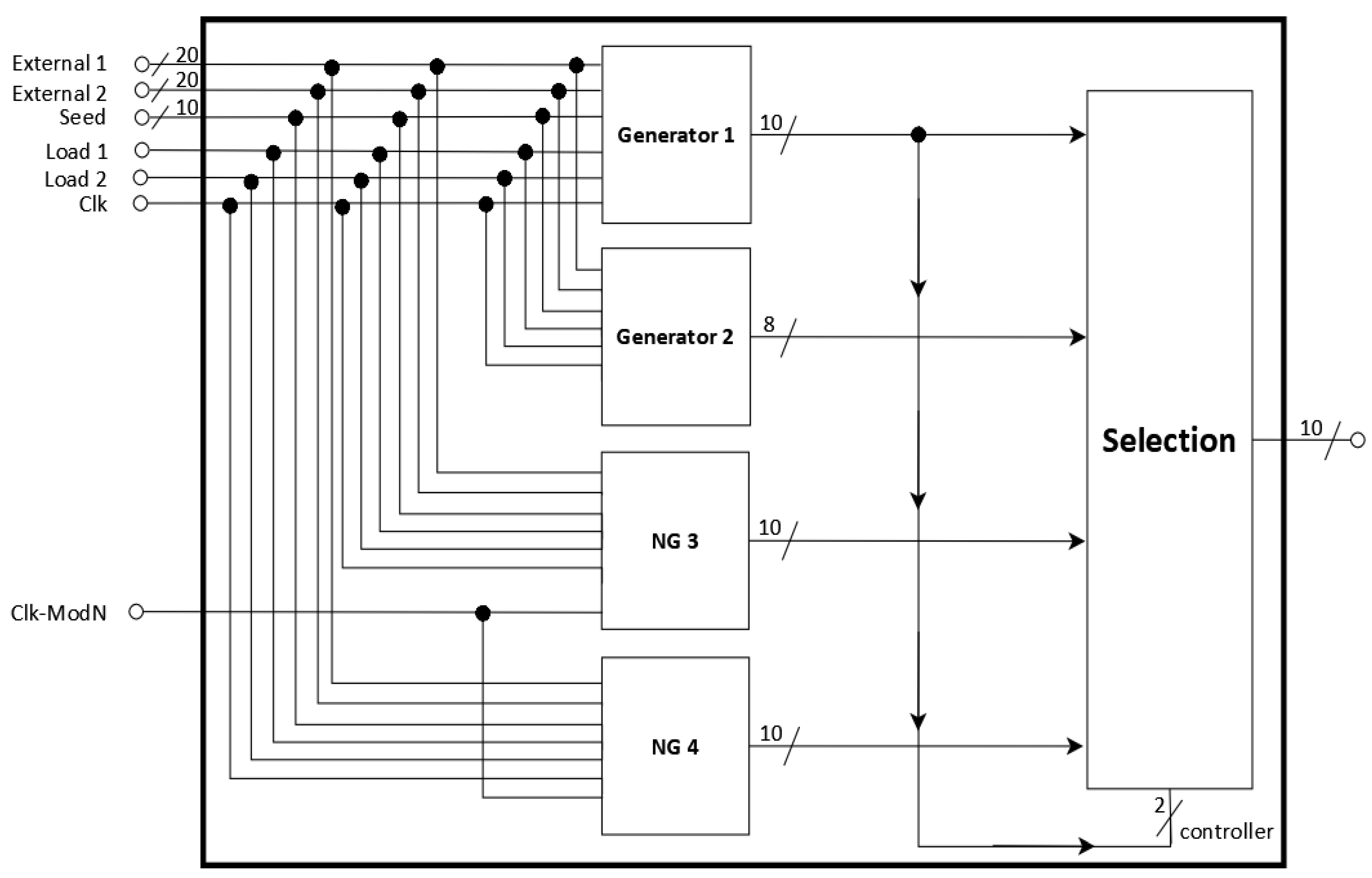
A system of pseudorandom number generators and neuro-generators was designed, as shown in
Figure 3. The proposed system consists of two PRNG generators (Generator 1 and Generator 2) and two neuro-generators (NG 1 and NG 2). Each of these was designed individually with specific conditions, to pass different NIST statistical tests with satisfactory pseudo-randomness results [
38,
47,
48,
49].
The system’s generators are connected to a selection device that determines, which set of bits is passed to the output. It features four input connections for initial data: External 1 and External 2 (each 20 bits) or Seed data (10 bits per generator). These inputs are loaded into the internal LFSRs of each generator, only when the Load signals are active. Additionally, the system includes an independent clock signal for the neuro-generator neuronal blocks, allowing their frequency to be adjusted without affecting the entire system. The sequences produced by each generator, along with different selection combinations, were validated by NIST statistical tests to confirm their pseudo-randomness.
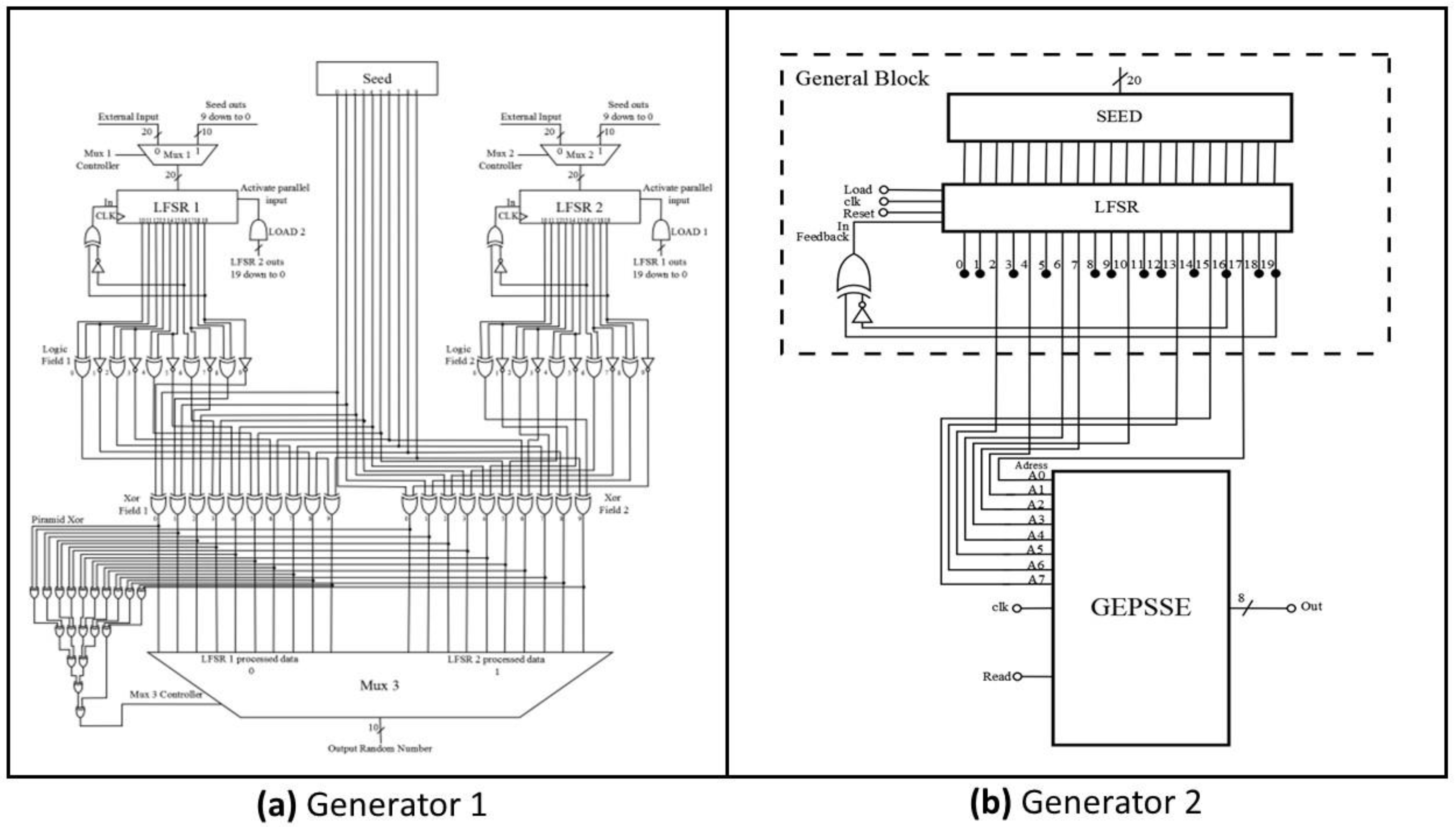
Generator 1, shown in
Figure 4 (
a) [
47], is a PRNG with a 10 bits output and two LFSR shift registers. These registers are loaded in parallel with either external data or seed data, depending on the
Load signals and the selection of the multiplexer, which is controlled by a controller [
47]. Once both LFSRs are loaded, each CLK signal pulse generate a 10-bit output, while simultaneously shifting a bit to the right, allowing a feedback bit to enter the register. This feedback is produced by an XOR gate, with one of its inputs negated, connected to bits 16 and 20 a configuration recommended by Xilinx to maximize the number of LFSR output sequences before repetition occurs. The outputs of LFSR1 and LFSR2 are further processed by two logic blocks, referred to as
Logic Field 1,
Logic Field 2,
Xor Field 1 and
Xor Field 2. The final output is determined by multiplexer
Mux 3, which directs the bit word to the generator output. The
Mux 3 Controller selects LFSR1 data when set to 0 and LFSR2 data when set to 1 [
47].
On the other hand, Generator 2, shown in
Figure 4b [
48], consists of a general block with an LFSR connected to a parallel register for seed data input. Similar to Generator 1, each CLK pulse shift the sequence one bit to the right, allowing the input of the feedback bit, while simultaneously producing the LFSR output sequence. In this design, outputs 2, 4, 6, 7, 10, 13, 15 and 17 are connected to an addressing bus, which enables random access to predefined words in the generator and produce the output sequence [
48].
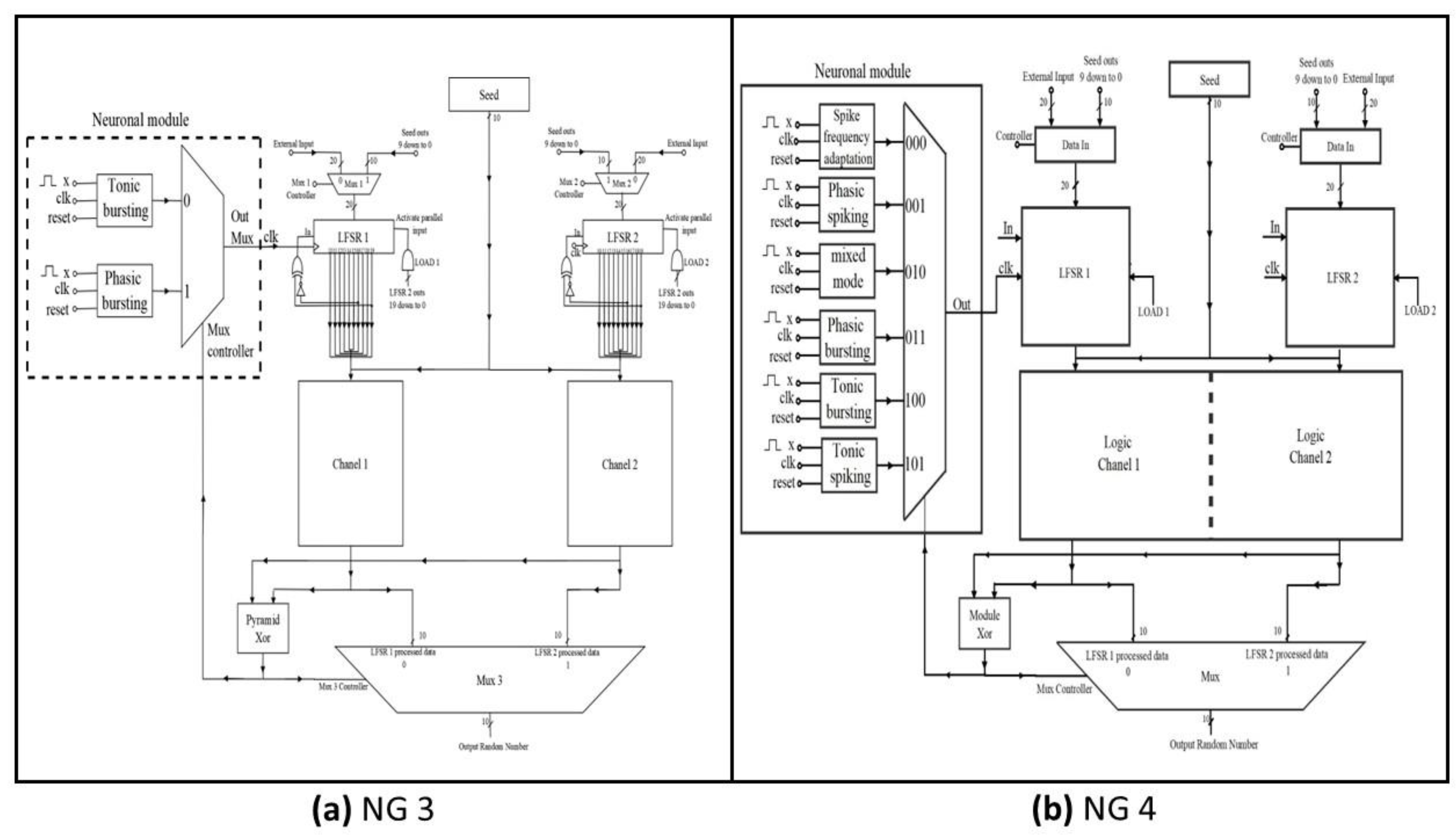
The NG 3 and NG 4 neuro-generators, shown in
Figure 5 [
38,
49], follow a similar topology to Generator 1, but incorporate a neuronal module connected to each neuro-generators. These modules generate a non-periodic clock signal that enters the CLK of the LFSR 1, causing the bits to shift and producing an output sequence whenever the CLK of the LFSR 1 receives a pulse from the neuronal module. Meanwhile, the LFSR 2 operates at a periodic frequency of 100 MHz [
38,
49].
The neuronal modules are designed with hardware impulse neurons operating at a 4 kHz clock signal, with the option to modify this frequency. Their behaviour is based on the Izhikevich biological neurons [
38,
49,
50,
51]. For neuro-generator NG 3, shown in
Figure 5a, the neuronal module exhibits phasic bursts, producing six impulses and tonic bursts, generating 16 impulses at the output. These impulses are triggered, only when the neuron is stimulated by an input impulse, without the need to remain in high state. On the other hand, the neuronal module of the neuro-generator NG 4, shown in
Figure 5b, consist of six impulse neurons with different behaviours: frequency adaptation, tonic impulse, mixed mode, phasic bursts, tonic bursts and phasic impulse. Each neuron produces a unique number of impulses per series, activated only upon stimulation [
38,
49,
50,
51]. In both neuro-generators, the output data from the LFSRs are processed by
Channel 1 and
Channel 2, which are then passed through a selection module to form the final output sequence. This sequence is subsequently validated by the NIST statistical tests.
3. Simulation and Implementation of the System Generators
The design of the generators and neuro-generators system was implemented using the VHDL hardware description language and developed in ISE 14.6, a software tool from the Xilinx AMD design platform [
52]. This software was used to simulate the system and test its operation. Additionally, it generated a txt text file containing the new output sequences, which were subsequently using NIST statistical tests. The system also provided occupation percentages, detailing the resource usage of each generator within the
Virtex 7 xc7vx485t-2ffg1761 reconfigurable FPGA device [
53].
3.1. Simulation Results
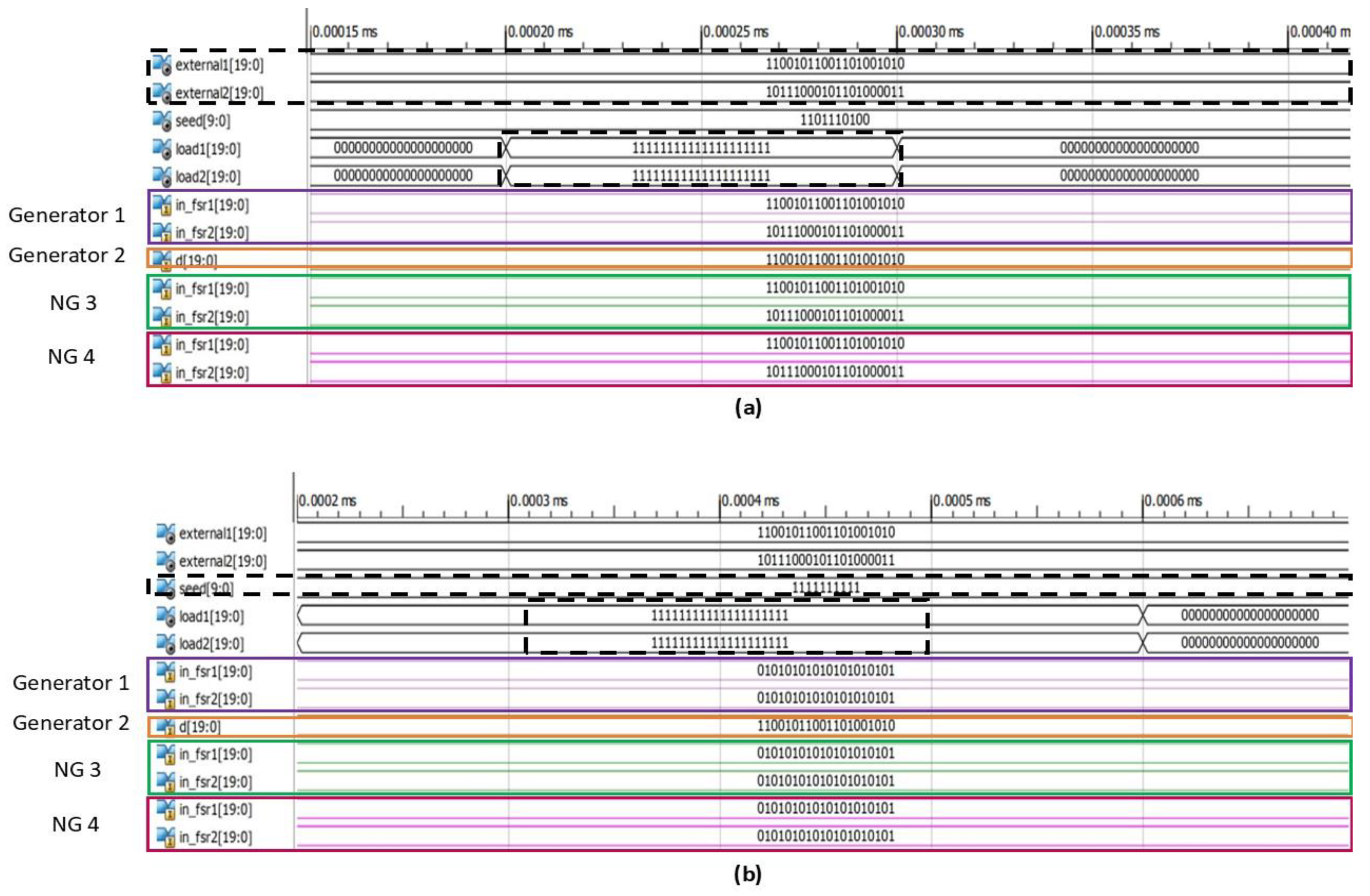
The simulation was performed at a frequency of 100 MHz for the entire system, including the neuronal modules of the neuro-generators. This is despite the fact that the clock frequency of the impulse neurons in hardware is 4 kHz. In
Figure 6a, the initial data (
external1 and
external2) are loaded into each of LFSR of the generators when the
Load signals are activated (set to 1). The loaded data is visible in the
in_lfsr signals, which are color coded, to indicate their respective generators. For Generator 2, represented by the brown
d signal, only a single shift register is used, and the
external1 data is loaded into it. A similar process occurs when the seed data is used instead of external data, as shown in
Figure 6b. However, in this case, the bits are distributed differently when loaded into the LFSR, due to the difference in the bit word length between each one.
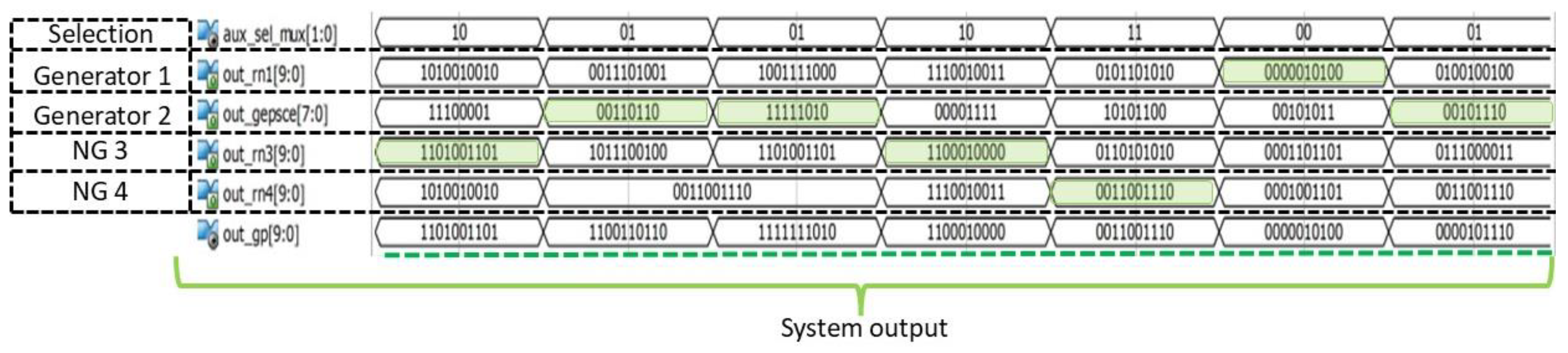
With the
Load signal disable, the data is processed by each of the generator stages to produce the system output sequences as shown in
Figure 7. The selector corresponding to the
aux_sel_mux signals, indicate the output data that form a new sequence. In this case, the corresponding bit word is marked in green, starting with 1101001101 of the neuro-generator NG 3 and ending with 00101110 of the Generator 2. In the latter, the output is eight bits, so in the ten bits word of the output system only the first eight bits change from right to left, keeping the last two bits of the previous word. As well as the generator sequences, this one is also validated by NIST statistical tests to demonstrate its pseudo-randomness in specific tests or the entire set.
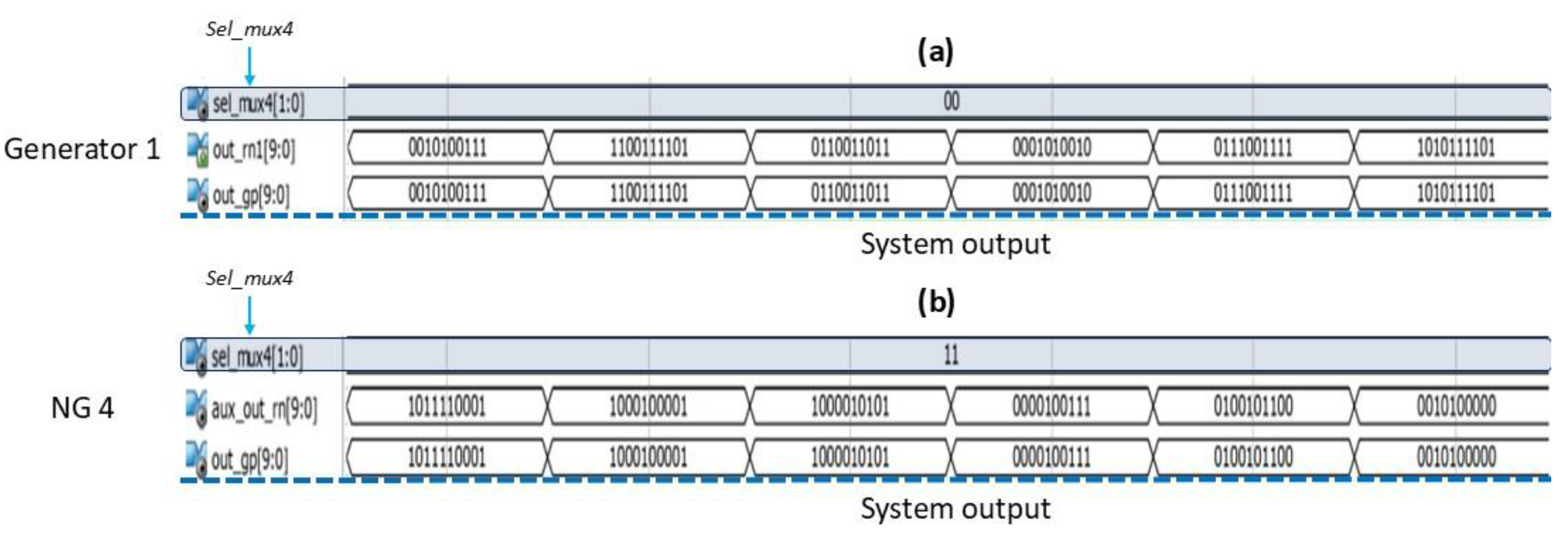
The design of this system has the flexibility to select the output of a single generator, to obtain the sequence already validated by NIST, as shown in
Figure 8. Where the
sel_mux4 signal in
Figure 8 (
a) shows only the output of Generator 1 with the combination 00 and in
Figure 8b of the neuro-generator NG 4 by having 11 in the selector. Therefore, the system is not limited to just the combination of the generators to produce new sequences, but it also has the option of obtaining the output of a specific generator immediately.
3.2. Occupancy Percentages of the System Generators and Neuro-Generators in the FPGA Virtex 7 xc7vx485T-2FFG1761
The resource occupancy percentages of the FPGA, for each of the system generators are shown in
Table 1, where all generators have a low percentage of resources used. Including the neuro-generators NG 3 and NG 4, which reach 20.04% and 31.70% of LUT-FF, as the number of highest resources. These results show that each of the generators can be implemented individually. However, in
Table 2 it can be observed that the system has the flexibility to be implemented in the same reconfigurable device as the generators and neuro-generators. This is due to the percentages that the design occupies in each of the resources, where none reaches 50% utilization, with 37.602% in LUT-FF, which is the number of Flip-Flops used by the system, being the resource with the highest percentage of occupation and the lowest the number of registers with 0.056%. In addition, it has 0.097% of RAM, which corresponds to the data storage block of Generator 2, 0.219% of LUTs
LookUp Table occupancy, 16.428% of IOBs inputs and outputs and 21.875% of BUFGs which are clock inputs and outputs.
4. Results and Discussion
The PRNG generators and neuro-generator of the system, were validated by NIST statistical tests to demonstrate that the sequences they produce are pseudorandom for a set or a specific test, as shown in
Table 3. In the case of Generator 1, the sequences produced by this design are considered pseudorandom for a set of ten statistical tests proposed by NIST. These are the Frequency (Monobit) test, Runs test, Binary Matrix Rank test, Non-overlapping Template Matching test, Maurer’s Universal Statistical test, Linear Complexity test, Approximate Entropy test, Cusums test, Random Excursion test and Random Excursion Variant test. Instead, Generator 2 is designed to meet the number of cycles required for the Random Excursion and the Random Excursion Variant tests, with satisfactory
P-Value values in some of the states that make up this test. The first neuro-generator NG 3 of the system, the sequence generated with the entire system at 100 MHz and then at 4 kHz is considered complex enough to be considered pseudorandom. The same occurs for the neuro-generator NG 4, which is also pseudorandom for the Frequency (Monobit) and Runs test.
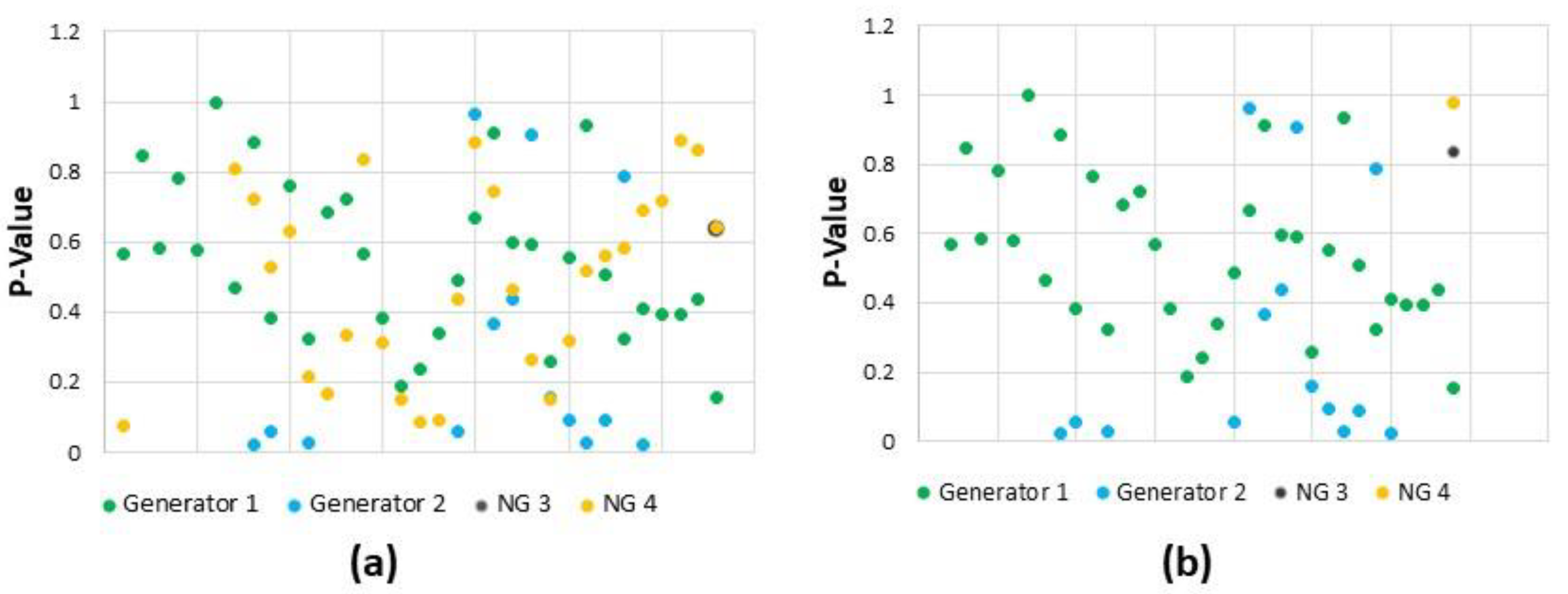
In the graph of
Figure 9, the distribution of the
P-Value of the validated output of each generator of the system can be observed, at a frequency of 100 MHz.
Figure 9a, shows the pseudo-randomness results, with the
external 1 and
external 2 data loaded to the LFSRs of the generators. Where it is observed that the majority of the
P-Value values are above 0.5, reaching values with a high level of pseudo-randomness, as in the case of Generator 1. The same occurs with the
P-Value data in
Figure 9 (b), where is observed that again Generator 1 maintain in some cases values of
P-Value=1.
Otherwise, when loading the seed data to the neuro-generators NG 3 and NG 4, the output sequence maintains its complexity and pseudo-randomness for the NIST Linear Complexity test. As shown in
Table 3 and
Figure 9. All the values of
P-Value can be consulted in [
38,
47,
48,
49], which corresponds to the scientific articles where the first results obtained from each generator were presented, with frequencies of 100 MHz and 4 kHz. With the aim of respecting the frequency of the neuronal module connected to the neuro-generator and with the initial seed and external data modified [
38,
47,
48,
49].
The first validation results of pseudo-randomness of the generators and neuro-generators system were with the entire system at a frequency of 4 kHz. Where, the external data and then the seed data were loaded. The results observed in
Table 4, show satisfactory conclusion for the Binary Matrix Rank test with
P-Value = 0.810078 and Linear Complexity test with
P-Value = 0.464674 when loading the external data. These same tests are approved when loading the seed data, but with a difference between the
P-Value values of 0.056173 for the first test and 0.191298 for the Linear Complexity test.
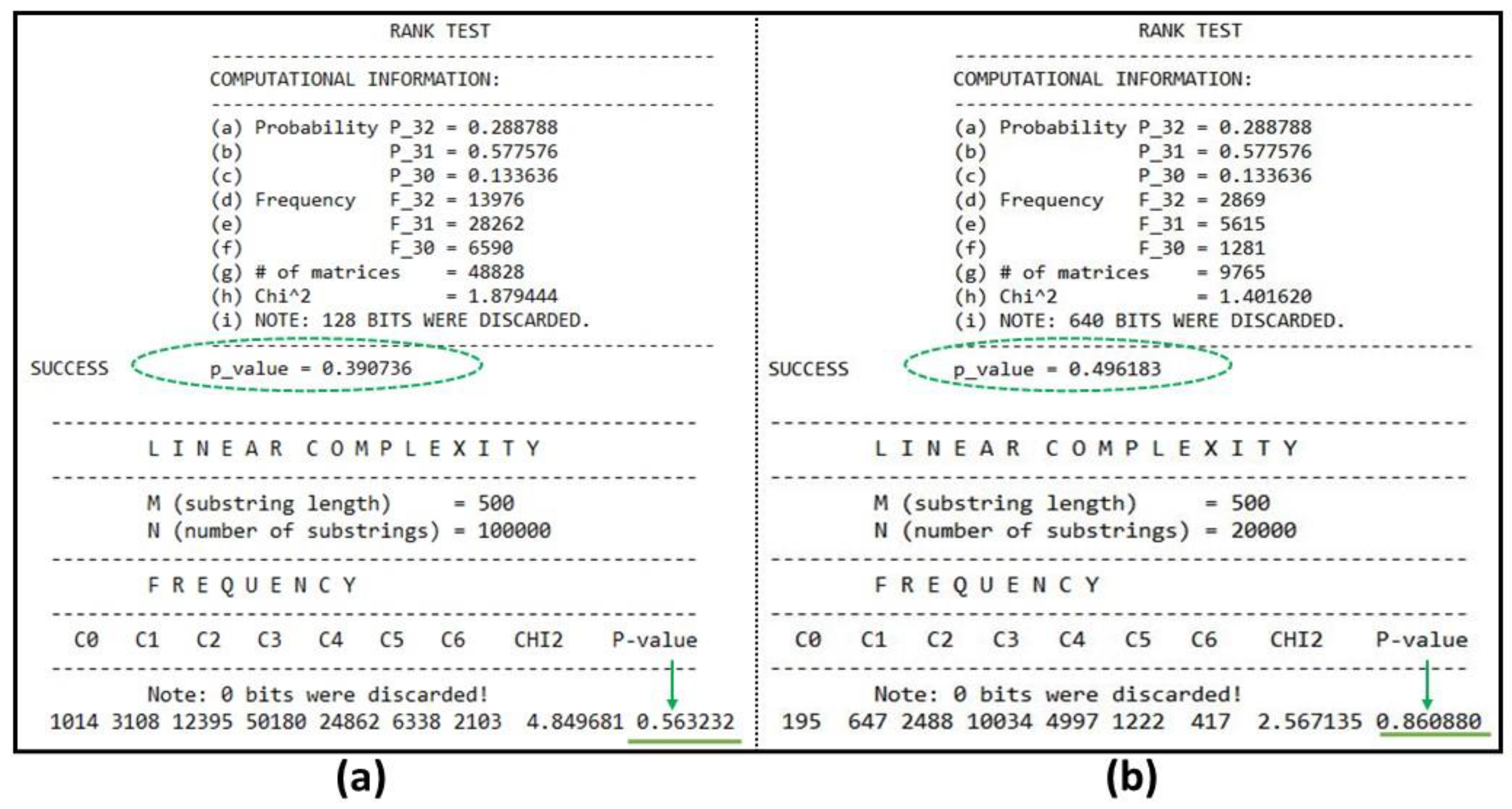
The results were also obtained with the system at a frequency of 100 MHz, including the neuronal module of each neuro-generator NG 3 and NG 4 and with the external data loaded to the LFSRs. Where the results were satisfactory for the Binary Matrix Rank test with
P-Value = 0.390736 and the Linear Complexity test with
P-Value = 0.563232, as observed in
Figure 10a. When the seed data was loaded, the results were greater than 0.01 for the same tests, but, with different levels of pseudo-randomness in
P-Value, as shown in
Figure 10b. This indicates that the system sequences maintain their complexity and pseudo-randomness without being influenced by the working frequency.
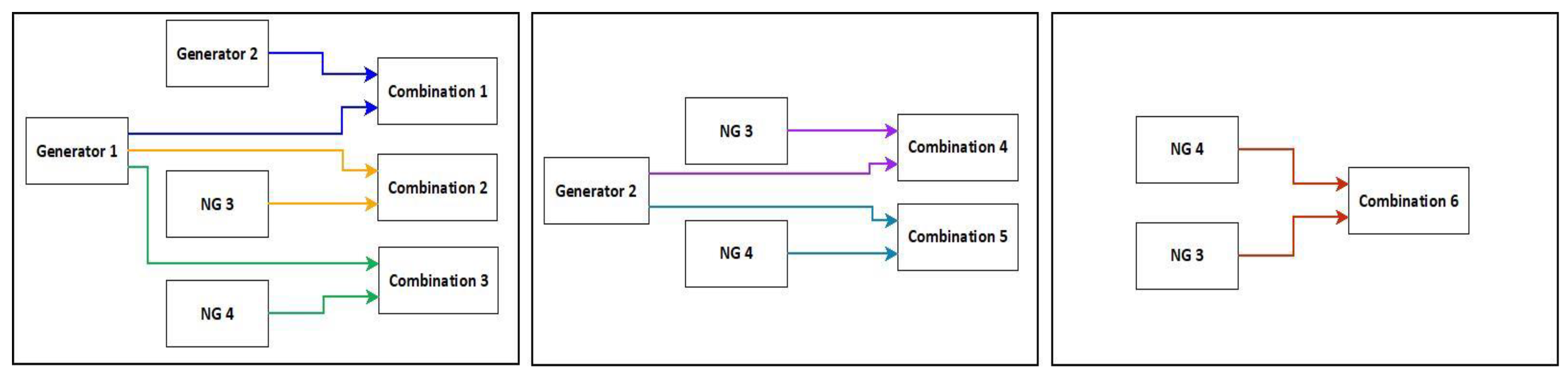
Keeping the system at 100 MHz, the combination between two different generators was made to obtain new pseudorandom sequences, which had good statistical properties to pass different NIST tests. These were performed following the combination shown in
Figure 11, where it begins with the selection of Generator 1 and Generator 2. Continuing with the same Generator, but now combined with neuro-generator NG 3 and NG 4. These with Generator 2 and the last combination with themselves.
For each case, the new output sequences of the system were validated by NIST statistical tests. The
P-Value results were satisfactory for the Binary Matrix Rank test and Linear Complexity test as seen in
Table 5. Which shows variation in the
P-Value value, without affecting the pseudorandomness of the sequence. However, when selecting only the neuro-generators NG 3 and NG 4, the sequence is pseudorandom for all states of the Random Excursions and Random Excursion Variant tests, as shown in
Table 6. Therefore, all sequences produced by the system when taking the bits from two generators, are complex and pseudorandom.
Considering the
P-Value results obtained in each situation in which the generators and neuro-generators system was put, it is demonstrated that the sequences with an adequate bit distribution are generated. In addition to being complex enough to pass different statistical tests proposed by NIST, such as the Frequency (Monobit) test, Runs test, Binary Matrix Rank test, Non-overlapping Template Matching test, Maurer´s Universal Statistical test, Linear Complexity test, Approximate Entropy test, Cumulative Sum (Cusums) test, Random Excursion test, Random Excursion Variant test and including the Frequency within a Block test and the Longest-Run-of-Ones in a Block test. These are added to the test approved by the generator and neuro-generator system, as shown in
Table 7 marked with X, with 12 tests approved out of 15 proposed by NIST. Even when combining the bits from two different generators as demonstrated by the results in
Table 5 and
Table 6, where different levels of pseudo-randomness were observed for the sequence obtained from each combination.
5. Conclusions
The system of generators and neuro-generators can produce sequences with adequate bit distribution and statistical properties at a frequency of 100 MHz and 4 kHz, respectively. As observed in the results section, the P-Value showed variation only in the levels of pseudo-randomness, due to the condition that each internal generator must pass tests independently or in specific sets. For the neuro-generators, the neuronal module operates at a 4 kHz, but it can be adjusted to operate at a frequency of 100 MHz without affecting the complexity and bit distribution of the output sequence. The same results are observed with Generators 1 and 2, which were designed to pass a specific set of tests, regardless of whether the working frequency matches that of the neuro-generators or whether the initial data were the external or seed data.
It was also demonstrated that the combination of two generators can produce pseudorandom sequences that pass the Binary Matrix Rank test, Linear Complexity test, and all the states of the Random Excursion and Random Excursion Variant tests. Therefore, the system of generators and neuro-generators is capable of generating sufficiently complex sequences, with adequate bit distribution, to pass 80% of the 15 NIST statistical tests proposed. This design offers flexibility, allowing for the selection of a specific generator to obtain a validated output sequence and the ability to adapt to different frequencies without affecting the pseudo-randomness of the sequences. This makes the system suitable for use for a wide range of different applications, including biological systems, mathematical systems simulation, electronic circuit testing, and even as initial data for other generators. In addition, it can be implemented in reconfigurable FPGA devices, such as the Virtex 7 xc7vx485T-2ffg1761.
Author Contributions
Conceptualization, J.J.R.P. and M.d.L.R.B.; methodology, J.J.R.P., and S.O.C.; software, E.C.B.A. and J.J.R.P.; validation, M.d.L.R.B. and J.J.R.P.; formal analysis, J.J.R.P. ; investigation, M.d.L.R.B., J.J.R.P., J.L.G.V.; resources, S.O.C., J.J.R.P.; data curation, J.J.R.P.; writing—original draft preparation, M.d.L.R.B. and J.J.R.P.; writing—review and editing, S.O.C., J.J.R.P. and M.d.L.R.B.; visualization, E.C.B.A.; supervision, J.J.R.P. and; project administration, J.J.R.P.; funding acquisition, S.O.C. All authors have read and agreed to the published version of the manuscript.
Funding
“This research received no external funding.
Data Availability Statement
The data presented in this study are available in this article.
Acknowledgments
The present work has been supported by the National Council of Humanities, Science and Technology (SECIHITI, Secretaría de Ciencia, Humanidades, Tecnología e Innovación), the University of Guadalajara and CINVESTAV Guadalajara for their support.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| PRNG |
Pseudorandom Number Generator |
| NIST |
National Institute of Standards and Technology |
| FPGA |
Field Programmable Gate Array |
| RNG |
Random Number Generator |
| QRNG |
Quantum Random Number Generator |
| TRNG |
True Random Number Generator |
| LCG |
Linear Congruential Generator |
| LFSR |
Linear Feedback Shift Register |
| JCR |
Journal Citation Report |
| NG |
Neuro-generator |
| VHDL |
Very High-Speed Integrated Circuits |
| MHz |
Mega Hertz |
| kHz |
Kilo Hertz |
References
- Malva, A.; Schwer, I.; Cámara, V.; Fumero, Y. Matemática Discreta, 1st ed.; Ediciones UNL, Secretaría de Extensión: Universidad Nacional del Litoral, Santa Fe, Argentina, 2005; pp. 214–217. ISBN: 987508431X.
- Steven, S. S. The Algorithm Design Manual, 2nd ed.; Springer London: Paises bajos, 2008; pp. 415-417. ISBN: 9781848000704, 1848000707.
- Liu, L.; Yang, J.; Wu, M.; Liu, J.; Huang, W.; Li, Y.; Xu, B. A Post-Processing Method for Quantum Random Number Generator Based on Zero-Phase Component Analysis Whitening. Entropy 2025, 27, 68. [CrossRef]
- Singh, M.; Singh, P.; Kumar, P. An Empirical Study of Non-Cryptographically Secure Pseudorandom Number Generators. 2020 International Conference on Computer Science, Engineering and Applications (ICCSEA), Gunupur, India, 2020. [CrossRef]
- Lee, J.; Seo, Y.; Heo, J. Analysis of random number generated by quantum noise source and software entropy source. 2018 International Conference on Information and Communication Technology Convergence (ICTC), Jeju, Korea (South), 2018. [CrossRef]
- Murillo-Escobar, D.; Murillo-Escobar, M. A.; Cruz Hernandez, C.; et al. Pseudorandom number generator base on novel 2D Hénon-Sine hyperchaotic map with microcontroller. Dyn no lineal 2022, Vol. 111, 6773-6789. [CrossRef]
- IDQ. Random numbers generation using quantum physics, white paper may 2020. Available online: https://marketing.idquantique.com. (accessed on: February 02, 2025).
- Mancilla Herrera, A. M. Números aleatorios. Historia, teoría y aplicaciones. Ingeniería y Desarrollo 2000, vol. 8. ISSN: 0122-3461.
- González de la Fuente, M. Generación de Números Aleatorios Físicos en Dispositivos Electrónicos. B.S, Universidad de Valladolid, September 2016.
- Patil, G. P.; Kotz, S.; Ord, J. K. A Modern Course on Statistical Distributions in Scientific Work. Springer Dordrecht: Calgary, Canada, 1974. [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo Method. Journal of the Americal Statistical Association 44:247, 335-341. [CrossRef]
- Otamendi, J. Las etapas en la gestación del Método de Montecarlo. In Historia de la Probabilidad y la Estadística (II). García Tomé, F. M., Eds.; Delta, Las rozas, Madrid, Spain, 2000; 1st ed., pp. 117-120. ISBN: 9788496477254, 8496477258.
- Askar, T.; Shukirgaliyev, B.; Lukac, M.; Abdikamalov, E. Evaluation of Pseudo-Random Number Generation on GPU Cards. Computation 2021, 9, 142. [CrossRef]
- IBM. ¿Qué es la simulación de Monte Carlo? Available online: https://www.ibm.com/mx-es/topics/monte-carlo-simulation (accessed on 13 february 2025.
- aws. ¿En qué consiste la simulación de Monte Carlo? Available online: https://aws.amazon.com/es/what-is/monte-carlo-simulation/ accessed on 13 february 2025.
- Garzon Gonzalez, J. A.; Rangel, M.; Muñoz, P. FPGA Implementation of a Multi-PRNG Base on a Multiscroll Chaotic Hopfield Neural Network. IEEE Transactions on Industrial Informatics. 2025, 1-10. [CrossRef]
- Caran, R. I. Comparative Analysis Between Counter Mode Deterministic Random Bit Generators and Chaos-Based Pseudo-Random Number Generators. 2024 International Conference on Development and Application Systems (DAS), Suceava, Romania, 2024. [CrossRef]
- Su, G. et al; A Method for Generating True Random Numbers With Multiple Distribution Characteristics. IEEE Access 2023, 11, 81753 – 81762. [CrossRef]
- Matuszewski, Ł.; Jessa, M.; Nikonowicz, J. Ring Oscillators with Additional Phase Detectors as a Random Source in a Random Number Generator. Entropy 2025, 27, 15. [CrossRef]
- Fei, C.; Zhang, X.; Wang, D.; Hu, H.; Huang, R.; Wang, Z. EPRNG: Effective Pseudo-Random Number Generator on the Internet of Vehicles Using Deep Convolution Generative Adversarial Network. Information 2025, 16, 21. [CrossRef]
- Gentle, J. E.; Random Number Generation and Monte Carlo Methods, 2nd ed.; Springer: USA, 1998. ISBN: 0-387-00178-6.
- García Gómez, J. A.; Martínez de la Cruz, A.; Jauregui Wade, L.; Valles Rivera, D.; Sánchez Vasconcelos, G. Importancia del uso de los generadores de números pseudoaleatorios en los contenidos de la asignatura de simulación del programa académico de ingeniería en sistemas computacionales, del Instituto Tecnológico de Villahermosa. Innovaciín y Desarrollo Tecnológico Revista Digital 2024, 16, 1358-1362. ISSN: 2007-4786.
- Kumar Panda, A.; Chandra, R. A Coupled Variable Input LCG Method and its VLSI Architecture for Pseudorandom Bit Generation. IEEE Transactions on Instrumentation and Measurement 2020, 69, 1011-1019. [CrossRef]
- Tezuka, S. Linear Congruential Generator. In Uniform Random Numbers. 1st ed.; Springer New York: New York, USA, 1995, pp. 57-82. ISBN: 978-0-7923-9572-0.
- Sujitha, A.; Lakshmi, L.; Mathan, N.; Narmadha, R. Analysis of an Efficient Linear Congruential Generator Architecture for Digital Applications. 2023 Fifth International Conference on Electrical, Computer and Communication Technologies (ICECCT), Erode, India, 2023. [CrossRef]
- Zulfikar, S.; Hubbul, W. Design and Implementations of Linear Congruential Generator into FPGA. International Journal of Electronics Communication and Computer Engineering, 2014, 5, 809-813. ISSN (online): 2249-071X.
- Pisharath, J. Linear Congruential Number Generators. Newer Math, Fall, 2023. Online Available: https://ow3.math.rutgers.edu/~greenfie/currentcourses/sem090/pdfstuff/jp.pdf.
- Van Tilborg, H. Encyclopedia of Cryptography and Security. Springer: New York, USA, 2005; p. 350. ISBN: 0-387-23483-7.
- Massey, J. L. Shift-Register Synthesis and BCH Decoding. IEEE Trans. Inf. Theory 1969, 15, 122-127. [CrossRef]
- Krishna, C. V.; Jas, A.; Touba, N. A. Test vector encoding using partial LFSR reseeding. In Proceeding International Test Conference 2021 (Cat. No01CH37260), Baltimore, MD, USA, 2001. [CrossRef]
- Grymel, M. New Programmable LFSR Counters with Automatic Encoding and State Extension. Electronics 2024, 13, 405. [CrossRef]
- Roshni, O.; Merin K, G.; Sharon, J. Study and Analysis of Various LFSR Architectures. In 2018 International Conference on Circuits and Systems in Digital Enterprise Technology (ICCSDET), Kottayam, India, 2018. [CrossRef]
- Wang, L. T. VLSI Test Principles and Architectures Design for Testability; Elsevier: San Francisco, CA, USA, 2006; pp. 272-275. ISBN: 9780080474793, 0080474799.
- Brown, R. G. Dieharder: A Random Number Test Suite. Version 3.31.1. Available online: https://webhome.phy.duke.edu/~rgb/General/dieharder.php (accessed on 11 February 2025).
- NIST Technical Series Publications, Available online: https://nvlpubs.nist.gov/nistpubs/legacy/sp/nistspecialpublication800-22r1a.pdf (accessed on 11 February 2025).
- Marek, T. Improvements to the Randomness Testing Toolkit. Bachelor’s Thesis, Masaryk University, Chequia, 2023.
- Lee, C. Y.; Bharathi, K.; Lansfor, J.; Khatri, S. P. NIST-Lite: Randomness Testing of RNGs on an Energy-Constrained Platform. In 2021 IEEE 39th International Conference on Computer Design (ICCD), Storrs, CT, USA, 2021. [CrossRef]
- Rivas Becerra, M.d.L.; Panduro, J.J.R.; Ortega Cisneros, S.; Becerra Álvarez, E.C.; Ríos Arrañaga, J.D. Diseño de un Nuevo Neurogenerador con un Módulo Neuronal para producir Secuencias Pseudoaleatorias y Perfectamente Pseudoaleatorias. Electrónica 2024, 13, 1955. [CrossRef]
- Chung, K. L. Elementary Probability Theory with Stochastic Processes, 2nd ed.; Gehring, F. W., Eds.; Springer-Verlag New York: Heidelberg, Berling, 1974. ISBN: 978-1-4757-5114-7.
- Maclaren, N. Cryptographic Pseudo-Random Numbers in Simulation. Cambridge Security Workshop on Fast Software Encryption; R. Anderson: Cambridge, UK, 1993; pp. 185-190.
- Dickinson Gibbons, J.; Chakraborti, S. Nonparametric Statistical Inference, 6th ed.; CRC Press Taylor & Francis Group: USA, 2021. ISBN: 9781315110479.
- Marsaglia, G.; Tsay, L. H. Matrices and the Structure of Random Number Sequence. Linear Algebra and Its Applications 1985, 67, 147-156.
- Maurer, U.M. A universal statistical test for random bit generators. J. Cryptology 1992, 5, 89-105. [CrossRef]
- Van Tilborg, H. Encyclopedia of Cryptography and Security. Springer: New York, USA, 2005; pp. 355-357. ISBN: 0-387-23483-7.
- Massey, J. L. Shift-Register Synthesis and BCH Decoding. IEEE Trans Inf. Theory 1969, 15, 122-127. [CrossRef]
- Spitzer, F. Principles of Random Walk, 2nd ed. Springer-Verlag: New York, USA, 2001. ISBN 0-387-95154-7.
- Panduro, J.J.R.; Alvarez, E.C.B.; Becerra, M.D.L.R.; Avila, C.A.O.; Valdovinos, M.L.B.; Ortega-Cisneros, S. Design and Implementation in FPGA a Random Number Generator of 10 bits validated by NIST Maurer’s “Universal Statistical” and Binary Matrix Rank tests. In Proceedings of the 2022 International Conference on Mechatronics, Electronics and Automotive Engineering (ICMEAE), Cuernavaca, Mexico, 5–9 December 2022; pp. 158–163. [CrossRef]
- Rivas Becerra, M.d.L.; Raygoza Panduro, J.J.; Susana, O.C.; Jose, L.G.V. Two new hardware implementations of random number generators on reconfigurable devices. In Proceedings of the 2023 3er Congreso Iberoamericano de Instrumentación y Ciencias Aplicadas SOMI XXXVII Congreso de Instrumentación, Bogotá, Colombia, 8–10 November 2023. ISSN 2395-8499.
- Rivas Becerra, M.d.L.; Raygoza Panduro, J.J.; Becerra Alvarez, C.E.; Rios Arrañaga, J.; Jimenez, M.; Ortega Cisneros, S. Impulse Neurons: Phasic Bursts and Tonic Bursts, to Generate Pseudorandom Sequences. In Proceedings of the 2023 IEEE International Autumn Meeting on Power, Electronics and Computing (ROPEC), Ixtapa, Mexico, 18–20 October 2023; pp. 1–6. [CrossRef]
- Izhikevich, E. M. Which Model to Use for Cortical Spiking Neurons? IEEE Transactions on neural networks 2004, 15, 1063-1070. [CrossRef]
- Salamanca Chavarin, J. A. Diseño e implementación de una neurona de impulsos en hardware reconfigurable, master thesis, Universidad de Guadalajara, Guadalajara Jalisco, september 2017.
- AMD XILINX. Available online: http://www.xilinx.com (accessed on 13 february 2025).
- Xilinx. 7 Series FPGAs Data Sheet: Overview. 2020. Available online: https://docs.amd.com/v/u/en-US/ds180_7Series_Overview (accessed 13 february 2025).
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).