Deep Reinforcement Learning Based Coverage Path Planning in Unknown Environments

Tianyao Zheng; Yuhui Jin; Haopeng Zhao; Zhichao Ma; Yongzhou Chen; Kunpeng Xu

doi:10.20944/preprints202503.0300.v1

Submitted:

03 March 2025

Posted:

05 March 2025

You are already at the latest version

Abstract

The Twin Delayed Deep Deterministic Policy Gradient (TD3) algorithm offers a robust solution for the coverage path planning problem, where a robot must effectively and efficiently cover a designated area, ensuring minimal redundancy and maximum coverage. Traditional methods for path planning often lack the adaptability required for dynamic and unstructured environments. In contrast, TD3 utilizes twin Q-networks to reduce overestimation bias, delayed policy updates for increased stability, and target policy smoothing to maintain smooth transitions in the robot's path. These features allow the robot to learn an optimal path strategy in real-time, effectively balancing exploration and exploitation. This paper explores the application of TD3 to coverage path planning, demonstrating that it enables a robot to adaptively and efficiently navigate complex coverage tasks, showing significant advantages over conventional methods in terms of coverage rate, total length, and adaptability.

Keywords:

deep reinforcement learning

;

coverage planning

;

path planning

Subject:

Computer Science and Mathematics - Robotics

I. Introduction

In recent years, the application of the Twin Delayed Deep Deterministic Policy Gradient (TD3) algorithm in coverage path planning has attracted increasing attention. Ma et al. conducted a study on real-time pill identification for visually impaired individuals using deep learning, significantly improving the accuracy and convenience of medication recognition [1]. Ma et al. carried out a comparative analysis of pneumonia X-ray image classification using deep learning algorithms, demonstrating the efficiency and accuracy of these techniques in medical diagnostics[2]. The core goal of coverage path planning is to enable a robot to efficiently and accurately cover a designated area, ensuring all target points or grid sections are visited or processed. This capability is essential in various applications, including home cleaning robots, agricultural monitoring, environmental inspection, and industrial equipment assessment[3,4]. The primary challenges in coverage path planning are to optimize the path for maximum coverage while minimizing redundant movements and overlap, ensuring minimal energy consumption and reduced task completion time[5].

Traditional path planning approaches often rely on rule-based coverage patterns, graph search algorithms (such as the A* algorithm), or heuristic path generation methods[6]. However, these methods can struggle in unstructured or dynamically changing environments, limiting their adaptability[7]. TD3, as a deep reinforcement learning algorithm, enables robots to learn an optimal coverage strategy through real-time interaction with the environment, making it highly adaptive and efficient in complex and dynamic scenarios[8,9].

Due to several key features, TD3 is particularly well-suited for coverage path planning tasks[10]. First, TD3 uses twin Q-networks, where two separate Q-networks estimate Q-values independently, and the minimum of the two is used to update the policy[11,12]. This reduces the common overestimation bias in traditional reinforcement learning, which is crucial in coverage path planning as it allows the robot to make more accurate assessments of each action’s effectiveness in covering new areas versus revisiting previously covered areas[13,14]. Second, TD3 incorporates delayed policy updates, meaning that the policy network is updated less frequently than the Q-networks, typically after every two Q-network updates. This delayed policy update effectively reduces the variance in policy learning, allowing the Q-networks to stabilize before the policy is adjusted, thus avoiding unstable learning and ensuring a smoother, more balanced coverage path[15].

Furthermore, TD3 introduces a target policy smoothing mechanism to further stabilize the policy[16]. By adding small, clipped noise to the target action, TD3 makes the policy less sensitive to minor fluctuations in actions, encouraging smoother, continuous coverage[17]. In coverage path planning, this is particularly advantageous, as it allows the robot to maintain a stable and continuous path even when navigating dense or complex areas, avoiding a decrease in coverage quality due to minor action changes[18].

In a TD3-based coverage path planning framework, the robot’s policy network (actor) learns to maximize expected coverage rate, while the twin Q-networks (critics) evaluate the value of actions, balancing between exploring uncovered areas and minimizing redundant coverage of known regions. In complex coverage scenarios, especially those requiring real-time decision-making in unstructured environments, TD3 enables a robot to balance exploration and exploitation, optimizing its coverage path to achieve the highest possible coverage rate in the fewest steps. This approach significantly enhances the efficiency and intelligence of coverage path planning, showing tremendous potential in applications like navigating complex terrains and inspecting large monitoring areas.

In summary, TD3 overcomes the instability and overestimation issues commonly found in traditional methods through its use of twin Q-networks, delayed policy updates, and target policy smoothing. These features allow a robot to adaptively learn in dynamic environments, balancing the exploration of new areas with efficient coverage of known regions. TD3 provides a robust and efficient solution for coverage path planning, making it highly effective in real-world robotic applications and advancing the development of automated and intelligent coverage path planning systems.

II. Methodology

A. Problem Description

In the domain of robot coverage path planning, the objective is to enable a robot to effectively cover a specified area, ensuring that all locations are visited or processed. This is critical in applications like cleaning robots, agricultural robots, and industrial inspection robots. The key challenge in coverage path planning is to optimize the path so that the area is covered in the shortest possible time while minimizing path overlap and unnecessary movements. Due to the uncertainty of environments and the dynamic nature of coverage demands, deep reinforcement learning (DRL) has shown significant advantages in addressing these challenges.

Firstly, the coverage planning problem can be modeled as a Markov Decision Process (MDP), where the state space

S

represents the robot’s position on a 2D plane along with relevant environmental information. The action space

A

represents the basic actions that the robot can execute, such as moving forward, backward, or turning. At each time step

t

, the robot is in state

s_{t} \in S

, takes an action

a_{t} \in A

, and transitions to the next state

s_{t + 1}

. The coverage rate

C_{t}

at time

t

measures the extent of area covered by the robot, defined as the ratio of the covered area to the total area. Typically, we aim to maximize this coverage rate within a given number of steps.

Within the DRL framework, the robot receives an immediate reward

r_{t}

at each state

s_{t}

. The design of the reward function

R (s, a)

is crucial for effective coverage planning. An appropriate reward function should encourage the robot to explore uncovered areas while avoiding excessive re-coverage. A typical reward function can be formulated as:

r_{t} = α \cdot (C_{t} - C_{t - 1}) - β \cdot d (s_{t}, s_{t - 1})

(1)

Where

C_{t} - C_{t - 1}

denotes the increase in coverage rate, and

d (s_{t}, s_{t - 1})

is the distance between consecutive states. The parameters

α

and

β

adjust the relative weighting of coverage efficiency and path optimization.

In DRL, a deep neural network is used to approximate the policy function

π (a | s; θ)

and the value function

V (s; θ)

, where

θ

represents the network weights. The policy function

π (a | s; θ)

outputs the probability distribution over actions, guiding the robot’s choice of actions in each state. To optimize the policy, policy-gradient-based algorithms such as Proximal Policy Optimization (PPO) or Deep Q-Network (DQN) are commonly employed. These algorithms update the parameters by minimizing the loss function:

L (θ) = E [{(r + γ V (s_{t + 1}; θ) - V (s_{t}; θ))}^{2}]

(2)

where

γ

is the discount factor, balancing short-term and long-term rewards.

During training, the DRL algorithm improves the robot’s coverage strategy through continual trial and error, maximizing cumulative rewards over time. To enhance coverage efficiency, the agent must balance exploration and exploitation. Initially, broad exploration of the environment is necessary, but as the coverage rate increases, the agent should focus on unexplored regions to converge on an optimal path.

Due to the dynamic and unstructured nature of real-world environments, traditional methods often rely on prior information, whereas DRL-based methods can adaptively learn optimal strategies even in variable conditions.

B. Twin Delayed Deep Deterministic Policy Gradient

The Twin Delayed Deep Deterministic Policy Gradient algorithm is an advanced actor-critic algorithm designed to address the limitations of traditional reinforcement learning methods in continuous action spaces. Developed as an enhancement of the Deep Deterministic Policy Gradient (DDPG) algorithm, TD3 introduces several modifications to improve learning stability and prevent the overestimation of Q-values, a common issue in value-based methods. TD3 has shown significant success in various continuous control tasks due to its robustness and efficiency.

TD3 builds upon the DDPG framework, where an actor network

π (s; θ^{π})

represents the policy that outputs actions based on the current state, and a critic network

Q (s, a; θ^{Q})

estimates the value of taking action

a

in state

s

. The goal of TD3 is to learn an optimal policy by maximizing expected returns while addressing potential overestimation in the Q-function.

In DDPG, the value function is approximated with a single Q-network, which can lead to the overestimation of Q-values due to the maximization bias in value estimation. TD3 mitigates this by using two Q-networks instead of one, each parameterized by separate weights

θ^{Q_{1}}

and

θ^{Q_{2}}

. These networks independently estimate Q-values, and the minimum of the two Q-values is used for policy updates, reducing overestimation.

TD3 utilizes two Q-networks

Q_{1} (s, a; θ^{Q_{1}})

and

Q_{2} (s, a; θ^{Q_{2}})

. The Q-value target is calculated by taking the minimum of these two Q-values to prevent overestimation:

y = r + γ \cdot \min (Q_{1} (s^{'}, π (s^{'}; θ^{π^{'}}); θ^{Q_{1}}), Q_{2} (s^{'}, π (s^{'}; θ^{Q_{2}}))

(3)

where

s'

is the next state,

γ

is the discount factor, and

r

is the immediate reward. The policy update is based on minimizing the temporal difference (TD) error using the above target

y

.

Another unique feature of TD3 is its delayed policy update mechanism. Instead of updating the policy at every time step, TD3 updates the policy (i.e., the actor network) and the target networks less frequently than the Q-networks. Typically, the policy is updated every two critic updates. This delay in policy updates reduces the variance in policy updates, providing more stable learning and allowing the Q-network to converge before updating the policy.

TD3 introduces target policy smoothing to further improve stability, which adds a small amount of noise to the target action during the Q-value target calculation. This noise is clipped to ensure it remains within a feasible range. This technique smooths the value estimation by averaging over a small range of actions around the target action, making the policy less sensitive to minor action changes. The target action with noise added can be written as:

\tilde{a} = π (s^{'}; θ^{π^{'}}) + ϵ

(4)

where

ε ~ clip (N (0, σ), - c, c)

, with

N (0, σ)

representing Gaussian noise and

c

a constant for clipping. The Q-value target is then computed as:

y = r + γ \cdot \min (Q_{1} (s^{'}, \tilde{a}; θ^{Q_{1}}), Q_{2} (s^{'}, \tilde{a}; θ^{Q_{2}}))

(5)

The TD3 algorithm alternates between updating the Q-networks and the policy network. The loss function for the Q-networks is based on the mean squared error between the Q-network predictions and the target Q-value:

L (θ^{Q_{i}}) = E_{(s, a, r, s^{'})} [{(Q_{i} (s, a; θ^{Q_{i}}) - y)}^{2}]

(6)

for

i = 1, 2

, where

y

is the Q-value target calculated as described above. After updating the Q-networks, if the policy update condition is met, the policy network is updated by maximizing the Q-value estimated by

Q_{1}

, the first Q-network, to improve the expected return.

\nabla_{θ^{π}} J (θ^{π}) = E_{s} [\nabla_{a} Q_{1} (s, a; θ^{Q_{1}}) |_{a = π (s; θ^{π})} \nabla_{θ^{π}} π (s; θ^{π})]

(7)

Lastly, TD3 employs soft updates for the target networks, where the parameters

θ^{Q_{i}^{'}}

and

θ^{π^{'}}

of the target networks

Q'_{i}

and

π^{'}

are updated slowly with respect to the current networks:

\begin{array}{l} θ^{Q_{i}^{'}} \leftarrow τ θ^{Q_{i}} + (1 - τ) θ^{Q_{i}^{'}} \\ θ^{π^{'}} \leftarrow τ θ^{π} + (1 - τ) θ^{π^{'}} \end{array}

(8)

where

τ

is a small constant controlling the update rate.

III. Experiments

In order to use randomly generated maps during training and ensure the generalization of the algorithm, we set up random maps and generate random obstacles in the map. Our map is usually a square grid matrix containing several obstacles. During the obstacle generation process, as much as possible, it is ensured that they are kept at a certain distance from each other and do not block the path between obstacles. The map sizes range from 40*40 to 500*500 to ensure that the generated paths are suitable not only for small indoor environments but also for large outdoor venues.

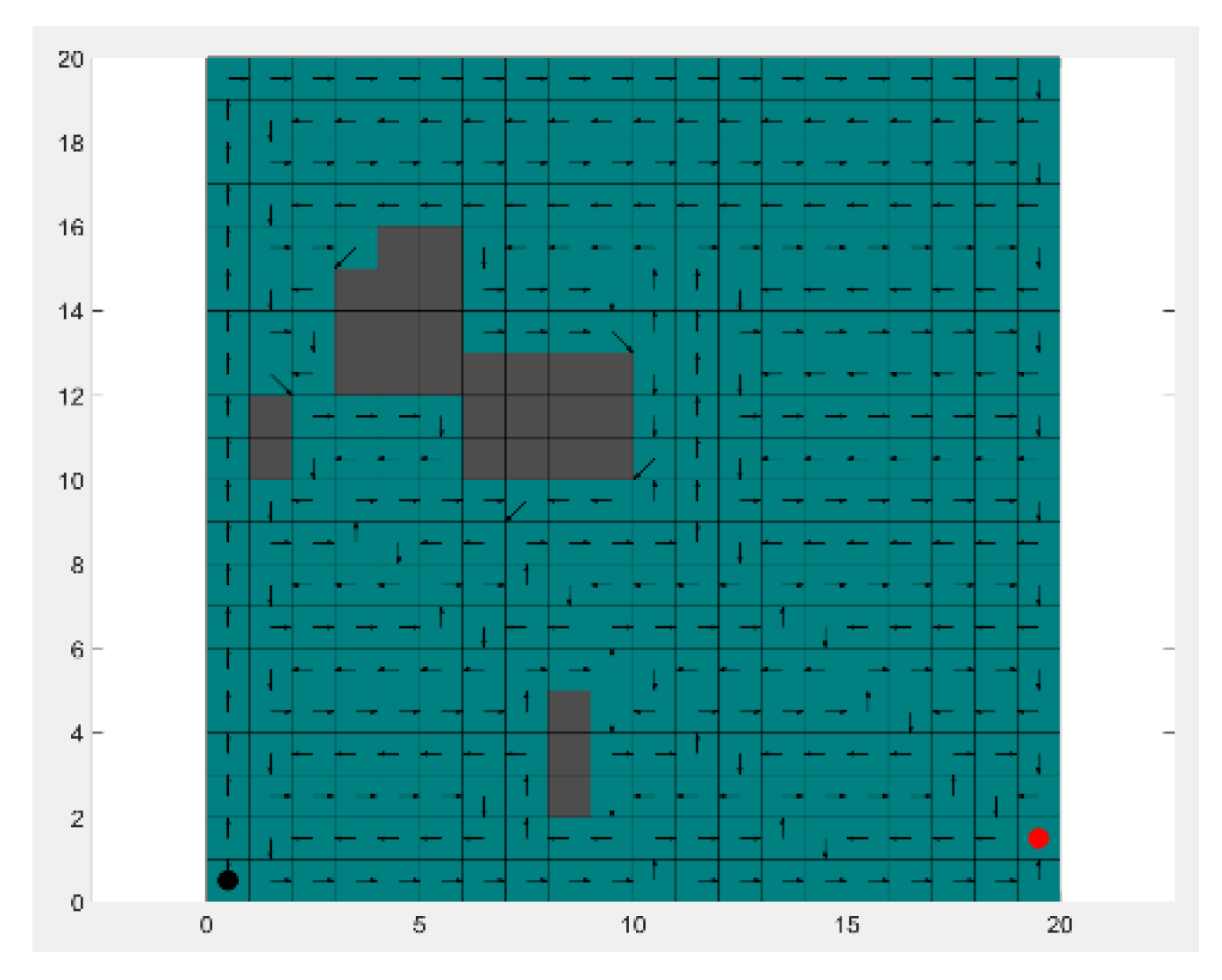
As shown in the Figure 1, the coverage path trained by our TD3 algorithm can completely cover the map, and the redundancy of the generated path is minimal. Among many algorithms, the total path length is the shortest.

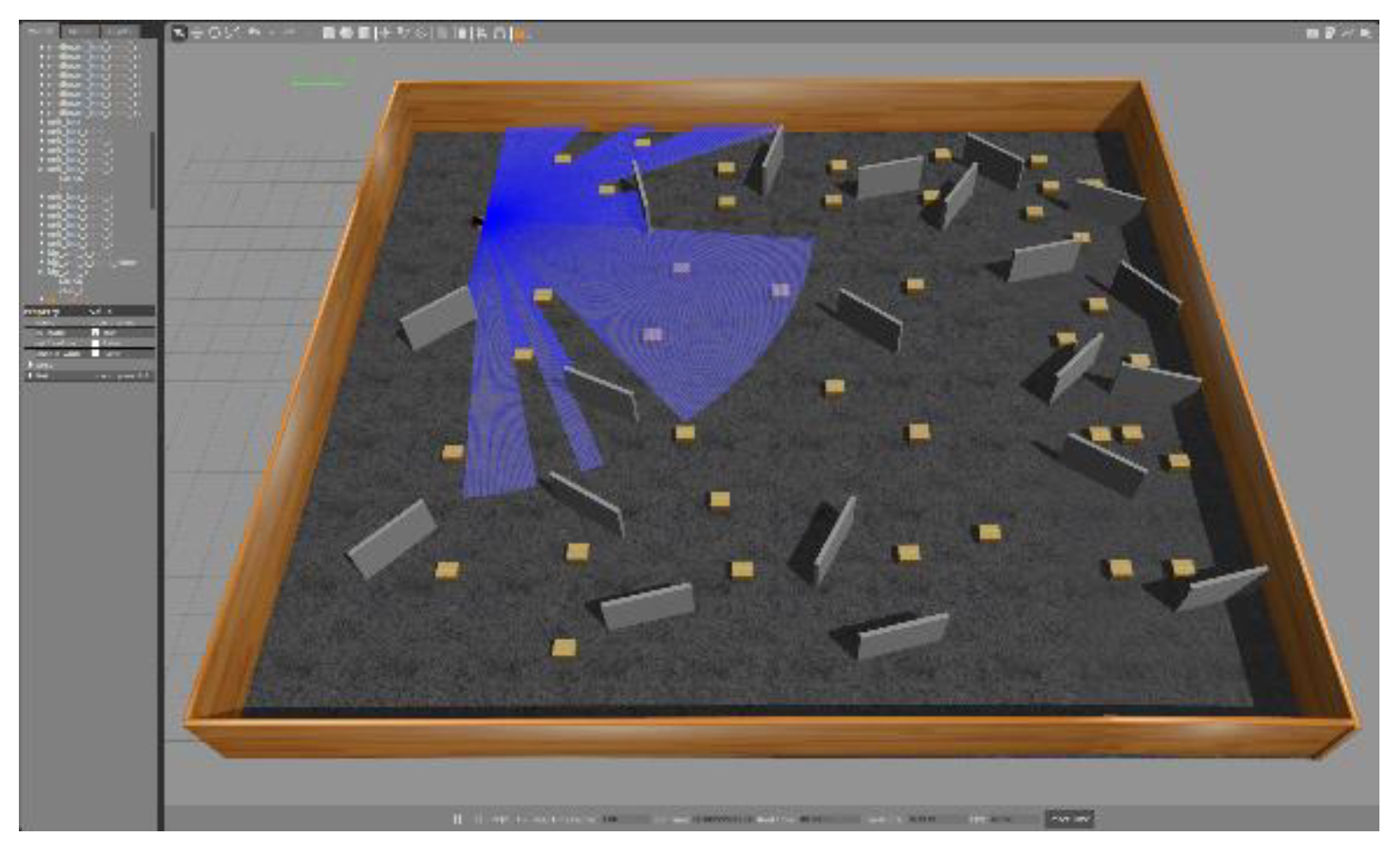
As shown in the Figure 2, we used a joint simulation environment of ROS (Robot Operating System) and Gazebo to implement and verify the application of TD3 algorithm in robot coverage path planning. The experimental environment was built on the Ubuntu operating system. ROS was used as the robot operating system for task allocation and communication, while Gazebo was used for physical simulation to provide a realistic virtual environment. In Gazebo, we built a two-dimensional simulation field with obstacles to simulate the complex environment and obstacle layout that robots may encounter in reality.

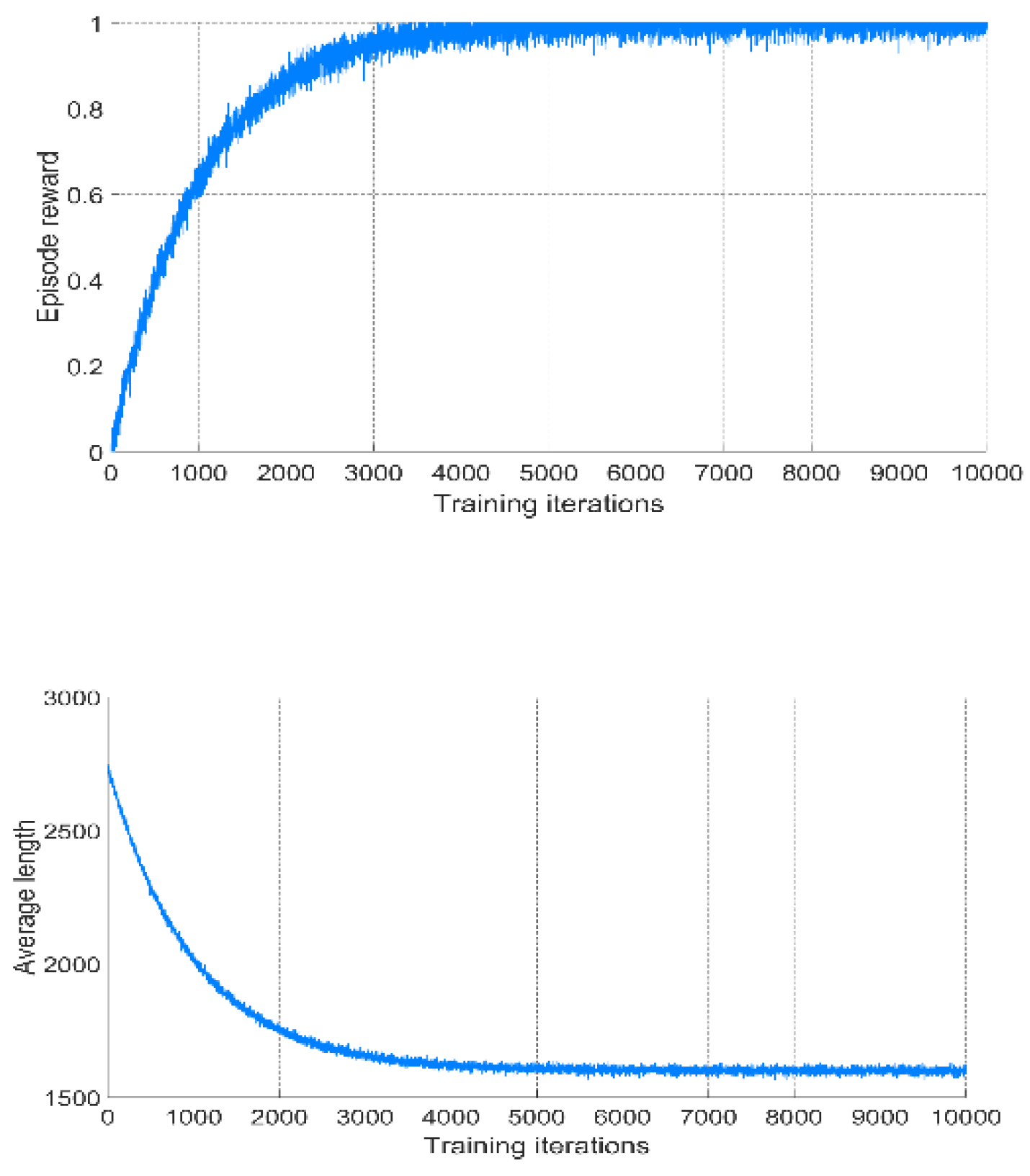
Table 1 and Figure 3 shows the performance indicators of different algorithms. Experiments show that the TD3-based method has obvious advantages over the traditional spiral method and intelligent optimization methods such as the ant colony algorithm (ACO) and genetic algorithm (GA) and DDPG. First, in terms of coverage, the TD3 algorithm can reach 100%, which meets the index requirements of coverage planning. Second, in terms of path length, the TD3 method has the smallest path length, which can ensure that the vehicle covers more areas under limited energy.

IV. Conclusions

In summary, the TD3 algorithm provides an effective approach for coverage path planning by addressing key challenges such as path optimization, redundancy reduction, and adaptability to dynamic environments. Through the dual Q network, TD3 reduces the overestimation bias, allowing for a more accurate assessment of the coverage efficiency of each action. Experimental results show that TD3 outperforms traditional heuristic and rule-based methods, achieving higher coverage with fewer redundant actions. The algorithm's ability to balance exploration and exploitation makes it a solid choice for practical applications in robotic coverage tasks.

References

Dang, B., Zhao, W., Li, Y., Ma, D., Yu, Q., & Zhu, E. Y. (2024). Real-Time Pill Identification for the Visually Impaired Using Deep Learning. 2024 6th International Conference on Communications, Information System and Computer Engineering (CISCE), 552–555. [CrossRef]
Ma, D., Yang, Y., Tian, Q., Dang, B., Qi, Z., & Xiang, A. (08 2024). Comparative analysis of X-ray image classification of pneumonia based on deep learning algorithm algorithm. [CrossRef]
Liu R, Xu X, Shen Y, et al. Enhanced detection classification via clustering svm for various robot collaboration task[J]. arXiv preprint arXiv:2405.03026, 2024. [CrossRef]
H. Liu, Y. Shen, C. Zhou, Y. Zou, Z. Gao and Q. Wang, "TD3 Based Collision Free Motion Planning for Robot Navigation," 2024 6th International Conference on Communications, Information System and Computer Engineering (CISCE), Guangzhou, China, 2024, pp. 247-250. [CrossRef]
Tao C, Fan X, Yang Y. Harnessing llms for api interactions: A framework for classification and synthetic data generation[J]. arXiv preprint arXiv:2409.11703, 2024. [CrossRef]
Yin J, Zheng Z, Pan Y, et al. Semi-supervised semantic segmentation with multi-reliability and multi-level feature augmentation[J]. Expert Systems with Applications, 2023, 233: 120973. [CrossRef]
Dan H C, Lu B, Li M. Evaluation of asphalt pavement texture using multiview stereo reconstruction based on deep learning[J]. Construction and Building Materials, 2024, 412: 134837. [CrossRef]
Tan L, Liu S, Gao J, et al. Enhanced self-checkout system for retail based on improved YOLOv10[J]. Journal of Imaging, 2024, 10(10): 248. [CrossRef]
Fan X, Tao C. Towards resilient and efficient llms: A comparative study of efficiency, performance, and adversarial robustness[J]. arXiv preprint arXiv:2408.04585, 2024. [CrossRef]
Zhang Y, Zhu M, Gui K, et al. Development and application of a monte carlo tree search algorithm for simulating da vinci code game strategies[J]. arXiv preprint arXiv:2403.10720, 2024. [CrossRef]
Y. Shen, H. Liu, C. Zhou, W. Wang, Z. Gao and Q. Wang, "Deep Learning Powered Estimate of The Extrinsic Parameters on Unmanned Surface Vehicles," 2024 9th Asia-Pacific Conference on Intelligent Robot Systems (ACIRS), Dalian, China, 2024, pp. 6-10. [CrossRef]
Fan X, Tao C. Towards resilient and efficient llms: A comparative study of efficiency, performance, and adversarial robustness[J]. arXiv preprint arXiv:2408.04585, 2024. [CrossRef]
Yin J, Peng N, Chen Y, et al. Class-level multiple distributions representation are necessary for semantic segmentation[C]//International Conference on Database Systems for Advanced Applications. Singapore: Springer Nature Singapore, 2024: 340-351.
Tao C, Fan X, Yang Y. Harnessing llms for api interactions: A framework for classification and synthetic data generation[J]. arXiv preprint arXiv:2409.11703, 2024. [CrossRef]
Liu X, Wang Z. Deep learning in medical image classification from mri-based brain tumor images[J]. arXiv preprint arXiv:2408.00636, 2024. [CrossRef]
Ru J, Yu H, Liu H, et al. A bounded near-bottom cruise trajectory planning algorithm for underwater vehicles[J]. Journal of Marine Science and Engineering, 2022, 11(1): 7. [CrossRef]
Peng X, Xu Q, Feng Z, et al. Automatic News Generation and Fact-Checking System Based on Language Processing[J]. arXiv preprint arXiv:2405.10492, 2024. [CrossRef]
Wang C, Sui M, Sun D, et al. Theoretical analysis of meta reinforcement learning: Generalization bounds and convergence guarantees[C]// Proceedings of the International Conference on Modeling, Natural Language Processing and Machine Learning. 2024: 153-159.

Figure 1. The path direction generated by the coverage planning algorithm. The black circle in the figure represents the starting point and the red circle represents the end point.

Figure 2. Gazebo Simulation Environment.

Figure 3. Coverage rate and average length of the TD3 algorithm during training process.

Table 1. Performance of different algorithms.

Approach	Total Length(m)	Running Time(s)	Coverage rate(%)
Spiral	2076	0.12	100
ACO	2434	3.78	98.3
Greedy Search	1875	42.37	100
GA	1948	4.61	97.8
DDPG	1864	0.75	100
TD3	1652	0.64	100

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Deep Reinforcement Learning Based Coverage Path Planning in Unknown Environments

Abstract

Keywords:

Subject:

I. Introduction

II. Methodology

A. Problem Description

B. Twin Delayed Deep Deterministic Policy Gradient

III. Experiments

IV. Conclusions

References

MDPI Initiatives

Important Links

Subscribe