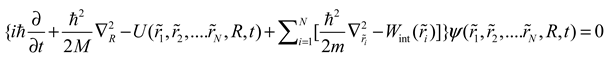2. On the Concept of the Physics of Evolution and the Problem of Irreversibility
The modern picture of the world, taking into account that the movement and interactions of bodies are general properties of matter, reflects the stationary state of surrounding objects [
3]. But only by adding evolution to these two properties of matter can we construct a picture of the world that determines the nature of the development of matter over time. Therefore, evolution can be called the third general property of matter. This is also confirmed by the fact that the task of all science is to determine the future state of a system based on its current state.
The concept of evolution originated in ancient Greece. It was related to biology, physics and sociology at the same time. The modern idea of the evolution of living matter is usually associated with the works of Charles Darwin and Gregor Mendel [
7,
8].
At present, the connection between the evolution of living and bone matter has been little studied. Moreover, the definitions of evolution for bone and living matter are different. Evolution for living matter is usually defined as the adaptation of organisms to changing conditions of their existence. And by the evolution of bone matter we understand the change in the picture of the world over time. Here, we propose to understand evolution as irreversible and nonlinear processes of the emergence, development and decay of natural objects.
If we proceed from the condition of the unity of nature and take into account that quantity gives birth to quality, then the principles and laws of the evolution of living matter must have their origin in the laws of the evolution of bone matter. Therefore, without understanding the laws of the evolution of bone matter, it is impossible to understand the more complex laws of the evolution of living matter. Consequently, there must be a cause-and-effect relationship between the evolution of bone and living matter. That is, the development of an evolutionary picture of the world, including living matter, should begin with the study of the laws of the evolution of bone matter. Its study is the subject of the recently proposed interdisciplinary section of physics
"Physics of Evolution", whose tasks include solving the problems of the emergence, development and decay of bone matter systems within the framework of the fundamental laws of physics [9].
The development of the "Physics of Evolution" has become especially relevant in recent years due to catastrophic changes in nature, climate, and society. The role of the "Physics of Evolution" for physics is especially clearly seen in the example of the construction of the cosmological evolutionary theory of the Universe. Today, this theory is based on classical mechanics, statistical physics, thermodynamics, and elementary particle physics. But its further development has encountered problems due to the limitations of the relevant sections, their insufficient consistency, fragmentation of physics, and violation of the principle of causality. The creation of a unified physical theory also encountered these problems [
10]. The main argument in favor of the existence of such a theory is the unity of the laws of nature, including the laws of evolution [
11]. To create a "unified theory of everything" and to construct the physics of evolution in particular, it is first necessary to eliminate the contradictions between classical mechanics, thermodynamics, and quantum mechanics.
Classical mechanics, one way or another, underlies all sections of physics. Therefore, it is natural that its limitations determine the limitations of all physics. Perhaps its main limitation, which hinders the study of evolution, is the reversibility of the dynamics of bodies, which contradicts the second law of thermodynamics [
12,
13,
14].
The first attempts to solve the problem of irreversibility belong to Boltzmann. To find its solution, he developed the molecular-kinetic theory of matter. On its basis, Boltzmann proposed a solution to the problem of irreversibility, which is essentially statistical [
3,
4,
15]. Today, this solution forms the basis of the generally accepted explanation of the mechanism of irreversibility. It is based on the positivity of the Lyapunov exponents for Hamiltonian systems and the resulting exponential instability of phase trajectories. This instability with arbitrarily small fluctuations of external parameters leads to irreversibility [
4,
5,
6]. And although this mechanism perfectly describes reality, it does not satisfy the principle of causality, does not allow us to answer the question, of how new properties of systems are born that their elements do not have [
16,
17,
18]. Therefore, this solution is difficult to use to construct an evolutionary picture of the world within the framework of the laws of physics.
Thus, all attempts to find the DMN within the framework of classical mechanics have failed to achieve their goal. The problem of irreversibility has been further aggravated by the advent of quantum mechanics, which is based on the uncertainty principle. The presence of this principle has even led to the assumption that the "arrow of time" is of a fundamental nature and is not simply a consequence of the laws of physics [
19,
20]. But if we proceed from the condition that the world is knowable and that it has a causality principle, without which the world could not have arisen by evolution, then the "arrow of time" must follow from the fundamental laws of physics. All this can only mean one thing -
the existing formalisms of classical mechanics have limitations that exclude the fundamental possibility of explaining the DMN. In this case, to solve the problem of irreversibility, it was necessary to find and exclude the existing limitations so that classical mechanics would contain the DMN [
21,
22]. That is, it was necessary to understand the nature of the limitations of classical mechanics that exclude the DMN. Only by identifying these limitations could we find a way to eliminate them.
It is necessary that the resulting extension satisfy the correspondence principle, since any new scientific theory
must include, as a special case, the old theory [
23]. This means, in particular, that the statistical mechanism of irreversibility must follow from it.
The problem of irreversibility has had a significant impact on the fact that the dynamics of bodies and their internal state are studied separately. As a result, physics today can be represented as two sections that are not well connected.
In the first section, as a rule, within the framework of classical mechanics, problems of the dynamics of interacting objects are solved. For this, the formalisms of classical mechanics are used, constructed under the condition of holonomic connections and potentiality of collective forces. Therefore, classical mechanics does not describe dissipative processes [
13]. But the dynamics of bodies without dissipation is not only reversible, it is impossible. This excludes the possibility of describing evolutionary processes [
14].
The second section studies the laws of behavior of internal states of bodies without taking into account their relationship with dynamics. For this, methods of statistical physics are used. But these methods are difficult to use to describe evolution processes, since they do not satisfy the principle of causality [
15]. Another difficulty in describing evolution is due to the fact that evolution is associated with both the dynamics of bodies and with changes in their internal states. Therefore, to construct the "Physics of Evolution" it is necessary to remove the contradictions between these two sections of physics. This means that statistical methods that describe the internal states of systems well enough must follow from the deterministic laws of physics.
Relatively recently, the necessary DMN was proposed. It opened up the possibility of constructing the "Physics of Evolution". This DMN follows from the equation of motion of the SB. The peculiarity of the equation of motion of the SB is that it takes into account the work of external forces on bodies, which changes not only the energy of motion, but also the internal energy. This led to the expansion of classical mechanics, eliminating the contradiction between mechanics and thermodynamics and opening up the possibility of describing the processes of evolution.
3. Equation of Motion of a Structured Body and Deterministic Mechanism of Irreversibility
Classical mechanics is based on Newton's equation of motion for MP. This equation can be obtained from the total energy of MP under the condition of its invariance [
25]. The total energy for MP consists only of the energy of motion, therefore all the work of external forces goes to the movement of MP.
The equation of motion of the SB in classical mechanics can be obtained by summing the equations of motion of each element of the SB [
13]. In this case, the work of external forces to change the internal energy remains unaccounted for, since the sum of the internal forces is zero. Therefore, the equation of motion of the SB in classical mechanics is valid only when all the work of external forces goes to moving the SB. This is true for structureless bodies or in the presence of homogeneous external forces. But if the external forces acting on the SB are non-homogeneous, then not only the energy of motion of the SB can change, but also its internal energy [
9,
24]. This is clear from the example of a parachutist whose speed reaches its maximum value over time. In this case, the force of gravity is equal to the force of friction and all the work of external forces goes to changing the internal energy of the SB. Therefore, in classical mechanics, the work of external forces to heat bodies is taken into account empirically, by determining the coefficient of friction. Consequently, the limitation of classical mechanics is due to the fact that it is impossible to determine that part of the work of external forces that goes to changing the internal energy of the body. This limitation excludes the possibility of describing evolution, since it is associated with the work of external forces to change the internal state of the system. That is; to
describe evolution, it is necessary to have an equation that takes into account both the work of external forces changing the energy of motion and the work to change the internal energy. Let us discuss how to obtain such an equation.
The equation of motion of the SB in classical mechanics is derived in the laboratory coordinate system. In it, the radius vector of each MP of the system consists of the sum of the radius vectors of the center of inertia and the radius vector of the MP relative to the center of inertia. The force determining the work on accelerating the SB is equal to the sum of the forces applied to each MP. But the sum of the internal forces is zero. And since each MP contributes both to the energy of motion and to the internal energy of the SB, then in the laboratory coordinate system it is impossible to determine the work on changing the internal energy. But it can be determined in the dual coordinate system specified by micro- and macrovariables. Moreover, microvariables determine the motion of each MP relative to the center of inertia, and macrovariables determine the motion of the center of intention of the SB. In the dual coordinate system, the total energy is represented as the sum of the energy of motion of the SB and its internal energy. Differentiating the total energy with respect to time, we obtain an equation that determines both the work of external forces on moving the center of inertia and the work they do on changing the internal energy. From this equation, we can find the equation of motion of SB. In it, unlike the equation of motion of MP, a second term will appear on the right-hand side, defining the forces that change the internal energy. It is obvious that the appearance of this term is due to the consideration of the structure of the body.
The derivation of the equation of motion of the SB in the dual coordinate system is equivalent to the fact that we expand classical mechanics by means of additional principles [
9].
The first principle includes the assertion that the evolution of natural objects is determined by two types of symmetry: symmetries of bodies and symmetries of space. We called this key assertion the principle of dualism of symmetry. It follows from it that the work of external forces goes both to the motion of bodies and to the change of their internal states. It is natural to call this the dualism of the work of external forces.
The second principle is the assertion that the physical laws that determine the behavior of bodies and the physical laws for their environment are unified. We call this assertion the principle of equivalence of the physical laws of a body and its environment. That is, the body and environment under study can be considered as two interacting systems that obey the general laws of physics. According to this principle, the direct and reverse flows of matter and energy for bodies and their environment are determined by general laws that follow from the symmetries of space and body.
The third principle is the assertion that the evolution of bodies is determined by the bilinear relationship between the symmetries of space and the symmetries of the body. Indeed, using the example of a body moving on an inclined surface, it is clear that the work of gravity, which goes into its movement, is interconnected with the work that, as a result of friction, goes into increasing its internal energy. That is, the invariant of the motion of SB is not the energy of motion, as in the case of MP, but the total energy, equal to the sum of the energies of motion of SB and its internal energy. Hence, the homogeneity of time, determined by the invariance of the energy of motion, is violated in the presence of a nonlinear transformation of the energy of motion of a body into internal energy. It follows from this principle that it is impossible to determine the evolution of bodies without taking into account the relationship between the dynamics of bodies and the change in their internal state. This is precisely, why evolution could not be studied without eliminating the contradictions between classical mechanics and thermodynamics.
Thus, differentiating the total energy with respect to time, represented through independent micro-and macrovariables in the form of the sum of the energy of motion and the internal energy, subject to its invariance, after simple transformations, we obtain the equation of motion of the SB [
9,
24]:
Here the mass of the SB; ; is a velocity of MP; is number of elements in the SB; is mass of the elements SB which is equal one for all MP; is external force acting on the - th element of the SB; ; ; ; is the force of interaction of the elements of the SB; ; ; .
The left term of equation (1) defines the inertial force. The first term on the right-hand side defines the active force for the displacement of the SB in space. It is equal to the sum of the external forces acting on all MP. Unlike Newton's equation of motion for MP, the second term has appeared on the right-hand side of equation (1). It defines the forces changing the internal energy due to the energy of motion. This term is nonzero only when the characteristic scales of the inhomogeneities of the external forces are smaller than or coincide with the characteristic scales of the SB. A similar term is also present in the equation of motion obtained on the basis of the statistical theory of fluctuations [
15]. No transformations of variables can exclude the second term on the right-hand side of equation (3), since it is determined by the law of conservation of total energy and characterizes the nonlinear transition of the energy of motion into internal energy. In the approximation of homogeneity of external forces or when neglecting the structure of bodies, this term disappears.
When the dissipative and active forces are equal, the acceleration of the SB is zero, and we have:
It was this particular case that led Aristotle to the conclusion that the speed of a body is proportional to the force acting on it [
27]. For low speeds, the second term of equation (1) can be neglected, and we arrive at Newton's equation of motion. Thus, equation (1) takes into account the complete work of external forces on the displacement of the body and the change in its internal state. In the general case, equation (1) for the SB and Newton's equations for each MP characterize the evolution of the system.
Based on the equation of motion (1), using the d'Alembert principle, it is possible to obtain extended formalisms of classical mechanics for SB without using hypotheses about the holonomy of connections or the potentiality of collective forces [
9]. These formalisms allow us to study evolution processes [
9].
Note that the second term, responsible for dissipation, enters equation (1) additively. This additivity makes it possible to study evolution using Newtonian mechanics by adding an empirical term to the canonical Hamiltonian, which is used in practice.
Equation (1) is not invariant with respect to time reversal, since for equilibrium SBs with inhomogeneities of external forces the energy of motion can transform into internal energy. That is, evolution is associated with the violation of time symmetry. Indeed, only if there is no change in the internal energy of the system, can the SB return to its initial state. But when the internal states change, the flow of time is irreversible, and the SB that has returned to the initial point in space will have a different state.
According to equation (1), the law of motion of the SB can be formulated as follows: the work of external forces goes both to accelerate the SB and to change the internal energy, provided that the total energy is preserved.
To determine the measure of work that goes into changing the internal energy, the concept of
D-entropy was introduced [
9,
28]. D-entropy is defined as the ratio of the increment of the internal energy of a system to its total value. D-entropy differs from existing concepts of entropy in that, firstly, it is determined by the total increment of internal energy as a result of the work of external forces; secondly, it is deterministic, since it follows from equation (1); thirdly, it characterizes the evolution of a dynamic system; fourthly, it is applicable to both large and small systems. Moreover, for small systems it can be both positive and negative [
28]. D-entropy characterizes the connection between the dynamics of bodies and their internal state. This is currently the only concept of entropy that is defined through dynamic parameters and allows us to study evolution processes.
According to calculations of the dependence of D-entropy on the number of elements in the system, performed on the basis of equation (1), it was found that when the number of particles in the system
N <100, D-entropy can be negative, but already at
N >100, it is always positive, and at
N > 1000 it reaches asymptotics [
33].
The nature of irreversibility can be understood by studying the nature of the transformation of the energy of motion into internal energy, taking into account that the mutual transformation of the energy of motion and the internal energy of a nonequilibrium system is determined by the equivalence principle. Indeed, according to equation (1), the transformation of the energy of motion into internal energy is determined by its second bilinear term on the right-hand side. Therefore, it has the second degree of smallness. The inverse transformation of the absorbed energy of motion, in accordance with the equivalence principle, will already have the fourth degree of smallness. Hence, the nature of the transformation of the energy of motion into internal energy is determined by the potential [
9]:
Here constants defined by equation (1); - a small parameter, for example, the increment of the average speed of the body's elements to their average value. Expression (2) displays the balance of the direct and inverse transformation of the energy of motion of bodies. The quantity , where are the roots of equation (2), for which irreversibility takes place. In the general case for N > >1, we will have , which corresponds to irreversibility.
Under the condition
there is a stationarity of systems. This unstable stationary state determines a special bifurcation point. Such a feature takes place for a macro description. It disappears if we move from the macro description of the dynamics of the SB to a micro description. That is, at the bifurcation point the dynamics of the body are uniquely determined by the dynamics of its elements. Therefore, the micro description allows us to remove the feature at the bifurcation point [
9,
29].
The transformation of the energy of motion into internal energy and its reverse transformation is not symmetrical by its nature. The symmetry is broken because the relative velocities of bodies in the coordinate system of their center of inertia decrease, which is not prohibited by the laws of conservation of energy and momentum. This is what determines the physics of irreversibility.
Thus, the expansion of classical mechanics, which arises as a result of taking into account the role of the structure of bodies in their dynamics, allows us to explain the second law of thermodynamics within the framework of the laws of classical mechanics. That is, equation (1) eliminates the contradictions between classical mechanics and thermodynamics.
From equation (1) it follows that
if we accept the condition of the evolutionary origin of the world, then matter must be infinitely divisible. Indeed, dissipation, without which there is no evolution, is possible only for SB. That is, if matter originated in an evolutionary way, then it must have structure at all its hierarchical levels [
29]. Thus, according to the laws of dynamics,
matter is infinitely divisible and represents a hierarchy of interconnected systems nested within each other [34]. This conclusion is due to the principle of dualism of symmetry and follows from the condition of conservation of total energy. And since the law of conservation of energy is a general law for all sections of physics, the conclusion about the infinite divisibility of matter is true for all physics and for all material objects. That is, the structure of matter should be taken into account at all its hierarchical levels. Let us generalize what taking into account the infinite divisibility of matter gives for classical physics.
4. The Role of the Structure of Matter for Physics
Problems with describing dissipation processes for the energy of motion of systems arose simultaneously with the creation of classical mechanics. Classical formalisms were built based on Newton's equation and d'Alembert's principle under the conditions of holonomy of connections and potentiality of collective forces. Therefore, they describe the dynamics of systems only when dissipation can be neglected, that is, when the dynamics of systems does not depend on their internal states [
25]. But evolution
is determined by the relationship between the dynamics of a system and changes in its internal state, which is not taken into account in classical mechanics. Therefore, it is quite natural that the nature of the problems of describing dissipation processes is associated with the limitations of mechanics. This explains the failure of many years of attempts to solve the problem of irreversibility within the framework of classical mechanics. This gave rise to the idea of searching for such an extension of classical mechanics that would nevertheless allow describing evolution within the framework of the laws of classical mechanics. As it turned out, such an extension arises as a result of taking into account the role of the structure of bodies in their dynamics. This is achieved by replacing Newton's equation with the equation of motion of the SB. Taking into account the role of the structurality of bodies in their dynamics leads to the possibility of describing changes in the internal states of bodies that arise as a result of their dynamics and interaction with other objects
. This meant that to describe evolution it was necessary to find such equation of motion that takes into account the work of external forces changing the internal energy. Such an equation is equation (1). As was shown above, from this equation follows the explanation of the DMN, which is a weighty argument in favor of the implementation of the principle of causality, the knowability of nature and its laws. Consequently,
taking into account the role of the structure of the body in its dynamics led to the expansion of classical mechanics, which eliminated the contradiction between mechanics and thermodynamics. According to expanded classical mechanics, the transformation of the energy of motion into internal energy is subject to the second law of thermodynamics. Moreover, the dynamics of bodies is characterized by the energy of motion, and the internal energy is characterized by D-entropy.
Thus, taking into account the role of the structure of bodies in their dynamics led to the possibility of describing evolutionary processes.
The most important conclusion that follows from the expansion of classical mechanics is the conclusion about the infinite divisibility of matter. This conclusion affects all sections of physics, since they, one way or another, were formed during the study of various hierarchical levels and types of matter. Moreover, it follows from this that
the knowledge of the world is an endless process. We also come to this conclusion in connection with the infinite diversity of the processes of the evolution of matter. This idea is shared by other researchers. Let us quote: “Science
does not reveal truisms. Rather, it is part of the greatness and beauty of science that we can learn, through our own critical research, that the world is completely different from what we ever imagined – until our imagination was fired by the refutation of our earlier theories. There seems to be no reason to think that this process will come to an end. The final theory is a goal that can be approached with any given accuracy, but never reached” [
30]. That is, there will always be an area of the unknown, although in nature there is no such phenomenon that cannot be understood.
The determinism of evolution does not mean that statistical methods of system analysis are unnecessary. Indeed, since the process of learning the truth is endless, this means that there is always an area of the unknown that introduces a share of uncertainty into our knowledge. This leaves room for statistics. Moreover, the use of statistical methods significantly simplifies the solution of many problems in processing and analyzing experimental data, which is important at the initial stage of studying the general patterns of system behavior.
Naturally, evolutionary development is characteristic of physics itself [
31]. This development, like the development of knowledge about matter, goes from the simple to the complex: “
Fundamental physical science becomes more complete due to the improvement in the quantity, variety, and accuracy of empirical data confirming predictions, and also due to rare unifications that reduce well-tested fundamental physical theories to the level of useful approximations to even more accurate theories” [
32].
In connection with the expansion of classical mechanics, questions arose concerning the need to construct distribution functions for nonequilibrium systems, since the Gibbs, Maxwell, Fermi-Dirac and Bose -Einstein statistics [
15,
35] were obtained only for systems close to equilibrium, when the second term on the right-hand side of equation (1) can be neglected. That is, these statistics are unacceptable for describing evolution processes.
Thus, the expansion of classical mechanics, which arose due to the consideration of the role of the structurality of bodies in their dynamics, led to the elimination of the contradiction between classical mechanics and thermodynamics, to the conclusion about the infinite divisibility of matter and to the possibility of constructing the "Physics of Evolution". But this does not yet solve all the problems of the possibility of describing evolution within the laws of physics. Another section of physics, without which it is impossible to create an evolutionary picture of the world, is quantum mechanics. Here we ask the question: how can the requirement of infinite divisibility of matter, the condition of the relationship between internal energy and the energy of motion, the nonlinearity of evolutionary processes be reflected in quantum mechanics.
5. Problems of Quantum Mechanics
The creation of quantum mechanics provided unprecedented progress in the development of physics. But at the same time, it revealed problems connected mainly with determinism and the principle of causality. Already at the very beginning of the creation of quantum mechanics, disputes about its essence and its limitations flared up. Among them, the dispute between Bohr and Einstein occupies a bright place [
39,
40]. Today these disputes not only do not fade away, but flare up with even greater force [
41,
42,
43,
44,
45]. As Weinberg states, so far "
Nobody has been able to devise a way to change quantum mechanics in such a way as to preserve its successes without leading to logical absurdities " [
46]. Dirac is the author of the statement:
It seems to me very probable that at some future time there will be an improved quantum mechanics which will contain a return to causality … But such a return can only be possible at the price of abandoning some other fundamental idea which we now accept unconditionally. If we are going to revive causality, we will have to pay for it, and at present we can only guess which idea might be sacrificed [
47].
The foundations of modern quantum mechanics are based on the Schrödinger wave equation [
36]:
This equation satisfies the superposition principle because it is linear. Having set the wave function at the initial moment of time, we can use it to find its values at all other moments of time. The square of the modulus of the wave function - determines the probability of a particle being in a given region of the configuration space:. Any dynamic quantity " f " in quantum mechanics, for example, energy and momentum, are determined by the wave function using the corresponding operator: - kinetic component of the energy of motion, - momentum. The quantities "f" characterizing the dynamics of particles are determined by averaging:.
Schrödinger obtained equation (3) based on the Hamilton-Jacobi formalism [
13,
25,
38]. It can also be obtained from the wave equation:
, replacing the parameters characterizing the waves with the parameters:
[
37]. This means that the properties of the Schrödinger equation and the wave equation are equivalent.
The Schrödinger equation can also be obtained from the expression for the total energy of the system
, if we replace the energy of motion and momentum with the corresponding operators:
, where
i are the numbers of the elements of the system [
37].
The Poisson brackets for the coordinates "q" and momenta "p" for a quantum particle satisfy the Heisenberg uncertainty relation: . This means that it is impossible to simultaneously determine the coordinates and momenta of a quantum particle. The physical essence of the uncertainty principle is clear from the fact that for a wave packet determined by a wave function, the uncertainty of energy and time follows from the condition: . Here is the width of the spectrum section where the amplitude of the Fourier harmonics differs significantly from zero, is the accuracy of the harmonic emission time.
It follows from the experiment that the energy and other dynamic parameters of the particles are quantized. An explanation of the nature of quantization was proposed by Bohr [
39]. According to his hypothesis, the classical action for stable orbits of an electron in an atom is equal to:
. The stationary orbits of electrons in an atom are determined not by their velocities, but by the frequency determined by Planck's formula:
.
In an attempt to solve the problem of the causality principle, Bohm, relying on the Hamilton-Jacobi formalism, constructed a system of equations for the amplitude and phase of the wave function. Formally, his proposal boils down to the fact that from the Schrödinger equation for the complex wave function go to the equations for amplitude – R ( x , t ) and phase – S ( x , t ).
Bohm's ideas are based on Einstein's assertion of the existence of "
hidden variables" in quantum mechanics that uniquely determine the state of the microworld. Bohm argued that
there must be a theory of hidden variables that, if experimental error is discounted, yields results that do not contradict the existence of cause-and-effect relationships. In Bohm's mechanics, the evolution of the system's configuration space, determined by the function
, is deterministic and continuous. In particular, when a particle passes through a double-slit screen, its state is determined by its initial position. At the same time, Bohm rejected the idea of exchange interaction, assuming a continuous model of matter. That is, in Bohm's model, particles are, as it were, defined by field clots [
48]. Bohm's model is consistent with the infinite divisibility of matter, but contradicts the condition of indivisibility of quantum particles [
37]. According to de Broglie-Bohm's ideas, it can be assumed that the simplest quantum particle is an oscillator. Bohm believed that the concepts of wave and particle merge at the atomic scale [
48]. Then, according to equations (3,4), the role of “hidden variables” will be played by microvariables.
The fact that quantum mechanics, like classical mechanics, is constructed for structureless particles means that it does not include evolution processes and is a certain approximation to reality. Indeed, evolution processes are nonlinear, and the Schrödinger equation is applicable to stationary states and linear processes. It is obvious that in practice, for sufficiently large energies of particle interaction, the indivisibility condition will be violated. Most likely, the critical interaction energy for particles should be determined by the condition: , where is the mass of the particle.
One of the most important conclusions that follows from the physics of evolution is the conclusion about the infinite divisibility of matter. According to this conclusion, all objects of nature represent a hierarchy of nested open nonequilibrium dynamic systems [
9] . Since this conclusion is general for all of physics, let us consider what it can lead to in quantum mechanics. From the condition of the structure of particles, we assume that
a quantum particle, in addition to the energy of motion, has internal energy. This means that the Hamiltonian operator is the sum of two operators. One of them corresponds to the internal energy of the particle, and the other corresponds to the motion of the particle in space. The validity of such a representation of the Hamiltonian function is beyond doubt, since we are actually writing the Schrödinger equation in new independent variables. But this is not an identical transformation. It allows us to determine the relationship between the energy of motion and the internal energy of the system. Then, representing the Hamiltonian of a system of
N particles as such a sum, from equation (3) we obtain the extended Schrödinger equation for the quantum SB [
49]:
Here the variables are designated in the same way as in
the equation of motion of the SB. R– coordinates of the
center of inertia of the system, – coordinates of i the
particle relative to the center of inertia of the system.
Equation (4), like equation (1), describes the evolution of the system. Obviously, the solutions of equations (3) and (4) differ in that equation (4) takes into account the change in internal energy during particle interactions, while equation (3) does not.
In the limit of infinite divisibility, a particle can be considered as a material field [
50]. That is, one can imagine that a particle is a "fluctuating cloud" of matter, possessing the energy of motion and internal energy. When such a particle moves in a non-uniform field of external forces, the energy of motion will be converted into internal energy, which is equivalent to dissipation.
The simplest model of a "fluctuating cloud" is an oscillator. Let us consider equation (4) for the case
N = 2, that is, for an oscillator. For a quantum oscillator from equation (4) in the stationary case we obtain:
Here are the kinetic components of the energy of motion of the oscillator and its internal energy; .
In equation (5), as in equation (1), in the general case, micro and macro variables are coupled due to the nonhomogeneous of the external potential. This means that the energy of motion and the internal energy of a quantum oscillator, as for a classical oscillator, can transform into each other in a nonhomogeneous field of external forces.
If the change in the external field on the scale of the system can be neglected, that is
, then the wave function can be written as follows:
, and equation (5) splits into two equations:
The solution of equation (5a) is determined by the external field. If =0, then we obtain the well-known equation of an oscillator freely moving in space.
The solution of equation (5c) under the condition that
, is the known equation for the oscillation of a particle near the equilibrium point. [
52]. This once again confirms the validity of equation (4).
It may turn out that , . If , where , then the oscillation of the classical oscillator corresponds to a de Broglie wave, for which the dispersion law holds: . This means that when a rarefied flow of such oscillators passes through a screen hole, a diffraction pattern typical of quantum particles will arise.
The presence of internal energy in the oscillator provides it with wave properties of dynamics. The presence of energy motion provides it with movement in space. Therefore, its state is determined by the frequency and phase of oscillation, the position of the center of inertia, the orientation of the axis. This is equivalent to the fact that the oscillator has quantum-wave dualism and its dynamics are described by a wave function.
From the standpoint of classical mechanics, a structureless particle cannot go beyond the region defined by its energy of motion. But for SB this is not so. Classical oscillator can pass through a potential barrier due to internal energy if the barrier is higher than the energy of motion but lower than the total energy. This is due to the relationship between the internal energy and the energy of motion of the oscillator [
51]. It is obvious that for a quantum oscillator, in addition to the quantum effect that allows passing through a potential barrier, which follows from equation (3), there will be an additional effect of passing through a potential barrier due to internal energy.
Thus, taking into account the infinite divisibility of matter in quantum mechanics preserves all of its basic principles, but at the same time it strengthens the position of determinism, giving quantum-wave dualism a relatively simple physical meaning.
It is obvious that further development of ideas related to the infinite divisibility of matter will require solving many problems. Among them, the most important question is how matter is connected with the field in the limit of infinite divisibility of natural objects. That is, how matter arises from the field. No less important questions will arise about the nature of the hierarchy of open nonequilibrium dynamic systems, about their stationarity, about the nature of forces. Of course, consideration of these and other questions will require great efforts. But without their solution, it is hardly possible to construct a self-consistent evolutionary picture of the world.