Submitted:
28 February 2025
Posted:
04 March 2025
You are already at the latest version
Abstract
The mechanical properties of additive manufactured (AM) short-fibre reinforced polymer (SFRP) composites are significantly influenced by infill patterns, fibre orientation, and fibre-matrix interactions. While previous studies have explored the role of process parameters in optimising AM components, the impact of infill geometry on anisotropy and mechanical performance remains underexplored, particularly in the context of machine learning (ML). This study develops an ML-driven framework to predict the tensile and flexural properties of AM SFRP composites with different infill patterns, including triangular, hexagonal, and rectangular. AM structures were fabricated and subjected to tensile and flexural tests, with the data used to train ML models, including LightGBM, XGBoost, and artificial neural networks (ANN). The results revealed that the triangular infill pattern exhibited the highest tensile strength and stiffness, while hexagonal infill showed lower flexural properties, and rectangular infill provided intermediate performance. The ML models demonstrated high prediction accuracy, with R-squared values exceeding 0.95. XGBoost performed best for predicting tensile properties of hexagonal infill, while ANN excelled with triangular and rectangular configurations. This study highlights the potential of ML to optimise the mechanical performance of AM SFRP composites by accounting for the interplay between infill geometry and fibre-matrix interactions, providing a pathway for the design of high-performance materials in applications such as biomedical devices.
Keywords:
1. Introduction
2. Materials and Experimental Methodology
2.1. Materials and Manufacturing Methods
2.2. ML Metrics and Assessment
2.2.1. Data Preprocessing
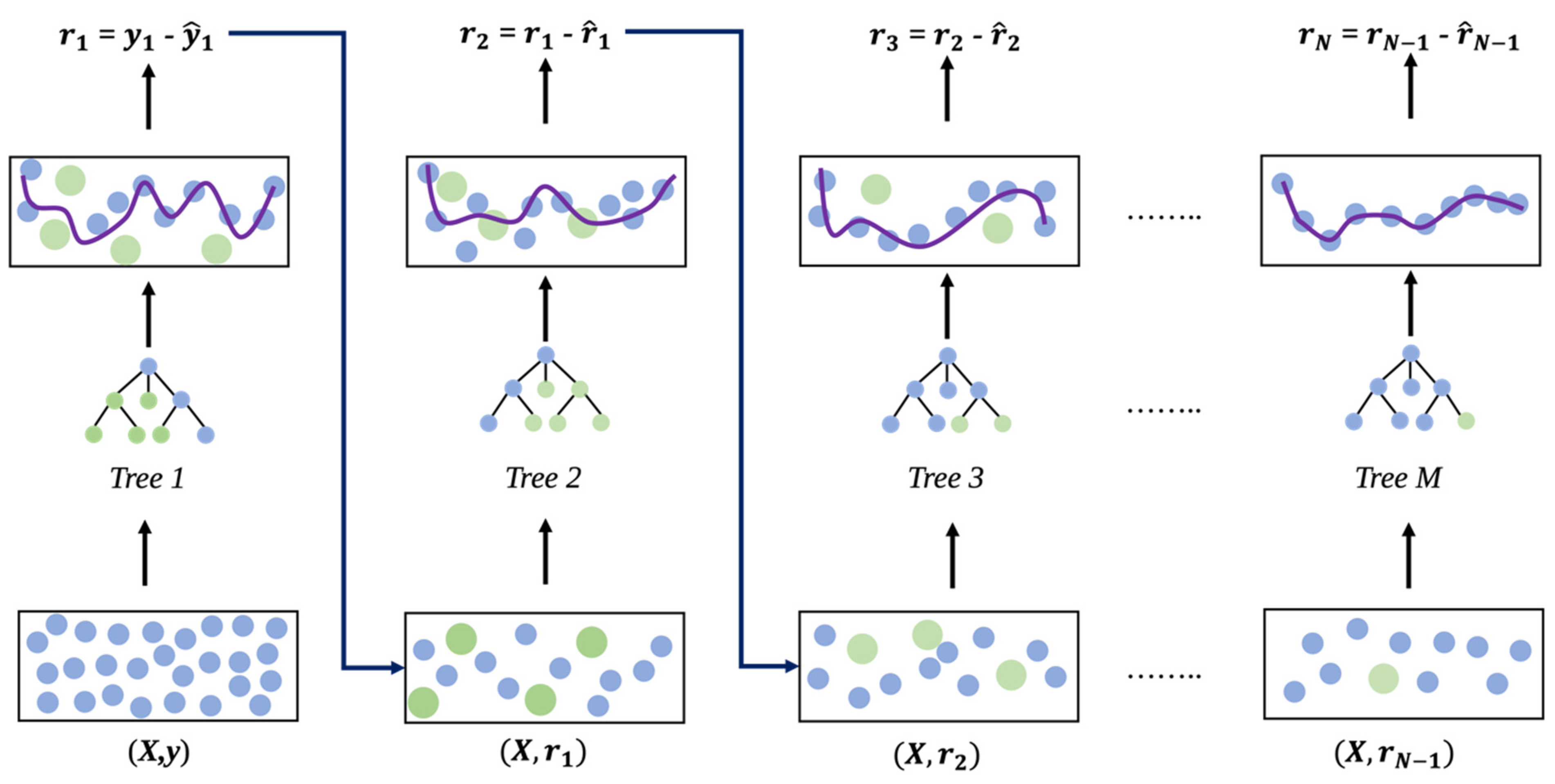
2.2.2. Selection of Regression Algorithms
3. Results and Discussion
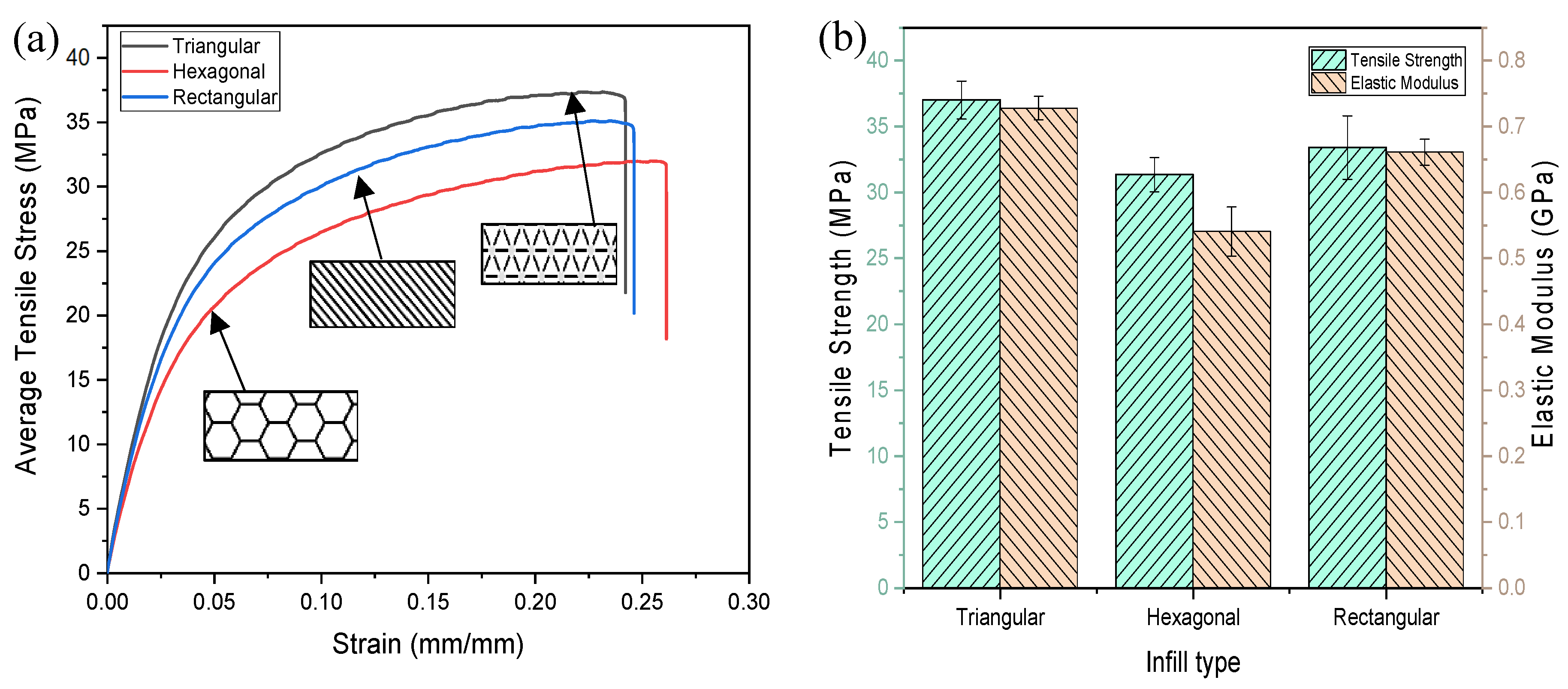
3.1. Tensile Results
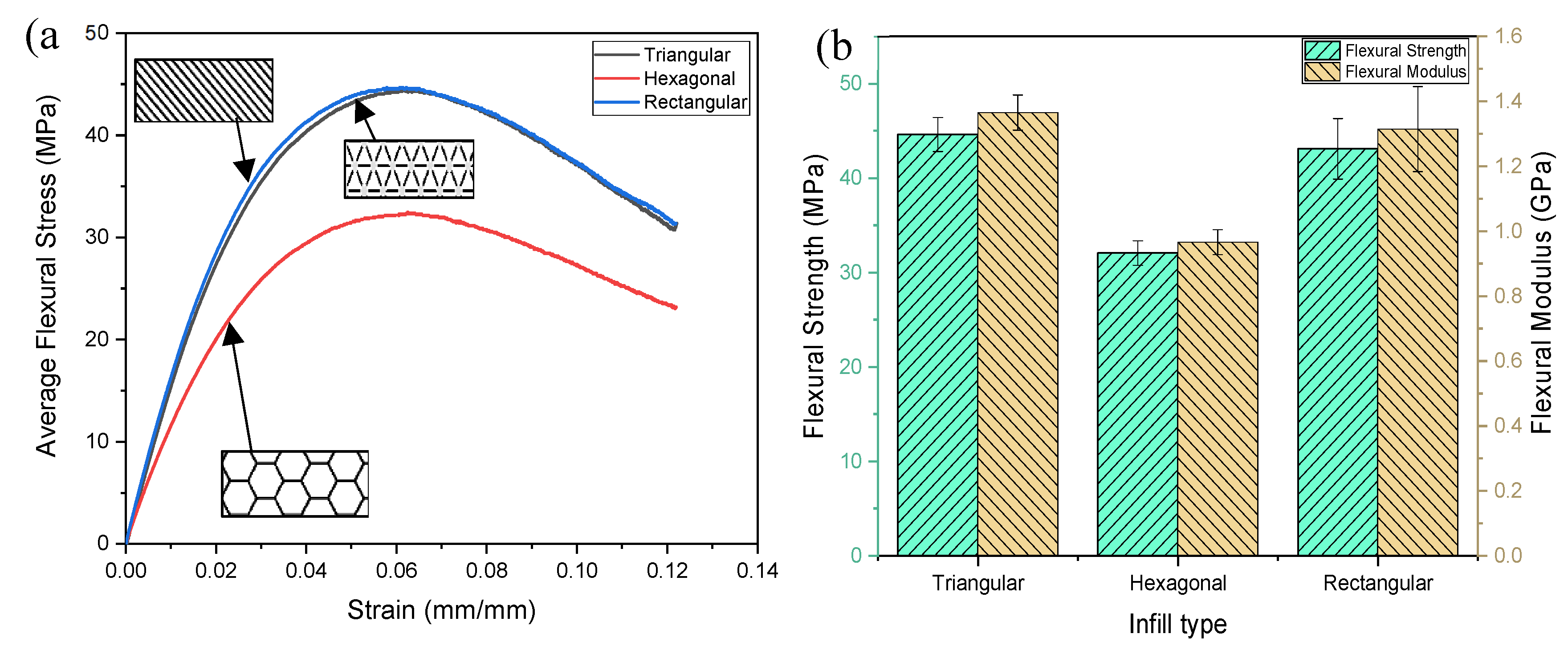
3.2. Flexural Results
3.3. ML set-up, results and discussion
3.3.1. ML Data Set Up
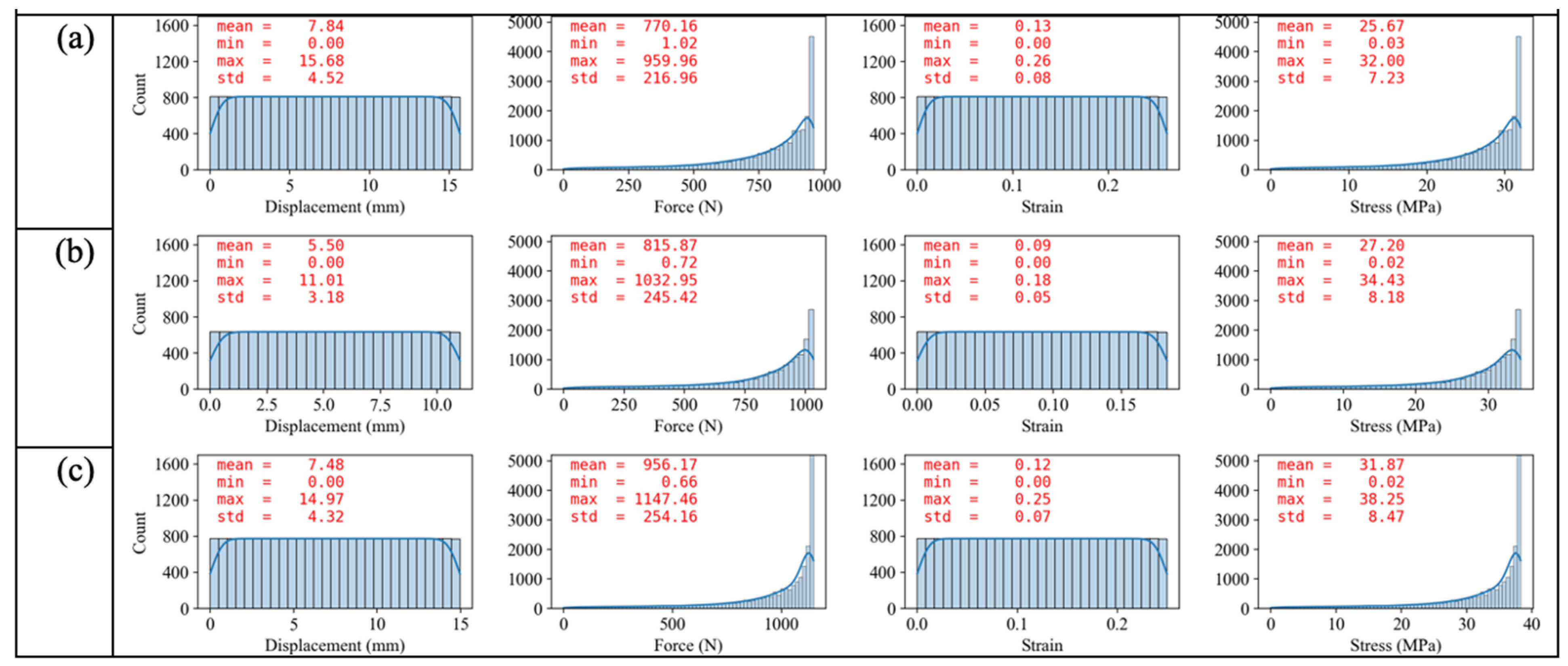
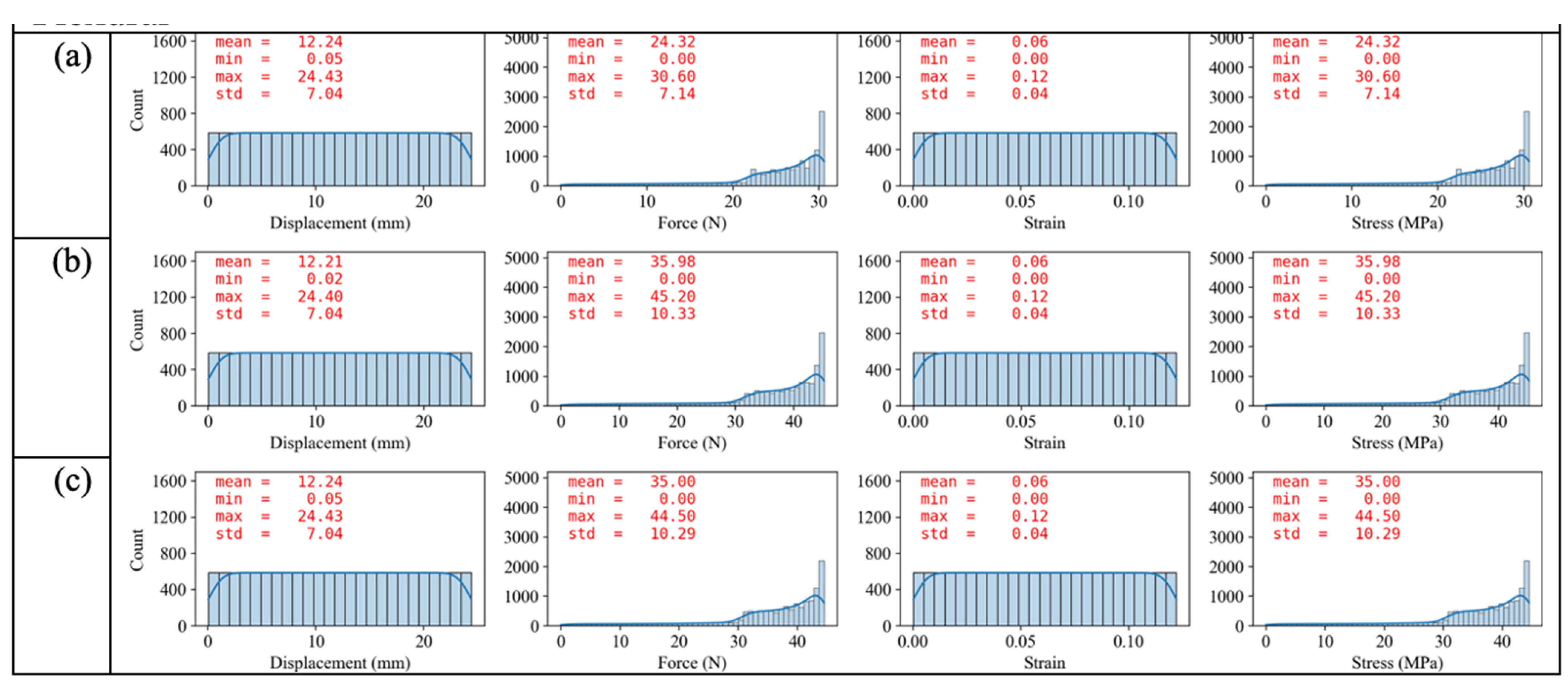
3.3.2. Data Assessment of Mechanical Properties
3.3.3. Evaluation of Regressor Algorithms
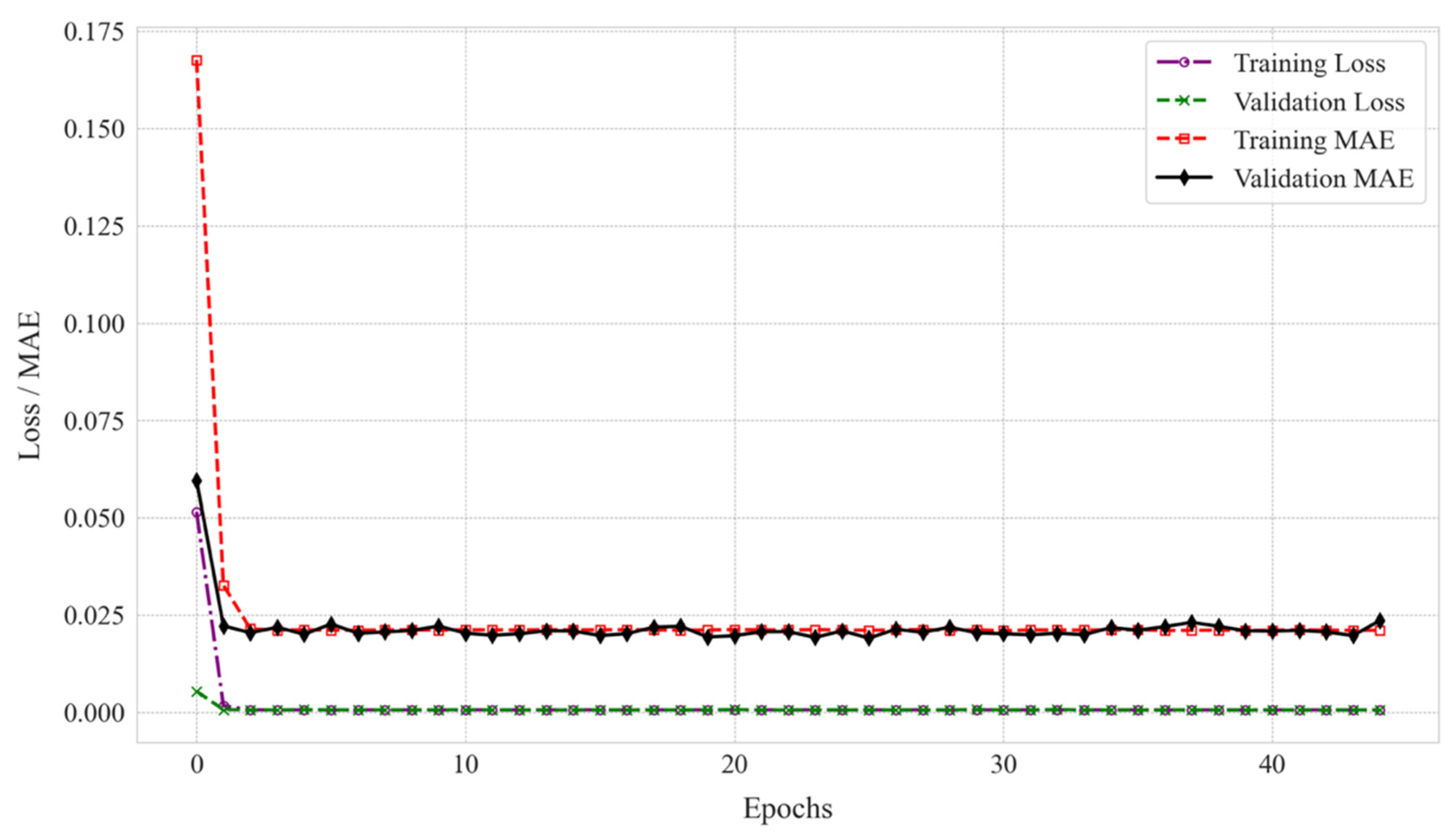
3.3.4. Hyper-Parameter Tuning Analysis
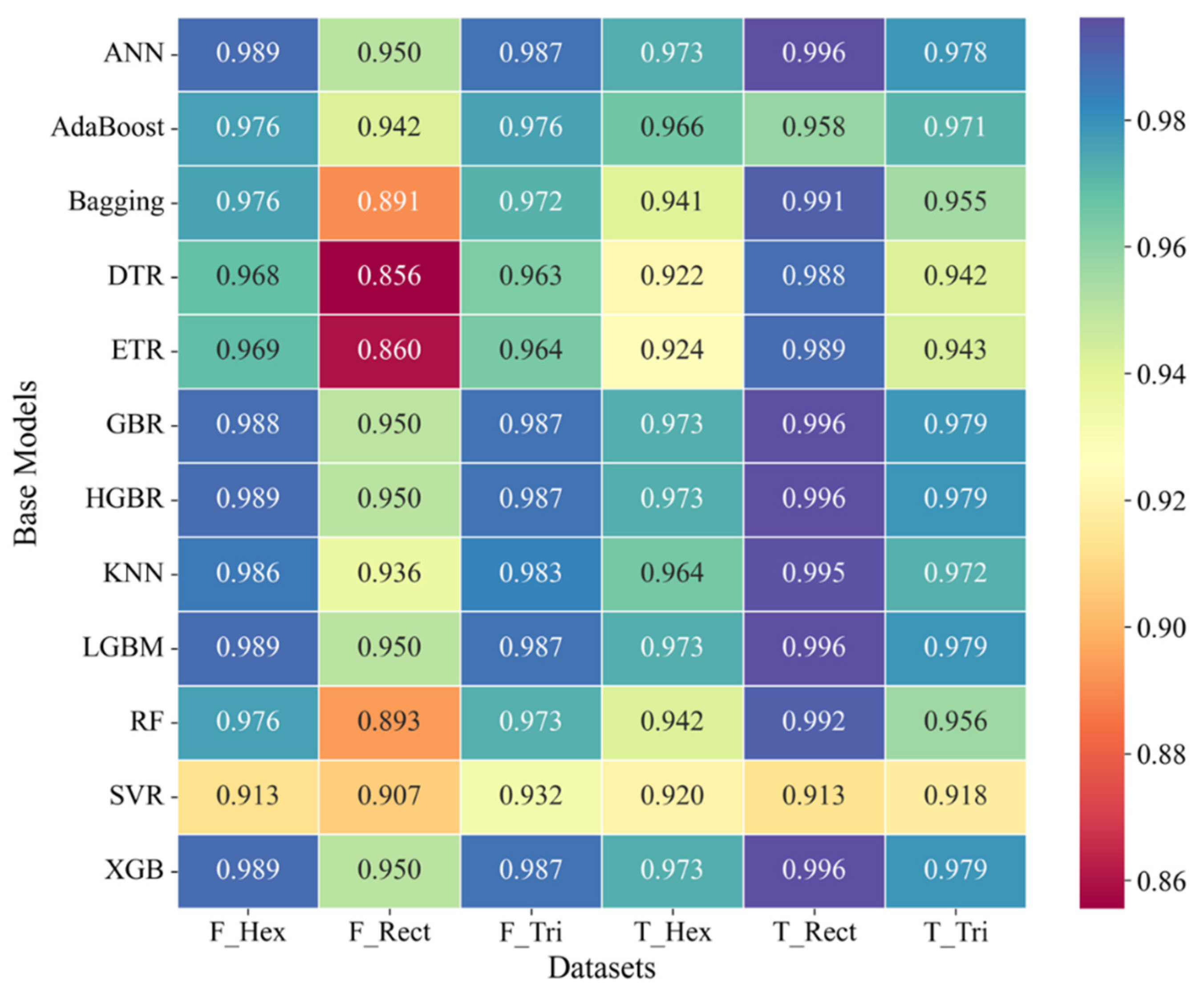
3.3.5. ML Model Performance
4. Conclusions
- The Triangular patterned samples exhibited superior tensile strength (37.01 ± 1.44 MPa) and stiffness (0.728 ± 0.018 GPa), surpassing Rectangular (33.40 ± 2.40 MPa; 0.661 ± 0.020 GPa) and Hexagonal (31.35 ± 1.30 MPa; 0.541 ± 0.037 GPa) configurations. Conversely, the hexagonal pattern displayed the weakest tensile strength and lowest stiffness, coupled with the highest variability in both properties (tensile SD = 1.30 MPa; stiffness SD = 0.037 GPa). Its superiority stems from its interconnected geometry, which facilitates uniform stress distribution and improves resistance to deformation, ensuring structural stability under load. Conversely, its weaknesses likely originate from its nodal junctions, which are susceptible to failure under stress, and its lightweight honeycomb structure, which reduces load-bearing efficiency.
- Regarding flexural properties, the triangular infill exhibited the highest bending strength (44.63 MPa) and flexural modulus (1.37 GPa), attributed to its efficient load distribution and structural integrity. In contrast, the hexagonal infill demonstrated the lowest bending strength (32.07 MPa) and flexural modulus (0.97 GPa), suggesting potential limitations in structural applications. The rectangular infill displayed intermediate values (43.1 MPa for strength and 1.31 GPa for modulus) but exhibited greater variability in performance.
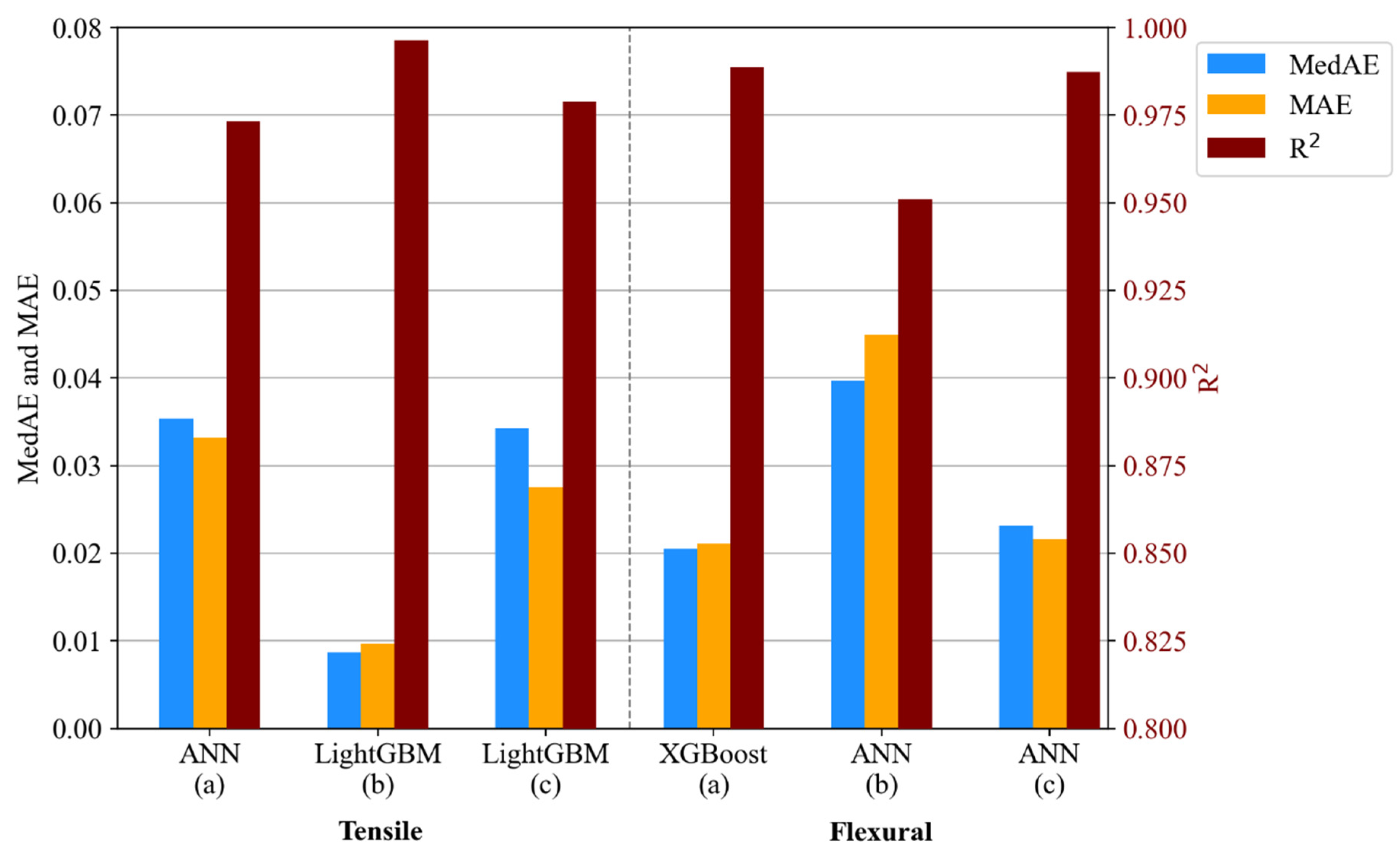
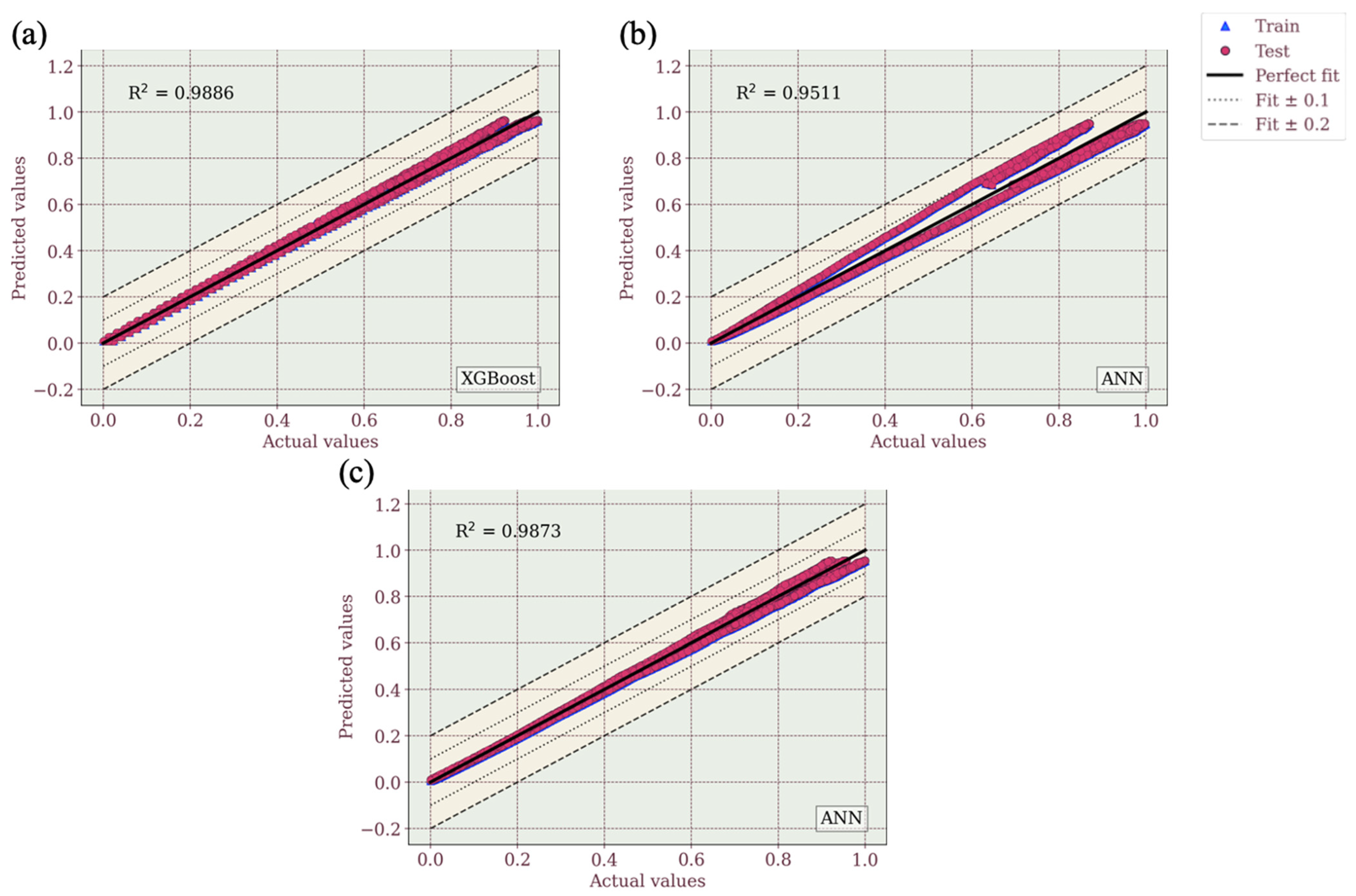
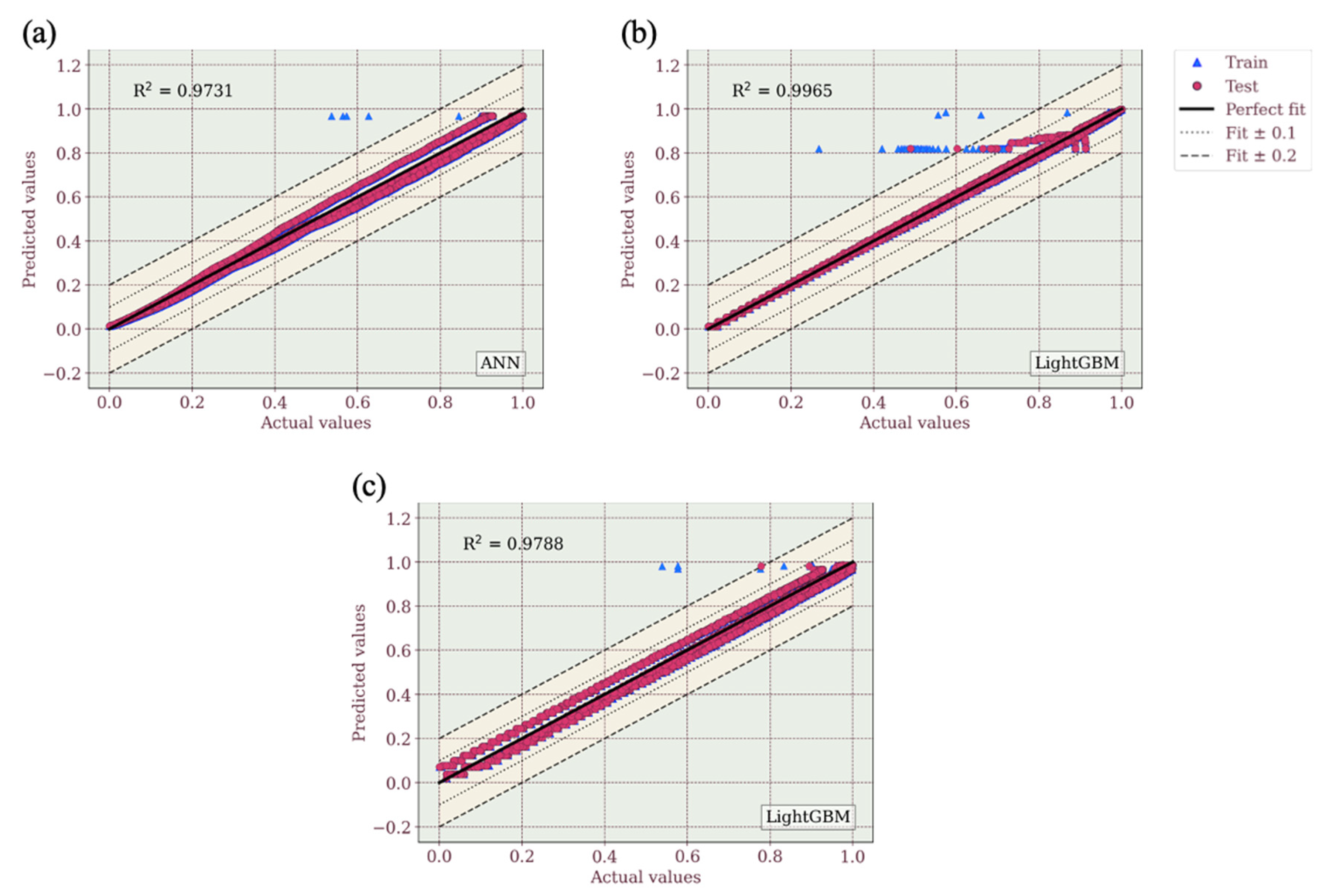
- The developed ML framework accurately predicts the tensile and flexural behaviour of Onyx composites across various infill parameters, with models like LightGBM, XGBoost, and ANN achieving R-squared values above 0.95. For tensile properties, XGBoost performed best for hexagonal stacking, while ANN excelled in rectangular and triangular configurations. In flexural properties, ANN outperformed in hexagonal sequences, whereas LightGBM achieved the highest accuracy for rectangular and triangular sequences, though its predictions for the rectangular sequence showed higher variability. This study highlights the potential of ML-driven modelling for material optimisation, particularly in biomedical applications. While ensemble learning and deep learning approaches show promise, further refinement and dataset expansion are needed to enhance model generalisability for real-world applications.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ning, F.; Cong, W.; Qiu, J.; Wei, J.; Wang, S. Additive Manufacturing of Carbon Fiber Reinforced Thermoplastic Composites Using Fused Deposition Modeling. Compos B Eng 2015, 80, 369–378. [Google Scholar] [CrossRef]
- Petersen, R. Carbon Fiber Biocompatibility for Implants. Fibers 2016, 4. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.; Hoglund, R.; Smith, D.E. Continuous Fiber Angle Topology Optimization for Polymer Composite Deposition Additive Manufacturing Applications. Fibers 2019, 7. [Google Scholar] [CrossRef]
- Tekinalp, H.L.; Kunc, V.; Velez-Garcia, G.M.; Duty, C.E.; Love, L.J.; Naskar, A.K.; Blue, C.A.; Ozcan, S. Highly Oriented Carbon Fiber-Polymer Composites via Additive Manufacturing. Compos Sci Technol 2014, 105, 144–150. [Google Scholar] [CrossRef]
- Arif, M.F.; Kumar, S.; Varadarajan, K.M.; Cantwell, W.J. Performance of Biocompatible PEEK Processed by Fused Deposition Additive Manufacturing. Mater Des 2018, 146, 249–259. [Google Scholar] [CrossRef]
- Durga Prasada Rao, V.; Rajiv, P.; Navya Geethika, V. Effect of Fused Deposition Modelling (FDM) Process Parameters on Tensile Strength of Carbon Fibre PLA. In Proceedings of the Materials Today: Proceedings; Elsevier Ltd, 2019; Vol. 18, pp. 2012–2018.
- Papon, E.A.; Haque, A. Fracture Toughness of Additively Manufactured Carbon Fiber Reinforced Composites. Addit Manuf 2019, 26, 41–52. [Google Scholar] [CrossRef]
- Ning, F.; Cong, W.; Hu, Y.; Wang, H. Additive Manufacturing of Carbon Fiber-Reinforced Plastic Composites Using Fused Deposition Modeling: Effects of Process Parameters on Tensile Properties. J Compos Mater 2017, 51, 451–462. [Google Scholar] [CrossRef]
- Wang, K.; Xie, X.; Wang, J.; Zhao, A.; Peng, Y.; Rao, Y. Effects of Infill Characteristics and Strain Rate on the Deformation and Failure Properties of Additively Manufactured Polyamide-Based Composite Structures. Results Phys 2020, 18. [Google Scholar] [CrossRef]
- Belarbi, Y.E.; Benmahiddine, F.; Hamami, A.E.A.; Guessasma, S.; Belhabib, S. Hygrothermal and Microstructural Investigation of PLA and PLA-Flax Printed Structures. Fibers 2022, 10. [Google Scholar] [CrossRef]
- Al Rashid, A.; Ikram, H.; Koç, M. Additive Manufacturing and Mechanical Performance of Carbon Fiber Reinforced Polyamide-6 Composites. In Proceedings of the Materials Today: Proceedings; Elsevier Ltd, January 1 2022; Vol. 62, pp. 6359–6363.
- Martulli, L.M.; Barriga Ruiz, P.; Rajan, A.; Bárnik, F.; Sága, M.; Bernasconi, A. Infill Shape Effects on Bending Stiffness of Additively Manufactured Short Fibre Reinforced Polymer Sandwich Specimens. Journal of Reinforced Plastics and Composites 2021, 40, 927–938. [Google Scholar] [CrossRef]
- Yasa, E.; Ersoy, K. Dimensional Accuracy and Mechanical Properties of Chopped Carbon Reinforced Polymers Produced by Material Extrusion Additive Manufacturing. Materials 2019, 12. [Google Scholar] [CrossRef] [PubMed]
- Breuer, K.; Stommel, M. Prediction of Short Fiber Composite Properties by an Artificial Neural Network Trained on an Rve Database. Fibers 2021, 9, 1–14. [Google Scholar] [CrossRef]
- Omigbodun, F.T.; Osa-Uwagboe, N.; Udu, A.G.; Oladapo, B.I. Leveraging Machine Learning for Optimized Mechanical Properties and 3D Printing of PLA/CHAP for Bone Implant. Biomimetics 2024. [Google Scholar] [CrossRef]
- Osa-uwagboe, N.; Udu, A.G.; Ghalati, M.K.; Silberschmidt, V. V.; Aremu, A.; Dong, H.; Demirci, E. A Machine Learning-Enabled Prediction of Damage Properties for Fiber-Reinforced Polymer Composites under out-of-Plane Loading. Eng Struct 2024, 308, 117970. [Google Scholar] [CrossRef]
- Gayatri, V.M.; Dave, A.; Chaganti, K. Artificial Neural Network Based Prediction of Tensile Strength of Hybrid Composites; 2018; Vol. 5.
- Huang, H.; Hadigheh, S.A.; Aghabalaei Baghaei, K. Influences of Fibre Shape on the Transverse Modulus of Unidirectional Fibre Reinforced Composites Using Finite Element and Machine Learning Methods. Compos Struct 2023, 312. [Google Scholar] [CrossRef]
- Cai, R.; Wen, W.; Wang, K.; Peng, Y.; Ahzi, S.; Chinesta, F. Tailoring Interfacial Properties of 3D-Printed Continuous Natural Fiber Reinforced Polypropylene Composites through Parameter Optimization Using Machine Learning Methods. Mater Today Commun 2022, 32. [Google Scholar] [CrossRef]
- Alhaddad, W.; He, M.; Halabi, Y.; Yahya Mohammed Almajhali, K. Optimizing the Material and Printing Parameters of the Additively Manufactured Fiber-Reinforced Polymer Composites Using an Artificial Neural Network Model and Artificial Bee Colony Algorithm. Structures 2022, 46, 1781–1795. [Google Scholar] [CrossRef]
- Meiabadi, M.S.; Moradi, M.; Karamimoghadam, M.; Ardabili, S.; Bodaghi, M.; Shokri, M.; Mosavi, A.H. Modeling the Producibility of 3d Printing in Polylactic Acid Using Artificial Neural Networks and Fused Filament Fabrication. Polymers (Basel) 2021, 13. [Google Scholar] [CrossRef]
- Agarwal, R.; Singh, J.; Gupta, V. Predicting the Compressive Strength of Additively Manufactured PLA-Based Orthopedic Bone Screws: A Machine Learning Framework. Polym Compos 2022, 43, 5663–5674. [Google Scholar] [CrossRef]
- Nikiema, D.; Balland, P.; Sergent, A. Study of the Mechanical Properties of 3D-Printed Onyx Parts: Investigation on Printing Parameters and Effect of Humidity. Chinese Journal of Mechanical Engineering: Additive Manufacturing Frontiers 2023, 2, 100075. [Google Scholar] [CrossRef]
- Petcharat, N.; Wiangkham, A.; Pichitkul, A.; Tantrairatn, S.; Aengchuan, P.; Bureerat, S.; Banpap, S.; Khunthongplatprasert, P.; Ariyarit, A. The Multi-Objective Optimization of Material Properties of 3D Print Onyx/Carbon Fiber Composites via Surrogate Model. Mater Today Commun 2023, 37. [Google Scholar] [CrossRef]
- Alexandropoulos, S.-A.N.; Kotsiantis, S.B.; Vrahatis, M.N. Data Preprocessing in Predictive Data Mining. Knowl Eng Rev 2019, 34, e1. [Google Scholar] [CrossRef]
- Luo, G. A Review of Automatic Selection Methods for Machine Learning Algorithms and Hyper-Parameter Values. Network Modeling Analysis in Health Informatics and Bioinformatics 2016, 5, 1–16. [Google Scholar] [CrossRef]
- Salman, M.T.; Siddle, D.R.; Udu, A.G. Machine Learning Approach to Predict the DC Bias for Adaptive OFDM Transmission in Indoor Li-Fi Applications. IEEE Access 2025, 13, 9627–9641. [Google Scholar] [CrossRef]
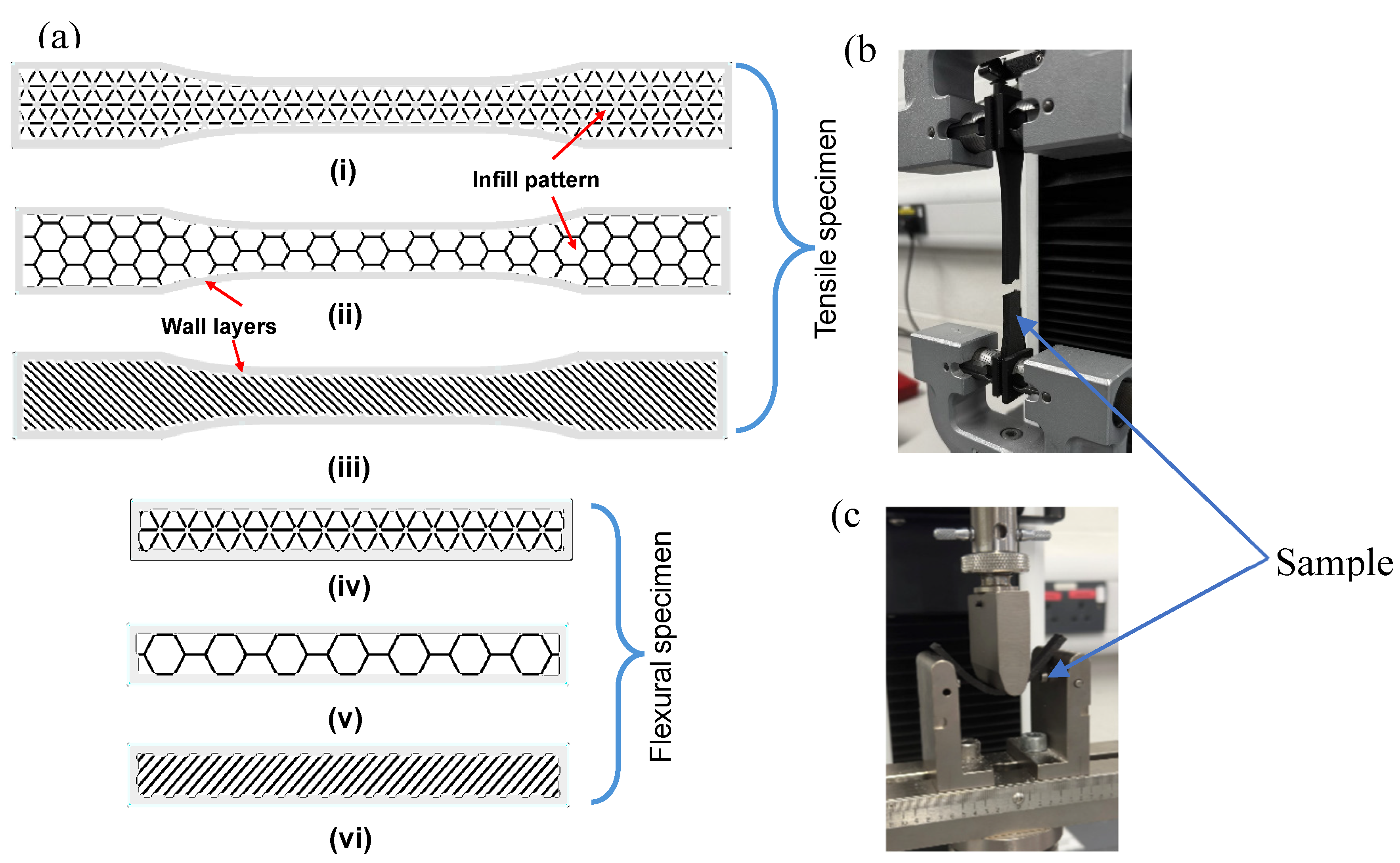
| Parameter | Value |
| Tensile Modulus | 2.4 GPa |
| Tensile stress at yield | 40 MPa |
| Tensile stress at break | 37 MPa |
| Flexural Strength | 71 MPa |
| Flexural Modulus | 3.6 GPa |
| Density | 1.4 g/cm3 |
| Parameter | Value |
| Layer height | 0.125 mm |
| No. of layers | 24 |
| Wall loops | 4 |
| Infill type | Triangular/Hexagonal/Rectangular |
| Infill | 28 % |
| Top/bottom layers | 4/4 |
| Model | Attribute | Range | Selected value | Mean test score |
| AdaBoost | learning rate | [0.01, 0.1, 0.5, 1] | 0.01 | 0.9745 |
| loss | ['linear', 'square', 'exponential'] | exponential | ||
| n_estimators | [50, 100, 200, 500] | 500 | ||
| ANN | activation | ['relu', 'tanh'] | relu | 0.9787 |
| alpha | [0.0001, 0.001, 0.01] | 0.01 | ||
| batch_size | [32, 64, 128, 200, ‘auto’] | 32 | ||
| hidden_layer_sizes | [(50,), (100,), (50, 50), (100,50)] | (100,50) | ||
| learning rate | ['constant', 'adaptive', 'invscaling'] | constant | ||
| max_iter | [200, 300, 400] | 200 | ||
| solver | ['lbfgs', 'sgd', 'adam'] | lbfgs | ||
| GBR | learning rate | [0.1, 0.01, 0.001] | 0.1 | 0.9787 |
| n_estimators | [100, 200, 300] | 100 | ||
| max_depth | [3, 5, 7] | 3 | ||
| min_samples_split | [2, 5, 10] | 10 | ||
| min_samples_leaf | [1, 2, 4] | 2 | ||
| max_features | ['auto', 'sqrt', 'log2'] | auto | ||
| Hist GBR | learning rate | [0.01, 0.05, 0.1] | 0.05 | 0.9787 |
| max_depth | [None, 5, 10, 20] | 5 | ||
| max_iter | [100, 200, 300] | 300 | ||
| min_leaf_nodes | [15, 31, 63] | 15 | ||
| min_samples_leaf | [10, 20, 50] | 20 | ||
| k-NN | algorithm | ['brute', 'kd_tree', 'ball_tree', 'auto'] | auto | 0.9744 |
| leaf_size | [5, 10, 20, 30] | 30 | ||
| n_neighbors | [3, 5, 7, 8] | 8 | ||
| weights | ['uniform', 'distance'] | uniform | ||
| LightGBM | learning rate | [1, 0.1, 0.01, 0.001] | 0.1 | 0.9787 |
| max_depth | [None, 1, 3, 5, 7, 10] | 3 | ||
| min_child_samples | [5, 10, 20, 30] | 5 | ||
| n_estimators | [100, 200, 300] | 100 | ||
| num_leaves | [31, 50, 100, 200] | 31 | ||
| XGBoost | colsample_bytree | [0.8, 0.9, 1.0] | 0.8 | 0.9787 |
| gamma | [0, 0.1, 0.2] | 0 | ||
| learning rate | [0.1, 0.01, 0.001] | 0.1 | ||
| max_depth | [3, 5, 7] | 3 | ||
| min_child_weight | [1, 3, 5] | 1 | ||
| n_estimators | [100, 200, 300] | 100 | ||
| subsample | [0.8, 0.9, 1.0] | 0.8 |
| Hex | Rect | Tri | ||||||||||||||||||
| R-squared | MedAE | MAE | R-squared | MedAE | MAE | R-squared | MedAE | MAE | ||||||||||||
| Model | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | ||
| AdaBoost | 0.9606 | 0.9610 | 0.0375 | 0.0376 | 0.0381 | 0.0381 | 0.9725 | 0.9737 | 0.0225 | 0.0227 | 0.0291 | 0.0290 | 0.9748 | 0.9749 | 0.0294 | 0.0295 | 0.0302 | 0.0303 | ||
| ANN | 0.9728 | 0.9731 | 0.0339 | 0.0340 | 0.0329 | 0.0329 | 0.9947 | 0.9963 | 0.0071 | 0.0070 | 0.0098 | 0.0095 | 0.9787 | 0.9787 | 0.0345 | 0.0346 | 0.0272 | 0.0274 | ||
| GBR | 0.9731 | 0.9727 | 0.0345 | 0.0349 | 0.0325 | 0.0329 | 0.9957 | 0.9963 | 0.0084 | 0.0085 | 0.0096 | 0.0097 | 0.9792 | 0.9785 | 0.0341 | 0.0349 | 0.0270 | 0.0276 | ||
| HistGBR | 0.9728 | 0.9730 | 0.0350 | 0.0350 | 0.0327 | 0.0329 | 0.9954 | 0.9965 | 0.0087 | 0.0086 | 0.0098 | 0.0096 | 0.9789 | 0.9788 | 0.0344 | 0.0349 | 0.0272 | 0.0275 | ||
| KNN | 0.9733 | 0.9657 | 0.0328 | 0.0370 | 0.0320 | 0.0365 | 0.9958 | 0.9955 | 0.0082 | 0.0092 | 0.0094 | 0.0105 | 0.9793 | 0.9732 | 0.0326 | 0.0369 | 0.0269 | 0.0308 | ||
| LightGBM | 0.9728 | 0.9730 | 0.0344 | 0.0344 | 0.0327 | 0.0328 | 0.9955 | 0.9965 | 0.0086 | 0.0087 | 0.0099 | 0.0097 | 0.9788 | 0.9788 | 0.0340 | 0.0343 | 0.0272 | 0.0275 | ||
| XGBoost | 0.9728 | 0.9730 | 0.0345 | 0.0344 | 0.0327 | 0.0328 | 0.9953 | 0.9964 | 0.0088 | 0.0087 | 0.0099 | 0.0097 | 0.9789 | 0.9788 | 0.0343 | 0.0345 | 0.0272 | 0.0275 | ||
| Hex | Rect | Tri | ||||||||||||||||||
| R-squared | MedAE | MAE | R-squared | MedAE | MAE | R-squared | MedAE | MAE | ||||||||||||
| Model | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | Train | Test | ||
| AdaBoost | 0.9542 | 0.9544 | 0.0356 | 0.0356 | 0.0392 | 0.0393 | 0.9248 | 0.9259 | 0.0477 | 0.0477 | 0.0523 | 0.0523 | 0.9507 | 0.9513 | 0.0362 | 0.0362 | 0.0401 | 0.0402 | ||
| ANN | 0.9884 | 0.9884 | 0.0192 | 0.0195 | 0.0209 | 0.0212 | 0.9503 | 0.9511 | 0.0396 | 0.0397 | 0.0449 | 0.0449 | 0.9868 | 0.9873 | 0.0240 | 0.0231 | 0.0219 | 0.0216 | ||
| GBR | 0.9887 | 0.9884 | 0.0194 | 0.0204 | 0.0207 | 0.0214 | 0.9508 | 0.9501 | 0.0409 | 0.0416 | 0.0451 | 0.0459 | 0.9870 | 0.9869 | 0.0233 | 0.0232 | 0.0217 | 0.0218 | ||
| HistGBR | 0.9886 | 0.9886 | 0.0200 | 0.0204 | 0.0208 | 0.0211 | 0.9505 | 0.9507 | 0.0410 | 0.0414 | 0.0453 | 0.0456 | 0.9869 | 0.9871 | 0.0238 | 0.0233 | 0.0218 | 0.0216 | ||
| KNN | 0.9889 | 0.9857 | 0.0193 | 0.0219 | 0.0204 | 0.0234 | 0.9512 | 0.9378 | 0.0412 | 0.0456 | 0.0443 | 0.0504 | 0.9871 | 0.9839 | 0.0220 | 0.0245 | 0.0215 | 0.0241 | ||
| LightGBM | 0.9886 | 0.9886 | 0.0200 | 0.0206 | 0.0208 | 0.0211 | 0.9505 | 0.9507 | 0.0412 | 0.0414 | 0.0453 | 0.0456 | 0.9868 | 0.9871 | 0.0236 | 0.0231 | 0.0218 | 0.0216 | ||
| XGBoost | 0.9887 | 0.9886 | 0.0200 | 0.0205 | 0.0208 | 0.0211 | 0.9505 | 0.9506 | 0.0411 | 0.0417 | 0.0452 | 0.0456 | 0.9869 | 0.9871 | 0.0239 | 0.0237 | 0.0218 | 0.0217 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





